Sinx область определения: Свойства функции y = sinx и её график — урок. Алгебра, 10 класс.

найдите область определения функции y=√ sin x — Учеба и наука

Лучший ответ по мнению автора

21. 05.15 Лучший ответ по мнению автора Ответ понравился автору вопроса

Ольга Читать ответы

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его . .. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.

как решить задачу 1,3,5,7,9,11,13,15 используя 3 числа чтоб ответ получился 30 одно и тоже число можно использовать несколько раз несколько раз

Решено

Из пункта А в пункт В,расположенный ниже по течению реки,отправился плот. Одновременно с ним из пункта А вышел катер.Дойдя до В,катер сразу же…

Решено

1)В остроугольном треугольникеMNP биссектриса угла M пересекает высоту NK в точке О, причем ОК =9см. Найдите расстояние от точки О до прямой МN.

сравните 10% от 40 и 40% от 10

Пользуйтесь нашим приложением

Найдите область определения и область значений данной функции. Постройте ее график..Алгебра и начала анализа. 10 класс. Колмогоров А.Н.№36

Найдите область определения и область значений данной функции.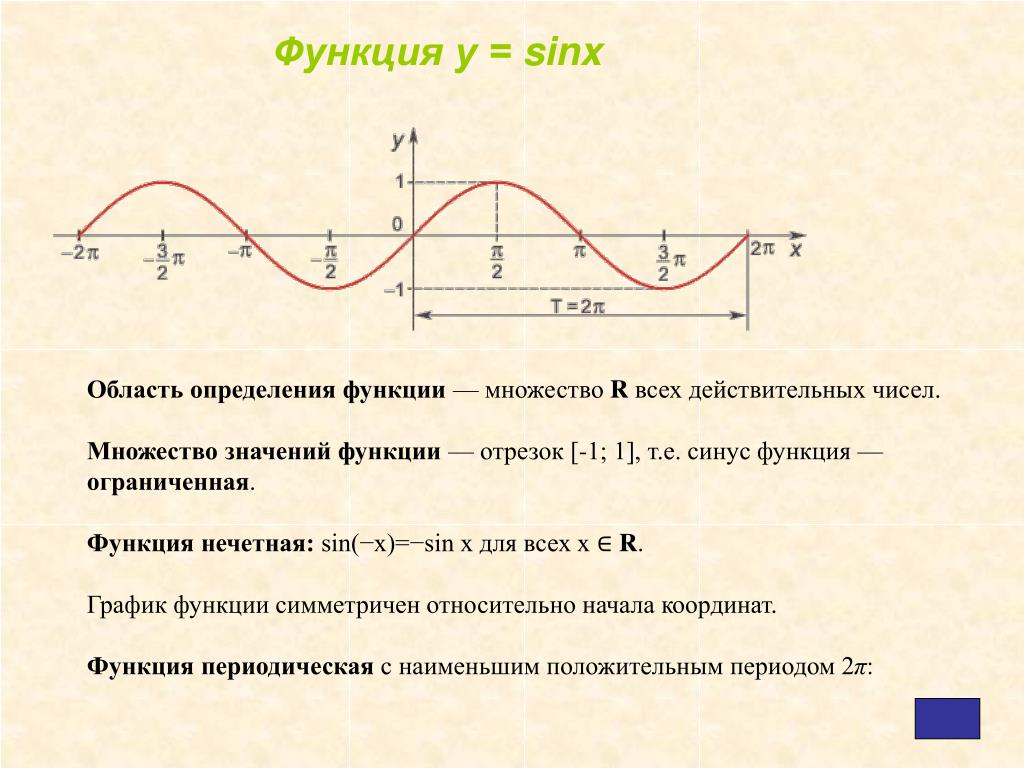 Постройте ее график..Алгебра и начала анализа. 10 класс. Колмогоров А.Н.№36 – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Прошу помощи зала)))Спасибо откликнувшимся 
а)   у = 2 + sin х;
в)   у = cos х — 1;
б) у = 1 + tg х;
г) y = 3 + sin х.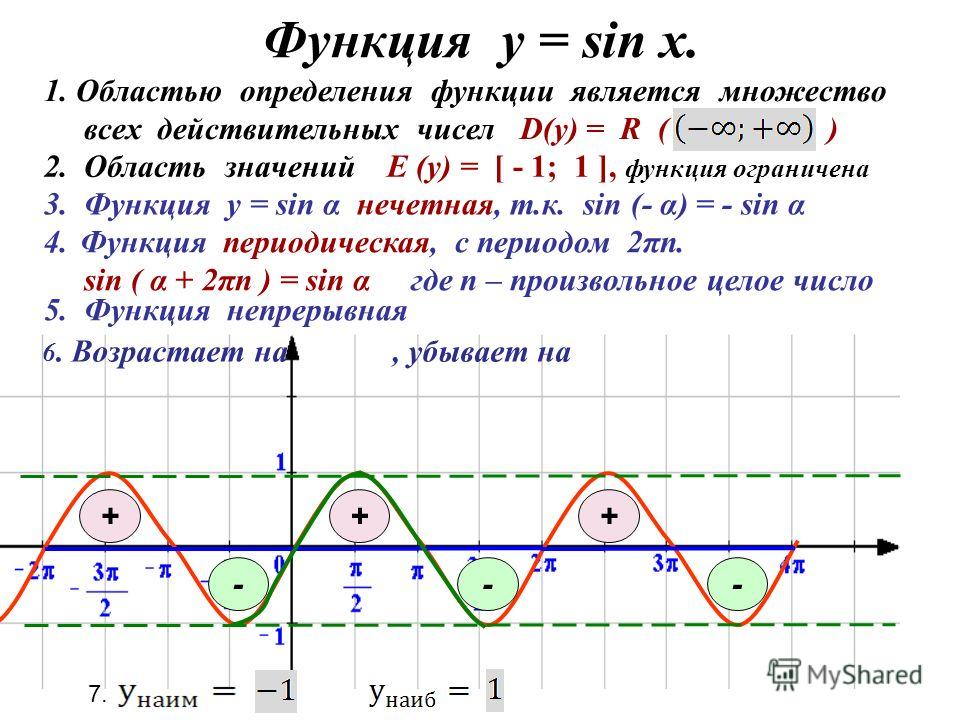
 

ответы

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

ЕГЭ

9 класс

11 класс

Химия

похожие вопросы 5

В какой момент времени ускорение движения будет наименьшим? Колмогоров Алгебра 10-11 класс Упр 309

Привет! Поможете с решением?)

Скорость изменяется по закону 
(скорость измеряется в метрах в секунду). В какой момент времени (Подробнее…)

ГДЗ11 классКолмогоров А.Н.10 классАлгебра

Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308

 Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее. ..)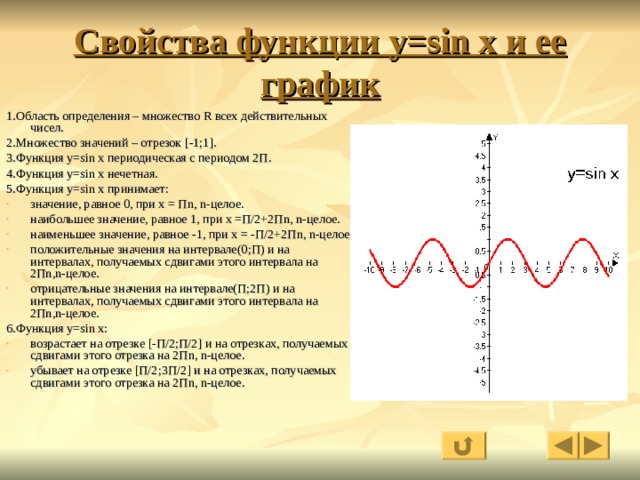

ГДЗ11 классКолмогоров А.Н.Алгебра

Почему сейчас школьники такие агрессивные ?

Читали новость про 10 классника который растрелял ? как вы к этому относитесь 

Новости10 классБезопасность

Это правда, что будут сокращать иностранные языки в школах?

 Хочется узнать, когда собираются сократить иностранные языки в школе? Какой в итоге оставят? (Подробнее…)

ШколаНовостиИностранные языки

ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…

18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)

ГДЗЕГЭРусский языкЦыбулько И.П.

Домен, диапазон и графики тригонометрических функций

Что такое домен и диапазон тригонометрических функций?

Входные и выходные значения тригонометрических функций — это область определения и диапазон тригонометрических функций соответственно. Мы знаем, что существует шесть тригонометрических функций, а именно

1. $\sin\theta$
2. $\cos\тета$
3. $\tan\theta$
4. $\cot\theta$
5. $\сек\тета$
6. $\csc\тета$

Угол и результирующее значение соответственно определяют область определения и диапазон тригонометрических функций. Область определения тригонометрических функций — это углы в градусах или радианах, а их диапазон — вещественное число.

Область определения тригонометрических функций задает значения углов, в которых определены тригонометрические функции, тогда как диапазон тригонометрических функций обозначает результирующее значение тригонометрической функции, соответствующее определенному углу в области определения.

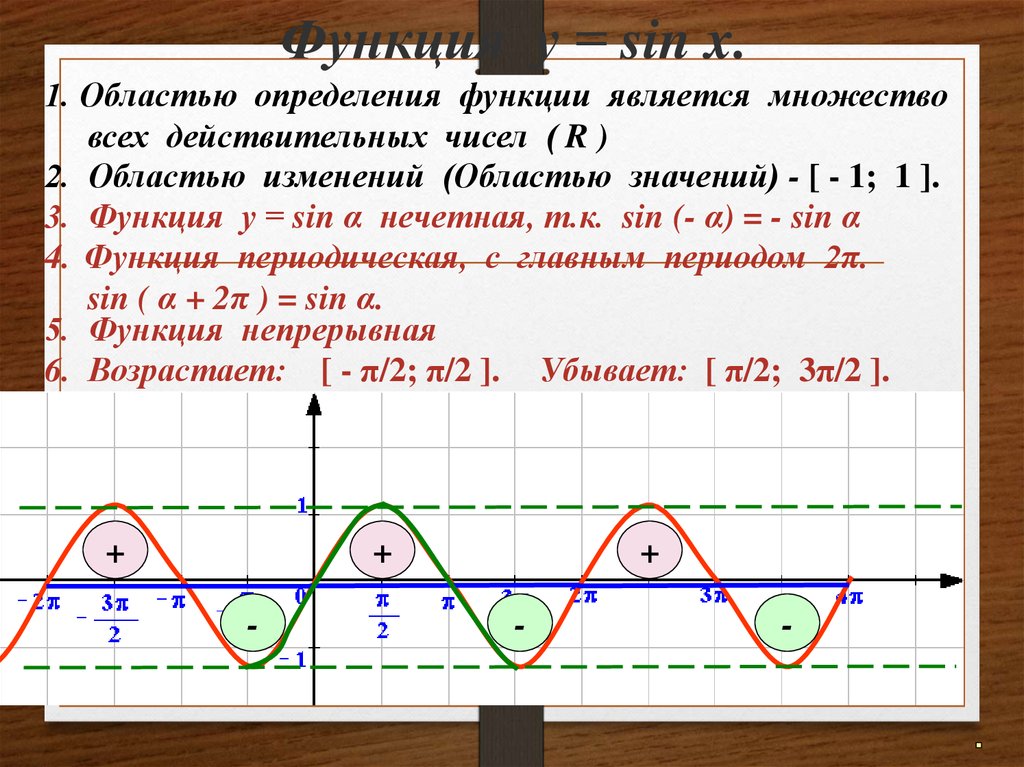
Домен и диапазон функции синуса

• $y=f(x)= Sin(x)$
• Домен функции синуса : Он определен для всех действительных значений $x$, т. е. $(-\infty , \infty)$
• Диапазон функции синуса: $-1 \leq y \leq 1$
• Период функции синуса: $2\pi$
• Это странная функция

График функции синуса

Другие графики функции синуса для $y=f(x)=2 \sin (x)$ и $y=f(x)=3 \sin (x)$

Мы видим, что диапазон увеличивается аналогичным образом

для $y=f(x)=\sin (2x)$

Мы видим, что диапазон остается, но график сжимается

Домен и диапазон функции косинуса

• $y=f(x)= cos(x)$
• Домен косинуса Функция: Определена для всех действительных значений $x$
• Диапазон функции косинуса: $-1 \leq y \leq 1$
• Период функции косинуса: $2\pi$
• Это четная функция

График функции cos(x)

Дополнительные графики содержат функцию для $y=f(x)=2 cos (x)$ и $y=f(x)=3 cos (x)$

Мы видим, что диапазон увеличивается аналогичным образом
для $y=f(x)=cos (2x)$

Мы видим, что диапазон остается, но график сжимается.

Область определения и диапазон касательной функции

• $y=f(x)=tan(x)$
• Область тангенса Функция: Определена для всех действительных значений x, кроме x ≠(2n + 1)(π/2), где n — любое целое число.
• Диапазон функции касательной: Все действительные числа
• Период функции касательной: π
• Это странная функция

График функции tan(x)

Область определения и диапазон функции котангенса

• $y=f(x)=cot(x)$
• Область определения котангенса Функция: Определяется для всех действительных значений $x$, кроме $x \neq n\pi$, где $n$ любое целое число
• Диапазон котангенса Функция: Все действительные числа
• Период функции котангенса: π
• Это странная функция

График функции кроватки(х)

Домен и диапазон секущей функции

• у=е(х)=сек(х)
• Область секущих Функция: Определена для всех действительных значений x, кроме x ≠(2n + 1)(π/2), где n — любое целое число
• Диапазон функции секанса: (-∞,-1] ∪ [1,∞)
• Период функции секущей: 2π
• Это четная функция

График функции sec(x)

Домен и диапазон функции косеканса

• $y=f(x)=cosec(x)$
• Область определения косеканса Функция: Определена для всех действительных значений x, кроме x ≠nπ, где n — любое целое число
• Диапазон функции косеканса: (-∞,-1] ∪ [1,∞)
• Период функции косеканса: 2π
• Нечетная функция

График функции cosec(x)

Область определения и диапазон тригонометрических функций Таблица

Мы можем записать диапазон для тригонометрических функций в сводной таблице ниже
• Тригонометрия
• Тригонометрические функции
• Домен, диапазон и график тригонометрических функций
• Тригонометрические тождества
• Тригонометрические уравнения
• Значения Sin 15, cos 15, tan 15, sin 75, cos 75, tan 75
• значений Sin 18, cos 18, tan 18, sin 36, cos 36, Sin 54, cos 72
• Вопросы
  • Вопросы по тригонометрическим уравнениям
  • Тригнометрические функции Вопросы
  • тригонометрические функции Класс 11 mcq

---

Пусть f(x)=sqrt(1-sinx) Какова область определения f(x), найдите f'(x), какова область определения f'(x) и напишите уравнение касательной прямой к графику f.

.. Цитата страницы Начать эссе значок-вопрос Спросите репетитора

Начать бесплатную пробную версию

Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой Делиться

Ссылайтесь на эту страницу следующим образом:

«Пусть f(x)=sqrt(1-sinx) Какова область определения f(x), найдите f'(x), какова область определения f'(x) и напишите уравнение для прямой, касательной к график f при x = 0″ Редакционная статья eNotes , 13 мая 2012 г., https://www.enotes.com/homework-help/let-f-x-sqrt-1-sinx-337781. Доступ 19декабрь 2022 г.

`f(x) = sqrt(1-sin(x))`

Домен f(x) —>

Домен sin(x) – это все действительные числа,  `x в R` . Для всех действительных чисел синус будет находиться в следующем диапазоне:

`-1lt=sin(x)lt=+1`

Следовательно, умножая на -1,

`+1=gt-sin(x) =gt-1`

Добавление +1,

`1+1=gt1-sin(x)=gt1-1`

Следовательно,

`2=gt1-sin(x)=gt0`

Мы знать, что для всех действительных чисел `1-sin(x)` будет положительным.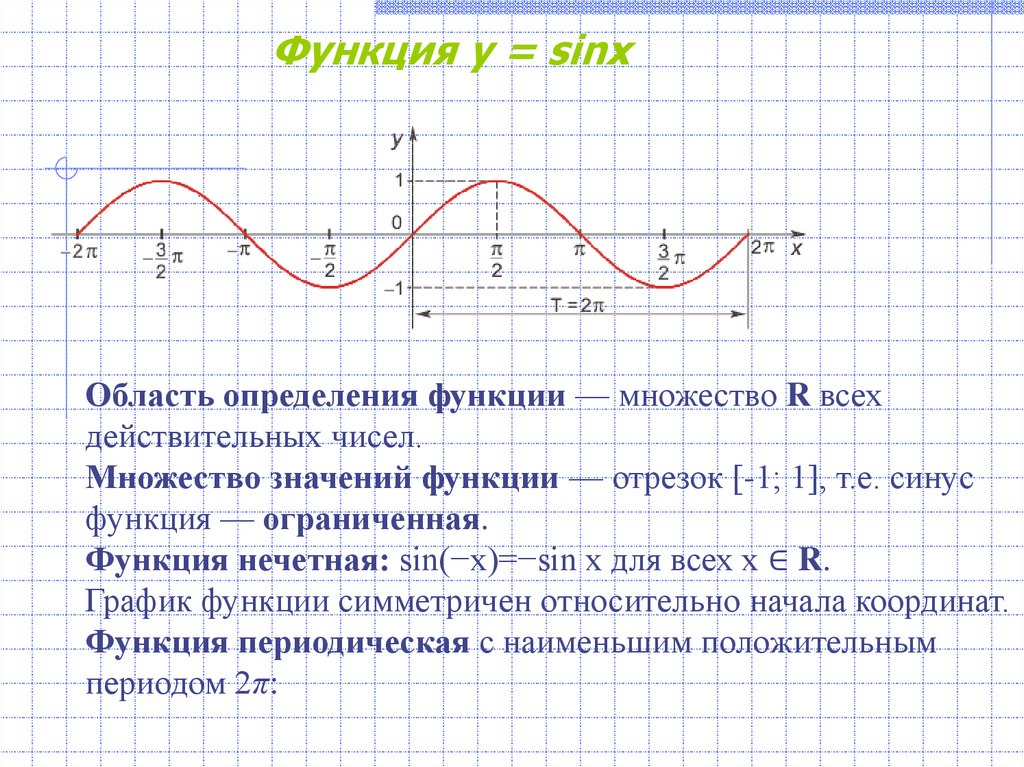 9n(pi/2)` , где n — любое целое число.

так что x` != {1/2pi, 5/2pi и 9/2pi…}`

или `x!= {1/2pi, 2pi+1/2pi и 4pi+1/2pi… }`

 

Следовательно, область определения f'(x) определяется как

Область определения `f'(x) = {x в R, x != 2npi+1/2pi, n в Z }`

 

Чтобы найти прямую, касательную f(x) в точке x = 0,

, мы должны найти f'(x) в точке x = 0.

`f'(0) = (-cos( 0))/(2sqrt(1-sin(0)))`

`f'(0) = (-1)/(2sqrt(1-0))`

`f'(0) = -1/2`

Это градиент линии,

и нам нужно f(0),

`f(0) = sqrt(1-sin(0) )`

`f(0) = sqrt(1-0)`

`f(0) = sqrt(1-sin(x))`

`f(0) = 1`

Это точка пересечения линии,

Следовательно, уравнение:

`y = mx+c`

`y = -1/2x+1`

Утверждено редакцией eNotes

Математика

Последний ответ опубликован 07 сентября 2010 г.