Свойства синуса, косинуса, тангенса и котангенса
В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.
Первое свойство — знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α. Второе свойство — периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и -α.
Знаки тригонометрических функций по четвертям
Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?
Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A0(1, 0) и, поворачивая ее вокруг точки O на угол α, попадем в точку A1(x, y). В зависимости от того, в какой четверти будет лежать точка A1(x, y), угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно.
Для наглядности приведем иллюстрацию.
Угол α=30° лежит в первой четверти. Угол -210° является углом второй четверти. Угол 585° — угол третьей четверти. Угол -45° — это угол четвертой четверти.
При этом углы ±90°, ±180°, ±270°, ±360° не принадлежат ни одной четверти, так как лежат на координатных осях.
Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.
Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A1(x, y). Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.
Косинус — это абсцисса точки A1(x, y). В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.
Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций.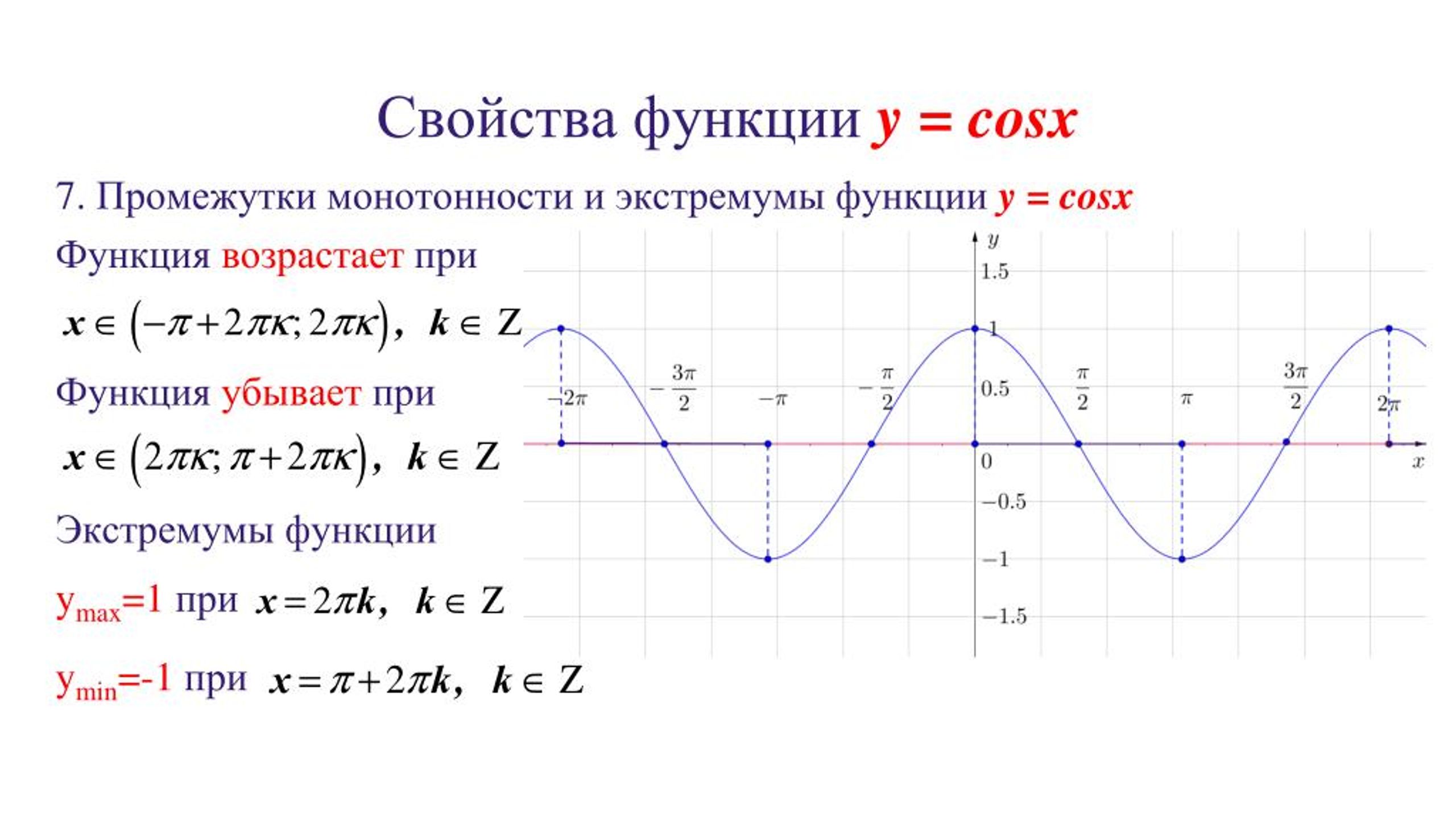 Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям.
Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям.
Важно помнить!
- Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус — в 3 и 4 четвертях.
- Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус — в 2 и 3 четвертях.
- Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
- Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
Свойство периодичности
Свойство периодичности — одно из самых очевидных свойств тригонометрических функций.
Свойство периодичностиПри изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.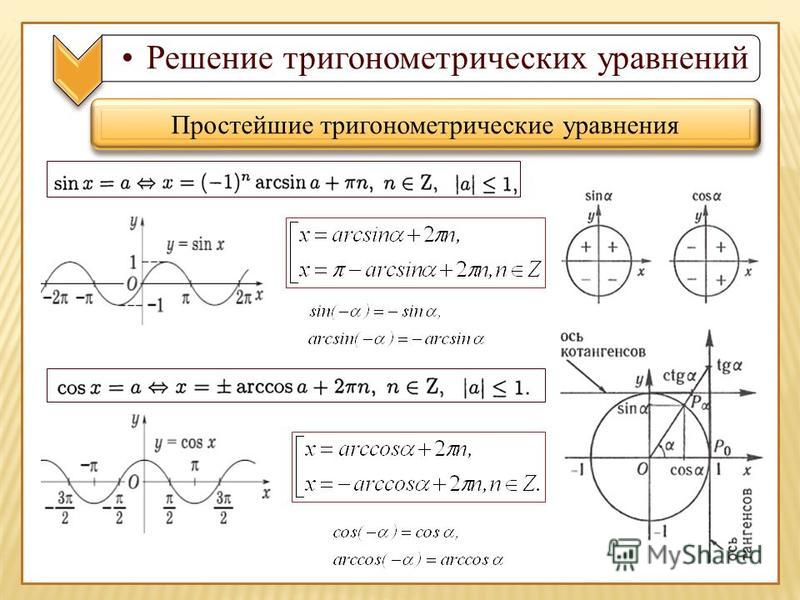
Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.
Математически данное свойство записывается так:
sinα+2π·z=sin αcosα+2π·z=cos αtgα+2π·z=tg αctgα+2π·z=ctg α
Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.
Приведем примеры.
sin13π5=sin3π5+2π=sin3π5
tg(-689°)=tg(31°+360°·(-2))=tg31°tg(-689°)=tg(-329°+360°·(-1))=tg(-329°)
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
Вновь обратимся к единичной окружности.
Точка A1(x, y) — результат поворота начальной точки A0(1, 0) вокруг центра окружности на угол α. Точка A2(x, -y) — результат поворота начальной точки на угол -α.
Точка A2(x, -y) — результат поворота начальной точки на угол -α.
Точки A1и A2 симметричны относительно оси абсцисс. В случае, когда α=0°, ±180°, ±360° точки A1и A2 совпадают. Пусть одна точка имеет координаты (x, y), а вторая — (x, -y). Вспомним определения синуса, косинуса, тангенса, котангенса и запишем:
sin α=y, cos α=x, tg α=yx, ctg α=xysin-α=-y, cos-α=x, tg-α=-yx, ctg-α=x-y
Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных угловsin-α=-sin αcos-α=cos αtg-α=-tg αctg-α=-ctg α
Согласно этому свойству, справедливы равенства
sin-48°=-sin 48°, ctgπ9=-ctg-π9, cos 18°=cos-18°
Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.
Решение задач
от 1 дня / от 150 р.
Свойства функций синуса, косинуса, тангенса и котангенса и их графики
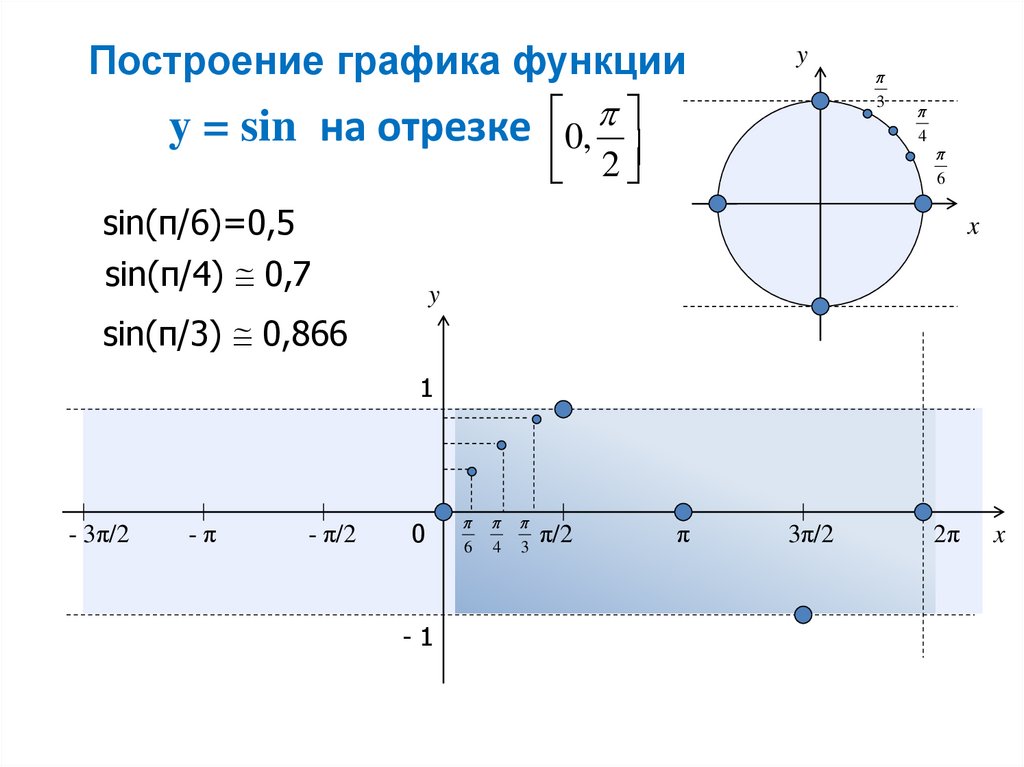
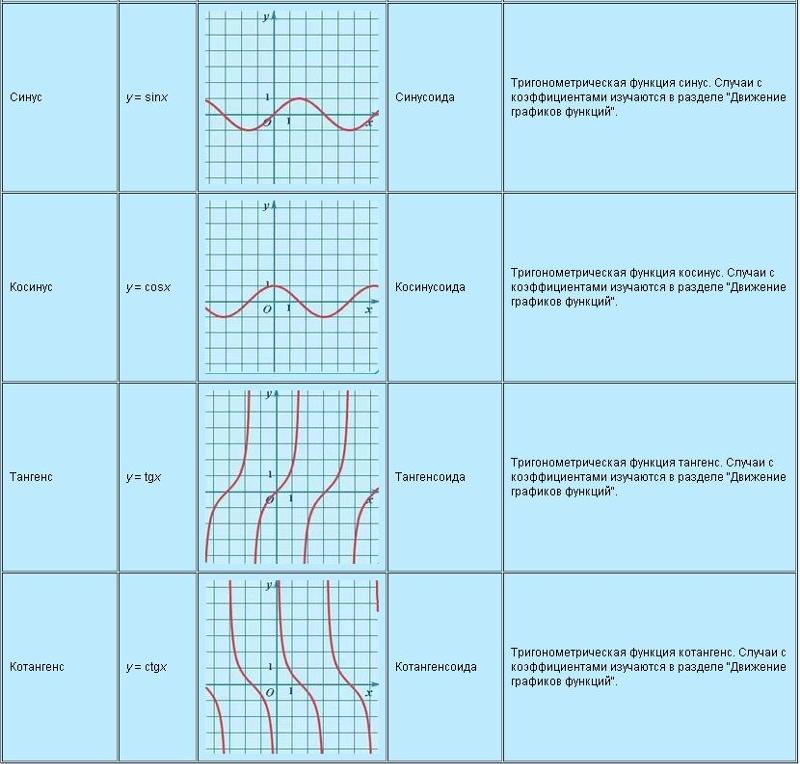
Свойства функции y=sin(x) и ее график.

График функции (синусоида)
Свойства функции
- Область определения: R (x — любое действительное число) т.е.
- Область значений:
-
Функция нечетная:
(график симметричен относительно начала координат).
- Функция периодическая с периодом
- Точки пересечения с осями координат:
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики: 1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания; 8) наибольшее и наименьшее значения функции.
Замечание. Абсциссы точек пересечения графика функции с осью Ох (то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.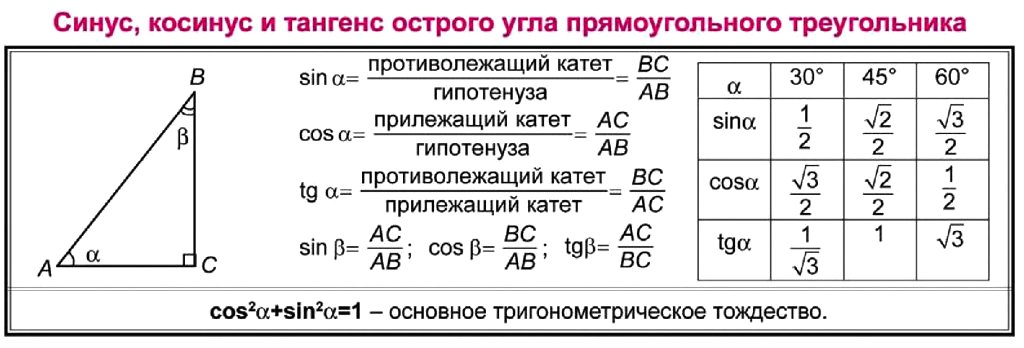
Напомним, что значение синуса — это ордината соответствующей точки единичной окружности (рис. 1).
Рис.1.
Поскольку ординату можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности всегда можно провести единственную прямую, перпендикулярную оси ординат), то область определения функции — все действительные числа. Это можно записать так:
Для точек единичной окружности ординаты находятся в промежутке [—1; 1] и принимают все значения от —1 до 1, поскольку через любую точку отрезка [—1; 1] оси ординат (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси ординат, и получить точку окружности, которая имеет рассматриваемую ординату. Таким образом, для функции область значений: . Это можно записать так:.Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при Наименьшее значение функции равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при.
Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при.
Синус — нечетная функция: , поэтому ее график симметричен относительно начала координат.
Синус — периодическая функция с наименьшим положительным периодом : , таким образом, через промежутки длиной вид графика функции повторяется. Поэтому при построении графика этой функции достаточно построить график на любом промежутке длиной , а потом полученную линию параллельно перенести вправо и влево вдоль оси Ox на расстояние , где k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение . Тогда соответствующее значение , то есть график функции проходит через начало координат.
На оси значение . Поэтому необходимо найти такие значения , при которых , то есть ордината соответствующей точки единичной окружности, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при (см. рис. 1).
рис. 1).
Промежутки знакопостоянства. Значения функции синус положительны (то есть ордината соответствующей точки единичной окружности положительна) в I и II четвертях (рис. 2). Таким образом, при всех , а также, учитывая период, при всех .
Значения функции синус отрицательны (то есть ордината соответствующей точки единичной окружности отрицательна) в III и IV четвертях, поэтому при .
Промежутки возрастания и убывания. Учитывая периодичность функции с периодом , достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке .
Если (рис. 3, а), то при увеличении аргумента ордината соответствующей точки единичной окружности увеличивается (то есть , следовательно, на этом промежутке функция возрастает. Учитывая периодичность функции , делаем вывод, что она также возрастает на каждом из промежутков
Рис.2 Рис.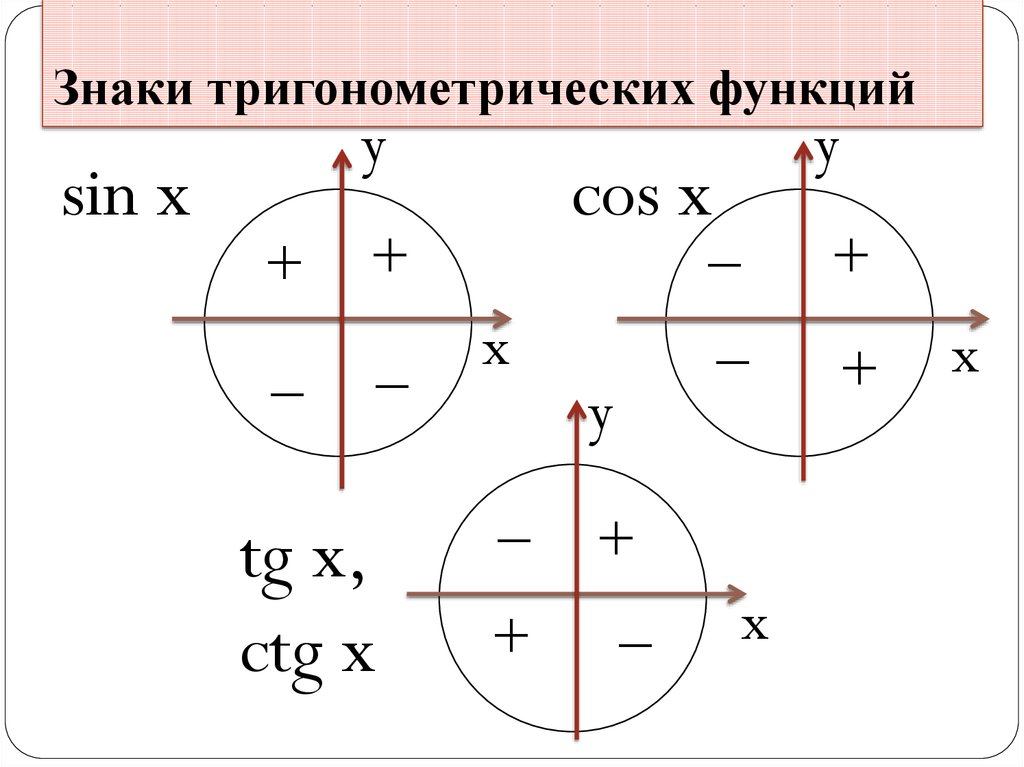 3
3
Если (рис.3,б), то при увеличении аргумента ордината соответствующей точки единичной окружности уменьшается (то есть ), таким образом, на этом промежутке функция убывает. Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков
Проведенное исследование позволяет обоснованно построить график функции . Учитывая периодичность этой функции (с периодом ), достаточно сначала построить график на любом промежутке длиной , например на промежутке . Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината соответствующей точки единичной окружности. На рисунке 4 показано построение графика функции на промежутке . Учитывая нечетность функции (ее график симметричен относительно начала координат), для построения графика на промежутке отображаем полученную кривую симметрично относительно начала координат (рис. 5).
Рис.4
Рис.5
Поскольку мы построили график на промежутке длиной , то, учитывая периодичность синуса (с периодом ), повторяем вид графика на каждом промежутке длиной (то есть переносим параллельно график вдоль оси на , где k — целое число). Получаем график, который называется синусоидой .(Рис.6)
Получаем график, который называется синусоидой .(Рис.6)
Рис.6
Замечание. Тригонометрические функции широко применяются в математике, физике и технике. Например, множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п., описываются функцией, которая задается формулой . Такие процессы называют гармоническими колебаниями.
График функции можно получить из синусоиды сжатием или растяжением ее вдоль координатных осей и параллельным переносом вдоль оси . Чаще всего гармоническое колебание является функцией времени t. Тогда оно задается формулой , где А — амплитуда
колебания, — частота, — начальная фаза, — период колебания.
СВОЙСТВА ФУНКЦИИ И ЕЕ ГРАФИК
График функции (косинусоида).
Свойства функции
- Область определения: R (x — любое действительное число).
- Область значений:
-
Функция четная:
(график симметричен относительно оси ).

- Функция периодическая с периодом :
- Точки пересечения с осями координат
- Промежутки знакопостоянства:
- Промежутки возрастания и убывания:
Объяснение и обоснование
Напомним, что значение косинуса — это абсцисса соответствующей точки единичной окружности (рис.7). Поскольку абсциссу можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности, всегда можно провести единственную прямую, перпендикулярную оси абсцисс), то область определения функции — все действительные числа. Это можно записать так:
.
Рис.7
Для точек единичной окружности абсциссы находятся в промежутке и принимают все значения от -1 до 1, поскольку через любую точку отрезка оси абсцисс (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси абсцисс, и получить
 Следовательно, область значений функции . Это можно записать так: .
Следовательно, область значений функции . Это можно записать так: .Как видим, наибольшее значение функции равно единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при .
Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть при .
Косинус — четная функция: , поэтому ее график симметричен относительно оси .
Косинус — периодическая функция с наименьшим положительным периодом : . Таким образом, через промежутки длиной вид графика функции повторяется.
Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение . Тогда соответствующее значение . На оси значение . Поэтому необходимо найти такие значения , при которых , то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при .
Промежутки знакопостоянства. Значения функции косинус положительны (то есть абсцисса соответствующей точки единичной окружности положительна) в I и IV четвертях (рис. 8). Следовательно, 0 при , а также, учитывая период, при всех .
Значения функции косинус отрицательны (то есть абсцисса соответствующей точки единичной окружности отрицательна) во II и III четвертях, поэтому при
Промежутки возрастания и убывания. Учитывая периодичность функции , достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке .
Если (рис. 9, а), то при увеличении аргумента абсцисса соответствующей точки единичной окружности уменьшается (то есть ), следовательно, на этом промежутке функция убывает. Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков .
Если (рис. 9, б), то при увеличении аргумента абсцисса соответствующей точки единичной окружности увеличивается (то есть ), таким образом, на этом промежутке функция возрастает.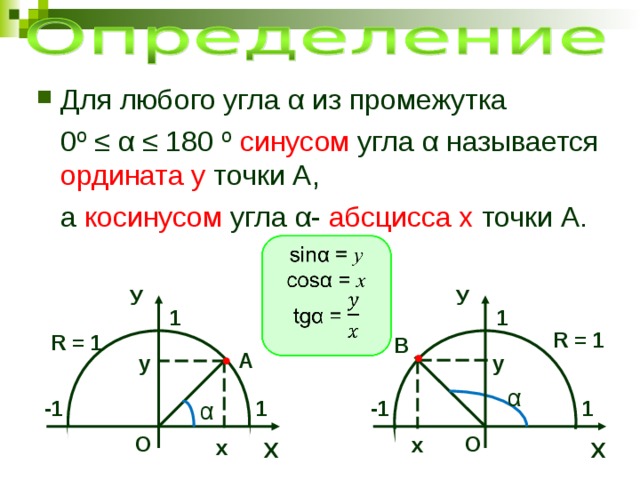 Учитывая периодичность функции , делаем вывод, что она возрастает также на каждом из промежутков .
Учитывая периодичность функции , делаем вывод, что она возрастает также на каждом из промежутков .
Рис.8 Рис.9
Проведенное исследование позволяет построить график функции аналогично тому, как был построен график функции . Но график функции можно также получить с помощью геометрических преобразований графика функции , используя формулу
Рис.10
Эту формулу можно обосновать, например, так. Рассмотрим единичную окружность (рис. 10), отметим на ней точки а также
абсциссы и ординаты этих точек. Так как , то при повороте
прямоугольника около точки на угол — против часовой стрелки он перейдет в прямоугольник . Но тогда . Следовательно, 00.
Укажем также формулы, которые нам понадобятся далее:.
Тогда,
Таким образом, .
Учитывая, что , график функции можно получить из графика функции его параллельным переносом вдоль оси на (рис. 11). Полученный график называется косинусоидой (рис. 12).
11). Полученный график называется косинусоидой (рис. 12).
Рис.11
Рис.12
График функции (тангенсоида)
Свойства функции :
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция периодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
График функции (котангенсоида)
Свойства функции :
1. Область определения:
2. Область значений:
3. Функция нечетная:
4. Функция переодическая с периодом
5. Точки пересечения с осями координат:
6. Промежутки знакопостоянства:
7. Промежутки возрастания и убывания:
8. Наибольшего и наименьшего значений функция не имеет.
Где синус положительный а где отрицательный. Свойства синуса, косинуса, тангенса и котангенса угла
Позволяют установить ряд характерных результатов – свойств синуса, косинуса, тангенса и котангенса . В этой статье мы рассмотрим три основных свойства. Первое из них указывает знаки синуса, косинуса, тангенса и котангенса угла α
в зависимости от того, углом какой координатной четверти является α
. Дальше мы рассмотрим свойство периодичности, устанавливающее неизменность значений синуса, косинуса, тангенса и котангенса угла α
при изменении этого угла на целое число оборотов. Третье свойство выражает зависимость между значениями синуса, косинуса, тангенса и котангенса противоположных углов α
и −α
.
В этой статье мы рассмотрим три основных свойства. Первое из них указывает знаки синуса, косинуса, тангенса и котангенса угла α
в зависимости от того, углом какой координатной четверти является α
. Дальше мы рассмотрим свойство периодичности, устанавливающее неизменность значений синуса, косинуса, тангенса и котангенса угла α
при изменении этого угла на целое число оборотов. Третье свойство выражает зависимость между значениями синуса, косинуса, тангенса и котангенса противоположных углов α
и −α
.
Если же Вас интересуют свойства функций синуса, косинуса, тангенса и котангенса, то их можно изучить в соответствующем разделе статьи .
Навигация по странице.
Знаки синуса, косинуса, тангенса и котангенса по четвертям
Ниже в этом пункте будет встречаться фраза «угол I , II , III и IV координатной четверти». Объясним, что же это за углы.
Возьмем единичную окружность , отметим на ней начальную точку А(1, 0)
, и повернем ее вокруг точки O
на угол α
, при этом будем считать, что мы попадем в точку A 1 (x, y)
.
Говорят, что угол α является углом I , II , III , IV координатной четверти , если точка А 1 лежит в I , II , III , IV четверти соответственно; если же угол α таков, что точка A 1 лежит на любой из координатных прямых Ox или Oy , то этот угол не принадлежит ни одной из четырех четвертей.
Для наглядности приведем графическую иллюстрацию. На чертежах ниже изображены углы поворота 30 , −210 , 585 и −45 градусов, которые являются углами I , II , III и IV координатных четвертей соответственно.
Углы 0, ±90, ±180, ±270, ±360, … градусов не принадлежат ни одной из координатных четвертей.
Теперь разберемся, какие знаки имеют значения синуса, косинуса, тангенса и котангенса угла поворота α в зависимости от того, углом какой четверти является α .
Для синуса и косинуса это сделать просто.
По определению синус угла α
— это ордината точки А 1
. Очевидно, что в I
и II
координатных четвертях она положительна, а в III
и IV
четвертях – отрицательна.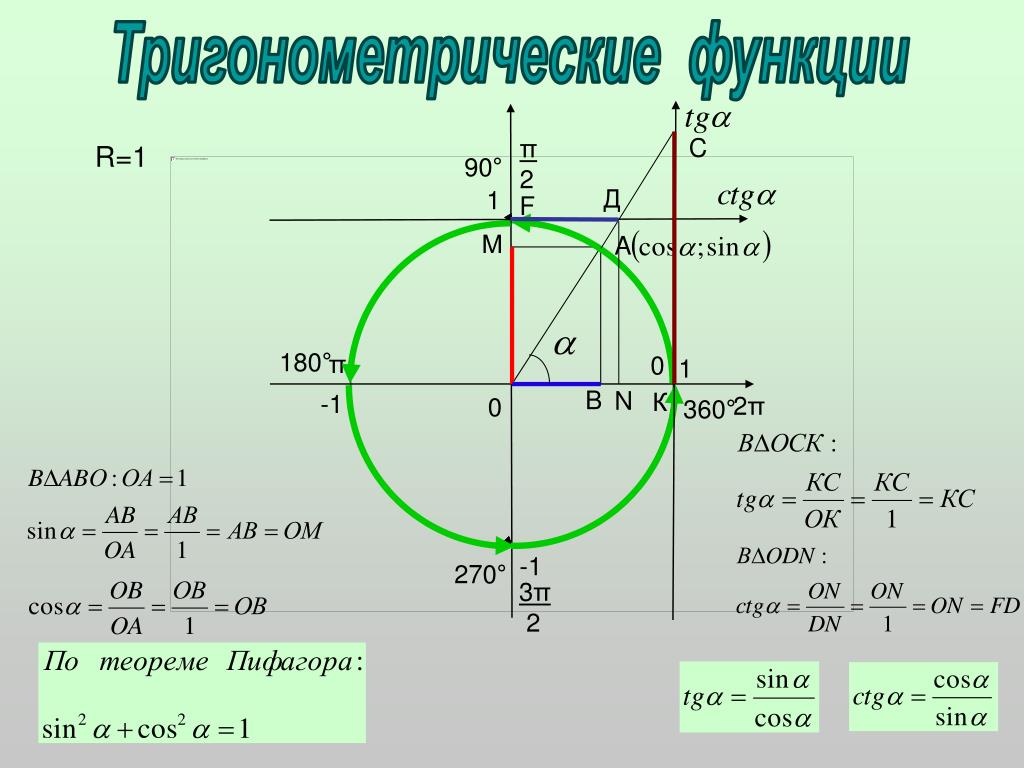 Таким образом, синус угла α
имеет знак плюс в I
и II
четвертях, а знак минус – в III
и VI
четвертях.
Таким образом, синус угла α
имеет знак плюс в I
и II
четвертях, а знак минус – в III
и VI
четвертях.
В свою очередь косинус угла α — это абсцисса точки A 1 . В I и IV четвертях она положительна, а во II и III четвертях – отрицательна. Следовательно, значения косинуса угла α в I и IV четвертях положительны, а во II и III четвертях – отрицательны.
Чтобы определить знаки по четвертям тангенса и котангенса нужно вспомнить их определения: тангенс – это отношение ординаты точки A 1 к абсциссе, а котангенс – отношение абсциссы точки A 1 к ординате. Тогда из правил деления чисел с одинаковыми и разными знаками следует, что тангенс и котангенс имеют знак плюс, когда знаки абсциссы и ординаты точки A 1 одинаковые, и имеют знак минус – когда знаки абсциссы и ординаты точки A 1 различны. Следовательно, тангенс и котангенс угла имеют знак + в I и III координатных четвертях, и знак минус – во II и IV четвертях.
Действительно, например, в первой четверти и абсцисса x
, и ордината y
точки A 1
положительны, тогда и частное x/y
, и частное y/x
– положительно, следовательно, тангенс и котангенс имеют знаки +
. А во второй четверти абсцисса x
– отрицательна, а ордината y
– положительна, поэтому и x/y
, и y/x
– отрицательны, откуда тангенс и котангенс имеют знак минус.
А во второй четверти абсцисса x
– отрицательна, а ордината y
– положительна, поэтому и x/y
, и y/x
– отрицательны, откуда тангенс и котангенс имеют знак минус.
Переходим к следующему свойству синуса, косинуса, тангенса и котангенса.
Свойство периодичности
Сейчас мы разберем, пожалуй, самое очевидное свойство синуса, косинуса, тангенса и котангенса угла. Оно состоит в следующем: при изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса этого угла не изменяются.
Это и понятно: при изменении угла на целое число оборотов мы из начальной точки А всегда будем попадать в точку А 1 на единичной окружности, следовательно, значения синуса, косинуса, тангенса и котангенса остаются неизменными, так как неизменны координаты точки A 1 .
С помощью формул рассматриваемое свойство синуса, косинуса, тангенса и котангенса можно записать так: sin(α+2·π·z)=sinα
, cos(α+2·π·z)=cosα
, tg(α+2·π·z)=tgα
, ctg(α+2·π·z)=ctgα
, где α
— угол поворота в радианах, z
– любое , абсолютная величина которого указывает количество полных оборотов, на которые изменяется угол α
, а знак числа z
указывает направление поворота.
Если же угол поворота α задан в градусах, то указанные формулы перепишутся в виде sin(α+360°·z)=sinα , cos(α+360°·z)=cosα , tg(α+360°·z)=tgα , ctg(α+360°·z)=ctgα .
Приведем примеры использования этого свойства. Например, , так как , а . Вот еще пример: или .
Это свойство вместе с формулами приведения очень часто используется при вычислении значений синуса, косинуса, тангенса и котангенса «больших» углов.
Рассмотренное свойство синуса, косинуса, тангенса и котангенса иногда называют свойством периодичности.
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
Пусть А 1 – точка, полученная в результате поворота начальной точки А(1, 0) вокруг точки O на угол α , а точка А 2 – это результат поворота точки А на угол −α , противоположный углу α .
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов базируется на достаточно очевидном факте: упомянутые выше точки А 1
и А 2
либо совпадают (при ), либо располагаются симметрично относительно оси Ox
. То есть, если точка A 1
имеет координаты (x, y)
, то точка А 2
будет иметь координаты (x, −y)
. Отсюда по определениям синуса, косинуса, тангенса и котангенса записываем равенства и .
То есть, если точка A 1
имеет координаты (x, y)
, то точка А 2
будет иметь координаты (x, −y)
. Отсюда по определениям синуса, косинуса, тангенса и котангенса записываем равенства и .
Сопоставляя их, приходим к соотношениям между синусами, косинусами, тангенсами и котангенсами противоположных углов α
и −α
вида .
Это и есть рассматриваемое свойство в виде формул.
Приведем примеры использования этого свойства. Например, справедливы равенства и .
Остается лишь заметить, что свойство синусов, косинусов, тангенсов и котангенсов противоположных углов, как и предыдущее свойство, часто используется при вычислении значений синуса, косинуса, тангенса и котангенса, и позволяет полностью уйти от отрицательных углов.
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Алгебра и начала анализа: Учеб.
 для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3. - Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Тригонометрия, как наука, зародилась на Древнем Востоке. Первые тригонометрические соотношения были выведены астрономами для создания точного календаря и ориентированию по звездам. Данные вычисления относились к сферической тригонометрии, в то время как в школьном курсе изучают соотношения сторон и угла плоского треугольника.
Тригонометрия – это раздел математики, занимающийся свойствами тригонометрических функций и зависимостью между сторонами и углами треугольников.
В период расцвета культуры и науки I тысячелетия нашей эры знания распространились с Древнего Востока в Грецию. Но основные открытия тригонометрии – это заслуга мужей арабского халифата. В частности, туркменский ученый аль-Маразви ввел такие функции, как тангенс и котангенс, составил первые таблицы значений для синусов, тангенсов и котангенсов. Понятие синуса и косинуса введены индийскими учеными. Тригонометрии посвящено немало внимания в трудах таких великих деятелей древности, как Евклида, Архимеда и Эратосфена.
Основные величины тригонометрии
Основные тригонометрические функции числового аргумента – это синус, косинус, тангенс и котангенс. Каждая из них имеет свой график: синусоида, косинусоида, тангенсоида и котангенсоида.
В основе формул для расчета значений указанных величин лежит теорема Пифагора. Школьникам она больше известна в формулировке: «Пифагоровы штаны, во все стороны равны», так как доказательство приводится на примере равнобедренного прямоугольного треугольника.
Синус, косинус и другие зависимости устанавливают связь между острыми углами и сторонами любого прямоугольного треугольника. Приведем формулы для расчета этих величин для угла A и проследим взаимосвязи тригонометрических функций:
Как видно, tg и ctg являются обратными функциями. Если представить катет a как произведение sin A и гипотенузы с, а катет b в виде cos A * c, то получим следующие формулы для тангенса и котангенса:
Тригонометрический круг
Графически соотношение упомянутых величин можно представить следующим образом:
Окружность, в данном случае, представляет собой все возможные значения угла α — от 0° до 360°. Как видно из рисунка, каждая функция принимает отрицательное или положительное значение в зависимости от величины угла. Например, sin α будет со знаком «+», если α принадлежит I и II четверти окружности, то есть, находится в промежутке от 0° до 180°. При α от 180° до 360° (III и IV четверти) sin α может быть только отрицательным значением.
Попробуем построить тригонометрические таблицы для конкретных углов и узнать значение величин.
Значения α равные 30°, 45°, 60°, 90°, 180° и так далее – называют частными случаями. Значения тригонометрических функций для них просчитаны и представлены в виде специальных таблиц.
Данные углы выбраны отнюдь не случайно. Обозначение π в таблицах стоит для радиан. Рад — это угол, при котором длина дуги окружности соответствует ее радиусу. Данная величина была введена для того, чтобы установить универсальную зависимость, при расчетах в радианах не имеет значение действительная длина радиуса в см.
Углы в таблицах для тригонометрических функций соответствуют значениям радиан:
Итак, не трудно догадаться, что 2π – это полная окружность или 360°.
Свойства тригонометрических функций: синус и косинус
Для того, чтобы рассмотреть и сравнить основные свойства синуса и косинуса, тангенса и котангенса, необходимо начертить их функции.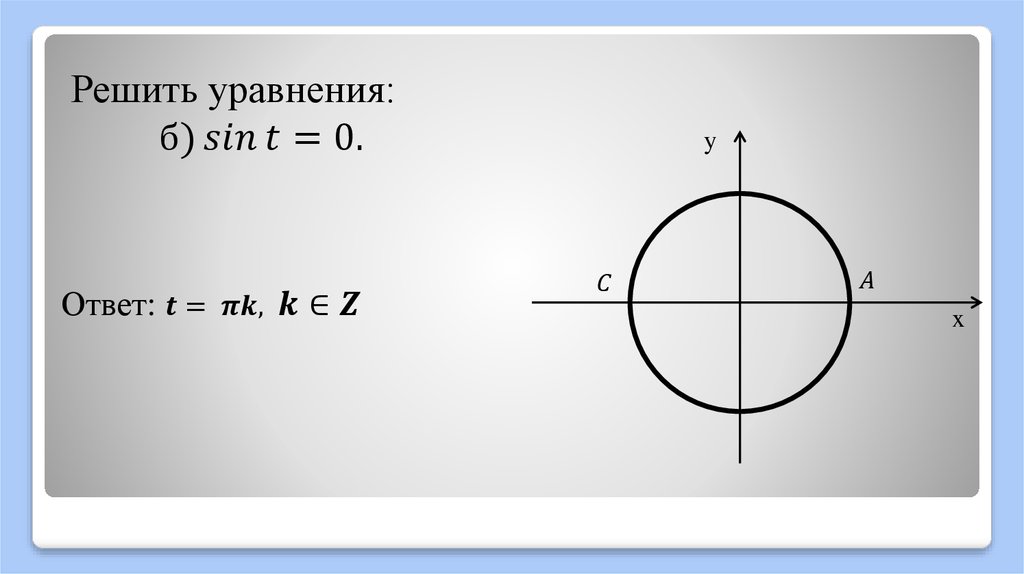 Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Сделать это можно в виде кривой, расположенной в двумерной системе координат.
Рассмотри сравнительную таблицу свойств для синусоиды и косинусоиды:
| Синусоида | Косинусоида |
|---|---|
| y = sin x | y = cos x |
| ОДЗ [-1; 1] | ОДЗ [-1; 1] |
| sin x = 0, при x = πk, где k ϵ Z | cos x = 0, при x = π/2 + πk, где k ϵ Z |
| sin x = 1, при x = π/2 + 2πk, где k ϵ Z | cos x = 1, при x = 2πk, где k ϵ Z |
| sin x = — 1, при x = 3π/2 + 2πk, где k ϵ Z | cos x = — 1, при x = π + 2πk, где k ϵ Z |
| sin (-x) = — sin x, т. е. функция нечетная | cos (-x) = cos x, т. е. функция четная |
| функция периодическая, наименьший период — 2π | |
| sin x › 0, при x принадлежащем I и II четвертям или от 0° до 180° (2πk, π + 2πk) | cos x › 0, при x принадлежащем I и IV четвертям или от 270° до 90° (- π/2 + 2πk, π/2 + 2πk) |
| sin x ‹ 0, при x принадлежащем III и IV четвертям или от 180° до 360° (π + 2πk, 2π + 2πk) | cos x ‹ 0, при x принадлежащем II и III четвертям или от 90° до 270° (π/2 + 2πk, 3π/2 + 2πk) |
| возрастает на промежутке [- π/2 + 2πk, π/2 + 2πk] | возрастает на промежутке [-π + 2πk, 2πk] |
| убывает на промежутках [ π/2 + 2πk, 3π/2 + 2πk] | убывает на промежутках |
| производная (sin x)’ = cos x | производная (cos x)’ = — sin x |
Определить является ли функция четной или нет очень просто. Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Достаточно представить тригонометрический круг со знаками тригонометрических величин и мысленно «сложить» график относительно оси OX. Если знаки совпадают, функция четная, в противном случае — нечетная.
Введение радиан и перечисление основных свойств синусоиды и косинусоиды позволяют привести следующую закономерность:
Убедиться в верности формулы очень просто. Например, для x = π/2 синус равен 1, как и косинус x = 0. Проверку можно осуществить обративших к таблицам или проследив кривые функций для заданных значений.
Свойства тангенсоиды и котангенсоиды
Графики функций тангенса и котангенса значительно отличаются от синусоиды и косинусоиды. Величины tg и ctg являются обратными друг другу.
- Y = tg x.
- Тангенсоида стремится к значениям y при x = π/2 + πk, но никогда не достигает их.
- Наименьший положительный период тангенсоиды равен π.
- Tg (- x) = — tg x, т. е. функция нечетная.
- Tg x = 0, при x = πk.

- Функция является возрастающей.
- Tg x › 0, при x ϵ (πk, π/2 + πk).
- Tg x ‹ 0, при x ϵ (— π/2 + πk, πk).
- Производная (tg x)’ = 1/cos 2 x .
Рассмотрим графическое изображение котангенсоиды ниже по тексту.
Основные свойства котангенсоиды:
- Y = ctg x.
- В отличие от функций синуса и косинуса, в тангенсоиде Y может принимать значения множества всех действительных чисел.
- Котангенсоида стремится к значениям y при x = πk, но никогда не достигает их.
- Наименьший положительный период котангенсоиды равен π.
- Ctg (- x) = — ctg x, т. е. функция нечетная.
- Ctg x = 0, при x = π/2 + πk.
- Функция является убывающей.
- Ctg x › 0, при x ϵ (πk, π/2 + πk).
- Ctg x ‹ 0, при x ϵ (π/2 + πk, πk).
- Производная (ctg x)’ = — 1/sin 2 x Исправить
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.
Первое свойство — знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α . Второе свойство — периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и — α .
Второе свойство — периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и — α .
Yandex.RTB R-A-339285-1
Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?
Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A 0 (1 , 0) и, поворачивая ее вокруг точки O на угол α , попадем в точку A 1 (x , y) . В зависимости от того, в какой четверти будет лежать точка A 1 (x , y) , угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно.
Для наглядности приведем иллюстрацию.
Угол α = 30 ° лежит в первой четверти. Угол — 210 ° является углом второй четверти. Угол 585 ° — угол третьей четверти. Угол — 45 ° — это угол четвертой четверти.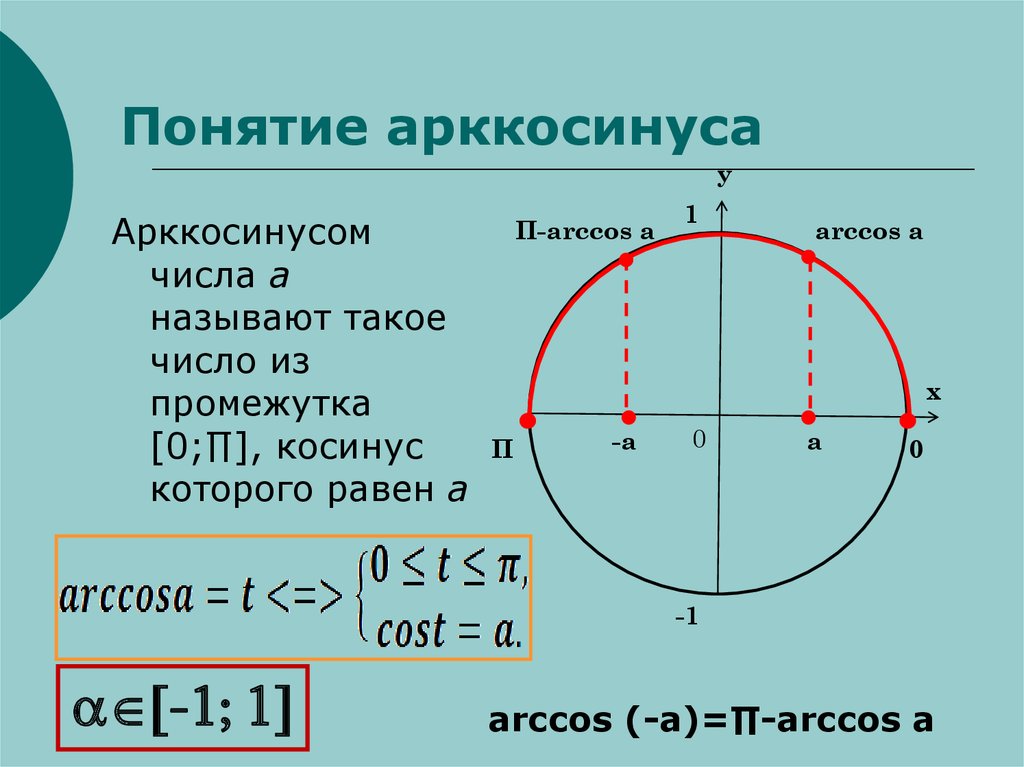
При этом углы ± 90 ° , ± 180 ° , ± 270 ° , ± 360 ° не принадлежат ни одной четверти, так как лежат на координатных осях.
Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.
Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A 1 (x , y) . Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.
Косинус — это абсцисса точки A 1 (x , y) . В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.
Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным.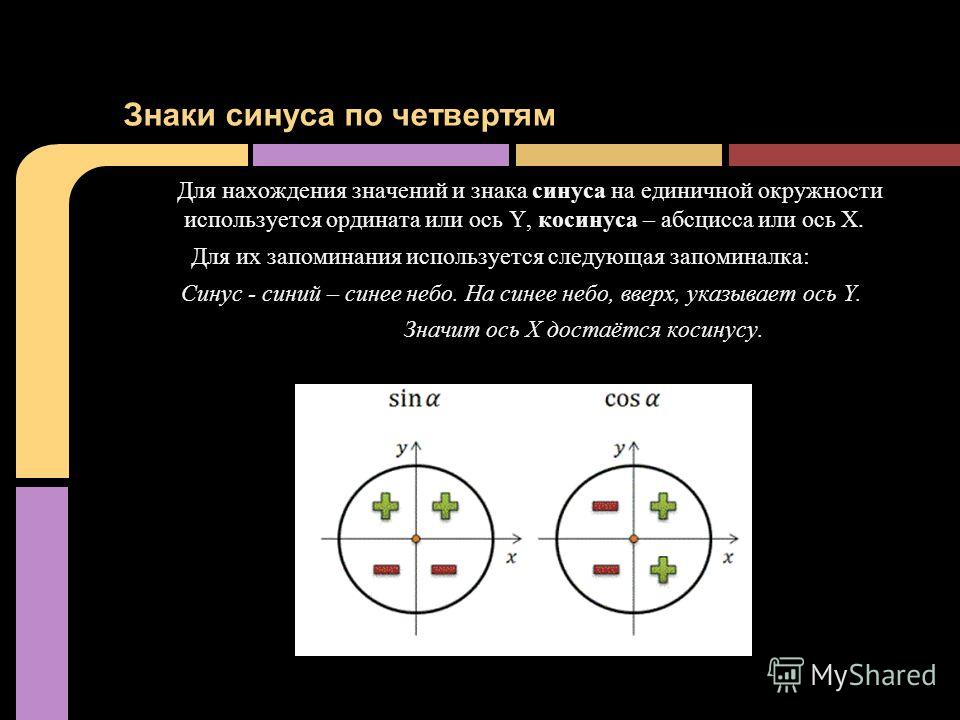 Аналогично определяются знаки котангенса по четвертям.
Аналогично определяются знаки котангенса по четвертям.
Важно помнить!
- Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус — в 3 и 4 четвертях.
- Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус — в 2 и 3 четвертях.
- Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
- Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
Свойство периодичности
Свойство периодичности — одно из самых очевидных свойств тригонометрических функций.
Свойство периодичности
При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.
Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A 1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.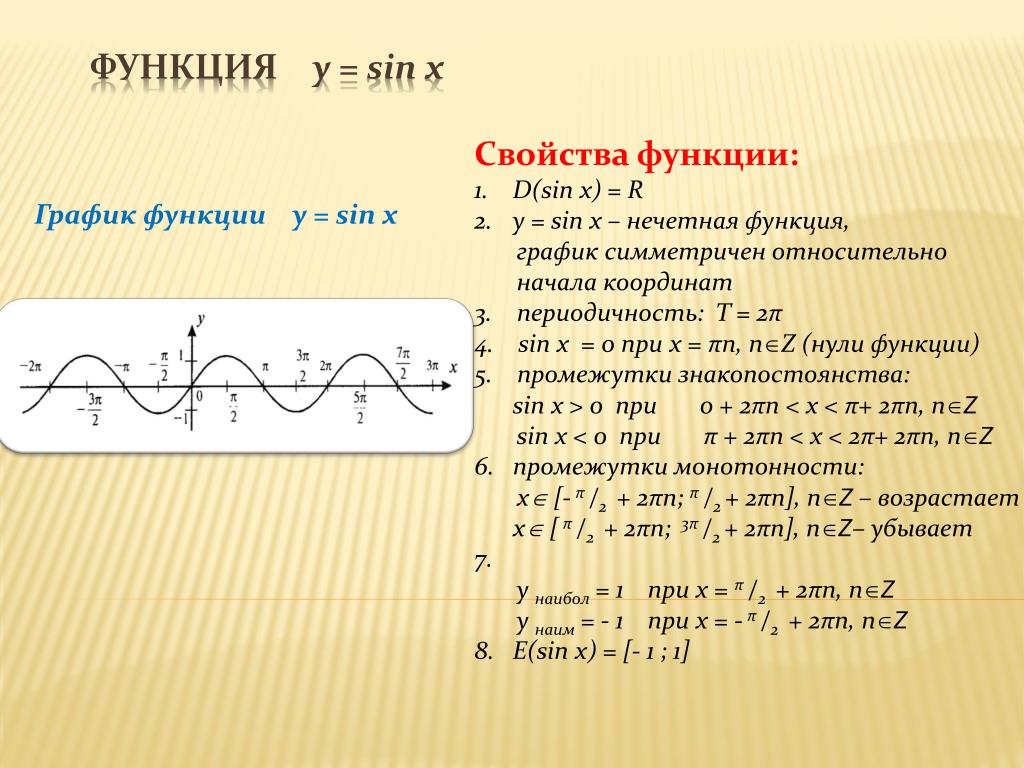
Математически данное свойство записывается так:
sin α + 2 π · z = sin α cos α + 2 π · z = cos α t g α + 2 π · z = t g α c t g α + 2 π · z = c t g α
Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.
Приведем примеры.
sin 13 π 5 = sin 3 π 5 + 2 π = sin 3 π 5
t g (- 689 °) = t g (31 ° + 360 ° · (- 2)) = t g 31 ° t g (- 689 °) = t g (- 329 ° + 360 ° · (- 1)) = t g (- 329 °)
Вновь обратимся к единичной окружности.
Точка A 1 (x , y) — результат поворота начальной точки A 0 (1 , 0) вокруг центра окружности на угол α . Точка A 2 (x , — y) — результат поворота начальной точки на угол — α .
Точки A 1 и A 2 симметричны относительно оси абсцисс. В случае, когда α = 0 ° , ± 180 ° , ± 360 ° точки A 1 и A 2 совпадают. Пусть одна точка имеет координаты (x , y) , а вторая — (x , — y) . Вспомним определения синуса, косинуса, тангенса, котангенса и запишем:
sin α = y , cos α = x , t g α = y x , c t g α = x y sin — α = — y , cos — α = x , t g — α = — y x , c t g — α = x — y
Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов
sin — α = — sin α cos — α = cos α t g — α = — t g α c t g — α = — c t g α
Согласно этому свойству, справедливы равенства
sin — 48 ° = — sin 48 ° , c t g π 9 = — c t g — π 9 , cos 18 ° = cos — 18 °
Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Использование предлога in в английском языке
Употребление и произношение in
Проектное занятие по теме «Свойства синуса, косинуса, тангенса и котангенса», алгебра, 9-й класс
Цели:
- Обеспечить усвоение знаний по теме “Свойства синуса, косинуса, тангенса и котангенса”.
- Сформировать умения и навыки в применении
свойств синуса, косинуса, тангенса и котангенса к
упрощению тригонометрических выражений.

Задачи:
- Изучить материалы соответствующего пункта учебного пособия, других источников в т.ч. сети Интернет.
- Вырабатывать умения и навыки применения свойств синуса, косинуса, тангенса и котангенса к упрощению тригонометрических выражений.
- Формировать навыки публичных выступлений.
Планируемый конечный результат (с позиции компетентностей, формируемых у школьников):
- Электронная презентация, выставленная на школьном сайте сети Интернет.
- Развитие информационной компетентности.
- Развитие коммуникативной компетентности.
Тип урока: проектное занятие.
Время реализации: 2 учебных часа.
Техническое обеспечение:
компьютер, сканер.
Программное обеспечение: MS Power Point, MS Word, Internet Explorer.
Другие ресурсы: учебные и дидактические материалы, набор карточек с заданиями, тесты.
Термины и понятия: свойства синуса, косинуса, тангенса и котангенса; нечетность функций синуса, тангенса и котангенса и четность функции косинус; неизменяемость значений синуса, косинуса, тангенса и котангенса при изменении угла на целое число оборотов.
Содержание занятия:
- Погружение в проблему.
- Организация деятельности.
- Осуществление деятельности.
- Презентация продукта деятельности учащихся.
- Оценка результата.
Ход занятия
I. Погружение в проблему.
Деятельность учителя. Осуществляет
мотивацию детей на изучение темы и работу над
проектом. Выделяет подтемы и ставит проблемные
вопросы. Обсуждает с учащимися подтемы проекта.
Показ электронной презентации предстоящей
работы.
Выделяет подтемы и ставит проблемные
вопросы. Обсуждает с учащимися подтемы проекта.
Показ электронной презентации предстоящей
работы.
Триада вопросов:
Основополагающий вопрос: Все ли призрачно в этом мире бушующем?
Проблемные вопросы учебной темы:
- Каким образом можно определить знаки синуса, косинуса, тангенса и котангенса по координатным четвертям?
- Почему синус, тангенс и котангенс – нечетные функции, а косинус – четная функция?
- Для чего в математике нам нужны эти формулы?
Частные вопросы:
- Что называется синусом угла косинусом угла , тангенсом угла , котангенсом угла ?
- Какие знаки имеет синус, косинус, тангенс и котангенс по координатным четвертям?
- При изменении угла на целое число оборотов значения синуса, косинуса, тангенса и котангенса изменяются?
Деятельность учащихся. Узнают тему
проекта, вопросы для исследования.
Узнают тему
проекта, вопросы для исследования.
Учащиеся активно обсуждают и предлагают варианты подтем, варианты конечного продукта.
Актуализация знаний учащихся.
Математический диктант.
Вариант 1.
- Углом какой четверти является угол a, если:
| a = 1850 a = –1850 a = 1020 a = –1020 a = 2500 a = –2500 a = 3750 |
a = 1450 a = –1450 a = 2250 a = –3150 a = 2100 a = 5900 a = –150 |
- Вычислите:
| cos 1800 + 5sin 900 sin 1800 – 3 cos 00 5ctg 900 – 7tg 1800 sin 600 + cos 300 |
cos 00 + 3sin 900 sin 2700 – 2cos 1800 6tg 1800 + 2ctg 900 1 + ctg 2700 – 5 tg 3600 |
Ответы:
1. III II II III III II I |
2. 4 –3 0 |
1. II III III I III III IV |
2. 4 1 0 1 |
II. Организация деятельности.
Деятельность учителя. Оказывает помощь в формировании творческих групп и распределении ролей и задач в группах.
Нацеливает на самостоятельную исследовательскую работу.
Формулирует задания для каждой группы.
Предлагает формы презентации результатов, помогает группам определиться.
Деятельность учащихся. Учащиеся
определили свои роли и группируются в
соответствии с ними в малые команды.
Определяют долю участия каждого в подборе информации, в соответствии со своими интересами, определяют этапы разработки проекта, даты получения первых результатов.
Учащиеся в группах, а затем в классе обсуждают формы представления результата исследовательской деятельности: презентаций (MS PowerPoint) и выставления работы на школьном сайте.
III. Осуществление деятельноти.
Деятельность учителя.
- Координирует работу между группами и учащихся в группе, улаживает споры.
- Мотивирует учащихся на выполнение проекта.
- Оказывает помощь в подборе и оформлении материала.
- Проводит тренировочные упражнения, направленные на отработку учебного материала. Предоставляет имеющийся материал для проекта.
- Наблюдает за работой учащихся.
- Оказывает техническую помощь в оформлении
результатов проекта.

Деятельность учащихся. Выполняют свою задачу (индивидуально или в паре): подбирают материал для проекта в Internet, библиотеке; решают тесты.
Оформляют результаты работы в группах.
Компетентностно-ориентированные задания (КОЗ)
Информационная компетентность.
Аспект – планирование и поиск информации (уровень2)
Аспект – извлечение первичной информации (уровень 2)
- Ребята, вам предоставляется возможность выставить электронную презентацию в сети Интернет, с тем, чтобы ее увидел весь мир. Для этого нам нужно немного поработать.
- Задание.
Определите значения знаков синуса, косинуса, тангенса и котангенса по координатным четвертям. Запишите результаты в таблицу.
Объясните свойства четности косинуса и
нечетности синуса, тангенса и котангенса.
Объясните, почему при изменении угла на целое
число оборотов значения синуса, косинуса,
тангенса и котангенса не изменяются.
I четв. |
II четв. |
III четв. |
IV четв. |
|
| Синус | ||||
| Косинус | ||||
| Тангенс | ||||
| Котангенс |
Синус – нечетная функция, т. к.
____________________________________
к.
____________________________________
Косинус – четная функция, т.к. ____________________________________
Тангенс – нечетная функция, т.к. ___________________________________
Котангенс – нечетная функция, т.к. _________________________________
При изменении угла на целое число оборотов значения синуса, косинуса, тангенса и котангенса не изменяются, т.к.__________________________________________________
_____________________________________________________________________________
- Информация, необходимая для решения данной задачи – п. 29 учебного пособия (можно найти информацию и в других источниках, обратитесь в библиотеку).
- Ключ:
| I четв. | II четв. | III четв. | IV четв. |
|
| Синус | + | + | – | – |
| Косинус | + | – | – | + |
| Тангенс | + | – | + | – |
| Котангенс | + | – | + | – |
Модельный ответ:
Синус – нечетная функция, т.к. sin (–a) = yc/R = –y/R = –sina
Косинус – четная функция, т.к. cos (–a) = xc/R = x/R = cosa
Тангенс – нечетная функция, т.к. tg (–a) = –yc/xc= –y/x = –tga
Котангенс – нечетная функция, т. к. ctg (–a) = xc/yc
= x/–y = –sina
к. ctg (–a) = xc/yc
= x/–y = –sina
При изменении угла на целое число оборотов значения синуса, косинуса, тангенса и котангенса не изменяются, т.к. при повороте радиуса ОА на угол ф получен радиус ОВ, тот же радиус получится при повороте ОА на угол, отличающийся от а на целое число оборотов.
Работа в малых группах по проблеме выработки умений и навыков применения свойств синуса, косинуса, тангенса и котангенса к упрощению тригонометрических выражений.
Выполнение теста.
Тест [4]
Вариант 1.
Часть А.
А1. Найдите значение выражения: –3 cos 600 + 1/3 tg 450
A2. Какое из значений может принимать sin a?
A3. Углом какой четверти является угол a, сos a>0, tg a <0?
| 1) I | 2) II | 3) III | 4) IV |
A4.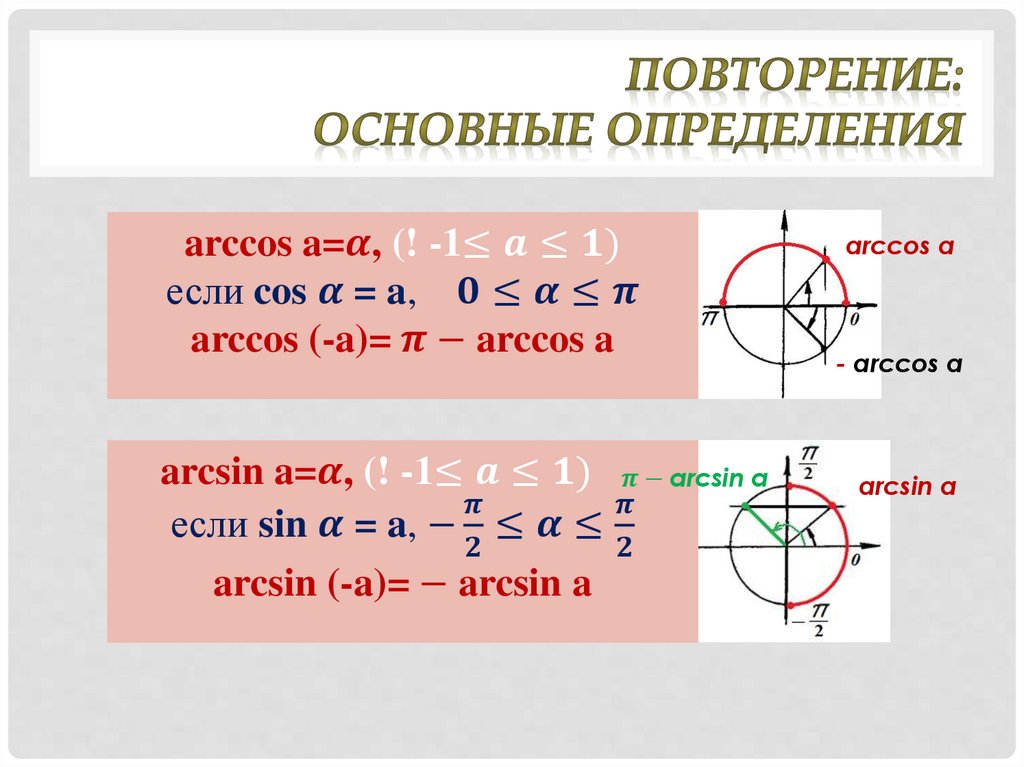 Вычислите значение выражения 2 sin2
450 + v3 ctg (–300).
Вычислите значение выражения 2 sin2
450 + v3 ctg (–300).
A5. Какое из данных выражений имеет отрицательное значение?
- sin 1700
- cos 1520
- sin 2520
- ctg 3000
- tg 1080 ctg 1080
Часть В.
В1. Найдите значение выражения 2cos 2a – 3 sin 3a при а = 300
Ответ: ______________________________________________
В2. Найдите наибольшее значение выражения 4 – 2 cos a.
Ответ: ______________________________________________
В3. Найдите значение выражения tg (–4950)
Ответ: ______________________________________________
Часть С.
С1. Углы треугольника пропорциональны числам 1, 2, 3.
Найдите их градусные меры.
Запишите ход решения на отдельном листе.
Вариант 2.
Часть А.
А1. Найдите значение выражения: 1/5 sin 300 — 4 ctg 450
A2. Какое из значений может принимать cos a ?
A3. Углом какой четверти является угол a, sin a<0, tg a >0?
| 1) I | 2) II | 3) III | 4) IV |
A4. Вычислите значение выражения v3 tg (–300) – 5 cos2 450
A5. Какое из данных выражений имеет положительное значение?
Часть В.
В1. Найдите значение выражения cos 3a – 2 sin 2a при а = 300
Ответ: ______________________________________________
В2. Найдите наибольшее значение выражения 5 – 3 sin a.
Ответ: ______________________________________________
В3. Найдите значение выражения ctg (–6750)
Ответ: ______________________________________________
Часть С.
С1. Углы треугольника пропорциональны числам 2, 2, 5.
Найдите их градусные меры.
Запишите ход решения на отдельном листе.
Ответы:
Вариант 1
Часть А
| № задания | А1 | А2 | А3 | А4 | А5 |
| Номер ответа | 2 | 1 | 4 | 2 | 3 |
Часть В
| № задания | В1 | В2 | В3 |
| Ответ | -2 | 6 | 1 |
Часть С
Ответ: 300, 600, 900
Вариант 2
Часть А
| № задания | А1 | А2 | А3 | А4 | А5 |
| Номер ответа | 2 | 3 | 3 | 4 | 1 |
Часть В
| № задания | В1 | В2 | В3 |
| Ответ | –3 | 2 | 1 |
Часть С
Ответ: 400, 400, 1000
IV.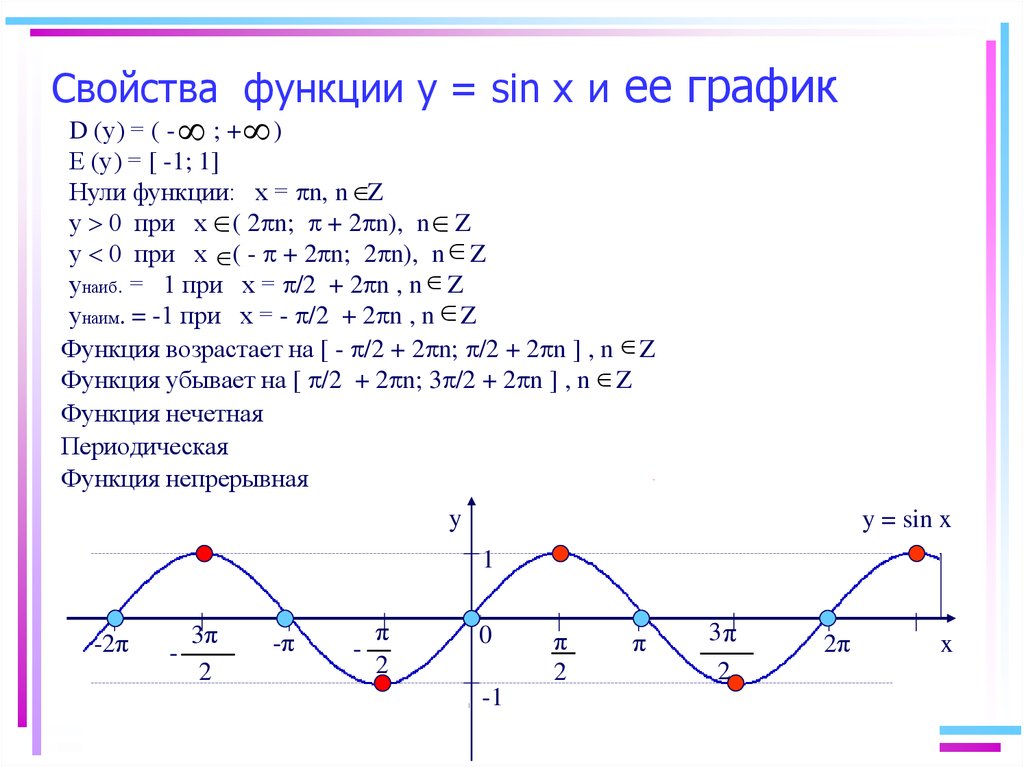 Презентация продукта деятельности
учащихся.
Презентация продукта деятельности
учащихся.
Деятельность учителя. Знакомится с презентацией, ставит вопросы по теме исследования группы, корректирует речевые ошибки, записывает типичные математические ошибки для последующей коррекционной работы.
Деятельность учащихся. Презентуют результат своей работы. Знакомятся и оценивают результаты работы других групп. Задают вопросы, высказывают свое мнение соблюдая культуру общения.
V. Оценка результата.
Деятельность учителя: Оценивает совместно с детьми результаты проекта, деятельности групп, деятельности каждого учащегося на основании наблюдений по ходу выполнения проекта. Делает анализ собственного участия в проекте.
Деятельность учащихся: Проводят
рефлексию своей деятельности при работе над
проектом. Анализируют результаты проекта,
степень участия в работе других учащихся.
Задание на дом: п.29 [2], № 902 (б).
Литература
- Министерство образования Российской Федерации. Программы для общеобразовательных школ. Математика. 5–11-е классы. М., “Дрофа”, 2001.
- Алгебра. Учебник для 9-го класса общеобразовательных учреждений. Под редакцией С.А.Теляковского. Авторы: Ю.Н.Макарычев и др. М.: “Просвещение”, 2002.
- Ю.Н.Макарычев и др. Дидактические материалы Алгебра. 9-й класс. М.: “Просвещение”, 2003.
- Ю.Н.Макарычев и др Сборник тестовых заданий для тематического и обобщающего контроля. Алгебра. 9-й класс. М.: “Интеллект-центр”, 2007.
- Методическое пособие для преподавателей по алгебре, 9-й класс, по учебнику Ю.Н.Макарычева.
Свойства синуса, косинуса, тангенса и котангенса
Нажмите для полного просмотра!
Вы можете ознакомиться и скачать презентацию на
тему Свойства синуса, косинуса, тангенса и котангенса.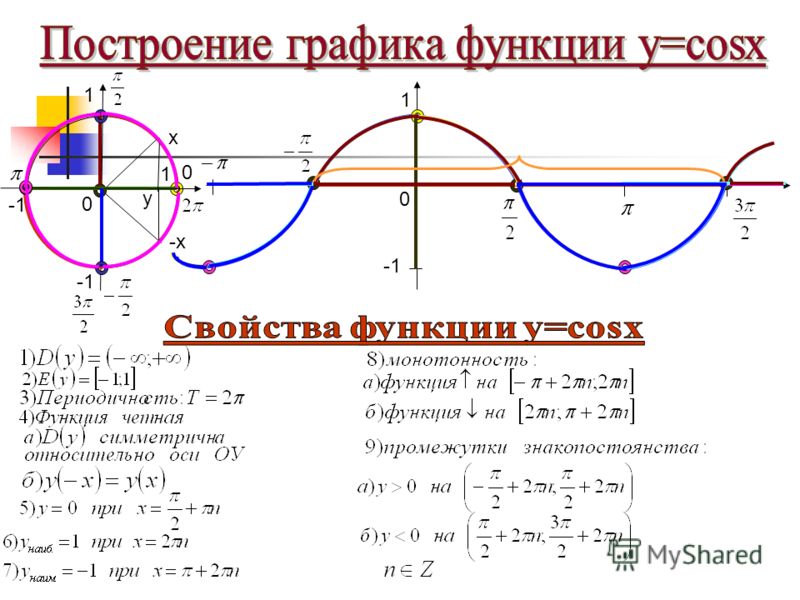 Доклад-сообщение содержит 41 слайдов.
Презентации для любого класса можно скачать бесплатно.
Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь
им с друзьями с помощью социальных кнопок и добавьте в закладки в своем
браузере.
Доклад-сообщение содержит 41 слайдов.
Презентации для любого класса можно скачать бесплатно.
Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь
им с друзьями с помощью социальных кнопок и добавьте в закладки в своем
браузере.
Слайды и текст этой презентации
Слайд 1
Описание слайда:
Слайд 2
Описание слайда:
Слайд 3
Описание слайда:
Слайд 4
Описание слайда:
Слайд 5
Описание слайда:
Слайд 6
Описание слайда:
Слайд 7
Описание слайда:
Слайд 8
Описание слайда:
Слайд 9
Описание слайда:
Слайд 10
Описание слайда:
Слайд 11
Описание слайда:
Слайд 12
Описание слайда:
Слайд 13
Описание слайда:
Слайд 14
Описание слайда:
Слайд 15
Описание слайда:
Слайд 16
Описание слайда:
Слайд 17
Описание слайда:
Слайд 18
Описание слайда:
Слайд 19
Описание слайда:
Слайд 20
Описание слайда:
Слайд 21
Описание слайда:
Слайд 22
Описание слайда:
Слайд 23
Описание слайда:
Слайд 24
Описание слайда:
Слайд 25
Описание слайда:
Слайд 26
Описание слайда:
Слайд 27
Описание слайда:
Слайд 28
Описание слайда:
Слайд 29
Описание слайда:
Слайд 30
Описание слайда:
Слайд 31
Описание слайда:
Слайд 32
Описание слайда:
Слайд 33
Описание слайда:
Слайд 34
Описание слайда:
Слайд 35
Описание слайда:
Слайд 36
Описание слайда:
Слайд 37
Описание слайда:
Слайд 38
Описание слайда:
Слайд 39
Описание слайда:
Слайд 40
Описание слайда:
Слайд 41
Описание слайда:
Теги Свойства синуса, косинуса, тангенса и котангенса
Похожие презентации
Презентация успешно отправлена!
Ошибка! Введите корректный Email!
Mypresentation. ru
ru
Закрыть (X)
1. Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол . С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. 2. К тригонометрическим функциям относятся следующие 6 функций: синус , косинус , тангенс ,котангенс , секанс и косеканс . Для каждой из указанных функций существует обратная тригонометрическая функция. 3. Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга . На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α. 4. Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r: 5. Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r: 6. 7. Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y: 8. Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y): 9. Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y): 10. В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом: 11. График функции синус 12. График функции косинус 13. График функции тангенс 14. График функции котангенс 15. График функции секанс Полезное
Реклама
Новое
|
Синус — График, Таблица, Свойства, Примеры
Синус угла представляет собой тригонометрическую функцию, которая обозначается sin x, где x — рассматриваемый угол. В прямоугольном треугольнике отношение перпендикуляра к гипотенузе называется синусоидой. Другими словами, это отношение стороны, противоположной рассматриваемому углу, а гипотенуза и ее значение изменяются при изменении угла. Функция синуса используется для представления звуковых и световых волн в области физики.
В прямоугольном треугольнике отношение перпендикуляра к гипотенузе называется синусоидой. Другими словами, это отношение стороны, противоположной рассматриваемому углу, а гипотенуза и ее значение изменяются при изменении угла. Функция синуса используется для представления звуковых и световых волн в области физики.
В этой статье мы изучим основные свойства sin x, синусоидального графика, его области определения и диапазона, производной, интеграла и разложения в степенной ряд. Функция синуса является периодической функцией и имеет период 2π. Мы решим несколько примеров, используя функцию синуса, чтобы лучше понять концепцию.
| 1. | Что такое синус? |
| 2. | Определение синуса |
| 3. | Формула функции синуса |
| 4. | Синусоидальные функции Домен и диапазон |
| 5. | Синусоидальный график |
6. | Таблица синуса |
| 7. | Свойства функции синуса |
| 8. | Синусоидальные тождества |
| 9. | Часто задаваемые вопросы о синусоидальной функции |
Что такое синус?
Синус угла прямоугольного треугольника представляет собой отношение стороны, противолежащей углу, и гипотенузы. Функция синуса является важной периодической функцией в тригонометрии и имеет период 2π. Чтобы понять вывод sin x, давайте рассмотрим единичный круг с центром в начале координат плоскости. Переменная точка P движется по границе (окружности) этой окружности. Заметьте, что P находится в первом квадранте, а OP образует острый угол x радиан с положительной осью x. PQ — перпендикуляр, опущенный из точки P на горизонтальную ось. Таким образом, треугольник образуется путем соединения точек O, P и Q, как показано на рисунке.
Следовательно, синусоидальная функция для приведенного выше случая может быть математически записана как sin x = PQ/OP.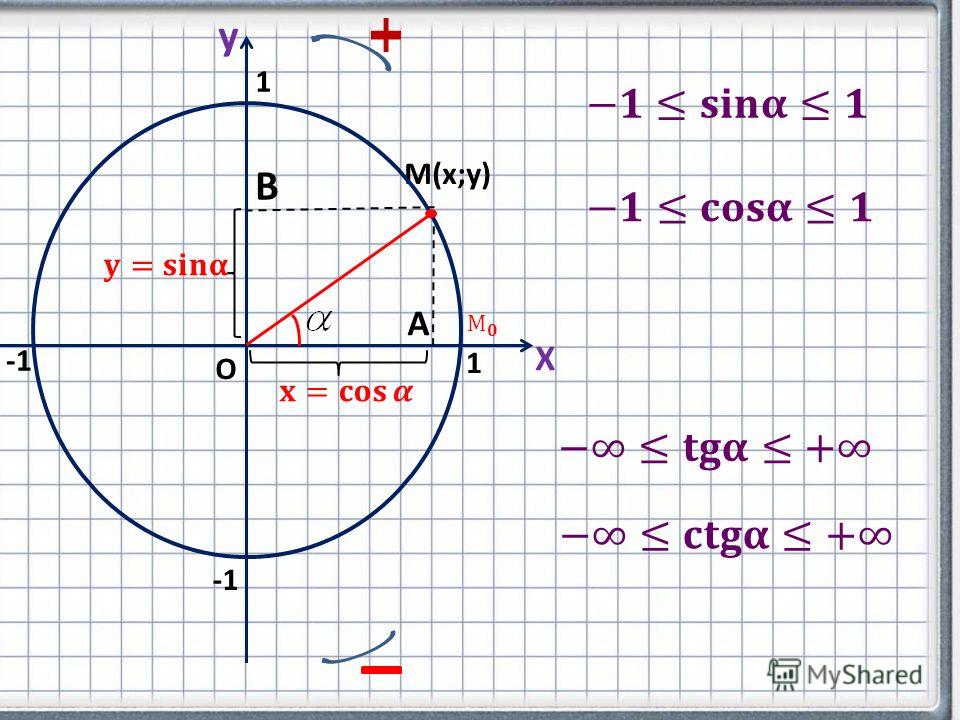 Здесь x — острый угол между гипотенузой и основанием прямоугольного треугольника OPQ.
Здесь x — острый угол между гипотенузой и основанием прямоугольного треугольника OPQ.
Определение синуса
Синус угла можно определить как отношение длины перпендикуляра к длине гипотенузы в прямоугольном треугольнике. Он дает значение функции синуса угла между основанием и гипотенузой прямоугольного треугольника. Математически он обозначается как sin x, где x — острый угол между основанием и гипотенузой прямоугольного треугольника.
Формула функции синуса
Функция синуса записывается как отношение длины перпендикуляра и гипотенузы прямоугольного треугольника. Математически формула функции синуса относительно сторон прямоугольного треугольника записывается так:
sin x = противоположная сторона/гипотенуза = перпендикуляр/гипотенуза
Область функции синуса и диапазон
Областью определения функции синуса являются все действительные числа, поскольку sin x определен для всех x в (-∞, ∞). Принимая во внимание, что диапазон sin x равен [-1, 1], так как значение sin x не выходит за его пределы. График синусоидальной функции выглядит как волна, которая колеблется между -1 и 1. Кроме того, период sin x равен 2π, поскольку его значение повторяется через каждые 2π радиан. Область определения и диапазон синусоидальной функции также можно наблюдать с помощью ее графика. В разделе ниже давайте посмотрим, как построен график sin x.
График синусоидальной функции выглядит как волна, которая колеблется между -1 и 1. Кроме того, период sin x равен 2π, поскольку его значение повторяется через каждые 2π радиан. Область определения и диапазон синусоидальной функции также можно наблюдать с помощью ее графика. В разделе ниже давайте посмотрим, как построен график sin x.
Синусоидальный график
Прежде чем перейти к графику функции синуса, давайте разберемся, как значения синуса изменяются на единичном круге, а затем нанесем их на график. Как показано на изображении выше, мы отмечаем, что sin x = PQ/OP = PQ/1 = PQ (поскольку радиус единичного круга равен 1, поэтому OP = 1). Поскольку x изменяется, значение sin x изменяется с изменением длины PQ. Теперь мы изучим изменение функции синуса в четырех квадрантах координатной плоскости.
Случай 1: Изменение PQ в первом квадранте.
Предположим, что изначально P находится на горизонтальной оси. Рассмотрим движение P на 90° или π/2 рад. На следующем рисунке показаны различные положения P для этого движения. Ясно, что длина PQ увеличилась от начального значения 0 (когда x равно 0 радианам) до конечного значения 1 (когда x равно π/2 радианам).
На следующем рисунке показаны различные положения P для этого движения. Ясно, что длина PQ увеличилась от начального значения 0 (когда x равно 0 радианам) до конечного значения 1 (когда x равно π/2 радианам).
Случай 2: Изменение PQ во втором квадранте.
Теперь мы проверим положение P во втором квадранте, как мы делали это в первом квадранте, и проверим, как изменяется значение функции синуса. P впоследствии перемещается из 9от 0° до положения 180°. В этой фазе движения длина PQ уменьшается от максимума 1 при 90° до минимума 0 при 180°.
Случай 3: Изменение PQ в третьем квадранте.
Когда P перемещается из положения 180° в положение 270°, хотя длина или величина PQ увеличивается. Но так как направление вдоль отрицательной оси y, фактическое значение синусоидальной функции уменьшается с 0 до -1. Таким образом, значение синусоидальной функции для угла x уменьшается.
Случай 4: Изменение PQ в четвертом квадранте.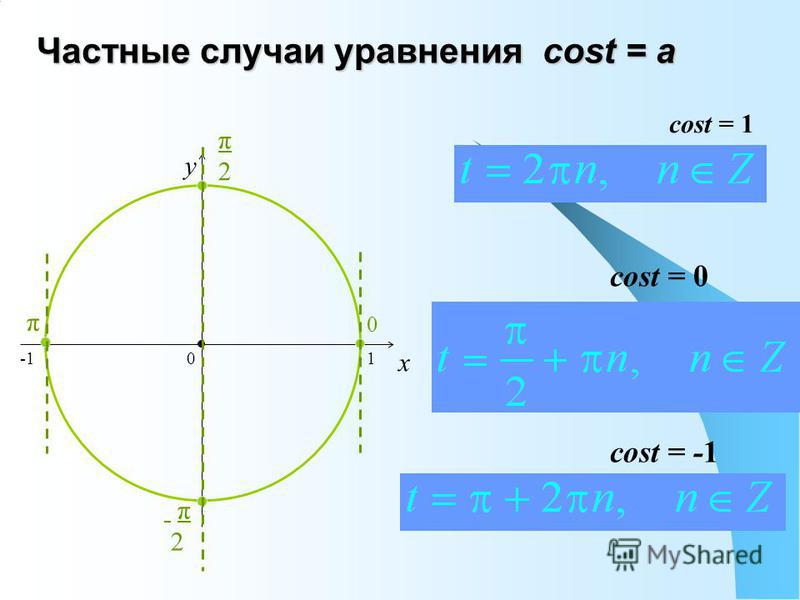
Наконец, когда P перемещается из положения 270° в положение 360°, sin x увеличивается с -1 до 0 (снова). Хотя длина или величина PQ уменьшается, значение величины PQ будет увеличиваться, потому что его направление направлено вдоль отрицательной оси y. Таким образом, значение синуса для угла x увеличивается.
Теперь мы можем изобразить это изменение на графике. Горизонтальная ось представляет входную переменную x как угол в радианах, а вертикальная ось представляет значение функции синуса. Объединив реакцию изменения значения PQ для всех четырех квадрантов, мы получили полный график зависимости PQ от x или sin x от x для одного полного цикла от 0 до 2π радиан (от 0° до 360°). Полученный таким образом синусоидальный график показан ниже:
Таблица синуса
Теперь давайте пройдемся по значениям функции синуса для некоторых конкретных углов, таких как 0°, 30°, 45°, 60°, 90° и т. д., поскольку их легко запомнить. Большинство приведенных ниже значений используются для решения различных задач по тригонометрии.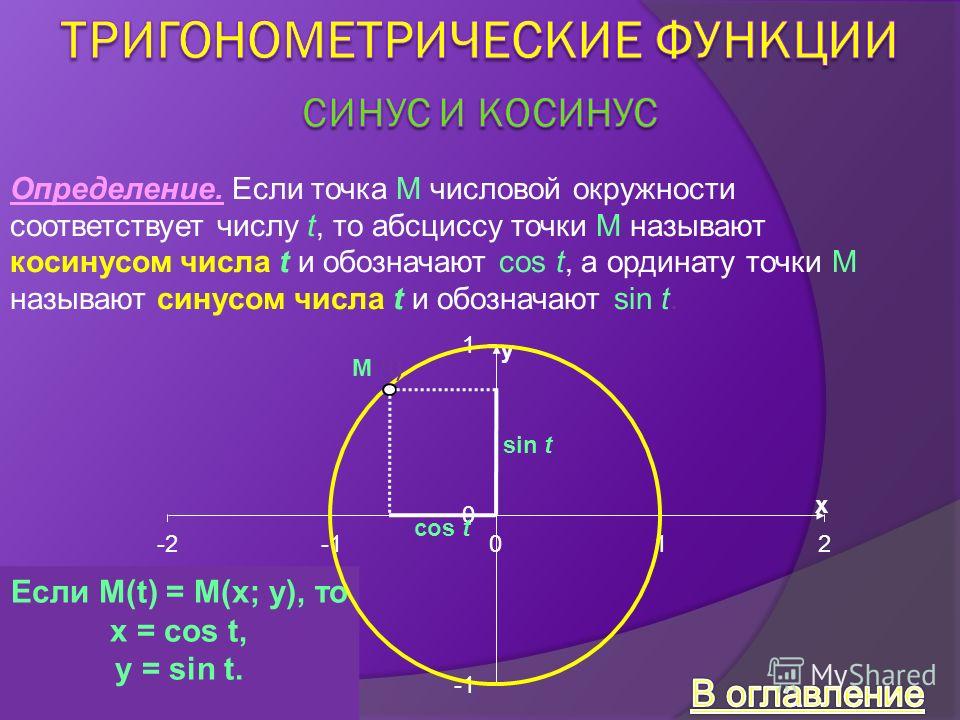 Значения sin x перечислены ниже в тригонометрической таблице:
Значения sin x перечислены ниже в тригонометрической таблице:
| Синус Градусы | Синус Радианы | Значение функции синуса (sin x) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| sin 0° | грех 0 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sin 30° | грех π/6 | 1/2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sin 45° | грех π/4 | 1/√2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sin 60° | грех π/3 | √3/2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sin 90° | грех π/2 | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sin 120° | грех 2π/3 | √3/2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sin 150° | грех 5π/6 | 1/2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sin 180° | грех π | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sin 270° | грех 3π/2 | -1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sin 360° | грех 2π | 0 9{2n+1}}{(2n+1)!}\) Синусоидальные тождестваВ тригонометрии есть несколько тождеств, связанных с функцией синуса. Эти тождества очень полезны при решении различных математических задач. Некоторые из них перечислены ниже:
☛ Связанные темы:
Важные примечания о функции синуса:
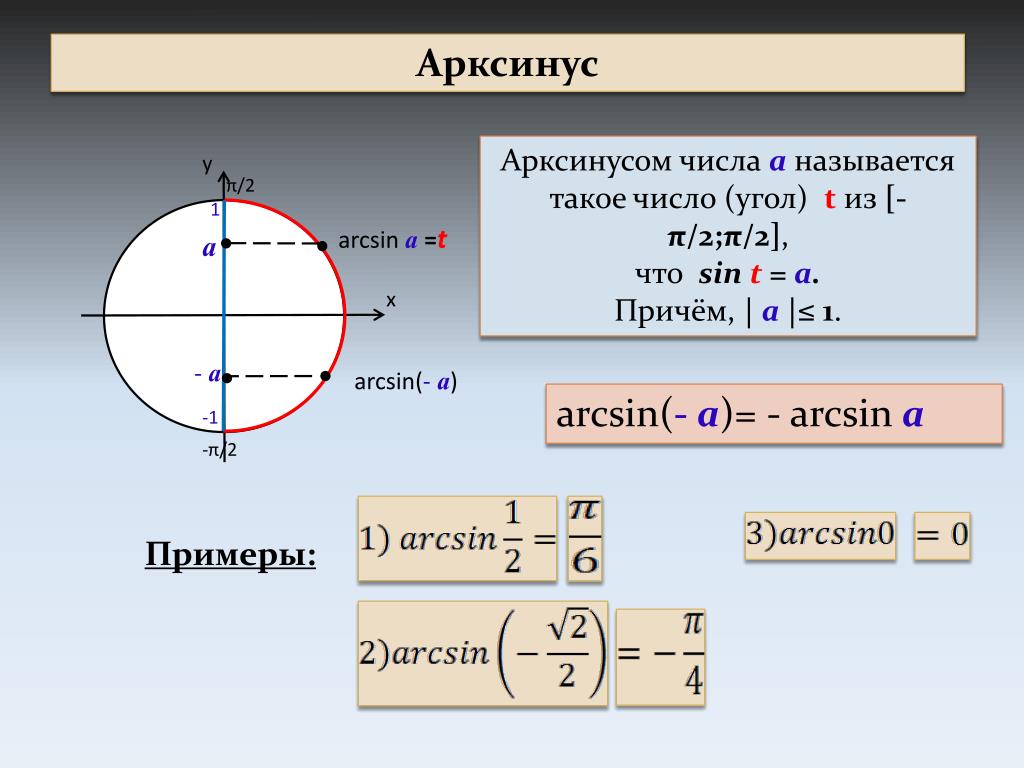
Часто задаваемые вопросы о синусоидальной функцииЧто такое синус в тригонометрии?синус угла является тригонометрической функцией, также известной как функция синуса. Отношение длин стороны, противоположной углу, и гипотенузы прямоугольного треугольника называется синусоидальной функцией, которая изменяется при изменении угла, и обозначается как sin x, где x — острый угол между основанием и гипотенуза. Как найти период синуса?Чтобы найти период синусоидальной функции f(x) = Asin Bx + C, мы используем формулу Period = 2π/|B|. Для синусоидальной функции f(x) = sin x мы имеем A = 1, B = 1, C = 0. Мы подставляем это значение B в формулу, чтобы найти период синусоидальной функции. Следовательно, период sin x определяется выражением Period = 2π/|1| = 2π. Что такое диапазон функции синуса? Диапазон функции синуса составляет [-1, 1], так как график sin x колеблется только между -1 и 1. Как найти амплитуду синуса?Амплитуда синусоидальной функции f(x) = Asin Bx + C определяется значением A. Для f(x) = sin x имеем A = 1, B = 1 , C = 0. Следовательно, амплитуда синусоидальной функции sin x равна 1. Является ли синусоидальная функция биективной?Синус Функция, определенная для всех действительных чисел, не является биективной. Однако, если мы ограничим область определения sin x значением [-π/2, π/2] и переопределим функцию как f(x) = sin x, f: [-π/2, π/2] → [-1 , 1], то функция синуса становится биективной. Что такое арксинус?Функция, обратная синусу, задается как sin -1 x = arcsin x, где x лежит в [-1, 1]. Функция, обратная синусу, читается как «арксинус x» или «синус, обратный x». Что такое формула функции синуса? Формула функции синуса задается как sin x = Противоположная сторона/Гипотенуза = Перпендикуляр/Гипотенуза. Эта формула помогает определить значение функции синуса sin x, которое можно определить, используя длины сторон треугольника или угол x. Синус непрерывен?Синусоидальная диаграмма является непрерывной, так как на ней нет разрывов или пробелов, и ее можно рисовать, не отрывая пера. Кроме того, синусоидальная функция определена для всех действительных чисел, поэтому график не прерывается и его можно рисовать непрерывно. Отсюда можно сделать вывод, что функция синуса непрерывна. Что такое период синуса?Период функции синуса равен 2π, так как значения sin x повторяются через каждые 2π радиан. Это также можно увидеть на графике синусоидальной функции, поскольку значения sin x колеблются между -1 и 1 и повторяются через каждые 2π радиан. Следовательно, период синусоидальной функции равен 2π. Функция синуса четная или нечетная?Функция синуса является нечетной функцией, она удовлетворяет определению нечетной функции, то есть f(-x) = -f(x) для всех x. Имеем f(-x) = sin(-x) = -sinx = -f(x). Следовательно, sin x — нечетная функция. Каково значение синуса? Значение синуса изменяется при изменении угла между основанием и гипотенузой прямоугольного треугольника. 9.1 Свойства синуса и косинуса9.1 Свойства синуса и косинусаСледующий: 9.2 Расчет Up: 9. Тригонометрические функции Предыдущий: 9. Тригонометрические функции   Индекс 9.1 Определение () Мы определяем функцию следующим образом. Если , то точка на единичной окружности такая, что длина из дуга, соединяющаяся с (измеряется против часовой стрелки) является равно . (Есть оптическая иллюзия на рисунке. Длина отрезка равна длине дуга.) Таким образом, чтобы найти , вы должны начать с и двигаться дальше
в
двигайтесь по кругу против часовой стрелки, пока не пройдете расстояние.
где – отражение относительно горизонтальной оси. Таким образом, если , то является в точка, полученная путем старта и движения по единичной окружности в в по часовой стрелке. Замечание . Определение зависит от нескольких идей, которых у нас нет.
определенный
или заявленные предположения о, например, длине дуги и против часовой стрелки
направление . Я считаю, что объем работы, необходимый для формализации этих
идеи в этом
точка не стоит усилий, так что я надеюсь, что ваша геометрическая интуиция поможет
ты
через эту главу. (В этой главе мы будем допускать довольно много
евклидовой геометрии и некоторые свойства площади, которые
не следуют из наших предположений, изложенных в главе 5. Более автономное рассмотрение тригонометрических функций можно найти в [44, глава 15], но трактовка, данная используются идеи, которые мы рассмотрим позже (например, производные, обратные функции, теорема о промежуточном значении и основная теорема исчисления) чтобы определить тригонометрические функции. У нас есть следующие значения для:
В целом
9,9 Определение (Синус и косинус.) В координатах пишем (Мы читаем «» как « косинус от ‘, а «’ читаем как « синус «.) Так как находится на единичной окружности, мы имеем а также Уравнения (9.3) — (9.8) показывают, что а также В уравнении (9.2) мы определили Таким образом, для , и отсюда следует, что С точки зрения компонентов и следовательно 903:00 Пусть — произвольные действительные числа. 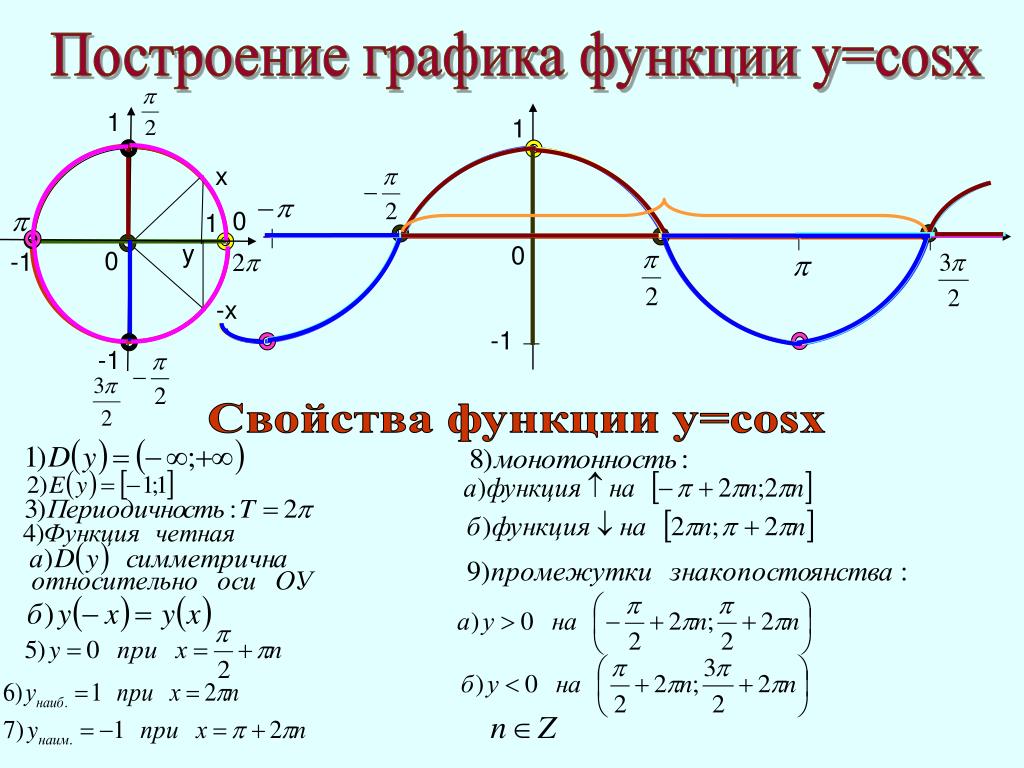 Тогда существуют целые числа и
такой, что а также
. Позволять Тогда существуют целые числа и
такой, что а также
. Позволять затем , так Предполагать (см. рисунок). Тогда длина дуги, соединяющей это что то же самое, что и длина дуга, соединяющаяся с . Поскольку равные дуги в окружность равные хорды, мы имеем и, следовательно
Вы можете убедиться, что это же соотношение выполняется, когда . 9.11 Теорема (Законы сложения для синуса и косинуса.) Для всех действительных чисел и ,
то есть, Следовательно Раскладывая квадраты и используя тот факт, что за все , мы заключаем, что
Это уравнение (9.13). Чтобы получить уравнение (9.12), замените на в (9.16). Если мы возьмем в уравнении (9.16) мы получить или же Если мы заменим на в этом уравнении получаем Теперь в уравнении (9.  16) заменить на
и получить 16) заменить на
и получить или же которое представляет собой уравнение (9.14). Наконец, замените на в этом последнем уравнение к получить (9.15). В процессе доказательства последней теоремы мы доказали следующее: 9.17 Теорема (Закон отражения для sin и cos.) Для всех ,
9.19 Теорема (Формулы двойного угла и половинного угла.) Для всех у нас есть 9,20 Упражнение. А Докажите четыре формулы теоремы 9.19. 9.21 Теорема (Произведения и разности sin и cos.) Для всех в ,
а также Складывая эти уравнения, получаем (9.22). Вычитая первое из второй, получаем (9.24). В уравнении (9.24) заменить на
и заменить на получить или же Это дает уравнение (9.  25). 25).9,27 Упражнение. Докажите уравнения (9.23) и (9.26). Из геометрического описания синуса и косинуса следует, что как увеличивается для , увеличивается от до и уменьшается от до . Тождествауказывают на то, что отражение относительно вертикальной линии через несет график sin на график cos и наоборот. Состояние указывает на то, что отражение о вертикальная ось несет график на себя. Отношение показывает, что т. е. граф переносится на себя поворотом на о происхождении. У нас есть а также , так а также (примерно). Имея эту информацию, мы можем сделать разумный набросок графика а также (см. рисунок выше) 9,28 Упражнение. Показать, что 9,29 Упражнение. А Заполните следующую таблицу синусов и косинусов: Большая часть материала из этого раздела обсуждался Клавдием Птолемеем (фл. 127-151 ОБЪЯВЛЕНИЕ). Функциями, рассматриваемыми Птолемеем, были не синус и косинус, а хорда , где хорда дуги — это длина отрезка, соединяющего это конечные точки.
Аккорды Птолемея являются функциями дуг (измеряемых в градусах), а не чисел. Птолемея закон сложения для was (грубо) где диаметр окружности, а Птолемей составил таблицы, эквивалентные таблицам для в интервалах . Все расчеты производились с точностью до 3-х шестидесятеричных (базовых) знаков. Этимология слова синус такова.
довольно любопытно[42, с. 615-616].
Функция, которую мы называем синусом, была первой
имя, данное Арьябхатой в начале шестого века нашей эры.
Название означало «половина аккорда». 9,31 Развлечения (Вычисление синусов.) Разработайте компьютерную программу, которая будет принимать введите а число между и , и рассчитает . (Я выбираю вместо того чтобы делать а не нужно знать значение сделать это.) Следующий: 9.2 Расчет Up: 9. Тригонометрические функции Предыдущий: 9. Тригонометрические функции Индекс Рэй Майер 2007-09-07 Свойства синуса и косинуса « Неизвиняющийся математик Блейз получил большую часть классических свойств синуса и косинуса в комментариях к последнему сообщению, так что я буду щедро копировать из его работы. Сначала рассмотрим функцию . Мы можем взять ее производную, используя правила для производных тригонометрических функций прошлого времени: Итак, эта функция является константой. Мы это легко проверяем, и так далее. Что это значит? Это говорит нам, что если и длины катетов прямоугольного треугольника, гипотенуза будет иметь длину . С другой стороны, точка с координатами в стандартной координатной плоскости будет лежать на единичной окружности. Мы еще не говорили об использовании интегрирования для вычисления длины пути на плоскости, но когда мы это сделаем, мы увидим, что длина дуги на окружности от до точно равна . Это дает нам другое определение функций синуса и косинуса — более близкое к обычному, которое люди видят в классе тригонометрии. Теперь, поскольку и оба неотрицательны, каждый из них должен быть ограничен сверху . Таким образом и . Точнее, в любое время, когда мы должны иметь . Мы знаем, что и , поэтому, если у нас когда-либо будет другая точка, где и у нас есть точка. Это связано с тем, что дифференциальное уравнение будет определять будущее поведение точно так же, как оно определяло поведение . На самом деле, если и , то будущее поведение будет точно отрицательным по отношению к поведению , и так со временем снова и снова. Признаться, я тут как бы размахиваю руками без доказательства существования/единственности решения дифференциальных уравнений. Итак, есть ли у синуса положительный нуль? То есть есть такие, что ? Если да, то наименьшее из таких должно быть (потому что положительные числа рядом имеют положительные синусы). Затем следующий будет с , и все повторится с точкой . Функция сначала возрастает, а затем уменьшается (поскольку . Если имеет максимум, то (ее производная) должна пересечь ноль. Затем она убывает, и она не может снова возрастать, пока снова не пересечет ноль. Но если снова пересечет ноль, она должна иметь прошел через локальный экстремум (Ролле) и, таким образом, не может снова возрастать до того, как сам пересечет нуль. уменьшится до некоторой асимптоты ниже Но для того, чтобы функция имела асимптоту, она должна приближаться к горизонтальная линия , а ее производная должна приближаться к . Но если приближается к асимптоте, то его производная также должна асимптотически приближаться к . Но эта производная есть то, что мы предполагаем приближается! Итак, ни одна из этих асимптот невозможна! Итак, функция синуса должна иметь положительный нуль: . Таким образом, синус и косинус (и все другие решения этого дифференциального уравнения) будут иметь период . Наконец, что это за значение? На самом деле, мы не можем сказать . Но это может пригодиться, поэтому мы определим этот номер и дадим ему новое имя: . Всякий раз, когда мы говорим, мы имеем в виду «первый положительный нуль синусоидальной функции». Здесь я хочу отметить, что несколько месяцев назад я оправдал свою похвальбу в другом блоге. В своих неустанных разглагольствованиях против -фетишизма, заполонившего гик-сообщество, я сказал кому-то, что в конечном счете его можно вывести исключительно из свойств реальной системы счисления. Нравится:Нравится Загрузка… 14 октября 2008 г. — Автор: Джон Армстронг | Анализ, Исчисление Базисные свойства p, q-синусоидальных функций
Proc Math Phys Eng Sci. doi: 10.1098/rspa.2014.0642 Информация об авторе Примечания к статье Информация об авторских правах и лицензиях Отказ от ответственности
Мы улучшаем известные в настоящее время пороги базисности семейства периодически расширенных p , q -синусоидальных функций. Наши результаты основаны на разложении Берлинга соответствующей замены координат в терминах операторов сдвига бесконечной кратности. Мы также определяем уточненные оценки константы Рисса, связанной с этим семейством. Эти результаты заполняют математические пробелы в существующей литературе по этому вопросу. Ключевые слова: базис Рисса, базис Шаудера, обобщенные тригонометрические функции Пусть p , q >1. Пусть F p , q :[0,1]→[0, π p , q /2] — интеграл Fp,q(y)=∫0ydx(1−xq)1/p, где π p , q = 2 F p , q (1). sinp,q(x)=Fp,q−1(x)для всех x∈[0,πp,q2] продлен до ℝ по правилам sinp,q(−x)=−sinp,q(x)andsinp,q(πp,q2−x)=sinp,q(πp,q2+x), которые делают их периодическими, непрерывными, нечетными относительно 0 и четными относительно π р , q /2. Это естественные обобщения функции синуса, действительно, sin 2,2 ( x ) = sin( x ) и π 2,2 = π , известно, что они обладают рядом замечательных свойств со своими классическими аналогами [1,2]. Среди этих свойств лежит фундаментальный вопрос о полноте и линейной независимости семейства S={sn}n=1∞, где s n ( x ) = sin p , q ( π p , q n x ). Положим en(x)=2sin(nπx), так что {en}n=1∞ является базисом Шаудера банахова пространства ,1) для всех r >1. The family 𝒮 is also a Schauder basis of L r if and only if the corresponding change of coordinates map , A : e n ↦ s n , продолжается до линейного гомеоморфизма 91(j)ejn=(∑j=1∞ajMj)en, так что замена координат принимает вид А=∑j=1∞ajMj. 1.1 Известно, что понятия «близости» между базисами банаховых пространств играют фундаментальную роль в классическом математическом анализе [11], с. На самом деле можно вызвать более элементарные методы, чтобы проверить обратимость изменения карты координат. Из (1.1) следует, что ∑j=3∞|aj|<|a1|⇒{A,A−1∈B(Lr)∥A∥ ∥A−1∥≤∑j=1∞|aj||a1|−∑j= 3∞|а|. 1,2 В Binding и др. [5] утверждалось, что левая часть (1.2) верна для всех сегмент (1,1211). Следовательно, 𝒮 будет базисом Шаудера всякий раз, когда p = q ∈ ( p 1 , ∞). О дальнейших разработках в этом отношении недавно сообщили Бушелл и Эдмундс [4]. Эти авторы ловко устранили пробел, первоначально опубликованный в [5, лемма 5], и заметили, что, поскольку левая часть (1. а1=∑j=3∞aj, 1,3 аргумент сломается для p = q рядом с p 2 ≈1,043989. Поэтому вопрос базисности для 𝒮 в режиме 9 следует решать разными способами.0402 p , q →1. Совсем недавно Edmunds et al. [3] использовал (1.2), чтобы показать обратимость A для общих пар ( p , q ), пока πp,q<16π2−8. 1,4 Поскольку (1.4) гарантируется всякий раз, когда pq(p−1)<4π2−8, 1,5 это позволяет q → 1 для p > 4/(12− π 2 ). Однако обратите внимание, что прямая замена p = q в (1.5) приводит только к субоптимальному условию p > π 2 /4−1≈1,467401. В §2 показано, что семейство 𝒮 является ω — линейно независимым для всех p , q >1, см. ∑j=3∞|aj|=a1, см. теорему 5.1, а также следствие 6.2. Для этого в § 4 мы находим еще два критерия, обобщающих (1.2) в условиях гильбертова пространства, см. следствия 4.3 и 4.4. В этом случае постоянная Рисса , r (𝒮) = ∥ А ∥ ∥ А −1 ∥ , 5характеризует, как 𝒮 отклоняется от ортонормированного базиса. Эти новые утверждения дают верхние оценки для r (𝒮), которые улучшают оценки, полученные из правой части (1.2), даже когда последняя применима. Формулировка представленных ниже альтернатив (1.2) в решающей степени зависит от работы, развитой в §3. Из леммы 3.1 вычисляем явно разложение Вольда изометрий M j : они оказываются сдвигами бесконечной кратности. Раздел 6 касается конкретных деталей случая равных индексов p = q и включает результаты как для общего случая r >1, так и для частного случая r =2. Довольно любопытно, что мы обнаружили еще один пробел, который делает доказательство обратимости 9 неполным.0402 A for p 1 < p <2 первоначально опубликовано в [5]. См. примечание 6.3. Более того, применение Бушелла и Эдмундса [4], теорема 4.5, достигает порога базисности 90 402 90 403 при p~1≈1,198236>1211, где p~1 определяется тождеством πp~1,p~1=2π2π2−8. 1,6 См. также [2], примечание 2.1. В теореме 6.5 мы показываем, что 𝒮 действительно является базисом Шаудера L r для p=q∈(p3,65), где p3≈1,087063<1211, см. [14], задача 1. Так как 65 >p~1, базисность теперь гарантируется для всех p = q > p 3 (). Открыть в отдельном окне Связь между различными утверждениями этой статьи с утверждениями ссылок [4,5], для случая p = q . Положения p 1 , p~2 и значение ε заданы только для иллюстрации, так как мы уверены только в том, что p2 В §7 мы сообщаем о наших текущих знаниях о различных порогах обратимости карты изменения координат как в случае равных индексов, так и в других случаях. На основе новых критериев, найденных в § 4, мы формулируем общий признак обратимости для A , который поддается аналитическому и численному исследованию. Все числовые величины, приведенные в этом документе, точны до последней цифры, которая округляется до ближайшего целого числа. В онлайн-версию этой рукописи, 1 , мы включили полностью воспроизводимые компьютерные коды, которые можно использовать для проверки представленных расчетов. Семейство {s~n}n=1∞ в банаховом пространстве называется ω -линейно независимым [12], с. 50, если ∑n=1∞fns~n=0 ⇒ fn=0 для всех n. Следовательно, 𝒮 является базисом Рисса L 2 тогда и только тогда, когда A ∈ ℬ( L 2 ) и RanA = L 2 . Фундаментальное разложение A , данное в (1.1), позволяет выделить подходящие компоненты, образованные операторами Теплица скалярного типа [15]. Чтобы идентифицировать эти компоненты, начнем с определения разложения Вольда изометрий М j , [15,16]. См. примечание 3.4. Пусть 𝔻 = {| з | < 1}. Пространства Харди функций из 𝔻 со значениями в банаховом пространстве 𝒞 обозначаются ниже как H γ (𝔻; 𝒞). Позволять б~(г)=∑k=0∞bkzk — голоморфная функция на D¯ и зафиксируйте j ∈ ℕ∖{1}. Позволять B~∈H∞(D;B(L0j)) определяется формулой B~(z)=b~(z)I. Пусть соответствующий оператор Теплица [15], (5-1) T(B~)∈B(h3(D;L0j)) задается формулой T(B~):f(z)↦B~(z)f(z). Позволять B=∑k=0∞bkMjk:L2⟶L2. 3. В силу леммы 3.1 (см. [15], §3.2 и 5.2) существует обратимая изометрия U:L2⟶h3(D;L0j) такой, что UB=T(B~)U. Ниже мы пишем M(b~)=maxz∈D¯|b~(z)|и m(b~)=minz∈D¯|b~(z)|. Доказательство (1.2) можно получить, применив следствие 3.3, предполагая, что Б = а 1 М 1 = a 1 I . Наша следующая цель — сформулировать конкретное достаточное условие обратимости A и соответствующие оценки на r (𝒮), улучшающие (1.2), когда r = 2. Для этой цели мы применяем следствие 3.3, предполагая, что B теперь имеет трехчленное разложение B = a 1 M 1 + a 3 M 3 + a 9 M 9 . Пусть T = { β < 1, β − α + 1 > 0, β + α + 1 > 0}. Позволять R1={|α(β+1)|<|4β|}∩{β>0}R3={|α(β+1)|<|4β|}∩{β<0}R2={| α(β+1)|≥|4β|}=R2∖(R1∪R3). Видеть . Открыть в отдельном окне Оптимальная область обратимости в лемме 4.1. Горизонтальная ось равна α и вертикальная ось β . Потому что SIN P , Q ( x )> 0 для всех x ∈ (0, π P , Следствия 4.3 и 4.4 являются следствием следствия 3.3 и леммы 4.1 и относятся к основным результатам этой статьи. Потому что а 1 >0, (4.1) заменяет (1.2) только тогда, когда пара ( p , q ) такова, что a 9 >0. Из этого следствия ниже мы видим, что замена координат обратима в окрестности порога, заданного условием (1.3). См. предложение 7.1 и и ]. Открыть в отдельном окне ( a – e ) Различные отношения и границы между областями ( p , q )-плоскость, где применимы теоремы 5.2(a) и (b), а также предложение 7.1 (с разными значениями k ). На всех графиках p соответствует горизонтальной оси, q — вертикальной оси, а пунктирная линия показывает p = q . (Онлайн-версия в цвете.) Далее мы видим, что следствие 4.3 немного полезнее, чем следствие 4.4, в контексте расширенных p , q -синусоидальных функций. Конечно, естественно спросить, какие следствия можно вывести из другого утверждения леммы 4.1. За (a3a1,a9a1)∈R3∩T, имеем ∥ B −1 ∥ −1 = a 1 −| а 3 |−| и 9 |. Следовательно, то же рассуждение, что и в доказательствах следствий 4.3 и 4.4, сводится к (1.2), и в этом случае улучшения нет. Наша первая цель в этом разделе — установить, что отображение замены координат, связанное с семейством 𝒮, обратимо вне области применимости (1.2). Мы начнем с напоминания о вычислении, которое было выполнено при доказательстве [3, предложение 4.1] и которое будет использовано несколько раз ниже. Пусть a ( t ) — функция, обратная sinp,q′(πp,qt). Затем, aj(p,q)=−22πp,qj2π2∫01sin(jππp,qa(t))dt. 5.1 Действительно, дважды проинтегрировав по частям и заменив переменную интегрирования на t=sinp,q′(πp,qx) урожаи aj(p,q)=2∫01sinp,q(πp,qx)sin(jπx) dx=22∫01/2sinp,q(πp,qx)sin(jπx) dx=22πp,qjπ ∫01/2sinp,q′(πp,qx)cos(jπx) dx=−22πp,qj2π2∫01/2[sinp,q′(πp,qx)]′sin(jπx) dx=−22πp ,qj2π2∫01sin(jππp,qa(t))dt. Теперь рассмотрим другие дальнейшие следствия следствий 4.3 и 4.4. Мы восстанавливаем [3], следствие 4.3 из части (a) этой теоремы, заметив, что для всех p , q >1, a1≥22∫01/22xsin(πx) dx=42π2. На самом деле, для ( p , q )∈(1,2) 2 лучшая оценка a1≥22∫01sin2(πx) dx=22, обеспечивает обратимость A для всех r >1 всякий раз, когда πp,q<2π2π2−8. 5,8 Смотрите и . Открыть в отдельном окне Область ( p , q )-плоскости, где применяется теорема 5.2(c). Даже когда мы знаем, что A обратимо в этой области вследствие теоремы 5.2(a), верхняя граница константы Рисса, обеспечиваемая (4.2), улучшает оценку, обеспечиваемую (1.2) (случай r = 2) . На этом графике p соответствует горизонтальной оси, а q относительно вертикальной оси, а пунктирная линия показывает p = q . Теперь рассмотрим более подробно частный случай p = q <2. Наш анализ требует установки различных точных верхних и нижних границ коэффициентов a j ( p , p ) для j =1,3,5,7,9. Это наша первая цель. Доказательство. —Все указанные границы определяются путем интегрирования подходящей аппроксимации sin p , p ( π p , p x ). Для каждого из них требуется свой набор точек квадратуры, но общая структура аргументов во всех случаях одинакова. Без дальнейшего упоминания в дальнейшем мы неоднократно используем тот факт, что в терминах гипергеометрических функций sinp,q−1(y)=∫0ydx(1−xq)1/p=y 2F 1(1p,1q;1q+1;yq)∀ y∈[0,1]. Связанный (а). Позволять {xj}j=03={0,16,13,12}и{yj}j=03={0,34,32,1}. Пусть ℓj(x)=yj+1−yjxj+1−xj(x−xj)+yj для j=0,1andℓ2(x)=1 (). sin4/3,4/3−1(y1)=(34) 2F 1(34,34;74;(34)4/3)<105100<110100<π24=π4/3,4/36 и sin p , p ( t ) является возрастающей функцией t ∈(0, π p , p , p09:00/2), затем sin 4/3,4/3 ( π 4/3,4/3 x 1 ) > y 1 . Открыть в отдельном окне Аппроксимации ℓ j ( x ) используются для демонстрации границы (a) в лемме 6.1. Для справки, мы также показываем SIN P 6 , P 6 ( π P 6 , P 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 903 Согласно Бушеллу и Эдмундсу [4], следствие 4.4, 2 sin p , p ( π p , p x ) увеличивается при любом фиксированном p | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

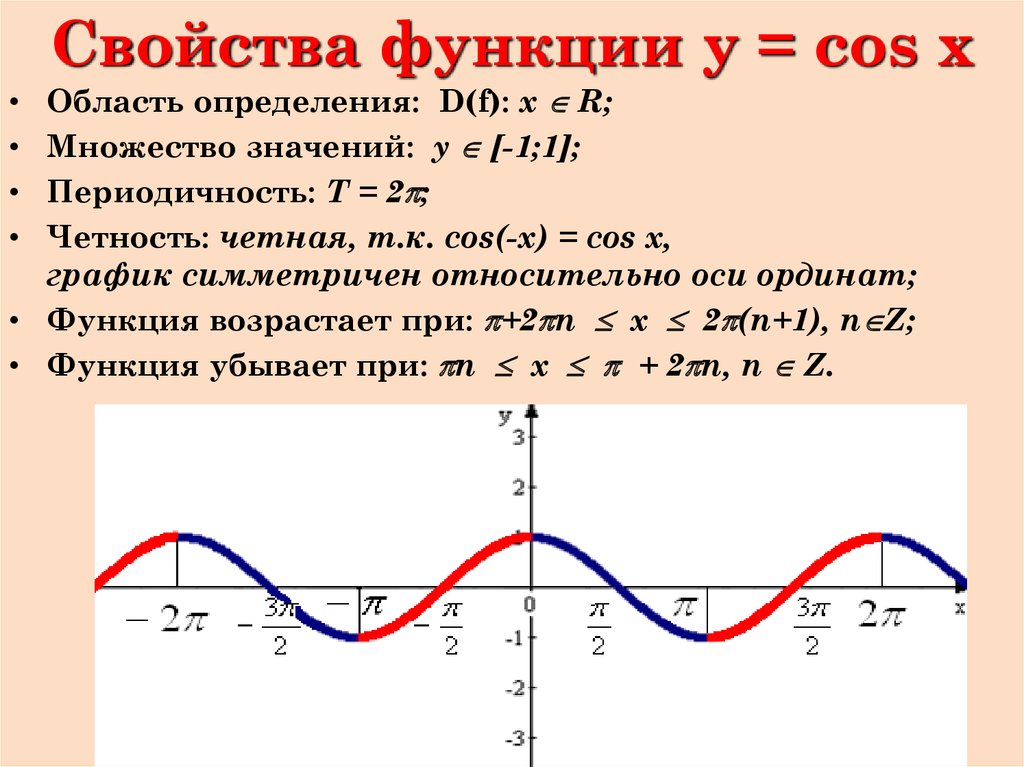
 для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.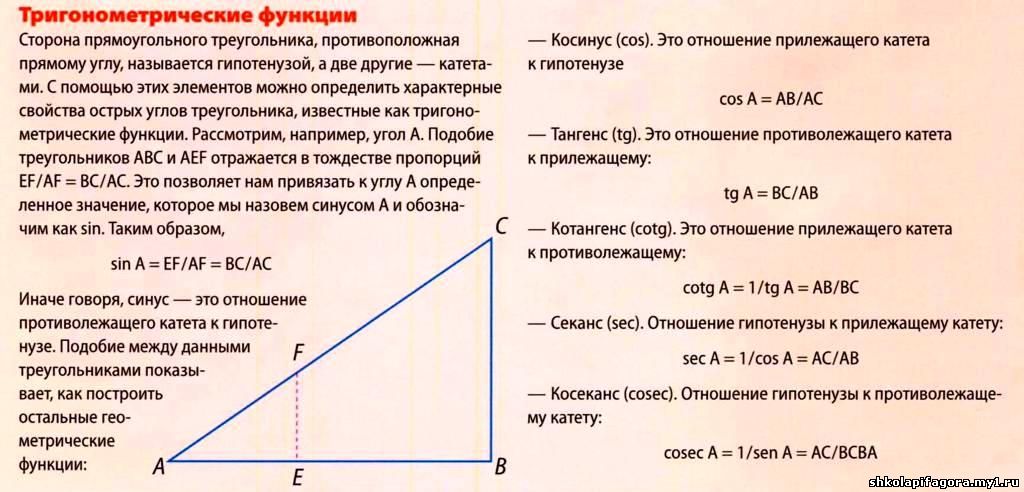




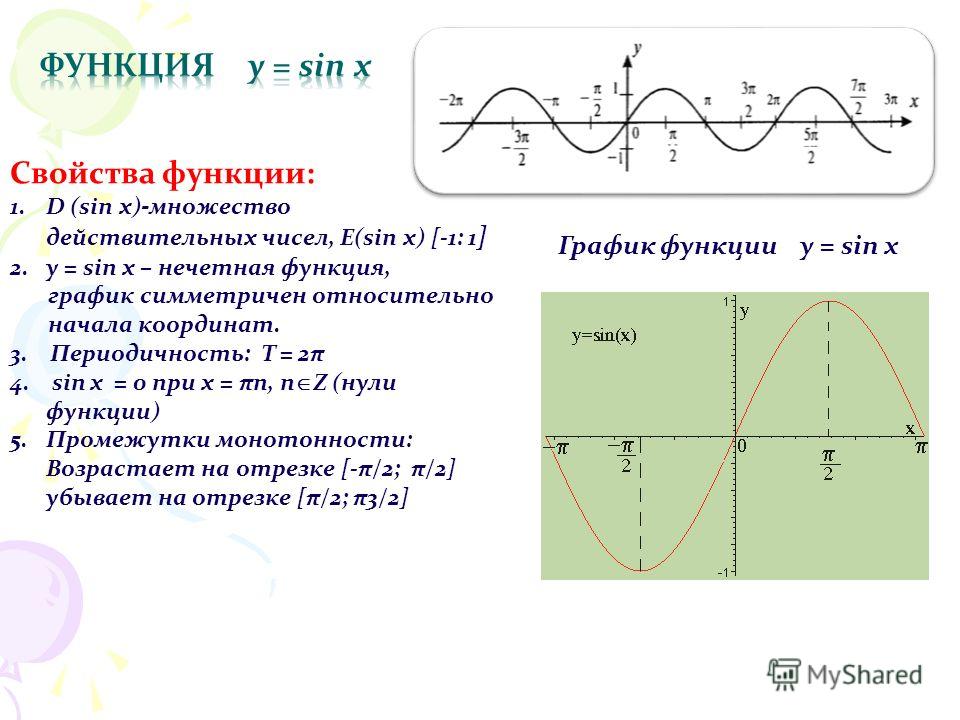
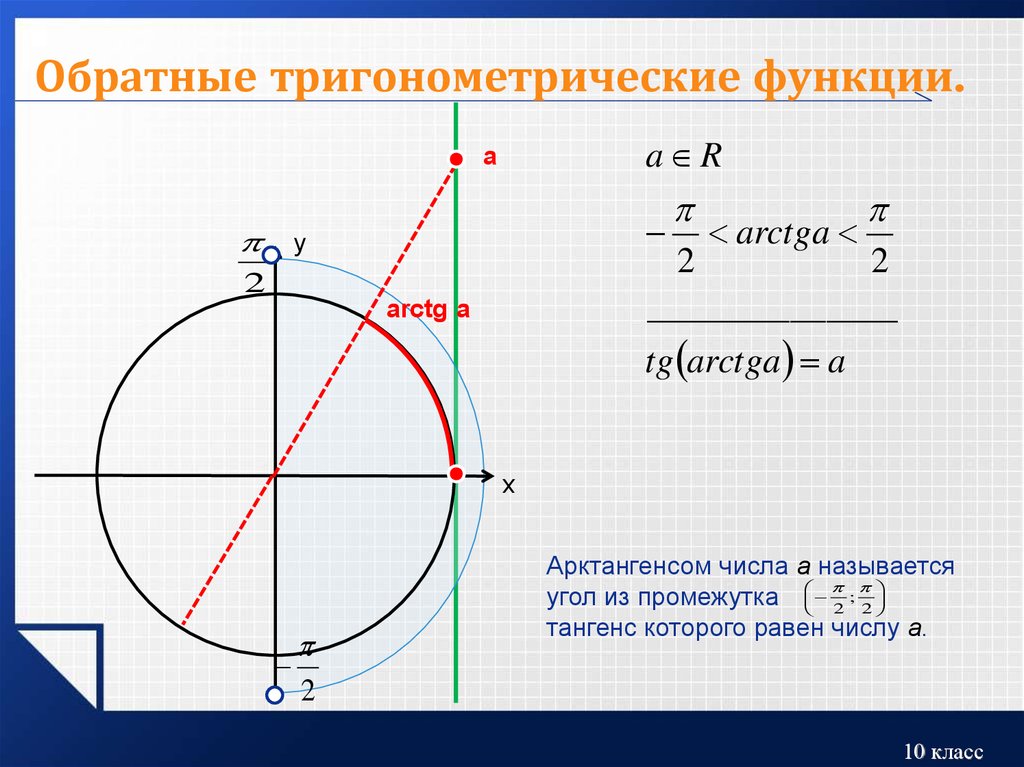 Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.
Наличие угла в 90 градусов дает возможность осуществлять различные операции, позволяющие по двум сторонам и одному углу либо по двум углам и одной стороне определять значения всех параметров рассматриваемой фигуры. В прошлом люди заметили эту закономерность и стали активно ею пользоваться при строительстве зданий, навигации, в астрономии и даже в искусстве.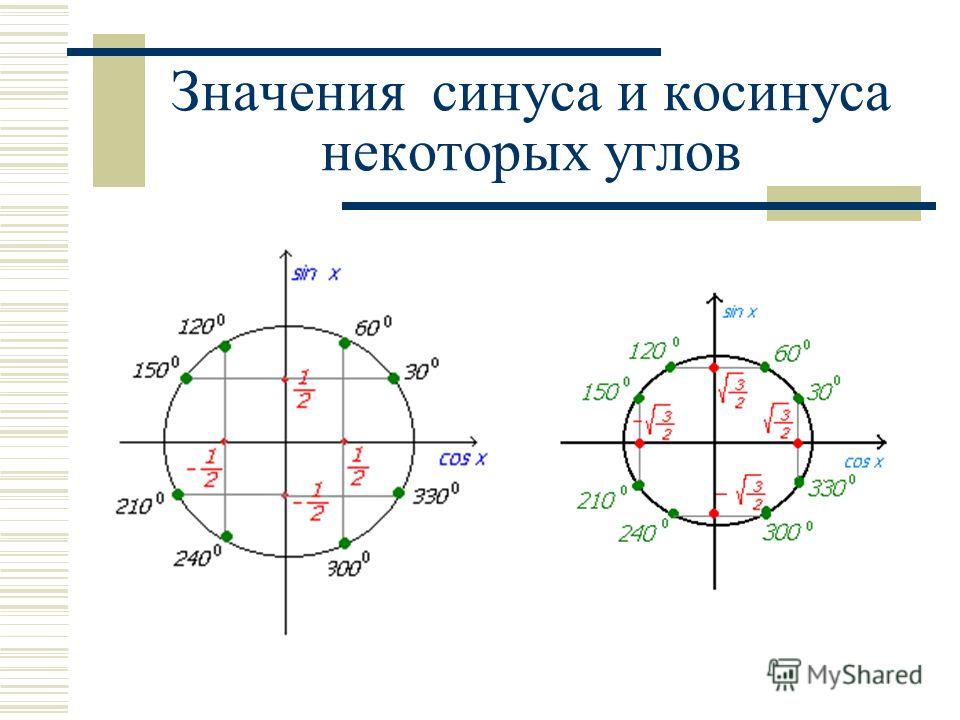 Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной».
Данный раздел не изучается в школе, однако знать о его существовании необходимо как минимум потому, что земная поверхность, да и поверхность любой другой планеты, является выпуклой, а значит, любая разметка поверхности будет в трёхмерном пространстве «дугообразной». Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.
Она является самой длинной. Мы помним, что по теореме Пифагора её численное значение равно корню из суммы квадратов двух других сторон.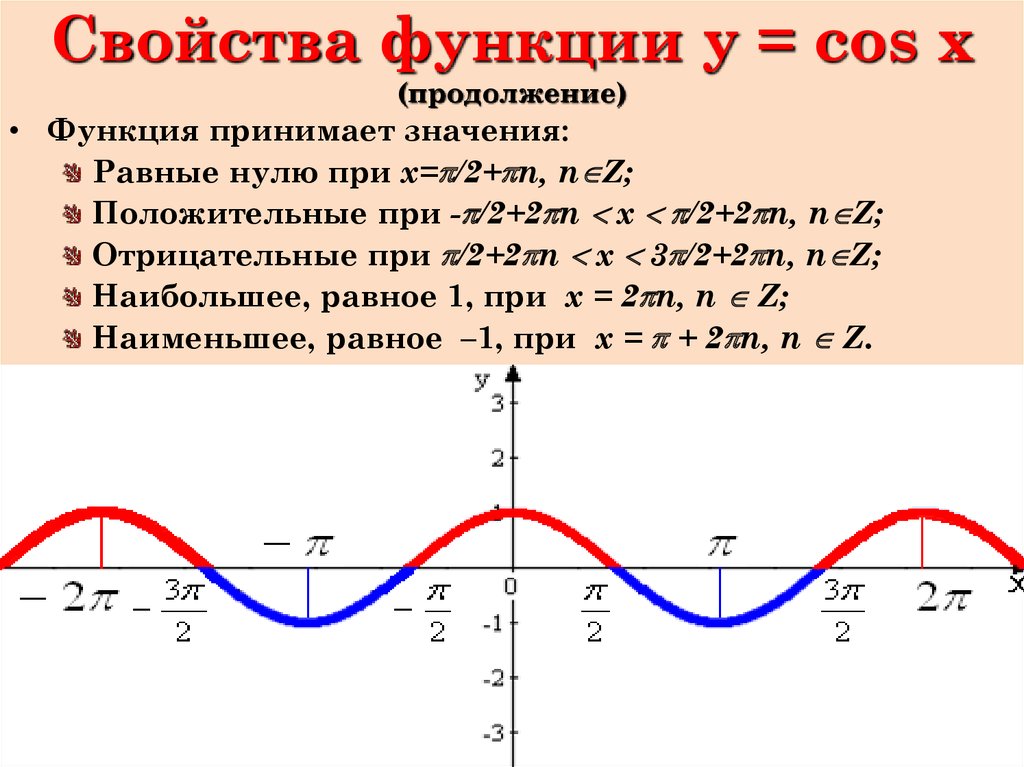 Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.
Таким образом, если у вас в ответе к задаче получился синус или косинус со значением, большим, чем 1, ищите ошибку в расчётах или рассуждениях. Этот ответ однозначно неверен.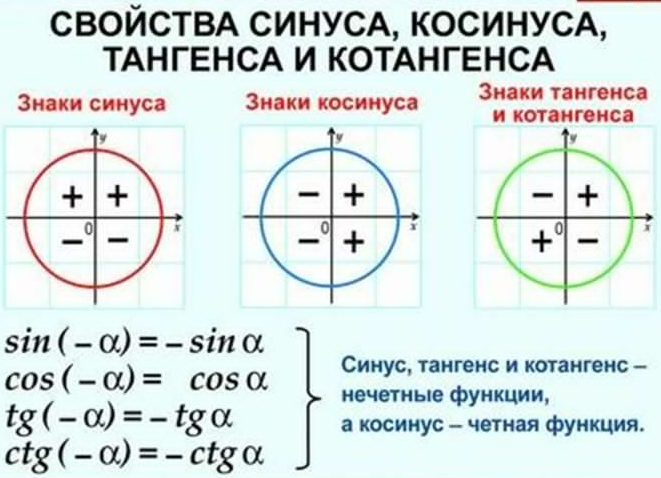 Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.
Данная формула является прямым следствием теоремы Пифагора, однако позволяет сэкономить время, если требуется узнать величину угла, а не стороны.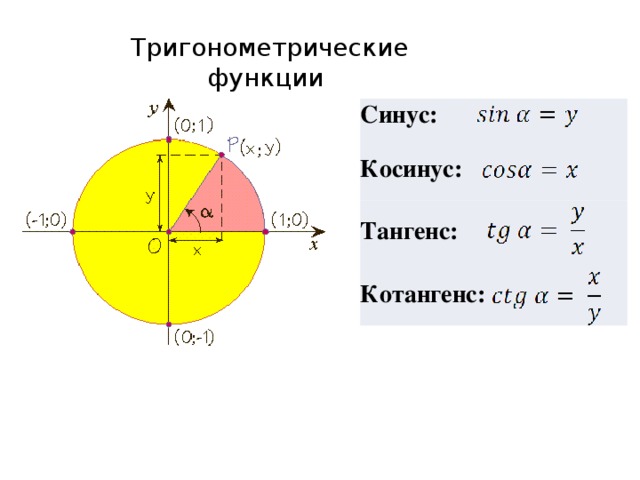
 Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов.
Оказывается, из суммы квадратов двух сторон вычесть их произведение, умноженное на двойной косинус смежного им угла — полученное значение окажется равно квадрату третьей стороны. Таким образом, теорема Пифагора оказывается частным случаем теоремы косинусов. То же касается округлений «некрасивых» чисел.
То же касается округлений «некрасивых» чисел. Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.
Без них нельзя построить здание, спроектировать автомобиль, рассчитать нагрузку на поверхность или траекторию движения предмета. И это только самые очевидные примеры! Ведь тригонометрия в том или ином виде используется повсюду, начиная от музыки и заканчивая медициной.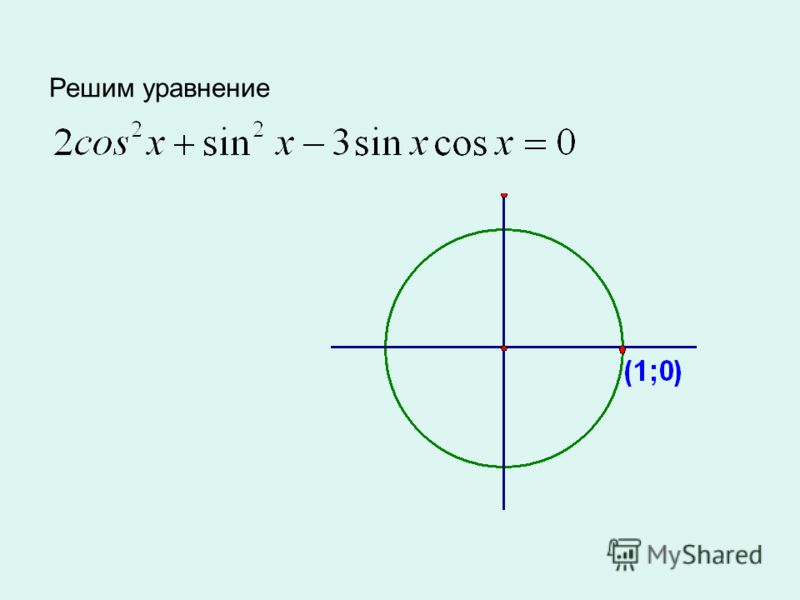
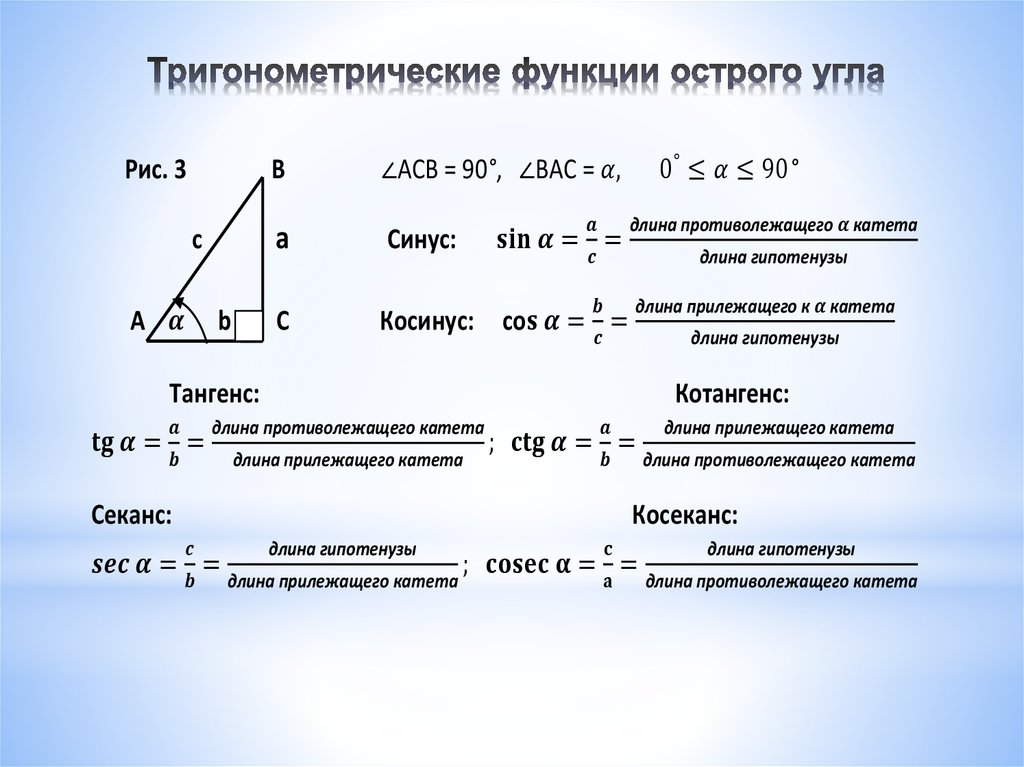
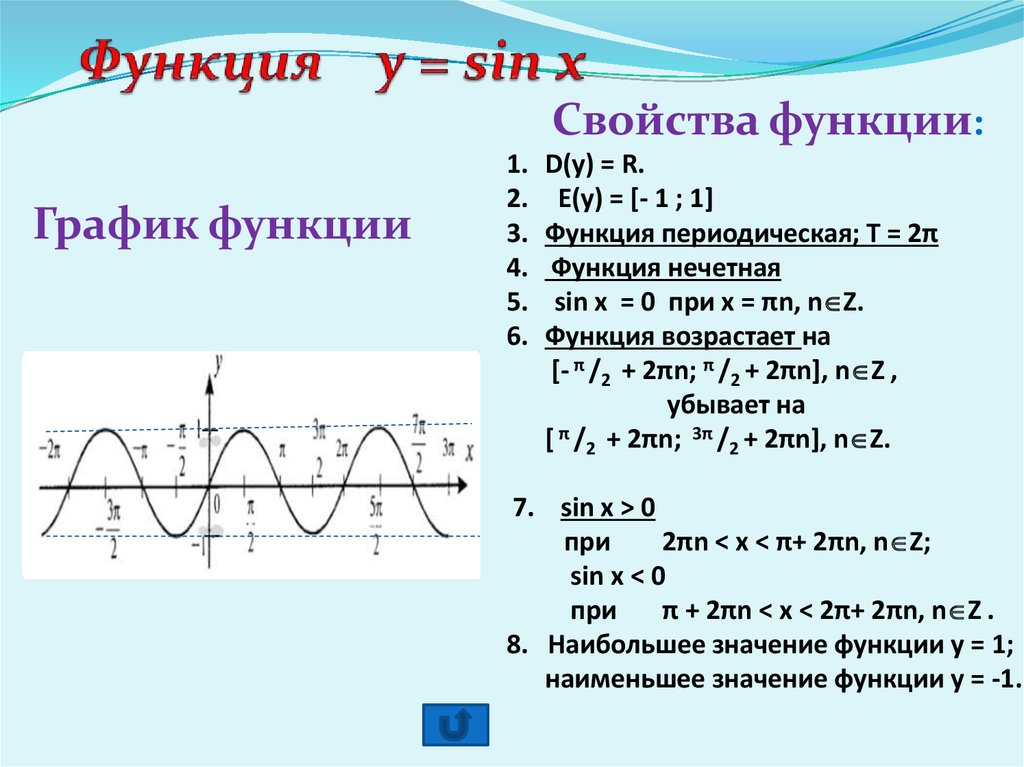 Представим единичную окружность с центром в начале декартовой системы координат.
Представим единичную окружность с центром в начале декартовой системы координат. В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
 cos t = x
cos t = x 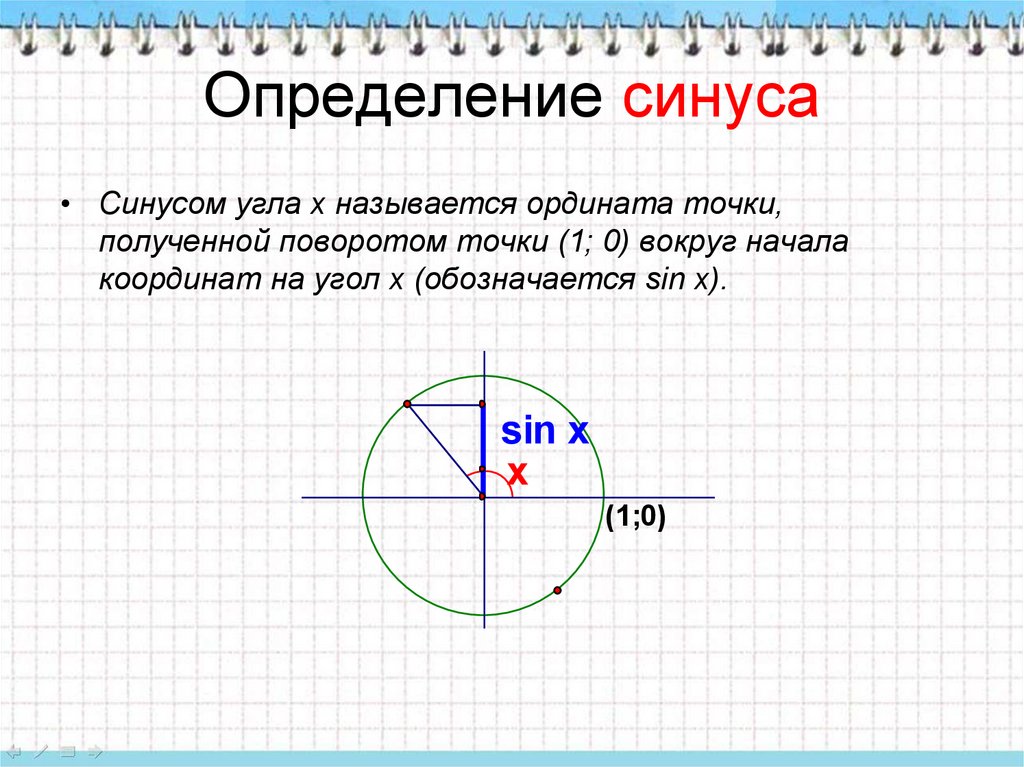 Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t . Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t . Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.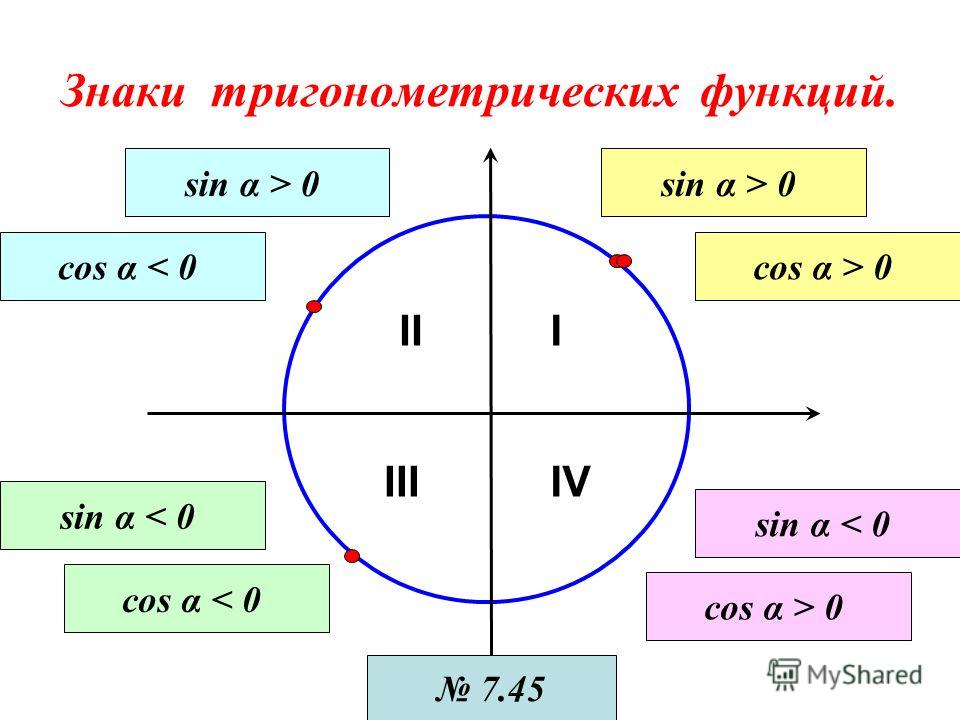 В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 (x , y) . Длина катета, противолежащего углу, равна ординате точки A 1 (x , y) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 (x , y) . Длина катета, противолежащего углу, равна ординате точки A 1 (x , y) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.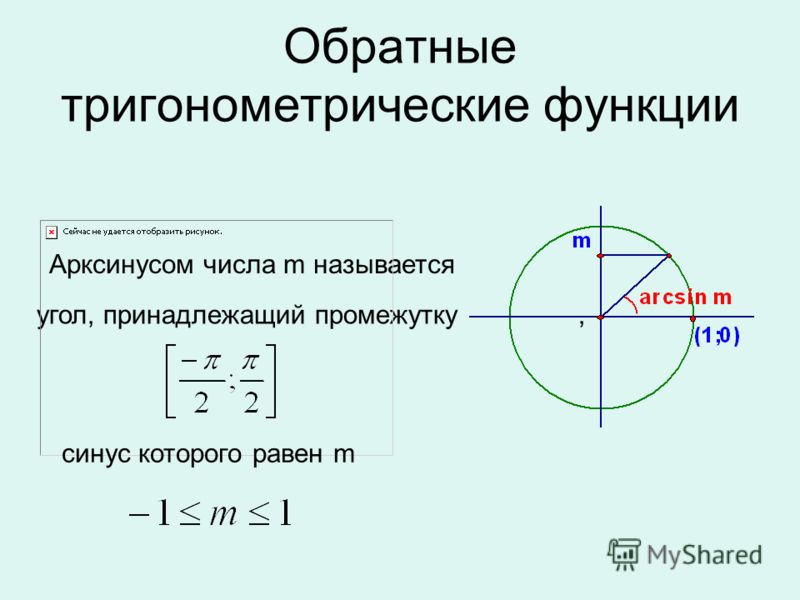 Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.
Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений. Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x:
Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x: 

 Значение функции синуса не выходит за пределы -1 и 1.
Значение функции синуса не выходит за пределы -1 и 1.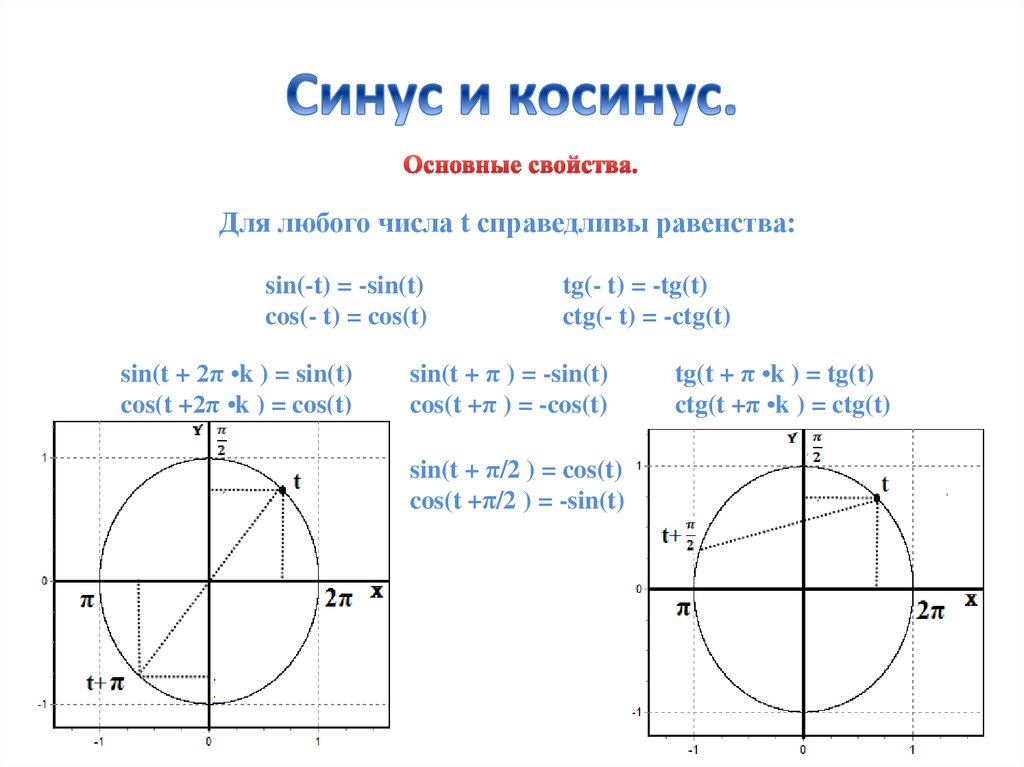
 Обычно используемые значения синуса: sin 0 = 0, sin π/6 = 1/2, sin π/4 = 1/√2, sin π/3 = √3/2 и sin π/2 = 1. , Мы можем определить эти значения, используя формулу синуса: sin x = Perpendicular/Hypotenuse.
Обычно используемые значения синуса: sin 0 = 0, sin π/6 = 1/2, sin π/4 = 1/√2, sin π/3 = √3/2 и sin π/2 = 1. , Мы можем определить эти значения, используя формулу синуса: sin x = Perpendicular/Hypotenuse. Поскольку длина окружности равна , мы видим, что .
(Здесь мы предполагаем, что Архимеда
результат, что площадь
круга равна половине длины окружности, умноженной на радиус.)
Если
, мы определяем
Поскольку длина окружности равна , мы видим, что .
(Здесь мы предполагаем, что Архимеда
результат, что площадь
круга равна половине длины окружности, умноженной на радиус.)
Если
, мы определяем )
) 6)
6) 13)
13) 22)
22) Для
оставшиеся значения
вам не нужно включать объяснение.
Для
оставшиеся значения
вам не нужно включать объяснение. и позже был сокращен до jya означает «аккорд». Индус
слово было переведено на арабский как джиба , что было бессмысленным
слово фонетически происходит от jya , но (поскольку гласные
по-арабски не писались) было написано так же, как jaib , что означает грудь. Когда араб был
в переводе на латынь это стало sinus . ( Jaib означает грудь, залив,
или грудь: sinus означает грудь, залив или складку тоги вокруг
грудь.) Английское слово синус фонетически происходит от синус .
и позже был сокращен до jya означает «аккорд». Индус
слово было переведено на арабский как джиба , что было бессмысленным
слово фонетически происходит от jya , но (поскольку гласные
по-арабски не писались) было написано так же, как jaib , что означает грудь. Когда араб был
в переводе на латынь это стало sinus . ( Jaib означает грудь, залив,
или грудь: sinus означает грудь, залив или складку тоги вокруг
грудь.) Английское слово синус фонетически происходит от синус .