Решение школьных задач: Решение задач за деньги — способ заработка по выполнению работ для школьников и студентов в интернете, примеры сайтов

• Семинар «Методология пошагового решения задач по физике», 04.

  12.2015

• Семинар «Методология пошагового решения задач по физике», 04.12.2015

• Семинар «Методология пошагового решения задач по физике», 04.12.2015

• Семинар «Методология пошагового решения задач по физике», 04.12.2015

• Семинар «Методология пошагового решения задач по физике», 04.12.2015

• Семинар «Методология пошагового решения задач по физике», 04.12.2015

• Семинар «Методология пошагового решения задач по физике», 04.12.2015

• Семинар «Методология пошагового решения задач по физике», 04.

  12.2015

• Семинар «Методология пошагового решения задач по физике», 04.12.2015

• Семинар «Методология пошагового решения задач по физике», 04.12.2015

• Семинар «Методология пошагового решения задач по физике», 04.12.2015

• Семинар «Методология пошагового решения задач по физике», 04.12.2015

• Семинар «Методология пошагового решения задач по физике», 04.12.2015

• Семинар «Методология пошагового решения задач по физике», 04.12.2015

• Семинар «Методология пошагового решения задач по физике», 04.

  12.2015

• Семинар «Методология пошагового решения задач по физике», 04.12.2015

• Семинар «Методология пошагового решения задач по физике», 04.12.2015

Структурное подразделение: 

• Физический факультет

Дата проведения: 

04.12.15

Время начала: 

Предмет: 

• Физика

Категория участников: 

• Учителя

Программа мероприятия: 

Отчет о проведении семинара «Методология пошагового решения задач по физике»,
04.12.2015, физический факультет МГУ

Решение задач по физике в средней школе – важный этап становления будущего специалиста в области естественных и технических наук. К сожалению, сокращение часов на изучение физики в школе привело к тому, что часть выпускников имеет размытое представление о физической науке, и уж, тем более, не умеет решать задачи. Работы ведущих преподавателей физического факультета МГУ сформировали систему решения школьных физических задач, основанную на пошаговых алгоритмах. Предлагаемые алгоритмы, их пошаговое содержание, методология их применения, связь с моделированием и олимпиадными задачами обсуждались в рамках семинара 04.12.15.

На семинар прибыло 23 учителя физики, в том числе 4 участника не проходили электронную регистрацию. Учителя приняли живое участие в дискуссии по предлагаемой теме, активно задавали вопросы выступающим, вносили предложения по содержанию рассмотренных алгоритмов.

Участники семинара по его окончании получили сертификат.

Краткие аннотации выступлений

Алгоритмический подход при решении задач динамики
П.Ю. Боков

Рассмотрен алгоритмический подход решения задач динамики как с применением законов Ньютона, так и с применением законов сохранения импульса и механической энергии. Показаны важность выбора моделей, роль системы отсчета на начальном этапе решения задачи, а также, актуальность анализа ответа не только с точки зрения размерности, но и с точки зрения соответствия действительности.
 

Решение задач отборочного тура олимпиады «Ломоносов-2015» с применением алгоритмов
А.В. Грачев

Предложен вариант решения двух задач динамики, предлагавшихся на отборочном туре олимпиады «Ломоносов-2015» по физике. Рассмотрена важность последовательности действий при решении задач.
 

Алгоритмизация задач механики и их решение с помощью вычислительных средств
Е.А. Михайлов

Алгоритмизация – важный этап написания компьютерной программы. Большая часть задач механики, не имеющих аналитического решения в рамках школьного курса физики и математики, современными школьниками может быть решена путем численного моделирования с использованием распространенных программных продуктов, например, таких как Microsoft Excel. В сообщении рассмотрен один из подходов к решению задач с применением вычислительных средств.

Регистрация на семинар начнется в 17.30. Одна из основных трудностей при освоении школьниками курса физики связанна с решением задач. Причем речь идет не только об олимпиадных задачах, речь, в том числе, о задачах, встречающихся в заданиях ГИА. В рамках семинара авторским коллективом нового УМК по физике (авт. Грачев А.В., Погожев В.А. и др.) предлагается рассмотреть варианты типизации школьных задач по физике и пошаговый подход к их решению.

Адрес: 

119991, ГСП-1, Москва, Ленинские горы, МГУ им. М.В.Ломоносова, дом 1, строение 2, Физический Факультет. Аудитория будет объявлена позднее.

Как проехать: 

Метро Университет, 1 остановка на любом транспорте по Ломоносовскому проспекту в сторону МГУ до остановки «ул.Лебедева». Здание №2 на карте http://www.msu.ru/info/lengory.html.

Решение задач как средство развития творческого мышления на уроках математики

Многие считают, что задача дается для того, чтобы ее просто решить. То есть найти правильный ответ или установить, что эта задача не имеет решения. Но оказывается, если задача решена, то в результате ее решения создана какая-то материальная и духовная ценность. Сейчас, более чем когда-либо в прошлом, современный мир нуждается в людях, стремящихся к открытиям и применению достижений науки, создающих более совершенные технические системы, новые технологии.

Развитие творческого мышления учащихся в процессе обучения является одной из актуальных задач, стоящих перед преподавателями математики в современной школе. Основным средством развития творческого мышления являются задачи. При обучении математики на решение задач отводится большая часть учебного времени. Математические задачи, содержащие в основных разделах школьных учебников, помогают учащимся узнать и усвоить новые математические факты, овладеть новыми математическими методами, накопить определенный опыт, научиться мыслить.

Самыми простейшими задачами правило являются стандартными. Главная цель стандартных задач в основном учебная: сформировать базовые знания, которые будут использоваться для решения других более сложных задач. Их решение требует от учащихся знаний, умений и навыков по какой-нибудь одной теме учебной программы.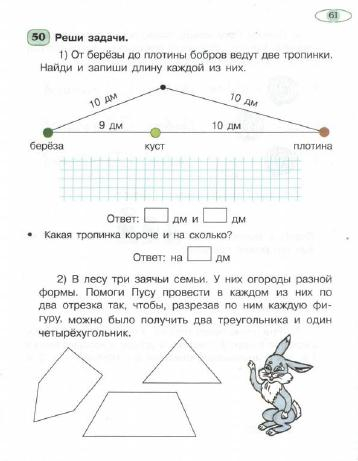 Каждая учебная задача может служить многим конкретным целям обучения. И все же главная их цель должна быть направлена на развитие творческого мышления учащихся. Достичь этой цели с помощью стандартных задач невозможно.

Средством развития творческого мышления все-таки являются нестандартные задачи. Нестандартные задачи – это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения. Такие задачи требуют от школьников наблюдательности, творчества и оригинальности. Необходимо тщательно отбирать нестандартные задачи и делать их содержательными, и привлекательными для учащихся. Наибольший интерес представляют задачи, которые решаются различными способами. Для развития творческого мышления гораздо полезнее одну задачу решить несколькими способами, и не жалеть на это времени, чем несколько однотипных задач одним способом. Из различных способов решения одной и той же задачи надо предложить учащимся выбрать наиболее рациональный. При отыскании различных способов решения задач, у школьников формируется познавательный интерес, развиваются не только творческие способности, но и вырабатываются исследовательские навыки.

В дальнейшем, на уроках математики исследовательские навыки используются при решении задач, включающие элементы исследования.

Простейшие исследования при решении задач следует предлагать уже с первых уроков. В дальнейшем обучении следует вводить и задачи, включающие исследования в качестве обязательной составной частью. При решении исследовательских задач, учащиеся приучаются к полной аргументации, учатся соблюдать формально-логические схемы рассуждений, обучаются лаконичному выражению мыслей. Правильно поставленное обучение решению исследовательских задач формирует особый научный стиль мышления, создают условия для проявления творческой активности учащегося.

Особое внимание следует обратить на решение проблемных задач. Проблемные задачи это только те задачи, решение которых предполагает на самостоятельный поиск еще неизвестному школьнику закономерностей, способов действия, правил. Такие задачи возбуждают активную мыслительную деятельность, а сделанное самими учащимися «открытие» приносит им эмоциональное удовлетворение. Наибольших эффект дают задачи, предполагающие открытие новых для учащихся причинно-следственных связей, закономерностей, общих признаков решения целого класса задач. Выбор задачи — проблемы зависит от наличия у школьников исходного минимума знаний или возможности до постановки проблемы ознакомить учащихся с необходимыми для самостоятельного решения сведениями. Вместе с тем нужно помнить, что эти знания должны служить опорой для поисков пути решения, а не «наводить», не подсказывать этот путь, иначе задача перестает быть проблемной. Для приобретения навыков решения довольно сложных задач нужно больше внимания уделять изучению полученного решения. Для этого можно предложить учащимся видоизменять условие задачи, придумывать задачи обратные решенным. Полезно так же предложить задачи, в которых неизвестно не только решение, но и плохо определены данные, либо цель, и потому как сама задача, так и ее решение могут быть весьма разнообразными. В таком случае учащиеся сами могут составить задачу и не только одну, а множество задач.

Конструирование задач — интересное для учащихся занятие, один из верных способов научиться решать задачи. Умение учащихся составлять нестандартные задачи, решаемые нестандартными способами, свидетельствует о культуре их мышления, хорошо развитых творческих способностях. При анализе решения задач полезно сопоставлять решение данной задачи с решениями других задач, установить возможность их обобщения. Учитель должен постоянно помнить, что решение задач является не самоцелью, а средством обучения и развития. Обсуждение найденного решения, поиск других способов решения, составление аналогичных задач или более сложных, обобщение данных задач — все это дает школьникам творчески развиваться. Именно через задачи учащиеся могут накопить определенный опыт, сформировать умения самостоятельно и творчески применять полученные знания.

Список литературы

1. Развитие мышления на уроках математики. / Е.М.Семенов, Е.Д.Горбунова Свердловск: Средне–уральское книжное издательство,1996г. – с.11-16.

2. Наглядность и моделирование в обучении. / Фридман Л.М. — М.: «Знание», 1984 г. – с.102-103.

3. Психолого-педагогические основы обучения математике в школе: Учителю математики о педагогической психологии. /Л.М.Фридман — М.: Просвещение, 2000. – с.68.

4. Сюжетные задачи по математике. История, теория, методика. / Л.М Фридман. — М.: Школьная пресса, 2002. – 208с.

5. Как научиться решать задачи. /Л.М.Фридман, Е.Н.Турецкий. — М.: Просвещение 1989.

6. Развитие логического мышления при изучении математики/ Н.В.Мельник – М.: Просвещение, 1997г. — с.21.

Методика решения задач | Методическая разработка по математике на тему:

В Федеральном государственном стандарте общего образования чётко сформулирована цель начального общего образования – « развитие личности обучающегося на основе освоения универсальных учебных действий, познания и освоения мира».

Ознакомившись с Федеральным государственным стандартом общего образования , мы видим, что одно из важнейших познавательных универсальных действий — умение решать проблемы или задачи.

Математические задачи, в которых есть хотя бы один объект, являющийся реальным предметом, принято называть текстовыми (сюжетными, практическими, арифметическими )

 Любая текстовая задача состоит из двух частей: условия и требования (вопроса).

Каждая задача – это единство условия и цели. Если нет одного из этих компонентов, то нет и задачи. Это очень важно иметь в виду, чтобы проводить анализ текста задачи с соблюдением такого единства.  

Можно выделить три типа задач:

-Задачи, решение которых состоит в стереотипном воспроизведении заученных действий. Степень трудности данных задач связана с тем, насколько сложным является навык воспроизведения действий и насколько он прочно освоен. Последний фактор становится основным.

-Задачи, решение которых требует некоторой модификации заученных действий в изменившихся условиях. Степень трудности в данном случае связана с количеством и разнородностью элементов, которое необходимо координировать наряду с описанными выше особенностями.

-Задачи, решение которых требует поиска новых, еще неизвестных способов действий. К данным задачам относятся такие, которые, требуют творческой активности, эвристического поиска новых, неизвестных схем действий или необычной комбинации известных.

     Решение задач – упражнение, развивающее мышление; оно способствует воспитанию терпения, настойчивости, воли, пробуждению интереса к самому процессу поиска решения, даёт возможность испытать глубокое удовлетворение, связанное с удачным решением, то есть формирует мотивационную сферу. Решение задач – одно из средств, помогающих формированию у детей таких важнейших качеств личности, как любовь к труду и потребность трудиться.

Что значит решить задачу?

  Современная методика предлагает делать это по следующему плану:

1.        Пропедевтика (подготовительная работа) к введению задач данного вида.

2.        Этап ознакомления с основными способами решения задач данного вида.

3.        Этап закрепления умения решать задачи данного вида.

       В начальный период знакомства с задачами чаще всего дети понимают, как дать ответ на поставленный в задаче вопрос (знают число). В случае, когда решается задача в одно действие, дети сразу после сообщения текста задачи учителем дают ответ на вопрос, не отвечая при этом, откуда этот ответ взялся («Подумал», «Догадался», «Посчитал», «Не знаю»), и если учитель говорит, что данное решение нельзя принять, дети обижаются. Поэтому следует четко провести грань между загадкой и задачей.

      Подготовительный этап очень важен для успешного формирования умений работать с текстовой задачей. В это время ученики усваивают конкретный смысл действий сложения и вычитания, учатся описывать задачные ситуации (без введения термина «задача»).

     На этом этапе учитель использует разнообразные виды заданий.

1.  Описание ситуаций по рисункам.

2. Составление к ситуациям вопросов со словом «сколько».

3. Постановка разных вопросов к одной ситуации.

4. Выполнение модели к ситуации и вопросу.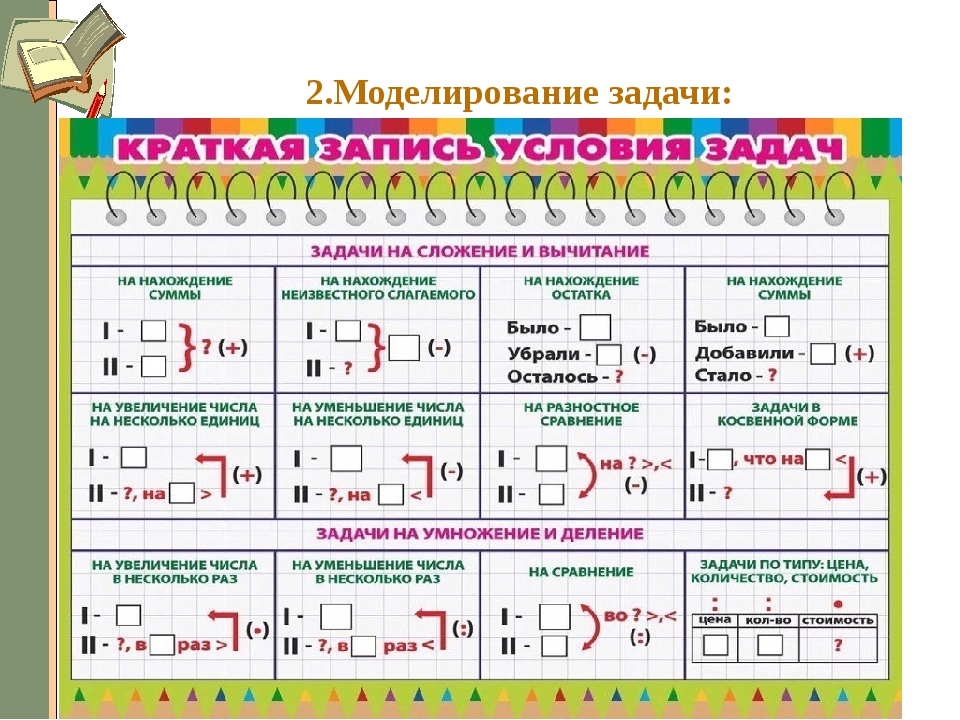

5. Описание ситуации при помощи чисел и знаков арифметических действий.

6. По данной модели описание ситуации и придумывание вопроса.

7. По данному выражению придумывание ситуации и вопроса.

8. Дополнение данной модели числами; придумывание ситуаций и вопросов к ним.

9. Подбор модели к данной ситуации. Объяснение соответствия одной модели и несоответствия других моделей.

10. Изменение модели с целью установления соответствия её данной ситуации.

11. Придумывание разных ситуаций к вопросу.

12. Придумывание заданий для товарища с целью проверки умений: описывать ситуации по рисункам, выражениям; моделировать ситуации; задавать разные вопросы к одной ситуации; придумывать разные ситуации к одному вопросу.

13. Определение видов заданий, которые даются легко, и видов заданий, которые вызывают трудности.

Работу над темой «Задача» с первого класса учитель организовывает так, чтобы ученики поняли:

 1) что в жизни люди постоянно встречаются с разными задачами;

 2) что в школе они будут иметь дело с задачами практически на всех уроках;

3) что часть задач могут решить, а часть решить не могут, так как не хватает знаний;

4) что среди огромного количества задач можно выделить такие, которые будут учиться решать на уроках математики, — это текстовые (математические) задачи;

5) что существуют общие приёмы работы над задачей.

 Для того чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких составных частей они состоят, каковы инструменты, с помощью которых производится решение задач.

                   Новые государственные стандарты начального общего образования по математике ориентируются на практические жизненные потребности человека в умении решать разные задачи. Таким целям отвечает не частный, а общий подход в обучении решению текстовых задач. Общий подход к решению задач по математике для начальной школы был разработан ещё в 80-е годы, но в действующем учебнике математики оставался частный подход к решению задач. В последнее десятилетие общий подход к решению задач, предполагающий деление процесса решения задач на этапы, постепенно становится приоритетным и в практике. При всём многообразии подходов к обучению решению задач основными считаются четыре этапа решения задачи. Каждый этап есть сложное умственное действие, входящее в состав ещё более сложного – решения задачи.

Первый этап- восприятие и осмысление задачи. Цель этапа — понять задачу, то есть выделить все множества и отношения, величины и зависимости между ними, числовые данные, лексическое значение слов. Основные приёмы работы на этом этапе:

 —  разбивка текста на смысловые части;

— постановка специальных вопросов;

-переформулировка, перефразирование, заменить описание термином, синонимом, убрать несущественные слова, конкретизировать;

— построить модель

С методической  точки зрения, для полноценной работы над этим этапом работы с задачей ребёнок должен:

а) уметь хорошо читать и понимать смысл прочитанного;

б) уметь анализировать текст задачи, выявляя его структуру и взаимоотношения между данными и искомым;

в) моделировать заданную в задаче ситуацию

Второй этап- поиск плана решения. Цель: связать вопрос и условие. Приёмы:

— рассуждения от условия к вопросу (синтетический способ), от вопроса к условию (аналитический способ), составление уравнения, рассуждение по модели, по словесному заданию отношений;

— название вида задачи;

— знание способа решения «таких» задач

Для организации процесса решения задач необходимо наличие программы конкретной деятельности учащихся, алгоритмов, системы приемов поиска решения задачи. Поэтому необходимы «ускорители» для приобретения навыков решения : иллюстрация, схемы, таблицы, дополнительные символы, условные знаки, стрелки, способствующие более конкретному наглядному представлению об отношениях между частями задачи, связях между величинами, порядке этих связей. Это позволяет стимулировать у учащихся развитие наглядно-действенного мышления и на основе его в дальнейшем – образного мышления.

Наибольший эффект при этом может быть достигнут в результате применения различных форм

записи содержания задачи:

1. Сокращенная форма записи, при которой из текста задачи выписывают числовые данные и только те слова и выражения, которые необходимы для понимания логического смысла задачи.

2. Сокращенно-структурная форма записи, при которой каждая логическая часть задачи записывается с новой строки.

3. Схематическая форма записи.

    Для некоторых задач использование схем, чертежей помогает обнаружить те скрытые связи между величинами, которые трудно выявить при использовании какого-либо вида разбора. Поиск пути решения и само решение проводятся с опорой на данный чертеж.

   Однако следует помнить о том, что краткая запись служит интересам ребенка при решении задачи, а не целью при решении (вспомогательное средство, при оценивании правильного решения задачи не следует осуждать ребёнка за то, что он сделал краткую запись не по образцу, показанному учителем, а так, как ему удобно, главное, что задача решена правильно.  

      Итак, как же искать план решения задачи? Профессор математики С.А. Яновская сказала, что «решить задачу – это свести её к уже решенным». Другими словами, разбить каждую задачу на систему подзадач, которые уже умеем решать.

       Третий этап- выполнение плана решения задачи.  Цель: выполнить операции в соответствующей математической области устно или письменно. Приёмы:

 1. оформление решения в виде записи решения:

— по действиям с ответом;

— по действиям с пояснениями после каждого действия;

— с вопросами перед каждым действием;

— по действиям с предварительной записью плана;

— числовым выражением;

— схематической моделью;

— комбинированным способом, включающим в себя несколько вышеперечисленных.

2. выполнение алгоритма решения «таких» задач;

3.название вида задачи

Четвёртый этап- проверка. Цель: убедиться в истинности выбранного плана и выполненных действий, после чего сформулировать ответ.

Приёмы — до решения: прикидка ответа или установление границ с точки зрения здравого смысла математики. Во время решения: по смыслу полученных выражений; осмысление хода решения по вопросам. После решения: решение другим способом, другим методом, подстановка результата в условие; сравнение с образцом; проверка на малых числах; составление и решение обратной задачи.

  Работа по формированию навыков контроля и самоконтроля при решении задач очень важна. Ведь проверка решенной задачи позволяет не только убедиться в правильности решения, но и способствует более глубокому пониманию и осмыслению ее математического содержания, осознанию связей между величинами, представленными в задаче.

   Для выработки у учащихся внутренней потребности проверять решение задачи необходимо научить их:

1.         При решении задачи обязательно объясните себе, почему решаете так, а не иначе.

2.        После решения задачи прочитайте снова текст задачи и проверьте, все ли требования задачи выполнены, правильно ли.

3.        Составьте план решения задачи. Какой пункт в решении задачи будет последним? (Работа над задачей заканчивается проверкой ее решения).

Способов проверки решения задачи много:

— Самый элементарный – прикидка ответа (установление границ искомого числа). Прикидка позволяет заметить неправильность рассуждения, несоответствие между величинами, но для многих задач не применим.

— Самый полезный, универсальный – составление и решение обратной задачи. Этот способ проверки развивает мышление, рассуждение, но громоздкий и отнимает много времени.

— Самый надежный способ проверки – решение задачи другим способом.

   Для проведения работы над задачей после ее решения используют следующие приемы: преобразование задачи, сравнение задач,  самостоятельное составление аналогичных задач, обсуждение разных способов решения задачи.

Однако следует отметить, что эффективное использование текстовых задач возможно только в том случае, когда учитель:

во-первых, может четко определить конкретную цель работы с каждой задачей на уроке;
          во-вторых, умеет организовать эту работу на уроке в строгом соответствии с поставленной целью, т.е.в зависимости от той или иной цели выбираются методические проблемы работы над задачей.

Выбор цели может осуществляться двумя взаимосвязанными путями:

1 – от общей цели урока к выбору задачи и конкретной цели работы с ней на уроке;
2 – от конкретной задачи к цели, для достижения которой эту задачу можно

Итак, изучив методическую литературу, мы пришли к следующим выводам:

− на современном этапе обучение младших школьников решению текстовых задач остается одним из важнейших направлений учебной деятельности, поскольку именно текстовые задачи являются связующим звеном между теоретическим обучением и применением знаний на практике;

− для всестороннего раскрытия понятия текстовой задачи и рассмотрения различных жизненных ситуаций в начальной школе предлагаются текстовые задачи, которые можно классифицировать по ряду оснований;

− решение любой текстовой задачи происходит по плану, включающему в себя ряд последовательных этапов;

− обучение решению задач проходит в двух направлениях: выработка общего умения решать текстовые задачи и выработка умений решать задачи определенного вида. Применительно к начальным классам чаще других реализуется первое из двух направлений.

− умение как психолого-педагогическая категория означает готовность и возможность человека (в данном контексте, младшего школьника) успешно выполнять какую-либо деятельность (в данном случае, решать текстовые задачи). В зависимости от уровня сформированности умения решать задачи учащихся можно разделить на три группы, соответственно с высоким, средним и низким уровнями. Критерии этих уровней описаны в методической литературе;

− для достижения поставленной дидактической цели в обучении младших школьников решению текстовых задач учителю необходимо варьировать и сочетать различные формы (индивидуальную, групповую, фронтальную) организации деятельности учащихся на уроках математики. Вспомогательные материалы, призванные оказать помощь учителю, содержатся в специально издаваемых методических пособиях, публикуются на страницах журналов и в сети Internet.

Приложение

Памятка по решению задачи

1.         Прочитай задачу, представь то, о чем говорится в задаче.

2.        Запиши задачу кратко, если необходимо, сделай чертеж или схему.

3.        Объясни, что показывает каждое число и назови вопрос задачи.

4.        Подумай, какое число должно получиться в результате (например, больше или меньше, чем данные числа и т.д.)

5.        Подумай, можно ли сразу ответить на вопрос задачи. Если нет, то почему? Что нужно узнать сначала? Что потом? Составь план решения задачи.

6.        Выполни решение.

7.        Проверь ответ и ответь на вопрос задачи.

8.        Подумай, можно ли решить задачу другим способом?

9.        Подумай, при каких условиях ответ задачи получился бы больше? Меньше?

Применительно к решению текстовых задач в отечественной начальной школе используется следующая шкала уровней.

• Высокому уровню сформированности умения решать задачи соответствуют работы и ответы, в которых ученик может самостоятельно и безошибочно решить задачу (составить план, решить, объяснить ход решения и точно сформулировать ответ на вопрос задачи).
• Среднему уровню сформированности умения решать задачи соответствуют работы и ответы, в которых ученик допускает отдельные неточности в формулировках, допускает ошибки в вычислениях и решениях задач, но исправляет их сам или с помощью учителя. При этом в работах не должно быть более одной грубой и трех-четырех негрубых ошибок.
• Низкому уровню сформированности умения решать задачи соответствуют работы и ответы, в которых ученик не справляется с решением задач и вычислениями в них даже с помощью учителя. Допускает 2 и более грубых ошибки.

Решение задач с параметрами как средство формирования исследовательских умений учащихся

В  материалах ЕГЭ регулярно содержатся задачи с параметром,  которые часто присутствовали на вступительных экзаменах в вуз с высокими требованиями к математической подготовке абитуриентов.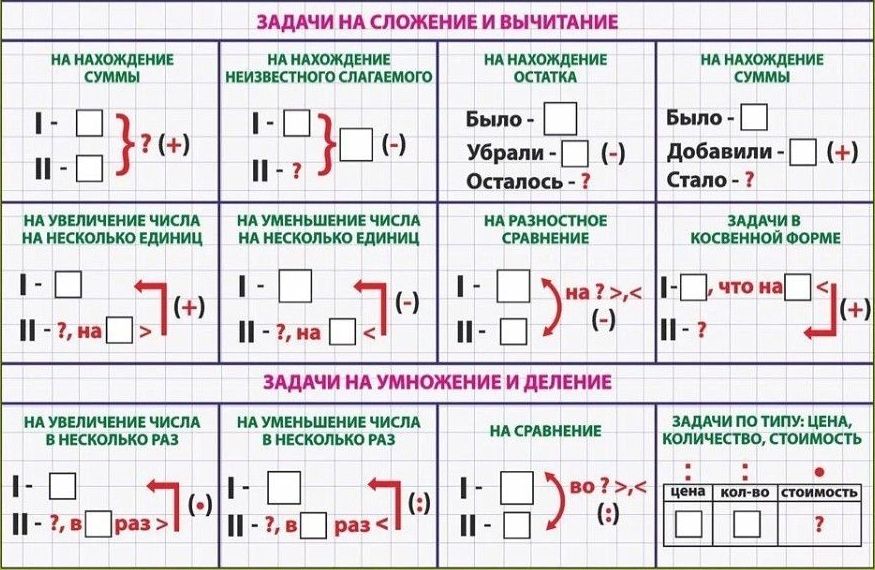 Контрольно-измерительные материалы для единого государственного экзамена создаются на основе кодификаторов элементов содержания и требований к уровню подготовки выпускников. Решение данных задач с одной стороны, относятся к элементам содержания «Уметь решать уравнения и неравенства», а с другой стороны, требуют определенного уровня сформированности умений наблюдать, сравнивать, анализировать, выдвигать и проверять гипотезы, оценивать результаты. Таким образом, решение задач с параметром можно считать деятельностью, близкой по своему характеру к исследовательской, а формирование указанной компетенции является одним из важных метапредметных результатов, реализуемого в рамках внедрения и апробации ФГОС среднего (полного) образования. В связи с этим, с одной стороны,  решение задач с параметрами важно использовать для развития математического мышления.

С другой стороны, школьники относят задачи с параметрами к самому сложному материалу, объясняя это несколькими причинами: трудность в выборе способа решения, отслеживания возникающих «ветвлений», исследования всех вариантов решений.

Таблица 1.

Общие результаты выполнения задания С5. 

 Кроме того, зачастую, учителя даже не рассматривают такие задачи с учениками, считая их заданиями повышенного уровня сложности, с  которыми слабые ученики априори не смогут справиться.

Аналогичное положение задач с параметрами в учебно-методических комплектах по математике, утвержденных или рекомендованных к использованию в общеобразовательной школе Министерством образования и науки РФ: их количество в любом из общефедеральных комплектов не превосходит 1%.  

Мирошин В.В. [2] выделяет отдельную часть математики – «абитуриентскую», которая существует отдельно от школьной программы. Действительно,  задачам с параметрами посвящены множество сборников для поступающих в вузы, в которых рассмотрены разнообразные приемы и методы решения. Однако педагоги сталкиваются с серьезными методическими проблемами при обучении решению таких задач, по причине того, что в большинстве этих пособий  не учат, как выбрать тот или иной способ решения, как научиться решать эти задачи.

Если же рассматривать решение задач с параметрами  не как  самоцель, а как средство развития активной творческой деятельности учащегося, его системного мышления, то целесообразно организовать учебно-исследовательскую  деятельность, в ходе которой ученик развивает умения самостоятельно приобретать и применять знания, формулировать и аргументировать позицию. Учащиеся, владеющие методами решения задач с параметрами, успешнее справляются (и опыт это подтверждает) [2] с другими задачами, поэтому в школьной математике таким задачам должно уделяться большое внимание.  

Известный  петербургский педагог В.И. Рыжик отмечает, что многолетняя ориентация на ЗУНы привела к тому, что основное внимание в школе уделяется учебной деятельности, в рамках которой, основным занятием стало усвоение алгоритмов и алгоритмических предписаний[3]. Уравнения (неравенства) с параметрами относятся к иному типу задач – задач, для решения которых необходимо прежде всего, умение проводить довольно разветвленные – логические построения и исследования. В теории обучения математике разработаны методические основы исследовательских задач, которые позволяют сравнить структуру типовой и исследовательской задачи [4,5]. На рис. 1 показано, что рассматриваемые в статье задачи обладают всеми признаками исследовательской задачи.

Проанализировав и обобщив ряд исследований[4,5,6,7,8], необходимо выделить общие положения в определениях учебно-исследовательской деятельности:  вид познавательной деятельности, цель которой не научные открытия учащихся, а развитие у них соответствующих личностных качеств, умений исследования как универсального способа освоения действительности.

Таблица 2.

Основные этапы учебного исследования

Рассмотренная задача с параметрами не является сложной, однако  иллюстрирует  важные свойства линейной функции, обладает высокой диагностической и прогностической ценностью. В процессе ее решения развиваются умения составлять соотношения, выдвижение различных предположений с обоснованием их возможности (гипотезы), формулирование обобщенного теоретического принципа, объясняющего сущность задачи.

Ниже приведем еще пример задачи с параметрами с описанием исследовательских умений, которые формулируются при их решении.

Задача: При каких значениях параметра а система уравнений

x+y=a

x²+y²=9  имеет единственное решение?

Задача может решаться несколькими способами.

Один из способов, так называемый аналитический,  получается, если из первого уравнения выразить y через х, подставить найденное выражение во второе уравнение, получив при этом квадратное, относительно х, далее проанализировать дискриминант уравнения.

Другой способ решения получается при рассмотрении геометрической интерпретации задачи: первое уравнение описывает прямую, расположенную под углом 45⁰ к оси Ох, а второе окружность с центром в начале координат и радиусом 3. При расположении прямой и окружности возможны три варианта:

1)    Прямая  пересекает окружность в двух точках;
2)    прямая касается окружности;
3)    прямая проходит вне окружности.

Легко увидеть, что единственное решение система будет иметь только при касании прямой СЕ и окружности с центром в начале координат и радиусом 3. При этом значение а можно определить как катет ОС равнобедренного прямоугольного треугольника ОСВ, в котором известна высота.

 
Рис.3 Графическая интерпретация задачи 

В процессе решения этой задачи у учащихся формируется умение  решать задачу несколькими способами, уметь конструировать новый способ на основе ранее изученных, уметь применять вспомогательный прием, умение решать задачу с необычным содержанием обычным способом, уметь проводить прямой и обратный ход рассуждений.

Ссылки на источники

1. И.В.Ященко, А.В.Семенов, И.Р.Высоцкий Методические рекомендации по некоторым аспектам совершенствования преподавания математики. – М.:ФИПИ, 2014.-34с.
2. Мирошин В.В. Решение задач с параметрами. Теория и практика/В.В.Мирошин.- М.:Издательство «Экзамен», 2009.-286с.
3. В.И.Рыжик Кризис среднего математического образования глазами учителя// Математика в школе, 2014,№1-с.3-9.
4. Колягин, Ю. М. Задачи в обучении математике. Ч.1. Математические задачи как средство обучения и развития учащихся [Текст] / Ю. М. Колягин. – М.: Просвещение, 1977. – 108с.
5. Крупич, В. И. Теоретические основы обучения решению школьных математических задач [Текст] / В. И. Крупич. – М.: Прометей, 1995. – 166с.
6. Далингер В.А. Поисково-исследовательская деятельность учащихся по математике: Учебное пособие. – Омск: Изд-во ОмГПУ, 2005. – 456 с.
7. Савенков А.И. Психологические основы исследовательского обучения щкольников// Физика : проблемы преподавания. -2007.-№7.-с.14-24
8. Алексеев Н. Г., Леонтович  А. В., Обухов  А. В., Фомина  Л. Ф. Концепция развития исследовательской деятельности учащихся // Исследовательская работа школьников. 2001. №. 1. С. 24-34.

Психолого-педагогические основы применения и решения школьных задач по химии

Психологи по-разному трактуют понятие «задача», связывая его с другими родственными понятиями. По словам А.И.Леонтьева, «задача – это цель, данная в определенных условиях» [6]. При характеристике процессов мышления задачу определяют как ситуацию, в которой субъект для достижения сформулированной цели должен выяснить неизвестное на основе использования его связи с известным.

Л.М.Фридман [8] считает, что задача – это «знаковая модель проблемной ситуации». А проблемная ситуация – это интеллектуальное затруднение человека, возникающее в случае, когда он не знает, как объяснить возникшее явление, факт, процесс действительности, не может достичь цели известным ему способом действия [5]. По определению Я.А.Пономарева, «задача есть… ситуация, которая определяет действие субъекта, удовлетворяющего потребность путем изменения ситуации» [3].

Решение задач есть вид творческой деятельности, а поиск решения – процесс изобретательства. Учебную же задачу принято считать частным случаем задачи вообще.

Таким образом, основным содержанием задач являются проблемные ситуации, решение которых возможно в результате творческого поиска. При этом необходимо учитывать как специфику изучаемого предмета, так и психологические закономерности процесса решения.

На основе анализа психологической и методической литературы химической задаче можно дать такое определение:

Химическая учебная задача – это модель проблемной ситуации, решение которой требует от учащихся мыслительных и практических действий на основе знания законов, теорий и методов химии, направленная на закрепление, расширение знаний и развитие химического мышления [4].

Решение задач не самоцель, а цель и средство обучения и воспитания учащихся. В связи с этим проблема решения задач является одной из основных для дидактики, педагогической психологии и частных методик.

Сформулировать задачу, приступить к решению с пониманием ее психологической сущности означает найти проявление тех внешних обстоятельств, через которые обеспечивается умственная активность школьников. Если эти обстоятельства станут предъявляться не в виде задачи, то они не будут вызывать у учащихся необходимых усилий и ограничатся лишь фиксацией отдельных бессвязных фактов.

Трудность решения задач зависит от объективного содержания и субъективного опыта. Задачи бывают репродуктивные и продуктивные. Механизм их решения различен. Репродуктивные – это типовые задачи, при решении которых возможно применение алгоритмов. В этом случае учитель сам объясняет ход их решения.

Продуктивные – творческие задачи, в них необходимо самостоятельно найти способы решения. Для этого недостаточно организованного опыта, необходим качественно иной опыт, заключающийся в умении логически мыслить, анализировать ситуацию в способности к интуитивному решению проблемы как высшего проявления логического мышления [1].

Психологический анализ обучения свидетельствует о том, что усвоение знаний происходит в процессе активной мыслительной работы учащегося при решении им задачи через выделение существенных сторон проблемы путем анализа, абстрагирования и обобщения. Решение задач предполагает целенаправленный, научно обоснованный ход деятельности. Бессистемно отобранные задачи, не связанные с теориями и законами, не обеспечивают должного развития мышления. Необходима продуманная система последовательно усложняющихся задач, отражающих явления в их взаимосвязи и развитии. Следует обращать внимание на применение полученных знаний на практике.

Правильно подобранные задачи в соответствии с уровнем развития учащихся не только реализуют их психологический потенциал, но и мобилизуют личность в целом, охватывая эмоциональную сферу, интересы, потребности.

Решение задач с психолого-педагогической точки зрения [9]:

• учит мыслить, ориентироваться в проблемной ситуации;
• предполагает активную продуктивную деятельность с определенной глубиной, широтой и самостоятельностью решения, которая должна быть направлена на установление переноса знаний на новые объекты;
• проявлять взаимосвязь представлений и понятий;
• содействует конкретизации и упрочению знаний;
• ведет к лучшему пониманию учащимися химических явлений в свете важнейших теорий;
• позволяет установить связь химии с другими предметами, особенно с физикой и математикой;
• является средством закрепления в памяти учащихся химических законов и важнейших понятий;
• служит одним из способов учета знаний и проверки навыков, полученных в процессе изучения предмета;
• воспитывает в процессе изучения у учащихся умение использовать полученные знания для решения практических проблем, тем самым, связывая обучение с жизнью и деятельностью человека.

Как видно, учебные задачи имеют огромное развивающее значение, поэтому важно понять природу мышления и знать механизмы их решения.

Природа внимания у школьника такова, что он не способен долго концентрировать его на одном предмете. Длительное решение подряд однотипных задач приводит к тому, что учащиеся новую предложенную задачу решают по-старому, не замечая, что ситуация в целом изменилась. Они перестают видеть существо предмета, действуя по шаблону. Проявляется некая инерция мысли, трудность перехода от одних представлений к другим. Учитывая это, учитель при работе над задачами должен обращать внимание на анализ их условий. При решении новых, более сложных задач ученики часто делают ошибки в простых действиях, которые им хорошо знакомы, т.е. при концентрации умственных усилий на решение относительно новой задачи наступает ослабление остроты осознания и мышления при выполнении привычных операций. Поэтому в разборе задач нового типа нужна четкость, не многословие, нет необходимости давать слишком много объяснений, ибо может ослабить внимание. Если учащимся что-то неясно, то этот момент при разъяснении следует повторить теми же словами, что и в первый раз, изменив лишь интонацию и ритм речи.

Психологами обнаружена закономерность в поведении человека при решении задач [7]. Он разбивает задачу на некоторое число более простых, т.е. ставит перед собой промежуточные вопросы (анализ задачи). Затем приступает к очередной проверке ряда простых задач, накапливая количественную информацию. Решив их, переходит к решению сложной – синтезирует. Таким образом, задачи решаются путем анализа и синтеза в совокупности. Иногда анализ протекает в скрытом виде (решающий провел анализ быстро, незаметно для себя, по шаблону), в таком случае создается впечатление, что имеет место только синтез. Поэтому цель учителя – не только подобрать задачи к уроку, но и обдумать, как он будет обучать учащихся разбивать подобранные задачи на более простые.

Проводя исследования в области решения задач, П.Линдсей и Д.Норман пришли к выводу, что при работе над любой сложной задачей «главным фактором, определяющим ход внутренних процессов решения задач и принятия решений, являются ограниченные возможности для кратковременного хранения информации».

У человека мала емкость оперативной памяти, это накладывает определенные ограничения на структуру и степень сложности процессов мышления. При решении ему приходится контролировать продвижение процесса решения и полученные промежуточные результаты; для этого он привлекает своего рода внешнюю память: записывает, делает пометки о путях решения задач. Чтобы облегчить положение, учитель должен обучать учеников рациональным способам записи условий и решения задач [2].

При подборе задачи для устного и письменного решения учителю необходимо уметь варьировать условие задачи, учить видеть скрытые данные.

Учащиеся первоначально не умеют выполнять действия по решению задач, им помогает в этом учитель. Постепенно они приобретают соответствующие умения, именно на этом этапе у них складывается химическое мышление, умение учиться. Для формирования обобщенного способа решения типовой химической задачи учащиеся должны решить несколько аналогичных задач на закрепление.

Таким образом, регуляция хода решения задач требует сформированности логически контролируемых, осознанных мыслительных действий. Процесс мыслительной деятельности должен управляться учителем, он требует максимального учета природы процесса, согласования каждого воздействия с закономерностями его протекания, что гарантирует достижение конечной цели.

Стратегии решения проблем родителей и учителей| Raising Children Network

Хорошие отношения между родителями и учителями

Хорошие отношения с учителем вашего ребенка и школой — отличная отправная точка для решения любых проблем, возникающих в школе.

Вы можете заложить основу для хороших отношений между родителями и учителями, представившись и познакомившись с учителем вашего ребенка как можно раньше. Общение и построение отношений с учителем вашего ребенка помогает вам работать вместе, когда возникает проблема.

Хорошие отношения между родителями и учителями означают, что дети:

• лучше успевают в учебе, эмоционально и социально
• счастливее в школе
• посещают школу более регулярно
• лучше себя ведут.

Проблемы в школе: что делать

У детей часто возникают проблемы в школе.

Некоторые проблемы  незначительные – например, пропуск школьного совета или забывание взять с собой правильную спортивную форму. Обычно вы и ваш ребенок сами можете решить эти проблемы, разговаривая и решая проблемы вместе.

Некоторые проблемы могут быть более сложными или длительными . Например, у вашего ребенка могут быть постоянные трудности на игровой площадке с другим ребенком, и стратегии, которые вы предложили своему ребенку, не сработали. С этими проблемами вам, возможно, придется поговорить с учителем вашего ребенка, чтобы найти решения.

Как решать школьные проблемы с учителями

Когда вам нужно поговорить с учителями о проблемах, спокойный и позитивный подход , скорее всего, принесет положительный результат для вашего ребенка. Вот что делать.

Пауза для успокоения
Если что-то только что расстроило вашего ребенка, это может расстроить и вас. Прежде чем что-то делать, постарайтесь успокоиться. Это поможет вам избежать того, о чем вы можете потом пожалеть, например, отправить гневное электронное письмо.

Можно сказать: «Я вижу, ты очень расстроен из-за этого, и я тоже расстроен». Нам нужно успокоиться, чтобы мы могли подумать о том, что делать». Это поможет вашему ребенку усвоить и эту стратегию.

Быть образцом для подражания
Даже в случае серьезной проблемы вы можете смоделировать позитивное решение проблемы для своего ребенка, если будете позитивно настроены, обдумывая решения и разговаривая с учителем о работе. Это лучше, чем жаловаться или быть агрессивным.

Можно сказать что-то вроде: «Давайте спросим мистера Смита, есть ли у него какие-нибудь идеи о том, как мы можем решить эту проблему». Такой подход показывает ребенку, что вы цените мнение учителя.

Говорите уважительно
Что бы вы ни думали, важно говорить позитивно и уважительно об учителе вашего ребенка, школе и других детях в присутствии вашего ребенка. Если вы жалуетесь или критикуете учителя или других детей и их семьи, ваш ребенок будет делать то же самое.

Используйте правильные каналы
Обычно это означает, что для начала нужно поговорить непосредственно с учителем вашего ребенка, а не с директором. Если обратиться прямо к директору, проблема может стать больше, чем она есть на самом деле.

Лучше записаться на прием к учителю. Таким образом, вы можете обсудить проблему наедине, и учитель сможет уделить вам все свое внимание.

В зависимости от проблемы и возраста вашего ребенка может быть уместно, чтобы ваш ребенок пришел на эту встречу.

Избегайте оборонительных действий
Когда возникают проблемы, люди иногда защищаются. Например, если вы или учитель чувствуете, что вас критикуют, вы оба можете занять оборонительную позицию.

Защитное поведение может помешать решению проблем, поэтому полезно попытаться увидеть точку зрения учителя и помочь учителю увидеть и вашу точку зрения. Например: «Я понимаю, что нереально ожидать, что ты проведешь обеденное время на детской площадке, помогая Итану, но я беспокоюсь, потому что он одинок и ему не с кем играть. Как мы оба можем помочь ему в этом?»

Шаги по решению проблем, которые можно использовать при встрече с учителями

Если вы решите, что вам нужно встретиться с учителем вашего ребенка по поводу серьезной проблемы, следующие шаги могут помочь вам и учителю работать вместе для достижения положительного результата.

1. Определите проблему
Четко и конкретно укажите, в чем состоит проблема, например, что происходит, как часто, кто участвует и кого затрагивает. Может помочь использование вопроса. Например, проблему «Как мы можем помочь Бренне завести друзей, с которыми можно играть?» решить легче, чем «Ни один из детей не будет играть с Бренной».

Также полезно спросить учителя вашего ребенка о проблеме. Так вы услышите о ситуации с точки зрения другого человека. Например, «Бренна говорит, что никто не хочет с ней играть. Судя по тому, что вы видели, это звучит правильно?»

2. Определите желания, потребности и опасения
Позвольте каждому определить свои потребности, желания и опасения. Если вы хотите, чтобы учитель вашего ребенка оценил ваши опасения, будет полезно, если вы покажете, что цените позицию учителя.

Используйте такие предложения, как «Я понимаю…», «Меня беспокоит…», «Мне нужно…» и «Я хочу…». Например: «Я понимаю, что это большой класс, но меня беспокоит, что Алистер отстает, потому что не понимает математику».

3. Придумайте возможные решения
Вместе с учителем придумайте как можно больше возможных решений проблемы. Учитель вашего ребенка имеет большой опыт решения проблем. У учителя также есть стратегии, которые работали в прошлом.

На данном этапе очень важно не осуждать идеи. Это увеличивает шансы найти правильное решение вашей проблемы.

4. Оцените решения
Когда вы и учитель перечислите как можно больше идей, подумайте о преимуществах, недостатках и последствиях каждого решения. Если решение имеет больше недостатков или негативных последствий, чем достоинств, вычеркните его из списка. Продолжайте делать это, пока не останутся только лучшие решения.

Когда вы делаете это, важно быть реалистом. Например, неразумно ожидать, что учитель будет сидеть с вашим ребенком во время трудных занятий, но разумно ожидать, что учитель будет время от времени проверять вашего ребенка.

5. Выберите одну и попробуйте
Выберите лучшую идею или комбинацию идей для опробования. Запишите, о чем вы договорились с учителем, кто что будет делать и когда. Решите, когда вы снова встретитесь, чтобы посмотреть, как работает решение. Дайте решению 1-2 недели, чтобы оно подействовало, прежде чем говорить о нем снова.

6. Оцените, как все прошло
Примите во внимание все мнения и отметьте все усилия, когда посмотрите, насколько хорошо сработало решение:

• Что сработало хорошо?
• Что не сработало?
• Что мы могли бы сделать по-другому, чтобы решение работало лучше?

Если проблема все еще не устранена или не улучшилась, возможно, вам потребуется привлечь других для помощи в поиске возможных решений. Эти люди могут включать директора школы или школьного координатора социального обеспечения. Рекомендуется сообщить учителю, что вы хотели бы поговорить с другими сотрудниками.

Если школа не может предоставить то, что нужно вашему ребенку, она должна иметь возможность направить вас в службу за пределами школы. Вы также можете поговорить со своим семейным врачом о других услугах и поддержке.

Решение задач в начальной школе | Edutopia

Образовательный фонд Джорджа Лукаса

Edutopia

Поиск

Грамотность

Учащиеся начальной школы практикуют методы решения проблем и самостоятельных вопросов для улучшения навыков чтения, социального и эмоционального обучения.

Морис Дж. Элиас

23 января 2019 г.

©iStock/Kobackpacko

В школьном округе Нью-Джерси, начиная с детского сада, каждый ребенок рассматривается как будущий решатель проблем с творческими идеями, которые могут помочь миру. Винс Капуто, руководитель школьного округа Метучен, объяснил, что на эту должность его привлекла «общая ценность всестороннего образования детей».

Первым, кто нанял Капуто в качестве суперинтенданта, был Рик Коэн, который работает директором школьной программы округа K-12 и директором начальной школы Мосс. Коэн стремится интегрировать социальное и эмоциональное обучение (SEL) в учебную программу и обучение, связывая когнитивные процессы и управляемый разговор с самим собой.

В первую очередь Коэн сосредоточился на воспитанниках детского сада. «Я рекомендовал учителям Moss обучать наших 6-летних детей только одному процессу решения проблем во всех областях академического содержания и предлагать учащимся использовать один и тот же процесс для решения социальных проблем», — пояснил он.

Moss В классах начальной школы используется особый процесс для развития навыков решения проблем, направленных на поддержание социальных и межличностных отношений. Процесс также концентрируется на развитии навыков чтения, в частности, декодирования и понимания.

Остановись, посмотри и подумай. Учащиеся формулируют задачу. Читая, они смотрят на картинки и текст в поисках подсказок, ищут информацию и задают вопрос: «Что важно, а что нет?» Аспект решения социальных проблем: учащиеся ищут признаки чувств в лицах, позах и тоне голоса других людей.

Сбор информации . Затем учащиеся выясняют, какие чувства они испытывают и какие чувства могут испытывать другие. Читая, они смотрят на начальный звук слова и спрашивают: «Что еще звучит так?» Аспект решения социальных проблем: учащиеся размышляют над такими вопросами, как «Какое слово или слова описывают чувства, которые вы видите или слышите в других? Какое слово описывает ваше чувство? Откуда ты знаешь и насколько ты уверен?»

Мозговой штурм . Затем учащиеся ищут разные решения. Читая, они задаются вопросом: «Правильно ли это звучит? Имеет ли это смысл? Как еще это могло звучать, чтобы иметь больше смысла? Какие еще звуки издают эти буквы?» Социальный аспект решения проблем: учащиеся размышляют над такими вопросами, как «Как вы можете решить проблему или улучшить ситуацию? Что еще вы можете придумать? Что еще вы можете попробовать? Какие еще идеи у вас есть?»

Выбери лучшего. Затем учащиеся оценивают решение. Во время чтения они ищут более мелкие слова, которые они знают, в более крупных и сложных словах. Они читают сложные слова так, как они думают, и спрашивают: «Будет ли это понятно другим людям?» Социальный аспект решения проблем: учащиеся обдумывают такие подсказки, как: «Выберите решение, которое, по вашему мнению, лучше всего подходит для решения проблемы. Спросите себя: «Что произойдет, если я сделаю это — для себя и для других участников?»

Перейти . На следующем этапе учащиеся составляют план и действуют. Они делают это, перечитывая текст. Аспект решения социальных проблем: студентов просят попробовать, что они скажут и как они скажут. Их просят выбрать подходящее время для этого, когда они захотят попробовать.

Чек . Наконец, учащиеся обдумывают и повторяют. После прочтения они обдумывают, что именно было сложным в прочитанном, и на основе этого решают, что делать дальше. Аспект решения социальных проблем: учащиеся размышляют над такими вопросами, как «Как это сработало? Вы решили проблему? Как другие относились к тому, что произошло? Что ты узнал? Что бы вы сделали, если бы то же самое повторилось?»

Вы можете посмотреть видео Moss Elementary Problem Solvers и увидеть аспекты этого процесса в действии.

Мосс Учащихся начальной школы и других школьников округа также учат структурированному самоанализу. Коэн отмечает: «Мы поняли, что многим из наших первоклассников будет трудно обобщить те же шаги и мыслительные навыки, которые они раньше использовали, чтобы понять неизвестное слово в тексте или разрешить социальные конфликты, чтобы обдумать сложные вопросы и исследовательские проекты». Решение? Научите учащихся задавать себе вопросы, зная, что они также могут применять эту эффективную стратегию в разных контекстах. Процесс самовопроса, который используют учащиеся, выглядит следующим образом:

Остановись и подумай. «Какой вопрос?»

Сбор информации. «Как собирать информацию? Каковы разные стороны проблемы?»

Придумай и выбери. «Как выбрать, упорядочить и выбрать информацию? Какие есть способы решения проблемы? Какой лучший выбор?»

Планируй и пробуй. «Как выглядит план? Когда и как это может произойти? Кого нужно привлечь?»

Проверка и проверка. «Как я могу предоставить информацию? Что я сделал хорошо? Как я могу улучшить?»

После использования процессов решения проблем и самостоятельных вопросов учащиеся начальной школы Moss за последние два года увеличили свои баллы на тестах PARCC по английскому языку для пятого класса. Однако, как делится Коэн, «более важным, чем подготовка наших студентов к тестам по государственным стандартам, является то, что мы также готовим их к тестам жизни».

Поделиться этой историей

, поданные в соответствии с