Корень 3 степени из 1728. Инженерный калькулятор
Если под рукой есть калькулятор, извлечь кубический корень из любого числа не составит никаких проблем. Но если калькулятора нет или вы просто хотите произвести впечатление на окружающих, извлеките кубический корень вручную. Большинству людей описываемый здесь процесс покажется довольно сложным, но с практикой извлекать кубические корни станет намного легче. Перед тем как приступить к чтению данной статьи, вспомните основные математические операции и вычисления с числами в кубе.
Шаги
Часть 1
Извлечение кубического корня на простом примере
Запишите задачу. Извлечение кубического корня вручную похоже на деление в столбик, но с некоторыми нюансами. Сначала запишите задачу в определенной форме.
- Запишите число, из которого нужно извлечь кубический корень. Число разбейте на группы по три цифры, причем отсчет начните с десятичной запятой.

Умножьте и вычтите. Умножьте последнюю цифру ответа (в нашем примере это 1) на найденный множитель (1261): 1*1261 = 1261. Запишите это число под 2000 и вычтите его из 2000. Вы получите 739 (это второй остаток).
Подумайте, является ли полученный ответ достаточно точным. Делайте это каждый раз, после того как завершите очередное вычитание. После первого вычитания ответ был равен 2, что не является точным результатом. После второго вычитания ответ равен 2,1.
- Чтобы проверить точность ответа, возведите его в куб: 2,1*2,1*2,1 = 9,261.
- Если вы считаете, что ответ достаточно точный, вычисления можно не продолжать; в противном случае проделайте еще одно вычитание.
Найдите второй множитель. Чтобы попрактиковаться в вычислениях и получить более точный результат, повторите действия, которые описаны выше.
Оцените второе число. Первое число вы нашли благодаря знанию кубов целых чисел. Теперь целое число превратите в десятичную дробь, приписав к нему (после десятичной запятой) некоторую цифру от 0 до 9. Необходимо найти десятичную дробь, куб которой будет близок, но меньше исходного числа.
- В нашем примере число 600 находится между числами 512 и 729. Например, к первому найденному числу (8) припишите цифру 5. Получится число 8,5.
- В нашем примере: 8 , 5 ∗ 8 , 5 ∗ 8 , 5 = 614 , 1. {\displaystyle 8,5*8,5*8,5=614,1.}
Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Если же куб полученного числа намного меньше исходного числа, оценивайте большие числа до тех пор, пока куб одного из них не превысит исходное число.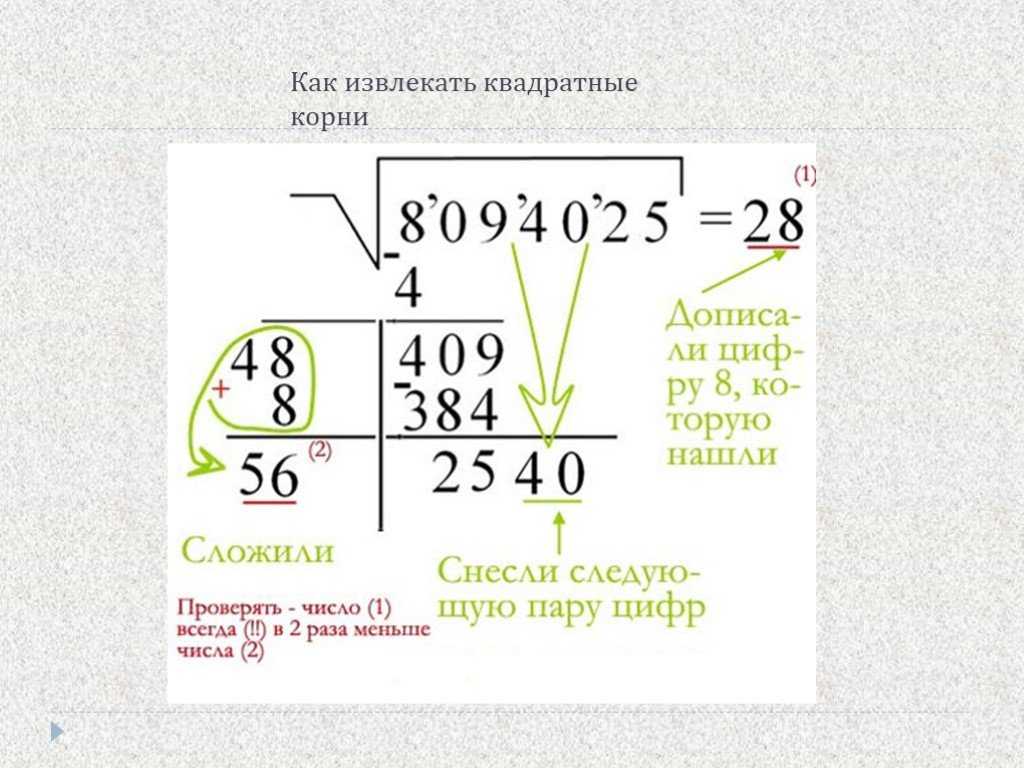
Если нужно, оцените другое число. Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Короче говоря, нужно найти такие два числа, кубы которых чуть больше и чуть меньше исходного числа.
- В нашем примере 8 , 44 ∗ 8 , 44 ∗ 8 , 44 = 601 , 2 {\displaystyle 8,44*8,44*8,44=601,2} . Это чуть больше исходного числа, поэтому оцените другое (меньшее) число, например, 8,43: 8 , 43 ∗ 8 , 43 ∗ 8 , 43 = 599 , 07 {\displaystyle 8,43*8,43*8,43=599,07} . Таким образом, значение кубического корня из 600 лежит между 8,43 и 8,44.
Выполняйте описанный процесс до тех пор, пока не получите ответ, точность которого вас устроит. Оцените следующее число, сравните его с исходным, затем, если нужно, оцените другое число и так далее. {3}=599,93}
, то есть результат меньше исходного числа менее чем на 0,1.
{3}=599,93}
, то есть результат меньше исходного числа менее чем на 0,1.
Размещенный на нашем сайте. Извлечение корня из числа часто используется в различных расчетах, а наш калькулятор — это отличный инструмент для подобных математических вычислений.
Онлайн калькулятор с корнями позволит быстро и просто сделать любые расчеты, содержащие извлечение корня. Корень третьей степени посчитает также легко, как и квадратный корень из числа, корень из отрицательного числа, корень из комплексного числа, корень из числа пи и т.д.
Вычисление корня из числа возможно вручную. Если есть возможность вычислить целый корень числа, то просто находим значение подкоренного выражения по таблице корней. В остальных случаях приближенное вычисление корней сводится к разложению подкоренного выражения на произведение более простых множителей, которые являются степенями и их можно убрать за знак корня, максимально упрощая выражение под корнем.
Но не стоит использовать такое решение корня. И вот, почему. Во-первых, придется потратить массу времени на подобные расчеты. Числа в корне, а точнее сказать, выражения могут быть достаточно сложными, а степень не обязательно квадратичной или кубической. Во-вторых, не всегда устраивает точность таких вычислений. И, в-третьих, есть онлайн калькулятор корней, который сделает за вас любое извлечение корня в считанные секунды.
И вот, почему. Во-первых, придется потратить массу времени на подобные расчеты. Числа в корне, а точнее сказать, выражения могут быть достаточно сложными, а степень не обязательно квадратичной или кубической. Во-вторых, не всегда устраивает точность таких вычислений. И, в-третьих, есть онлайн калькулятор корней, который сделает за вас любое извлечение корня в считанные секунды.
Извлечь корень из числа — значит найти такое число, которое при его возведении в степень n будет равно значению подкоренного выражения, где n — это степень корня, а само число — основание корня. Корень 2 степени называют простым либо квадратным, а корень третьей степени — кубическим, опуская в обоих случаях указание степени.
Решение корней в онлайн калькуляторе сводится лишь к написанию математического выражения в строке ввода. Извлечение из корня в калькуляторе обозначается как sqrt и выполняется с помощью трех клавиш — извлечение квадратного корня sqrt(x), извлечение корня кубического sqrt3(x) и извлечение корня n степени sqrt(x,y). Более детальная информация о панели управления представлена на странице .
Более детальная информация о панели управления представлена на странице .
Извлечение квадратного корня
Пример решения квадратных корней в калькуляторе:
Если под корнем отрицательное число, а степень корня четная, то ответ будет представлен в виде комплексного числа с мнимой единицей i.
Квадратный корень из отрицательного числа:
Корень третьей степени
Используйте эту клавишу, когда нужно извлечь кубический корень. Она вставляет в строке ввода запись sqrt3(x).
Корень 3 степени:
Корень степени n
Естественно, онлайн калькулятор корней позволяет извлекать не только квадратный и кубический корень из числа, но также корень степени n. Нажатие этой кнопки выведет запись вида sqrt(x x,y).
Корень 4 степени:
Точный корень n степени из числа можно извлечь только, если само число является точным значением степени n.
Корень 5 степени с приблизительным результатом:
Корень из дроби
Вычислить корень калькулятор может из различных чисел и выражений. Нахождение корня дроби сводится к отдельному извлечению корня из числителя и знаменателя.
Квадратный корень из дроби:
Корень из корня
В случаях когда корень выражения находится под корнем, по свойству корней их можно заменить одним корнем, степень которого будет равняться произведению степеней обоих. Проще говоря, чтобы извлечь корень из корня, достаточно перемножить показатели корней. В приведенном на рисунке примере выражение корень третьей степени корня второй степени можно заменить одним корнем 6-ой степени. Указывайте выражение так, как вам удобно. Калькулятор в любом случае все рассчитает верно.
Пример, как извлечь корень из корня:
Степень в корне
Корень степени калькулятор позволяет рассчитать в одно действие, без предварительного сокращения показателей корня и степени.
Квадратный корень из степени:
Все функции нашего бесплатного калькулятора собраны в одном разделе.
Решение корней в онлайн калькуляторе was last modified: Март 3rd, 2016 by Admin
Поздравляю: сегодня мы будем разбирать корни — одну из самых мозговыносящих тем 8-го класса.:)
Многие путаются в корнях не потому, что они сложные (чего там сложного-то — пара определений и ещё пара свойств), а потому что в большинстве школьных учебников корни определяются через такие дебри, что разобраться в этой писанине могут разве что сами авторы учебников. Да и то лишь с бутылкой хорошего виски.:)
Поэтому сейчас я дам самое правильное и самое грамотное определение корня — единственное, которое вам действительно следует запомнить. А уже затем объясню: зачем всё это нужно и как это применять на практике.
Но сначала запомните один важный момент, про который многие составители учебников почему-то «забывают»:
Корни бывают чётной степени (наш любимый $\sqrt{a}$, а также всякие $\sqrt{a}$ и даже $\sqrt{a}$) и нечётной степени (всякие $\sqrt{a}$, $\sqrt{a}$ и т.
{2}}=1$.
Кубические корни тоже часто встречаются — не надо их бояться:
\[\begin{align} & \sqrt{27}=3; \\ & \sqrt{-64}=-4; \\ & \sqrt{343}=7. \\ \end{align}\]
Ну, и парочка «экзотических примеров»:
\[\begin{align} & \sqrt{81}=3; \\ & \sqrt{-32}=-2. \\ \end{align}\]
Если вы не поняли, в чём разница между чётной и нечётной степенью — перечитайте определение ещё раз. Это очень важно!
А мы тем временем рассмотрим одну неприятную особенность корней, из-за которой нам и потребовалось вводить раздельное определение для чётных и нечётных показателей.
Зачем вообще нужны корни?
Прочитав определение, многие ученики спросят: «Что курили математики, когда это придумывали?» И вправду: зачем вообще нужны все эти корни?
Чтобы ответить на этот вопрос, вернёмся на минутку в начальные классы. Вспомните: в те далёкие времена, когда деревья были зеленее, а пельмени вкуснее, основная наша забота была в том, чтобы правильно умножать числа. Ну, что-нибудь в духе «пять на пять — двадцать пять», вот это вот всё. Но ведь можно умножать числа не парами, а тройками, четвёрками и вообще целыми комплектами:
Ну, что-нибудь в духе «пять на пять — двадцать пять», вот это вот всё. Но ведь можно умножать числа не парами, а тройками, четвёрками и вообще целыми комплектами:
\[\begin{align} & 5\cdot 5=25; \\ & 5\cdot 5\cdot 5=125; \\ & 5\cdot 5\cdot 5\cdot 5=625; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5=3125; \\ & 5\cdot 5\cdot 5\cdot 5\cdot 5\cdot 5=15\ 625. \end{align}\]
Однако суть не в этом. Фишка в другом: математики — людишки ленивые, поэтому им было в лом записывать умножение десяти пятёрок вот так:
Поэтому они придумали степени. Почему бы вместо длинной строки не записать количество множителей в виде верхнего индекса? Типа вот такого:
Это же очень удобно! Все вычисления сокращаются в разы, и можно не тратить кучу листов пергамента блокнотиков на запись какого-нибудь 5 183 . Такую запись назвали степенью числа, у неё нашли кучу свойств, но счастье оказалось недолгим.
После грандиозной пьянки, которую организовали как раз по поводу «открытия» степеней, какой-то особо упоротый математик вдруг спросил: «А что, если нам известна степень числа, но неизвестно само число?» Вот, действительно, если нам известно, что некое число $b$, допустим, в 5-й степени даёт 243, то как нам догадаться, чему равно само число $b$?
Проблема эта оказалась гораздо более глобальной, чем может показаться на первый взгляд. {n}}=a\]
{n}}=a\]
Не спорю: зачастую эти корни легко считаются — мы видели несколько таких примеров выше. Но всё-таки в большинстве случаев, если вы загадаете произвольное число, а затем попробуете извлечь из него корень произвольной степени, вас ждёт жестокий облом.
Да что там! Даже самый простой и всем знакомый $\sqrt{2}$ нельзя представить в привычном нам виде — как целое число или дробушка. А если вы вобьёте это число в калькулятор, то увидите вот это:
\[\sqrt{2}=1,414213562…\]
Как видите, после запятой идёт бесконечная последовательность цифр, которые не подчиняются никакой логике. Можно, конечно, округлить это число, чтобы быстро сравнить с другими числами. Например:
\[\sqrt{2}=1,4142…\approx 1,4 \lt 1,5\]
Или вот ещё пример:
\[\sqrt{3}=1,73205…\approx 1,7 \gt 1,5\]
Но все эти округления, во-первых, довольно грубые; а во-вторых, работать с примерными значениями тоже надо уметь, иначе можно словить кучу неочевидных ошибок (кстати, навык сравнения и округления в обязательном порядке проверяют на профильном ЕГЭ).
Поэтому в серьёзной математике без корней не обойтись — они являются такими же равноправными представителями множества всех действительных чисел $\mathbb{R}$, как и давно знакомые нам дроби и целые числа.
Невозможность представить корень в виде дроби вида $\frac{p}{q}$ означает, что данный корень не является рациональным числом. Такие числа называются иррациональными, и их нельзя точно представить иначе как с помощью радикала, либо других специально предназначенных для этого конструкций (логарифмов, степеней, пределов и т.д.). Но об этом — в другой раз.
Рассмотрим несколько примеров, где после всех вычислений иррациональные числа всё же останутся в ответе.
\[\begin{align} & \sqrt{2+\sqrt{27}}=\sqrt{2+3}=\sqrt{5}\approx 2,236… \\ & \sqrt{\sqrt{-32}}=\sqrt{-2}\approx -1,2599… \\ \end{align}\]
Естественно, по внешнему виду корня практически невозможно догадаться о том, какие числа будут идти после запятой. {2}}$:
{2}}$:
График квадратичной функции даёт два корня: положительный и отрицательный
Попробуем с помощью этого графика посчитать $\sqrt{4}$. Для этого на графике проведена горизонтальная линия $y=4$ (отмечена красным цветом), которая пересекается с параболой в двух точках:${{x}_{1}}=2$ и ${{x}_{2}}=-2$. Это вполне логично, поскольку
С первым числом всё понятно — оно положительное, поэтому оно и есть корень:
Но что тогда делать со второй точкой? Типа у четвёрки сразу два корня? Ведь если возвести в квадрат число −2, мы тоже получим 4. Почему бы тогда не записать$\sqrt{4}=-2$? И почему учителя смотрят на подобные записи так, как будто хотят вас сожрать?:)
В том-то и беда, что если не накладывать никаких дополнительных условий, то квадратных корней у четвёрки будет два — положительный и отрицательный. И у любого положительного числа их тоже будет два. А вот у отрицательных чисел корней вообще не будет — это видно всё по тому же графику, поскольку парабола нигде не опускается ниже оси y , т. {3}}$:
{3}}$:
Кубическая парабола принимает любые значения, поэтому кубический корень извлекается из любого числа
Из этого графика можно сделать два вывода:
- Ветви кубической параболы, в отличие от обычной, уходят на бесконечность в обе стороны — и вверх, и вниз. Поэтому на какой бы высоте мы ни проводили горизонтальную прямую, эта прямая обязательно пересечётся с нашим графиком. Следовательно, кубический корень можно извлечь всегда, абсолютно из любого числа;
- Кроме того, такое пересечение всегда будет единственным, поэтому не нужно думать, какое число считать «правильным» корнем, а на какое — забить. Именно поэтому определение корней для нечётной степени проще, чем для чётной (отсутствует требование неотрицательности).
Жаль, что эти простые вещи не объясняют в большинстве учебников. Вместо этого нам начинают парить мозг всякими арифметическими корнями и их свойствами.
Да, я не спорю: что такое арифметический корень — тоже надо знать. И я подробно расскажу об этом в отдельном уроке. Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.
И я подробно расскажу об этом в отдельном уроке. Сегодня мы тоже поговорим о нём, поскольку без него все размышления о корнях $n$-й кратности были бы неполными.
Но сначала надо чётко усвоить то определение, которое я дал выше. Иначе из-за обилия терминов в голове начнётся такая каша, что в итоге вообще ничего не поймёте.
А всего-то и нужно понять разницу между чётными и нечётными показателями. Поэтому ещё раз соберём всё, что действительно нужно знать о корнях:
- Корень чётной степени существует лишь из неотрицательного числа и сам всегда является неотрицательным числом. Для отрицательных чисел такой корень неопределён.
- А вот корень нечётной степени существует из любого числа и сам может быть любым числом: для положительных чисел он положителен, а для отрицательных — как намекает кэп, отрицательный.
Разве это сложно? Нет, не сложно. Понятно? Да вообще очевидно! Поэтому сейчас мы немного потренируемся с вычислениями.
Основные свойства и ограничения
У корней много странных свойств и ограничений — об этом будет отдельный урок. {2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение.
{2}}$, напротив, означает, что мы сначала извлекаем корень из некого числа $a$ и лишь затем возводим результат в квадрат. Поэтому число $a$ ни в коем случае не может быть отрицательным — это обязательное требование, заложенное в определение.
Таким образом, ни в коем случае нельзя бездумно сокращать корни и степени, тем самым якобы «упрощая» исходное выражение. Потому что если под корнем стоит отрицательное число, а его показатель является чётным, мы получим кучу проблем.
Впрочем, все эти проблемы актуальны лишь для чётных показателей.
Вынесение минуса из-под знака корня
Естественно, у корней с нечётными показателями тоже есть своя фишка, которой в принципе не бывает у чётных. А именно:
\[\sqrt{-a}=-\sqrt{a}\]
Короче говоря, можно выносить минус из-под знака корней нечётной степени. Это очень полезное свойство, которое позволяет «вышвырнуть» все минусы наружу:
\[\begin{align} & \sqrt{-8}=-\sqrt{8}=-2; \\ & \sqrt{-27}\cdot \sqrt{-32}=-\sqrt{27}\cdot \left(-\sqrt{32} \right)= \\ & =\sqrt{27}\cdot \sqrt{32}= \\ & =3\cdot 2=6. \end{align}\]
\end{align}\]
Это простое свойство значительно упрощает многие вычисления. Теперь не нужно переживать: вдруг под корнем затесалось отрицательное выражение, а степень у корня оказалась чётной? Достаточно лишь «вышвырнуть» все минусы за пределы корней, после чего их можно будет умножать друг на друга, делить и вообще делать многие подозрительные вещи, которые в случае с «классическими» корнями гарантированно приведут нас к ошибке.
И вот тут на сцену выходит ещё одно определение — то самое, с которого в большинстве школ и начинают изучение иррациональных выражений. И без которого наши рассуждения были бы неполными. Встречайте!
Арифметический корень
Давайте предположим на минутку, что под знаком корня могут находиться лишь положительные числа или в крайнем случае ноль. Забьём на чётные/нечётные показатели, забьём на все определения, приведённые выше — будем работать только с неотрицательными числами. Что тогда?
А тогда мы получим арифметический корень — он частично пересекается с нашими «стандартными» определениями, но всё же отличается от них. {n}}=a$.
{n}}=a$.
Как видим, нас больше не интересует чётность. Взамен неё появилось новое ограничение: подкоренное выражение теперь всегда неотрицательно, да и сам корень тоже неотрицателен.
Чтобы лучше понять, чем арифметический корень отличается от обычного, взгляните на уже знакомые нам графики квадратной и кубической параболы:
Область поиска арифметического корня — неотрицательные числа
Как видите, отныне нас интересуют лишь те куски графиков, которые расположены в первой координатной четверти — там, где координаты $x$ и $y$ положительны (или хотя бы ноль). Больше не нужно смотреть на показатель, чтобы понять: имеем мы право ставить под корень отрицательное число или нет. Потому что отрицательные числа больше в принципе не рассматриваются.
Возможно, вы спросите: «Ну и зачем нам такое кастрированное определение?» Или: «Почему нельзя обойтись стандартным определением, данным выше?»
Что ж, приведу всего одно свойство, из-за которого новое определение становится целесообразным. {2}}}=\sqrt{4} \gt 0. \\ \end{align}$
{2}}}=\sqrt{4} \gt 0. \\ \end{align}$
Как видите, в первом случае мы вынесли минус из-под радикала (имеем полное право, т.к. показатель нечётный), а во втором — воспользовались указанной выше формулой. Т.е. с точки зрения математики всё сделано по правилам.
WTF?! Как одно и то же число может быть и положительным, и отрицательным? Никак. Просто формула возведения в степень, которая прекрасно работает для положительных чисел и нуля, начинает выдавать полную ересь в случае с отрицательными числами.
Вот для того, чтобы избавиться от подобной неоднозначности, и придумали арифметические корни. Им посвящён отдельный большой урок, где мы подробно рассматриваем все их свойства. Так что сейчас не будем на них останавливаться — урок и так получился слишком затянутым.
Алгебраический корень: для тех, кто хочет знать больше
Долго думал: выносить эту тему в отдельный параграф или нет. В итоге решил оставить здесь. Данный материал предназначен для тех, кто хочет понять корни ещё лучше — уже не на среднем «школьном» уровне, а на приближенном к олимпиадному. {n}}=a \right. \right\}\]
{n}}=a \right. \right\}\]
Принципиальное отличие от стандартного определения, приведённого в начале урока, состоит в том, что алгебраический корень — это не конкретное число, а множество. А поскольку мы работаем с действительными числами, это множество бывает лишь трёх типов:
- Пустое множество. Возникает в случае, когда требуется найти алгебраический корень чётной степени из отрицательного числа;
- Множество, состоящее из одного-единственного элемента. Все корни нечётных степеней, а также корни чётных степеней из нуля попадают в эту категорию;
- Наконец, множество может включать два числа — те самые ${{x}_{1}}$ и ${{x}_{2}}=-{{x}_{1}}$, которое мы видели на графике квадратичной функции. Соответственно, такой расклад возможен лишь при извлечении корня чётной степени из положительного числа.
Последний случай заслуживает более подробного рассмотрения. Посчитаем парочку примеров, чтобы понять разницу.
Пример. Вычислите выражения:
\[\overline{\sqrt{4}};\quad \overline{\sqrt{-27}};\quad \overline{\sqrt{-16}}.
\]
Решение. С первым выражением всё просто:
\[\overline{\sqrt{4}}=\left\{ 2;-2 \right\}\]
Именно два числа входят в состав множества. Потому что каждое из них в квадрате даёт четвёрку.
\[\overline{\sqrt{-27}}=\left\{ -3 \right\}\]
Тут мы видим множество, состоящее лишь из одного числа. Это вполне логично, поскольку показатель корня — нечётный.
Наконец, последнее выражение:
\[\overline{\sqrt{-16}}=\varnothing \]
Получили пустое множество. Потому что нет ни одного действительного числа, которое при возведении в четвёртую (т.е. чётную!) степень даст нам отрицательное число −16.
Финальное замечание. Обратите внимание: я не случайно везде отмечал, что мы работаем с действительными числами. Потому что есть ещё комплексные числа — там вполне можно посчитать и $\sqrt{-16}$, и многие другие странные вещи.
Однако в современном школьном курсе математики комплексные числа почти не встречаются. Их вычеркнули из большинства учебников, поскольку наши чиновники считают эту тему «слишком сложной для понимания».
y».
Корень третьей степени можно вычислить и в программе MS Excel. Для этого введите в любую клетку «=» и выберите значок «вставка » (fx). Выберите в появившемся окошке функцию «СТЕПЕНЬ» и нажмите кнопку «Ок». В появившемся окошке введите значение числа, для которого необходимо вычислить корень третьей степени. В «Степень» введите число «1/3». Число 1/3 набирайте именно в таком виде – как обыкновенную . После этого нажмите кнопку «Ок». В той клетке таблицы, где создавалась , появится кубический корень из заданного числа.
Если корень третьей степени приходится вычислять постоянно, то немного усовершенствуйте описанный выше метод. В качестве числа, из которого требуется извлечь корень, укажите не само число, а клетку таблицы. После этого, просто каждый раз вводите в эту клетку исходное число – в клетке с формулой будет появляться его кубический корень.
Видео по теме
Обратите внимание
Заключение. В данной работе были рассмотрены различные методы вычисления значений кубического корня.
Выяснилось, что значения кубического корня можно находить с помощью метода итераций, также можно аппроксимировать кубический корень, возводить число в степень 1/3, искать значения корня третьей степени с помощью Microsoft Office Ecxel, задавая формулы в ячейках.
Полезный совет
Корни второй и третьей степени употребляются особенно часто и поэтому имеют специальные названия. Квадратный корень: В этом случае показатель степени обычно опускается, а термин «корень» без указания степени чаще всего подразумевает квадратный корень. Практическое вычисление корней Алгоритм нахождения корня n-ной степени. Квадратные и кубические корни обычно предусмотрены во всех калькуляторах.
Источники:
- корень третий степени
- Как извлечь квадратный корень в N степени в Excel
Операцию нахождения корня третьей степени обычно называют извлечением «кубического» корня, а заключается она в нахождении такого вещественного числа, возведение которого в куб даст значение равное подкоренному числу.
Операция извлечения арифметического корня любой степени n эквивалентна операции возведения в степень 1/n. Для практического вычисления кубического корня можно использовать несколько способов.
При решении некоторых технических задач бывает нужно посчитать корень третьей степени . Иногда это число еще называют кубическим корнем. Корнем третьей степени из данного числа называют такое число, куб (третья степень) которого равняется данному. То есть если y – корень третьей степени числа x, то должно выполняться условие: y?=x (икс равно игрек куб).
Вам понадобится
- калькулятор или компьютер
Инструкция
- Чтобы посчитать корень третьей степени , воспользуйтесь калькулятором. Желательно, чтобы это был не обычный калькулятор, а калькулятор, используемый для инженерных расчетов. Однако даже на таком калькуляторе вы не найдете специальную кнопку для извлечения корня третьей степени .
Поэтому используйте функцию для возведения числа в степень. Извлечению корня третьей степени соответствует возведение в степень 1/3 (одна треть).
- Для возведения числа в степень 1/3 наберите на клавиатуре калькулятора само число. После чего нажмите на клавишу «возведение в степень». Такая кнопка, в зависимости от типа калькулятора, может выглядеть как xy (у – в виде верхнего индекса). Так как в большинстве калькуляторов нет возможности работать с обычными (недесятичными) дробями, то вместо числа 1/3 наберите его приблизительное значение: 0,33. Чтобы получить большую точность вычислений, необходимо увеличить количество «троек», например, набрать 0,33333333333333. Затем, нажмите кнопку «=».
- Чтобы посчитать корень третьей степени на компьютере, воспользуйтесь стандартным калькулятором Windows. Порядок действий полностью аналогичен описанному в предыдущем пункте инструкции. Единственное отличие — это обозначение кнопки возведения в степень. На «компьютерном» калькуляторе она выглядит как x^y.
- Если корень третьей степени приходится считать систематически, то воспользуйтесь программой MS Excel. Чтобы посчитать корень третьей степени в «Екселе», введите в любую клетку знак «=», а затем, выберите значок «fx» — вставка функции. В появившемся окошке в списке «Выберите функцию» выберите строку «СТЕПЕНЬ». Нажмите кнопку «Ок». Во вновь появившемся окошке введите в строку «Число» значение числа, из которого нужно извлечь корень. В строку «Степень» введите число «1/3» и нажмите «Ок». В клетке таблицы появится искомое значение кубического корня из исходного числа.
Как находить кубический корень из числа
Кубический корень. Как извлечь квадратный корень из большого числа без калькулятора мы уже разобрали. В этой статье рассмотрим как извлечь кубический корень (корень третьей степени). Оговорюсь, что речь идёт о натуральных числах. Как вы думаете, сколько времени нужно, чтобы устно вычислить такие корни как:
Совсем немного, а если потренируетесь два-три раза минут по 20, то любой такой корень вы сможете извлечь за 5 секунд устно.
*Нужно отметить, что речь идёт о таких числах стоящих под корнем, которые являются результатом возведения в куб натуральных чисел от 0 до 100.
Так вот, число а, которое мы будем находить – это натуральное число от 0 до 100. Посмотрите на таблицу кубов этих чисел (результаты возведения в третью степень):
Вы без труда сможете извлечь кубический корень из любого числа в этой таблице. Что нужно знать?
1. Это кубы чисел кратных десяти:
Я бы даже сказал, что это «красивые» числа, запоминаются они легко. Выучить несложно.
2. Это свойство чисел при произведении.
Его суть заключается в том, что при возведении в третью степень какого-либо определённого числа, результат будет иметь особенность. Какую?
Например, возведём в куб 1, 11, 21, 31, 41 и т.д. Можно посмотреть по таблице.
1 3 = 1, 11 3 = 1331, 21 3 = 9261, 31 3 = 26791, 41 3 = 68921 …
То есть, при возведении в куб числа с единицей на конце в результате у нас всегда получится число с единицей в конце.
При возведении в куб числа с двойкой на конце в результате всегда получится число с восьмёркой в конце.
Покажем соответствие в табличке для всех чисел:
Знания представленных двух моментов вполне достаточно.
Извлечь кубический корень из 21952.
Данное число находится в пределах от 8000 до 27000. Это означает, что результат корня лежит в пределах от 20 до 30. Число 29952 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 28.
Извлечь кубический корень из 54852.
Данное число находится в пределах от 27000 до 64000. Это значит, что результат корня лежит в пределах от 30 до 40. Число 54852 заканчивается на 2. Такой вариант возможен только тогда, когда в куб возводится число с восьмёркой в конце. Таким образом, результат корня равен 38.
Извлечь кубический корень из 571787.
Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90.
Число 571787 заканчивается на 7. Такой вариант возможен только тогда, когда в куб возводится число с тройкой в конце. Таким образом, результат корня равен 83.
Извлечь кубический корень из 614125.
Данное число находится в пределах от 512000 до 729000. Это значит, что результат корня лежит в пределах от 80 до 90. Число 614125 заканчивается на 5. Такой вариант возможен только тогда, когда в куб возводится число с пятёркой в конце. Таким образом, результат корня равен 85.
Думаю, что вы теперь без труда сможете извлечь кубический корень из числа 681472.
Конечно, чтобы извлекать такие корни устно, нужна небольшая практика. Но восстановив две указанные таблички на бумаге, вы без труда в течение минуты, в любом случае, такой корень извлечь сможете.
После того, как нашли результат обязательно сделайте проверку (возведите его с третью степень). *Умножение столбиком никто не отменял 😉
На самом ЕГЭ задач с такими «страшненькими» корнями нет. Например, в Задаче 27125 требуется извлечь кубический корень из 1728.
Думаю, что это теперь для вас не проблема.
Если вы знаете какие-то интересные приёмы вычислений без калькулятора, присылайте, со временем опубликую. На этом всё. Успеха Вам!
Онлайн калькулятор для расчета кубического корня для положительных и отрицательных чисел.
Кубический корень из a, обозначающийся как или как a 1/3 — решение уравнения x 3 = a (обычно подразумеваются вещественные решения).
Кубический корень — нечётная функция. В отличие от квадратного корня, кубический корень может быть извлечён и из отрицательных чисел.
Калькулятор кубического корня
Онлайн калькулятор для расчета кубического корня для положительных и отрицательных чисел.
Алгоритм извлечения кубического корня
Перед началом необходимо разделить число на тройки (целую часть — справа налево, дробную — слева направо). Когда Вы достигли десятичной запятой, в конце результата необходимо поставить десятичную запятую.
- Найдите число, куб которого меньше первой группы цифр, но при её увеличении на 1 она становиться больше. Выпишите найденное число справа от данного числа. Под ним запишите число 3.
- Запишите куб найденного числа под первой группой цифр и произведите вычитание. Результат после вычитания запишите под вычитаемым. Далее снесите следующую группу цифр.
- Далее найденный промежуточный ответ заменим буквой a. Вычислите по формуле 300× a 2 × x+30× a × x 2 +x 3 такое число x, что его результат меньше нижнего числа, но при увеличении на 1 становится больше. Запишите найденное x справа от ответа. Если достигнута необходимая точность, прекратите вычисления.
- Запишите под нижним числом результат вычисления по формуле 300 × a 2 × x+30 × a × x 2 +x 3 и произведите вычитание. Перейдите к пункту 3.
В создании этой статьи участвовала наша опытная команда редакторов и исследователей, которые проверили ее на точность и полноту.
Количество источников, использованных в этой статье: 14. Вы найдете их список внизу страницы.
Команда контент-менеджеров wikiHow тщательно следит за работой редакторов, чтобы гарантировать соответствие каждой статьи нашим высоким стандартам качества.
Если под рукой есть калькулятор, извлечь кубический корень из любого числа не составит никаких проблем. Но если калькулятора нет или вы просто хотите произвести впечатление на окружающих, извлеките кубический корень вручную. Большинству людей описываемый здесь процесс покажется довольно сложным, но с практикой извлекать кубические корни станет намного легче. Перед тем как приступить к чтению данной статьи, вспомните основные математические операции и вычисления с числами в кубе.
Как вычислить кубический корень? – Обзоры Вики
Мы знаем, что 5 × 5 × 5 = 125. Следовательно, 125 называется кубом числа 5. С другой стороны, кубический корень числа является обратным процессом куба числа и обозначается ∛.
...
Список кубических корней чисел.
Кубический корень 1 Кубический корень 2 Кубический корень 1000 Кубический корень 1331 Кубический корень 1728 Кубический корень 4096 Отсюда, какова экспоненциальная форма числа 9? Экспонентные таблицы и шаблоны
Полномочия 3 Полномочия 9 31 = 3 91 = 9 32 = 9 92 = 81 33 = 27 93 = 729 34 = 81 94 = 6561 Что такое куб числа 8? Поскольку кубический корень из 8 — целое число, 8 — совершенный куб.
…
Кубический корень из 8 в радикальной форме: ∛8.
1. Что такое кубический корень из 8? 3. Является ли кубический корень из 8 иррациональным? 4. Часто задаваемые вопросы о Cube Root of 8 Дополнительно Что такое куб √ 3? Следовательно, кубический корень из 8 равен 2, а из 27 равен 3. Кубический корень любого числа n — это число x, например x 3 = п.
…
Как найти кубический корень из 3?
Число (х) Куб числа (x 3 ) 2 2 × 2 × 2 = 8 3 3 × 3 × 3 = 27 4 4 × 4 × 4 = 64 5 5 × 5 × 5 = 125 Что такое кубические корни в математике? Кубический корень числа это множитель, который мы умножаем на себя трижды, чтобы получить это число. Символом кубического корня является 3 кубический корень из, конец кубический корень . Нахождение кубического корня числа противоположно возведению числа в куб.
Что такое 9 * 9 как степень?
9 в квадрате как экспонента будет 92 .
Если выразить это, это будет 9 x 9 = 81.
Что означает число 9 в 9-й степени? 9 в степени 9 = 99 = 387,420,489. Почему мы используем возведения в степень, такие как 99 так или иначе? Что ж, нам намного проще писать умножения и выполнять математические операции как с большими, так и с маленькими числами, когда вы работаете с числами с большим количеством конечных нулей или большим количеством десятичных знаков.
Как найти степень 9? Формула – Как рассчитать показатель степени 9 чисел
Показатель 9 числа равен получается умножением этого числа само на себя 9 раз.
Что такое куб 10?
Кубический корень из 10 выражается как ∛10 в радикальной форме и как (10) ⅓ or (10) 0 . 33 в экспоненциальной форме.
…
Кубический корень из 10 в радикальной форме: ∛10.
1. Что такое кубический корень из 10? 2. Как вычислить кубический корень из 10? 3. Является ли кубический корень из 10 иррациональным? Также Что такое кубический корень из 3 27? Значение кубического корня из 27 равно 3. Это действительное решение уравнения x 3 = 27.
…
Кубический корень из 27 в радикальной форме: ∛27.
1. Что такое кубический корень из 27? 3. Является ли кубический корень из 27 иррациональным? 4. Часто задаваемые вопросы о Cube Root of 27 Что такое куб 5?
Кубический корень из 5 выражается как ∛5 в радикальной форме и как (5) ⅓ или (5) 0 . 33 в экспоненциальной форме.
…
Кубический корень из 5 в радикальной форме: ∛5.
1. Что такое кубический корень из 5? 3. Является ли кубический корень из 5 иррациональным? 4. Часто задаваемые вопросы о Cube Root of 5 Чему равен куб корня 2 из 2? Кубический корень из 2 выражается как ∛2 в радикальной форме и как (2) ⅓ или (2) 0 . 33 в экспоненциальной форме.
…
Кубический корень из 2 в радикальной форме: ∛2.
1. Что такое кубический корень из 2? 2. Как вычислить кубический корень из 2? 3. Является ли кубический корень из 2 иррациональным? 4. Часто задаваемые вопросы о Cube Root of 2 Что такое 9-й квадратный номер?
«Можно ли воссоздать это до 12 × 12?»
0 в квадрате = 0 6 в квадрате = 36 7 в квадрате = 49 8 в квадрате = 64 9 в квадрате = 81 Кубический корень равен 1 3?
Кубический корень – это число, которое при возведенный в куб, равно заданному числу.
Обозначается показателем степени «1/3». Например, кубический корень из 27 равен 27.1/3 = 3.
Почему число 9 волшебное? 9 называют магическим числом потому что сумма цифр кратных 9 всегда равна 9.
Есть ли ноль в квадрате?
Квадрат нуля будет равен нулю потому что, когда вы возводите число в квадрат, вы просто умножаете число само на себя. 0²=0*0=0, потому что 0, умноженный на любое число, всегда будет равен нулю.
Что такое число 9? 9 (число)
← 8 9 10 → -1 0 1 2 3 4 5 6 7 8 9 → Список чисел — Целые числа ← 0 10 20 30 40 50 60 70 80 90 → Кардинальный 9 порядковый 9-й (девятый) Система счисления девятеричный Что такое 9 в степени 5?
Ответ: 9 в степени 5 равно 59049.
Какова четвертая степень числа 9? 9 в 4-й степени, или 94, это 6,561.
Что такое 9 в степени 3?
Ответ: 9 в степени 3 можно выразить как 93 = 9 × 9 × 9 = 729.
Как записать 10 в степени 9? Ответ: 10 в степени 9 можно представить как 10.9 = 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 × 10 = 1,000,000,000.
арифметика / Возможно ли извлечь кубический корень из -8? / Математика
Без использования мнимых чисел.
Я еще понимаю, почему нельзя извлечь квадратный корень из отрицательного числа. Ведь если у нас есть четное количество отрицательных множителей, то результатом будет положительное число. Но в случае с третьей степенью ситуация другая!
Ведь по сути, что такое извлечение кубического корня? Это ответ на вопрос «какое число при трехкратном умножении на само себя даст данное число»?
Предположим, перед нами -8.
арифметика
задан 1 Апр ’13 16:03
Tsukune
51●2●7●27
95% принятыхстарыеновыеценные
Корень извлечь возможно, но калькулятор действует по-другому. Он рассматривает корень третьей степени как возведение в степень 1/3. А вот это уже нельзя применять к отрицательным числам.
Причина тут в том, что число 1/3 задается не только парой (1, 3), но и, например, (2, 6), 1/3 =2/6.
Как возвести в степень 2/6? Сначала извлечь корень 6-ой степени, потом возвести в квадрат. Но это невозможно для отрицательных чисел.
Для калькулятора такое ограничение естественно, так как вычисления производятся приближенно. Например, 1/3 приближенно равна 0,333, и какой же корень здесь извлекать?
ссылка
отвечен 1 Апр ’13 16:09
DocentI
9.9k●2●20●52
Когда я учился в школе, у нас было понятие «арифметического корня $%n$%-й степени».
3= -8 т е обратная связь
ссылка
отвечен 7 Апр ’15 2:44
сергей000001
1●1Ваш ответ
Если вы не нашли ответ, задайте вопрос.
Вычисление кубического корня : Чулан (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Побережный Александр
Вычисление кубического корня
01.06.2011, 09:31
29/07/08
533
В различного рода вычислениях требуется вычислить кубический корень из числа.

Есть ли простые и быстрые способы его извлечения?
Обычный подбор довольно трудоемкий.
Я использую такой: ~
Я использую наличие в моем калькуляторе операции извлечения корня квадратного. Всего нажимаются кнопки калькулятора пять раз.
Полученное число находится около действительного значения. Затем подбором довожу до необходимой точности.
Аналогичным способом я добываю корень пятого порядка.
Sonic86
Re: Вычисление кубического корня
01.06.2011, 10:25
Заслуженный участник 08/04/08
8524
Используйте метод Ньютона для решения
Для натуральных чисел можно и цепные дроби использовать.
Батороев
Re: Вычисление кубического корня
01.06.2011, 10:51
23/01/07
3361
Новосибирск
Побережный Александр в сообщении #452527 писал(а):
В различного рода вычислениях требуется вычислить кубический корень из числа.
y»-«m».
gris
Re: Вычисление кубического корня
01.06.2011, 11:12
Заслуженный участник 13/08/08
13978
Ну если компьютер под рукой, или продвинутый калькулятор, то и разговора нет.

Тут речь идёт о самом простом калькуляторе, где нет ни логарифмов, ни экспоненты. Корень, как правило, бывает всегда.
Я делаю абсолютно так же. Приближаю показатель степени двоичной дробью и далее перевожу это дело в цепочку умножений, делений и извлечения квадратного корня. Для кубического корня лучше подходит 11/32 или даже 21/64, что экономичнее следующих приближений.
А для уточнения я использую ряд Тейлора с центром в найденном приближении.
obar
Re: Вычисление кубического корня
01.06.2011, 16:13
Заслуженный участник 13/04/11
564
В данном случае гораздо точнее сразу по Тейлору:
с ошибкой меньше 0.01 (точное значение 1.7099).
gris
Re: Вычисление кубического корня
01.06.2011, 16:53
Заслуженный участник 13/08/08
13978
ну не скажите.
Это надо столько возиться.
а для конкретно кубического корня из последовательное нажатие
даёт одну итерацию, а пять итераций уже дают 4 знака. Да можно сколько угодно повторять эти нажатия, пока необходимое количество цифр не стабилизируется.
alex1910
Re: Вычисление кубического корня
01.06.2011, 16:58
21/07/10
555
Сколько угодно нельзя из-за нарастания погрешности.
Joker_vD
Re: Вычисление кубического корня
01.06.2011, 17:46
Заслуженный участник 09/09/10
3729
alex1910 в сообщении #452653 писал(а):
Сколько угодно нельзя из-за нарастания погрешности.
Да вы что, да вы что… метод последовательных итераций тем и хорош, что обычно сглатывает вычислительные погрешности. Попробуйте хоть на windows-овском калькуляторе решить — решение стабилизируется и больше уже не меняется.
Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию
Страница 1 из 1 [ Сообщений: 8 ] Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей
Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения
Найти: Кубический корень — Что такое кубический корень?
При трехкратном умножении числа (x) полученное число называется кубом этого числа.
Куб для числа (x) представлен как x 3 и читается как «x в кубе» (или) «x в степени 3» (или) «x в степени 3». Например, возьмем число 5. Мы знаем, что 5 × 5 × 5 = 125. Следовательно, 125 называется кубом из 5. С другой стороны, нахождение кубического корня числа включает процесс, обратный куб числа и обозначается ∛. В том же примере 5 называется кубическим корнем числа 125 и записывается как ∛125 = 5. На этой странице мы узнаем больше о кубах и кубических корнях числа.
1. Определение кубического корня 2. Как найти кубический корень числа? 3. Формула кубического корня 4. Что такое куб числа? 5. Список кубических корней чисел 6. Часто задаваемые вопросы о Cube Root Определение кубического корня
Когда мы думаем о словах «куб» и «корень», первая картина, которая может прийти нам на ум, — это буквальный куб и корни дерева.
Не так ли? Ну идея похожа. Корень означает первоисточник или происхождение. Итак, нам просто нужно подумать «куб какого числа нужно взять, чтобы получить данное число». В математике определение кубического корня записывается как Кубический корень — это число, которое нужно умножить три раза, чтобы получить исходное число. Теперь давайте посмотрим на формулу кубического корня, где у — кубический корень из х. ∛х = у. Подкоренной знак ∛ используется как символ кубического корня для любого числа с маленькой цифрой 3, написанной в верхнем левом углу знака. Другой способ обозначить кубический корень — написать 1/3 как показатель степени числа.
Кубический корень — операция, обратная кубу числа.
Совершенные кубы
Совершенный куб — это целое число, которое можно представить как произведение трех одинаковых или равных целых чисел. Например, 125 — это совершенный куб, потому что 5 3 = 5 × 5 × 5 = 125. Однако 121 не является совершенным кубом, потому что не существует числа, которое при трехкратном умножении дает произведение 121.
Другими словами, совершенный куб — это число, кубический корень которого является целым числом. Его также называют «кубическим числом». В следующей таблице показаны совершенные кубы первых 10 натуральных чисел.
Число/кубический корень Совершенный куб 1 1 2 8 3 27 4 64 5 125 6 216 7 343 8 512 9 729 10 1000 Как найти кубический корень числа?
Кубический корень числа можно определить с помощью метода простой факторизации. Чтобы найти кубический корень числа:
- Шаг 1: Начните с разложения заданного числа на простые множители.
- Шаг 2: Затем разделите полученные множители на группы, состоящие из трех одинаковых множителей.
- Шаг 3: После этого уберите символ кубического корня и перемножьте множители, чтобы получить ответ. Если останется какой-либо множитель, который нельзя разделить поровну на группы по три, это означает, что данное число не является полным кубом, и мы не можем найти кубический корень из этого числа.
Пример: Посмотрим, как найти кубический корень из 15625.
Формула кубического корня
Формула кубического корня помогает вычислить кубический корень любого заданного числа, выраженного в радикальной форме с помощью символа ∛. Его можно рассчитать, сначала выяснив разложение данного числа на простые множители, а затем применив формулу кубического корня. Предположим, что x — любое число такое, что x = y × y × y.
Формула для вычисления кубического корня выглядит следующим образом:
- Кубический корень из x = ∛x = ∛(y × y × y) = y
где y — кубический корень из любого числа x.
Это также означает, что число x будет идеальным кубом, если y имеет целочисленное значение.
Применение формулы кубического корня
Ниже приведены несколько основных применений формулы кубического корня,
- для решения кубических уравнений.
- найдите размеры куба, если задан объем.
- указать более точный размер квартиры и т.д.
Что такое куб числа?
Когда мы трижды умножаем число само на себя, полученное число (произведение) называется кубом исходного числа. Мы называем его кубом, потому что он используется для представления объема куба. Другими словами, число, возведенное в степень 3, называется кубом этого числа. Например, куб числа 3 равен 27. Это означает, что 3 × 3 × 3 = 27, и это можно записать как 3·9.0003 3 . Точно так же куб числа 4 равен 64, куб числа 5 равен 125 и так далее.
Чтобы найти куб числа, сначала умножьте это число само на себя, а затем снова умножьте полученное произведение на исходное число.
Таким же образом найдем куб числа 7. Мы знаем, что куб числа N равен N × N × N. Итак, куб числа 7 равен 7 × 7 × 7. Теперь, чтобы найти куб числа 7, сначала найдем значение 7 × 7. , Это значение равно 49. Теперь мы найдем 49 × 7. Это равно 343. Следовательно, мы можем сказать, что куб числа 7 равен 343.
Куб дроби
Подобно кубу числа, куб дроби можно найти, умножив его три раза. Например, куб дроби (2/5) можно записать как 2/5 × 2/5 × 2/5. Упрощая его дальше, мы получаем значение куба как (2 × 2 × 2) / (5 × 5 × 5). Это равно (2 3 / 5 3 ) = 8/125.
Куб отрицательных чисел
Процесс нахождения куба отрицательного числа такой же, как и для целого числа и дроби. Здесь всегда помните, что куб отрицательного числа всегда отрицателен, а куб положительного числа всегда положителен. Например, попробуем найти куб числа -7. Мы знаем, что куб числа -7 равен (-7) × (-7) × (-7). Теперь, чтобы найти куб (-7), мы сначала найдем значение (-7) × (-7).
Это значение равно 49. Теперь мы найдем 49 × (-7). Это равно -343. Следовательно, мы можем сказать, что куб числа -7 равен -343. Формула кубического корня для отрицательных чисел:
- Выполнить метод простой факторизации данного числа.
- Разделите полученные факторы на три группы, каждая из которых должна содержать одинаковый набор факторов.
- Умножьте множители любой группы, чтобы получить кубический корень.
- Просто произведение трех отрицательных значений дает отрицательный результат. который представлен отрицательным знаком с кубическим корнем отрицательного числа.
☛ Похожие темы:
Прочтите эти интересные статьи, связанные с кубическим корнем.
- Калькулятор кубического корня
- Квадраты и квадратные корни
- Радикальный
Список кубических корней чисел
Примеры кубического корня
Пример 1: Является ли число 729 идеальным кубом?
Решение:
Да, 729является совершенным кубом, потому что когда мы умножаем 9 × 9 × 9 = 9 3 = 729.
Это означает, что кубический корень из 729 равен 9.
Ответ: Да.
Пример 2: Возраст отца Эмили 27 лет. Найдите возраст Эмили, если ее возраст равен кубическому корню из возраста ее отца.
Решение:
Дано, возраст отца Эмили = 27 лет. Следовательно, возраст Эмили = кубический корень из 27 = ∛27 лет = 3 года.
Ответ: 3 года.
Пример 3: Проверить, является ли 512 совершенным кубом или нет.
Решение:
Найти: Является ли 512 идеальным кубом или нет.
Используя формулу кубического корня,
Кубический корень из 512 = ∛512=∛(2×2×2×2×2×2×2×2×2)=∛(8×8×8)
= 8, что является целым числом. Следовательно, 512 — совершенный куб.
Следовательно, 512 — идеальный куб.
Ответ: Да, это так.
перейти к слайдуперейти к слайдуперейти к слайду
Хотите создать прочную основу в математике?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними.
Испытайте Cuemath и приступайте к работе.
Записаться на бесплатный пробный урок
Практические вопросы по кубическому корню
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о Cube Root
Что такое кубический корень числа?
Кубический корень является обратным кубу числа и обозначается ∛. Например, ∛216, то есть кубический корень из 216 = 6, потому что, когда 6 умножается трижды на себя, получается 216. Другими словами, поскольку 6 3 = 216, мы имеем ∛216 = 6,
. В чем разница между кубом и кубическим корнем?
- Когда число умножается само на себя 3 раза, произведение равно кубу данного числа. Например, куб 3 равен 27, потому что 3 × 3 × 3 = 27,9.0148
- Кубический корень числа — это число, куб которого равен данному числу. Например, кубический корень из 27 равен
.Для чего используется кубический корень?
Кубический корень используется для решения кубических уравнений.
Они также используются для нахождения длины стороны куба, если известен его объем.
Как упростить кубический корень?
Кубический корень можно упростить, используя метод простой факторизации. Сначала выполните простую факторизацию данного числа, затем выньте общие делители в группах по 3. Умножьте эти общие делители, взяв только один из каждой группы, чтобы получить ответ.
Можно ли упростить отрицательный кубический корень?
Да, упрощение отрицательных кубических корней такое же, как и положительных кубических корней. Единственным отличием является наличие знака минус при кубическом корне из отрицательного числа.
Что не является идеальным кубом?
Число не является идеальным кубом, если мы не можем составить 3 равные группы делителей числа после разложения на простые множители. Например, 144 не является совершенным кубом, потому что не существует числа, которое при 3-кратном умножении само на себя дает 144 в качестве произведения. Другими словами, если кубический корень числа не является целым числом, то это не совершенный куб.
Что такое куб нечетного натурального числа?
Куб нечетного натурального числа всегда является нечетным числом. Например, 5 3 = 125, 7 3 = 343, 9 3 = 729 и т. д.
Может ли кубический корень любого нечетного числа быть четным?
Нет, кубический корень из нечетного числа всегда нечетный. Например, кубический корень из 27 = (27) 1/3 = 3. Здесь и 3, и 27 — нечетные числа.
Как легко вычислить кубический корень любого числа?
Самый простой и простой метод нахождения кубического корня любого числа — это метод разложения на простые множители.
Что такое формула кубического корня в алгебре?
В математике формула кубического корня используется для представления любого числа в форме его кубического корня, например, для любого числа x его кубический корень будет равен 3 √x = x 1/3 . Например, кубический корень из 125 равен 5 125 1/3 = (5 3 ) 1/3 = 5.
Что такое формула кубического корня для отрицательных чисел?
Да, можно найти кубический корень из отрицательных чисел. Например, -64 = (-4) × (-4) × (-4). Мы можем записать -64 как произведение трех отрицательных четверок. Таким образом, ∛-64 = -4, потому что произведение трех отрицательных значений дает отрицательный результат.
Как использовать формулу кубического корня?
Чтобы использовать формулу кубического корня
- Шаг 1: Определите простые множители числа, скажем x, используя метод разложения на простые множители.
- Шаг 3: Составьте группы полученных таким образом множителей, где каждая группа представляет собой произведение 3 одинаковых множителей.
- Шаг 3: Запишите это в виде 3 √x = 3 √(y×y×y), где y соответствует кубическому корню из x.
Как написать формулу кубического корня словами?
Кубический корень из любого числа — это число, возведенное в степень 1/3.
арифметика — Как вручную вычислить кубические корни
Используйте мой метод: Естественный алгоритм
См. расчетное представление алгоритма внизу: 92-3x+1$ начиная с $x=1$
- Пока $n>0$, делаем $x=x+1$ и продолжаем вычитание.
- Когда $n=0$, этот этап останавливается и число $N$ имеет действительный кубический корень из $x$.
- Когда $n<0$, этот этап останавливается, ближайший действительный кубический корень равен $x-1$, и мы продолжаем второй этап, чтобы найти числа после запятой.
Второй этап: Нахождение чисел после запятой:
Пусть $x$ — ближайший действительный кубический корень из $N$ 92+3s+1)=1518799-483607=1035192…(i=2)$
$s=402: b=1035192-486019=549173…(i=3)$
$s=403: b=549173 -488437=60736…(i=4)$
$s=404: b=60736-4=-430125$
Поскольку результат $b$ меньше нуля:
Делаем $i$ количеством вычитаний на шаге 3, не считая времени, в течение которого получилось $b<0$: $$i=4$$
- 92+3s+1)=11759079-4
В пробеле после запятой пишем число $i$: $$\sqrt[3]66≈4,04$$
67=-37242088$ …
Вычислительное представление алгоритма в JavaScript:
https://codepen.
io/am_trouzine/pen/GRyoWbM
Вычисление N-го корня:
25 https://m.youtube.com/watch?v=uEpv6_4ZBG4&feature=youtu.be
Мои заметки:
https://github.com/am-trouzine/Арифметические-алгоритмы-в-различных-системах счисления/ blob/master/Arithmetic%20algorithms%20in%20 Different%20numeral%20systems.pdf
Алгоритм Mental Cube Roots — World Mental Calculation
Существует множество способов мысленного вычисления кубических корней (для чисел, не являющихся точно кубическими). В этой статье мы объясним быстрый метод, который работает с любым числом и похож на метод, описанный для мысленного вычисления квадратных корней.
Введение:Этот метод легче понять, если мы сначала посмотрим на ответ в квадрате. Например, мы найдем кубический корень из 397758. Мы можем записать это как:
3 √397758 = ab.cdef… = 10*a + 1*b + 0,1*c + 0,01*d + 0,001* е + 0,0001*f + …
Следовательно, образуя куб из левой и правой частей:
397758 =
1000 * a³
+ 100 * 3a²b
+ 10 * [3a²c + 3ab²] 9 *
5 3a²d + 6abc + b³]
+ 0,1 * [3a²e + 6abd + 3ac² + 3b²c]
+ 0,01 * [ и так далее ]
внизу из-за факторов 1000, 100, 10 и т.
Метод: Шаг 1:д. Поэтому мы можем начать с вычисления a, вычитания верхней строки и использования второй строки для вычисления b, вычитания второй строки и использования третьей строки для вычисления c и т. д.
Вычислите первую цифру ответа. Здесь оно равно 7, потому что:
70³ = 343000 ≤ 397758 < 512000 = 80³
Шаг 2:Величина 3a² часто фигурирует в приведенном выше объяснении, поэтому мы вычислим ее сейчас, чтобы помочь нам позже:
3a² = 3*7*7 = 147
Шаг 3:Мы использовали первую строку объяснения (1000 * a³) для вычисления первой цифры a, поэтому мы можем вычесть эту первую строку. В первой строке используются только числа, кратные 1000, поэтому мы можем упростить умственную работу, используя только самые большие цифры:
397 – 343 = 54
Далее мы воспользуемся второй строкой алгоритма, в которой используются числа, кратные 100, поэтому теперь нам нужно рассмотреть следующую (четвертую) цифру числа 397758.
Из объяснения мы теперь есть:
547 = 3a²b + [все остальные строки, но это небольшие числа, которые мы проигнорируем позже]
Чтобы вычислить b, нам нужно разделить на 3a², и мы знаем, что в этом примере 3a² = 147
547 / 147 = 3 остаток 106
Итак, b = 3, и пока что ответ равен 73.
Шаг 4:Мы закончили с одной строкой и переходим к следующей. Переносим следующую цифру исходного числа 397758 в остаток:
106 -> 1065
Тогда следующая (третья) строка объяснения дает нам:
1065 = 3a²c + 3ab² + [все остальные строки]
Мы знаем a=7 и b=3, поэтому мы можем вычесть член 3ab² = 3 * 7 * 3 * 3 = 189:
1065 – 189 = 3a² * c + [все остальные строки]
876 = 147 * c + [все остальные строки]
876 / 147 = 5 (оставшееся 141)
Таким образом, c = 5, и ответ пока равен 73,5…
Шаг 5:Повторите шаг 4 для каждой новой цифры, которую вы хотите вычислить.
Таким образом, для каждой новой цифры:
- умножьте остаток на 10 и добавьте следующую цифру из исходного вопроса
.- вычесть все термины из следующей строки объяснения, кроме термина с новой неизвестной буквой
- разделить результат на 3a². Ответом является следующая цифра ответа, а остаток будет использоваться для вычисления следующей цифры.
Иногда необходимо выбрать меньшее число для ответа, чтобы (сверхбольшой) остаток был достаточно большим для вычитания членов на следующем шаге. См. непосредственно ниже пример этого.
Для иллюстрации приведем продолжение текущего примера:
- 141 * 10 + 8 = 1418
- 6abc = 6*7*3*5 = 630; 1418 – 630 = 788; б³ = 27; 788 – 27 = 761
- 761 / 147 = 4 (остаток 173)
Обратите внимание, что хотя 761 / 147 = 5 (остаток 26), это приведет к тому, что 260 – 630 – 525 – 135 < 0 при вычислении следующей цифры! Поэтому мы берем меньшее делимое (4), чтобы получить большой остаток.
К сожалению, это происходит очень часто во время этого алгоритма.
Назад к правильному ответу:
- 173 * 10 + 0 = 1730 (+0, потому что исходный вопрос был 397758,0…)
- 6абд = 6*7*3*4 = 504; 1730 – 504 = 1226; 3ac² = 3*7*5*5 = 525; 1226 – 525 = 701; 3b²c = 3*3*3*5 = 135; 701 – 135 = 566
- 566 / 147 = 3 (остаток 125)
Это дает нам ответ:
3 √397758 = 73,543 (Фактический ответ: 73,542712…)
РЕЗУМЮТСЯ:Требуется. некоторая интуиция, чтобы выбрать размер, необходимый для остатков.
Альтернативные методы, которые обобщаются на четвертый, пятый и более глубокие корни, включают:
- более быстрый метод оценки, обеспечивающий точность около 3 цифр для кубических корней.
- более продвинутый метод с использованием логарифмов.
Для практики с кубическими корнями и более глубокими корнями вы можете использовать учебное программное обеспечение Pegasus, указанное на этом веб-сайте.
Неточные кубические корни из 6-значных целых чисел были сложной задачей на чемпионате мира по умственным вычислениям 2012 года. Результаты и контрольные вопросы здесь.
Если у вас есть какие-либо вопросы или вы хотели бы получить от меня специализированный коучинг, вы можете связаться со мной здесь.
Как вычислять кубические корни в уме
Вот способ произвести впечатление на людей. Попросите кого-нибудь придумать число, состоящее не более чем из 3 цифр, и назвать вам его куб (для этого можно использовать калькулятор). Используя метод, о котором я собираюсь вам рассказать, вы можете вычислить исходное число, кубический корень из числа, которое вам дано, без необходимости выполнять какие-либо промежуточные вычисления, кроме сложения и вычитания чисел, содержащих не более 2 цифры. Если вы сможете выполнять эти промежуточные вычисления с нормальной скоростью, вы, вероятно, сможете вычислить кубический корень в течение минуты, при некоторой практике.
Предположим, что вам дали число (так что это исходное число, кубический корень, который вы пытаетесь найти).
Вы будете знать, что имеет не более 3 цифр. Если вы используете этот метод, вы будете вычислять три цифры одну за другой. Начальную и конечную цифры можно вычислить почти сразу; средняя цифра — это та, которую вы потратите большую часть своего времени на вычисление, потому что это часть вычислений, где вам нужно выполнить некоторые сложения и вычитания.
1. Последняя цифра
Чтобы найти конечную цифру, вы можете использовать тот факт, что для каждой пары чисел и , и имеют одинаковую конечную цифру тогда и только тогда, когда и имеют одинаковую конечную цифру. Другими словами, последняя цифра предсказуема по последней цифре . Можно использовать следующую таблицу.
Последняя цифра 0 1 2 3 4 5 6 7 8 9 Последняя цифра 0 1 8 7 4 5 6 3 2 9 Таблицу несложно запомнить.
Просто запомните это так: если последняя цифра 0, 1, 4, 5, 6 или 9, то последняя цифра такая же, иначе (если последняя цифра 2, 3, 7 или 8 ), последняя цифра равна 10 минус последняя цифра .
Если вам не интересно, почему это работает, вы можете пропустить несколько абзацев вперед. Но если да, то я объясню, почему это работает. Во-первых, обратите внимание, что для каждого числа последняя цифра является остатком от деления на 10, т. е. уникальным целым числом таким, что и для некоторого целого числа . Например, и . Кубирование обеих частей последнего уравнения дает
Теперь, если мы позволим быть последней цифрой , то есть остатком от деления на 10, то есть уникальным целым числом таким, что и для некоторого целого числа мы тогда имеем
откуда видно, что это также остаток от деления на 10, то есть последняя цифра . Это показывает, что для каждого числа последняя цифра является последней цифрой , где является последней цифрой .
Давайте составим таблицу, показывающую, какова последняя цифра для каждого из 10 возможных значений . Последние цифры каждого числа во второй строке выделены жирным шрифтом.
0 1 2 3 4 5 6 7 8 9 0 1 8 2 7 6 4 12 5 21 6 34 3 51 2 72 9 Теперь, возвращаясь к поставленной задаче, мы знаем конечную цифру , которая также является конечной цифрой , где последняя цифра .
Назовем этот номер. Из приведенной выше таблицы видно, что если равно 1, то равно 1; если 3, то 7; если 6, то 6; если 8, то 2 и так далее. На самом деле, для каждого возможного значения существует только одно возможное значение , и поэтому мы можем прочитать значение , найдя уникальную ячейку в нижней строке, содержащую число, последняя цифра которого равна , и увидев, какое число находится в ячейке. выше. Отсюда исходная таблица.
Это доказательство принципиально опирается на тот факт, что для каждого возможного значения существует только одно возможное значение . Если вы попытаетесь сделать то же самое, скажем, с квадратными корнями, вы обнаружите, что существуют некоторые возможные значения, для которых существует несколько возможных значений , и поэтому, хотя этот метод может сузить возможные значения, он не может дать вам точное значение.
2. Начальная цифра
Чтобы найти начальную цифру, взгляните на таблицу выше, в которой показаны кубы каждого из неотрицательных целых чисел меньше 10.
Вам нужно будет запомнить эту таблицу, к сожалению, для него нет простой сводки, как для другой таблицы. Однако знание первых 10 неотрицательных совершенных кубов полезно во многих ситуациях, когда вам нужно произвести расчеты в уме, а не только в этой ситуации.
Прежде всего, вам нужно записать как 9-значное число. Это означает, что если он имеет менее 9 цифр, ставьте перед ним 0, пока он не станет 9 цифр. Теперь посмотрите на первые 3 цифры числа , когда оно записывается так; это дает вам 3-значное число. Используя свои знания о первых 10 неотрицательных совершенных кубах, определите наибольший совершенный куб, который не больше этого трехзначного числа. Первая цифра — это кубический корень из этого совершенного куба. Вы также можете использовать следующую таблицу.
Первые 3 цифры 000 001–007 008–026 027–063 064–124 Первая цифра 0 1 2 3 4
Первые 3 цифры 125–215 216–342 343–511 512–728 729–999 Первая цифра 5 6 7 8 9 Чтобы понять, почему это работает, обратите внимание, что для каждого числа, состоящего не более чем из 3 цифр, первая цифра — это уникальное целое число, такое что , где — количество цифр .
Например, и . Кубирование каждой части этого неравенства дает . Например, и . И если наблюдается выполнение неравенства вида последнего для некоторого значения , то из кубических корней каждой части можно получить неравенство вида первого, тем самым показывая, что первая цифра числа является .
Кстати, эта часть метода не опирается на тот факт, что это идеальный куб; он также будет работать для нахождения первой цифры иррациональных кубических корней. Его также можно обобщить без усложнения, чтобы найти первую цифру корней любого порядка: квадратные корни, корни 4-й степени и т. д.
3. Средняя цифра
Самая умная часть метода — вычисление средней цифры . В отличие от начальной и конечной цифр, нет простой характеристики того, как средняя цифра относится ко всему числу. Вместо этого мы воспользуемся довольно неясным фактом, который связывает три цифры числа . Таким образом, среднюю цифру можно вычислить только тогда, когда известны две другие цифры. Этот неясный факт заключается в том, что для каждого числа остаток от деления на 11 такой же, как остаток от деления на 11 переменной суммы цифр числа .
Под знакопеременной суммой цифр я понимаю сумму цифр при разрядах, соответствующих четным степеням числа 10 (разряды единиц, разряды сотен, разряды десятков тысяч и т. д.) минус сумма цифр при места, соответствующие нечетным степеням числа 10 (разряд десятков, разряд тысяч, разряд сотен тысяч и т. д.). Например, альтернированная сумма цифр числа 121281 равна , и, конечно, у нас есть , а , поэтому остатки 121281 и -5 при делении на 11 одинаковы. На практике, чтобы вычислить переменную сумму , вы смотрите на каждую цифру по очереди, двигаясь справа налево (а не в том порядке, в котором записываются цифры, то есть слева направо!) и чередуетесь между добавлением и вычитанием цифры из Общая; вот почему это называется альтернирующей суммой. Может быть полезно взять цифры группами по два и сначала найти разницу между двумя цифрами в группе, а затем добавить ее к сумме; таким образом, вы с меньшей вероятностью запутаетесь, поскольку будете делать одно и то же на каждом этапе. Например, чтобы вычислить переменную сумму 121281, вы видите это и устанавливаете итог в , затем вы видите это и устанавливаете итог в , и, наконец, вы видите это и устанавливаете итог в .
Кстати, если сумма переменных неотрицательна и меньше 11, то она равна остатку от деления на 11; в противном случае, хотя оно часто будет достаточно маленьким, чтобы вы могли сразу увидеть его остаток при делении на 11, вы могли бы найти альтернированную сумму цифр альтернированной суммы, повторив процесс, чтобы получить еще меньшее число.
Если вы просто хотите посмотреть, как вычислить среднюю цифру, пропустите вперед, но вам может быть интересно, почему эти два остатка одинаковы, поэтому я приведу вам доказательство. Предположим, это целое число с цифрами. Пусть это будет его цифра единиц, пусть это будет цифра десятков, … и пусть будет его цифра s, так что
Мы также можем записать это как
Для каждого целого числа, такого что , расширяется в сумму, которую можно записать как для некоторого целого числа (потому что каждый член в сумме, кроме имеет по крайней мере один фактор 11). Следовательно, у нас есть
, из которого видно, что остаток от деления на 11 будет таким же, как остаток от деления на 11 (по той же логике, которую мы использовали выше, чтобы показать это, и имели те же остатки при делении на 10) .
Это завершает доказательство.
Итак, как использовать этот факт для вычисления средней цифры? Ну, во-первых, обратите внимание, что для каждого числа, если мы позволим быть остатком от деления на 11, то это остаток от деления на 11. Мы доказали это выше для деления на 10, а не для деления на 11, и доказательство для деления к 11 почти то же самое. Просто замените ссылки на 10 ссылками на 11. Поэтому я не буду здесь подробно рассматривать доказательство. Вместо этого мы можем сразу же увидеть, каков остаток от деления на 11 для каждого из 11 возможных значений . В следующей таблице термины «частное от» и «остаток от» следует рассматривать как относящиеся к частному и остатку от деления на 11; внутри таблицы просто нет места для полного описания.
0 1 2 3 4 5 6 7 8 9 10 0 1 8 27 64 125 216 343 512 729 1000 Частное 0 0 0 2 5 11 19 31 46 66 90 Остаток 0 1 8 5 9 4 7 2 6 3 10 Опять же, эта таблица имеет удобное свойство, заключающееся в том, что для каждого возможного значения существует только одно возможное значение , и поэтому мы можем использовать ее для нахождения значения заданного значения .
Или, что более удобно, мы можем использовать следующую перевернутую форму таблицы.
0 1 2 3 4 5 6 7 9 10 0 1 7 9 5 3 8 6 2 4 10 К сожалению, нет простого способа обобщить содержимое этой таблицы, как это было с предыдущей. Это просто более или менее случайное соответствие, которое вы должны запомнить. Вот почему вам нужно немного практики, чтобы иметь возможность быстро выполнять вычисления.
Но если вы постараетесь и будете проверять себя через равные промежутки времени в течение пары дней, вы, вероятно, сможете успешно запомнить соответствие.
Итак, чтобы найти среднюю цифру, вы находите остаток от деления на 11, вычисляя альтернированную сумму цифр (и беря остаток от деления на 11 этой альтернирующей суммы, хотя часто это будет не -отрицательный и меньше 11, и в этом случае он совпадает с его остатком). Затем вы используете приведенную выше таблицу, чтобы найти остаток от деления на 11. Принимая во внимание тот факт, что мы говорили выше об остатках от деления на 11, возможно, теперь вы понимаете, что делать. Переменная сумма цифр , где начальная цифра , является средней цифрой и является последней цифрой . Вы можете вычислить значения и , и вы также знаете, что остаток от деления на 11 этой переменной суммы равен . В этот момент вы можете сразу увидеть, что должно быть, но его значение можно вычислить систематически: у нас есть для некоторого целого числа , поэтому , которое показывает, что это остаток от деления на 11 от .
Это немного сложно, поэтому пример будет полезен. Предполагать . Конечная цифра также должна быть 6 (используя таблицу), а начальная цифра должна быть 6, так как . Следующим шагом является вычисление альтернированной суммы цифр : . Из таблицы следует, что остаток от деления на 11 равен 9. Следовательно, остаток от деления на 11 числа , т. е. где средняя цифра числа , должен быть 9. Тогда легко видеть, что должно быть 3, так . Последний шаг также можно сделать, отметив, что . Попробуйте воспользоваться калькулятором, чтобы убедиться в этом.
4. Резюме
Здесь я все подробно объяснил, поэтому может показаться, что этот метод очень сложен, но на самом деле это не так. Вот пошаговое описание метода с приблизительными оценками того, сколько времени вам потребуется для выполнения каждого шага.
- Посмотрите на последнюю цифру и используйте свои знания о соответствии, чтобы найти последнюю цифру . (Если заканчивается на 2, 3, 7 или 8, это 10 минус последняя цифра , а в противном случае заканчивается той же цифрой, что и .
)
- Найдите первые 3 цифры 9-значного числа. Используйте свои знания о первых десяти неотрицательных совершенных кубах и найдите наибольшее целое число, меньшее полученного трехзначного числа. Первая цифра .
- Найдите чередующуюся сумму цифр числа , и при необходимости повторите процесс, чтобы получить остаток от деления на 11.
- Используйте свои знания соответствия, чтобы найти остаток от деления на 11 из .
- Вычислите и найдите остаток от деления на 11. Средняя цифра .
Если вы все запомнили, я думаю, что шаг 1 займет не более 2 секунд, шаг 2 займет, возможно, немного больше времени, но все же не более 5 секунд, шаг 3 займет большую часть вашего времени, максимум 30 секунд , с потенциалом длиться намного дольше, если вы запутаетесь, шаг 4 займет не более 2 секунд, а шаг 5 займет не более 10 секунд. Поэтому я могу с уверенностью сказать, что вы сможете вычислить кубический корень за минуту.
Я узнал об этом из этого поста на Dead Reckonings.
Если вас это интересует, взгляните на этот пост — он охватывает множество других методов ментального расчета в более сжатой форме, чем этот пост. Не знаю, как вы, но пока я не наткнулся на этот пост, я всегда ассоциировал тему вычислений в уме с утомительным выполнением алгоритмов и поэтому считал это неинтересным и не совсем «настоящей математикой». Но по мере того, как вы приобретаете больше математических знаний, вы обнаружите, что расчеты в конечном итоге становятся своего рода творческим процессом, когда вы часто не придерживаетесь одного метода, а импровизируете способ решения проблемы, опираясь на то, что вы знаете, так что это можно решить как можно быстрее. Также интересно посмотреть, почему эти алгоритмы работают, и подумать, как их можно было бы придумать. Если вам интересно, вы можете попробовать придумать аналогичные алгоритмы для других видов корней. Или, возможно, посмотреть, есть ли способ нахождения кубических корней чисел с числом больше 9.цифры (хотя я понятия не имею, как вы можете это сделать).
Нравится:
Нравится Загрузка…
Запись опубликована в рубрике Математика с метками математика, вычисление в уме. Добавьте постоянную ссылку в закладки.
Квадратные и кубические корни действительных чисел
Определение квадратных и кубических корней
Квадратный корень Это число, которое при умножении само на себя дает исходное число. числа — это число, которое при умножении само на себя дает исходное число. Например, 4 — это квадратный корень из 16, потому что 42=16. Поскольку (−4)2=16, мы можем сказать, что −4 также является квадратным корнем из 16. Каждое положительное действительное число имеет два квадратных корня, один положительный и один отрицательный. По этой причине мы используем радикальный знак. Символ используется для обозначения квадратного корня. для обозначения главного (неотрицательного) квадратного корняНеотрицательный квадратный корень. и знак минус перед радикалом - для обозначения отрицательного квадратного корня.
16=4 Положительный квадратный корень из 16−16=−4 Отрицательный квадратный корень 2 с нулевым квадратным корнем 15 900 ровно единица с квадратным корнем 15 900.
0=0
Если подкоренное число и число внутри радикала, число внутри знака радикала, не равно нулю и может быть разложено на множители как квадрат другого ненулевого числа, то квадратный корень числа очевиден. В этом случае имеем следующее свойство:
a2=a, if a≥0
Важно отметить, что и должны быть неотрицательными. Обратите внимание, что (−3)2≠−3, потому что радикал обозначает главный квадратный корень. Вместо этого
(−3)2=9=3
Это различие будет тщательно рассмотрено позже в курсе.
Пример 1
Извлечение квадратного корня:
- 121
- 0,25
- 49
Решение:
- 121=112=11
- 0,25=0,52=0,5
- 49=(23)2=23
Пример 2
Найдите отрицательный квадратный корень:
- −64
- −1
Решение:
- −64=−82=−8
- −1=−12=−1
Подкоренное число не всегда может быть правильным квадратом.
Если натуральное число не является полным квадратом, то его квадратный корень будет иррациональным. Рассмотрим 5, мы можем получить приближение, оценив его с помощью идеальных квадратов 4 и 92≈5
Далее рассмотрим квадратный корень из отрицательного числа. Чтобы определить квадратный корень из -9, вы должны найти число, которое при возведении в квадрат дает -9,
-9=? or ( ? )2= −9
Однако возведение в квадрат любого действительного числа всегда дает положительное число,
(3)2=9 и (−3)2=9
оставил неопределенным. Попробуйте вычислить −9 на своем калькуляторе; что он говорит? А пока скажем, что −9 не является действительным числом. Квадратный корень из отрицательного числа определяется позже в курсе.
Кубический кореньЧисло, которое при трехкратном умножении само на себя дает исходное число, обозначаемое как 3, — это число, которое при трехкратном умножении само на себя дает исходное число. Кроме того, мы обозначаем кубический корень, используя символ 3, где 3 называется индексом.
Положительное целое число n в обозначении n, которое используется для обозначения n -го корня. Например,
83=2, потому что 23=8
Произведение трех равных множителей будет положительным, если множитель положительный, и отрицательным, если множитель отрицательный. По этой причине любое действительное число будет иметь только один действительный кубический корень. Следовательно, технические особенности, связанные с главным корнем, не применяются. Например,
−83=−2, потому что (−2)3=−8
В общем, для любого действительного числа a мы имеем следующее свойство:
a33=a
При упрощении кубических корней ищите факторы, являющиеся совершенными кубами.
Пример 3
Найдите кубический корень:
- 1253
- 03
- 8273
Решение:
- 1253=533=5
- 03=033=0
- 8273=(23)33=23
Пример 4
Найдите кубический корень:
- −273
- −13
Решение:
- −273=(−3)33=−3
- -13=(-1)33=-1
Возможно, подкоренное число не является совершенным кубом.
Если это так, то его кубический корень будет иррациональным. Например, 23 — иррациональное число, которое можно приблизительно приблизить на большинстве калькуляторов с помощью корневой кнопки x. В зависимости от калькулятора мы обычно вводим индекс перед нажатием кнопки, а затем подкоренное число следующим образом: 93≈2
Позже в этом курсе мы расширим эти идеи, используя любое целое число в качестве индекса. Важно отметить, что квадратный корень имеет индекс 2; следовательно, следующие эквивалентны:
a2=a
Другими словами, если индекс не указан, предполагается, что он представляет собой квадратный корень.
Упрощение квадратных и кубических корней
Не всегда подкоренное число является полным квадратом. Если нет, мы используем следующие два свойства, чтобы упростить выражение. Даны действительные числа An и Bn, где B≠0,
Для заданных действительных чисел An и Bn A⋅Bn=An⋅Bn.
Для заданных действительных чисел An и Bn ABn=AnBn.
Упрощенный радикал Радикал, в котором подкоренное число не состоит ни из каких множителей, которые могут быть записаны в виде совершенных степеней индекса.
— это тот, где подкоренное число не состоит из каких-либо множителей, которые можно записать в виде совершенных степеней индекса. Учитывая квадратный корень, идея состоит в том, чтобы определить наибольший квадратный множитель подкоренного числа, а затем применить свойство, показанное выше. Например, чтобы упростить 12, обратите внимание, что 12 не является идеальным квадратом. Однако у числа 12 есть совершенный квадратный множитель, 12=4⋅3. Примените свойство следующим образом: 12=4⋅3 Применить правило произведения для радикалов. =4⋅3 Упростить.=2⋅3 Число 23 — это упрощенное иррациональное число. Вас часто просят найти примерный ответ, округленный до определенного знака после запятой. В этом случае используйте калькулятор, чтобы найти десятичную аппроксимацию, используя либо исходную задачу, либо ее упрощенный эквивалент. 12=23≈3,46 Для проверки посчитайте 12 и 23 на калькуляторе и убедитесь, что оба результата приблизительно равны 3,46.
Пример 5
Упростите: 135.
Решение:
Начните с нахождения наибольшего квадрата числа 135. 135 = 9om15 Примените правило продукта для радикалов. = 9om15 Simplify. = 3 %
Ответ: 315
Пример 6
Упрощение: 108169.
Решение:
Мы начинаем с нахождения основных факторов. как 108, так и 169. Это позволит нам легко определить самые большие совершенные квадратные множители.
108 = 22 ОТДЕЛА 33 = 22 ОТДЕЛА 32 ОТ 3169 = 132
Следовательно,
108169 = 22 %32 ОТДЫХ 3132 Применить правило продукта и коэффициент для радикалов. = 22 ОТ 322 ОТ 3132. 313=6313
Ответ: 6313
Пример 7
Упрощение: −5162.
Решение:
−5162=−5⋅81⋅2=−5⋅81⋅2=−5⋅9⋅2=−45⋅2=−452
Ответ: −452
Попробуйте это
6 ! Упростите: 4150.
Ответ: 206
(нажмите, чтобы посмотреть видео)
Кубический корень упрощается, если он не содержит множителей, которые можно записать в виде идеальных кубов.
Идея состоит в том, чтобы определить наибольший кубический коэффициент подкоренного числа, а затем применить правило произведения или частного для радикалов. Например, чтобы упростить число 803, обратите внимание, что число 80 не является идеальным кубом. Однако 80=8⋅10, и мы можем написать 9.0005
803=8⋅103 Применить правило произведения для радикалов. = 83om103 Упростить. = 2 %03
Пример 8
Упростить: 1623.
Решение:
Начните с найдя самый большой коэффициент совершенного куба 162.
162 = 34 ОТ = 27z6
Следовательно,
1623 = 27 ОБЛАСТИ Примените правило продукта для радикалов. = 273om63 Упрощение. = 3 %
Ответ: 363
Пример
Упрощайте: -163433.
Решение:
−163433=−1⋅8⋅23733=−13⋅83⋅23733=−1⋅2⋅237=−2 237
Ответ: −2 237
02 это! Упростите: −2 −2563.
Ответ: 8 43
(щелкните, чтобы посмотреть видео)
Рассмотрим следующие два вычисления:
81=92=981=92=(9)2=(3)2=9
имеет значение, применяем ли мы сначала показатель степени или сначала извлекаем квадратный корень.
Это верно для любого положительного действительного числа. У нас есть следующее,
a2=(a)2=a, if a≥0
Пример 10
Упростить: (10)2.
Решение:
Примените тот факт, что (a)2=a, если a неотрицательно.
(10)2=10
Теорема Пифагора
Прямоугольный треугольникТреугольник с углом, равным 90°. треугольник, у которого один из углов равен 90°. Сторона, противоположная прямому углу, является самой длинной стороной, называемой гипотенузой. Самая длинная сторона прямоугольного треугольника; это всегда будет сторона, противоположная прямому углу., а две другие стороны называются катетами. Стороны прямоугольного треугольника, которые не являются гипотенузой. Эта геометрическая фигура используется во многих реальных приложениях. Теорема ПифагораГипотенуза любого прямоугольного треугольника равна квадратному корню из суммы квадратов длин сторон треугольника. утверждает, что для любого прямоугольного треугольника с сторонами, равными a и b единиц, квадрат меры гипотенузы c равен сумме квадратов мер катетов, a2+b2=c2.
Другими словами, гипотенуза любого прямоугольного треугольника равна квадратному корню из суммы квадратов его катетов.
Пример 11
Вычислите диагональ квадрата со сторонами, равными 5 единицам.
Решение:
Диагональ квадрата образует равнобедренный прямоугольный треугольник, в котором две равные стороны равны 5 единиц каждая.
Мы можем использовать теорему Пифагора, чтобы определить длину гипотенузы.
c=a2+b2=52+52=25+25=50=25⋅2=25⋅2=5⋅2
Ответ: 52 единицы
Теорема Пифагора фактически утверждает, что длины сторон удовлетворяют свойству a2 +b2=c2 — необходимое и достаточное условие прямоугольных треугольников. Другими словами, если мы можем показать, что сумма квадратов длин катетов треугольника равна квадрату гипотенузы, то это должен быть прямоугольный треугольник.
Пример 12
Определите, является ли треугольник с катетами a=1 см, b=2 см и гипотенузой b=5 см прямоугольным.
Решение:
Если катеты удовлетворяют условию a2+b2=c2, то теорема Пифагора гарантирует, что треугольник прямоугольный.
a2+b2=c2(1)2+(2)2=?(5)21+4=55=5✓
Ответ: Да, описанный треугольник прямоугольный.
Ключевые выводы
- Квадратный корень из числа — это число, которое при возведении в квадрат дает исходное число. Главный квадратный корень из положительного действительного числа — это положительный квадратный корень. Квадратный корень из отрицательного числа в настоящее время не определен.
- При упрощении квадратного корня числа ищите совершенные квадратные множители подкоренного числа. Примените правило произведения или частного для радикалов, а затем упростите.
- Кубический корень числа — это число, которое при возведении в куб дает исходное число. Каждое действительное число имеет только один действительный кубический корень.
- При упрощении кубических корней ищите совершенные кубические множители подкоренного числа. Примените правило произведения или частного для радикалов, а затем упростите.
- Теорема Пифагора дает нам необходимое и достаточное условие прямоугольных треугольников: a2+b2=c2 тогда и только тогда, когда a , b и c представляют длины сторон прямоугольного треугольника.
Тематические упражнения
Часть A. Квадратные и кубические корни
Упрощение.
81
49
−16
−100
2516
964
14
1100
−1
−25
0,36
1,21
(−5)2
(−6)2
264
336
−104
−825
643
1253
−273
−13
03
0,0083
0,0643
−−83
−10003
(−8)33
(−15)33
12163
27643
−183
−1273
5 3433
4 5123
−10 83
−6 −643
8−83
Используйте калькулятор, чтобы округлить до сотых.

3
10
19
7
35
−23
33
63
283
93
4 103
−3 123
Определите множество, состоящее из квадратов первых двенадцати натуральных чисел.
Определите множество, состоящее из кубов первых двенадцати натуральных чисел.
Часть B: Упрощение квадратных и кубических корней
Упрощение.
18
50
24
40
5081
5425
472
327
−580
−6128
3−40
5−160
163
543
813
243
481253
135643
7 5003
25 6863
−2 −1623
5 −963
(64)2
(25)2
(2)2
(6)2
Часть C: Теорема Пифагора
Если длина двух катетов прямоугольного треугольника равна 3 единицам и 4 единицам, найдите длину гипотенузы.
Если длина двух катетов прямоугольного треугольника равна 6 единицам и 8 единицам, найдите длину гипотенузы.
Если длина двух равных катетов равнобедренного прямоугольного треугольника равна 7 единицам, то найдите длину гипотенузы.
Если длина двух равных катетов равнобедренного прямоугольного треугольника равна 10 единицам, то найдите длину гипотенузы.
Вычислите диагональ квадрата со стороной 3 сантиметра.
Вычислите диагональ квадрата со стороной 10 сантиметров.
Вычислите диагональ квадрата со стороной 6 см.
Вычислите диагональ квадрата со стороной 10 сантиметров.
Вычислите длину диагонали прямоугольника размером 4 см на 8 см.
Вычислите длину диагонали прямоугольника размером 8 на 10 метров.
Вычислите длину диагонали прямоугольника размером 3 метра на 2 метра.
Вычислите длину диагонали прямоугольника размером 6 метров на 10 метров.
Чтобы вновь построенные ворота были квадратными, измеренная диагональ должна совпадать с расстоянием, рассчитанным по теореме Пифагора. Если ворота имеют размеры 4 фута на 4 фута, то какая диагональ должна быть в дюймах? (Округлить до десятых долей дюйма.
)
Если дверная рама имеет размеры 3,5 фута на 6,6 фута, какова должна быть диагональ, чтобы рама была идеальным прямоугольником?
Определите, является ли данный треугольник с катетами a и b и гипотенузой c прямоугольным или нет.
а=3, б=7 и с=10
а=5, б=12 и с=13
а=8, б=15 и с=17
а=7, б=24 и с=30
а=3, б=2 и с=13
а=7, б=4 и с=11
а=4, б=3 и с=19
а=6, б=15 и с=21
Часть D: Дискуссионная доска
Что говорит ваш калькулятор после извлечения квадратного корня из отрицательного числа? Поделитесь своими результатами на доске обсуждений и объясните, почему это так.
Исследуйте и обсудите историю теоремы Пифагора.
Исследовать и обсудить историю извлечения квадратного корня.
Обсудите значение главного квадратного корня. Почему та же проблема не возникает с кубическими корнями? Приведите несколько примеров с вашим объяснением.
Ответы
9
−4
54
12
Не настоящее число.
0,6
5
16
−20
4
−3
0
0,4
−10
−15
34
−13
32
24
1,73
4,36
6,71
1,44
3,04
8,62
{1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144}
32
26
529
242
−205
Не настоящее число.
2 23
3 33
2 635
35 43
6 63
64
2
5 шт.
72 шт.
32 сантиметра
23 см
45 см
7 метров
Диагональ должна составлять примерно 67,9дюймы.
Не прямоугольный треугольник.
Прямоугольный треугольник.
Прямоугольный треугольник.
Прямоугольный треугольник.
Ответ может отличаться
Ответ может отличаться
Калькулятор кубического корня
Калькулятор кубического корня
Пожалуйста, введите реальный номер: Результат кубического корня: Введите числовое значение от —
- 72036854775807 до +
- 72036854775807.
Котировки Что такое кубический корень?
Определение кубического корня
Кубический корень числа а — это число х такое, что х 3 = а, другими словами, число х, кубом которого является а. Например, 0 — это кубический корень из 0, потому что 0 3 = 0•0•0 = 0, —0 — это кубический корень из —0, потому что (-0) 3 = (—0)•(—0) •(-0) = -0.
Perfect Cube Coots Table 1-100
См. Также нашу кубическую корневую таблицу от 1 до 1000.
x Корень Куба 1 1 1 1 0008 1 1 8 2 27 3 64 4 125 5 216 6 343 7 512 8 729 9 1000 10 1331 11 1728 12 2197 13 2744 14 3375 15 4096 16 4913 17 5832 18 6859 19 8000 20 9261 21 10648 22 12167 22 12167 22 12167 22 12167 22 12167 22 22 0010 23 13824 24 15625 25
x Cube Root 17576 26 19683 27 21952 28 24389 29 27000 30 29791 31 29791 31 001032768 32 35937 33 39304 34 42875 35 46656 36 50653 37 54872 38 59319 39 64000 40 68921 41 68921 41 9000 68921 41 74088 42 79507 43 85184 44 45 97336 46 103823 47 110592 48 117649 49 125000 50
X
3 X0068 Cube Root 132651 51 140608 52 148877 53 157464 54 166375 55 175616 56 185193 57 195112 58 205379 59 216000 59 216000 0010 60 226981 61 238328 62 250047 63 262144 64 274625 65 287496 66 300763 67 314432 68 328509 69 343000 69 343000 343000 343000 69 328509 0009 70 357911 71 373248 72 389017 73 405224 74 421875 75
x Cube Root 438976 76 456533 474552 9000 78474552 9000 78474552 9000 78474552 9000474552 9000474552 9000474552 77 00104 79 512000 80 531441 81 551368 82 571787 83 5 84 614125 85 636056 658503 87 681472 88 681472 88 681472 681472 9000681472 9000681472 90000013 681472 9000704969 89 729000 90 753571 91 778688 92 804357 93 830584 94 857375 95 884736 96 3 97 941192 98 941192 98 9000 941192 98 970299 99 1000000 100 Cube Croot Calculator
Пожалуйста, свяжите на этой странице! Просто щелкните правой кнопкой мыши на изображении выше, затем выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.



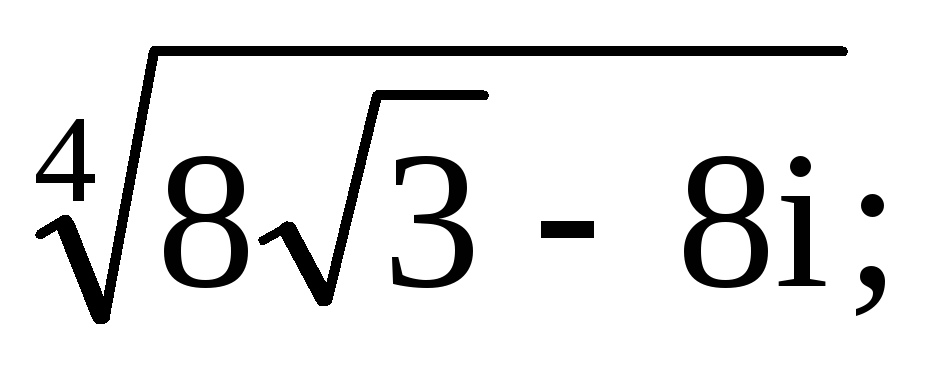 {2}}=1$.
{2}}=1$. \]
\] y».
y». Выяснилось, что значения кубического корня можно находить с помощью метода итераций, также можно аппроксимировать кубический корень, возводить число в степень 1/3, искать значения корня третьей степени с помощью Microsoft Office Ecxel, задавая формулы в ячейках.
Выяснилось, что значения кубического корня можно находить с помощью метода итераций, также можно аппроксимировать кубический корень, возводить число в степень 1/3, искать значения корня третьей степени с помощью Microsoft Office Ecxel, задавая формулы в ячейках. Операция извлечения арифметического корня любой степени n эквивалентна операции возведения в степень 1/n. Для практического вычисления кубического корня можно использовать несколько способов.
Операция извлечения арифметического корня любой степени n эквивалентна операции возведения в степень 1/n. Для практического вычисления кубического корня можно использовать несколько способов. Поэтому используйте функцию для возведения числа в степень. Извлечению корня третьей степени соответствует возведение в степень 1/3 (одна треть).
Поэтому используйте функцию для возведения числа в степень. Извлечению корня третьей степени соответствует возведение в степень 1/3 (одна треть).


 Число 571787 заканчивается на 7. Такой вариант возможен только тогда, когда в куб возводится число с тройкой в конце. Таким образом, результат корня равен 83.
Число 571787 заканчивается на 7. Такой вариант возможен только тогда, когда в куб возводится число с тройкой в конце. Таким образом, результат корня равен 83. Думаю, что это теперь для вас не проблема.
Думаю, что это теперь для вас не проблема.

 ..
.. 
 Если выразить это, это будет 9 x 9 = 81.
Если выразить это, это будет 9 x 9 = 81.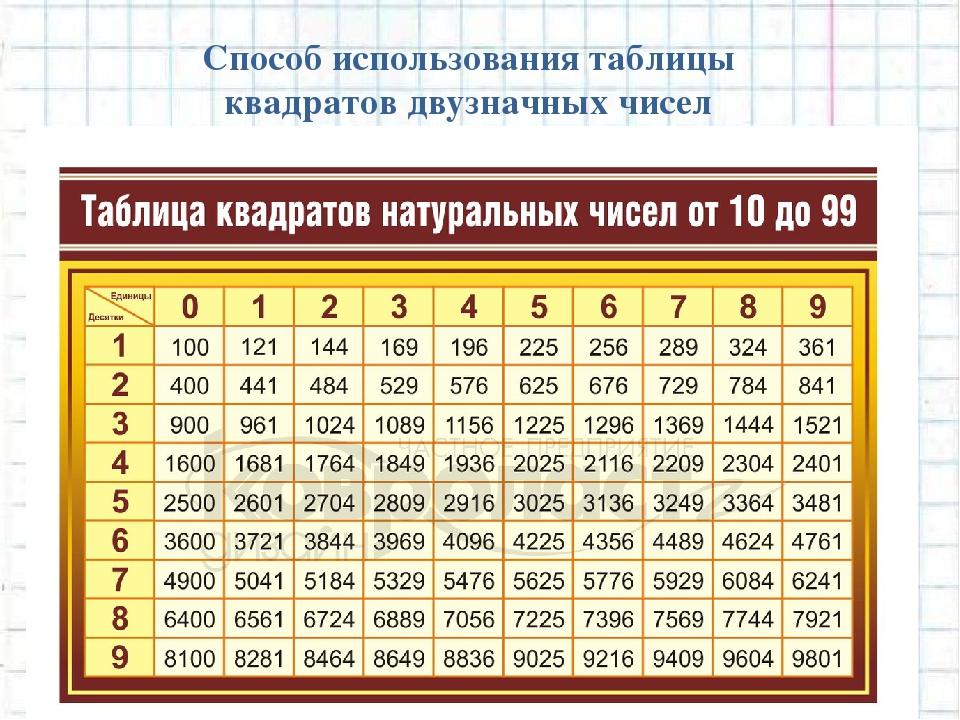

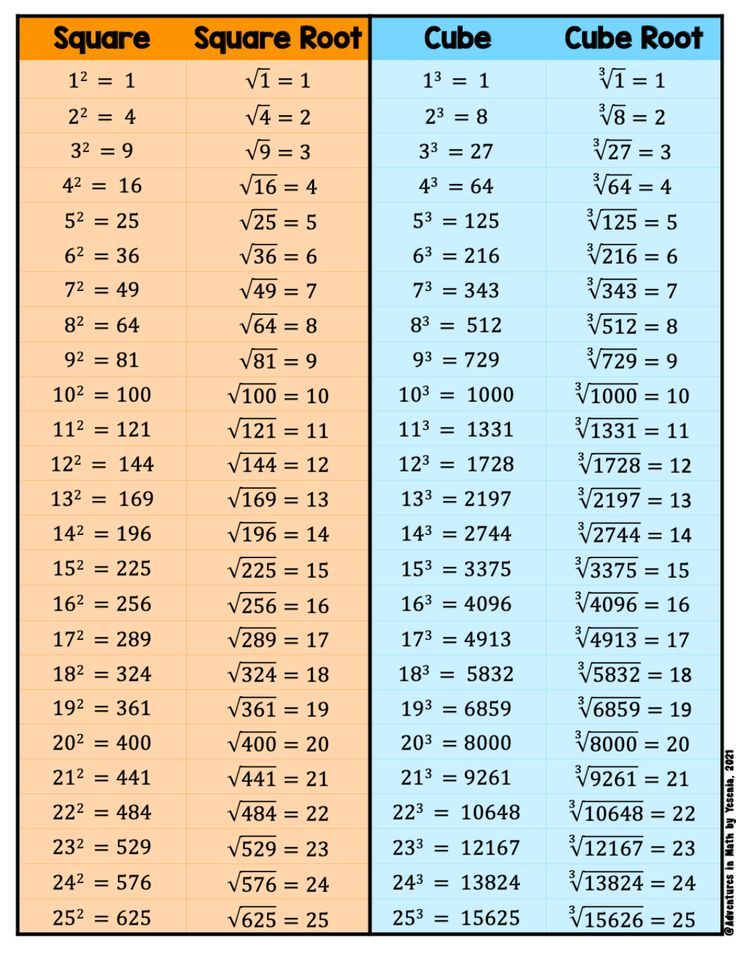 Обозначается показателем степени «1/3». Например, кубический корень из 27 равен 27.1/3 = 3.
Обозначается показателем степени «1/3». Например, кубический корень из 27 равен 27.1/3 = 3.
 Как возвести в степень 2/6? Сначала извлечь корень 6-ой степени, потом возвести в квадрат. Но это невозможно для отрицательных чисел.
Как возвести в степень 2/6? Сначала извлечь корень 6-ой степени, потом возвести в квадрат. Но это невозможно для отрицательных чисел. 3= -8 т е обратная связь
3= -8 т е обратная связь

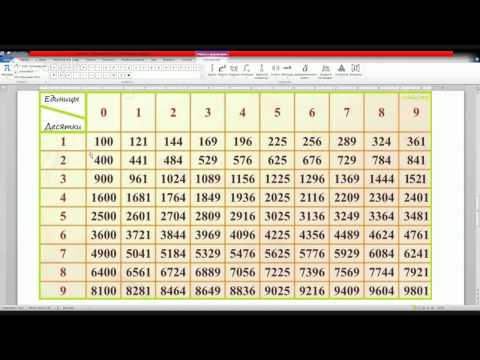
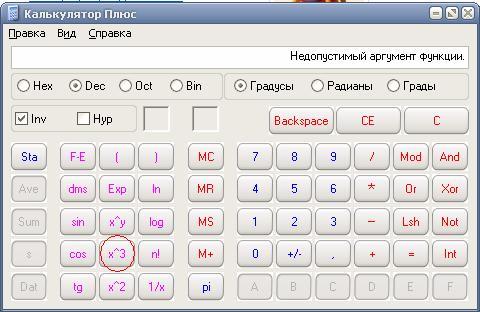 y»-«m».
y»-«m».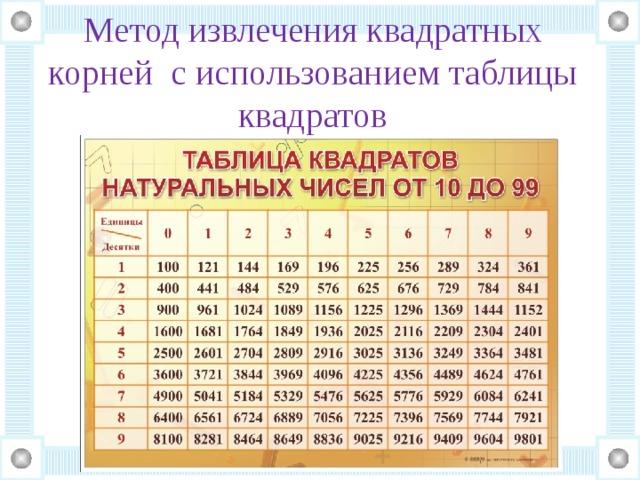
 01 (точное значение 1.7099).
01 (точное значение 1.7099). Это надо столько возиться.
Это надо столько возиться. 
 Куб для числа (x) представлен как x 3 и читается как «x в кубе» (или) «x в степени 3» (или) «x в степени 3». Например, возьмем число 5. Мы знаем, что 5 × 5 × 5 = 125. Следовательно, 125 называется кубом из 5. С другой стороны, нахождение кубического корня числа включает процесс, обратный куб числа и обозначается ∛. В том же примере 5 называется кубическим корнем числа 125 и записывается как ∛125 = 5. На этой странице мы узнаем больше о кубах и кубических корнях числа.
Куб для числа (x) представлен как x 3 и читается как «x в кубе» (или) «x в степени 3» (или) «x в степени 3». Например, возьмем число 5. Мы знаем, что 5 × 5 × 5 = 125. Следовательно, 125 называется кубом из 5. С другой стороны, нахождение кубического корня числа включает процесс, обратный куб числа и обозначается ∛. В том же примере 5 называется кубическим корнем числа 125 и записывается как ∛125 = 5. На этой странице мы узнаем больше о кубах и кубических корнях числа. Не так ли? Ну идея похожа. Корень означает первоисточник или происхождение. Итак, нам просто нужно подумать «куб какого числа нужно взять, чтобы получить данное число». В математике определение кубического корня записывается как Кубический корень — это число, которое нужно умножить три раза, чтобы получить исходное число. Теперь давайте посмотрим на формулу кубического корня, где у — кубический корень из х. ∛х = у. Подкоренной знак ∛ используется как символ кубического корня для любого числа с маленькой цифрой 3, написанной в верхнем левом углу знака. Другой способ обозначить кубический корень — написать 1/3 как показатель степени числа.
Не так ли? Ну идея похожа. Корень означает первоисточник или происхождение. Итак, нам просто нужно подумать «куб какого числа нужно взять, чтобы получить данное число». В математике определение кубического корня записывается как Кубический корень — это число, которое нужно умножить три раза, чтобы получить исходное число. Теперь давайте посмотрим на формулу кубического корня, где у — кубический корень из х. ∛х = у. Подкоренной знак ∛ используется как символ кубического корня для любого числа с маленькой цифрой 3, написанной в верхнем левом углу знака. Другой способ обозначить кубический корень — написать 1/3 как показатель степени числа. Другими словами, совершенный куб — это число, кубический корень которого является целым числом. Его также называют «кубическим числом». В следующей таблице показаны совершенные кубы первых 10 натуральных чисел.
Другими словами, совершенный куб — это число, кубический корень которого является целым числом. Его также называют «кубическим числом». В следующей таблице показаны совершенные кубы первых 10 натуральных чисел.
 Это также означает, что число x будет идеальным кубом, если y имеет целочисленное значение.
Это также означает, что число x будет идеальным кубом, если y имеет целочисленное значение. Таким же образом найдем куб числа 7. Мы знаем, что куб числа N равен N × N × N. Итак, куб числа 7 равен 7 × 7 × 7. Теперь, чтобы найти куб числа 7, сначала найдем значение 7 × 7. , Это значение равно 49. Теперь мы найдем 49 × 7. Это равно 343. Следовательно, мы можем сказать, что куб числа 7 равен 343.
Таким же образом найдем куб числа 7. Мы знаем, что куб числа N равен N × N × N. Итак, куб числа 7 равен 7 × 7 × 7. Теперь, чтобы найти куб числа 7, сначала найдем значение 7 × 7. , Это значение равно 49. Теперь мы найдем 49 × 7. Это равно 343. Следовательно, мы можем сказать, что куб числа 7 равен 343. Это значение равно 49. Теперь мы найдем 49 × (-7). Это равно -343. Следовательно, мы можем сказать, что куб числа -7 равен -343. Формула кубического корня для отрицательных чисел:
Это значение равно 49. Теперь мы найдем 49 × (-7). Это равно -343. Следовательно, мы можем сказать, что куб числа -7 равен -343. Формула кубического корня для отрицательных чисел: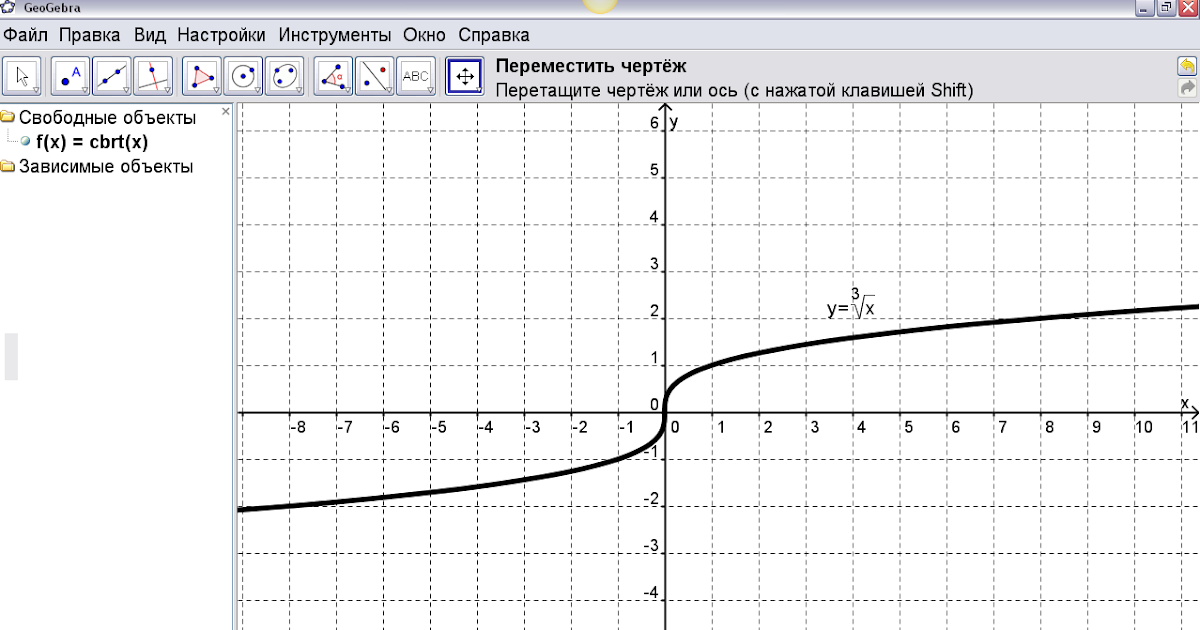 Это означает, что кубический корень из 729 равен 9.
Это означает, что кубический корень из 729 равен 9.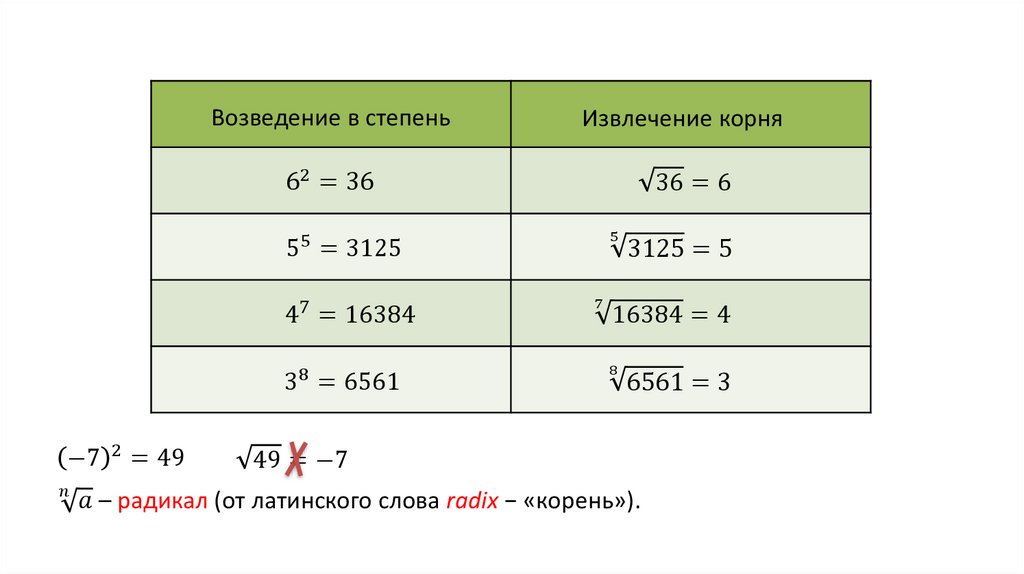 Испытайте Cuemath и приступайте к работе.
Испытайте Cuemath и приступайте к работе.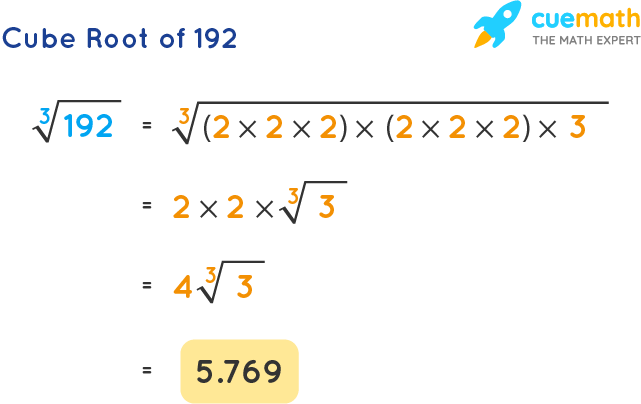 Они также используются для нахождения длины стороны куба, если известен его объем.
Они также используются для нахождения длины стороны куба, если известен его объем.


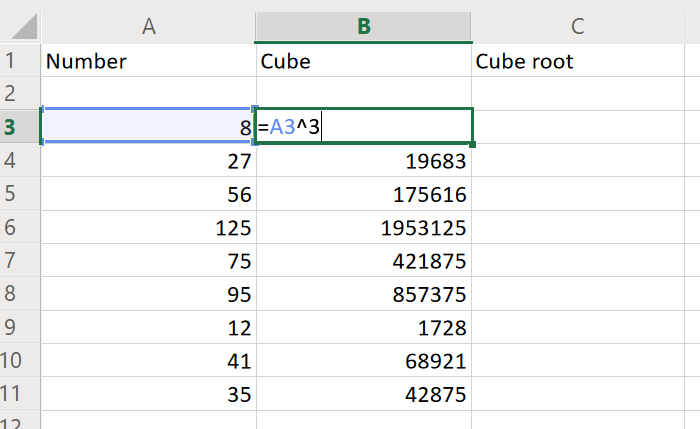 io/am_trouzine/pen/GRyoWbM
io/am_trouzine/pen/GRyoWbM д. Поэтому мы можем начать с вычисления a, вычитания верхней строки и использования второй строки для вычисления b, вычитания второй строки и использования третьей строки для вычисления c и т. д.
д. Поэтому мы можем начать с вычисления a, вычитания верхней строки и использования второй строки для вычисления b, вычитания второй строки и использования третьей строки для вычисления c и т. д. Из объяснения мы теперь есть:
Из объяснения мы теперь есть: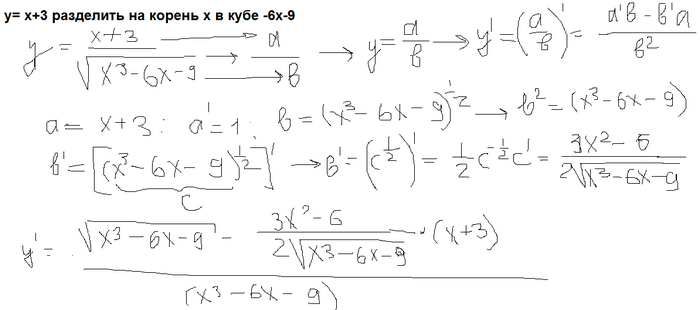 Таким образом, для каждой новой цифры:
Таким образом, для каждой новой цифры: К сожалению, это происходит очень часто во время этого алгоритма.
К сожалению, это происходит очень часто во время этого алгоритма.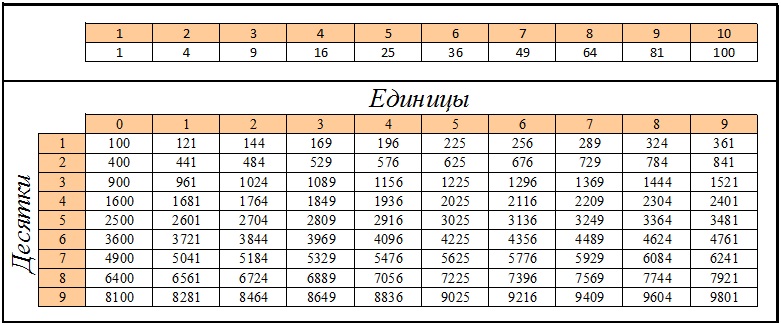
 Вы будете знать, что имеет не более 3 цифр. Если вы используете этот метод, вы будете вычислять три цифры одну за другой. Начальную и конечную цифры можно вычислить почти сразу; средняя цифра — это та, которую вы потратите большую часть своего времени на вычисление, потому что это часть вычислений, где вам нужно выполнить некоторые сложения и вычитания.
Вы будете знать, что имеет не более 3 цифр. Если вы используете этот метод, вы будете вычислять три цифры одну за другой. Начальную и конечную цифры можно вычислить почти сразу; средняя цифра — это та, которую вы потратите большую часть своего времени на вычисление, потому что это часть вычислений, где вам нужно выполнить некоторые сложения и вычитания. Просто запомните это так: если последняя цифра 0, 1, 4, 5, 6 или 9, то последняя цифра такая же, иначе (если последняя цифра 2, 3, 7 или 8 ), последняя цифра равна 10 минус последняя цифра .
Просто запомните это так: если последняя цифра 0, 1, 4, 5, 6 или 9, то последняя цифра такая же, иначе (если последняя цифра 2, 3, 7 или 8 ), последняя цифра равна 10 минус последняя цифра . Давайте составим таблицу, показывающую, какова последняя цифра для каждого из 10 возможных значений . Последние цифры каждого числа во второй строке выделены жирным шрифтом.
Давайте составим таблицу, показывающую, какова последняя цифра для каждого из 10 возможных значений . Последние цифры каждого числа во второй строке выделены жирным шрифтом.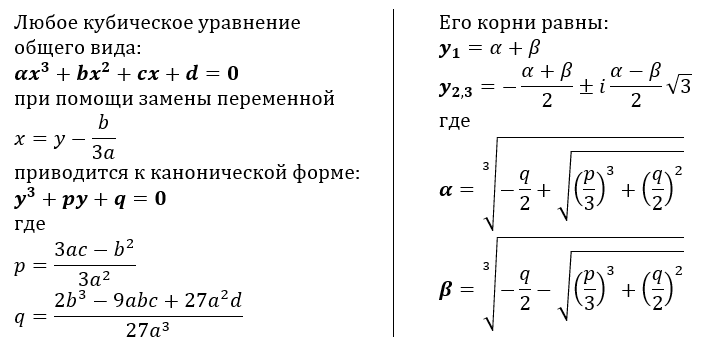 Назовем этот номер. Из приведенной выше таблицы видно, что если равно 1, то равно 1; если 3, то 7; если 6, то 6; если 8, то 2 и так далее. На самом деле, для каждого возможного значения существует только одно возможное значение , и поэтому мы можем прочитать значение , найдя уникальную ячейку в нижней строке, содержащую число, последняя цифра которого равна , и увидев, какое число находится в ячейке. выше. Отсюда исходная таблица.
Назовем этот номер. Из приведенной выше таблицы видно, что если равно 1, то равно 1; если 3, то 7; если 6, то 6; если 8, то 2 и так далее. На самом деле, для каждого возможного значения существует только одно возможное значение , и поэтому мы можем прочитать значение , найдя уникальную ячейку в нижней строке, содержащую число, последняя цифра которого равна , и увидев, какое число находится в ячейке. выше. Отсюда исходная таблица. Вам нужно будет запомнить эту таблицу, к сожалению, для него нет простой сводки, как для другой таблицы. Однако знание первых 10 неотрицательных совершенных кубов полезно во многих ситуациях, когда вам нужно произвести расчеты в уме, а не только в этой ситуации.
Вам нужно будет запомнить эту таблицу, к сожалению, для него нет простой сводки, как для другой таблицы. Однако знание первых 10 неотрицательных совершенных кубов полезно во многих ситуациях, когда вам нужно произвести расчеты в уме, а не только в этой ситуации. Например, и . Кубирование каждой части этого неравенства дает . Например, и . И если наблюдается выполнение неравенства вида последнего для некоторого значения , то из кубических корней каждой части можно получить неравенство вида первого, тем самым показывая, что первая цифра числа является .
Например, и . Кубирование каждой части этого неравенства дает . Например, и . И если наблюдается выполнение неравенства вида последнего для некоторого значения , то из кубических корней каждой части можно получить неравенство вида первого, тем самым показывая, что первая цифра числа является . Под знакопеременной суммой цифр я понимаю сумму цифр при разрядах, соответствующих четным степеням числа 10 (разряды единиц, разряды сотен, разряды десятков тысяч и т. д.) минус сумма цифр при места, соответствующие нечетным степеням числа 10 (разряд десятков, разряд тысяч, разряд сотен тысяч и т. д.). Например, альтернированная сумма цифр числа 121281 равна , и, конечно, у нас есть , а , поэтому остатки 121281 и -5 при делении на 11 одинаковы. На практике, чтобы вычислить переменную сумму , вы смотрите на каждую цифру по очереди, двигаясь справа налево (а не в том порядке, в котором записываются цифры, то есть слева направо!) и чередуетесь между добавлением и вычитанием цифры из Общая; вот почему это называется альтернирующей суммой. Может быть полезно взять цифры группами по два и сначала найти разницу между двумя цифрами в группе, а затем добавить ее к сумме; таким образом, вы с меньшей вероятностью запутаетесь, поскольку будете делать одно и то же на каждом этапе. Например, чтобы вычислить переменную сумму 121281, вы видите это и устанавливаете итог в , затем вы видите это и устанавливаете итог в , и, наконец, вы видите это и устанавливаете итог в .
Под знакопеременной суммой цифр я понимаю сумму цифр при разрядах, соответствующих четным степеням числа 10 (разряды единиц, разряды сотен, разряды десятков тысяч и т. д.) минус сумма цифр при места, соответствующие нечетным степеням числа 10 (разряд десятков, разряд тысяч, разряд сотен тысяч и т. д.). Например, альтернированная сумма цифр числа 121281 равна , и, конечно, у нас есть , а , поэтому остатки 121281 и -5 при делении на 11 одинаковы. На практике, чтобы вычислить переменную сумму , вы смотрите на каждую цифру по очереди, двигаясь справа налево (а не в том порядке, в котором записываются цифры, то есть слева направо!) и чередуетесь между добавлением и вычитанием цифры из Общая; вот почему это называется альтернирующей суммой. Может быть полезно взять цифры группами по два и сначала найти разницу между двумя цифрами в группе, а затем добавить ее к сумме; таким образом, вы с меньшей вероятностью запутаетесь, поскольку будете делать одно и то же на каждом этапе. Например, чтобы вычислить переменную сумму 121281, вы видите это и устанавливаете итог в , затем вы видите это и устанавливаете итог в , и, наконец, вы видите это и устанавливаете итог в . Кстати, если сумма переменных неотрицательна и меньше 11, то она равна остатку от деления на 11; в противном случае, хотя оно часто будет достаточно маленьким, чтобы вы могли сразу увидеть его остаток при делении на 11, вы могли бы найти альтернированную сумму цифр альтернированной суммы, повторив процесс, чтобы получить еще меньшее число.
Кстати, если сумма переменных неотрицательна и меньше 11, то она равна остатку от деления на 11; в противном случае, хотя оно часто будет достаточно маленьким, чтобы вы могли сразу увидеть его остаток при делении на 11, вы могли бы найти альтернированную сумму цифр альтернированной суммы, повторив процесс, чтобы получить еще меньшее число. Это завершает доказательство.
Это завершает доказательство. Или, что более удобно, мы можем использовать следующую перевернутую форму таблицы.
Или, что более удобно, мы можем использовать следующую перевернутую форму таблицы. Но если вы постараетесь и будете проверять себя через равные промежутки времени в течение пары дней, вы, вероятно, сможете успешно запомнить соответствие.
Но если вы постараетесь и будете проверять себя через равные промежутки времени в течение пары дней, вы, вероятно, сможете успешно запомнить соответствие.
 )
) Если вас это интересует, взгляните на этот пост — он охватывает множество других методов ментального расчета в более сжатой форме, чем этот пост. Не знаю, как вы, но пока я не наткнулся на этот пост, я всегда ассоциировал тему вычислений в уме с утомительным выполнением алгоритмов и поэтому считал это неинтересным и не совсем «настоящей математикой». Но по мере того, как вы приобретаете больше математических знаний, вы обнаружите, что расчеты в конечном итоге становятся своего рода творческим процессом, когда вы часто не придерживаетесь одного метода, а импровизируете способ решения проблемы, опираясь на то, что вы знаете, так что это можно решить как можно быстрее. Также интересно посмотреть, почему эти алгоритмы работают, и подумать, как их можно было бы придумать. Если вам интересно, вы можете попробовать придумать аналогичные алгоритмы для других видов корней. Или, возможно, посмотреть, есть ли способ нахождения кубических корней чисел с числом больше 9.цифры (хотя я понятия не имею, как вы можете это сделать).
Если вас это интересует, взгляните на этот пост — он охватывает множество других методов ментального расчета в более сжатой форме, чем этот пост. Не знаю, как вы, но пока я не наткнулся на этот пост, я всегда ассоциировал тему вычислений в уме с утомительным выполнением алгоритмов и поэтому считал это неинтересным и не совсем «настоящей математикой». Но по мере того, как вы приобретаете больше математических знаний, вы обнаружите, что расчеты в конечном итоге становятся своего рода творческим процессом, когда вы часто не придерживаетесь одного метода, а импровизируете способ решения проблемы, опираясь на то, что вы знаете, так что это можно решить как можно быстрее. Также интересно посмотреть, почему эти алгоритмы работают, и подумать, как их можно было бы придумать. Если вам интересно, вы можете попробовать придумать аналогичные алгоритмы для других видов корней. Или, возможно, посмотреть, есть ли способ нахождения кубических корней чисел с числом больше 9.цифры (хотя я понятия не имею, как вы можете это сделать).

 Если натуральное число не является полным квадратом, то его квадратный корень будет иррациональным. Рассмотрим 5, мы можем получить приближение, оценив его с помощью идеальных квадратов 4 и 92≈5
Если натуральное число не является полным квадратом, то его квадратный корень будет иррациональным. Рассмотрим 5, мы можем получить приближение, оценив его с помощью идеальных квадратов 4 и 92≈5 Положительное целое число n в обозначении n, которое используется для обозначения n -го корня. Например,
Положительное целое число n в обозначении n, которое используется для обозначения n -го корня. Например, Если это так, то его кубический корень будет иррациональным. Например, 23 — иррациональное число, которое можно приблизительно приблизить на большинстве калькуляторов с помощью корневой кнопки x. В зависимости от калькулятора мы обычно вводим индекс перед нажатием кнопки, а затем подкоренное число следующим образом: 93≈2
Если это так, то его кубический корень будет иррациональным. Например, 23 — иррациональное число, которое можно приблизительно приблизить на большинстве калькуляторов с помощью корневой кнопки x. В зависимости от калькулятора мы обычно вводим индекс перед нажатием кнопки, а затем подкоренное число следующим образом: 93≈2 — это тот, где подкоренное число не состоит из каких-либо множителей, которые можно записать в виде совершенных степеней индекса. Учитывая квадратный корень, идея состоит в том, чтобы определить наибольший квадратный множитель подкоренного числа, а затем применить свойство, показанное выше. Например, чтобы упростить 12, обратите внимание, что 12 не является идеальным квадратом. Однако у числа 12 есть совершенный квадратный множитель, 12=4⋅3. Примените свойство следующим образом:
12=4⋅3 Применить правило произведения для радикалов. =4⋅3 Упростить.=2⋅3
Число 23 — это упрощенное иррациональное число. Вас часто просят найти примерный ответ, округленный до определенного знака после запятой. В этом случае используйте калькулятор, чтобы найти десятичную аппроксимацию, используя либо исходную задачу, либо ее упрощенный эквивалент.
12=23≈3,46
Для проверки посчитайте 12 и 23 на калькуляторе и убедитесь, что оба результата приблизительно равны 3,46.
— это тот, где подкоренное число не состоит из каких-либо множителей, которые можно записать в виде совершенных степеней индекса. Учитывая квадратный корень, идея состоит в том, чтобы определить наибольший квадратный множитель подкоренного числа, а затем применить свойство, показанное выше. Например, чтобы упростить 12, обратите внимание, что 12 не является идеальным квадратом. Однако у числа 12 есть совершенный квадратный множитель, 12=4⋅3. Примените свойство следующим образом:
12=4⋅3 Применить правило произведения для радикалов. =4⋅3 Упростить.=2⋅3
Число 23 — это упрощенное иррациональное число. Вас часто просят найти примерный ответ, округленный до определенного знака после запятой. В этом случае используйте калькулятор, чтобы найти десятичную аппроксимацию, используя либо исходную задачу, либо ее упрощенный эквивалент.
12=23≈3,46
Для проверки посчитайте 12 и 23 на калькуляторе и убедитесь, что оба результата приблизительно равны 3,46.
 Идея состоит в том, чтобы определить наибольший кубический коэффициент подкоренного числа, а затем применить правило произведения или частного для радикалов. Например, чтобы упростить число 803, обратите внимание, что число 80 не является идеальным кубом. Однако 80=8⋅10, и мы можем написать 9.0005
Идея состоит в том, чтобы определить наибольший кубический коэффициент подкоренного числа, а затем применить правило произведения или частного для радикалов. Например, чтобы упростить число 803, обратите внимание, что число 80 не является идеальным кубом. Однако 80=8⋅10, и мы можем написать 9.0005 Это верно для любого положительного действительного числа. У нас есть следующее,
Это верно для любого положительного действительного числа. У нас есть следующее, Другими словами, гипотенуза любого прямоугольного треугольника равна квадратному корню из суммы квадратов его катетов.
Другими словами, гипотенуза любого прямоугольного треугольника равна квадратному корню из суммы квадратов его катетов.
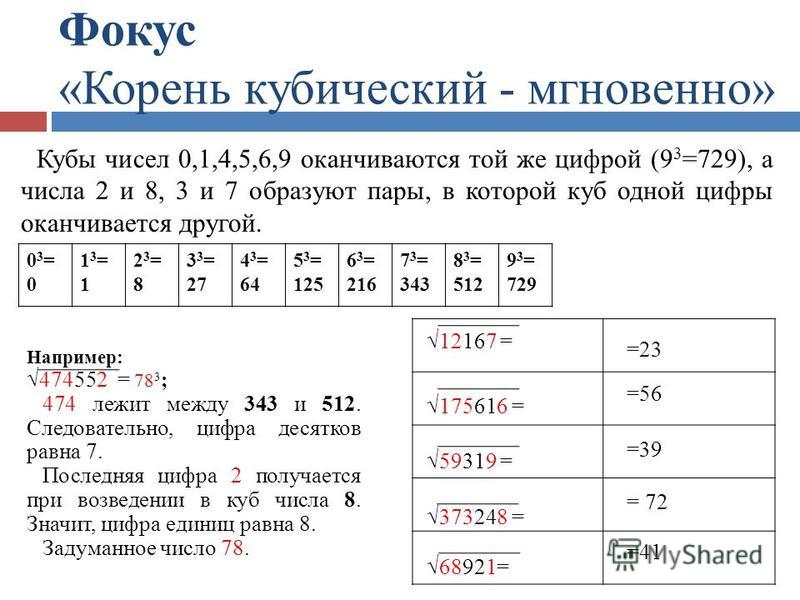




 )
)