Таблица-шпаргалка логарифмов: десятичных, по основанию 2
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
Ниже представлена таблица логарифмов (по основанию 2, 10 и числу e), которую можно использовать для выполнения быстрых расчетов, а также, проверки своих знаний.
| x | log10x | log2x | logex |
| 0 | — | — | — |
| 0+ | — ∞ | — ∞ | — ∞ |
| 0001″ data-order=»0.0001″>0.0001 | -4 | -13.287712 | -9.210340 |
| 0.001 | -3 | 965784″ data-order=»-9.965784″>-9.965784 | -6.907755 |
| 0.01 | -2 | -6.643856 | -4.605170 |
| 1″ data-order=»0.1″>0.1 | -1 | -3.321928 | -2.302585 |
| 1 | 0 | 0 | 0 |
| 2 | 301030″ data-order=»0.301030″>0.301030 | 1 | 0.693147 |
| 3 | 0.477121 | 1.584963 | 098612″ data-order=»1.098612″>1.098612 |
| 4 | 0.602060 | 2 | 1.386294 |
| 5 | 698970″ data-order=»0.698970″>0.698970 | 2.321928 | 1.609438 |
| 6 | 0.778151 | 2.584963 | 791759″ data-order=»1.791759″>1.791759 |
| 7 | 0.845098 | 2.807355 | 1.945910 |
| 8 | 903090″ data-order=»0.903090″>0.903090 | 3 | 2.079442 |
| 9 | 0.954243 | 3.169925 | 197225″ data-order=»2.197225″>2.197225 |
| 10 | 1 | 3.321928 | 2.302585 |
| 20 | 301030″ data-order=»1.301030″>1.301030 | 4.321928 | 2.995732 |
| 30 | 1.477121 | 4.906891 | 401197″ data-order=»3.401197″>3.401197 |
| 40 | 1.602060 | 5.321928 | 3.688879 |
| 50 | 698970″ data-order=»1.698970″>1.698970 | 5.643856 | 3.912023 |
| 60 | 1.778151 | 5.906991 | 094345″ data-order=»4.094345″>4.094345 |
| 70 | 1.845098 | 6.129283 | 4.248495 |
| 80 | 903090″ data-order=»1.903090″>1.903090 | 6.321928 | 4.382027 |
| 90 | 1.954243 | 6.491853 | 499810″ data-order=»4.499810″>4.499810 |
| 100 | 2 | 6.643856 | 4.605170 |
| 200 | 301030″ data-order=»2.301030″>2.301030 | 7.643856 | 5.298317 |
| 300 | 2.477121 | 8.228819 | 703782″ data-order=»5.703782″>5.703782 |
| 400 | 2.602060 | 8.643856 | 5.991465 |
| 500 | 698970″ data-order=»2.698970″>2.698970 | 8.965784 | 6.214608 |
| 600 | 2.778151 | 9.228819 | 396930″ data-order=»6.396930″>6.396930 |
| 700 | 2.845098 | 9.451211 | 6.551080 |
| 800 | 903090″ data-order=»2.903090″>2.903090 | 9.643856 | 6.684612 |
| 900 | 2.954243 | 9.813781 | 802395″ data-order=»6.802395″>6.802395 |
| 1000 | 3 | 9.965784 | 6.907755 |
| 10000 | 4 | 287712″ data-order=»13.287712″>13.287712 | 9.210340 |
microexcel.ru
Смотрите также: “Функция логарифма в Excel: формула расчета”
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Таблица логарифмов по основанию для школьников и студентов
log22 — log2100
log22 = 1. 0000
0000
log23 = 1.5850
log24 = 2.0000
log25 = 2.3219
log26 = 2.5850
log27 = 2.8074
log28 = 3.0000
log29 = 3.1699
log210 = 3.3219
log211 = 3.4594
log212 = 3.5850
log213 = 3.7004
log214 = 3.8074
log215 = 3.9069
log216 = 4.0000
log217 = 4.0875
log218 = 4.1699
log219 = 4.2479
log220 = 4.3219
log221 = 4.3923
log222 = 4.4594
log223 = 4.5236
log224 = 4.5850
log225 = 4.6439
log226 = 4.7004
log227 = 4.7549
log228 = 4.8074
log230 = 4.9069
log231 = 4.9542
log232 = 5.0000
log233 = 5.0444
log234 = 5.0875
log235 = 5.
 1293
1293log236 = 5.1699
log237 = 5.2095
log238 = 5.2479
log239 = 5.2854
log240 = 5.3219
log241 = 5.3576
log242 = 5.3923
log243 = 5.4263
log244 = 5.4594
log245 = 5.4919
log246 = 5.5236
log247 = 5.5546
log248 = 5.5850
log249 = 5.6147
log250 = 5.6439
log251 = 5.6724
log252 = 5.7004
log253 = 5.7279
log254 = 5.7549
log255 = 5.7814
log256 = 5.8074
log257 = 5.8329
log258 = 5.8580
log259 = 5.8826
log260 = 5.9069
log261 = 5.9307
log262 = 5.9542
log263 = 5.9773
log264 = 6.0000
log265 = 6.0224
log266 = 6.0444
log267 = 6.0661
log268 = 6.
 0875
0875log269 = 6.1085
log270 = 6.1293
log271 = 6.1497
log272 = 6.1699
log273 = 6.1898
log274 = 6.2095
log275 = 6.2288
log276 = 6.2479
log277 = 6.2668
log278 = 6.2854
log279 = 6.3038
log280 = 6.3219
log281 = 6.3399
log282 = 6.3576
log283 = 6.3750
log284 = 6.3923
log286 = 6.4263
log287 = 6.4429
log288 = 6.4594
log289 = 6.4757
log290 = 6.4919
log291 = 6.5078
log292 = 6.5236
log293 = 6.5392
log294 = 6.5546
log295 = 6.5699
log296 = 6.5850
log297 = 6.5999
log298 = 6.6147
log299 = 6.6294
log2100 = 6.6439
log32 — log3100
log32 = 0. 6309
6309
log33 = 1.0000
log34 = 1.2619
log35 = 1.4650
log36 = 1.6309
log37 = 1.7712
log38 = 1.8928
log39 = 2.0000
log310 = 2.0959
log311 = 2.1827
log312 = 2.2619
log314 = 2.4022
log315 = 2.4650
log316 = 2.5237
log317 = 2.5789
log318 = 2.6309
log319 = 2.6801
log320 = 2.7268
log321 = 2.7712
log322 = 2.8136
log323 = 2.8540
log324 = 2.8928
log325 = 2.9299
log326 = 2.9656
log327 = 3.0000
log328 = 3.0331
log329 = 3.0650
log330 = 3.0959
log331 = 3.1257
log332 = 3.1546
log333 = 3.1827
log334 = 3.2098
log335 = 3.
 2362
2362log336 = 3.2619
log337 = 3.2868
log338 = 3.3111
log339 = 3.3347
log340 = 3.3578
log341 = 3.3802
log3
log343 = 3.4236
log344 = 3.4445
log345 = 3.4650
log346 = 3.4850
log347 = 3.5046
log348 = 3.5237
log349 = 3.5425
log350 = 3.5609
log351 = 3.5789
log352 = 3.5966
log353 = 3.6139
log354 = 3.6309
log355 = 3.6476
log356 = 3.6640
log357 = 3.6801
log358 = 3.6960
log359 = 3.7115
log360 = 3.7268
log361 = 3.7419
log362 = 3.7567
log363 = 3.7712
log364 = 3.7856
log365 = 3.7997
log366 = 3.8136
log367 = 3.8273
log368 = 3.
 8408
8408log369 = 3.8540
log370 = 3.8671
log371 = 3.8801
log372 = 3.8928
log373 = 3.9053
log374 = 3.9177
log375 = 3.9299
log376 = 3.9420
log377 = 3.9539
log378 = 3.9656
log379 = 3.9772
log380 = 3.9887
log381 = 4.0000
log382 = 4.0112
log383 = 4.0222
log384 = 4.0331
log385 = 4.0439
log386 = 4.0545
log387 = 4.0650
log388 = 4.0754
log389 = 4.0857
log390 = 4.0959
log391 = 4.1060
log392 = 4.1159
log393 = 4.1257
log394 = 4.1355
log395 = 4.1451
log396 = 4.1546
log397 = 4.1641
log398 = 4.1734
log399 = 4.1827
log3100 = 4.1918
log42 — log4100
log 5000
5000
log43 = 0.7925
log44 = 1.0000
log45 = 1.1610
log46 = 1.2925
log47 = 1.4037
log48 = 1.5000
log49 = 1.5850
log410 = 1.6610
log411 = 1.7297
log412 = 1.7925
log413 = 1.8502
log414 = 1.9037
log415 = 1.9534
log416 = 2.0000
log417 = 2.0437
log418 = 2.0850
log419 = 2.1240
log420 = 2.1610
log421 = 2.1962
log422 = 2.2297
log423 = 2.2618
log424 = 2.2925
log425 = 2.3219
log426 = 2.3502
log427 = 2.3774
log428 = 2.4037
log429 = 2.4290
log430 = 2.4534
log431 = 2.4771
log433 = 2.5222
log434 = 2.5437
log435 = 2.
 5646
5646log436 = 2.5850
log437 = 2.6047
log438 = 2.6240
log439 = 2.6427
log440 = 2.6610
log441 = 2.6788
log442 = 2.6962
log443 = 2.7131
log444 = 2.7297
log445 = 2.7459
log446 = 2.7618
log447 = 2.7773
log448 = 2.7925
log449 = 2.8074
log450 = 2.8219
log451 = 2.8362
log452 = 2.8502
log453 = 2.8640
log454 = 2.8774
log455 = 2.8907
log456 = 2.9037
log457 = 2.9164
log458 = 2.9290
log459 = 2.9413
log461 = 2.9654
log462 = 2.9771
log463 = 2.9886
log464 = 3.0000
log465 = 3.0112
log466 = 3.0222
log467 = 3.0330
log468 = 3.
 0437
0437log469 = 3.0543
log470 = 3.0646
log471 = 3.0749
log472 = 3.0850
log473 = 3.0949
log474 = 3.1047
log475 = 3.1144
log476 = 3.1240
log477 = 3.1334
log478 = 3.1427
log479 = 3.1519
log480 = 3.1610
log481 = 3.1699
log482 = 3.1788
log483 = 3.1875
log484 = 3.1962
log485 = 3.2047
log486 = 3.2131
log487 = 3.2215
log 488 = 3.2297
log489 = 3.2379
log490 = 3.2459
log491 = 3.2539
log492 = 3.2618
log493 = 3.2696
log494 = 3.2773
log495 = 3.2849
log496 = 3.2925
log497 = 3.3000
log498 = 3.3074
log499 = 3.3147
log4100 = 3.3219
log52 — log5100
log52 = 0. 4307
4307
log53 = 0.6826
log54 = 0.8614
log55 = 1.0000
log56 = 1.1133
log57 = 1.2091
log58 = 1.2920
log59 = 1.3652
log510 = 1.4307
log511 = 1.4899
log512 = 1.5440
log513 = 1.5937
log514 = 1.6397
log516 = 1.7227
log517 = 1.7604
log518 = 1.7959
log519 = 1.8295
log520 = 1.8614
log521 = 1.8917
log522 = 1.9206
log523 = 1.9482
log524 = 1.9746
log525 = 2.0000
log526 = 2.0244
log527 = 2.0478
log528 = 2.0704
log529 = 2.0922
log530 = 2.1133
log531 = 2.1337
log532 = 2.1534
log533 = 2.1725
log534 = 2.1911
log535 = 2.
 2091
2091log536 = 2.2266
log537 = 2.2436
log538 = 2.2602
log539 = 2.2763
log540 = 2.2920
log541 = 2.3074
log542 = 2.3223
log543 = 2.3370
log544 = 2.3512
log545 = 2.3652
log546 = 2.3789
log547 = 2.3922
log548 = 2.4053
log549 = 2.4181
log550 = 2.4307
log551 = 2.4430
log552 = 2.4550
log553 = 2.4669
log554 = 2.4785
log555 = 2.4899
log556 = 2.5011
log557 = 2.5121
log558 = 2.5229
log559 = 2.5335
log560 = 2.5440
log561 = 2.5542
log562 = 2.5643
log563 = 2.5743
log564 = 2.5841
log565 = 2.5937
log566 = 2.6032
log567 = 2.6125
log568 = 2.
 6217
6217log569 = 2.6308
log570 = 2.6397
log571 = 2.6486
log572 = 2.6572
log573 = 2.6658
log574 = 2.6743
log575 = 2.6826
log576 = 2.6908
log577 = 2.6990
log578 = 2.7070
log579 = 2.7149
log580 = 2.7227
log581 = 2.7304
log582 = 2.7380
log583 = 2.7456
log584 = 2.7530
log585 = 2.7604
log586 = 2.7676
log587 = 2.7748
log588 = 2.7819
log589 = 2.7889
log590 = 2.7959
log591 = 2.8028
log592 = 2.8095
log593 = 2.8163
log594 = 2.8229
log595 = 2.8295
log596 = 2.8360
log597 = 2.8424
log598 = 2.8488
log599 = 2.8551
log5100 = 2.8614
log62 — log6100
log62 = 0. 3869
3869
log63 = 0.6131
log64 = 0.7737
log65 = 0.8982
log66 = 1.0000
log67 = 1.0860
log68 = 1.1606
log69 = 1.2263
log610 = 1.2851
log611 = 1.3383
log612 = 1.3869
log613 = 1.4315
log614 = 1.4729
log615 = 1.5114
log616 = 1.5474
log617 = 1.5812
log618 = 1.6131
log619 = 1.6433
log620 = 1.6720
log621 = 1.6992
log622 = 1.7251
log623 = 1.7500
log624 = 1.7737
log625 = 1.7965
log626 = 1.8184
log627 = 1.8394
log628 = 1.8597
log629 = 1.8793
log630 = 1.8982
log631 = 1.9165
log632 = 1.9343
log633 = 1.9514
log634 = 1.9681
log635 = 1. 9843
9843
log636 = 2.0000
log637 = 2.0153
log638 = 2.0302
log639 = 2.0447
log640 = 2.0588
log641 = 2.0726
log642 = 2.0860
log643 = 2.0992
log644 = 2.1120
log645 = 2.1245
log646 = 2.1368
log647 = 2.1488
log648 = 2.1606
log649 = 2.1721
log650 = 2.1833
log651 = 2.1944
log652 = 2.2052
log653 = 2.2159
log654 = 2.2263
log655 = 2.2365
log656 = 2.2466
log657 = 2.2565
log658 = 2.2662
log659 = 2.2757
log660 = 2.2851
log661 = 2.2943
log662 = 2.3034
log663 = 2.3123
log664 = 2.3211
log665 = 2.3298
log666 = 2.3383
log667 = 2.3467
log668 = 2. 3550
3550
log669 = 2.3631
log670 = 2.3711
log671 = 2.3790
log672 = 2.3869
log673 = 2.3946
log674 = 2.4021
log675 = 2.4096
log676 = 2.4170
log677 = 2.4243
log678 = 2.4315
log679 = 2.4386
log680 = 2.4457
log681 = 2.4526
log682 = 2.4594
log683 = 2.4662
log684 = 2.4729
log685 = 2.4795
log686 = 2.4860
log687 = 2.4925
log688 = 2.4988
log689 = 2.5052
log690 = 2.5114
log691 = 2.5176
log692 = 2.5237
log693 = 2.5297
log694 = 2.5357
log695 = 2.5416
log696 = 2.5474
log697 = 2.5532
log698 = 2.5589
log699 = 2.5646
log6100 = 2.5702
log72 — log7100
log72 = 0. 3562
3562
log73 = 0.5646
log74 = 0.7124
log75 = 0.8271
log76 = 0.9208
log77 = 1.0000
log78 = 1.0686
log79 = 1.1292
log710 = 1.1833
log711 = 1.2323
log712 = 1.2770
log713 = 1.3181
log714 = 1.3562
log715 = 1.3917
log716 = 1.4248
log717 = 1.4560
log718 = 1.4854
log719 = 1.5131
log720 = 1.5395
log721 = 1.5646
log722 = 1.5885
log723 = 1.6113
log724 = 1.6332
log725 = 1.6542
log726 = 1.6743
log727 = 1.6937
log728 = 1.7124
log729 = 1.7304
log730 = 1.7479
log731 = 1.7647
log732 = 1.7810
log733 = 1.7968
log734 = 1.8122
log735 = 1. 8271
8271
log736 = 1.8416
log737 = 1.8556
log738 = 1.8693
log739 = 1.8827
log740 = 1.8957
log741 = 1.9084
log742 = 1.9208
log743 = 1.9329
log744 = 1.9447
log745 = 1.9562
log746 = 1.9675
log747 = 1.9786
log748 = 1.9894
log749 = 2.0000
log750 = 2.0104
log751 = 2.0206
log752 = 2.0305
log753 = 2.0403
log754 = 2.0499
log755 = 2.0594
log756 = 2.0686
log757 = 2.0777
log758 = 2.0867
log759 = 2.0954
log760 = 2.1041
log761 = 2.1126
log762 = 2.1209
log763 = 2.1292
log764 = 2.1372
log765 = 2.1452
log766 = 2.1531
log767 = 2.1608
log768 = 2. 1684
1684
log769 = 2.1759
log770 = 2.1833
log771 = 2.1906
log772 = 2.1978
log773 = 2.2049
log774 = 2.2119
log775 = 2.2187
log776 = 2.2256
log777 = 2.2323
log778 = 2.2389
log779 = 2.2455
log780 = 2.2519
log781 = 2.2583
log782 = 2.2646
log783 = 2.2708
log784 = 2.2770
log785 = 2.2831
log786 = 2.2891
log787 = 2.2950
log788 = 2.3009
log789 = 2.3067
log790 = 2.3124
log791 = 2.3181
log792 = 2.3237
log793 = 2.3293
log794 = 2.3348
log795 = 2.3402
log796 = 2.3456
log797 = 2.3509
log798 = 2.3562
log799 = 2.3614
log7100 = 2.3666
log82 — log8100
log82 = 0. 3333
3333
log83 = 0.5283
log84 = 0.6667
log85 = 0.7740
log86 = 0.8617
log87 = 0.9358
log88 = 1.0000
log89 = 1.0566
log810 = 1.1073
log811 = 1.1531
log812 = 1.1950
log813 = 1.2335
log814 = 1.2691
log815 = 1.3023
log816 = 1.3333
log817 = 1.3625
log818 = 1.3900
log819 = 1.4160
log820 = 1.4406
log821 = 1.4641
log822 = 1.4865
log823 = 1.5079
log824 = 1.5283
log825 = 1.5480
log826 = 1.5668
log827 = 1.5850
log828 = 1.6025
log829 = 1.6193
log830 = 1.6356
log831 = 1.6514
log832 = 1.6667
log833 = 1.6815
log834 = 1.6958
log835 = 1. 7098
7098
log836 = 1.7233
log837 = 1.7365
log838 = 1.7493
log839 = 1.7618
log840 = 1.7740
log841 = 1.7859
log842 = 1.7974
log843 = 1.8088
log844 = 1.8198
log845 = 1.8306
log846 = 1.8412
log847 = 1.8515
log848 = 1.8617
log849 = 1.8716
log850 = 1.8813
log851 = 1.8908
log852 = 1.9001
log853 = 1.9093
log854 = 1.9183
log855 = 1.9271
log856 = 1.9358
log857 = 1.9443
log858 = 1.9527
log859 = 1.9609
log860 = 1.9690
log861 = 1.9769
log862 = 1.9847
log863 = 1.9924
log864 = 2.0000
log865 = 2.0075
log866 = 2.0148
log867 = 2.0220
log868 = 2. 0292
0292
log869 = 2.0362
log870 = 2.0431
log871 = 2.0499
log872 = 2.0566
log873 = 2.0633
log874 = 2.0698
log875 = 2.0763
log876 = 2.0826
log877 = 2.0889
log878 = 2.0951
log879 = 2.1013
log880 = 2.1073
log881 = 2.1133
log882 = 2.1192
log883 = 2.1250
log884 = 2.1308
log885 = 2.1365
log886 = 2.1421
log887 = 2.1476
log888 = 2.1531
log889 = 2.1586
log890 = 2.1640
log891 = 2.1693
log892 = 2.1745
log893 = 2.1797
log894 = 2.1849
log895 = 2.1900
log896 = 2.1950
log897 = 2.2000
log898 = 2.2049
log899 = 2.2098
log8100 = 2.2146
log92 — log9100
log92 = 0. 3155
3155
log93 = 0.5000
log94 = 0.6309
log95 = 0.7325
log96 = 0.8155
log97 = 0.8856
log98 = 0.9464
log99 = 1.0000
log910 = 1.0480
log911 = 1.0913
log912 = 1.1309
log913 = 1.1674
log914 = 1.2011
log915 = 1.2325
log916 = 1.2619
log917 = 1.2895
log918 = 1.3155
log919 = 1.3401
log920 = 1.3634
log921 = 1.3856
log922 = 1.4068
log923 = 1.4270
log924 = 1.4464
log925 = 1.4650
log926 = 1.4828
log927 = 1.5000
log928 = 1.5166
log929 = 1.5325
log930 = 1.5480
log931 = 1.5629
log932 = 1.5773
log933 = 1.5913
log934 = 1.6049
log935 = 1. 6181
6181
log936 = 1.6309
log937 = 1.6434
log938 = 1.6555
log939 = 1.6674
log940 = 1.6789
log941 = 1.6901
log942 = 1.7011
log943 = 1.7118
log944 = 1.7223
log945 = 1.7325
log946 = 1.7425
log947 = 1.7523
log948 = 1.7619
log949 = 1.7712
log950 = 1.7804
log951 = 1.7895
log952 = 1.7983
log953 = 1.8070
log954 = 1.8155
log955 = 1.8238
log956 = 1.8320
log957 = 1.8401
log958 = 1.8480
log959 = 1.8558
log960 = 1.8634
log961 = 1.8709
log962 = 1.8783
log963 = 1.8856
log964 = 1.8928
log965 = 1.8998
log966 = 1.9068
log967 = 1.9136
log968 = 1. 9204
9204
log969 = 1.9270
log970 = 1.9336
log971 = 1.9400
log972 = 1.9464
log973 = 1.9527
log974 = 1.9589
log975 = 1.9650
log976 = 1.9710
log977 = 1.9770
log978 = 1.9828
log979 = 1.9886
log980 = 1.9943
log981 = 2.0000
log982 = 2.0056
log983 = 2.0111
log984 = 2.0166
log985 = 2.0219
log986 = 2.0273
log987 = 2.0325
log988 = 2.0377
log989 = 2.0429
log990 = 2.0480
log991 = 2.0530
log992 = 2.0580
log993 = 2.0629
log994 = 2.0677
log995 = 2.0726
log996 = 2.0773
log997 = 2.0820
log998 = 2.0867
log999 = 2.0913
log9100 = 2.0959
log102 — log10100
log102 = 0. 3010
3010
log103 = 0.4771
log104 = 0.6021
log105 = 0.6990
log106 = 0.7782
log107 = 0.8451
log108 = 0.9031
log109 = 0.9542
log1010 = 1.0000
log1011 = 1.0414
log1012 = 1.0792
log1013 = 1.1139
log1014 = 1.1461
log1015 = 1.1761
log1016 = 1.2041
log1017 = 1.2304
log1018 = 1.2553
log1019 = 1.2788
log1020 = 1.3010
log1021 = 1.3222
log1022 = 1.3424
log1023 = 1.3617
log1024 = 1.3802
log1025 = 1.3979
log1026 = 1.4150
log1027 = 1.4314
log1028 = 1.4472
log1029 = 1.4624
log1030 = 1.4771
log1031 = 1.4914
log1032 = 1.5051
log1033 = 1.5185
log1034 = 1. 5315
5315
log1035 = 1.5441
log1036 = 1.5563
log1037 = 1.5682
log1038 = 1.5798
log1039 = 1.5911
log1040 = 1.6021
log1041 = 1.6128
log1042 = 1.6232
log1043 = 1.6335
log1044 = 1.6435
log1045 = 1.6532
log1046 = 1.6628
log1047 = 1.6721
log1048 = 1.6812
log1049 = 1.6902
log1050 = 1.6990
log1051 = 1.7076
log1052 = 1.7160
log1053 = 1.7243
log1054 = 1.7324
log1055 = 1.7404
log1056 = 1.7482
log1057 = 1.7559
log1058 = 1.7634
log1059 = 1.7709
log1060 = 1.7782
log1061 = 1.7853
log1062 = 1.7924
log1063 = 1.7993
log1064 = 1.8062
log1065 = 1.8129
log1066 = 1. 8195
8195
log1067 = 1.8261
log1068 = 1.8325
log1069 = 1.8388
log1070 = 1.8451
log1071 = 1.8513
log1072 = 1.8573
log1073 = 1.8633
log1074 = 1.8692
log1075 = 1.8751
log1076 = 1.8808
log1077 = 1.8865
log1078 = 1.8921
log1079 = 1.8976
log1080 = 1.9031
log1081 = 1.9085
log1082 = 1.9138
log1083 = 1.9191
log1084 = 1.9243
log1085 = 1.9294
log1086 = 1.9345
log1087 = 1.9395
log1088 = 1.9445
log1089 = 1.9494
log1090 = 1.9542
log1091 = 1.9590
log1092 = 1.9638
log1093 = 1.9685
log1094 = 1.9731
log1095 = 1.9777
log1096 = 1.9823
log1097 = 1.9868
log1098 = 1. 9912
9912
log1099 = 1.9956
log10100 = 2.0000
log112 — log11100
log112 = 0.2891
log113 = 0.4582
log114 = 0.5781
log115 = 0.6712
log116 = 0.7472
log117 = 0.8115
log118 = 0.8672
log119 = 0.9163
log1110 = 0.9603
log1111 = 1.0000
log1112 = 1.0363
log1113 = 1.0697
log1114 = 1.1006
log1115 = 1.1293
log1116 = 1.1563
log1117 = 1.1815
log1118 = 1.2054
log1119 = 1.2279
log1120 = 1.2493
log1121 = 1.2697
log1122 = 1.2891
log1123 = 1.3076
log1124 = 1.3254
log1125 = 1.3424
log1126 = 1.3587
log1127 = 1.3745
log1128 = 1. 3896
3896
log1129 = 1.4043
log1130 = 1.4184
log1131 = 1.4321
log1132 = 1.4453
log1133 = 1.4582
log1134 = 1.4706
log1135 = 1.4827
log1136 = 1.4944
log1137 = 1.5059
log1138 = 1.5170
log1139 = 1.5278
log1140 = 1.5384
log1141 = 1.5487
log1142 = 1.5587
log1143 = 1.5685
log1144 = 1.5781
log1145 = 1.5875
log1146 = 1.5967
log1147 = 1.6056
log1148 = 1.6144
log1149 = 1.6230
log1150 = 1.6314
log1151 = 1.6397
log1152 = 1.6478
log1153 = 1.6557
log1154 = 1.6635
log1155 = 1.6712
log1156 = 1.6787
log1157 = 1.6861
log1158 = 1.6933
log1159 = 1.7005
log1160 = 1. 7075
7075
log1161 = 1.7144
log1162 = 1.7211
log1163 = 1.7278
log1164 = 1.7344
log1165 = 1.7409
log1166 = 1.7472
log1167 = 1.7535
log1168 = 1.7597
log1169 = 1.7658
log1170 = 1.7718
log1171 = 1.7777
log1172 = 1.7835
log1173 = 1.7893
log1174 = 1.7949
log1175 = 1.8005
log1176 = 1.8061
log1177 = 1.8115
log1178 = 1.8169
log1179 = 1.8222
log1180 = 1.8274
log1181 = 1.8326
log1182 = 1.8377
log1183 = 1.8428
log1184 = 1.8478
log1185 = 1.8527
log1186 = 1.8576
log1187 = 1.8624
log1188 = 1.8672
log1189 = 1.8719
log1190 = 1.8766
log1191 = 1.8812
log1192 = 1. 8857
8857
log1193 = 1.8902
log1194 = 1.8947
log1195 = 1.8991
log1196 = 1.9035
log1197 = 1.9078
log1198 = 1.9121
log1199 = 1.9163
log11100 = 1.9205
Таблица логарифмов — frwiki.wiki
Для одноименных статей см. Таблицу (значения) .
Таблицы логарифмов Бувара и Ратине , книжный магазин Hachette, 1957 г.
Таблица натуральных логарифмов от 0,01 до 100 с пятью десятичными знаками, «естественное чтение» (числа показаны полностью).
Таблица логарифмов является табличным представлением логарифмов , как правило , в основании 10, целых числа от 1 до N. Наиболее часто N 10000, как и в таблице Bouvart и Ratinet , весьма распространенных во Франции до появления вычислителей , или 100000 .
Достаточно знать десятичный логарифм целых чисел от 10 n до 10 n + 1 , поскольку логарифм других чисел может быть легко получен; изменяется только часть перед запятой или характеристика. По этой причине в таблице чаще всего приводятся только цифры после запятой, называемые мантиссой.
По этой причине в таблице чаще всего приводятся только цифры после запятой, называемые мантиссой.
Пример:
- Логарифм 2 равен 0,30103…;
- логарифм 20 равен 1,30103…;
- логарифм 200 равен 2,30103…;
- в таблице мы просто прочитаем 301 03.
Когда в таблице приведены логарифмы чисел до 10 n , мы получаем логарифмы для всех чисел, имеющих не более n значащих цифр. Логарифмы чисел с более значащими цифрами вычисляются методом линейной интерполяции . Часто таблицы содержат таблицы на полях для облегчения интерполяции.
Логарифмические таблицы помогают при вычислении произведений, частных или степеней. Однако мы также можем вычислить сумму двух чисел, логарифм которых известен, либо используя специальную таблицу аддитивных логарифмов (например, прилагаемую к таблице Хоуэля ), либо используя тригонометрию и таблицы логарифмов тригонометрических функций, которые почти всегда приводятся после таблицы. логарифмов целых чисел. Тригонометрия также позволяет составить большое количество формул, вычисляемых по логарифму .
Тригонометрия также позволяет составить большое количество формул, вычисляемых по логарифму .
Резюме
- 1 рассказ
- 1.1 Принцип
- 1.2 Иллюстрация, построение таблицы десятичного логарифма
- 1.2.1 Первый шаг
- 1.2.2 Второй шаг
- 2 Использование таблицы логарифмов
- 2.1 Чтение
- 2.2 Расчеты
- 3 Примечания и ссылки
- 4 См. Также
- 4.1 Связанные статьи
- 4.2 Внешние ссылки
История
Первые логарифмические таблицы отображаются в начале XVII — го века , с тем чтобы облегчить астрономические вычисления. В то время как все расчеты производятся вручную, они позволяют переводить продукты в суммы. Чтобы вычислить произведение a на b, достаточно найти логарифм a и b. Суммируя эти два логарифма, мы получаем логарифм числа ab. Затем продукт ab легко найти, прочитав таблицу вверх ногами . Именно Джон Напье (Непер) опубликовал первые логарифмические таблицы, которые представляют собой таблицы синус-логарифмов ( Mirifici Loagarithmorum Canonis Descriptio — 1614). Генри Бриггс, который работает в сотрудничестве с Непером, имеет идею связать число 10 с числом 1 и таким образом построить первую таблицу десятичного логарифма или десятичного логарифма (1615). В то же время (1603 — 1611) астроном Йост Бюрджи, который работает вместе с Кеплером, разрабатывает тригонометрические таблицы и таблицу антилогарифмов, которые будут опубликованы в 1620 году.
Именно Джон Напье (Непер) опубликовал первые логарифмические таблицы, которые представляют собой таблицы синус-логарифмов ( Mirifici Loagarithmorum Canonis Descriptio — 1614). Генри Бриггс, который работает в сотрудничестве с Непером, имеет идею связать число 10 с числом 1 и таким образом построить первую таблицу десятичного логарифма или десятичного логарифма (1615). В то же время (1603 — 1611) астроном Йост Бюрджи, который работает вместе с Кеплером, разрабатывает тригонометрические таблицы и таблицу антилогарифмов, которые будут опубликованы в 1620 году.
Эти цифровые таблицы построены по принципу, описанному ниже, с использованием только простых операций (сложения, линейной интерполяции). Полученная точность, 14 знаков после запятой, например для таблицы Бриггса, позволяет представить количество вычислений, которые необходимо было выполнить для их построения. Это является ценным инструментом как для сложности ее конструкции , чем для ее практической полезности, которая растет хорошо в XVII — м веке . Они широко используются в расчетах в течение более трех столетий , прежде чем свергнутый в конце XX — го века путем размещения на рынке мощных вычислителей.
Они широко используются в расчетах в течение более трех столетий , прежде чем свергнутый в конце XX — го века путем размещения на рынке мощных вычислителей.
Таблицы логарифмов, титульный лист, издан в 1792 г.
Принцип
Принцип построения состоит в соединении арифметической последовательности и геометрической последовательности, которые развиваются вместе. Непер, объясняя свой принцип, по существу говорит:
- «Логарифм синуса — это число, которое также увеличивается в равные разы, в то время как синус пропорционально уменьшается. Два движения происходят одновременно и начинаются с одинаковой скоростью » .
Иллюстрация, построение таблицы десятичного логарифма
Мы можем представить упрощенную версию конструкции, представив себе, как построить последовательные степени 1.01. Расчеты выполняются вручную из основных операций (сложение, линейная интерполяция), поэтому уже требуется много времени, чтобы получить точность до трех или четырех знаков после запятой.
Первая ступень
Определяем последовательность степеней числа 1.01 до достижения числа 10 (основания): начинаем с первой степени (1.01), затем складываем число, сдвинутое вправо на две цифры (умноженное на 0,01), и получить следующую мощность:
- 1,01 + 0,0101 = 1,0201.
Продолжаем так, затем округляем результаты, усекая цифры после четвертого десятичного знака:
- Третья степень 1,01 равна 1,0303;
- 4 — й мощность равна 1.0406; … Используя классические правила округления, например:
- 11 — й мощности 1,1155;
- 12 — й мощности затем 1,1155 + 0,0112 = 1,1267; …
- Наконец, 231- я степень — 9 959; а 232- я степень — 10.
 059.
059.
Мы останавливаемся, когда превышено 10. Тогда мы получим следующую таблицу:
| нет | 1.01 п |
|---|---|
| 1 | 1.01 |
| 2 | 1.0201 |
| 3 | 1.0303 |
| 4 | 1,0406 |
| … | … |
| 11 | 1,1155 |
| 12 | 1,1267 |
| … | … |
| 231 | 9,959 |
| 232 | 10,059 |
Вклад Непера состоит в том, чтобы учесть, что движение непрерывно, то есть мы можем заполнить пробелы. Поскольку для n = 231 мы получаем 9,959, а для n = 232 — 10,059, именно между этими двумя числами мы получим 10. Затем мы можем рассмотреть линейную интерполяцию: разность 1 в левом столбце соответствует отклонению в одну десятую в правом столбце. Чтобы получить 10 из 9,959, добавьте 0,41 десятых. Поэтому мы должны добавить 0,41 единицы в левый столбец. Таким образом, число 10 соответствует 231,41. Если вы хотите сопоставить число 10 с числом 1, вам просто нужно разделить все члены в левом столбце на 231,41. Таким образом, мы получаем приблизительные значения десятичных логарифмов всех степеней 1,01 (представлены в правом столбце таблицы ниже).
Таким образом, число 10 соответствует 231,41. Если вы хотите сопоставить число 10 с числом 1, вам просто нужно разделить все члены в левом столбце на 231,41. Таким образом, мы получаем приблизительные значения десятичных логарифмов всех степеней 1,01 (представлены в правом столбце таблицы ниже).
Второй шаг
Затем мы строим таблицу соответствий, которую достаточно заполнить для промежуточных значений, используя линейную интерполяцию.
| нет | в | журнал (а) |
|---|---|---|
| 1 | 1.01 | 0,00432 |
| 2 | 1.0201 | 0,00864 |
| 3 | 1.0303 | 0,01296 |
| 4 | 1.0406 | 0,01728 |
| … | … | … |
| 11 | 1,1155 | 0,04753 |
| 12 | 1,1267 | 0,05185 |
| … | … | … |
| 69 | 1,9867 | 0,29818 |
| 70 | 2,0066 | 0,30250 |
. .. .. | … | … |
| 231 | 9,959 | 0,99827 |
| 231,4 | 10 | 1 |
Чтобы определить, например, десятичный логарифм числа 2, просто просмотрите таблицу степеней 1,01 и 2,00 чтения, которые находятся между 69- й степенью (1,9867) и 70- й степенью 1,01 (2,0066). При линейной интерполяции 2 получается степень 69,66, поэтому 1,01⋅ 69,66 ≈ 2, то есть 69,66⋅log (1.01) ≈ log (2).
Чтобы определить логарифм 2 по основанию 10, остается только выполнить деление 69,66 / 231,4 ≈ 0,30104, что хорошо соответствует приблизительному значению log (2).
На самом деле таблицы логарифмов были построены вручную с большей точностью, например, начиная со степеней 1,000001. Если мы затем произвольно присвоим значение 0,000001 логарифму 1,000001, мы получим значение 1 для логарифма 2,71828, тем самым придав законность натуральному (или неперианскому) логарифму основания e .
Если мы затем произвольно присвоим значение 0,000001 логарифму 1,000001, мы получим значение 1 для логарифма 2,71828, тем самым придав законность натуральному (или неперианскому) логарифму основания e .
Использование таблицы логарифмов
Чтение
Простые таблицы логарифмов с пятью десятичными знаками обычно расширяются так, что числа, образованные из первых двух цифр (от 10 до 99), образуют левый край таблицы, а последние цифры (от 0 до 9) появляются вверху таблицы. столбец.
Таблица логарифмов выглядит так:
N 0 1 2 3 … 9 10 0000 0043 0086 0128 … 0374 11 0414 0453 0492 0531 … 0756 12 0792 0828 0864 0899 … 1106 13 1139 1173 1206 1239 … 1430 14 1461 1492 1523 1553 … 1732 15 1761 1790 1818 1847 … 2014 16 2041 2068 2095 2122 … 2279 17 2304 2330 2355 2380 … 2529 18 2553 2577 2601 2625 … 2765 19 2788 2810 2833 2856 … 2989 · · · · · · · · · · · · · · · · · · 99 9956 9957 9957 9958 … 9960
Здесь единица и десятая цифра числа N появляются в левом столбце, а сотые цифры — в первой строке. На пересечении строки и столбца читаем журнал (N).
На пересечении строки и столбца читаем журнал (N).
Пример 1 : Как определить журнал (1,53)?
- Переходим к строке 15 и столбцу 3 и читаем
1847. Таким образом, мы можем заключить, что - журнал (1,53) 0,1847
Пример 2 : Как определить лог (0,00153)?
- Мы знаем, что характеристика этого числа — –3, а его мантисса — log (1.53).
- Итак, log (0,00153) = –3 + 0,1847 ≃ –2,8153.
Пример 3 : Как определить журнал (18,27)?
- Мы знаем, что его характеристика равна 1, а мантисса — log (1827). Таким образом, мы помещаем себя в строку 18 между столбцами 2 и 3. Затем необходимо выполнить линейную интерполяцию.
- log (1,82) 0,2601 и log (1,83) ≃ 0,2625, то есть разница в 24 десятитысячных. Линейная интерполяция аппроксимирует логарифмы чисел от 1,82 до 1,83 следующим образом
- журнал (1,821) ≃ 0,2601 + 0,00024
- журнал (1,822) ≃ 0,2601 + 0,00048
- …
- журнал (1,827) 0,2601 + 7 × 0,00024 ≃ 0,2618
- журнал (18,27) 1,2618
Пример 4 : Какое число имеет логарифм 1,208?
- Мы знаем, что характеристика равна 1, и поэтому число записывается как N × 10 с log (N) = 0,208.

- В таблице логарифмов
2080находится между2068и2095(разница 27). Число2068находится в строке 16 и в столбце 1, поэтому 0,2068 = log (1,61). Аналогично 0,2095 = журнал (1,62). Поэтому переходим к линейной интерполяции - 0,2068 + 0,00027 = 0,20707 = журнал (1,611)
- 0,20707 + 0,00027 = 0,20734 = лог (1,612)
- …
- 0,2068 + 4 × 0,00027 = 0,20788 = журнал (1,614)
- 0,2068 + 5 × 0,00027 = 0,20815 = журнал (1,615)
- 0,208 ≃ лог (1,614)
- 10 1,208 ≃ 16,14
Расчеты
Примечания и ссылки
- ↑ a и b А. Дахан-Далмедико и Дж. Пайффер , История математики: дороги и лабиринты ,[ подробности изданий ], стр 214
Смотрите также
Статьи по Теме
- Теория приближений
- Линейная интерполяция
- Логарифм
- Логарифмическая линейка
- Мари-Анри Андойе
- Гаспар де Прони , используя разделение труда в своей логарифмической фабрике в 1793 году.

- Адриан Влак
- Zacharias Dase
- Тригонометрический стол
- Цифровой стол
Внешние ссылки
- LOCOMAT — Коллекция математических таблиц Loria
- Таблицы логарифмов Ж. Дюпюи, 1880 г. (Галлика)
- Таблицы логарифмов по Дж де — Ла — Ланде , 1841 (Галльский)
<img src=»//fr.wikipedia.org/wiki/Special:CentralAutoLogin/start?type=1×1″ alt=»» title=»»>
Натуральные логарифмы чисел (Таблица)
I. Таблица натуральные логарифмы чисел
1)1)Натуральный логарифм числа, не содержащегося среди аргументов таблицы, находится следующим образом. Пусть ищется ln 753. Имеем: ln 753 = ln (7,53 • 102) = ln 7,53 4- 2 ln 10. Первое слагаемое находим по таблице натуральных логарифмов, второе — по таблице III. Получаем: ln 753 = 2,0189 + 4,6052 = 6,6241. Таким же образом находим ln 0,00753 = ln (7,53 • 10″3) = 2,0189 — 6,9078 = -4,8889.
| N | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 1,0 | 0,0000 | 0,0100 | 0,0198 | 0,0296 | 0,0392 | 0,0488 | 0,0583 | 0,0677 | 0,0770 | 0,0862 |
| 1,1 | 0,0953 | 0,1044 | 0,1133 | 0,1222 | 0,1310 | 0,1398 | 0,1484 | 0,1570 | 0,1655 | 0,1740 |
| 1,2 | 0,1823 | 0,1906 | 0,1989 | 0,2070 | 0,2151 | 0,2231 | 0,2311 | 0,2390 | 0,2469 | 0,2546 |
| 1,3 | 0,2624 | 0,2700 | 0,2776 | 0,2852 | 0,2927 | 0,3001 | 0,3075 | 0,3148 | 0,3221 | 0,3293 |
| 1,4 | 0,3365 | 0,3436 | 0,3507 | 0,3577 | 0,3646 | 0,3716 | 0,3784 | 0,3853 | 0,3920 | 0,3988 |
| 1,5 | 0,4055 | 0,4121 | 0,4187 | 0,4253 | 0,4318 | 0,4383 | 0,4447 | 0,4511 | 0,4574 | 0,4637 |
| 1,6 | 0,4700 | 0,4762 | 0,4824 | 0,4886 | 0,4947 | 0,5008 | 0,5068 | 0,5128 | 0,5188 | 0,5247 |
| 1,7 | 0,5306 | 0,5365 | 0,5423 | 0,5481 | 0,5539 | 0,5596 | 0,5653 | 0,5710 | 0,5766 | 0,5822 |
| 1,8 | 0,5878 | 0,5933 | 0,5988 | 0,6043 | 0,6098 | 0,6152 | 0,6206 | 0,6259 | 0,6313 | 0,6366 |
| 1,9 | 0,6419 | 0,6471 | 0,6523 | 0,6575 | 0,6627 | 0,6678 | 0,6729 | 0,6780 | 0,6831 | 0,6881 |
| 2,0 | 0,6931 | 0,6981 | 0,7031 | 0,7080 | 0,7129 | 0,7178 | 0,7227 | 0,7275 | 0,7324 | 0,7372 |
| 2,1 | 0,7419 | 0,7467 | 0,7514 | 0,7561 | 0,7608 | 0,7655 | 0,7701 | 0,7747 | 0,7793 | 0,7839 |
| 2,2 | 0,7885 | 0,7930 | 0,7975 | 0,8020 | 0,8065 | 0,8109 | 0,8154 | 0,8198 | 0,8242 | 0,8286 |
| 2,3 | 0,8329 | 0,8372 | 0,8416 | 0,8459 | 0,8502 | 0,8544 | 0,8587 | 0,8629 | 0,8671 | 0,8713 |
| 2,4 | 0,8755 | 0,8796 | 0,8838 | 0,8879 | 0,8920 | 0,8961 | 0,9002 | 0,9042 | 0,9083 | 0,9123 |
| 2,5 | 0,9163 | 0,9203 | 0,9243 | 0,9282 | 0,9322 | 0,9361 | 0,9400 | 0,9439 | 0,9478 | 0,9517 |
| 2,6 | 0,9555 | 0,9594 | 0,9632 | 0,9670 | 0,9708 | 0,9746 | 0,9783 | 0,9821 | 0,9858 | 0,9895 |
| 2,7 | 0,9933 | 0,9969 | 1,0006 | 1,0043 | 1,0080 | 1,0116 | 1,0152 | 1,0188 | 1,0225 | 1,0260 |
| 2,8 | 1,0296 | 1,0332 | 1,0367 | 1,0403 | 1,0438 | 1,0473 | 1,0508 | 1,0543 | 1,0578 | 1,0613 |
| 2,9 | 1,0647 | 1,0682 | 1,0716 | 1,0750 | 1,0784 | 1,0818 | 1,0852 | 1,0886 | 1,0919 | 1,0953 |
| 3,0 | 1,0986 | 1,1019 | 1,1053 | 1,1086 | 1,1119 | 1,1151 | 1,1184 | 1,1217 | 1,1249 | 1,1282 |
| 3,1 | 1,1314 | 1,1346 | 1,1378 | 1,1410 | 1,1442 | 1,1474 | 1,1506 | 1,1537 | 1,1569 | 1,1600 |
| 3,2 | 1,1632 | 1,1663 | 1,1694 | 1,1725 | 1,1756 | 1,1787 | 1,1817 | 1,1848 | 1,1878 | 1,1909 |
| 3,3 | 1,1939 | 1,1969 | 1,2000 | 1,2030 | 1,2060 | 1,2090 | 1,2119 | 1,2149 | 1,2179 | 1,2208 |
| 3,4 | 1,2238 | 1,2267 | 1,2296 | 1,2326 | 1,2355 | 1,2384 | 1,2413 | 1,2442 | 1,2470 | 1,2499 |
| 3,5 | 1,2528 | 1,2556 | 1,2585 | 1,2613 | 1,2641 | 1,2669 | 1,2698 | 1,2726 | 1,2754 | 1,2782 |
| 3,6 | 1,2809 | 1,2837 | 1,2865 | 1,2892 | 1,2920 | 1,2947 | 1,2975 | 1,3002 | 1,3029 | 1,3056 |
| 3,7 | 1,3083 | 1,3110 | 1,3137 | 1,3164 | 1,3191 | 1,3218 | 1,3244 | 1,3271 | 1,3297 | 1,3324 |
| 3,8 | 1,3350 | 1,3376 | 1,3403 | 1,3429 | 1,3455 | 1,3481 | 1,3507 | 1,3533 | 1,3558 | 1,3584 |
| 3,9 | 1,3610 | 1,3635 | 1,3661 | 1,3686 | 1,3712 | 1,3737 | 1,3762 | 1,3788 | 1,3813 | 1,3838 |
| 4,0 | 1,3863 | 1,3888 | 1,3913 | 1,3938 | 1,3962 | 1,3987 | 1,4012 | 1,4036 | 1,4061 | 1,4085 |
| 4,1 | 1,4110 | 1,4134 | 1,4159 | 1,4183 | 1,4207 | 1,4231 | 1,4255 | 1,4279 | 1,4303 | 1,4327 |
| 4,2 | 1,4351 | 1,4375 | 1,4398 | 1,4422 | 1,4446 | 1,4469 | 1,4493 | 1,4516 | 1,4540 | 1,4563 |
| 4,3 | 1,4586 | 1,4609 | 1,4633 | 1,4656 | 1,4679 | 1,4702 | 1,4725 | 1,4748 | 1,4770 | 1,4793 |
| 4,4 | 1,4816 | 1,4839 | 1,4861 | 1,4884 | 1,4907 | 1,4929 | 1,4951 | 1,4974 | 1,4996 | 1,5019 |
| 4,5 | 1,5041 | 1,5063 | 1,5085 | 1,5107 | 1,5129 | 1,5151 | 1,5173 | 1,5195 | 1,5217 | 1,5239 |
| 4,6 | 1,5261 | 1,5282 | 1,5304 | 1,5326 | 1,5347 | 1,5369 | 1,5390 | 1,5412 | 1,5433 | 1,5454 |
| 4,7 | 1,5476 | 1,5497 | 1,5518 | 1,5539 | 1,5560 | 1,5581 | 1,5602 | 1,5623 | 1,5644 | 1,5665 |
| 4,8 | 1,5686 | 1,5707 | 1,5728 | 1,5748 | 1,5769 | 1,5790 | 1,5810 | 1,5831 | 1,5851 | 1,5872 |
| 4,9 | 1,5892 | 1,5913 | 1,5933 | 1,5953 | 1,5974 | 1,5994 | 1,6014 | 1,6034 | 1,6054 | 1,6074 |
| 5,0 | 1,6094 | 1,6114 | 1,6134 | 1,6154 | 1,6174 | 1,6194 | 1,6214 | 1,6233 | 1,6253 | 1,6273 |
| 5,1 | 1,6292 | 1,6312 | 1,6332 | 1,6351 | 1,6371 | 1,6390 | 1,6409 | 1,6429 | 1,6448 | 1,6467 |
| 5,2 | 1,6487 | 1,6506 | 1,6525 | 1,6544 | 1,6563 | 1,6582 | 1,6601 | 1,6620 | 1,6639 | 1,6658 |
| 5,3 | 1,6677 | 1,6696 | 1,6715 | 1,6734 | 1,6752 | 1,6771 | 1,6790 | 1,6808 | 1,6827 | 1,6845 |
| 5,4 | 1,6864 | 1,6882 | 1,6901 | 1,6919 | 1,6938 | 1,6956 | 1,6974 | 1,6993 | 1,7011 | 1,7029 |
| 5,5 | 1,7047 | 1,7066 | 1,7084 | 1,7102 | 1,7120 | 1,7138 | 1,7156 | 1,7174 | 1,7192 | 1,7210 |
| 5,6 | 1,7228 | 1,7246 | 1,7263 | 1,7281 | 1,7299 | 1,7317 | 1,7334 | 1,7352 | 1,7370 | 1,7387 |
| 5,7 | 1,7405 | 1,7422 | 1,7440 | 1,7457 | 1,7475 | 1,7492 | 1,7509 | 1,7527 | 1,7544 | 1,7561 |
| 5,8 | 1,7579 | 1,7596 | 1,7613 | 1,7630 | 1,7647 | 1,7664 | 1,7681 | 1,7699 | 1,7716 | 1,7733 |
| 5,9 | 1,7750 | 1,7766 | 1,7783 | 1,7800 | 1,7817 | 1,7834 | 1,7851 | 1,7867 | 1,7884 | 1,7901 |
| 6,0 | 1,7918 | 1,7934 | 1,7951 | 1,7967 | 1,7984 | 1,8001 | 1,8017 | 1,8034 | 1,8050 | 1,8066 |
| 6,1 | 1,8083 | 1,8099 | 1,8116 | 1,8132 | 1,8148 | 1,8165 | 1,8181 | 1,8197 | 1,8213 | 1,8229 |
| 6,2 | 1,8245 | 1,8262 | 1,8278 | 1,8294 | 1,8310 | 1,8326 | 1,8342 | 1,8358 | 1,8374 | 1,8390 |
| 6,3 | 1,8405 | 1,8421 | 1,8437 | 1,8453 | 1,8469 | 1,8485 | 1,8500 | 1,8516 | 1,8532 | 1,8547 |
| 6,4 | 1,8563 | 1,8579 | 1,8594 | 1,8610 | 1,8625 | 1,8641 | 1,8656 | 1,8672 | 1,8687 | 1,8703 |
| 6,5 | 1,8718 | 1,8733 | 1,8749 | 1,8764 | 1,8779 | 1,8795 | 1,8810 | 1,8825 | 1,8840 | 1,8856 |
| 6,6 | 1,8871 | 1,8886 | 1,8901 | 1,8916 | 1,8931 | 1,8946 | 1,8961 | 1,8976 | 1,8991 | 1,9006 |
| 6,7 | 1,9021 | 1,9036 | 1,9051 | 1,9066 | 1,9081 | 1,9095 | 1,9110 | 1,9125 | 1,9140 | 1,9155 |
| 6,8 | 1,9169 | 1,9184 | 1,9199 | 1,9213 | 1,9228 | 1,9242 | 1,9257 | 1,9272 | 1,9286 | 1,9301 |
| 6,9 | 1,9315 | 1,9330 | 1,9344 | 1,9359 | 1,9373 | 1,9387 | 1,9402 | 1,9416 | 1,9430 | 1,9445 |
| 7,0 | 1,9459 | 1,9473 | 1,9488 | 1,9502 | 1,9516 | 1,9530 | 1,9544 | 1,9559 | 1,9573 | 1,9587 |
| 7,1 | 1,9601 | 1,9615 | 1,9629 | 1,9643 | 1,9657 | 1,9671 | 1,9685 | 1,9699 | 1,9713 | 1,9727 |
| 7,2 | 1,9741 | 1,9755 | 1,9769 | 1,9782 | 1,9796 | 1,9810 | 1,9824 | 1,9838 | 1,9851 | 1,9865 |
| 7,3 | 1,9879 | 1,9892 | 1,9906 | 1,9920 | 1,9933 | 1,9947 | 1,9961 | 1,9974 | 1,9988 | 2,0001 |
| 7,4 | 2,0015 | 2,0028 | 2,0042 | 2,0055 | 2,0069 | 2,0082 | 2,0096 | 2,0109 | 2,0122 | 2,0136 |
| 7,5 | 2,0149 | 2,0162 | 2,0176 | 2,0189 | 2,0202 | 2,0215 | 2,0229 | 2,0242 | 2,0255 | 2,0268 |
| 7,6 | 2,0281 | 2,0295 | 2,0308 | 2,0321 | 2,0334 | 2,0347 | 2,0360 | 2,0373 | 2,0386 | 2,0399 |
| 7,7 | 2,0412 | 2,0425 | 2,0438 | 2,0451 | 2,0464 | 2,0477 | 2,0490 | 2,0503 | 2,0516 | 2,0528 |
| 7,8 | 2,0541 | 2,0554 | 2,0567 | 2,0580 | 2,0592 | 2,0605 | 2,0618 | 2,0631 | 2,0643 | 2,0656 |
| 7,9 | 2,0669 | 2,0681 | 2,0694 | 2,0707 | 2,0719 | 2,0732 | 2,0744 | 2,0757 | 2,0769 | 2,0782 |
| 8,0 | 2,0794 | 2,0807 | 2,0819 | 2,0832 | 2,0844 | 2,0857 | 2,0869 | 2,0882 | 2,0894 | 2,0906 |
| 8,1 | 2,0919 | 2,0931 | 2,0943 | 2,0956 | 2,0968 | 2,0980 | 2,0992 | 2,1005 | 2,1017 | 2,1029 |
| 8,2 | 2,1041 | 2,1054 | 2,1066 | 2,1078 | 2,1090 | 2,1102 | 2,1114 | 2,1126 | 2,1138 | 2,1150 |
| 8,3 | 2,1163 | 2,1175 | 2,1187 | 2,1199 | 2,1211 | 2,1223 | 2,1235 | 2,1247 | 2,1258 | 2,1270 |
| 8,4 | 2,1282 | 2,1294 | 2,1306 | 2,1318 | 2,1330 | 2,1342 | 2,1353 | 2,1365 | 2,1377 | 2,1389 |
| 8,5 | 2,1401 | 2,1412 | 2,1424 | 2,1436 | 2,1448 | 2,1459 | 2,1471 | 2,1483 | 2,1494 | 2,1506 |
| 8,6 | 2,1518 | 2,1529 | 2,1541 | 2,1552 | 2,1564 | 2,1576 | 2,1587 | 2,1599 | 2,1610 | 2,1622 |
| 8,7 | 2,1633 | 2,1645 | 2,1656 | 2,1668 | 2,1679 | 2,1691 | 2,1702 | 2,1713 | 2,1725 | 2,1736 |
| 8,8 | 2,1748 | 2,1759 | 2,1770 | 2,1782 | 2,1793 | 2,1804 | 2,1815 | 2,1827 | 2,1838 | 2,1849 |
| 8,9 | 2,1861 | 2,1872 | 2,1883 | 2,1894 | 2,1905 | 2,1917 | 2,1928 | 2,1939 | 2,1950 | 2,1961 |
| 9,0 | 2,1972 | 2,1983 | 2,1994 | 2,2006 | 2,2017 | 2,2028 | 2,2039 | 2,2050 | 2,2061 | 2,2072 |
| 9,1 | 2,2083 | 2,2094 | 2,2105 | 2,2116 | 2,2127 | 2,2138 | 2,2148 | 2,2159 | 2,2170 | 2,2181 |
| 9,2 | 2,2192 | 2,2203 | 2,2214 | 2,2225 | 2,2235 | 2,2246 | 2,2257 | 2,2268 | 2,2279 | 2,2289 |
| 9,3 | 2,2300 | 2,2311 | 2,2322 | 2,2332 | 2,2343 | 2,2354 | 2,2364 | 2,2375 | 2,2386 | 2,2396 |
| 9,4 | 2,2407 | 2,2418 | 2,2428 | 2,2439 | 2,2450 | 2,2460 | 2,2471 | 2,2481 | 2,2492 | 2,2502 |
| 9,5 | 2,2513 | 2,2523 | 2,2534 | 2,2544 | 2,2555 | 2,2565 | 2,2576 | 2,2586 | 2,2597 | 2,2607 |
| 9,6 | 2,2618 | 2,2628 | 2,2638 | 2,2649 | 2,2659 | 2,2670 | 2,2680 | 2,2690 | 2,2701 | 2,2711 |
| 9,7 | 2,2721 | 2,2732 | 2,2742 | 2,2752 | 2,2762 | 2,2773 | 2,2783 | 2,2793 | 2,2803 | 2,2814 |
| 9,8 | 2,2824 | 2,2834 | 2,2844 | 2,2854 | 2,2865 | 2,2875 | 2,2885 | 2,2895 | 2,2905 | 2,2915 |
| 9,9 | 2,2925 | 2,2935 | 2,2946 | 2,2956 | 2,2966 | 2,2976 | 2,2986 | 2,2996 | 2,3006 | 2,3016 |
II.
 Таблица для перехода от натуральных логарифмов к десятичным
Таблица для перехода от натуральных логарифмов к десятичным (таблица умножения на М = log е = 0,4342945…)
| 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | |
| 0 | 0,0000 | 4,3430 | 8,6859 | 13,0288 | 17,3718 | 21,7147 | 26,0577 | 30,4006 | 34,7436 | 39,0865 |
| 1 | 0,4343 | 4,7772 | 9,1202 | 13,4631 | 17,8061 | 22,1490 | 26,4920 | 30,8349 | 35,1779 | 39,5208 |
| 2 | 0,8686 | 5,2115 | 9,5545 | 13,8974 | 18,2404 | 22,5833 | 26,9263 | 31,2692 | 35,6122 | 39,9551 |
| 3 | 1,3029 | 5,6458 | 9,9888 | 14,3317 | 18,6747 | 23,0176 | 27,3606 | 31,7035 | 36,0464 | 40,3894 |
| 4 | 1,7372 | 6,0801 | 10,4231 | 14,7660 | 19,1090 | 23,4519 | 27,7948 | 32,1378 | 36,4807 | 40,8237 |
| 5 | 2,1715 | 6,5144 | 10,8574 | 15,2003 | 19,5433 | 23,8862 | 28,2291 | 32,5721 | 36,9150 | 41,2580 |
| 6 | 2,6058 | 6,9487 | 11,2917 | 15,6346 | 19,9775 | 24,3205 | 28,6634 | 33,0064 | 37,3493 | 41,6923 |
| 7 | 3,0401 | 7,3830 | 11,7260 | 16,0689 | 20,4118 | 24,7548 | 29,0977 | 33,4407 | 37,7836 | 42,1266 |
| 8 | 3,4744 | 7,8173 | 12,1602 | 16,5032 | 20,8461 | 25,1891 | 29,5320 | 33,8750 | 38,2179 | 42,5609 |
| 9 | 3,9086 | 8.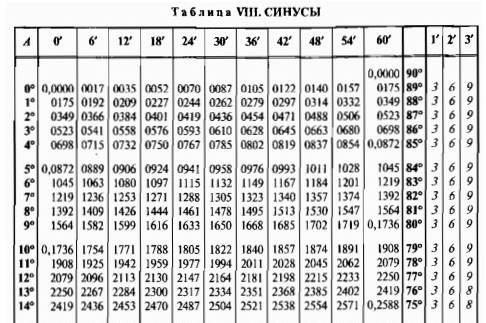 2516 2516 |
12,5945 | 16,9375 | 21,2804 | 25,6234 | 29,9663 | 34,3093 | 38,6522 | 42,9952 |
III. Таблица для перехода от десятичных логарифмов к натуральным
(таблица умножения на i = In 10 = 2,302585)
| 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | |
| 0 | 0,0000 | 23,026 | 46,052 | 69,078 | 92,103 | 115,129 | 138,155 | 161,181 | 184,207 | 207,233 |
| 1 | 2,3026 | 25,328 | 48,354 | 71,380 | 94,406 | 117,431 | 140,458 | 163,484 | 186,509 | 209,535 |
| 2 | 4,6052 | 27,631 | 50,657 | 73,683 | 96,709 | 119,734 | 142,760 | 165,786 | 188,812 | 211,838 |
| 3 | 6,9078 | 29,934 | 52,959 | 75,985 | 99,011 | 122,037 | 145,062 | 166,089 | 191,115 | 214,140 |
| 4 | 9,2103 | 32,236 | 55,262 | 78,288 | 101,314 | 124,340 | 147,365 | 170,391 | 193,417 | 216,443 |
| 5 | 11,513 | 34,539 | 57,565 | 80,590 | 103,616 | 126,642 | 149,668 | 172,694 | 195,720 | 218,746 |
| 6 | 13,816 | 36,841 | 59,867 | 82,893 | 105,919 | 128,945 | 151,971 | 174,997 | 198,022 | 221,048 |
| 7 | 16,118 | 39,144 | 62,170 | 85,196 | 108,221 | 131,247 | 154,273 | 177,299 | 200,325 | 223,351 |
| 8 | 18,421 | 41,447 | 64,472 | 87,498 | 110,524 | 133,550 | 156,576 | 179,602 | 202,627 | 225,653 |
| 9 | 20,723 | 43,749 | 66,775 | 89,801 | 112,827 | 135,853 | 158,878 | 181,904 | 204,930 | 227,956 |
_______________
Источник информации: Справочник по высшей математике / М.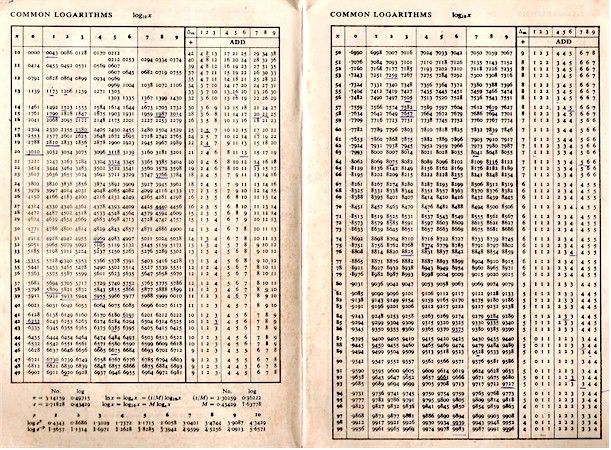 Я. Выгодский. — М.: ACT: Астрель, 2006.
Я. Выгодский. — М.: ACT: Астрель, 2006.
Десятичные и натуральные логарифмы: определения, свойства и примеры
- Десятичный логарифм и его свойства
- Натуральный логарифм и его свойства
- Примеры
п.1. Десятичный логарифм и его свойства
Логарифмы чисел по основанию 10 называют десятичными.
Для десятичных логарифмов принято специальное обозначение: \begin{gather*} \log_{10}x\overset{def}{=}\lg x \end{gather*}
Основание десятичных логарифмов \(10\gt 1\), поэтому они обладают всеми свойствами логарифмов с основанием больше единицы (см. §30 данного справочника).
Но у десятичных логарифмов есть также целых ряд дополнительных свойств, благодаря которым в докомпьютерную эпоху они широко использовались для трудоемких вычислений. Роль калькулятора тогда выполняли логарифмическая таблица и логарифмическая линейка.
Целая часть десятичного логарифма \([\lg x]\) называется характеристикой, а дробная часть \(\left\{\lg x\right\}\) – мантиссой. n\)
n\)
характеристика равна порядку числа \([\lg b]=n\), мантисса \(\left\{\lg b\right\}=\lg a\)
О стандартном виде числа, см. §41 справочника для 8 класса.
Например:
| Число b | Стандартный вид | Характеристика | Мантисса b | Унифицированная запись | Логарифм числа \(\lg b\) |
| 420 | 4,2·102 | 2 | 0,623 | 2,623 | 2,623 |
| 42 | 4,2·101 | 1 | 0,623 | 1,623 | 1,623 |
| 4,2 | 4,2 | 2 | 0 | 0,623 | 0,623 |
| 0,42 | 4,2·10–1 | –1 | 0,623 | \(\overline{1},623\) | –0,377 |
| 0,042 | 4,2·10–2 | –2 | 0,623 | \(\overline{2},623\) | –1,377 |
\(\lg 4,2\approx 0. 623\)
623\)
Если использовать унифицированную запись, как в представленной таблице, то мантисса всегда лежит в промежутке \(0\lt \lg a\lt 1\). У чисел, отличающихся только порядком, мантисса одинакова. Можно составить таблицы мантисс и пользоваться ими для умножения и деления, «разбавляя» их несложным сложением и вычитанием целых характеристик по необходимости.
Первые таблицы логарифмов были изданы в 1617 году оксфордским математиком Бригсом. Таблицы пересчитывались, дополнялись и переиздавались вплоть до 70-х гг. ХХ века, когда на столах стали появляться калькуляторы.
Таблицы Брадиса, которыми по традиции пользуются наши школьники с 1921 года, издаются до сих пор и постепенно перекочевывают в Интернет.
Непосредственная связь десятичных логарифмов с десятичной системой исчисления делает их удобным инструментом для оценки порядка числа и сравнения чисел.
В практике приближенных вычислений используется следующая оценочная таблица:
\(\lg 1\)
\(\lg 2\)
\(\lg 3\)
\(\lg 4\)
\(\lg 5\)
\(\lg 8\)
0
0,3
0,5
0,6
0,7
0,9
Относительная погрешность этих приближений (кроме \(\lg 3)\) \(\delta\sim 0,5\text{%}\)
Например:
Сравним \(\log_23\) и \(log_58\)
Сравнивая с помощью оценки, получаем: \begin{gather*} \log_23=\frac{\lg 3}{\lg 2}\approx\frac{0,5}{0,3}=\frac53,\ \ \log_58=\frac{\lg 8}{\lg 5}\approx\frac{0,9}{0,7}=\frac97\\ \frac{35}{21}\gt \frac{27}{21}\Rightarrow \frac53\gt \frac97\Rightarrow\log_23\gt\log_58 \end{gather*}
п.
 {3} = 1000; \cdots$
{3} = 1000; \cdots$
Будем говорить, что эти числа представляются единицей с нулями (с последующими нулями, если $n > 0$, и с предшествующими нулями, если $n
Десятичный логарифм числа, представляемого единицей с нулями, равен числу нулей в этом числе, если оно есть единица с последующими нулями, и числу нулей с противоположным знаком, если оно есть единица с предшествующими нулями.
Например:
$lg 0,0001=-4, lg 0,01=-2, lg 1000 = 3, lg 1000000 = 6$.
Десятичный логарифм любого числа, не равного целой степени десяти, является числом дробным (вообще говоря, иррациональным).
Напомним, что всякое число (рациональное или иррациональное) однозначно разлагается на сумму своей целой части и дробней части. При этом целой частью данного числа называется наибольшее целое число, не превосходящее данного; дробная часть любого числа заключена между нулем и единицей:
$3,176 = 3 + 0,176; — 2,143 = — 3 + 0,857 = \overline{3},857$. {-3} \leq 0,0032 $\cdots \cdots$
{-3} \leq 0,0032 $\cdots \cdots$
Неравенства (3) показывают, что
$- l \leq lg N
т. е. характеристика логарифма $lg N$ равна $-l$.
Итак, характеристика десятичного логарифма положительного числа, меньшего единицы, равна взятому со знаком минус числу нулей в данном числе, предшествующих первой значащей цифре, включая и нуль целых.
Например:
$lg 0,3052 = \overline{1}, \cdots; lg 0,0587 = \overline{2} \cdots; lg 0,0096 = \overline{3}, \cdots$
Мы выяснили, что характеристика десятичного логарифма числа определяется непосредственно по виду самого числа, если оно целое или представлено в виде десятичной дроби. Для определения характеристики, таким образом, не нужны никакие вычисления (и таблицы). Что же касается мантиссы, то она, как правило, берется из таблиц (например, из таблиц Брадиса). При этом следует пользоваться одним замечательным свойством мантиссы: если в логарифмируемом числе перенести запятую на любое количество знаков влево или вправо, то мантисса десятичного логарифма от этого не изменится (изменится только характеристика логарифма). {4} = 4$.
{4} = 4$.
Log Values От 1 до 10
В математике логарифмирование является наиболее удобным способом выражения больших чисел. Определение логарифма можно сформулировать как степень, в которую нужно возвести любое число, чтобы получить некоторые значения. Логарифмы также называют процессом, обратным возведению в степень. В этой статье; мы изучим логарифмические функции, свойства логарифмических функций, таблицу значений журнала, значения журнала от 1 до 10 для основания журнала 10, а также значения журнала от 1 до 10 для основания журнала e.
Логарифмические значения важны в математике и других связанных предметах, таких как физика. Студенты должны обратиться к значениям журнала для нахождения различных сумм, связанных с логарифмами. Значение log 1 по основанию 10 равно нулю. Значения журнала можно определить с помощью функции логарифмирования. Существуют различные типы логарифмических функций. Функции журнала полезны для поиска длинных вычислений и экономии времени. Использование логарифмической функции также упрощает решение сложной задачи. Используя логарифмические функции, учащиеся могут сократить операции от умножения до сложения и от деления до вычитания. Прочтите здесь, чтобы узнать больше о функциях логарифмирования.
Использование логарифмической функции также упрощает решение сложной задачи. Используя логарифмические функции, учащиеся могут сократить операции от умножения до сложения и от деления до вычитания. Прочтите здесь, чтобы узнать больше о функциях логарифмирования.
Логарифмическая функция
Логарифмическая функция определяется как функция, обратная возведению в степень.
Функция логарифмов задается как
F(x) = loga x
Здесь основание логарифма равно a. Его можно прочитать как логарифмическую базу x. Наиболее часто используемые функции логарифмирования по основанию 10 и основанию e.
Правила логарифмирования
Существуют некоторые правила логарифмирования, и учащиеся должны знать эти правила для решения вопросов. Правила приведены здесь:
Логарифмическая функция с основанием 10 известна как функция десятичного логарифма. Он выражается как log10.
F(x) =log10 x
Логарифмическая функция по основанию e известна как функция натуральных логарифмов. Выражается как loge.
F(x) = loge x
Правило произведения
В правиле произведения два числа будут умножены на одно и то же основание, а затем будут добавлены степени.
Logb MN = Logb M + Logb N
Правило частного
В правиле частного два числа будут разделены по одному основанию, а затем будут вычтены степени, Logb M/N = Logb M — Logb N
Степенное правило
В степенном правиле выражения степени возводятся в степень, а затем степени умножаются.
Logb Mp = P logb M
Правила нулевого порядка
Loga = 1
Изменение базового правила
Logb (x) = in x/ In b или logb (x) = log10 x / log10 bЗначение от Log 1 до log 10 для Log Base 10 Таблица
Log Таблица от 1 до 10 для Log Base 10
Common log to a number (log10X) | Log Values |
Log 1 | 0 |
Log 2 | 0,3010 |
Log 3 | 0. |
Log 4 | 0.6020 |
Log 5 | 0.6989 |
Log 6 | 0,7781 |
log 7 | 0,8450 |
Log 8 | 0,9030 | 0,9030 | 0,9030 | 91920,9030 | 91890,9030 | 0,9030 | 0,9030 |
| .0083 log 9003 | 0,9542 |
log 10 | 1 |
ЗДЕСЬ. ЗДЕСЬ ПРОДОЛЖЕНИЕ ВАМАЛЕВА.
ЗДЕСЬ ПРОДОЛЖЕНИЕ ВАМАЛЕВА.
Журнал Таблица с 1 по 10 для логарифмической базы E
Обычный логарифм до числа (Loge X) | LN0002 0 | |
ln (2) | 0.6 | |
ln (3) | 1.098612 | |
ln (4) | 1.386294 | |
ln (5) | 1.609438 | |
ln (6) | 1.7 | |
ln (7) | 1. | |
ln (8) | 2. | |
ln (9) | 2.1 | |
ln (10) | 2.302585 |
В соответствии с определением логарифмической функции logan=x можно записать в виде экспоненциальной функции:
Тогда ax = b
Если значение log 1 не задано, вы можете взять основание равным 10. Таким образом, вы можно выразить как log 1 как log10 1.
Теперь, согласно определению логарифма, мы знаем значение a =10 и b =1. Таким образом,
Log 10 x = 1
Мы также можем записать это как:
10x= 1
Мы уже знаем, что все, что возведено в степень 0, равно 1. Таким образом, 10, возведенное в степень 0, покажет что приведенное выше выражение верно.
Итак, 100 = 1
Это общее условие для базового значения log, и основание, возведенное в нулевую степень, даст вам значение 1.
Это доказывает, что значение журнала 1 равно 0.
Альтернативный метод поиска журнала 1 или записи по базе e?
Мы также можем найти логарифмическое значение 1
Log (b) = loge (b)
Таким образом, Ln(1) = loge(1)
Или ex = 1
∴ e0 = 1
Следовательно , Ln(1) = loge(1) = 0
Важные моменты, которые следует помнить
Учащиеся должны помнить несколько важных моментов, связанных с логарифмами. Некоторые важные моменты, которые следует помнить:
Индия была первой страной во 2 веке до нашей эры, которая использовала логарифм.
Обратный процесс логарифмирования также известен как возведение в степень
Если нужно выполнить теоретическую работу, лучше всего подойдут натуральные логарифмы.
 Их легко вычислить количественно.
Их легко вычислить количественно.Наиболее важным преимуществом использования логарифмов по основанию 10 является то, что их легко вычислить в уме для некоторых чисел. Например, логарифмическая база 10 из 1 00 000 равна 5, и вам нужно считать только нули.
Решенные примеры
Решите следующее для значения x для log3 x = log34 + log37, используя свойства логарифма?
Решение: log3x = log34 + log37
= log34 + log37 = log3 (4 x 7) (с использованием правила сложения)
= log3(28)
Следовательно, x = 28
10 9003 Evalue : log1 – log 0
Решение: log1 – log 0 (дано)
Значение журнала 1 = 0 и значение журнала 0 = — ∞
Следовательно, log 1+ log 0 = 0-(-∞) = ∞
Найдите значение log 2 (64)
Решение: x =64 (Дано)
Используя 90 Базовая формула,
Log 2 x = log 10 x/ log 10 2
= log 2 64 = log 10 64/ log 10 2 9000 2
= 64/ log 10 2 9000 2
= 1,80416 = 1,80418 = 1,80418 = 1,80418 = 1,80418 = 1,80418 = 1,80418 = 1,80418 = 1,80418 = 1,80418 = 1,80418 = 1,80418 = 1,80418 = 1,80416 = 1,80418 = 1,80416.
Quiz Time
1. Логарифмические функции являются обратной экспонентой
а. Стихи
б. Функции
c. Номера
д. Цифры
2. Как записать уравнение 53= 125 в логарифмической форме
a. Лог 3 (125) =5
б. Лог 125 (5) = 3
c. Лог 5 (125) = 3
д. Журнал 5 (3 = 124)
3. Чему будет равен лог 9, если лог 27 = 1,431?
а. 0,934
б. 0,945
в. 0,954
г. 0,958
Таблица десятичного логарифма
Таблица десятичного логарифмаТаблица десятичного логарифма
В таблице ниже перечислены десятичные логарифмы (с основанием 10) для числа от 1 до 10.
Логарифм выделен жирным шрифтом. Например, первая запись в третьем столбце
означает, что общий логарифм 2,00 равен 0,3010300.
Примечание. Эта таблица довольно длинная, и ее загрузка может занять несколько секунд! Вы также можете скачать таблицу в виде электронной таблицы Excel. Печать в ландшафтном режиме на двух страницах должна дать удовлетворительные результаты.
| 1.000 | 0,00000000 | 2,00 | 3,00 | 4,00 | 9624″ x:fmla=»=LOG(I1)-FLOOR(LOG(I1),1)»> 0,6020600 | 5,00 | 698 | 6,00 | 0,7781513 | 7,00 | 0,8450980 | 8,00 | 164374649943″ x:fmla=»=LOG(S34)-FLOOR(LOG(S34),1)»>54″ x:fmla=»=LOG(Q1)-FLOOR(LOG(Q1),1)»> 0, | 00 | 9,00 | 1,001 | 929E-4″ x:fmla=»=LOG(A2)»> 0,00043408 | 2,01 | 3,01 | 32″ x:fmla=»=LOG(C80)-FLOOR(LOG(C80),1)»>34″ x:fmla=»=LOG(G2)-FLOOR(LOG(G2),1)»> 0,4785665 | 4. 01 01 | 0,6031444 | 5,01 | 0,6998377 | 6.01 | 0,7788745 | 7,01 | 8.01 | 0, | 9.01 | 82449″ x:fmla=»=LOG(M3)-FLOOR(LOG(M3),1)»>3″ x:fmla=»=LOG(S2)-FLOOR(LOG(S2),1)»> 0, | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,002 | 0,00086772 | 2,02 | 3,02 | 480006 | 4,02 | 0,6042261 | 5,02 | 0,7007037 | 6,02 | 82449″ x:fmla=»=LOG(M3)-FLOOR(LOG(M3),1)»> 0,77 | 7,02 | 0,8463371 | 8.02 | 0,44 | 9.02 | 1,003 | 2,03 | 3074 | 289″ x:fmla=»=LOG(E4)-FLOOR(LOG(E4),1)»> 0,3074960 | 3,03 | 0,4814426 | 4,03 | 0,6053050 | 5,03 | 6,03 | 0,7803173 | 7,03 | 8.03 | 0,55 | 9,03 | 1,004 | 0,00173371 | 2,04 | 30 | 3,04 | 0,4828736 | 4,04 | 0,6063814 | 5,04 | 0,7024305 | 6,04 | 7,04 | 1222″ x:fmla=»=LOG(O5)-FLOOR(LOG(O5),1)»> 0,8475727 | 8.04 | 0, | 60 | 9.04 | 1.005 | 0,00216606 | 2,05 | 31175386105575426″ x:fmla=»=LOG(E6)-FLOOR(LOG(E6),1)»> 0,3117539 | 3,05 | 8583″ x:fmla=»=LOG(G6)-FLOOR(LOG(G6),1)»> 0,4842998 | 4,05 | 0,6074550 | 5,05 | 6,05 | 0,7817554 | 7,05 | 65″ x:fmla=»=LOG(O6)-FLOOR(LOG(O6),1)»> 0,8481891 | 8,05 | 59 | 9,05 | 001″> 1,006 | 719 | 72E-3″ x:fmla=»=LOG(A7)»> 0,002597982,06 | 3,06 | 0,4857214 | 4,06 | 0,6085260 | 5,06 | 6,06 | 0,7824726 | 7,06 | 0,8488047 | 8.06 | 0, | 50 | 9,06 | 8181312″ x:fmla=»=LOG(S7)-FLOOR(LOG(S7),1)»> 0,82 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,007 | 536176745E-3″ x:fmla=»=LOG(A8)»> 0,00302947 | 2,07 | 3,07 | 0,4871384 | 4,07 | 5,07 | 3604″ x:fmla=»=LOG(K8)-FLOOR(LOG(K8),1)»> 0,7050080 | 6,07 | 3873768″ x:fmla=»=LOG(E14)-FLOOR(LOG(E14),1)»>25757″ x:fmla=»=LOG(M8)-FLOOR(LOG(M8),1)»> 0,7831887 | 7,07 | 84941 | 6721541778″ x:fmla=»=LOG(S93)-FLOOR(LOG(S93),1)»>791633″ x:fmla=»=LOG(C87)-FLOOR(LOG(C87),1)»>45″ x:fmla=»=LOG(O8)-FLOOR(LOG(O8),1)»> 0,84 | 8.07 | 0, | 35 | 9,07 | 1,008 | 2.08 | 3,08 | 0,4885507 | 4,08 | 0,6106602 | 5,08 | 705863712283 | » x:fmla=»=LOG(K9)-FLOOR(LOG(K9),1)»> 0,7058637 | 6,08 | 3491″ x:fmla=»=LOG(M9)-FLOOR(LOG(M9),1)»> 0,7839036 | 7,08 | 8.08 | 0, | 14 | 9,08 | 1,009 | 5E-3″ x:fmla=»=LOG(A10)»> 0,00389117 | 2,09 | 0,3201463 | 3,09 | 4,09 | 61172330800734176″ x:fmla=»=LOG(I10)-FLOOR(LOG(I10),1)»> 0,6117233 | 5,09 | 0,7067178 | 6,09 | 7,09 | 0,8506462 | 8,09 | 161227224″ x:fmla=»=LOG(Q10)-FLOOR(LOG(Q10),1)»> 0, | 859,09 | 1,010 | 0,00432137 | 1.10 | 158225077E-2″ x:fmla=»=LOG(C11)-FLOOR(LOG(C11),1)»> 0,0413927 | 2.10 | 082192319765″ x:fmla=»=LOG(Q58)-FLOOR(LOG(Q58),1)»>339193″ x:fmla=»=LOG(E11)-FLOOR(LOG(E11),1)»> 0,3222193 | 3,10 | 37E-3″ x:fmla=»=LOG(A21)»>6 | 27269″ x:fmla=»=LOG(G11)-FLOOR(LOG(G11),1)»> 0,44.10 | 5.10 | 6.10 | 0,7853298 | 7.10 | 0,8512583 | 8.10 | 0, | 509.10 | 09027 | 87″ x:fmla=»=LOG(S43)-FLOOR(LOG(S43),1)»>09353″ x:fmla=»=LOG(S11)-FLOOR(LOG(S11),1)»> 0,95||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0109999999999988″ x:fmla=»=A11+0.001″> 1,011 | 1.11 | 2.11 | 3.11 | 4.11 | 0,6138418 | 5.11 | 0,7084209 | 6.11 | 0,7860412 | 7.11 | 8.11 | 0,90 | 9. 11 11 | 1,012 | 1,12 | 2,12 | 144″ x:fmla=»=LOG(E13)-FLOOR(LOG(E13),1)»> 0,3263359 | 3,12 | 4.12 | 5,12 | 0516 | 348″ x:fmla=»=LOG(S52)-FLOOR(LOG(S52),1)»>60073″ x:fmla=»=LOG(K13)-FLOOR(LOG(K13),1)»> 0,70 | 6,12 | 78675142214556115″ x:fmla=»=LOG(M13)-FLOOR(LOG(M13),1)»> 0,7867514 | 7,12 | 8.12 | 7529″ x:fmla=»=LOG(Q13)-FLOOR(LOG(Q13),1)»> 0, | 60 | 9.12 | 1,013 | 602798149E-3″ x:fmla=»=LOG(A14)»> 0,00560945 | 1,13 | 0,0530784 | 2,13 | 3,13 | 4,13 | 615 | 5,13 | 0,7101174 | 6,13 | 0,7874605 | 7,13 | 8.13 | 05 | 9.13 | 1.014 | 1,14 | 0,0569049 | 2,14 | 3,14 | 496807321494″ x:fmla=»=LOG(G15)-FLOOR(LOG(G15),1)»> 0,46 | 4,14 | 0,6170003 | 5,14 | 6,14 | 0,7881684 | 7,14 | 0,8536982 | 8.14 | 9.14 | 573383144″ x:fmla=»=LOG(S15)-FLOOR(LOG(S15),1)»> 0, 62 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,015 | 1,15 | 0635361165E-2″ x:fmla=»=LOG(C16)-FLOOR(LOG(C16),1)»> 0,0606978 | 2,15 | 3,15 | 4,15 | 5,15 | 0,7118072 | 6,15 | 0,7888751 | 7,15 | 0,8543060 | 8,15 | 76 | 9,15 | 0159999999999982″ x:fmla=»=A16+0.001″> 1.016 | E-3″ x:fmla=»=LOG(A17)»> 0,00689371 | 1,16 | E-2″ x:fmla=»=LOG(C17)-FLOOR(LOG(C17),1)»> 0,0644580 | 2,16 | 0,3344538 | 3,16 | 4,16 | 5,16 | 6,16 | 7,16 | 8,16 | 91169015875386117″ x:fmla=»=LOG(Q17)-FLOOR(LOG(Q17),1)»> 0, | 02 | 9,16 | 1,017 | 1,17 | 0,0681859 | 2,17 | 3,17 | 4,17 | 5,17 | 6,17 | 0,7 | 2 | 7,17 | 855516780012″ x:fmla=»=LOG(O18)-FLOOR(LOG(O18),1)»> 0,8555192 | 8,17 | 0, | 219,17 | 1,018 | 0,00774778 | 1,18 | 0,0718820 | 2,18 | 3,18 | 0,5024271 | 4,18 | 0,6211763 | 5,18 | 6,18 | 79098847508881587″ x:fmla=»=LOG(M19)-FLOOR(LOG(M19),1)»> 0,75 | 7,18 | 0,8561244 | 8,18 | 0, | 33 | 9,18 | 1,019 | 0,00817418 | 1,19 | 2,19 | 0,3404441 | 3,19 | 0,5037907 | 4,19 | 622214022535″ x:fmla=»=LOG(I20)-FLOOR(LOG(I20),1)»> 0,6222140 | 5,19 | 0,7151674 | 6,19 | 7,19 | 0,8567289 | 8,19 | 0, | 399,19 | 1,020 | 1,20 | 2,20 | 0,3424227 | 3,20 | 505149990605″ x:fmla=»=LOG(G21)-FLOOR(LOG(G21),1)»> 0,5051500 | 4,20 | 45″ x:fmla=»=LOG(I21)-FLOOR(LOG(I21),1)»> 0,6232493 | 5,20 | 0,7160033 | 6,20 | 49825389″ x:fmla=»=LOG(M21)-FLOOR(LOG(M21),1)»> 0,7 | 7 | 7,20 | 8,20 | 0, | 39 | 9,20 | 1.021 | 02574208690 | E-3″ x:fmla=»=LOG(A22)»> 0,004 | 1,21 | 0,0827854 | 2,21 | 68511072″ x:fmla=»=LOG(E22)-FLOOR(LOG(E22),1)»> 0,3443923 | 3,21 | 0,5065050 | 4,21 | 5,21 | 6,21 | 6 | 7,21 | 8,21 | 914343157111″ x:fmla=»=LOG(Q22)-FLOOR(LOG(Q22),1)»> 0,32 | 9,21 | 1,022 | 5958″ x:fmla=»=LOG(M57)-FLOOR(LOG(M57),1)»>4E-3″ x:fmla=»=LOG(A23)»> 0,00 | 1,22 | 0,0863598 | 2,22 | 3,22 | 4,22 | 5,22 | 0,7176705 | 6,22 | 738469081864″ x:fmla=»=LOG(M23)-FLOOR(LOG(M23),1)»> 0,74 | 7,22 | 8,22 | 181754005042″ x:fmla=»=LOG(Q23)-FLOOR(LOG(Q23),1)»> 0, | 18 | 9,22 | 362934″ x:fmla=»=LOG(S23)-FLOOR(LOG(S23),1)»> 0, | 09 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,023 | 0,00987563 | 1,23 | 31E-2″ x:fmla=»=LOG(C24)-FLOOR(LOG(C24),1)»> 0,0899051 | 2,23 | 0,3483049 | 3,23 | 3499999999999908″>2233110286″ x:fmla=»=LOG(G24)-FLOOR(LOG(G24),1)»> 0,50 | 4,23 | 0,6263404 | 5,23 | 0,7185017 | 6,23 | 7,23 | 8,23 | 983521226986″ x:fmla=»=LOG(Q24)-FLOOR(LOG(Q24),1)»> 0, | 98 | 9,23 | 1,024 | 1,24 | 3421685162235063E-2″ x:fmla=»=LOG(C25)-FLOOR(LOG(C25),1)»> 0,0 | 7 | 2,24 | 0,3502480 | 3,24 | 0,5105450 | 4,24 | 7″ x:fmla=»=LOG(I25)-FLOOR(LOG(I25),1)»> 0,6273659 | 5,24 | 6,24 | 7,24 | 8,24 | 7211622″ x:fmla=»=LOG(Q25)-FLOOR(LOG(Q25),1)»> 0,72 | 9,24 | 1,025 | 1,25 | 0,00 | 2,25 | 0,3521825 | 3,25 | 4,25 | 031049″ x:fmla=»=LOG(I26)-FLOOR(LOG(I26),1)»> 0,6283889 | 2499999999999902″> 5,25 | 6,25 | 7,25 | 0,8603380 | 8,25 | 004732038163″ x:fmla=»=LOG(Q27)-FLOOR(LOG(Q27),1)»>3 | 9 | » x:fmla=»=LOG(Q26)-FLOOR(LOG(Q26),1)»> 0, | 9,25 | 1,026 | 1,26 | 10037054511756291″ x:fmla=»=LOG(C27)-FLOOR(LOG(C27),1)»> 0,1003705 | 2,26 | 0,3541084 | 3,26 | » x:fmla=»=LOG(G27)-FLOOR(LOG(G27),1)»> 0,5132176 | 4,26 | 9910271788″ x:fmla=»=LOG(I27)-FLOOR(LOG(I27),1)»> 0,62 | 5,26 | 0,7209857 | 6,26 | 7,26 | 2599999999999891″> 8,26 | 9,26 | » x:fmla=»=LOG(S27)-FLOOR(LOG(S27),1)»> 0, 10 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1,027 | 1,27 | 2,27 | 3,27 | 0,5145478 | 4,27 | 0,6304279 | 5,27 | 0,7218106 | 2699999999999898″> 6,27 | 7,27 | 0,8615344 | 8,27 | 9,27 | 1.028 | 1,28 | 2,28 | 3,28 | 0,5158738 | 2799999999999896″> 4,28 | 0,6314438 | 5,28 | 381142″ x:fmla=»=LOG(K29)-FLOOR(LOG(K29),1)»> 0,7226339 | 6,28 | 7,28 | 8,28 | 033678487966″ x:fmla=»=LOG(Q29)-FLOOR(LOG(Q29),1)»> 0, | 03 | 9,28 | 1,029 | 0,01241537 | 1,29 | 110589 | 2,29 | 0,3598355 | 3,29 | 4,29 | 5,29 | 0,7234557 | 6,29 | 0,7986506 | 7,29 | 8,29 | 102378411046″ x:fmla=»=LOG(Q32)-FLOOR(LOG(Q32),1)»>45 | 9,29 | 28″ x:fmla=»=LOG(S30)-FLOOR(LOG(S30),1)»> 0,57 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.030 | 0,01283722 | 1,30 | 230683679″ x:fmla=»=LOG(C31)-FLOOR(LOG(C31),1)»> 0,1139434 | 2,30 | 0,3617278 | 3,30 | 788619″ x:fmla=»=LOG(G31)-FLOOR(LOG(G31),1)»> 0,5185139 | 4,30 | 63346845557 | 5,30 | 6,30 | 4 | 8102″ x:fmla=»=LOG(M31)-FLOOR(LOG(M31),1)»> 0,79 | 7,30 | 0,8633229 | 8.30 | 52E-2″ x:fmla=»=LOG(A34)»>80 | 07341″ x:fmla=»=LOG(Q31)-FLOOR(LOG(Q31),1)»> 0,919.30 | » x:fmla=»=LOG(S31)-FLOOR(LOG(S31),1)»> 0, 29 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0309999999999966″ x:fmla=»=A31+0.001″> 1,031 | 0,01325867 | 1,31 | 2,31 | 3,31 | 71742″ x:fmla=»=LOG(G32)-FLOOR(LOG(G32),1)»> 0,5198280 | 4,31 | 0,6344773 | 5,31 | 99999999802″>08146821″ x:fmla=»=LOG(K32)-FLOOR(LOG(K32),1)»> 0,7250945 | 6,31 | 3365″ x:fmla=»=LOG(M32)-FLOOR(LOG(M32),1)»> 0,8000294 | 3099999999999898″> 7,31 | 8,31 | 9,31 | 1,032 | 1,32 | 2,32 | 0,3654880 | 3,32 | 0,5211381 | 4,32 | 0,6354837 | 3199999999999896″> 5,32 | 6,32 | 0,8007171 | 7,32 | 0,8645111 | 8,32 | 9,32 | 1235398084″ x:fmla=»=LOG(S33)-FLOOR(LOG(S33),1)»> 0,96 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,033 | 1,33 | 2,33 | 367355601711″ x:fmla=»=LOG(E34)-FLOOR(LOG(E34),1)»> 0,3673559 | 3,33 | 0,5224442 | 4,33 | 5,33 | 0,7267272 | 6,33 | 0,8014037 | 7,33 | 8,33 | 9,33 | 0339999999999963″ x:fmla=»=A34+0.001″> 1,034 | 1,34 | 0,1271048 | 2,34 | 3,34 | 0,5237465 | 4,34 | 5,34 | 0,7275413 | 6,34 | 7,34 | 8656 |
| 8,34 | 9,34 | 1,035 | » x:fmla=»=LOG(O84)-FLOOR(LOG(O84),1)»> | 1,35 | 2,35 | 0,3710679 | 3,35 | 0,5250448 | 4,35 | 63848 | » x:fmla=»=LOG(E56)-FLOOR(LOG(E56),1)»>585225671328″ x:fmla=»=LOG(Q49)-FLOOR(LOG(Q49),1)»>5463632″ x:fmla=»=LOG(I36)-FLOOR(LOG(I36),1)»> 0,6384893 | 5,35 | 0,7283538 | 6,35 | 7,35 | 0,8662873 | 8,35 | 9,35 | 1,036 | 651018″ x:fmla=»=LOG(E39)-FLOOR(LOG(E39),1)»>55E-2″ x:fmla=»=LOG(A37)»> 0,01535976 | 1,36 | 13353890837021754″ x:fmla=»=LOG(C37)-FLOOR(LOG(C37),1)»> 0,1335389 | 2,36 | 3,36 | 8984276″ x:fmla=»=LOG(G37)-FLOOR(LOG(G37),1)»> 0,5263393 | 4,36 | 8498″ x:fmla=»=LOG(I37)-FLOOR(LOG(I37),1)»> 0,63 | 5,36 | 21″ x:fmla=»=LOG(K37)-FLOOR(LOG(K37),1)»> 0,72 | 6,36 | 0,8034571 | 7,36 | 0,8668778 | 8,36 | 627743901595″ x:fmla=»=LOG(Q37)-FLOOR(LOG(Q37),1)»> 0,63 | 9,36 | 1,037 | 0,01577876 | 1,37 | 0,1367206 | 2,37 | 0,3747483 | 3,37 | 0,5276299 | 4,37 | 5,37 | 3699999999999903″> 6,37 | 3534979″ x:fmla=»=LOG(M38)-FLOOR(LOG(M38),1)»> 0,8041394 | 7,37 | 0,8674675 | 8,37 | 624″ x:fmla=»=LOG(E66)-FLOOR(LOG(E66),1)»>45″ x:fmla=»=LOG(Q38)-FLOOR(LOG(Q38),1)»> 0, | 559,37 | 1,038 | 1,38 | 0,1398791 | 2,38 | 3799999999999901″> 3,38 | 0,5289167 | 4,38 | 0,6414741 | 5,38 | 0,7307823 | 6,38 | 0,8048207 | 7,38 | 0,8680564 | 8,38 | 9,38 | 1,039 | 6615547557175616E-2″ x:fmla=»=LOG(A40)»> 0,01661555 | 1,39 | 0,1430148 | 2,39 | 3,39 | 4,39 | 0,6424645 | 5,39 | 0,7315888 | 6,39 | 0,8055009 | 7,39 | 8,39 | 1 | 9,39 | 1.040 | 78514E-2″ x:fmla=»=LOG(A41)»> 0,01703334 | 1,40 | 0,1461280 | 2,40 | 0,3802112 | 3,40 | 0,5314789 | 4,40 | 0,6434527 | 5,40 | 636180664″ x:fmla=»=LOG(C78)-FLOOR(LOG(C78),1)»>822» x:fmla=»=LOG(K41)-FLOOR(LOG(K41),1)»> 0,7323938 | 3999999999999897″> 6,40 | 7,40 | 8,40 | » x:fmla=»=LOG(I46)-FLOOR(LOG(I46),1)»> | 6188114″ x:fmla=»=LOG(Q41)-FLOOR(LOG(Q41),1)»> 0,9,40 | 1,041 | 1,41 | 14921911265537988″ x:fmla=»=LOG(C42)-FLOOR(LOG(C42),1)»> 0,14 | 2,41 | 0,3820170 | 3,41 | 4,41 | 5,41 | 6,41 | 7,41 | 8,41 | 5991161″ x:fmla=»=LOG(Q42)-FLOOR(LOG(Q42),1)»> 0, | 60 | 9,41 | 1,042 | 1,42 | 0,1522883 | 2,42 | 0,3838154 | 3,42 | 0,5340261 | 4,42 | 5,42 | 5499999999999901″>3838609″ x:fmla=»=LOG(K43)-FLOOR(LOG(K43),1)»> 0,7339993 | 6,42 | 0,8075350 | 7,42 | 0,8704039 | 8,42 | 9 327292″ x:fmla=»=LOG(S48)-FLOOR(LOG(S48),1)»>209149 | 9″ x:fmla=»=LOG(Q43)-FLOOR(LOG(Q43),1)»> 0, | 9,42 | 1,043 | 0,01828431 | 1,43 | 0,1553360 | 4299999999999899″> 2,43 | 0,3856063 | 3,43 | 4,43 | 0,6464037 | 5,43 | 6,43 | 7,43 | 0,8709888 | 8,43 | 9,43 | 95 | 69968″ x:fmla=»=LOG(Q53)-FLOOR(LOG(Q53),1)»>32796″ x:fmla=»=LOG(S44)-FLOOR(LOG(S44),1)»> 0,17 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,044 | 0,01870050 | 1,44 | 2,44 | 0,3873898 | 3,44 | 0,5365584 | 4,44 | 5,44 | 6,44 | 0,8088859 | 4399999999999897″> 7,44 | 8,44 | 9,44 | 1,045 | 0,01 | 91,45 | 2,45 | 0,38 | 3,45 | 4,45 | 648360010980» x:fmla=»=LOG(I46)-FLOOR(LOG(I46),1)»> 0,6483600 | 5,45 | 6,45 | 7,45 | 0,8721563 | 8,45 | 6708 | 185″ x:fmla=»=LOG(Q46)-FLOOR(LOG(Q46),1)»> 0, | 67 | 9,45 | 1,046 | 1,46 | 0,1643529 | 4599999999999902″> 2,46 | 3883221» x:fmla=»=LOG(S10)-FLOOR(LOG(S10),1)»>1 | 3,46 | 20070002″ x:fmla=»=LOG(O54)-FLOOR(LOG(O54),1)»>4″ x:fmla=»=LOG(G47)-FLOOR(LOG(G47),1)»> 0,53 | 4,46 | 5,46 | 6,46 | 45″ x:fmla=»=LOG(M47)-FLOOR(LOG(M47),1)»> 0,8102325 | 7,46 | 0,8727388 | 8,46 | 95 | 69968″ x:fmla=»=LOG(Q53)-FLOOR(LOG(Q53),1)»>036303902298″ x:fmla=»=LOG(Q47)-FLOOR(LOG(Q47),1)»> 0, | 95 | 69968″ x:fmla=»=LOG(Q53)-FLOOR(LOG(Q53),1)»>04 | 9,46 | 1,047 | 1,47 | 0,1673173 | 2,47 | 0 | 3,47 | 4,47 | 46999999999999″> 5,47 | 0,7379873 | 6,47 | 0,8109043 | 7,47 | 0,8733206 | 8,47 | 9,47 | 1,048 | 0,02036128 | 1,48 | 2,48 | 68082621457″ x:fmla=»=LOG(E49)-FLOOR(LOG(E49),1)»> 0,3 | 84073323461180549″ x:fmla=»=LOG(M94)-FLOOR(LOG(M94),1)»>7 | 3,48 | 975″ x:fmla=»=LOG(G49)-FLOOR(LOG(G49),1)»> 0,5415792 | 4,48 | 0,6512780 | 5,48 | 0,7387806 | 6,48 | 0,8115750 | 7,48 | 46076″ x:fmla=»=LOG(O49)-FLOOR(LOG(O49),1)»> 0,8739016 | 8,48 | » x:fmla=»=LOG(E56)-FLOOR(LOG(E56),1)»>585225671328″ x:fmla=»=LOG(Q49)-FLOOR(LOG(Q49),1)»> 0, | 4799999999999898″> 9,48 | 1,049 | 625E-2″ x:fmla=»=LOG(A50)»> 0,02077549 | 1,49 | 0,1731863 | 2,49 | 3,49 | 4,49 | 0,6522463 | 5,49 | 6,49 | 812244636859″ x:fmla=»=LOG(M50)-FLOOR(LOG(M50),1)»> 0,8122447 | 7,49 | 8,49 | 9,49 | 1.050 | 5E-2″ x:fmla=»=LOG(A51)»> 0,02118930 | 1,50 | 0,1760913 | 2,50 | 3,50 | 0,5440680 | 4999999999999902″> 4,50 | 0,6532125 | 5,50 | 11″ x:fmla=»=LOG(K51)-FLOOR(LOG(K51),1)»> 0,7403627 | 6,50 | 0,8129134 | 7,50 | 0,8750613 | 8,50 | 892571429219″ x:fmla=»=LOG(Q51)-FLOOR(LOG(Q51),1)»> 0, | 89 | 9,50 | 1,051 | 0,02160272 | 1,51 | 17872 | 43″ x:fmla=»=LOG(C52)-FLOOR(LOG(C52),1)»> 0,1789769 | 2,51 | 3,51 | 0,5453071 | 4,51 | 5,51 | 0,7411516 | 6,51 | 0,8135810 | 7,51 | 8,51 | 5099999999999891″> 9,51 | 348″ x:fmla=»=LOG(S52)-FLOOR(LOG(S52),1)»> 0,05 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1.052 | 0.02201574 | 1,52 | 254″ x:fmla=»=LOG(C53)-FLOOR(LOG(C53),1)»> 0,1818436 | 2,52 | 0,4014005 | 3,52 | 0,5465427 | 4,52 | 0,6551384 | 5,52 | 772919809″ x:fmla=»=LOG(K53)-FLOOR(LOG(K53),1)»> 0,7419391 | 5199999999999898″> 6,52 | 7,52 | 0,8762178 | 8,52 | 95 | 69968″ x:fmla=»=LOG(Q53)-FLOOR(LOG(Q53),1)»> 0, | 96 | 9,52 | 1,053 | 0,02242837 | 1,53 | 0,1846914 | 2,53 | 0,4031205 | 3,53 | 0,5477747 | 5299999999999896″> 4,53 | 0,6560982 | 5,53 | 0,7427251 | 6,53 | 0,8149132 | 7,53 | 8,53 | 9,53 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,054 | 0,02284061 | 1,54 | 0,1875207 | 5399999999999898″> 2,54 | » x:fmla=»=LOG(E55)-FLOOR(LOG(E55),1)»> 0,4048337 | 3,54 | 0,54 | 4,54 | 0,6570559 | 5,54 | 6,54 | 0,8155777 | 7,54 | 8,54 | 155690604″ x:fmla=»=LOG(K63)-FLOOR(LOG(K63),1)»>787068900454″ x:fmla=»=LOG(Q55)-FLOOR(LOG(Q55),1)»> 0, | 74155690604″ x:fmla=»=LOG(K63)-FLOOR(LOG(K63),1)»>79 | 9,54 | 1,055 | 1,55 | 0,17 | 2,55 | 3,55 | 0,5502284 | 4,55 | 5,55 | 12267544″ x:fmla=»=LOG(K56)-FLOOR(LOG(K56),1)»> 0,7442930 | 5499999999999901″> 6,55 | 0,8162413 | 7,55 | 162918768″ x:fmla=»=LOG(O56)-FLOOR(LOG(O56),1)»> 0,8779470 | 8,55 | 9,55 | 0,9800034 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,056 | 1,56 | 2,56 | 5599999999999898″> 3,56 | 4,56 | 5,56 | 0,7450748 | 6,56 | 7,56 | 8,56 | 9,56 | 0,9804579 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,057 | 407498730742369E-2″ x:fmla=»=LOG(A58)»> 0,02407499 | 1,57 | 2,57 | 3,57 | 0,5526682 | 4,57 | 0,6599162 | 5,57 | 6,57 | 7,57 | 5699999999999896″> 8,57 | 9,57 | 684305″ x:fmla=»=LOG(S58)-FLOOR(LOG(S58),1)»> 0,9809119 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,058 | 0,02448567 | 1,58 | 263″ x:fmla=»=LOG(C59)-FLOOR(LOG(C59),1)»> 0,1986571 | 2,58 | 3,58 | 0,5538830 | 4,58 | 0,6608655 | 5,58 | 746634198 | 799″ x:fmla=»=LOG(K59)-FLOOR(LOG(K59),1)»> 0,7466342 | 6,58 | » x:fmla=»=LOG(M59)-FLOOR(LOG(M59),1)»> 0,8182259 | 7,58 | 8,58 | 9,58 | 0,9813655 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,059 | 1,59 | 2,59 | 5899999999999901″> 3,59 | 4,59 | 0,6618127 | 5,59 | 0,7474118 | 6,59 | 21″ x:fmla=»=LOG(M60)-FLOOR(LOG(M60),1)»> 0,8188854 | 7,59 | 8,59 | 32 | 9,59 | 0,9818186 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 001″> 1.060 | 0,02530587 | 1,60 | 0,2041200 | 2,60 | 3,60 | 0,5563025 | 4,60 | 0,6627578 | 5,60 | 0,7481880 | 6,60 | 7,60 | 0,8808136 | 5999999999999908″> 8,60 | 845124356723″ x:fmla=»=LOG(Q61)-FLOOR(LOG(Q61),1)»> 0, | 85 | 9,60 | 1,061 | 0,02571538 | 1,61 | 0,2068259 | 2,61 | 0,4166405 | 3,61 | 0,5575072 | 4,61 | 5,61 | 748125616063″ x:fmla=»=LOG(K62)-FLOOR(LOG(K62),1)»> 0,7489629 | 6,61 | 7,61 | 0,8813847 | 8,61 | 9,61 | 0,9827234 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,062 | 0,02612452 | 1,62 | 2,62 | 6199999999999899″> 3,62 | 0,5587086 | 4,62 | 5,62 | 6,62 | 7,62 | 8,62 | 9,62 | 0,9831751 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,063 | 65332645232 | 306757E-2″ x:fmla=»=LOG(A82)»>E-2″ x:fmla=»=LOG(A64)»> 0,02653326 | 1,63 | 2,63 | 3,63 | 0,5599066 | 4,63 | 5,63 | 6,63 | 0,8215135 | 7,63 | 6299999999999901″> 8,63 | 07 | 08 | 9,63 | 0,9836263 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,064 | 1,64 | 0,2148438 | 2,64 | 0,4216039 | 3,64 | 0,5611014 | 4,64 | 0,6665180 | 6399999999999899″> 5,64 | 0,7512791 | 6,64 | 7,64 | 8,64 | 374247889274″ x:fmla=»=LOG(Q65)-FLOOR(LOG(Q65),1)»> 0, | 37 | 9,64 | 0,9840770 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,065 | 1,65 | 6721541778″ x:fmla=»=LOG(S93)-FLOOR(LOG(S93),1)»>390627″ x:fmla=»=LOG(C66)-FLOOR(LOG(C66),1)»> 0,2174839 | 6499999999999901″> 2,65 | 3,65 | 0,5622929 | 4,65 | 5,65 | 6,65 | 0,8228216 | 7,65 | 0,8836614 | 8,65 | 610746481367″ x:fmla=»=LOG(Q66)-FLOOR(LOG(Q66),1)»> 0, | 61 | 9,65 | 98452731334379207″ x:fmla=»=LOG(S66)-FLOOR(LOG(S66),1)»> 0,9845273 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,066 | 0,02775720 | 1,66 | 0.2201081 | 2,66 | 0,4248816 | 3,66 | 75655″ x:fmla=»=LOG(M93)-FLOOR(LOG(M93),1)»>44″ x:fmla=»=LOG(G67)-FLOOR(LOG(G67),1)»> 0,5634811 | 4,66 | 0,6683859 | 5,66 | 0,7528164 | 6,66 | 82347422917030044″ x:fmla=»=LOG(M67)-FLOOR(LOG(M67),1)»> 0,8234742 | 7,66 | 8,66 | 9,66 | 1,067 | 1,67 | 0,2227165 | 2,67 | 0,4265113 | 3,67 | 0,5646661 | 6699999999999902″> 4,67 | 0,66 | 5,67 | 0,7535831 | 6,67 | 0,8241258 | 7,67 | 8,67 | 9020971″ x:fmla=»=LOG(Q68)-FLOOR(LOG(Q68),1)»> 0, | 91 | 9,67 | 0,9854265 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,068 | 8571252692534566E-2″ x:fmla=»=LOG(A69)»> 0,02857125 | 1,68 | 0,2253093 | 2,68 | 3,68 | 0,5658478 | 4,68 | 0,6702459 | 5,68 | 0,7543483 | 6,68 | 0,8247765 | 7,68 | 0,8853612 | 8,68 | 006″ x:fmla=»=LOG(G80)-FLOOR(LOG(G80),1)»>97 | 9,68 | 0,9858754 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1,069 | 1,69 | 0,2278867 | 2,69 | 3,69 | 0,5670264 | 4,69 | 0,6711728 | 6899999999999897″> 5,69 | 6,69 | 0,8254261 | 7,69 | 0,8859263 | 8,69 | 4866597″ x:fmla=»=LOG(Q70)-FLOOR(LOG(Q70),1)»> 0,93
|

 059.
059.
