Градусы перевести в радианы: Онлайн калькулятор: Перевод градусов в радианы

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(30 град. )
4	Найти точное значение	sin(60 град. )
5	Найти точное значение	tan(30 град. )
6	Найти точное значение	arcsin(-1)
7	Найти точное значение	sin(pi/6)
8	Найти точное значение	cos(pi/4)
9	Найти точное значение	sin(45 град. )
10	Найти точное значение	sin(pi/3)
11	Найти точное значение	arctan(-1)
12	Найти точное значение	cos(45 град. )
13	Найти точное значение	cos(30 град. )
14	Найти точное значение	tan(60)
15	Найти точное значение	csc(45 град. )
16	Найти точное значение	tan(60 град. )
17	Найти точное значение	sec(30 град. )
18	Найти точное значение	cos(60 град. )
19	Найти точное значение	cos(150)
20	Найти точное значение	sin(60)
21	Найти точное значение	cos(pi/2)
22	Найти точное значение	tan(45 град. )
23	Найти точное значение	arctan(- квадратный корень из 3)
24	Найти точное значение	csc(60 град. )
25	Найти точное значение	sec(45 град. )
26	Найти точное значение	csc(30 град. )
27	Найти точное значение	sin(0)
28	Найти точное значение	sin(120)
29	Найти точное значение	cos(90)
30	Преобразовать из радианов в градусы	pi/3
31	Найти точное значение	tan(30)
32	Преобразовать из градусов в радианы	45
33	Найти точное значение	cos(45)
34	Упростить	sin(theta)^2+cos(theta)^2
35	Преобразовать из радианов в градусы	pi/6
36	Найти точное значение	cot(30 град. )
37	Найти точное значение	arccos(-1)
38	Найти точное значение	arctan(0)
39	Найти точное значение	cot(60 град. )
40	Преобразовать из градусов в радианы	30
41	Преобразовать из радианов в градусы	(2pi)/3
42	Найти точное значение	sin((5pi)/3)
43	Найти точное значение	sin((3pi)/4)
44	Найти точное значение	tan(pi/2)
45	Найти точное значение	sin(300)
46	Найти точное значение	cos(30)
47	Найти точное значение	cos(60)
48	Найти точное значение	cos(0)
49	Найти точное значение	cos(135)
50	Найти точное значение	cos((5pi)/3)
51	Найти точное значение	cos(210)
52	Найти точное значение	sec(60 град. )
53	Найти точное значение	sin(300 град. )
54	Преобразовать из градусов в радианы	135
55	Преобразовать из градусов в радианы	150
56	Преобразовать из радианов в градусы	(5pi)/6
57	Преобразовать из радианов в градусы	(5pi)/3
58	Преобразовать из градусов в радианы	89 град.
59	Преобразовать из градусов в радианы	60
60	Найти точное значение	sin(135 град. )
61	Найти точное значение	sin(150)
62	Найти точное значение	sin(240 град. )
63	Найти точное значение	cot(45 град. )
64	Преобразовать из радианов в градусы	(5pi)/4
65	Найти точное значение	sin(225)
66	Найти точное значение	sin(240)
67	Найти точное значение	cos(150 град. )
68	Найти точное значение	tan(45)
69	Вычислить	sin(30 град. )
70	Найти точное значение	sec(0)
71	Найти точное значение	cos((5pi)/6)
72	Найти точное значение	csc(30)
73	Найти точное значение	arcsin(( квадратный корень из 2)/2)
74	Найти точное значение	tan((5pi)/3)
75	Найти точное значение	tan(0)
76	Вычислить	sin(60 град. )
77	Найти точное значение	arctan(-( квадратный корень из 3)/3)
78	Преобразовать из радианов в градусы	(3pi)/4
79	Найти точное значение	sin((7pi)/4)
80	Найти точное значение	arcsin(-1/2)
81	Найти точное значение	sin((4pi)/3)
82	Найти точное значение	csc(45)
83	Упростить	arctan( квадратный корень из 3)
84	Найти точное значение	sin(135)
85	Найти точное значение	sin(105)
86	Найти точное значение	sin(150 град. )
87	Найти точное значение	sin((2pi)/3)
88	Найти точное значение	tan((2pi)/3)
89	Преобразовать из радианов в градусы	pi/4
90	Найти точное значение	sin(pi/2)
91	Найти точное значение	sec(45)
92	Найти точное значение	cos((5pi)/4)
93	Найти точное значение	cos((7pi)/6)
94	Найти точное значение	arcsin(0)
95	Найти точное значение	sin(120 град. )
96	Найти точное значение	tan((7pi)/6)
97	Найти точное значение	cos(270)
98	Найти точное значение	sin((7pi)/6)
99	Найти точное значение	arcsin(-( квадратный корень из 2)/2)
100	Преобразовать из градусов в радианы	88 град.

Формулы перевода градусов в радианы (градусной меры угла в радианную), длин, площадей и объемов основных геометрических фигур.

		Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.
Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация/ / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Формулы перевода градусов в радианы (градусной меры угла в радианную), длин, площадей и объемов основных геометрических фигур. Поделиться:    Формулы перевода градусов в радианы (градусной меры угла в радианную), длин, площадей и объемов основных геометрических фигур. Вариант для печати. Во первых, под числом «π» Администрация Сайта понимает величину близкую к: 3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679… (100 знаков после запятой) Формулы перевода Формулы расчета длины Формулы расчета площади Формулы расчета объема ФОРМУЛЫ ПЕРЕВОДА Перевод радиан в градусы Зная, что углу 2•π соответствует угол 360 градусов: Ad = Ar • 180 / π Где Ad — угол в градусах, Ar — угол в радианах. Перевод градусов в радианы Зная, что углу 360 градусов соответствует угол 2 • π: Ar = Ad • π / 180 Где Ad — угол в градусах, Ar — угол в радианах. ФОРМУЛЫ РАСЧЕТА ДЛИНЫ Длина окружности L = 2 • π • R Где L — длина окружности, R — радиус окружности. L = π • D Где L — длина окружности, D — диаметр окружности. Длина дуги окружности L = A • R Где L — длина дуги окружности, R — радиус окружности, A — центральный угол, выраженный в радианах. Так, для окружности, A = 2•π (360 градусов), получим L = 2 • π • R ФОРМУЛЫ РАСЧЕТА ПЛОЩАДИ Площадь треугольника. Формула Герона площади треугольника. S = (p • (p-a) • (p-b) • (p-c))1/2. Где S — площадь треугольника, a, b, c — длины сторон, p=(a+b+c)/2 — полупериметр. Площадь круга S = π • R2 Где S — площадь круга, R — радиус круга. Площадь сектора S = (Ld • R)/2 = (A • R2)/2 Где S — площадь сектора, R — радиус круга, Ld — длина дуги. Площадь поверхности шара (сферы) S = 4 • π • R2 Где S — площадь поверхности шара, R — радиус шара. Площадь боковой поверхности цилиндра S = 2 • π •R • H Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра. Площадь полной поверхности цилиндра S = 2 • π • R • H + 2 • π • R2 Где S — площадь боковой поверхности цилиндра, R — радиус основания цилиндра, H — высота цилиндра. Площадь боковой поверхности конуса S = π • R • L Где S — площадь боковой поверхности конуса, R — радиус основания конуса, L — длина образующей конуса. Площадь полной поверхности конуса S = π • R • L + π • R2 Где S — площадь полной поверхности конуса, R — радиус основания конуса, L — длина образующей конуса. ФОРМУЛЫ РАСЧЕТА ОБЪЕМА Объем шара V = 4 / 3 • π • R3 Где V — объем шара, R — радиус шара. Объем цилиндра (прямого, круглого) V = π • R2 ·H Где V — объем цилиндра, R — радиус основания цилиндра, H — высота цилиндра. Объем конуса (прямого, круглого) V = π • R • L = π • R • H/cos (A/2) = π • R • R/sin (A/2) Где V — объем конуса, R — радиус основания конуса, L — длина образующей конуса, A — угол при вершине конуса. Поиск в инженерном справочнике DPVA. Введите свой запрос: Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела: Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая поддержка сайта: Zavarka Team	Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

как перевести, формула, таблица преобразования

Содержание:

• Градусы в радианы
  • Краткое описание
  • В чем можно измерять угол
• Связь между градусами и радианами
  • Мера угла
  • Формула соотношения
• Формулы перевода
  • Градусы в радианы
  • Радианы в градусы
• Таблица перевода градусов в радианы
• Примеры расчета градусов и минут в радианы

Содержание

• Градусы в радианы
  • Краткое описание
  • В чем можно измерять угол
• Связь между градусами и радианами
  • Мера угла
  • Формула соотношения
• Формулы перевода
  • Градусы в радианы
  • Радианы в градусы
• Таблица перевода градусов в радианы
• Примеры расчета градусов и минут в радианы

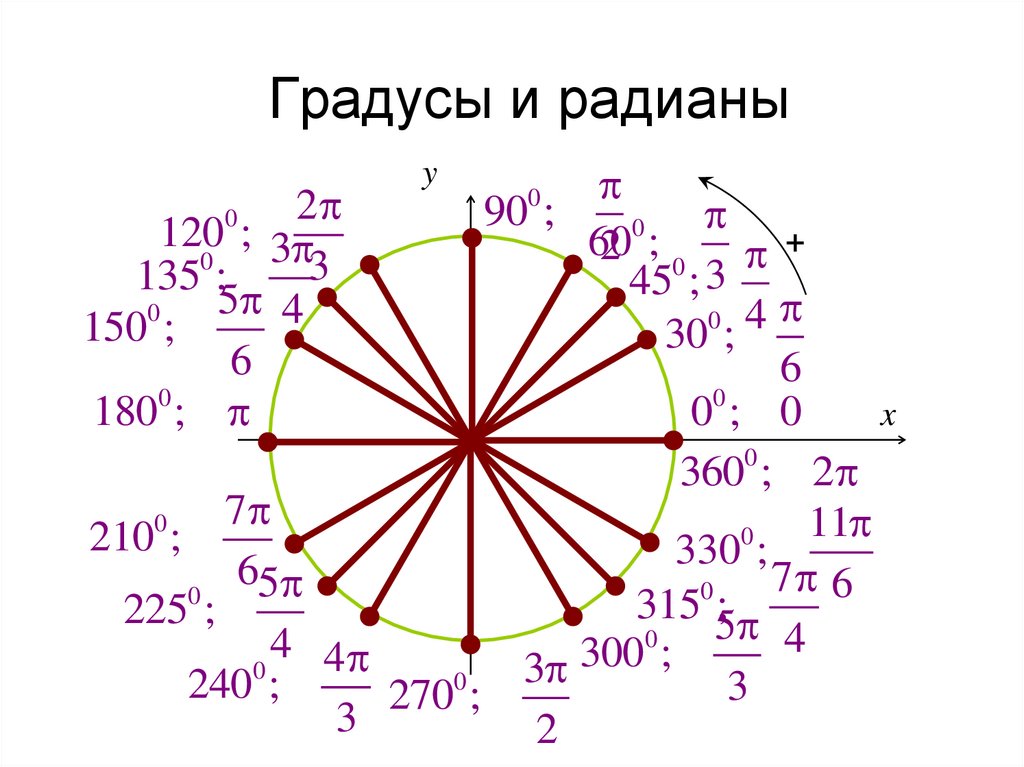
Градусы в радианы

Краткое описание

Угол — это два луча, выходящие из одной точки. Эта точка называется вершиной. Взяв за единицу измерения некий конкретный угол, можно определить величину любого угла, выяснив, сколько раз в нем укладывается такой единичный угол. При измерении угла исходят из двух его свойств:

1. Величины равных углов равны.
2. Величина суммы двух углов равна сумме их величин.

Если ясно, о чем идет речь, вместо «величина угла» говорят просто «угол».

Равные углы с вершиной в центре окружности будут создавать на ней дуги одинаковой длины. Их сумма будет равняться сумме стягиваемых ими дуг. Поэтому единицы измерения углов можно задавать, указывая, какую часть окружности составляет соответствующая дуга.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В чем можно измерять угол

Наиболее распространены две единицы измерения:

• градус, равный дуге в 1/360 всей окружности;
• радиан — центральный угол, высекающий дугу, равную радиусу окружности. \circ\;=3,3915\;рад\)

  Насколько полезной была для вас статья?

  У этой статьи пока нет оценок.

  Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

  Поиск по содержимому

  Перевод градусов в радианы, перевод радианов в градусы

  Пример решили: 111287 раз Сегодня решили: 0 раз

  Введите градусы или радианы

  Угол Градусы (°)Радианы (rad)

  Скачать решение в PDF

  Порекомендуйте наш сервис друзьям

  Вконтакте

  Facebook

  Twitter

  Одноклассники

  Google+

  Данный онлайн-сервис позволяет совершить перевод градусов в радианы, а также перевод радианов в градусы.

  Градус — единица измерения плоских углов. Один оборот имеет 360°.
  Градус содержит в себе 60 минут, а минута в себе 60 секунд.

  Радиан — основная единица измерения плоских углов. 0$$

Попробуйте другие сервисы

• Вычисление косинуса

• Вычисление синуса

• Вычисление тангенса

• Вычисление котангенса

• Вычисление секанса

История решений

Перевод из радиан в. Как перевести градусы в радианы

Калькулятор онлайн выполняет перевод градусов в радианы , перевевод радиан в градусы , перевод дробных градусов (градусы представленные десятичной дробью) в вид градусов, минут и секунд и выводит формулы с подробным решением.

Перевести градусы в радианы : градусы необходимо умножить на π/180. Если градусы заданы в виде «градусов, минут и секунд», то вначале их необходимо перевести в десятичную форму по формуле: градусы + минуты/60 + секунды/3600;

Формула перевода радиан в градусы : если угол равен α rad радиан, то он равен формула перевода радиан в градусы градусов, где π ≈ 3,1415.

Перевести радианы в градусы : радианы необходимо умножить на 180/π. Целая часть полученного произведения — это количество градусов. Чтобы перевести дробную часть в минуты, необходимо ее умножить на 60. Целая часть полученного произведения — количество минут. Для вычисления секунд необходимо снова умножить дробную часть от предыдущей операции на 60, округлить полученное произведение до ближайшего целого — это количество секунд.

Формула перевода градусов в радианы : если угол равен α deg радиан, то он равен формула перевода градусы в радианы радиан, где π ≈ 3,1415.

Дано:		Решение:
Перевод градусов, минут и секунд в радианы
α° deg = градусов		перевод градусов в радианы
α» deg = минут
α» deg = секунд
Перевод радиан в градусы, минуты и секунды
α rad = радиан		перевод радиан в градусы, минуты и секунды
Перевод десятичных градусов в вид градусов, минут и секунд
α deg = градусов		выделение из десятичных градусов градусов, минут и секунд перевод десятичных градусов в вид градусов, минут и секунд
округление до 1 2 3 4 5 знаков после запятой

Помощь на развитие проекта сайт

Уважаемый Посетитель сайта.
Если Вам не удалось найти, то что Вы искали — обязательно напишите об этом в комментариях, чего не хватает сейчас сайту. Это поможет нам понять в каком направлении необходимо дальше двигаться, а другие посетители смогут в скором времени получить необходимый материал.
Если же сайт оказался Ваме полезен — подари проекту сайт всего 2 ₽ и мы будем знать, что движемся в правильном направлении.

Спасибо, что не прошели мимо!

I. Примечание:

1. Округление результатов расчета выполняется до указанного количества знаков после запятой (по умолчанию — округление до десятитысячных).

II. Для справки:

1. Градусна мера угла — угловая мера, в которой за единицу принимается угол в 1 градус и показывающая сколько раз градус и его части (минута и секунда) укладывается в данном угле.
2. Радианная мера угла — угловая мера, в которой за единицу принимается угол в 1 радиан и показывающая сколько раз радиан укладывается в данном угле.
3. Градусы и радианы — единицы измерения плоских углов в геометрии.
4. Один градус равен 1/180 части развернутого угла.
5. Радиан — угол, соответствующий дуге, длина которой равна ее радиусу.

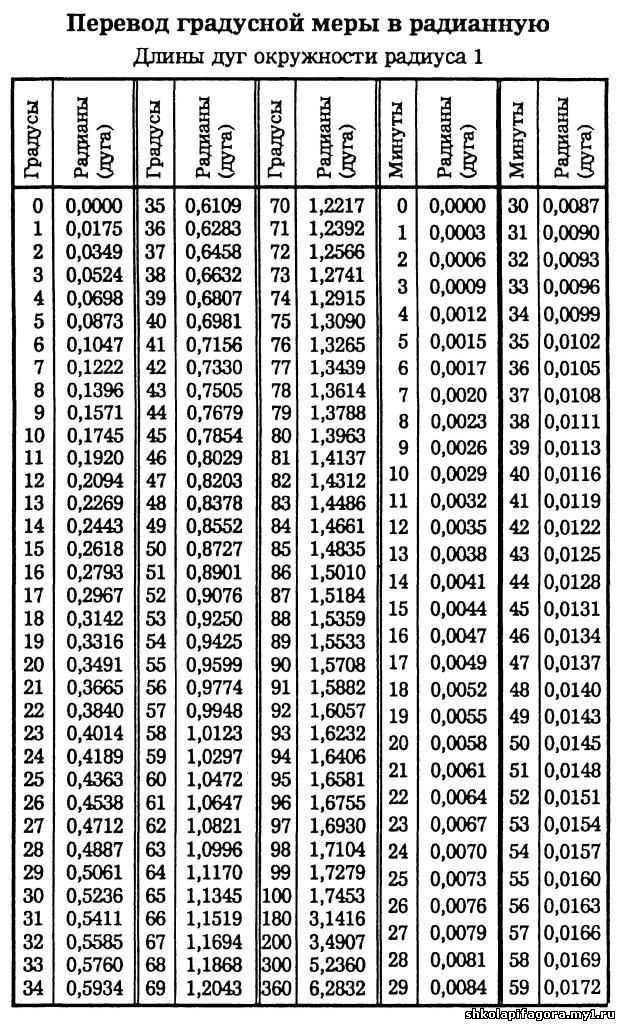
Номограмма для перевода радиан в градусы и градусов в радианы.

Люди в математической науке довольно часто сталкиваются с такой задачей, как перевод градусов в радианы или наоборот. Выполнить данную задачу довольно просто и для этого не нужно иметь глубокие познания в различных прикладных науках или математике. Итак, для начала необходимо разобраться с этими величинами измерения. Градус и радиан – это основные единицы, которыми измеряются плоские углы в математике и физике. Ещё данные единицы используют в картографии для определения координат в любой точке земного шара.

Эти величины измерения обозначаются следующим образом:

• рад – радиан
• градус — º

Как перевести градусы в радианы

Для начала, чтобы стала понятной формула перевода градусов в радианы, нужно научиться переводить угол в радианы и радианы в угол:

• 1 рад = (180/π)ºπ 57,295779513, где известно, что π = 3,14
• 1° = (π/180) рад π 0,017453293 рад

По вышеизложенным формулам сразу же становиться ясно, что π рад = 180°, именно из них и берут своё начало понятные всем и простые формулы для перевода величин измерения.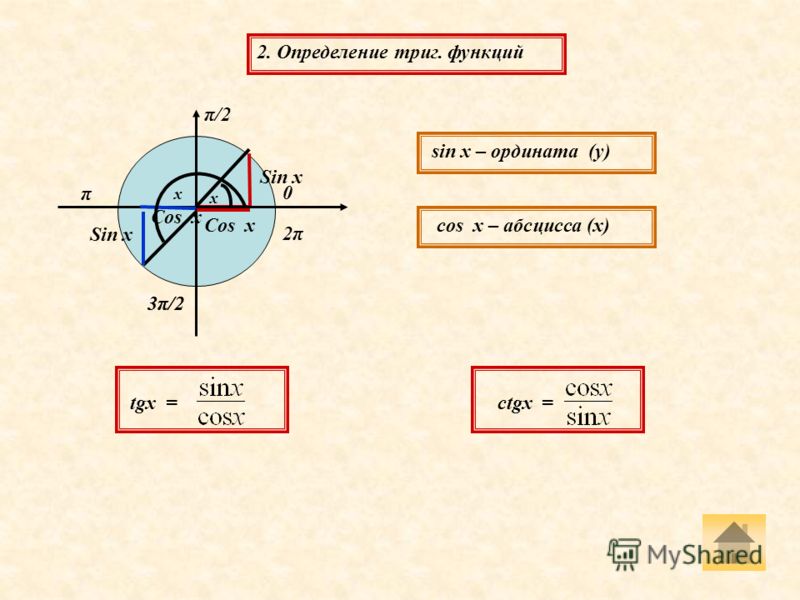 Сейчас рассмотрим основные формулы, которые используются при переводе:

1. Градусы в радианы

Zº=Z рад × (180/π), где Zº — угол в градусах, а Z рад – угол в радианах, π = 3,14

2. Радианы в градусы

Z рад = Z° × (π/180)

Теперь рассмотрим пример, чтобы стало понятней, как пользоваться вышеприведёнными формулами на практике. Для этого возьмём два угла 20º и 100º:

1. Перевод градусов в радианы

• 20º = 20 рад × (π/180) π 0,35 рад
• 100º = 100 рад × (180/π) π 1, 7453 рад

2. Перевод радиан в градусы

• 20 рад = 20º × (180/π) π 1146,15, где π = 3,14
• 100 рад = 100° × (180/π) π 5729, 577, где π = 3,14

Рассмотрев формулы для перевода величин измерения, становиться понятно, что справиться с поставленой задачей довольно просто. Для тех людей, которые самостоятельно не хотят проводить расчеты, в интернете существует множество сайтов, на которых с помощью он-лайн калькуляторов можно перевести градусы в радианы или наоборот, их использование значительно облегчит вам выполнение различных задач по тригонометрии.

Функция РАДИАНЫ (на английском RADIANS) – это одна из математических и тригонометрических функций, которая часто применяется для инженерных расчетов. Данная функция в Excel легко преобразует градусы в радианы – угол, соответствующий дуге, а длина этой дуги равна ее радиусу.

Как работает функция индекс в Excel?

ПРИМЕР 1. Для инженерных расчетов связанных с движением по окружности зачастую необходимо вычислять угловые скорости и переводить градусы в радианы и радианы в градусы. В Excel для этого предусмотрены специальные функции. Для упрощения математических расчетов может потребоваться выразить в одной и второй величине.

Нам необходимо найти сколько будет в Радианах 180°. Нажимаем кнопку fx возле строки формул для вызова окна выбора функций «Вставка функции» (SHIFT+F3) и в окне поиска вводим функцию «РАДИАНЫ». Выбираем высветившуюся нужную функцию, как показано на ниже рисунке.

Появляется окно, в которое нужно ввести аргументы функции. Вводим значение 180, так как нам нужно найти сколько будет радиан в 180 градусах. Жмем ОК.




В 180 градусах будет 3,1415 радиан.

Найдем радианы для угла в 90°. Откроем окно функций и введем функцию, что необходимо вычислить. Находим ее в окне мастера функций и выбираем аргумент 90.




ОК. В 90 градусах будет 1,5707 радиан.

В следующих примерах рассмотрим, как конвертировать эти единицы измерения углов в обоих направлениях.



Как перевести Радианы в Градусы средствами Excel

ПРИМЕР 2. Иногда нужно единицу измерения углов rad перевести в значение gradus° . Для этого предусмотрена функция ГРАДУСЫ. Она позволяет перевести значения выраженные в радианах в градусы в десятичном исчислении.

Нам нужно найти сколько будет в градусах 4,1 радианы. Нажимаем кнопку fx для вызова окна выбора функции и в окне поиска вводим соответствующее название функции.




Появляется окно в которое нужно ввести аргументы функции. Вводим значение 4,1, так как нам следует найти сколько будет gradus° в 4,1 rad . Нажимаем ОК.

Для исходного значения 4,1 получаем ровно 235 градусов.

Таким образом выполняется перевод из радиан в градусы в Excel.

Сколько радиан в нескольких значениях градуса?

ПРИМЕР 3. Иногда нужно определить сколько радиан в сразу нескольких значениях градуса и вводить тогда каждый раз аргумент очень долго. В таком случае можно воспользоваться немного иным способом конвертирования величин для измерения углов.

Требуется найти сколько будет в Радианах 45, 67, 23, 12, 57 градусов. Нажимаем кнопку fx (SHIFT+F3) для вызова окна выбора функции и в окне поиска вводим необходимо функцию как показано ниже на рисунке. Указываем на высветившуюся функцию.

Необходимость в измерении углов появилась у людей с тех пор, как цивилизация достигла минимального технического уровня. Всем известна феноменальная точность соблюдения наклона и ориентации по странам света, обеспеченная строителями египетских пирамид. Современную градусную меру углов, как сейчас считается, изобрели древние аккадцы.

Что такое градусы?

Градус — общепринятая единица измерения углов. В полной окружности 360 градусов. Причина выбора именно этого числа неизвестна. Вероятно, аккадцы разделили окружность на сектора, используя угол равностороннего треугольника, а затем полученные сегменты снова разделили на 60 частей согласно своей системе счисления. Градус тоже делится на 60 минут, а минуты — на 60 секунд. Общепринятыми обозначениями являются:

° — угловые градусы

’ — минуты,

’’ — секунды.

За тысячелетия градусная мера углов прочно вошла во многие сферы человеческой деятельности. Она и сейчас незаменима во всех областях науки и техники — от картографии до расчета орбит искусственных спутников Земли.

Что такое радианы?

Архимеду приписывается открытие постоянства соотношения длины окружности и ее диаметра. Мы называем его числом π. Оно иррационально, то есть не может быть выражено в виде обычной или периодической дроби. Чаще всего используется значение числа π с точностью до двух знаков после запятой — 3,14. Длина окружности L с радиусом R легко вычисляется по формуле: L=2πR.

Окружность радиуса R=1 имеет длину 2π. Это соотношение используется в геометрии как формулировка радианной меры угла.

По определению, радиан — угол с вершиной в центре окружности, опирающийся на дугу с длиной, равной радиусу окружности. Международное обозначение радиана — rad, отечественное — рад. Размерности он не имеет.

Дуга окружности с радиусом R с угловой величиной α радиан, имеет длину α * R.

Зачем понадобилось вводить новую единицу измерения угла?

Развитие науки и техники привело к появлению тригонометрии и математического анализа, необходимых для точных расчетов механических и оптических устройств. Одной из его задач является измерение длины кривой линии. Самый распространенный случай — определение длины дуги окружности. Использование для этой цели градусной меры углов крайне неудобно. Идея сопоставить длину дуги с радиусом окружности возникала у многих математиков, но сам термин «радиан» был введен в научный обиход только во второй половине XIX века. Сейчас все тригонометрические функции в математическом анализе по умолчанию используют радианную меру угла.

Как переводить градусы в радианы

Из формулы длины окружности вытекает, что в нее укладывается 2π радиусов. Отсюда вытекает, что: 1⁰=2π/360= π/180 рад.

И простая формула перевода из радианов в градусы: 1 рад = 180/π.

Пусть мы имеем угол в N градусов. Тогда формула для перевода из градусов в радианы будет такой: α(радиан) = N/(180/π) = N*π/180.

Остались вопросы?

Ответы на них можно найти , где подробно разъяснены понятия длины окружности, радианной меры углов и на конкретных примерах показан перевод градусов в радианы. Знания упомянутого крайне важны для понимания математики, без которой невозможно существование современной цивилизации.

сколько градусов в радиане, формула перевода

С давних времён люди измеряют углы. Но что такое угол? Геометрия даёт нам ответ: «Угол — это два луча, проведённые из заданной точки». Углы бывают разные: тупые, острые, прямые, развёрнутые, центральные, смежные. Возьмём точку O и проведём из неё луч O. A. Теперь из этой же точки проведём луч OB, параллельный лучу OA и направленный с ним в одну сторону. Про такие лучи говорят, что угол между ними составляет 0° (ноль градусов). Если мы теперь направим луч OB параллельно лучу OA, но в противоположную сторону, то получим развёрнутый угол, равный 180°.

…

Оглавление:

• Что означают градус и радиан
• Как перевести градусы в радианы и обратно
• Примеры решения задач
• Минуты и секунды

Что означают градус и радиан

Так вот, мерой расхождения двух лучей, проведённых из одной точки друг от друга, будет градусное расстояние. Что такое градус? В переводе «градус» означает «шаг». Всего таких «шагов» может быть 360°. Это число было придумано ещё в глубокой древности математиками и астрономами, пользовавшимися шестидесятиричной системой счисления. Они брали круг, из центра которого проводили два радиуса. Мерой расхождения этих радиусов друг от друга был градус. Когда расстояние между радиусами в градусах отсчитывали против часовой стрелки, такой угол считался положительным, а когда против часовой — отрицательным.

Это интересно: умножение на 0 — правило для любого числа.

Вращая один радиус относительно другого против часовой стрелки, мы будем получать разные углы. Когда эти отрезки совпадают, то между ними будет 0°, когда же отрезки отсекают сектор круга, равный одной четверти полного круга, то угол между ними составит 90°. Вращая дальше таким образом, мы получим следующие углы: 180° — радиусы лежат на диаметре круга и делят его пополам, 270° — радиусы отсекают три четверти круга, 360° — радиусы совпадают. Таким образом, полный круг составляет 360°. Для измерения углов существует транспортир.

Кроме градусной меры для измерения углов применяют меру радианную. Радиан — это мера центрального угла. «Радиан» означает «связанный с радиусом». Если из центра окружности радиусом R провести два луча, то они на ней отсекут дугу, длина которой l. Так вот, угол α между указанными лучами называется центральным. Чтобы его измерить, нужно длину дуги окружности разделить на её радиус: α=l/R. Получится значение, выраженное в радианах (рад). Поскольку любому углу на плоскости можно сопоставить такой же центральный угол, то встаёт вопрос, как от обычной градусной меры перейти к радианной.

Это интересно: признак перпендикулярности прямой и плоскости, теория и практика.

Как перевести градусы в радианы и обратно

Мы знаем, что центральному углу в 360° соответствует вся окружность, длина которой вычисляется по известной формуле l=2•π•R. Разделим это выражение на R и получим: α= 2•π•R/R=2•π рад≈6,28 рад. Если взять какое-то угловое расстояние в A град., то его радианная мера α получится из пропорции: А/360°=α/(2•π). Решив это уравнение, получим формулу перевода градусов в радианы — α=(π/180°)•А, или формулу перевода радиан в градусы — А=(180°/π)•α. Из этих формул мы придём к следующим соотношениям:

• 1 рад=180°/π≈57,2958°;
• 1°=π/180 рад≈0,01745 рад.

Сколько составит 180 градусов в радианах и 90 градусов в радианах? Воспользовавшись полученными выше формулами, придём к таким соотношениям:

• 90°=π/2 рад≈1,571 рад;
• 180°=π рад≈3,142 рад.

Итак, как правильно переводить градусную меру в радианную и обратно? В этом вам поможет следующее правило:

Чтобы найти число радиан, нужно градусную меру умножить на число π и поделить на 180. Чтобы найти число градусов, нужно радианную меру умножить на 180 и поделить на число π.

Примеры решения задач

Задача 1. Чему равна длина дуги окружности, если R=1 см, α=1 рад?

Решение. По формуле длины дуги найдём: l=R•α=1•1=1 см.

Задача 2. Сколько рад в 45°?

Решение. Используя правило, получим: α=45•π/180=π/4 рад.

Задача 3. Сколько град. в π² рад?

Решение. Используя правило, найдём: А=π²•180/π=180π град.≈565,5°.

Задача 4. Чему равен средний угловой размер лунного диска, если среднее расстояние до Луны равно R=384399 км, а диаметр самой Луны D=3476 км?

Решение. Если мысленно на Луну с Земли провести два луча, которые пройдут через крайние точки диаметра её диска, мы получим центральный угол, исходящий из глаз наблюдателя. Поскольку расстояние до Луны намного превышает её диаметр, то этот диаметр можно будет приравнять длине дуги l окружности, образуемой радиусом R, т. е. D≈l=α•R. Тогда искомый угловой размер составит: α≈D/R=3476/384399=0,00904268742 рад=0,51810782462°≈31’05»≈0,5°. Итак, видимый угловой диаметр Луны равен полградуса.

Это интересно: что такое разность в математике?

Минуты и секунды

Издревле для измерения углов пользовались так называемой шестидесятиричной системой исчисления. В этой системе вся окружность делится на 360°. Затем каждый градус делят на 60 минут, а каждую минуту — на 60 секунд. Минуты обозначаются значком «’», а секунды — значком «»». Отсюда пошло измерение времени. Кроме того, циферблат — это символ круга, а стрелки часов отмеряют центральные углы. Для перевода этих единиц используйте следующие соотношения:

• 1°=60’=3600»;
• 1’=(1/60)°=60»;
• 1»=(1/3600)°=(1/60)’;
• 1 рад≈3438′. Приставочный способ вы найдете ответ по ссылке.

градусов в радианы — Преобразование, Формула, Примеры

Градусы в радианы — это форма преобразования, используемая для преобразования единиц измерения углов в геометрии. Точно так же, как у каждой величины есть единица измерения, углы также измеряются в разных единицах в зависимости от области применения. Для измерения углов в качестве единиц измерения используются градусы и радианы. Для человека важно знать, как преобразовать градусы в радианы, поскольку чаще всего радианы используются вместо градусов для измерения углов.

Вот некоторые из распространенных применений измерения в радианах: площадь сектора круга, длина дуги и угловая скорость. В основном следует использовать радианы, когда они имеют дело либо с объектом, движущимся по круговым путям, либо с частями кругового пути. В постановке задачи угол может быть измерен в градусах, но мы всегда должны преобразовывать углы в градусах в радианы, прежде чем использовать их в каких-либо вычислениях. В этой статье давайте узнаем о формуле преобразования градусов в радианы и таблице преобразования с решенными примерами.

1.	Что такое преобразование градусов в радианы?
2.	Градусов в Радиан Формула
3.	Как преобразовать градусы в радианы?
4.	градусов в радианы Таблица перевода
5.	Часто задаваемые вопросы о градусах в радианах

Что такое преобразование градусов в радианы?

Для измерения углов используются две единицы измерения: градусы и радианы. Мы можем преобразовать меру любого угла, заданного в градусах, в радианы в соответствии с нашим удобством. Это преобразование может быть выполнено после некоторых очень простых вычислений. Давайте разберемся в концепции обеих единиц и установим взаимосвязь между ними.

Градус

Градус, который называют градусом дуги или градусом дуги, является единицей измерения плоского угла. Обозначается символом (°). 360° — это угловая мера полного оборота. Полный оборот обозначается углом, измеряющим 360°, а инструмент, используемый для измерения угла в градусах, известен как транспортир.

Радиан

Радиан — еще одна единица измерения угла в геометрии. Один радиан — это угол, образованный в центре окружности дугой, длина которой равна радиусу r окружности. Один полный оборот против часовой стрелки равен 2π в радианах. На приведенном ниже изображении мера одного радиана равна 57,296 °. Кроме того, прямой угол выражается как π/2 радиан, а прямой угол выражается как π радиан.

Мы можем сравнить меру углов полного оборота в радианах и градусах как,

360 градусов = 2π радиан
180 градусов = π радиан

Градусов в Радиан Формула

Формула преобразования градусов в радианы — это обобщенная формула, используемая для преобразования заданного значения в градусах в значение в радианах. Мы можем сказать, что для преобразования градусов в радианы мы умножаем угол (в градусах) на π / 180.

Радианы = Градусы × π / 180

Перевод градусов в радианы Формула

В пересчете на градусы один полный против часовой стрелки оборот составляет 360 °, а в радианах один полный оборот против часовой стрелки равен 2π. Эти утверждения можно приравнять к:

Один полный оборот против часовой стрелки в градусах = 360°
Один полный оборот против часовой стрелки в радианах = 2π

градусов в радианы Уравнение: Связь между градусной мерой и мерой в радианах может быть представлена ​​следующим уравнением:

360° = 2π радиан.

Следовательно, 180° = π радиан.

Получаем уравнение

1° = (π)/180 радиан.

Это дает нам формулу для преобразования градусов в радианы и наоборот.

Таким образом, чтобы преобразовать градусы в радианы, используйте эту формулу = Градусная мера × (π/180°). 1° = (π)/180 радиан = 0,017453 радиан.

Чтобы найти значение 1°, как описано выше, используйте значение π, равное 3,1415926535…

Как преобразовать градусы в радианы?

Чтобы перевести градусы в радианы вручную, мы используем формулу: Радианы = градусы × (π/180°). Мы можем выполнить шаги, указанные ниже, чтобы вычислить меру угла, выраженную в градусах и радианах.

• Запишите величину угла, указанную в градусах.
• Мы знаем, что 1°= (π)/180 радиан. Итак, чтобы преобразовать угол, указанный в градусах, в радианы, мы умножаем его на π/180°.
  Угол в радианах = Угол в градусах × π/180°.
• Упростите значения и выразите ответ в радианах.

Пример: Преобразование 90 градусов в радианы.

Решение: 90° = 90° × (π/180°) = π/2.

Таблица преобразования градусов в радианы

В таблице ниже показаны значения радиана для соответствующих мер угла в градусах. В первой таблице показано преобразование углов в градусы в радианы от 0° до 90°.

Степень	0°	30°	45°	60°	90°
Радиан	0	π/6	№/4	№/3	№/2

Во второй таблице показано преобразование углов в градусах в радианы от 120° до 360°.

Степень	120º	135º	150º	180º	270º	360º
Радиан	(2π)/3	(3π)/4	(5π)/6	№	(3π)/2	2π

Таблица градусов в радианах

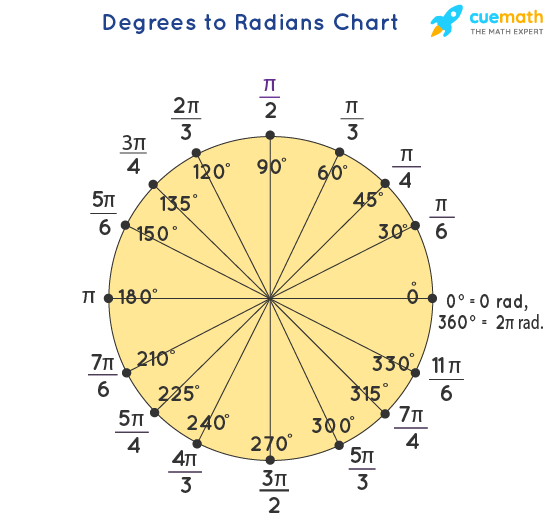
В приведенной ниже таблице показаны меры в градусах и соответствующие им меры в радианах. Мы также можем использовать эту диаграмму для преобразования градусов в радианы, чтобы сделать вычисления проще и быстрее. На приведенной ниже диаграмме мы видим, что 0° равняется 0 рад, а 360° равняется 2π рад

☛ Важные примечания о градусах в радианах

Вот несколько пунктов, которые следует помнить при изучении градусов в радианах:

• Углы измеряются в градусах и радианах.
• Один полный оборот равен 2π рад (или) 360°.
• 1° = 0,017453 радиана и 1 рад = 57,2958°.
• Чтобы преобразовать угол из градусов в радианы, мы умножаем его на π/180°.
• Чтобы преобразовать угол из радианов в градусы, мы умножаем его на 180°/π.

☛ Похожие статьи о градусах в радианах

Ознакомьтесь со следующими страницами, связанными с градусами в радианах:

• Радианы в градусы Калькулятор
• Калькулятор градусов в радианы
• Формула для поворота на 180 градусов
• Радиан
• градусов

Градусы в Радианы Примеры

1. Пример 1: В окружности с центром O точки A и B являются двумя точками на окружности. ∠AOB = 60°. Преобразование меры угла ∠AOB из градусов в радианы.

   Решение:

   Имеем ∠AOB = 60°.

   Формула преобразования градусов в радианы дается как (Градусы × π)/180°

   Таким образом, преобразуя данный угол, мы получаем,

   ∠AOB в радианах = ∠AOB в градусах × (π/180°)

   ∠AOB в радианах = 60° × (π/180°)

   ∠AOB в радианах = π/3

   Ответ: ∠AOB = π/3 рад.

2. Пример 2: Кэти купила пиццу в ближайшем магазине. Ее мать дала ей кусок, который составлял (1/4) часть полной пиццы. Кэти спросила мать о центральном угле, который образовал ее кусок пиццы. Можете ли вы помочь Кэти найти измерение угла в градусах и радианах?

   Решение:

   Здесь порция, которую получила Кэти, = (1/4) всей пиццы. Поскольку форма пиццы круглая, а угол для полного круга = 360°, мы можем заключить, что:

   Угол для всей пиццы = 360°

   Угол для (1/4)-го куска = 360°/4 = 90°

   Мы знаем,

   Значение этого угла в радианах = значение в градусах × (π/180°)

   = 90° × (π/180°) = π/2 рад

   Ответ: Угол среза Кэти в градусах равен 90°, а при переводе из градусов в радианы его мера равна π/2 рад.

3. Пример 3. Преобразуйте следующую градусную меру в радианную.

   a) 20 градусов b) 28 градусов

   Решение: Чтобы преобразовать следующую градусную меру в радианы, мы будем использовать следующие шаги:

   a) 20° × (π/180°) = π/ 9 радиан.

   б) 28° × (π/180°) = 7π/45 радиан.

перейти к слайдуперейти к слайдуперейти к слайду

Разбивайте сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Градусы в радианы

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о градусах в радианах

Как перевести градусы в радианы?

Чтобы преобразовать градусы в радианы, мы должны умножить заданный угол (то есть в градусах) на π/180°. Для этого воспользуемся формулой: радианы = градусы × π/180°.

Что такое градусы в формуле радианов?

Формула преобразования градусов в радианы относится к формуле, которая преобразует заданную меру угла в градусах в его эквивалентное значение в радианах. Формула перевода градусов в радианы выглядит так: радианы = градусы × π / 180°.

Как преобразовать 30 градусов в радианы?

Сначала нам нужно преобразовать данные градусы (30°) в радианы, используя формулу Радианы = градусы × π/180°. Радианы = 30° × π/180° = π/6 рад. Следовательно, 30 градусов можно представить как π/6 рад.

Как преобразовать 90 градусов в радианы?

Чтобы преобразовать 90 градусов в радианы, давайте умножим угол 90° на π/180°. Здесь мы используем формулу: радианы = (градусы × π)/180°. Радианы = (90° × π)/180° = π/2 = 0,785 рад. Таким образом, прямой угол выражается как π/2 радиан.

Сколько 60 градусов конвертируются в радианы?

Преобразуем 60 градусов в радианы, умножив угол 60° на π/180°. Используемая формула: радианы = (градусы × π)/180°. Радианы = (60° × π)/180° = π/3. Следовательно, 60 градусов, преобразованные в радианы, равны π/3.

Что такое 180 градусов в радианах?

Сначала нам нужно преобразовать данные градусы (180°) в радианы, используя формулу Радианы = (Градусы × π)/180°. Радианы = (180° × π)/180° = π рад. Следовательно, прямой угол 180° можно выразить как π радиан.

Как радианы используются в повседневной жизни?

Вот некоторые способы использования радианов в повседневной жизни:

• Для вычисления площади сектора и длины дуги.
• Для аппроксимации длины хорды, когда заданы центральный угол и радиус.
• Для решения задач, связанных с угловой скоростью.

Как преобразовать 150 градусов в радианы?

Сначала нам нужно преобразовать заданные градусы (150°) в радианы, используя формулу Радианы = Градусы × π/180°. Радианы = 150° × π/180° = 5π/6 рад. Следовательно, 150 градусов можно представить как 5π/6 рад.

Почему радианы более полезны в реальном мире, чем градусы?

Хотя для измерения углов в качестве единиц измерения используются как градусы, так и радианы, чаще всего математики предпочитают использовать радианы вместо градусов для измерения углов. Радианные меры можно использовать при вычислении площади сектора круга, длины дуги и угловой скорости. Очень важно всегда использовать радианы, когда они имеют дело либо с объектом, движущимся по круговым путям, либо с частями кругового пути. Даже если в исходной постановке задачи угол измеряется в градусах, мы всегда должны переводить эти углы в радианы, прежде чем использовать их в каких-либо вычислениях.

Как преобразовать 135 градусов в радианы?

Сначала нам нужно преобразовать данные градусы (135°) в радианы, используя формулу Радианы = Градусы × π/180°. Радианы = 135° × π/180° = 3π/4 рад. Следовательно, 135 градусов можно представить как 3π/4 рад.

Как использовать формулу преобразования градусов в радианы?

Чтобы преобразовать градусы в радианы с помощью формулы градусы в радианы,

• Шаг 1: Проверьте значение, указанное в градусах
• Шаг 2: Умножьте заданный угол (в градусах) на π/180°. То есть радианы = (градусы × π)/180°.

Что такое формула преобразования степени в радианы для преобразования отрицательного градуса в радианы?

Для преобразования отрицательного градуса в радиан тот же метод используется для положительных градусов. Просто умножьте заданное значение угла в градусах на π/180.

Как вывести формулу преобразования градусов в радианы?

Поскольку один полный оборот против часовой стрелки представляет меру в градусах и радианах как 360° и 2π, таким образом, 2π = 360°. Также π = 180°. Таким образом, формула выводится как радианы = градусы × π / 180,9.0003

Как преобразовать 120 градусов в радианы?

Сначала нам нужно преобразовать данные градусы (120°) в радианы, используя формулу Радианы = Градусы × π/180°. Радианы = 120° × π/180° = 2π/3 рад. Следовательно, 120 градусов можно представить как 2π/3 рад.

Градусы и радианы – объяснение и примеры

Как и любая другая величина, углы также имеют единицы измерения.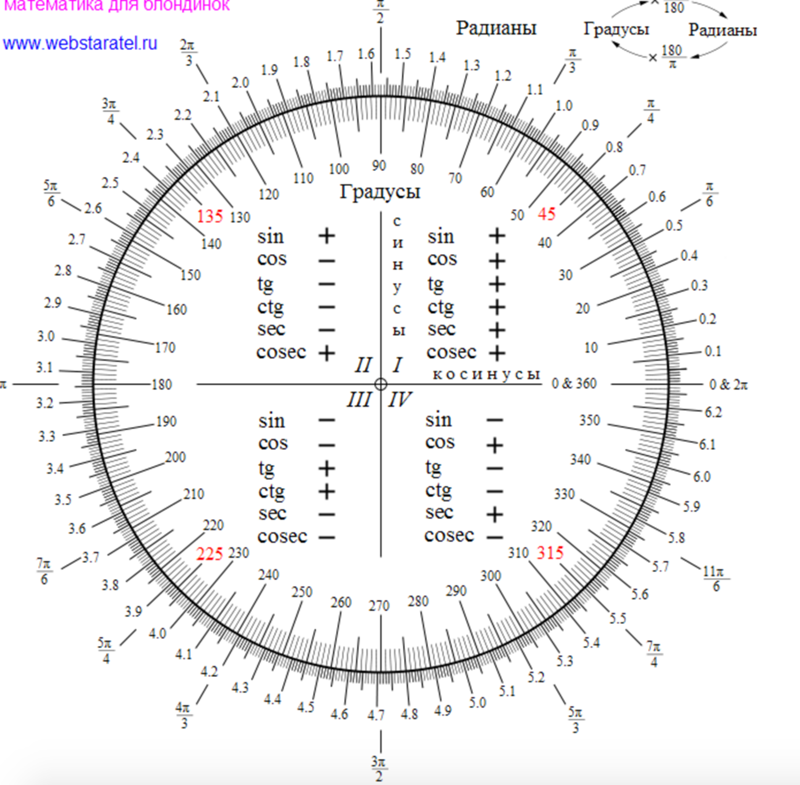 Радианы и градусы — две основные единицы измерения углов . Существуют и другие единицы измерения углов (например, 9).0077 град и MRAD), но в старших классах вы увидите только эти две единицы.

Что такое градусы и радианы?

Наиболее популярной единицей измерения углов, с которой знакомо большинство людей, является градус (°). Единицами градуса являются минуты и секунды. Есть 360 градусов, 180 градусов для полукруга (полукруга) и 90 градусов для четверти круга (прямоугольный треугольник) в полном круге или одном полном обороте.

Градусы в основном указывают направление и величину угла . Лицом к северу означает, что вы смотрите в направлении 0 градусов. Если вы поворачиваетесь на юг, вы смотрите в направлении 90 градусов. Если вы вернетесь на север после полного вращения, вы повернетесь на 360 градусов. Обычно направление против часовой стрелки считается положительным. Если повернуть на запад с севера, угол будет либо -90 градусов, либо +270 градусов.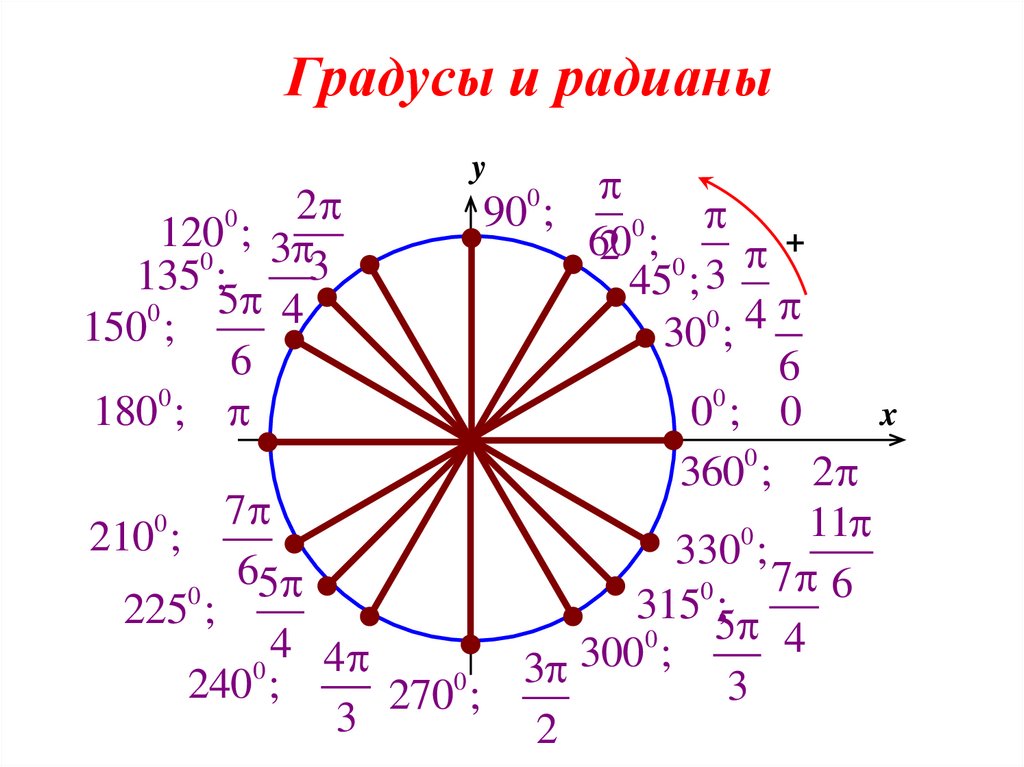

В геометрии есть еще одна единица измерения углов, известная как радиан ( Рад ).

Итак, зачем нам нужны радианы, когда мы уже привыкли к углам?

В большинстве расчетов в математике используются числа. Поскольку градусы на самом деле не являются числами, то предпочтительнее использовать радианы, которые часто требуются для решения задач.

Хорошим примером , который похож на эту концепцию, является использование десятичных дробей, когда у нас есть проценты . Хотя процент может быть показан числом, за которым следует знак %, мы преобразуем его в десятичную дробь (или дробь).

Понятие нахождения угла по длине дуги использовалось давно. Радиан был введен намного позже. Роджер Котес дал понятие радианам в 1714 году, но не дал ему этого названия, а просто назвал его круговой мерой угла.

Термин « радиан » впервые был использован в 1873 году. Позднее это название привлекло всеобщее внимание и получило официальное признание.

В этой статье вы узнаете, как преобразовать градусы в радианы и наоборот (радианы в градусы). Давайте взглянем.

Как перевести градусы в радианы?

Чтобы преобразовать градусы в радианы, мы умножаем заданный угол (в градусах) на π/180.

Угол в градусах (°) x π/180 = угол в радианах (рад)

Где π = 22/7 или 3,14

Пример 1

9000
1. 0°
2. 30°
3. 45°
4. 60°
5. 90°
6. 120°
7. 150°
8. 180 °
9. 210 °
10. 240 °
11. 360 °

раствор

Угла в градусах (°) x π/180 = угла в radian (Rad)

1. 0 ° ° x/180 = угла в Radian (Rad)

1. 0 ° ° x/180 = угла в Radian (Rad) 9000 3

1. 0 ° ° x/180 = угла в Radian (Rad) 180

= 0 RAD

2. 30 ° x π/180

= π/6

= 0,5 RAD

3. 45 ° x π/180

= π/4

= 0,785 RAD

. 4. 60° x π/180

= π/3

= 1,047 Рад

5. 90° x π/180

= π/2

= 1,571 Рад

6. 120 ° x π/180

= 2π/3

= 2,094 RAD

7. 150 ° x π/180

= 5π/6

= 2,618 RAD

8. 180 ° ° x π. /180

= π

= 3,14 RAD

9. 210 ° x π/180

= 7π/6

= 3,665 RAD

10. 240 ° x/180

= 3π/2

. = 4,189 Рад

11. 360° x π/180

= 2π

= 6,283 Рад

Пример 2

Преобразовать 70 градусов в радианы.

Решение

Угол в градусах (°) x π/180 = угол в радианах (рад)

Подстановка:

Угол в радианах (рад) = 700 x π/180.

= 35 π/9

= 12,21 Рад.

Пример 3

Преобразование – 300° в радианы.

Решение

Угол в радианах = -300° x π/180.

= – 5π/3

= – 5,23 Рад

Пример 4

Преобразовать – 270° в радианы.

Решение

Угол в радианах = -270° x π/180.

= – 3π/2

= -4,71 рад.

Пример 5

Преобразование 43 градусов, 6 минут и 9 секунд в радианы.

Решение

Сначала выразите 43 градуса, 6 минут и 9 секунд только в градусах.

43° 6′ 9″ = 43,1025°

43,1025° x π/180 = угол в радианах

= 0,752 рад.

Пример 6

Преобразование 102° 45′ 54″ в радианы.

Решение

102° 45′ 54″ равно 102,765°

Угол в радианах = 102,765°x π/180.

= 1,793 рад.

 

Как преобразовать радианы в градусы?

Чтобы преобразовать радианы в градусы, умножьте радианы на 180/π. Итак, формула имеет вид:

Угол в радианах x 180/ π = Угол в градусах.

Пример 7

Преобразуйте каждый из следующих углов в радианах в градусы.

1. 1,46
2. 11π/6
3. π/12
4. 3. 491
5. 7,854
6. -8,14
7. π/180
• π/180
9000 2 .
1. 46 х 180/π

= 83,69 градуса.

1. 11π/6 x 180/ π

= 330 градусов.

1. π/12 x 180/ π

= 15 градусов.

3. 491 х 180/ π

= 200,1 градуса

7. 854 х 180/ π

= 450,2 градуса.

8. -8,14 х 180/ π

= – 466,6 градуса.

1. π/180 x 180/ π

= 1 градус.

Пример 8

Преобразуйте угол π ​/5 радиан в градусы.

Решение

Угол в радианах x 180/ π = Угол в градусах.

Путем замены

π ​/5 x 180/ π = 36 градусов.

Пример

Преобразовать угол — π /8 Радиан в градусы

Решение

-π /8 x 180/π = –22,5 градуи.

Пример 10

Радиус куска пиццы равен 9 см. Если периметр куска равен 36,850 см, найдите угол куска пиццы в радианах и градусах.

Решение

Пусть длина дуги куска = x

Периметр = 9 + 9 + x

36,850 см = 18 + x

Вычтите 18 с обеих сторон.

18,85 = x

Итак, длина дуги куска равна 18,85 см.

Но, длина дуги = θr

Где θ = угол в радианах, а r = радиус.

18,85 см = 9 θ

Разделить обе стороны на 9

θ = 2,09 рад

θ в градусах:

Угол в радианах x 180/ π = Угол в градусах.

= 2,09 х 180/ π

= 120 градусов.

Пример 11

Радиус сектора 3 м, площадь 3π/4 м ² . Найдите центральный угол сектора в градусах и радианах.

Решение

Учитывая, что

Площадь сектора = (r ² θ)/2

Где θ = центральный угол в радианах.

Заменитель.

3π/4 = (3 ² θ)/2

3π/4 = 9θ/2

Перекрестное умножение.

6 π = 36 θ

Разделите обе стороны на 36, чтобы получить

θ = 0,52 рад.

Преобразование угла в градусы.

= 0,52 х 180/π

= 29,8 градуса.

Пример 12

Найдите центральный угол сектора радиусом 56 см и площадью 144 см ² .

Решение

A= (θ/360) πr ²

144 = (θ/360) x 3,14 x 56 x 56,

144 = 27,353 θ

Разделите обе части на θ.

θ = 5,26

Таким образом, центральный угол равен 5,26 градуса.

Пример 13

Площадь сектора 625 мм ² . Если радиус сектора равен 18 мм, найдите центральный угол сектора в радианах.

Решение

Площадь сектора = (θ r ² )/2

625 = 18 x 18 x θ/2

2 625 = 1960003

Разделите обе части на 162.

θ = 3,86 радиана.

Как преобразовать градусы в радианы

2π радиан на 360°.

Вам нужно знать, как преобразовать градусов в радианы и радианов в градусов в геометрии, тригонометрии и естественных науках. Радиан — производная единица измерения углов в системе СИ. Это безразмерное значение или имеет символ единицы r или рад. При этом степень ( °) измеряет плоский угол, при котором полный оборот составляет 360 °. Градус легко измерить и находит практическое применение в астрономии и географии.

2π = 360°
π = 180°

Вот формулы преобразования градусов в радианы и радианы в градусы и примеры, показывающие, как работать с преобразованием углов.

Формула преобразования градусов в радианы

Формула преобразования градусов в радианы:

радианы = градусы x π/180

Обратите внимание, что при измерениях в радианах сохраняется π. Вы можете сообщать измерения в радианах в виде десятичных значений примерно на пи как 3,14, но это не является распространенным явлением.

Как преобразовать градусы в радианы

Вот этап преобразования градусов в радианы:

1. Запишите угол в градусах.
2. Умножьте на π/180.
3. Сохраните π и упростите дробь.

Если вам нужно измерение в радианах в десятичном формате, помните, что значение числа пи примерно равно 3,14 или 9.0830 22 / ₇ .

Градусы в радианы Пример

Например, конвертируйте 90° в радианы.

радианы = градусы x π/180
радианы = 90 x π/180 = π/2

Радианы в градусы Формула

Формула для преобразования радианов в градусы:

градусов = радианы x 180/π

8

Градусы — это либо целые числа, либо десятичные числа. Но вы по-прежнему хотите сохранить значение π в радианах (вместо того, чтобы преобразовывать его в десятичное число), чтобы оно сокращалось при расчете.

Как преобразовать радианы в градусы

Вот шаги для преобразования радианов в градусы:

1. Запишите значение в радианах.
2. Умножьте это значение на 180 и разделите на π.

Если значение в радианах содержит π, то оно исключается из формулы, и все, что вам действительно нужно сделать, это умножить дробь на 180, чтобы получить ответ!

Радианы в градусы Пример

Например, переведите π/6 в градусы.

градуса = радианы x 180/π = π/6 x 180/π = 180/6 = 30°.

Отрицательные градусы или радианы

Преобразование единиц нормально работает с отрицательными градусами или радианами.

Например, конвертируйте -180° в радианы.

радиан = градусы x π/180 = -180 x π/180 = -π

Например, преобразуйте -3π/2 радиан в градусы.

градусы = радианы x 180/π = -3π/2 x 180/π = -1,5 x 180 = -270°

Таблица преобразования градусов в радианы

1030 Angle in Degrees Angle in Radians 0° 0 rad 30° π/6 ≈ 0. 524 rad 45° π/ 4 ≈ 0.785 rad 60° π/3 ≈ 1.047 rad 90° π/2 ≈ 1.571 rad 120° 2π/3 ≈ 2,094 rad 150° 5π/6 ≈ 2.618 rad 180° π ≈ 3.14 rad 210° 7π/6 ≈ 3.665 rad 270 ° 3π/2 ≈ 4.713 RAD 360 ° 2π ≈ 6. 283 RAD

Что на 1 -й или 1 рад?

• Один градус равен π/180, что приблизительно равно 0,0174533 радиана.
• Один радиан равен примерно 57,2958°.

Ссылки

• Каджори, Флориан (1929). История математических обозначений . 2. Дуврские публикации. ISBN 0-486-67766-4.
• Мор, Дж. К.; Филлипс, WD (2015). «Безразмерные единицы в СИ». Метрология . 52 (1): 40–47. doi:10.1088/0026-1394/52/1/40
• Мьюир, Тхос. (1910). «Термин «радиан» в тригонометрии». Природа . 83 (2110): 156. doi:10.1038/083156a0
• Проттер, Мюррей Х.; Морри, Чарльз Б. младший (1970). Колледж исчисления с аналитической геометрией (2-е изд.). Чтение: Эддисон-Уэсли.

---

Преобразование градусов в радианы (и радианы в градусы) • datagy

В этом руководстве вы узнаете, как использовать Python для преобразования градусов в радианы и радианы в градусы. Вы узнаете, как соотносятся градусы и радианы. Затем вы узнаете, как использовать библиотеку math и numpy библиотека для использования Python для преобразования градусов в радианы и радианы в градусы.

Быстрый ответ: Используйте math.radians() и math.степени()

Содержание

Что такое градусы и радианы?

Градусы и радианы являются широко используемыми метриками, которые используются для представления углов. Из-за их полезности полезно знать, как конвертировать между ними.

Формула, используемая для вычисления градуса с известным радианом:

градуса = r * (180° / pi)

Формула, используемая для расчета радиана, с известным числом градусов:

радиан = градус * (pi / 180°)

Теперь, когда вы знаете взаимосвязь между градусами и радианами, давайте рассмотрим, как преобразовать их с помощью библиотеки math .

Хотите узнать больше о вычислении квадратного корня в Python? Посмотрите мой туториал, который научит вас различным способам вычисления квадратного корня, как без функций Python, так и с помощью функций.

Использование математики для преобразования градусов в радианы

Библиотека math содержит полезную функцию radians() , которая позволяет нам преобразовывать градусы в радианы. Функция math.radians() принимает один вход, значение, представляющее градус, и возвращает значение, представляющее радиан.

Давайте попробуем несколько практических примеров. Мы знаем, основываясь на формуле, что если бы мы передали значение pi , мы смогли бы вернуть значение 180 .

Давайте попробуем это сделать, используя константу pi библиотеки math , доступ к которой можно получить с помощью math.pi :

 # Использование математики для преобразования градусов в радианы
импортировать математику
печать (математика.  градусы (математика. пи))
# Возвращает: 180.0 

Здесь мы видим, что возвращается правильное значение. Теперь давайте попробуем передать другое значение:

 # Используйте математику для преобразования градусов в радианы.
импортировать математику
печать (математика. Степени (3))
# Возвращает: 171.88733853924697 

В следующем разделе вы узнаете, как использовать библиотеку math для преобразования радиан в градусы.

Хотите узнать больше о циклах for Python? Ознакомьтесь с моим подробным руководством, которое превратит вас из новичка в опытного пользователя циклов for! Хотите вместо этого посмотреть видео? Посмотрите мой туториал на YouTube.

Использовать математику для преобразования радианов в градусы

Подобно тому, как библиотека math имеет функцию для преобразования радианов в градусы, мы можем использовать радиана функции для преобразования градусов в радианы.

Из формулы мы знаем, что если мы передадим значение 180 градусов, то должно быть возвращено значение пи .

Давайте попробуем сделать это с помощью Python:

 # Используйте математику для преобразования радианов в градусы
импортировать математику
печать (математика. радианы (180))
# Возвращает: 3.141592653589793 

Теперь, когда мы подтвердили это, давайте попробуем передать другое значение:

 # Используйте математику для преобразования радианов в градусы
импортировать математику
печать (математика. радианы (90))
# Возвращает: 1.5707963267948966 

В следующем разделе вы узнаете, как преобразовать градусы в радианы с помощью Python и numpy.

Хотите узнать больше о механизмах списков Python? Ознакомьтесь с этим подробным учебным пособием, которое охватывает все, что вам нужно знать, с практическими примерами. Больше визуального обучения, ознакомьтесь с моим руководством на YouTube здесь.

Используйте Numpy для преобразования радианов в градусы

Подобно тому, как библиотека math поставляется со встроенными функциями для преобразования между радианами и градусами, популярная числовая библиотека numpy имеет аналогичные функции.

Чтобы использовать numpy для преобразования градусов в радианы, мы можем использовать функцию radians() .

Давайте еще раз попробуем преобразовать значение pi , чтобы увидеть, возвращает ли оно значение 180:

 # Используйте numpy для преобразования радианов в градусы
импортировать numpy как np
импортировать математику
печать (np. степени (math.pi))
# Возвращает: 180.0 

Теперь давайте попробуем другой numpy, чтобы увидеть его результат:

 # Используйте numpy для преобразования радианов в градусы
импортировать numpy как np
печать (np.степени (3))
# Возвращает: 171.88733853924697 

В следующем разделе вы будете использовать numpy для преобразования радианов в градусы.

Нужно проверить, существует ли ключ в словаре Python? Ознакомьтесь с этим учебным пособием, в котором рассказывается о пяти различных способах проверки наличия ключа в словаре Python, в том числе о том, как вернуть значение по умолчанию.

Использование Numpy для преобразования градусов в радианы

Подобно использованию numpy для преобразования градусов в радианы, мы также можем использовать numpy для преобразования радианов в градусы. Для этого мы будем использовать np.radians() функция. Эта функция принимает один вход, значение, которое представляет радианы, и возвращает один выход, значение, которое представляет градусы.

Давайте снова передадим значение 180 и посмотрим, вернет ли оно значение pi :

 # Используйте numpy для преобразования градусов в радианы
импортировать numpy как np
печать (np.radians (180))
# Возвращает: 3.141592653589793 

Теперь, когда это подтверждено, давайте проверим другое значение:

 # Используйте numpy для преобразования градусов в радианы
импортировать numpy как np
печать (np. radians (90))
# Возвращает: 1.5707963267948966 

Хотите научиться красиво печатать файл JSON с помощью Python? Изучите три различных способа достижения этого с помощью этого подробного руководства здесь.

Заключение

Из этого руководства вы узнали, как использовать Python для преобразования радианов в градусы и градусов в радианы. Вы также узнали, как использовать библиотеки math и numpy для преобразования радианов в градусы.

Чтобы узнать больше о math , ознакомьтесь с официальной документацией здесь.

Преобразование градусов в радианы | Brilliant Math & Science Wiki

Содержание

• Измерение углов
• Длина дуги
• Примеры

Существуют две разные системы измерения углов: градусы и радианы. \circ360∘ в градусах, то длина дуги окружности, высеченной углом, равна длине окружности радиусом 111, или 2π⋅1=2π,2 \pi \cdot 1 = 2\pi,2π⋅1=2π. Для любого другого измерения угла в градусах мы можем вычислить долю длины дуги, вырезанную путем преобразования градусов в радианы, как показано в следующем примере:\circ = \pi \text{ радианы}. \end{array}​30∘=6π​ радиан,​60∘=3π​ радиан,​90∘=2π​ радиан,​180∘=π радиан.​

Для обычной окружности с радиусом rrr, если угол θ\thetaθ (данный в радианах) образован с положительной осью xxx, тогда длина дуги части окружности, вырезанной углом, равна

(Arc Длина)=rθ. \text{(Длина дуги)} = r \theta. (Длина дуги) = rθ.

Как мы видели, для окружности с радиусом r=1,r=1,r=1 длина дуги равна просто углу θ\thetaθ в радианах. 9\круг} \\ &= \pi \text{ радианы}. \ _\площадь \end{выровнено} 60∘180∘​=60∘⋅360∘2π радиан=3π радиан=180⋅360∘2π радиан=π радиан. □​​

Чему равен центральный угол θ\thetaθ (в радианах), опирающийся на дугу длины 4 и радиуса 2?

---

Подход 1:

Если длина дуги равна ее радиусу, то центральный угол, опирающийся на дугу, равен 1 радиану.
Поскольку в этой задаче длина дуги окружности вдвое больше радиуса, центральный угол равен 2 радианам. □_\квадрат□​

Подход 2:

Длина lll дуги радиуса rrr и центрального угла θ\thetaθ определяется по формуле l=rθ.l=r\тета.l=rθ. Для этой задачи у нас есть l=rθ4=2θθ=2 радиана. □ \begin{выровнено} л &= г \ тета \\ 4 &= 2\тета\\ \тета &= 2 \текст{ радианы}.\ _ \квадрат \end{выровнено} l4θ​=rθ=2θ=2 радиан. □​​

Цитировать как: Преобразование градусов и радианов. Brilliant.org . Извлекаются из https://brilliant.org/wiki/степени-радиан/

Как преобразовать градусы в радианы: шаги и примеры решений

Namrata Das

Exams Prep Master | Обновлено 5 апреля 2022 г.

В геометрии и градусы, и радианы представляют собой меру угла . Полный поворот против часовой стрелки можно выразить в 2π (радианах) или 360° (градусах). Следовательно, градусы и радианы равны следующим образом: 2π = 360°, Когда π = 180°, и, таким образом, 180 градусов равны π радианам. Градус, или градус дуги, или градус дуги — это единица измерения горизонтальных углов. Радианы — еще одна мера угла геометрии. Радиус — это угол, образованный в центре окружности дугой, длина которой равна радиусу r окружности. В общей геометрии угловое расстояние обычно считается в градусах (°). Давайте подробнее рассмотрим преобразование градусов в радианы и обсудим некоторые важные вопросы.

Содержание Как перевести градусы в радианы? Преобразование радианов в градусы Radian to Degree Equation Degrees to Radian Formula Negative degree to radians Degrees to radians chart Things to Remember Sample Questions

Подробнее:  Формула формы периметра

Радианы обычно учитываются при измерении углов тригонометрических или периодических функций. Радианы всегда выражаются в пи, а значение пи равно 22/7 или 3,14.

Некоторые градусы имеют части, выраженные в минутах и ​​секундах. Это преобразование является наиболее важной частью тригонометрических приложений.

• Grade xπ / 180 = radial
• Radial x 180 / π = degree
• 360 degrees = 2π radial
• 180 degrees = π radial

Also check: 

---

Как преобразовать градусы в радианы?

Значение 180° всегда равно π радианам. Чтобы преобразовать любой заданный угол из градусов в радианы, значение необходимо умножить на π / 180.

Угол в радианах = угол в градусах * \(\frac{\pi}{180}\)

Угол в радианах = угол в градусах /180.

Где π = 22/7 или значение 3,14

Подробнее:  Разница между площадью и объемом

Следующие шаги показывают, как преобразовать углы в градусах в радианы.

• Запишите числовое значение меры заданного угла в градусах.
• Умножить число, записанное в шаге 1, на π/180
• Упростить формулу, сократив общие элементы числа
• Результат после упрощения — радиальное угловое расстояние.
Преобразование градусов в радианы

Рассмотрим примеры преобразования различных угловых величин.

Пример 1. Преобразование 90 градусов в радианы.

Решение: 90 градусов — заданный угол, π/2 в радианах.

Также проверьте: 

---

Преобразование радианов в градусы

Как уже объяснялось, как преобразовать градусы в радианы для любого заданного угла. Теперь мы увидим, как преобразовать радианы в градусы для любого заданного угла. Формула преобразования радианов в градусы выглядит следующим образом: Радиал x (180 / π) = градусы

Пример 2: Преобразование π / 6 в градусы.

Решение: Используя приведенную выше формулу,

π / 6 × (180 / π) = 180/6 = 30 градусов

Подробнее:

---

Радиан в градус Уравнение

Как уже известно, полный оборот, т. е. против часовой стрелки в плоскости XY равен 2π (радиан) или 360° (градусов). Следовательно, и градусы, и радианы могут образовывать уравнение, поэтому:

2π = 360 °, Также π = 180 °

Подробнее:

---

Градусы в радиан Формула

Вы можете использовать ту же формулу, что и в предыдущий раздел, чтобы преобразовать градусы в радианы.

Градус x π/180 = радианы

Пример 3: Преобразование 15 градусов в радианы.

Решение: Используя приведенную выше формулу,

15xπ / 180 = π / 12

Пример 4. Преобразование 330 градусов в радианы.

Решение: Использование вышеупомянутой формулы,

330xπ / 180 = 11π / 6

также проверьте:

---

Отрицательный степень с Radians

. Метод конвертации отрицательных градусов в Radian что касается положительных степеней. Умножьте указанное значение угла в градусах на π/180.

Например, если вам нужно перевести -180 градусов в радианы:

Радиан = (π/180) x (градусы)

Радиал = (π/180) x (-180°)

Радиальный угол = — π

Подробнее:

---

Градусы в радианы Таблица

Ниже приведена таблица, в которой некоторые углы в градусах конвертируются в радианы.

Угол (градусы)	Угол (радианы)
0°	0
30°	π/6 = 0.524 Rad
45°	π/4 = 0.785 Rad
60°	π/3 = 1.047 Rad
90°	π/2 = 1.571 Rad
120°	2π/3 = 2.094 Rad
150°	5π/6 = 2.618 Rad
180°	π = 3,14 Рад
210°	7π/6 = 3.665 Rad
270°	3π/2 = 4. 713 Rad
360°	2π = 6.283 Rad

---

Things To Remember

• This is indicated символом (°). 360° — это мера угла одного оборота. Полный оборот указывается под углом 360°, а инструмент, используемый для измерения угла в градусах, известен как транспортир.
• Полный оборот против часовой стрелки равен 2π в радианах. На следующем изображении показано измерение одной радиальной оси 57,29.6°. Прямые углы представлены π / 2 радианами, а прямые углы представлены π радианами.
• В общей геометрии угловое расстояние обычно измеряется в градусах (°). Радиалы обычно рассматриваются при измерении углов тригонометрических или периодических функций. Радиалы всегда выражаются в пи, а значение пи равно 22/7 или 3,14.
• Формула для преобразования радиан в градусы: Радиал x (180 / π) = уклон
• Чтобы преобразовать угол данного градуса в радиальное направление, значение необходимо умножить на π / 180.

Читайте также:

---

Примеры вопросов

Вопросы: Преобразуйте 200 градусов в радианы. (2 балла)

Ответ: По известной нам формуле;

Угол в радиусе = Угол в градусах x π / 180 

Следовательно, радиальный 200 градусов = 200 × π / 180 

= 10π / 9 = 3491 рад

Вопрос: Преобразуйте 450 градусов в радианы. (2 балла)

Ответ: По известной нам формуле;

Угол в радиусе = Угол в градусах x π / 180

Следовательно, радиальные 450 градусов = 450 × π / 180

= 7854 колеса.

Подробнее:

Вопрос: Какова формула преобразования радианов в градусы? (2 балла)

Ответ: Чтобы преобразовать значение угла из радиан в градусы, нужно умножить указанное значение на 180 / π. Например, значение 2π:

2π x180 / π = 360 градусов

Вопрос: Как преобразовать 30 градусов в радианы? (2 балла)

Ответ: Умножьте 30 градусов на π/180.

30 x (π/180) = π/6

Следовательно, 30 градусов равны π/6 в радианах.

Подробнее:

Запрос: преобразовать следующую степень в отношении степени в Radian меру: (3 балла)

(I) 60 °

(II) 150 °

9007 (III) (II) 150 °

9000 2 (III) (II) 240°

(iv) -320°

Ответ: (i) 1° = π / 180 радиан

Следовательно, 60° = π / 180 x 60 радиан = π / 3 радиана

(ii) 150° = π / 180 x 150 радиан = 5π / 6 радиан

(iii) 240° = π / 180 x 240 радианы = 4π / 3 радиана

(iv) -320° = π / 180 x -320 радиан = -6π / 9 радиан

Вопрос: Почему число пи равно 180 градусам? (2 балла)

Ответ: Один оборот против часовой стрелки в плоскости XY дает 2π (радиан) или 360° (градусов). Следовательно, мы можем написать: 2π = 360°, Также π = 180°.

No related posts.