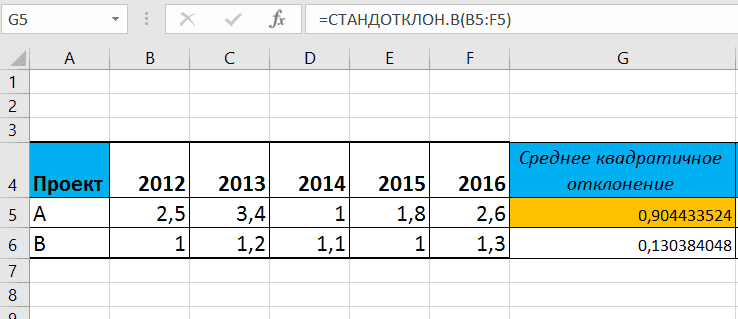
Рассчитать онлайн среднее квадратичное отклонение: Среднее квадратичное отклонение | Онлайн калькулятор

Содержание

Калькулятор Среднеквадратичное Отклонение

Онлайн-калькулятор среднеквадратичное отклонение поможет вам среднеквадратичное отклонение калькулятор, дисперсию, среднее значение и сумму квадратов набора данных. Низкое значение стандартного отклонения указывает на то, что точки близки к среднему значению, тогда как большее значение указывает на то, что числа сильно отличаются от среднего. Среднее также известно как среднее значение чисел в наборе данных. Наш калькулятор среднего и SD работает для следующих двух наборов данных:

Для образца
Для населения

Стандартное отклонение – это одна из мер дисперсии, которая говорит нам, насколько значения в наборе данных отличаются от среднего. Это квадратный корень из дисперсии набора данных. Кроме того, он часто используется для измерения статистических результатов, например, погрешности. В этом случае стандартное отклонение называется стандартной ошибкой среднего. Для удобства вы можете попробовать наш онлайн-калькулятор среднеквадратическое отклонение ошибки, который поможет вам рассчитать стандартную ошибку для данного набора исходных данных.

n \)

Кроме того, этот простой, но высокоточный калькулятор ковариации будет эффективно оценивать ковариацию между двумя случайными величинами X и Y во время экспериментов по вероятности и статистике.

Применение стандартного отклонения:

Стандартное отклонение широко используется для тестирования моделей на реальных данных экспериментально и в промышленных условиях. Его можно использовать, чтобы найти минимальную и максимальную стоимость некоторого продукта, когда продукт имеет высокий процент. Если значения выходят за пределы допустимого диапазона, то необходимо изменить производство, чтобы улучшить качество продукта. Этот показатель дисперсии широко используется в различных областях науки, например, в прогнозировании погоды для прогнозирования погоды, в финансах для измерения колебаний цен на продукцию и многих других. Вы можете легко определить нормальный или средний диапазон набора данных чего угодно с помощью решателя стандартных отклонений. Это широко используется в области социальных наук в исследовательских целях для анализа статистики здоровья, результатов тестов и демонстрации различных моделей культурного поведения.

Как найти стандартное отклонение (шаг за шагом):

Наш среднего и калькулятор среднеквадратическое отклонение выполняет мгновенные вычисления, чтобы найти статистическую меру разнообразия или изменчивости в наборе данных, который является S.D. Вам просто нужно следовать следующим пунктам, чтобы производить точные вычисления вручную:

Узнайте количество выборки из совокупности
Рассчитать среднее
Найдите разницу между каждым образцом и средним значением
Возвести каждое значение в квадрат
Найдите сумму квадратов каждого значения
Разделите на N-1, чтобы получить дисперсию набора данных.
Взяв квадратный корень из значения, вы можете определить калькулятор среднее квадратическое отклонение набора данных.

Здесь у нас есть пример решения вручную для лучшего понимания.

Читать дальше!

Пример:
Найти стандартное отклонение от среднего для выборки с 6 числами 3, 4, 9, 7, 2, 5?

Решение:

Шаг 1:

Вычислите среднее значение чисел, для этого разделите сумму всех чисел на общее число:

\ (µ = {\ frac {3 + 4 + 9 + 7 + 2 + 5} {6}} \)

\ (µ = 30/6 \)

\ (µ = 5 \)

Шаг 2:

Найдите квадрат разницы каждого значения со средним значением:

\ (x_1-µ = 3 – 5 = -2 \)

\ (x_2-µ = 4 – 5 = -1 \)

\ (x_3-µ = 9 – 5 = 4 \)

\ (x_4-µ = 7 – 5 = 2 \)

\ (x_5-µ = 2 – 5 = -3 \)

\ (x_6-µ = 5 – 5 = 0 \)

Сейчас же,

\ ((x_1-µ) ^ 2 = (-2) ^ 2 = 4 \)

\ ((x_2-µ) ^ 2 = (-1) ^ 2 = 1 \)

\ ((x_3-µ) ^ 2 = (-4) ^ 2 = 16 \)

\ ((x_4-µ) ^ 2 = (2) ^ 2 = 4 \)

\ ((x_5-µ) ^ 2 = (-3) ^ 2 = 9 \)

\ ((x_6-µ) ^ 2 = (0) ^ 2 = 0 \)

Шаг 3:

Вычислить стандартное отклонение:

\ (s = \ sqrt {\ frac {4 + 1 + 16 + 4 + 9 + 0} {6-1}} \)

\ (s = \ sqrt {\ frac {34} {5}} \)

\ (s = \ sqrt {6. 2 = 6,8 \)

Просто учтите этот калькулятор среднеквадратичное отклонение и введите значения в соответствующие поля. Калькулятор дисперсии и стандартного отклонения помогает выполнять вычисления как для простых, так и для сложных вычислений стандартных отклонений и дисперсии.

Стандартное отклонение в гистограммах:

Набор данных представлен в виде гистограммы, которая представляет числа в виде полос разной высоты. На гистограмме столбцы представляют диапазон набора данных. Более длинный столбец представляет более высокий диапазон набора данных, в то время как более широкий столбец указывает на большее стандартное отклонение, а более узкий столбец указывает на меньшее стандартное отклонение. Приведем пример:

Тестовые отметки 600 студентов со средним значением 100, ориентация гистограммы следующая:

Оценки за тесты по математике SD = 8,5

Оценки по английскому языку SD = 18,3

Оценки по физике SD = 25,8

По всем трем предметам тест по физике имеет самое высокое стандартное отклонение.

Как среднеквадратичное отклонение калькулятор с помощью калькулятора SD:

Несомненно, вычисление стандартного отклонения набора данных – непростая задача. Но наш калькулятор SD лучше всего подходит для быстрого определения S.D.

Входы:

Сначала выберите вариант: значение вашего набора данных в форме выборки или генеральной совокупности.
Затем введите значения для набора данных
Наконец, нажмите кнопку расчета

Выходы:

Калькулятор показывает:

Стандартное отклонение набора данных
Дисперсия набора данных
Среднее значение набора данных
Всего чисел
Сумма квадратов чисел
Пошаговый расчет

Этот поисковик stdev использует ваш набор данных и отображает всю работу, необходимую для ваших расчетов.

Конечное примечание:

Стандартное отклонение называется мерой разброса чисел в данном наборе данных от его среднего значения. Эта статистическая модель используется почти во всех областях, включая исследования финансового рынка, прогноз климата, фармацевтику, материаловедение и т. Д. калькулятор среднее квадратическое отклонение помогает исследователю проводить эксперименты, когда сбор всех данных невозможен. Когда дело доходит до расчета стандартного отклонения, это очень сложно сделать вручную. Поэтому для удобства попробуйте этот онлайн-калькулятор среднеквадратичное отклонение , который поможет вам определить стандартное отклонение набора данных с другими статистическими показателями.

Other Languages: Standard Deviation Calculator, Standart Sapma Hesaplama, Odchylenie Standardowe Kalkulator, Kalkulator Standar Deviasi, Standardabweichung Rechner, 標準偏差計算, 표준편차 계산기, výpočet směrodatné odchylky, Calculadora De Desvio Padrão, Calculadora De Desviacion Estandar, Calcul Ecart Type, Calcolo Deviazione Standard Online, حساب الانحراف المعياري, Keskihajonta Laskin.

Среднее квадратическое отклонение, Линейное отклонение

Среднее квадратическое отклонение

Среднее квадратичное отклонение определяется как обобщающая характеристика размеров вариации признака в совокупности. Оно равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической, т.е. корень из дисперсии и может быть найдена так:

1. Для первичного ряда:

2. Для вариационного ряда:

Преобразование формулы среднего квадратичного отклонени приводит ее к виду, более удобному для практических расчетов:

Среднее квадратичное отклонение определяет на сколько в среднем отклоняются конкретные варианты от их среднего значения, и к тому же является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, и поэтому хорошо интерпретируется.

Примеры нахождения cреднего квадратического отклонения: Пример 1, Пример 2

Для альтернативных признаков формула среднего квадратичного отклонения выглядит так:

где р — доля единиц в совокупности, обладающих определенным признаком;

q — доля единиц, не обладающих этим признаком.

Понятие среднего линейного отклонения

Среднее линейное отклонение определяется как средняя арифметическая абсолютных значений отклонений отдельных вариантов от их средних арифметических.

1. Для первичного ряда:

2. Для вариационного ряда:

где сумма n — сумма частот вариационного ряда.

Пример нахождения cреднего линейного отклонения: Пример 1

Преимущество среднего абсолютного отклонения как меры рассеивания перед размахом вариации, очевидно, так как эта мера основана на учете всех возможных отклонений. Но этот показатель имеет существенные недостатки. Произвольные отбрасывания алгебраических знаков отклонений могут привести к тому, что математические свойства этого показателя являются далеко не элементарными. Это сильно затрудняет использование среднего абсолютного отклонения при решении задач, связанных с вероятностными расчетами.

Поэтому среднее линейное отклонение как мера вариации признака применяется в статистической практике редко, а именно тогда, когда суммирование показателей без учета знаков имеет экономический смысл. С его помощью, например, анализируется оборот внешней торговли, состав работающих, ритмичность производства и т. д.

Среднее квадратическое

Среднее квадратическое применяется, например, для вычисления средней величины сторон n квадратных участков, средних диаметров стволов, труб и т. д. Она подразделяется на два вида.

Средняя квадратичная простая. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратичной средней величиной.

Она является квадратным корнем из частного от деления суммы квадратов отдельных значений признака на их число:

Средняя квадратичная взвешенная вычисляется по формуле:

где f — признак веса.

Средняя кубическая

Средняя кубическая применяется, например, при определении средней длины стороны и кубов. Она подразделяется на два вида.
Средняя кубическая простая:

Средняя кубическая взвешенная:

При расчете средних величин и дисперсии в интервальных рядах распределения истинные значения признака заменяются центральными значениями интервалов, которые отличны от средней арифметической значений, включенных в интервал. Это приводит к возникновению систематической погрешности при расчете дисперсии. В.Ф. Шеппард определил, что погрешность в расчете дисперсии, вызванная применением сгруппированных данных, составляет 1/12 квадрата величины интервала как в сторону повышения, так и в сторону понижения величины дисперсии.

Поправка Шеппарда должна применяться, если распределение близко к нормальному, относится к признаку с непрерывным характером вариации, построено по значительному количеству исходных данных (n > 500). Однако исходя из того, что в ряде случаев обе погрешности, действуя в разных направлениях компенсируют друг друга, можно иногда отказаться от введения поправок.

Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее совокупность и тем более типичной будет средняя величина.
В практике статистики часто возникает необходимость сравнения вариаций различных признаков. Например, большой интерес представляет сравнение вариаций возраста рабочих и их квалификации, стажа работы и размера заработной платы, себестоимости и прибыли, стажа работы и производительности труда и т. д. Для таких сопоставлений показатели абсолютной колеблемости признаков непригодны: нельзя сравнивать колеблемость стажа работы, выраженного в годах, с вариацией заработной платы, выраженной в рублях.

Для осуществления таких сравнений, а также сравнений колеблемости одного и того же признака в нескольких совокупностях с разными средним арифметическим используется относительный показатель вариации — коэффициент вариации.

Структурные средние

Для характеристики центральной тенденции в статистических распределениях не редко рационально вместе со средней арифметической использовать некоторое значение признака X, которое в силу определенных особенностей расположения в ряду распределения может характеризовать его уровень.

Это особенно важно тогда, когда в ряду распределения крайние значения признака имеют нечеткие границы. В связи с этим точное определение средней арифметической, как правило, невозможно, либо очень сложно. В таких случаях средний уровень можно определить, взяв, например, значение признака, которое расположено в середине ряда частот или которое чаще всего встречается в текущем ряду.

Такие значения зависят только от характера частот т. е. от структуры распределения. Они типичны по месту расположения в ряду частот, поэтому такие значения рассматриваются в качестве характеристик центра распределения и поэтому получили определение структурных средних. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.

Источник: Балинова B.C. Статистика в вопросах и ответах: Учеб. пособие. — М.: ТК. Велби, Изд-во Проспект, 2004. — 344 с.

Расчет НМЦК — начальной (максимальной) цены контракта, онлайн калькулятор

Главная
Расчет НМЦК

Расчет начальной (максимальной) цены контракта

методом сопоставимых рыночных цен (анализа рынка)

Предмет (товар/работа/услуга) удалить

Количество (объем) закупаемого товара (работы, услуги)

Единицы измерения

Код ОКПД2

Цена из реестра контрактов

Ценовая информация	Цена за единицу (руб)
Источник удалить

Добавить ценовое предложение

Средняя арифметическая цена за единицу

Среднее квадратичное отклонение

Коэффициент вариации цен
Значение коэффициента вариации не превышает порог в 33%, совокупность ценовых значений является ОДНОРОДНОЙ
Значение коэффициента вариации превышает порог в 33%, совокупность ценовых значений является НЕОДНОРОДНОЙ, требуется дополнительное изучение рынка и характеристик предмета закупок

Цена за единицу с учетом округления вниз

НМЦК

Добавить товар/работу/услугу

Ответственное лицо за расчет

Сохранить Скачать . docx

Необходимо Зарегистрироваться или Войти

Фамилия Имя Отчество

Номер телефона

Отправляя сообщение и при дальнейшем использовании настоящим интернет-ресурсом Вы соглашаетесь с правилами пользования форумом и политикой конфиденциальности

Прайс

Тариф	Тариф 1	Тариф 2	Тариф 3
Информирование об изменениях законодательства о контрактной системе
Сервис по поиску ОКПД 2
Доступ к вебинарам
Доступ к справочно-правовой системе
Расширенный доступ к сервису поиска кода ОКПД2
Ресурс по подготовке пакета документов, необходимого для применения профессионального стандарта «специалист в сфере закупок»
Ресурс по подготовке локальных актов, регламентирующих закупочную деятельность организации
Ресурс по формированию контрактов и ведению реестра закупок по 44-ФЗ
Ресурс по формированию договоров и ведению реестра закупок по 223-ФЗ
Юридическое сопровождение в формате письменных консультаций
Абонентское годовое обслуживание для государственных и муниципальных заказчиков
Обучение (повышение квалификации или профессиональная переподготовка)
Доступ к калькулятору пени с возможностью формирования претензии
Ресурс по подготовке расчета НМЦК		с ограничением
Калькулятор расчета сроков проведения закупки
Конструктор закупок по 44-ФЗ
Конструктор технического задания (в разработке)

Регистрация

Дисперсия и среднее квадратичное отклонение.

Примеры вычисления

Математическое ожидание не дает достаточно полной информации о случайной величине, поскольку одному и тому же значению математического ожидания может соответствовать множество случайных величин, будут различаться не только возможными значениями, но и характером распределения и самой природой возможных значений.

Например. Законы распределения двух случайных величин и заданные таблицами:

Вычислить математическое ожидание и

Решение. Находим математическое ожидание по класической формуле

Получили, что для двух различных законов распределения математическое ожидание принимает одинаковое значения (0), при этом возможные значения случайных величин и различаются. Из приведенного примера видно, что в случае равенства математических ожиданий случайные величин и имеют тенденцию к колебаниям относительно и причем имеет больший размах рассеяния относительно сравнительно случайной величине относительно . Поэтому математическое ожидание еще называют центром рассеяния. Для определения рассеяния вводится числовая характеристика, называемая дисперсией.

Для определения дисперсии рассматривается отклонение случайной величины от своего математического ожидания

Математическое ожидание такого отклонения случайной величины всегда равна нулю. В этом легко убедиться из следующего соотношения

Таки образом, отклонение не может быть мерой рассеивания случайной величины.

Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от своего математического ожидания

Для дискретной случайной величины дисперсия вычисляется по формуле

для непрерывной находят интегрированием

Если непрерывная величина заданная на интервале то дисперсия равна интегралу с постоянными пределами интегрирования

Дисперсия обладает следующими свойствами

1. Если случайная величина состоит из одной тотчки — постоянная величина, то дисперсия равна нулю

2. Дисперсия от произведения постоянной на случайную величину равна квадрату постоянной умноженной на дисперсию случайной величины

3. Если и — постоянные величины, то для дисперсии справедлива зависимость

Это следует из двух предыдущих свойств.

Дисперсию можно вычислить по упрощенной формуле:

которая в случае дискретной случайной величины имеет вид

для непрерывной определяется зависимостью

и для непрерывной на промежутке соотношением

Приведенные формулы очень удобны в вычислениях, и их, в отличие от предыдущих, используют в обучении

Также следует помнить, что дисперсия всегда принимает неотрицательные значения . Она характеризует рассеяние случайной величины относительно своего математического ожидания. Если случайная величина измерена в некоторых единицах, то дисперсия будет измеряться в этих же единицах, но в квадрате.

Для сравнения удобно пользоваться числовыми характеристиками одинаковой размерности случайной величиной. Для этого вводят в рассмотрение среднее квадратичное отклонение – корень квадратный из дисперсии. Ее обозначают греческой буквой «сигма»

—————————————-

Рассмотрим примеры для ознакомления с практической стороной определения этих величин.

Пример 1. Закон распределения дискретной случайной величины заданы таблицей:

Вычислить дисперсию и среднее квадратическое отклонение .

Решение. Согласно свойствами дисперсии получим:

—————————————-

Пример2. Есть четыре электрические лампочки, каждая из которых имеет дефект с вероятностью ( — вероятность того, что лампочка без дефекта). Последовательно берут по одной лампочке, вкручивают в патрон и включают электрический ток. При включении тока лампочка может перегореть, и ее заменяют на другую. Построить закон распределения дискретной случайной величины — число лампочек, которые будут опробованы. Вычислить среднее квадратическое отклонение

Решение. Дискретная случайная величина — число лампочек, которые будут опробованы — приобретает такие возможных значений:

Вычислим соответствующие вероятности:

Последнюю вероятность можно трактовать следующим образом: четвертая лампочка будет испытана, когда третья перегорит, а четвертая — нет, или если и четвертая перегорит.

В табличной форме закон распределения иметь следующий вид:

Для нахождения среднего квадратического отклонения найдем сначала значение дисперсии. Для дискретной случайной величины она примет значение:

Среднее квадратичное отклонение находим добычей корня квадратного из дисперсии.

—————————————-

Пример 3. Закон распределения вероятностей дискретной случайной величины заданы в виде функции

Вычислить среднее квадратическое отклонение и дисперсию

Решение. С помощью функции распределения вероятностей формируем закон распределения в виде таблицы

На основе таблицы распределения вычисляем дисперсию

————————

Подобных примеров можно привести множество, основная их суть в правильном применении приведенных в начале статьи формул для вычисления дисперсии и математического ожидания. Применяйте их там где это необходимо и не допускайте ошибок при определении дисперсии.

Что такое дисперсия и стандартное отклонение?

Содержание

— Как связаны стандартное отклонение и дисперсия?
— В чем разница между дисперсией и средним квадратическим отклонением?
— Что такое дисперсия в теории вероятности?
— Как найти дисперсию по выборке?
— Как рассчитать среднее отклонение?
— Что такое дисперсия в покере?
— Что такое дисперсия в статистике простыми словами?
— Что характеризует среднее квадратичное отклонение?
— Что такое дисперсия?
— Как найти дисперсию в теории вероятности?
— Для чего служит дисперсия?

— Как найти математическое ожидание и дисперсию?
— Как найти дисперсию признака?
— Как найти генеральную дисперсию?

Дисперсия и стандартное отклонение, основанные на квадрате отклонений, являются двумя наиболее широко используемыми мерами дисперсии: Дисперсия определяется как среднее квадратов отклонений от среднего значения. Стандартное отклонение — это положительный квадратный корень дисперсии.

Как связаны стандартное отклонение и дисперсия?

Квадратный корень из дисперсии называется стандартным отклонением. Стандартное отклонение измеряется в тех же единицах, что и сама случайная величина, а дисперсия измеряется в квадратах этой единицы измерения.

В чем разница между дисперсией и средним квадратическим отклонением?

Дисперсия — это не что иное, как среднее квадратов отклонений. С другой стороны, стандартное отклонение является среднеквадратичным отклонением. … В отличие от стандартного отклонения, которое выражается в тех же единицах, что и значения в наборе данных. Дисперсия показывает, насколько далеко распределены люди в группе.

Что такое дисперсия в теории вероятности?

Определение Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания. обозначает математическое ожидание.

Как найти дисперсию по выборке?

Для того, чтобы оценить дисперсию по выборке необходимо: — Вычислить математические ожидания данных (выборочное среднее — среднее арифметическое значений вариант в выборке). — Вычитаем математическое ожидание из исходного значения для всех данных из выборки и возводим результат в квадрат.

Как рассчитать среднее отклонение?

Чтобы найти среднеквадратическое отклонение, нужно взять квадратный корень из дисперсии.

Что такое дисперсия в покере?

Дисперсия — это отклонение между реальными результатами и математическим ожиданием на дистанции.

Что такое дисперсия в статистике простыми словами?

Простыми словами дисперсия – это средний квадрат отклонений. То есть вначале рассчитывается среднее значение, затем берется разница между каждым исходным и средним значением, возводится в квадрат, складывается и затем делится на количество значений в данной совокупности.

Что характеризует среднее квадратичное отклонение?

Среднеквадратическое отклонение равно квадратному корню из дисперсии: Среднее квадратическое отклонение характеризует разброс значений относительно среднего (математического ожидания). …

Что такое дисперсия?

Дисперсия (химия) — образования из двух или более фаз (тел), которые совершенно или практически не смешиваются и не реагируют друг с другом химически. Дисперсия (биология) — термин, обозначающий разнообразие признаков в популяции.

Как найти дисперсию в теории вероятности?

Дисперсия случайной величины Х вычисляется по следующей формуле: D(X)=M(X−M(X))2, которую также часто записывают в более удобном для расчетов виде: D(X)=M(X2)−(M(X))2. Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.

Для чего служит дисперсия?

Дисперсия характеризует разброс случайной величины вокруг ее математического ожидания. … Оно используется для оценки масштаба возможного отклонения случайной величины от ее математического ожидания.

Как найти математическое ожидание и дисперсию?

Математическое ожидание находим по формуле m = ∑xipi. Математическое ожидание M[X]. Дисперсию находим по формуле d = ∑x2ipi — M[x]2.

Как найти дисперсию признака?

дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.

Как найти генеральную дисперсию?

Генеральной дисперсией называют среднее арифметическое квадратов отклонения значений признака X от их среднего значения xг. Рассеяние значений количественного признака X в выборке вокруг своего среднего значения`x характеризует выборочная дисперсия.

Интересные материалы:

Какие животные взяты под охрану в тундре?
Какие животные живут в лесотундре?
Какие знаки Зодиака самые богатые?
Какие зодчие построили Благовещенский собор в Москве?
Какие зубы считаются передними?
Какие звуки глухие и звонкие?
Какие звуки может издавать новорожденный?
Каким было количество английских колоний в Северной Америке в последней четверти xviii века?
Каким числам относится 0?
Каким должен быть журналист?

Дисперсия случайной величины и ее свойства. Среднее квадратическое отклонение. Теория вероятностей и математическая статистика

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Краткая теория

Дисперсия и формула для ее вычисления

На практике часто требуется оценить рассеяние возможных значений случайной величины вокруг ее среднего значения. Например, в артиллерии важно знать, насколько кучно лягут снаряды вблизи цели, которая должна быть поражена.

На первый взгляд может показаться, что для оценки рассеяния проще всего вычислить все возможные значения отклонения случайной величины и затем найти их среднее значение. Однако такой путь ничего не даст, так как среднее значение отклонения, т. е. M[X-M(X)], для любой случайной величины равно нулю. Это свойство объясняется тем, что одни возможные отклонения положительны, а другие — отрицательны; в результате их взаимного погашения среднее значение отклонения равно нулю. Эти соображения говорят о целесообразности заменить возможные отклонения их абсолютными значениями или их квадратами. Так и поступают на деле. Правда, в случае, когда возможные отклонения заменяют их абсолютными значениями, приходится оперировать с абсолютными величинами, что приводит иногда к серьезным затруднениям. Поэтому чаще всего идут по другому пути, то есть вычисляют среднее значение квадрата отклонения, которое и называют дисперсией.

Дисперсией называется математическое ожидание квадрата отклонения случайной величины от :

Для того чтобы найти дисперсию, достаточно вычислить сумму произведений возможных значений квадрата отклонения на их вероятности.

Для вычисления дисперсии на практике удобно пользоваться следующей формулой:

Свойства дисперсии

Свойство 1.

Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания.

Свойство 2.

Дисперсия константы равна нулю:

Свойство 3.

Постоянный множитель выносится из-под знака дисперсии в квадрате:

Свойство 4.

Дисперсия суммы случайных величин:

где – ковариация случайных величин и

Если не находите примера, аналогичного вашему, если сами не успеваете выполнить работу, если впереди экзамен по предмету и нужна помощь — свяжитесь со мной:

ВКонтакте
WhatsApp
Telegram

Я буду работать с вами, над вашей проблемой, пока она не решится.

Следствия из свойств дисперсии.

В частности, если и независимы, то

Прибавление константы в случайной величине не меняет ее дисперсии:

Дисперсия разности равна сумме дисперсий:

Среднеквадратическое отклонение

Для оценки рассеяния возможных значений случайной величины вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики. К их числу относится среднее квадратическое отклонение.

Стандартное (среднее квадратичное) отклонение случайной величины определяется как корень из дисперсии и обозначается

Легко показать, что дисперсия имеет размерность, равную квадрату размерности случайной величины. Так как среднее квадратическое отклонение равно квадратному корню из дисперсии, то ее размерность совпадает с размерностью X. Поэтому в тех случаях, когда желательно, чтобы оценка рассеяния имела размерность случайной величины, вычисляют среднее квадратическое отклонение, а не дисперсию. Например, если X выражается в линейных метрах, то среднее квадратичное отклонение X будет выражаться также в линейных метрах, a дисперсия X — в квадратных метрах.

Смежные темы решебника:

Математическое ожидание и его свойства
Дискретная случайная величина
Непрерывная случайная величина

Примеры решения задач

Пример 1

В коробке 20 конфет, из которых 4 с вареньем. Х – число конфет с вареньем среди двух случайно выбранных. Найти дисперсию случайной величины Х.

Решение

ВКонтакте
WhatsApp
Telegram

Я буду работать с вами, над вашей проблемой, пока она не решится.

Случайная величина – число конфет с вареньем, может принимать значения 0,1,2

Найдем соответствующие вероятности:

Проверка:

Получаем следующий закон распределения СВ :

	0	1	2
	0. 6316	0.3368	0.0316

Математическое ожидание:

Дисперсию можно вычислить по формуле:

Искомая дисперсия:

Пример 2

Даны законы распределения независимых случайных величин X и Y:

x_i	0	1
n_i	0.4	0.6

y_i	2	3
m_i	0. 5	0.5

Найти закон распределения суммы (X+Y). Проверить равенство D(X+Y)=D(X)+D(Y).

Решение

ВКонтакте
WhatsApp
Telegram

Я буду работать с вами, над вашей проблемой, пока она не решится.

Распределение суммы :

	0+2	0+3	1+2	1+3

Окончательно получаем:

	2	3	4	Итого
	0. 2	0.5	0.3	1

Вычислим математические ожидания:

Вычислим дисперсии:

Проверим равенство :

Равенство выполняется.

Пример 3

Вероятность изготовления бракованной детали на первом станке составляет 3%, на втором станке 5%. На первом станке было изготовлено 20 деталей, на втором 40 деталей. Найти математическое ожидание и дисперсию числа бракованных деталей.

Решение

Математическое ожидание биномиального распределения:

Дисперсия:

Математическое ожидание величины – числа бракованных деталей на 1-м станке:

Дисперсия:

Математическое ожидание величины – числа бракованных деталей на 2-м станке:

Дисперсия:

Математическое ожидание числа бракованных деталей:

Дисперсия числа бракованных деталей:

Ответ: ; .

Пример 4

Случайные величины X,Y распределены по закону Пуассона. Найдите M{(X+Y)²}, если M(X)=40 и M(Y)=70, а коэффициент корреляции X и Yравен 0,8.

Решение

ВКонтакте
WhatsApp
Telegram

Я буду работать с вами, над вашей проблемой, пока она не решится.

Поскольку случайные величины и распределены по закону Пуассона и известны их математические ожидания, соответствующие дисперсии равны:

Пользуясь свойствами математического ожидания и дисперсии:

Подставляя числовые значения, получаем:

Ответ: .

Задачи контрольных и самостоятельных работ

Задача 1

Независимые случайные величины X и Y заданы следующими законами:

x	2. 3	2.5	2.7	2.9
p	0.4	0.3	0.2	0.1

y	1	2	3
p	0.3	0.5	0.2

Укажите законы распределения случайной величины X+Y, X-Y и найдите их математическое ожидание и дисперсию.

Задача 2

Найти дисперсию, математическое ожидания, среднекваратическое отклонение ДСВ X, заданной законом распределения.

x	-5	2	3	4
p	0,4	0,3	0,1	0,2

Написать F(x) и построить ее график.

Задача 3

Случайная величина X имеет плотность вероятности

Требуется найти дисперсию D_x.

ВКонтакте
WhatsApp
Telegram

Я буду работать с вами, над вашей проблемой, пока она не решится.

Задача 4

Вероятность того, что прибор исправен, равна 0,8. X – число исправных приборов из двух выбранных. Найти дисперсию случайной величины X.

Задача 5

Случайные величины X и Y независимы. Найти дисперсию случайной величины Z=2X+3Y, если известно, что D(X)=4, D(Y)=5.

Задача 6

Найти дисперсию дискретной случайной величины X – числа отказов элемента некоторого устройства в десяти независимых опытах, если вероятность отказа элемента в каждом опыте равна 0,9.

Задача 7

Дискретная случайная величина X имеет только два возможных значения: x₁ и x₂, причем x₂>x₁. Вероятность того, что X примет значение x₁, равна 0,6. Найти закон распределения величины X, если математическое ожидание и дисперсия известны: M(X)=1,4; D(X)=0,24.

Задача 8

Закон распределения случайной величины ξ имеет вид:

ξ	-1	2	3	5
P	1/4	1/2	1/8	1/8

Найти функцию распределения случайной величины ξ, вычислить ее математическое ожидание, дисперсию и среднее квадратическое отклонение. Вычислить вероятность P{5⁄2<ξ<5}.

Задача 9

Дискретная случайная величины X принимает лишь два значения. Большее из значений 3 она принимает с вероятностью 0,4. Кроме того, известна дисперсия случайной величины D(X)=6. Найти математическое ожидание случайной величины.

Задача 10

Найти дисперсию по заданному непрерывному закону распределения случайной величины X, заданному плотностью вероятности при и в остальных точках.

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Калькулятор стандартного отклонения

Укажите числа, разделенные запятыми, для расчета стандартного отклонения, дисперсии, среднего значения, суммы и погрешности.

Калькулятор связанных вероятностей | Калькулятор размера выборки | Калькулятор статистики

Стандартное отклонение в статистике, обычно обозначаемое как σ , является мерой вариации или дисперсии (относится к степени растяжения или сжатия распределения) между значениями в наборе данных. Чем ниже стандартное отклонение, тем ближе точки данных к среднему (или ожидаемому значению)9.0006 мк . И наоборот, более высокое стандартное отклонение указывает на более широкий диапазон значений. Подобно другим математическим и статистическим понятиям, существует множество различных ситуаций, в которых можно использовать стандартное отклонение, и, следовательно, множество различных уравнений. В дополнение к выражению изменчивости населения стандартное отклонение также часто используется для измерения статистических результатов, таких как предел погрешности. При таком использовании стандартное отклонение часто называют стандартной ошибкой среднего или стандартной ошибкой оценки относительно среднего. Приведенный выше калькулятор вычисляет стандартное отклонение генеральной совокупности и стандартное отклонение выборки, а также приближения доверительного интервала.

Стандартное отклонение совокупности

Стандартное отклонение совокупности, стандартное определение σ , используется, когда можно измерить всю совокупность, и представляет собой квадратный корень из дисперсии заданного набора данных. В случаях, когда каждый член совокупности может быть отобран, для определения стандартного отклонения всей совокупности можно использовать следующее уравнение:

Где

x _i — индивидуальное значение
μ среднее/ожидаемое значение
N общее количество значений

Для тех, кто не знаком с обозначениями суммирования, приведенное выше уравнение может показаться сложным, но если рассматривать его отдельные компоненты, это суммирование не представляет особой сложности. i=1 в суммировании указывает начальный индекс, т. е. для набора данных 1, 3, 4, 7, 8, i=1 будет 1, i=2 будет 3 и т. д. . Следовательно, обозначение суммирования просто означает выполнение операции (x _i — μ) ² для каждого значения до N , что в данном случае равно 5, поскольку в этом наборе данных 5 значений.

ПРИМЕР: μ = (1+3+4+7+8) / 5 = 4,6
σ = √[(1 — 4,6) ² + (3 — 4,6) ² + . .. + (8 — 4,6) ² )]/5
σ = √(12,96 + 2,56 + 0,36 + 5,76 + 11,56)/5 = 2,577

Стандартное отклонение выборки

Во многих случаях невозможно провести выборку каждого члена совокупности, что требует изменения приведенного выше уравнения таким образом, чтобы стандартное отклонение можно было измерить с помощью случайной выборки изучаемой совокупности. Общая оценка для σ — стандартное отклонение выборки, обычно обозначаемое как s . Стоит отметить, что существует множество различных уравнений для расчета стандартного отклонения выборки, поскольку, в отличие от среднего значения выборки, стандартное отклонение выборки не имеет какой-либо единственной оценки, которая была бы беспристрастной, эффективной и имела максимальную вероятность. Уравнение, представленное ниже, представляет собой «скорректированное стандартное отклонение выборки». Это скорректированная версия уравнения, полученная путем изменения уравнения стандартного отклонения совокупности с использованием размера выборки в качестве размера совокупности, что устраняет некоторую погрешность в уравнении. Однако беспристрастная оценка стандартного отклонения очень сложна и варьируется в зависимости от распределения. Таким образом, «скорректированное стандартное отклонение выборки» является наиболее часто используемой оценкой стандартного отклонения генеральной совокупности и обычно называется просто «стандартным отклонением выборки». Это гораздо лучшая оценка, чем ее нескорректированная версия, но все же она имеет значительную погрешность для малых размеров выборки (N

Где

x _i — одно значение выборки
x̄ — среднее значение выборки
N — размер выборки

Пример работы с суммированием см. в разделе «Стандартное отклонение генеральной совокупности». Уравнение по существу такое же, за исключением члена N-1 в уравнении скорректированного выборочного отклонения и использования выборочных значений.

Применение стандартного отклонения

Стандартное отклонение широко используется в экспериментальных и промышленных условиях для проверки моделей на реальных данных. Примером этого в промышленных приложениях является контроль качества некоторых продуктов. Стандартное отклонение можно использовать для расчета минимального и максимального значения, в пределах которого должен находиться какой-либо аспект продукта в течение некоторого большого процента времени. В случаях, когда значения выходят за расчетный диапазон, может потребоваться внести изменения в производственный процесс для обеспечения контроля качества.

Стандартное отклонение также используется в погоде для определения различий в региональном климате. Представьте себе два города, один на побережье и один в глубине страны, в которых средняя температура одинакова — 75°F. Хотя это может привести к убеждению, что температуры в этих двух городах практически одинаковы, реальность может быть замаскирована, если учитывать только среднее значение и игнорировать стандартное отклонение. Прибрежные города, как правило, имеют гораздо более стабильную температуру из-за регулирования большими водоемами, поскольку вода имеет более высокую теплоемкость, чем земля; по сути, это делает воду гораздо менее восприимчивой к изменениям температуры, а прибрежные районы остаются теплее зимой и прохладнее летом из-за количества энергии, необходимой для изменения температуры воды. Следовательно, в то время как прибрежный город может иметь диапазон температур от 60 ° F до 85 ° F в течение определенного периода времени, что приводит к среднему значению 75 ° F, внутренний город может иметь температуру от 30 ° F до 110 ° F. получается одно и то же среднее.

Еще одной областью, в которой широко используется стандартное отклонение, являются финансы, где оно часто используется для измерения риска, связанного с колебаниями цен на некоторые активы или портфели активов. Использование стандартного отклонения в этих случаях обеспечивает оценку неопределенности будущих доходов от данной инвестиции. Например, при сравнении акции А со средней доходностью 7 % и стандартным отклонением 10 % с акцией Б, имеющей такую же среднюю доходность, но со стандартным отклонением 50 %, первая акция явно будет более безопасным вариантом. поскольку стандартное отклонение акции B значительно больше при той же доходности. Это не означает, что акции А определенно являются лучшим вариантом для инвестиций в этом сценарии, поскольку стандартное отклонение может искажать среднее значение в любом направлении. В то время как Акция А имеет более высокую вероятность средней доходности, близкой к 7%, Акция Б потенциально может обеспечить значительно большую прибыль (или убыток).

Это лишь несколько примеров того, как можно использовать стандартное отклонение, но существует гораздо больше. Как правило, вычисление стандартного отклонения полезно всякий раз, когда требуется узнать, насколько далеко от среднего может быть типичное значение распределения.

Калькулятор стандартного отклонения

Использование калькулятора

Стандартное отклонение — это статистическая мера разнообразия или изменчивости в наборе данных. Низкое стандартное отклонение указывает на то, что точки данных обычно близки к среднему или среднему значению. Высокое стандартное отклонение указывает на большую изменчивость точек данных или более высокий разброс от среднего значения.

Этот калькулятор стандартного отклонения использует ваш набор данных и показывает работу, необходимую для расчетов.

Введите набор данных, разделенный пробелами, запятыми или разрывами строк. Нажмите «Рассчитать», чтобы найти стандартное отклонение, дисперсию, количество точек данных. n , среднее значение и сумма квадратов. Вы также можете увидеть работу, выполненную для расчета.

Вы можете копировать и вставлять строки точек данных из таких документов, как электронные таблицы Excel или текстовые документы, с запятыми или без них в форматах, показанных в таблице ниже.

Формула стандартного отклонения

Стандартное отклонение набора данных представляет собой квадратный корень из рассчитанной дисперсии набора данных.

Формула дисперсии (s ² ) представляет собой сумму квадратов разностей между каждой точкой данных и средним значением, деленную на количество точек данных.

При работе с данными из полной совокупности сумма квадратов разностей между каждой точкой данных и средним значением делится на размер набора данных, 92} \)

Для дополнительного объяснения стандартного отклонения и того, как оно связано с распределением кривой нормального распределения, см. {n}x_i \] 9{2}}{n — 1} \]

Допустимые форматы данных

Столбец (новые строки)

42
54
65
47
59
40
53

42, 54, 65, 47, 59, 40, 53

Разделенные запятыми (CSV)

42,
54, г.
65,
47, г.
59, г.
40, г.
53, г.

или

42, 54, 65, 47, 59, 40, 53

Пробелы

42 54
65 47
59 40
53

или

42 54 65 47 59 40 53

42, 54, 65, 47, 59, 40, 53

Смешанные разделители

42
54 65, 47,59,
40 53

42, 54, 65, 47, 59, 40, 53

Расчет стандартного отклонения

Стандартное отклонение (SD) измеряет волатильность или изменчивость набора данных. Это мера разброса чисел в наборе данных от их среднего значения и может быть представлена с помощью символа сигма (σ). Следующий алгоритмический инструмент расчета позволяет легко быстро определить среднее значение, дисперсию и стандартное отклонение набора данных.

Математические формулы

Среднее значение = сумма значений / N (количество значений в наборе)
Дисперсия = ((n ₁ — Среднее) ² + … n _n — Среднее) ² ) / N-1 (количество значений в наборе — 1)
Стандартное отклонение σ = √Дисперсия
Стандартное отклонение населения = используйте N в знаменателе дисперсии, если у вас есть полный набор данных. Причина, по которой 1 вычитается из стандартных показателей дисперсии в более ранней формуле, заключается в том, чтобы расширить диапазон, чтобы «исправить» тот факт, что вы используете только неполную выборку из более широкого набора данных.

Пример расчета

для набора данных 1,8,-4,9,6 вычислить SD и SD населения .

SD Расчет

Сумма:
1+8+-4+9+6 = 20

Среднее значение:
20/5 Числа =
Среднее 4

Вариант: 9000 40004 (1-

: 9000 40004 (1-

4) ² + (8-4) ² + (-4-4) ² + (9-4) ² + (6-4) ² ) / (N-1) =
((-3) ² +( 4) ² + (-8) ² + (5) ² + (2) ² ) / 4 =
(9+16+64+25+4)/4 =
118/4 = 29,5

Стандартное отклонение:
√29,5= 5,43139

Расчет стандартного отклонения населения

Стандартное отклонение населения:
((1-4) ² + (8-4) 900 900 ² + (9-4) ² + (6-4) ² ) / N =
((-3) ² +(4) ² + (-8) ² + (5) ² + (2) ² ) / 5 =
(9+16+64+25+4) / 5 =
118 / 5 = 23,6

Стандартное отклонение населения:

4 √28,709 7 8 4,

Стандартное отклонение: что это такое, важность и использование в реальных условиях один? А как насчет глобальной статистики экономического неравенства? Как насчет риска, связанного с инвестициями?

Если вы все еще задаете эти вопросы, вы попали по адресу. В этом разделе вы узнаете, как определить стандартное отклонение, почему оно важно и как его можно использовать в реальном мире.

Что такое стандартное отклонение?

В статистике, стандарт отклонение (SD) — это мера того, насколько разбросаны числа в данном наборе, показаны точки отклонения. Он говорит нам, в какой степени набор чисел рассредоточены вокруг среднего.

Дисперсия – это разница между фактическим значением и среднее значение в наборе. В принципе, чем шире дисперсия, тем выше стандартное отклонение.

Его значение представлено греческой буквой сигма (σ), показывающей, какая часть данных разбросана вокруг среднего (также называемого средним).

SD может принимать значения от 0 до бесконечности. Получающий 0 указывает на то, что все наборы чисел равны, что означает, что они не разбросаны в какой-либо степени.

Что такое среднее значение? Это среднее математическое значение всех числа в наборе, представленном греческой буквой мю (µ). Чтобы вычислить среднее, сложите значения всех чисел, затем разделите его на общее количество значений в заданном наборе.

Среднее значение = сумма всех значений / N (количество значений в наборе)

Что предполагает стандартное отклонение?

Низкое стандартное отклонение указывает на то, что числа близки к среднему набору .
Высокое стандартное отклонение означает, что числа рассредоточены в более широком диапазоне .

Чтобы лучше понять SD, мы должны визуализировать, как это отображается на графике. В частности, давайте обсудим график нормального распределения, также известный как кривая нормального распределения.

Гауссовая кривая и отклонения от среднего

В совершенно нормальном распределение, большинство точек данных относительно схожи. Это выглядит симметричный, что означает, что половина наблюдений данных находится по обе стороны от график. Это указывает на то, что данные попадают в диапазон значений с несколькими выбросы в нижней или верхней точках графика.

Элементы Нормальное распределение:

Имеет среднее значение, медиану или моду. Среднее значение — это среднее число чисел в группе, медиана — это среднее число в списке чисел, а мода — это число, которое чаще всего встречается в наборе чисел.
50% значений меньше среднего
50% значений больше среднего

Кривая нормального распределения также является теоретической представление о том, как часто эксперимент будет давать тот или иной результат.

Как выглядит стандартное отклонение на графике нормального распределения? См. пример изображения ниже.

Каждая окрашенная секция представляет 1 стандартное отклонение от среднего . Например, 1σ означает 1 стандартное отклонение от среднего значения и так далее. Точно так же -1σ также на 1 стандартное отклонение от среднего, но в противоположном направлении.

Проценты показывают, сколько данных приходится на каждый раздел. В этом примере 34,1% данных находятся в диапазоне 1 стандартное отклонение от среднего . Поскольку он отражает другую половину графика, 34,1% данных также появляются на -1σ от среднего.

Этот график выше показывает, что большинство данных, 95,5%, находятся ближе к среднему значению. Это указывает на то, что имеет низкое стандартное отклонение .

График выше показывает, что только 4,6% данных были получены после 2 стандартных отклонений.

Кроме того, данные имеют тенденцию находиться в типичном диапазоне согласно графику нормального распределения:

Около 68% попадают между -1 и 1
Около 95% попадают в диапазон от -2 до 2
Около 99% попадают в диапазон от -3 до 3

Стандартное отклонение в гистограммах

Данные также могут быть представлены в виде гистограммы, которая демонстрирует числа с использованием столбцов разной высоты. На гистограмме столбцы группируют числа в диапазоны. Более высокая полоса указывает на более высокий диапазон.

Более широкая гистограмма предполагает большее стандартное отклонение, а более узкая — более низкое стандартное отклонение. См. примеры ниже.

Например, следующие изображения иллюстрируют ориентацию гистограммы наблюдаемых результатов тестов, основанных на 800 учащихся, со средним баллом 100.

Результаты тестов по английскому языку SD = 7,5
Результат тестов по математике SD = 15,3
Результаты тестов по физике SD = 30,8

Из трех примеров результаты тестов по физике демонстрируют самое высокое стандартное отклонение.

Нахождение стандартного отклонения

Основная формула для SD (формула генеральной совокупности):

Где,

σ — стандартное отклонение
∑ это сумма
X — каждое значение в наборе данных
µ — среднее значение всех значений в наборе данных
N — количество значений в набор данных

В основном, стандартное отклонение σ = √Дисперсия

Что такое дисперсия? Это среднее квадратов отличий от среднего.
Стандартная формула дисперсии:
V = ((n ₁ – Среднее) ² + … n _n – Среднее) ² ) / N-1 (количество значений в наборе – 1 )

Как найти дисперсию:

Найти среднее (получить среднее значение).
Для каждого значения вычтите среднее значение и возведите результат в квадрат. Это квадрат разницы.
Затем найдите среднее значение квадратов разностей.

Например, 5 друзей только что измерили свой рост в сантиметрах. Используя приведенный ниже пример, найдите среднее значение, дисперсию и стандартное отклонение.

Среднее = сумма всех значений / N (количество значений в наборе)
Среднее = 157,48 + 165,099 + 172,72 + 152,4 + 167,64 / 5
= 815,339 / 5
= 163,0678 см
В этом примере средний или средний рост 163,0678 см.

Чтобы найти дисперсию, возьмите каждое отличие от среднего, возведите его в квадрат, а затем найдите среднее значение результата.

Корин: 163,0678 – 157,48 = 5,5878
Джен: 163,0678 – 165,099 = -2,0312
Раффи: 163,0678 – 172,72 = -9,6522
Джесси: 163,0678 – 152,4 = 10,6678
Кэт: 163,0678 – 167,64 = -4,5722

σ ² = 5.5878 ² + (-2.0312) ² + (-9.6522) ² + 10.6678 ² + (-4.5722) ² / 5
= 31.22351 + 4.12577 + 93.16496 + 113,80196 + 20,/5
= 263,22121/5
= 52,644242

Разница составляет 52,644242 . Поскольку стандартное отклонение представляет собой квадратный корень из дисперсии,
σ = √52,644242
= 7,2556352
Стандартное отклонение в этом примере равно 7,2556 см .

Если мы нанесем это на график, то теперь сможем показать, какие высоты находятся в пределах 1 стандартного отклонения от среднего. Теперь, когда мы знаем «стандарт», мы можем определить, какова обычная высота, а что слишком низко или слишком высоко.

Судя по этому небольшому набору, Раффи выше среднего человека более чем на 1σ при росте 172,72 см.

Конечно, вы можете сделать это быстрее, используя калькулятор в верхней части этой страницы.

Вы также можете использовать Excel, Google Таблицы или любую подобную программу. Это экономит время, если вы находите стандартное отклонение для большого набора чисел.

Просто введите формулу =stdevp () , затем выберите числа, которые необходимо рассчитать. См. пример ниже.

Значение и практическое использование

Нахождение стандартного отклонения позволяет нам определить нормальный или средний диапазон для всего, что касается набора данных. Он широко используется в исследованиях в области социальных наук для анализа записей, таких как результаты тестов, статистика здоровья и болезней, а также данных, показывающих модели культурного поведения.

При анализе опросов общественного мнения, таких как выборы или потребительские предпочтения, стандартные отклонения имеют решающее значение для расчета пределов погрешности. Хотя он измеряет непротиворечивость статистической гипотезы, его также можно проверить на точность. Это помогает исследователям определять нормальные модели поведения, чтобы делать точные прогнозы.

В финансах стандартное отклонение цен или показателей данных волатильность инвестиций, таких как отдельные ценные бумаги, инвестиционные фонды и портфели.

Например, фондовые рынки обычно имеют высокую волатильность (высокое стандартное отклонение), тогда как рынки облигаций демонстрируют низкую волатильность (низкое стандартное отклонение).

Более того, одна из самых значимых фигур в портфеле менеджмент это Шарп Соотношение, названное в честь лауреата Нобелевской премии и экономиста Уильяма Шарп.

Коэффициент Шарпа использует стандартное отклонение для измерения доходности с поправкой на риск, которая указывает доходность инвестиций путем измерения суммы риска, связанного с получением этой доходности.

Итог

Стандартное отклонение (SD) является важным инструментом для анализа статистических данных. Он предоставляет исследователям оценку среднего значения, которое является нормальным диапазоном, что позволяет им устанавливать стандарты.

SD используется в широкой области социальных исследований, включая медицину, образование, правительство и культурные исследования. В финансах, SD измеряет волатильность, когда дело доходит до анализа фондовых рынков.

Это практический инструмент, который позволяет исследователям измерять надежность статистической гипотезы, а также помочь предсказать будущие результаты.

Об авторе

Корин — страстный исследователь и автор финансовых тем, изучающих экономические тенденции, их влияние на население, а также то, как помочь потребителям принимать более разумные финансовые решения. Другие ее тематические статьи можно прочитать на Inquirer.net и Manileno.com. Она имеет степень магистра творческого письма Филиппинского университета, одного из ведущих учебных заведений мира, и степень бакалавра коммуникативных искусств Колледжа Мириам.

Вы позитивны? Cartoon

Формула стандартного отклонения и его использование в сравнении с дисперсией

Что такое стандартное отклонение?

Стандартное отклонение — это статистика, которая измеряет дисперсию набора данных относительно его среднего значения и рассчитывается как квадратный корень из дисперсии. Стандартное отклонение рассчитывается как квадратный корень из дисперсии путем определения отклонения каждой точки данных относительно среднего значения.

Если точки данных находятся дальше от среднего значения, в наборе данных имеется более высокое отклонение; таким образом, чем больше разбросаны данные, тем выше стандартное отклонение.

Основные выводы:

Стандартное отклонение измеряет дисперсию набора данных относительно его среднего значения.
Рассчитывается как квадратный корень из дисперсии.
Стандартное отклонение в финансах часто используется как мера относительной рискованности актива.
Волатильные акции имеют высокое стандартное отклонение, тогда как отклонение стабильных акций «голубых фишек» обычно довольно низкое.
Как недостаток, стандартное отклонение рассчитывает всю неопределенность как риск, даже когда это в пользу инвестора, например, доход выше среднего.

Стандартное отклонение

Понимание стандартного отклонения

Стандартное отклонение — это статистическое измерение в финансах, которое применительно к годовой доходности инвестиций проливает свет на историческую волатильность этих инвестиций.

Чем больше стандартное отклонение ценных бумаг, тем больше разница между каждой ценой и средним значением, которое показывает больший ценовой диапазон. Например, волатильная акция имеет высокое стандартное отклонение, в то время как отклонение стабильной акции «голубых фишек» обычно довольно низкое.

Формула стандартного отклонения

Стандартное отклонение рассчитывается путем извлечения квадратного корня из значения, полученного в результате сравнения точек данных, с коллективным средним значением генеральной совокупности. {th} \text{ точки в наборе данных}\\ &\overline{x}= \text{Среднее значение набора данных}\\ &n = \text{Количество точек данных в наборе данных} \end{выровнено} Стандартное отклонение=n−1∑i=1n(xi−x)2, где:xi=значение i-й точки в наборе данныхx=среднее значение набора данныхn=количество точек данных в набор данных

Расчет стандартного отклонения

Стандартное отклонение рассчитывается следующим образом:

Вычислить среднее значение всех точек данных. Среднее значение рассчитывается путем сложения всех точек данных и деления их на количество точек данных.
Рассчитайте дисперсию для каждой точки данных. Дисперсия для каждой точки данных рассчитывается путем вычитания среднего значения из значения точки данных.
Возведение в квадрат дисперсии каждой точки данных (из шага 2).
Сумма квадратов значений дисперсии (из шага 3).
Разделите сумму квадратов значений дисперсии (из шага 4) на количество точек данных в наборе данных за вычетом 1.
Извлеките квадратный корень из частного (из шага 5).

Использование стандартного отклонения

Стандартное отклонение — особенно полезный инструмент в стратегиях инвестирования и торговли, поскольку он помогает измерять волатильность рынка и ценных бумаг, а также прогнозировать тенденции производительности. Что касается инвестирования, например, индексный фонд, скорее всего, будет иметь низкое стандартное отклонение по сравнению с эталонным индексом, поскольку целью фонда является воспроизведение индекса.

С другой стороны, можно ожидать, что фонды агрессивного роста будут иметь высокое стандартное отклонение от относительных фондовых индексов, поскольку их портфельные менеджеры делают агрессивные ставки, чтобы получить доход выше среднего.

Более низкое стандартное отклонение не обязательно предпочтительно. Все зависит от инвестиций и готовности инвестора взять на себя риск. Имея дело с величиной отклонения в своих портфелях, инвесторы должны учитывать свою терпимость к волатильности и свои общие инвестиционные цели. Более агрессивным инвесторам может быть удобной инвестиционная стратегия, которая выбирает инструменты с волатильностью выше среднего, в то время как более консервативным инвесторам может не понравиться.

Стандартное отклонение — одна из ключевых фундаментальных мер риска, которую используют аналитики, портфельные менеджеры, консультанты. Инвестиционные фирмы сообщают о стандартном отклонении своих взаимных фондов и других продуктов. Большая дисперсия показывает, насколько доходность фонда отклоняется от ожидаемой нормальной доходности. Поскольку это легко понять, эта статистика регулярно сообщается конечным клиентам и инвесторам.

Стандартное отклонение и дисперсия

Дисперсия получается путем взятия среднего значения точек данных, вычитания среднего значения из каждой точки данных в отдельности, возведения в квадрат каждого из этих результатов, а затем взятия другого среднего значения этих квадратов. Стандартное отклонение — это квадратный корень из дисперсии.

Дисперсия помогает определить размер разброса данных по сравнению со средним значением. По мере того, как дисперсия становится больше, возникает больше различий в значениях данных, и может быть больший разрыв между одним значением данных и другим. Если значения данных близки друг к другу, дисперсия будет меньше. Однако это труднее понять, чем стандартное отклонение, потому что дисперсии представляют собой результат в квадрате, который не может быть осмысленно выражен на том же графике, что и исходный набор данных.

Стандартные отклонения обычно легче изобразить и применить. Стандартное отклонение выражается в той же единице измерения, что и данные, что не обязательно относится к дисперсии. Используя стандартное отклонение, статистики могут определить, имеют ли данные нормальную кривую или другое математическое соотношение.

Если данные ведут себя по нормальной кривой, то 68% точек данных будут находиться в пределах одного стандартного отклонения от средней или средней точки данных. Большие отклонения приводят к тому, что большее количество точек данных выходит за пределы стандартного отклонения. Меньшие отклонения приводят к большему количеству данных, близких к среднему.

Стандартное отклонение графически изображается как ширина колоколообразной кривой вокруг среднего значения набора данных. Чем шире ширина кривой, тем больше стандартное отклонение набора данных от среднего значения.

Сильные стороны стандартного отклонения

Стандартное отклонение является широко используемой мерой дисперсии. Многие аналитики, вероятно, лучше знакомы со стандартным отклонением, чем с другими статистическими расчетами отклонения данных. По этой причине стандартное отклонение часто используется в самых разных ситуациях, от инвестирования до актуариев.

Стандартное отклонение включает все наблюдения. Каждая точка данных включена в анализ. Другие измерения отклонения, такие как дальность, измеряют только самые разбросанные точки без учета промежуточных точек. Поэтому стандартное отклонение часто считается более надежным и точным измерением по сравнению с другими наблюдениями.

Стандартное отклонение двух наборов данных можно объединить с помощью специальной формулы комбинированного стандартного отклонения. Аналогичных формул для других измерений наблюдения дисперсии в статистике нет. Кроме того, стандартное отклонение можно использовать в дальнейших алгебраических вычислениях, в отличие от других средств наблюдения.

Ограничения стандартного отклонения

Есть некоторые недостатки, которые следует учитывать при использовании стандартного отклонения. Стандартное отклонение на самом деле не измеряет, насколько далеко точка данных находится от среднего значения. Вместо этого он сравнивает квадрат различий, тонкую, но заметную разницу фактической дисперсии со средним значением.

Выбросы оказывают более сильное влияние на стандартное отклонение. Это особенно верно, если учесть, что разница со средним значением равна квадрату, что приводит к еще большему количеству по сравнению с другими точками данных. Поэтому помните, что стандартное наблюдение, естественно, придает больший вес экстремальным значениям.

Наконец, стандартное отклонение может быть трудно рассчитать вручную. В отличие от других измерений дисперсии, таких как диапазон (наибольшее значение меньше наименьшего значения), стандартное отклонение требует нескольких громоздких шагов и с большей вероятностью приведет к вычислительным ошибкам по сравнению с более простыми измерениями. Это препятствие можно обойти с помощью терминала Bloomberg.

Рассмотрите возможность использования Excel при расчете стандартного отклонения. После ввода данных используйте формулу СТАНДОТКЛОН.С, если ваш набор данных является числовым, или формулу СТАНДОТКЛОН, если вы хотите включить текст или логические значения. Существует также несколько конкретных формул для расчета стандартного отклонения для всей совокупности.

Пример стандартного отклонения

Скажем, у нас есть точки данных 5, 7, 3 и 7, что в сумме дает 22. Затем вы должны разделить 22 на количество точек данных, в данном случае на четыре, что даст среднее значение 5,5. Это приводит к следующим определениям: x̄ = 5,5 и N = 4.

Дисперсия определяется путем вычитания среднего значения из каждой точки данных, в результате чего получаются -0,5, 1,5, -2,5 и 1,5. Затем каждое из этих значений возводится в квадрат, в результате чего получаются 0,25, 2,25, 6,25 и 2,25. Затем квадратные значения складываются вместе, что дает в сумме 11, которые затем делятся на значение N минус 1, что равно 3, что дает дисперсию приблизительно 3,67.

Затем вычисляется квадратный корень из дисперсии, в результате чего стандартное отклонение составляет примерно 1,915.

Или рассмотрим акции Apple (AAPL) сроком на пять лет. Историческая доходность акций Apple составляла 12,49% за 2016 год, 48,45% за 2017 год, -5,39% за 2018 год, 88,98% за 2019 год и по состоянию на сентябрь 60,91% за 2020 год. Таким образом, средняя доходность за пять лет составила 41,09%.

Величина годового дохода за вычетом среднего значения тогда составляла -28,6%, 7,36%, -46,48%, 47,89.% и 19,82% соответственно. Затем все эти значения возводятся в квадрат, чтобы получить 8,2%, 0,54%, 21,6%, 22,93% и 3,93%. Сумма этих значений равна 0,572. Разделите это значение на 4 (N минус 1), чтобы получить дисперсию (0,572/4) = 0,143. Квадратный корень дисперсии берется для получения стандартного отклонения 0,3781, или 37,81%.

Что означает высокое стандартное отклонение?

Большое стандартное отклонение указывает на то, что наблюдаемые данные сильно отличаются от среднего значения. Это указывает на то, что наблюдаемые данные весьма разбросаны. Небольшое или низкое стандартное отклонение вместо этого указывает на то, что большая часть наблюдаемых данных плотно сгруппирована вокруг среднего значения.

О чем говорит стандартное отклонение?

Стандартное отклонение описывает, насколько рассредоточен набор данных. Он сравнивает каждую точку данных со средним значением всех точек данных, а стандартное отклонение возвращает вычисленное значение, которое описывает, находятся ли точки данных в непосредственной близости или они разбросаны. В нормальном распределении стандартное отклонение говорит вам, насколько далеко значения от среднего.

Как быстро найти стандартное отклонение?

Если вы посмотрите на распределение некоторых наблюдаемых данных визуально, вы увидите, является ли фигура относительно худой или толстой. Более толстые распределения имеют большие стандартные отклонения. В качестве альтернативы Excel имеет встроенные функции стандартного отклонения в зависимости от набора данных.

Как рассчитать стандартное отклонение?

Стандартное отклонение рассчитывается как квадратный корень из дисперсии. В качестве альтернативы он рассчитывается путем нахождения среднего значения набора данных, нахождения разницы каждой точки данных со средним значением, возведения в квадрат различий, сложения их вместе, деления на количество точек в наборе данных за вычетом 1 и нахождение квадрата корень.

Почему важно стандартное отклонение?

Стандартное отклонение важно, поскольку оно может помочь пользователям оценить риск. Рассмотрим вариант инвестирования со средней годовой доходностью 10% в год. Однако это среднее значение было получено на основе доходности за последние три года в размере 50%, -15% и -5%. Рассчитав стандартное отклонение и поняв низкую вероятность фактического среднего значения в 10% в любой отдельно взятый год, вы будете лучше подготовлены к принятию обоснованных решений и выявлению лежащего в основе риска.

Калькулятор стандартного отклонения. Вычисляет стандартное отклонение выборки и генеральной совокупности. Стандартное отклонение для биномиальных данных. Калькулятор также выводит дисперсию

, среднее арифметическое (среднее), диапазон, количество и стандартную ошибку среднего (SEM) .

Быстрая навигация:

Что такое стандартное отклонение?
Формула стандартного отклонения
Как интерпретировать стандартное отклонение?
Практические приложения и примеры

Статистический вывод
Финансы
Погода

Что такое стандартное отклонение?

Стандартное отклонение — это термин в статистике и теории вероятностей, используемый для количественной оценки количества дисперсии в наборе числовых данных, то есть того, насколько далеки от нормы (среднего значения) точки интереса данных. «Стандартное отклонение» часто объединяется с 9.0284 SD или StDev и обозначается греческой буквой sigma σ при ссылке на оценку генеральной совокупности на основе выборки и строчной латинской буквой s при ссылке на стандартное отклонение выборки, которое рассчитывается напрямую.

Стандартное отклонение рассчитывается как квадратный корень из дисперсии , а сама дисперсия представляет собой среднее квадратов отличий от среднего арифметического. Мы возводим в квадрат различия так, что большие отклонения от среднего наказываются строже, а также имеет побочный эффект одинаковой обработки отклонений в обоих направлениях (положительных ошибок и отрицательных ошибок). Стандартное отклонение предпочтительнее дисперсии при описании статистических данных, поскольку оно выражается в тех же единицах, что и значения в данных. Наш калькулятор стандартного отклонения также рассчитает для вас дисперсию.

Для непрерывных переменных результатов вам потребуется весь необработанный набор данных, в то время как для биномиальных данных — доли, коэффициенты конверсии, коэффициенты восстановления, коэффициенты выживаемости и т. д. вы можете рассчитать дисперсию и стандартное отклонение, используя всего две сводные статистики: количество наблюдений ( размер выборки) и частота интересующих событий (которая также является средним значением). Наш калькулятор стандартного отклонения поддерживает как непрерывные, так и биномиальные данные.

Низкое стандартное отклонение σ означает, что точки данных сгруппированы вокруг среднего значения выборки, в то время как высокое стандартное отклонение указывает на то, что набор данных разбросан по широкому диапазону значений. Приведенный ниже график иллюстрирует этот момент путем сравнения двух распределений по 18 элементов в каждом с разными стандартными отклонениями (2,26 и 8,9).4):

Вы можете проверить числа в наборах данных и полученные расчеты в нашем калькуляторе SD здесь для набора 1 и здесь для набора 2.

Формула стандартного отклонения , в зависимости от того, рассчитываете ли вы стандартное отклонение на основе выборки из совокупности или на основе всей совокупности.

Чтобы найти стандартное отклонение по выборке , применяется формула стандартного отклонения выборки, а именно:

Если набор данных представляет всю интересующую совокупность , найдите стандартное отклонение по формуле:

read «x bar») — среднее арифметическое, а n — количество элементов в наборе данных (количество). Суммирование выполняется для стандартной суммы от i=1 до i=n. Как уже отмечалось, стандартное отклонение в обоих случаях равно квадратному корню из дисперсии. Наш калькулятор стандартного отклонения поддерживает обе формулы одним щелчком переключателя.

В большинстве случаев вам придется использовать формулу выборочного стандартного отклонения, так как большую часть времени вы будете делать выборку из совокупности и не будете иметь доступа к данным обо всей совокупности. Формула, используемая нашим калькулятором в этом случае, известна как «скорректированное стандартное отклонение выборки», и она не уникальна, поскольку, в отличие от среднего значения выборки и дисперсии, не существует единой формулы, которая является оптимальной оценкой для всех распределений. Эта формула, например, может быть сильно смещена для n

В некоторых случаях у вас будет информация обо всем населении, например, если интересующее нас население — это учащиеся класса или школы, в определенный момент времени можно получить оценки для всех из них. Однако чаще всего интересующая нас популяция охватывает время и охватывает слишком много людей, чтобы их можно было измерить на практике.

Если вам нужно рассчитать стандартное отклонение для пропорциональных данных, частоты событий и т. д., используйте простую формулу:

, где p — это доля населения, которое сталкивается с интересующим событием или имеет интересующую характеристику. Поскольку пропорция — это всего лишь особый тип среднего значения, эта формула стандартного отклонения получается путем простого преобразования приведенных выше. Наш калькулятор стандартного отклонения поддерживает пропорции, для которых необходимо знать только размер выборки и частоту событий, чтобы оценить разницу между наблюдаемым результатом и ожидаемым.

Как интерпретировать стандартное отклонение?

Как уже было показано в приведенном выше примере, более низкое стандартное отклонение означает меньшую дисперсию в наборе данных — числа больше сгруппированы вокруг среднего значения. Это качество означает, что меры и оценки стандартного отклонения могут использоваться для обозначения точности измерительных инструментов, инструментов или процедур в физике, медицине, биологии, физиологии, химии и т. д. Его можно рассматривать как измерение неопределенности данных — ожидаемых, известных или принятых, в зависимости от контекста.

Во многих ситуациях вам будет представлена статистическая точка отсечки в стандартных отклонениях. Их можно приравнять к процентилям — какой процент случаев соответствует x стандартным отклонениям от ожидаемого значения. Вот некоторые ключевые уровни и пороговые значения процентилей:

Таблица часто используемых пороговых значений стандартного отклонения для нормально распределенных переменных:

Общие пороговые значения стандартного отклонения
Стандартное отклонение	Процентиль (односторонний)	Процентиль (2-сторонний)
0,3186σ	50,00%	25,00%
0,5000σ	69,15%	38,29%
0,6745σ	75,00%	50,00%
0,8416σ	80,00%	60,00%
1,0000σ	84,13%	68,27%
1,2816σ	90,00%	80,00%
1,6448σ	95,00%	90,00%
1,9599σ	97,50%	95,00%
2,3263σ	99,00%	98,00%
2,5758σ	99,50%	99,00%
3,7190σ	99,99%	99,98%

Итак, , если наблюдение составляет 1,645 стандартных отклонений от ожидаемого значения, оно находится в верхнем 10-м процентиле интересующей совокупности . 2-стороннее относится к направлению интересующего вас эффекта. В большинстве практических сценариев 1-сторонний номер является релевантным. В популяционных исследованиях двусторонний процентиль эквивалентен доле в пределах, определяемых стандартным отклонением.

Геометрическая интерпретация будет состоять в том, что стандартное отклонение представляет часть площади распределения, которая включена или исключена.

Практические приложения и примеры

Стандартные отклонения имеют множество практических применений, в первую очередь связанных со статистикой и измерениями, поэтому этот онлайн-инструмент находится в нашей категории «Статистика».

Статистический вывод

Статистический вывод до статистические тесты с нулевой гипотезой процедура заключается в том, чтобы установить, каково ожидаемое распределение результатов теста, предполагая, что набор условий верен, а затем сравнить фактически наблюдаемые данные (преобразованные в меры стандартного отклонения) с ожидаемым результатом. Если наблюдаемые экспериментальные данные значительно отклоняются от ожидаемых, можно сделать вывод о прорыве. Такие результаты часто называют «статистически значимыми». При статистическом выводе имеют дело с выборками из совокупности, следовательно, необходимо применить формулу стандартного отклонения выборки для оценки стандартного отклонения генеральной совокупности .

Различные практические ситуации требуют различных порогов (уровней статистической значимости), которые могут быть выражены в терминах стандартных отклонений, скажем, 2 стандартных отклонения от ожидаемого, или в терминах процентной вероятности наблюдения ниже нуля: 5%, 1 % и т. д. Значение, рассчитанное как 1,96 стандартного отклонения от нулевого порога, будет видно только в 5% случаев, если нулевая гипотеза действительно верна. Число стандартных отклонений наблюдения часто называют Z-оценкой. Например, эксперименты в ЦЕРН, в ходе которых были обнаружены гравитационные волны, имели порог 6 сигм, поэтому наблюдения в ходе эксперимента должны были быть крайне маловероятными, прежде чем объявлялось об открытии.

Одной из причин, по которой стандартное отклонение среднего (стандартная ошибка среднего, SEM) является выбранной статистикой, является то, что оно обычно нормально распределено, даже если базовые данные не . Таким образом, очень часто с ожидаемым средним значением и стандартным отклонением среднего значения сравнивается среднее значение экспериментальных данных, а не отдельные точки данных.

Финансы

Стандартное отклонение колебаний цен финансового актива (акции, облигации, имущество и т. д.) широко используется для оценки суммы риск отдельных активов или портфелей активов финансовыми менеджерами и научными работами. Однако это горячо обсуждаемый вопрос, и многие видные финансовые практики осуждают уравнение риска и стандартного отклонения. Популярный инструмент технического анализа — полосы Боллинджера — эффективно строит линии, рассчитанные так, чтобы они представляли собой два стандартных отклонения в любом направлении от средней цены за данный скользящий период.

Поскольку стандартное отклонение и другие статистические инструменты применяются только к стационарным рядам, а некоторые финансовые данные являются нестационарными, их необходимо преобразовать, удалив тренд, сезонность и автокорреляцию из набора данных, обычно путем разности с использованием сложных регрессии, такие как ARIMA (AutoRegressive Integrated Moving Average) и модели экспоненциального сглаживания.

Погода

Расчеты стандартного отклонения часто сопровождают климатические данные, такие как среднесуточные максимальные и минимальные температуры, поскольку они помогают нам понять, как часто и насколько сильно они колеблются. Например, прибрежные районы часто имеют меньшие отклонения температуры по сравнению с внутренними районами, что делает типичную погоду совершенно другой, даже если они имеют одинаковую среднюю температуру.

Калькулятор стандартного отклонения со встроенным динамическим учебным пособием

Пусть вас не пугает формула!

По моему мнению, если бы «сильные мира сего» действительно хотели привлечь детей к занятиям математикой, они использовали бы котят, щенков, кроликов и т. д. в качестве математических символов, а не греческих букв.

Хотите напугать ученика с проблемами в математике, чтобы тот закрыл учебник по математике так быстро, что задует свечи в комнате? Покажите им это:

σ ² =

_N	(X _i — μ) ²
Σ
ⁱ⁼¹

σ = √

σ ²

Это страшная формула для расчета дисперсии ( σ ²) и стандартная отклонения ( σ ).

Но подождите! Держите свечи горящими!

Как вы увидите в примере ниже на странице, шаги по вычислению дисперсии и стандартного отклонения намного проще, чем пытаться расшифровать греческую формулу гика.

Что такое стандартное отклонение?

Стандартное отклонение — это просто один из нескольких методов суммирования дисперсии значений в наборе данных.

В частности, стандартное отклонение представляет собой квадратный корень из дисперсии, который пытается суммировать изменчивость или разброс значений относительно среднего значения всего набора.

Небольшое стандартное отклонение указывает на то, что значения тесно сгруппированы вокруг среднего (среднего) набора данных.

Большое стандартное отклонение указывает на то, что значения не плотно сгруппированы вокруг среднего (среднего) набора данных.

Население против выборочной статистики

Население: Набор данных представляет собой общий набор элементов, представляющих интерес для данной проблемы. Параметры населения в формулах на этой странице обозначены цифрой σ и μ .

Выборка: Набор данных представляет только часть населения, как определено выше. Примеры параметров в формулах на этой странице обозначены s и X.

4 простых шага

Как я уже говорил ранее, расчет стандартного отклонения намного проще, чем показано в формуле. Вот 4 простых шага:

Найдите среднее значение набора данных.
Найдите сумму квадратов отличий от среднего.
Разделите результат шага 2 на n (население) или n — 1 (выборка), где n — количество элементов в наборе.
Найдите квадратный корень из результата шага №3.

Чтобы понять, насколько просты вышеуказанные шаги, позвольте мне показать вам пример.

Пример задачи

Чтобы проиллюстрировать, насколько просто вычислить дисперсию и стандартное отклонение, я буду использовать следующий набор данных:

5, 4, 7, 9, 6, 8, 7, 5, 4, 5

Примечание. Десятичные числа в этом примере округляются до 2-х разрядов перед их отображением на экране.

Шаг №1: вычислить среднее

Среднее — это среднее всех чисел в наборе данных. Чтобы вычислить среднее значение набора чисел, вы складываете все элементы вместе, а затем делите результат на количество элементов в наборе.

Набор данных: 5, 4, 7, 9, 6, 8, 7, 5, 4, 5

Набор данных содержит 10 позиций

Среднее значение = (5 + 4 + 7 + 9 + 6 + 8 + 7 + 5 + 4) ÷ 10

Среднее значение = 60 ÷ 10

Среднее значение = 6

Шаг # 6

6 Шаг # # # 2: Найдите сумму квадратов расстояний от среднего.
Для каждого элемента в наборе данных мы: (1) вычитаем среднее значение всего набора из элемента, (2) возводим результат в квадрат, а затем (3) суммируем все результаты в квадрате, например:

(1) ²²²²
Цнт п X X — μ (X — μ ) ²
1 5 5 — 6 = -1 (-1) ² = 1
2 4 4 — 6 = -2 (-2) ² = 4
3 7 7 — 6 = 1 (1) ² 7 — 6 = 1 (1) ^{2
2} 7 — 6 = 1 (1) ² 7 — 6 = 1 7 — 6 = 1 7 — 6 = 1 7 — 6 = 1 7 — 6.
4 9 9 — 6 = 3 (3) ² = 9
5 6 6 — 6 = 0 (0) ² = 0
6 8 8 — 6 = 2 8 8 — 6 = 2 (2) ⁷ .
7 7 7 — 6 = 1 (1) ² = 1
8 5 5 — 6 = -1 (-1) ² = 1
9 4 4 — 6 = -2 (-2) ² = 4
10 5 5 — 6 = -1 (-1) ² = 1
n = 10 Sum = 60 Σ (X — μ) ² = 26

Шаг № 3: Рассчитайте дисперсию.
Этот шаг зависит от того, представляет ли набор, с которым вы работаете, общие данные (совокупность) или частичные данные (выборка). Вот как вы вычисляете отклонение от результатов шага 2 для любого случая ( μ и x являются символами для среднего , с единственной реальной разницей, указанной красным текстом):
9998). ² =
Дисперсия популяции ( σ ²)
Σ (X — μ ) ² = 26 = 2.60
n 10

Sample Variance ( s ² )

s ² = Σ (X — X) ² = 26 = 2.89
n — 1 9
Шаг №4: Вычислите квадратный корень из дисперсии.

No related posts.