Свойства tg: Функция y = tgx и её свойства — урок. Алгебра, 11 класс.

.3. СВОЙСТВА ФУНКЦИИ y=tg⁡x И ЕЕ ГРАФИК

Объяснение и обоснование

Напомним, что . Таким образом, областью определения функции y=будут все значения аргумента, при которых , то есть все значения x, kZ. Получаем

Этот результат можно получить и геометрически. Значения тангенса – это ордината соответствующей точки  на линии тангенсов (рис.91). Поскольку точки Aи B единичной окружности лежат на прямых ОА и ОВ, параллельных линии тангенсов, мы не сможем найти значение тангенса дляx, kZ.

Для всех других значений аргумента мы можем найти соответствующую точку на линии тангенсов и ее ординату — тангенс. Следовательно, все

Значенияx входят в область определения функции y=tgx.

Для точек единичной окружности (которые не совпадают с точками А и В) ординаты соответствующих т

очек на линии тангенсов принимают

все значения до +, поскольку для любого действительного числа

мы можем указать соответствующую точку на оси ординат, а значит, и соответствующую точку на оси тангенсов.

Учитывая, что точка О лежит

внутри окружности, а точка   вне ее (или на самой окружности), получаем, что прямая  имеет с окружностью хотя бы одну общую точку

(на самом деле их две). Следовательно, для любого действительного числа

найдется аргумент х, такой, что tan x равен данному действительному числу.

Поэтому область значений функции y= tg x — все действительные числа,

то есть R. Это можно записать так: E (=tgx) = R. Отсюда следует, что наибольшего и наименьшего значений функция tan x не имеет.

Как было показано в § 13, тангенс — нечетная функция:tg(-x)=tg x, следовательно, ее график симметричен относительно начала координат.

Тангенс — периодическая функция с наименьшим положительным периодом

Поэтому при построении графика

этой функции достаточно построить график на любом промежутке длиной π,

а потом полученную линию перенести параллельно вправо и влево вдоль оси

Ox на расстоянияkT = πk, где k — любое натуральное число.

Чтобы найти точки пересечения графика функции с осями координат,

напомним, что на оси Oy значение x = 0. Тогда соответствующее значение

y = tg 0 = 0, то есть график функции y = tg x проходит через начало координат.

На оси Ox значение y = 0. Поэтому необходимо найти такие значения x,

при которых tg x, то есть ордината соответствующей точки линии тангенсов, равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при x = πk, k ∈ Z.

Промежутки знакопостоянства. Как было обосновано в § 13, значения

функции тангенс положительны (то есть ордината соответствующей точкилинии тангенсов положительна) в І и ІІІ четвертях. Следовательно, tgx > 0 при

а также, учитывая период, при всех

Значения функции тангенс отрицательны (то есть ордината соответствующей точки линии тангенсов отрицательна) во ІІ и ІV четвертях. Такимобразом,

Промежутки возрастания и убывания.           

 Учитывая периодичность функции tgx (период T = π), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной π,

например на промежутке . Если x (рис. 92), то при увеличении аргумента x (x2>x1) ордината соответствующей точки линии

тангенсов увеличивается (то есть tgx2>tgx1). Таким образом, на этом

промежутке функция tgx возрастает. Учитывая периодичность функции

tgx, делаем вывод, что она возрастает также на каждом из промежутков

Проведенное исследование позволяет обоснованно построить график

функции y = tg x. Учитывая периодичность этой функции (с периодом π),

сначала построим график на любом промежутке длиной π, например на промежутке . Для более точного построения точек графика воспользуемся также тем, что значение тангенса — это ордината соответствующей точки

линии тангенсов. На рисунке 93 показано построение графика функции

y = tg x на промежутке.

Далее, учитывая периодичность тангенса (с периодом π), повторяем вид

графика на каждом промежутке длиной π (то есть параллельно переносим

график вдоль оси Ох на πk, где k — целое число).

Получаем график, приведенный на рисунке 94, который называется тангенсоидой.

14.4. СВОЙСТВА ФУНКЦИИ y = ctg x И ЕЕ ГРАФИК

Объяснение и обоснование

Так как  =, то областью определения котангенса будут все значения аргумента, при которых sin х ≠ 0, то есть x ≠ πk, k ∈ Z. Такимобразом,

D (ctg x): x ≠ πk, k ∈ Z.

Тот же результат можно получить, используя геометрическую иллюстрацию. Значение котангенса — это абсцисса соответствующей точки на линии

котангенсов (рис. 95).

 Поскольку точки А и В единичной окружности лежат на прямых ОА

и ОВ, параллельных линии котангенсов, мы не можем найти значение котангенса для x = πk, k ∈ Z. Длядругихзначенийаргументамыможемнайтисоответствующуюточкуна линии котангенсов и ее абсциссу — котангенс. Поэтому все значения x ≠ πk входят в область определения функции у = ctg х.

Для точек единичной окружности (которые не совпадают с точками А и В) абсциссы соответствующих точек на линии котангенсов принимают все значения от –× до +×, поскольку для любого действительного числа мы можем указать соответствующую точку на оси абсцисс, а значит, и соответствующую точку Qх на оси котангенсов. Учитывая, что точка О лежит внутри окружности, а точка Qх — вне ее (или на самой окружности), получаем, что прямая ОQх имеет с окружностью хотя бы одну общую точку (на самом деле их две). Следовательно, для любого действительного числа найдется аргумент х, такой, что сtg x равен данному действительному числу. Таким образом,

область значений функции y = ctg x — все действительные числа, то есть R.

Это можно записать так: E (ctgx) = R.Из приведенных рассуждений также вытекает, что наибольшего и наименьшего значений функция ctgxне имеет.

Как было показано в § 13, котангенс — нечетная функция: ctg (-x) = -ctgx, поэтому ее график симметричен относительно начала координат.

Там же было обосновано, что котангенс — периодическая функция с наи­меньшим положительным периодом T= : ctg (x+ ) = ctg x, поэтому через промежутки длиной п вид графика функции ctgxповторяется.

Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси Oyзначение x= 0. Но ctg0 не существует, значит, график функции y= ctg x не пересекает ось Oy.

На оси Оx значение y= 0. Поэтому необходимо найти такие значения x, при которых ctgx, то есть абсцисса соответствующей точки линии котанген­сов, равна нулю. Это будет тогда и только тогда, когда на единичной окруж­ности будут выбраны точки C или D(рис. 95), то есть при

Промежутки знакопостоянства. Как было обосновано в § 13, значения функции котангенс положительны (то есть абсцисса соответствующей точки линии котангенсов положительна) в I и III четвертях (рис. 96). Тогда ctgx> 0 при всех . Учитывая период, получаем, что ctgx> 0 при всех

         Значения функции котангенс отрицательны (то есть абсцисса соответ­ствующей точки линии котангенсов отрицательна) во II и IV четвертях, та­ким образом, ctgx< 0 при .

 

     Промежутки возрастания и убывания

 Учитывая периодичность функции ctg x (наименьший положительный период T = ), достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке (0; ). Если (0; ) (рис. 97), то при увеличении аргумента x (x₂>x₁) аб­сцисса соответствующей точки линии котангенсов уменьшается (то есть ctgx₂<ctgx₁), следовательно, на этом промежутке функция ctg x убывает. Учитывая периодичность функции y= ctgx, делаем вывод, что она также убывает на каждом из промежутков

 Проведенное исследование позволяет построить график функции y= ctg x аналогично тому, как был построен график функции y= tg x. Но график функции у = ctg x можно получить также с помощью геометрических пре­образований графика функции у = tg х. По формуле, приведенной на с. 172, , то есть Поэтому график функции у = ctg x можно получить из графика функции у = tg х параллельным переносом вдоль оси Ох на (− ) и симметричным отображением полученного графика относительно оси Ох.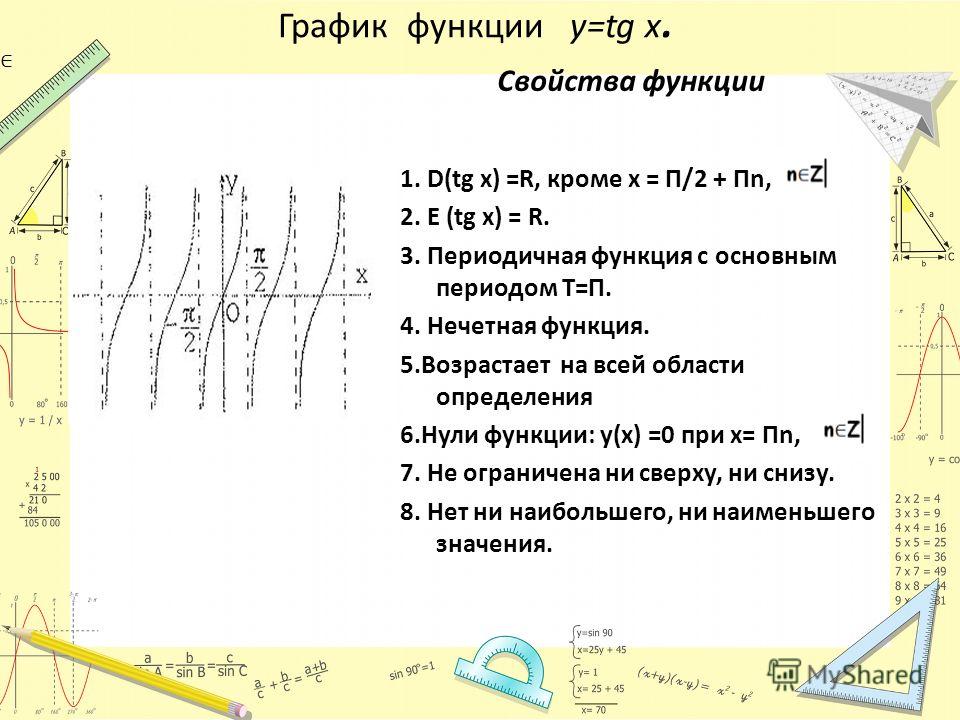

Получаем график, который называется котангенсоидой (рис. 98).

 

Функция y = tg x, свойства и график косинуса с примерами

1. Развертка тангенса движения точки по числовой окружности в функцию от угла
2. Свойства функции y=tgx
3. Примеры

п.1. Развертка тангенса движения точки по числовой окружности в функцию от угла

При движении точки по числовой окружности на вертикальной касательной, проведенной через точку (1;0), отображаются значения тангенсов соответствующих углов (см. §3 данного справочника).

Рассмотрим, как изменяется тангенс, если точка описывает полный круг, и угол x изменяется в пределах: 0≤x≤2π и построим график y=tgx на этом отрезке.

Если мы продолжим движение по окружности для углов x > 2π, кривые продолжатся вправо; если будем обходить числовую окружность в отрицательном направлении (по часовой стрелке) для углов x<0, кривые продолжатся влево.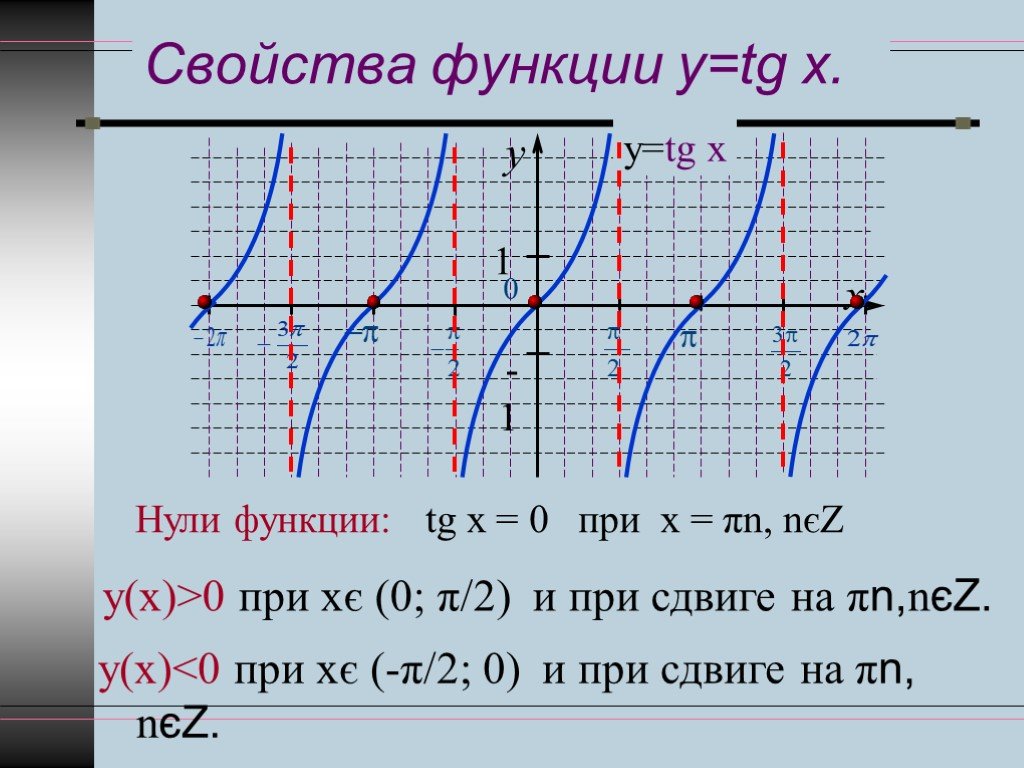

В результате получаем график y=tgx для для всех x из области допустимых значений.

График y=tgx называют тангенцоидой.
Часть тангенцоиды c \(-\frac\pi2\lt x\lt \frac\pi2\) называют главной ветвью тангенцоиды.

п.2. Свойства функции

y=tgx⁡

1. Область определения \(x\ne\frac\pi2+\pi k\) — множество действительных чисел, кроме точек, в которых \(cosx=0\).

2. Функция не ограничена сверху и снизу. Область значений \(y\in\mathbb{R}\)

3. Функция нечётная $$ tg(-x)=-tgx $$

4. Функция периодическая с периодом π $$ tg(x+\pi k)=tgx $$

5. Функция стремится к \(+\infty\) при приближении слева к точкам \(x=\frac\pi2+\pi k\).
Приближение к точке a слева записывается как \(x\rightarrow a-0\) $$ \lim_{x\rightarrow\frac\pi2+\pi k-0} tgx=+\infty $$ Функция стремится к \(-\infty\) при приближении справа к точкам \(x=\frac\pi2+\pi k\).
Приближение к точке a справа записывается как \(x\rightarrow a+0\) $$ \lim_{x\rightarrow\frac\pi2+\pi k+0} tgx=-\infty $$ Нули функции \(y_{0}=0\) достигаются в точках \(x_0=\pi k\)

6.  Функция возрастает на всей области определения.

7. Функция имеет разрывы в точках \(x=\frac\pi2+\pi k\), через эти точки проходят вертикальные асимптоты. На интервалах между асимптотами \(\left(-\frac\pi2+\pi k;\ \frac\pi2+\pi k\right)\) функция непрерывна.

п.3. Примеры

Пример 1.Найдите наименьшее и наибольшее значение функции y=tgx на заданном промежутке:

a) \(\left[\frac{2\pi}{3}; \frac{3\pi}{2}\right)\) $$ y_{min}=tg\left(\frac{2\pi}{3}\right)=-\sqrt{3},\ \ y_{max}=\lim_{x\rightarrow\frac{3\pi}{2}-0}tgx=+\infty $$ б) \(\left(\frac{\pi}{2}; \pi\right]\) $$ y_{min}=\lim_{x\rightarrow\frac{\pi}{2}+0}tgx=-\infty,\ \ y_{max}=tg(\pi)=0 $$ в) \(\left[\frac{3\pi}{4}; \frac{7\pi}{6}\right]\) $$ y_{min}=tg\left(\frac{3\pi}{4}\right)=-1,\ \ y_{max}=tg\left(\frac{7\pi}{6}\right)=\frac{1}{\sqrt{3}} $$

Пример 2. Решите уравнение:
a) \(tgx=-\sqrt{3}\)
Бесконечное множество решений: \(x=\frac{2\pi}{3}+\pi k,\ k\in\mathbb{Z}\)

б) \(tg\left(x-\frac\pi2\right)=0\)
\(x-\frac\pi2=\pi k\)
Бесконечное множество решений: \(x=\frac{\pi}{2}+\pi k,\ k\in\mathbb{Z}\)

в) \(tg(2x)=1\)
\(2x=\frac\pi4+\pi k\)
Бесконечное множество решений: \(x=\frac{\pi}{8}+\frac{\pi k}{2},\ k\in\mathbb{Z}\)

г) \(tg\left(\frac{x}{3}-1\right)=-1\)
\(\frac{x}{3}-1=-\frac{\pi}{4}+\pi k\)
\(\frac{x}{3}=1-\frac{\pi}{4}+\pi k\)
Бесконечное множество решений: \(x=3-\frac{3\pi}{4}+3\pi k,\ k\in\mathbb{Z}\)

Пример 3. 2+tgx\ne \left[ \begin{array} -y(x)\\ y(x) \end{array} \right. $$ Функция ни чётная, ни нечётная.

Пример 4. Если \(tg(7\pi-x)=\frac34\), то чему равны \(tgx,\ \ ctgx\)?
Т.к. период тангенса равен π, получаем: \begin{gather*} tg(7\pi-x)=tg(-x)=-tgx=\frac34\Rightarrow tgx=-\frac34\\ ctgx=\frac{1}{tgx}=-\frac43 \end{gather*} Ответ: \(-\frac34,\ \ -\frac43\)

TG Недвижимость — Отзывы и недвижимость на продажу

TG Недвижимость — Отзывы и недвижимость на продажу | ОценитьМойАгент

searchSearch

filter_hdrUnclaimed Profile

Познакомьтесь с командой

Познакомьтесь с 9 агентами TG Real Estate. Просмотреть профиль

Посмотреть профиль

Дэвид Фрай

Посмотреть профиль

Marci English

Посмотреть профиль

Michael Gaia

Посмотреть профиль

Вы TG Real Estate?

Вы TG Real Estate? Свяжитесь с нами по адресу help@ratemygent. com, и один из наших дружных коллективов поможет вам получить бесплатный профиль, запросить и получить первый отзыв.

О нас

TG Real Estate — агентство недвижимости. В настоящее время у них 24 активных объекта недвижимости и 195 проданных объектов недвижимости за последние 12 месяцев на сумму 30 405 998 долларов США .

Наши отзывы

3 отзыва в 3 разных местах, показывая 3.

звезда звезда звезда звезда звезда

25 дней назад дома моей матери. Она была очень профессиональна. Своевременно ответил на все наши вопросы. Помогли нам со всеми документами. Я настоятельно рекомендую всем, кто хочет купить или продать дом, позвонить Джинни.

Ginny Rudolphi

star   5   (3 отзыва)

star star star star star

12 месяцев назад

Работа с Джинни Р.

Очень профессионально, легко связаться, когда у нас возникали вопросы, и ответы были быстрыми. Продажа дома с момента выставления на продажу до закрытия была очень быстрой, с большим количеством хороших советов.

Джинни Рудольфи

star   5   (3 отзыва)

star star star star star star

более 1 года назад

Первоклассный риелтор

Знающий, честный и сделает все возможное, чтобы продать дом.

Брюс Шаффнер

звезда   5   (1 отзыв)

Наша недвижимость на продажу

TG Real Estate имеет 24 объекта в настоящее время для продажи, показывая 4.

Подробнее >

На продажу

9 0002 $159 900

819 Алмасы Drive

Campbell OH 44405

направления_автомобиль1

Джинни Рудольфи

звезда   5   (3 отзыва)

Подробнее >

Продажа

120 000 $

681 North Rd

Niles OH 44446

direction_car2

Rollin Gos ney

Подробнее >

На продажу

170 000 $

257 Apple St

Salem OH 44460

direction_car1

David Frye

Подробнее >

Продажа

449 999 $

14831 Robinson Rd

9 0002 Ньютон-Фолс, Огайо, 44444

direction_car4

Rollin Gosney

Показать все 24 свойства

Вы TG Real Estate?

Вы TG Real Estate? Свяжитесь с нами по адресу help@ratemygent.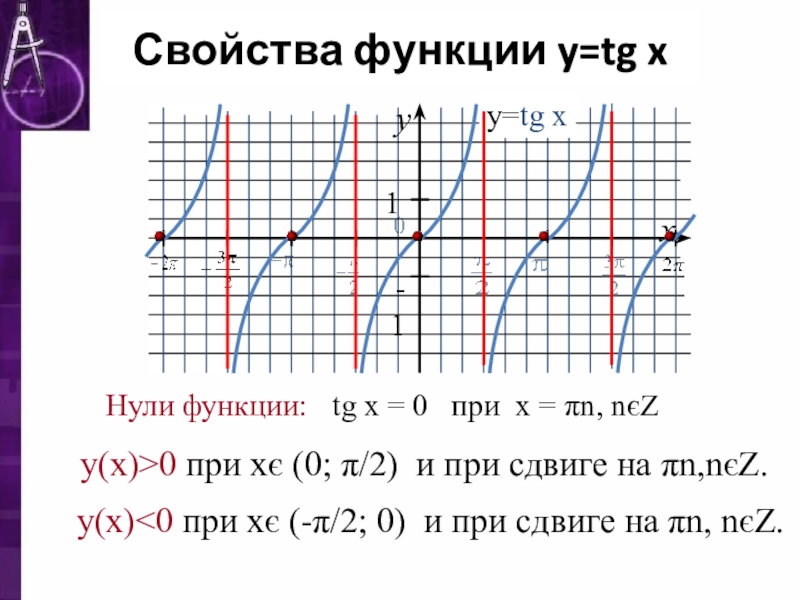 com, и один из наших дружных коллективов поможет вам получить бесплатный профиль, запросить и получить первый отзыв.

Связаться с TG Real Estate

Какая информация вам нужна?

Просмотр ближайших местоположений

Это физическое или юридическое лицо не заявило права на этот профиль. Несмотря на то, что этот профиль находится на RateMyAgent, это не означает, что они одобряют сайт, связаны с сайтом или подтверждают, что списки или данные о продажах, которые мы показываем о них, или любая другая общедоступная информация, являются точными в любом случае. . Подробнее

TG Real Estate

Отдел продаж:

+1 213-699-2001

Электронная почта:

[email protected]

Агент • Карта сайта

Заявленный профиль позволяет пользователю отвечать на отзывы. , попросите клиентов написать отзывы и многое другое. Любая компания может претендовать на свой профиль и попросить клиентов просмотреть его бесплатно.

Сывороточные свойства растительных стеролов и станолов снижать уровень ТГ связаны со снижением секреции ЛПОНП печенью

1. Ву Т., Фу Дж., Ян Ю., Чжан Л., Хан Дж. 2009. Влияние фитостеролов/станолов на липидный профиль крови: систематический обзор с метаанализом. Азия Пак. Дж. Клин. Нутр. 18: 179–186. [PubMed] [Google Scholar]

2. Бруфау Г., Канела М. А., Рафекас М. 2008. Фитостеролы: физиологические и метаболические аспекты, связанные со свойствами снижения уровня холестерина. Нутр. Рез. 28: 217–225. [PubMed] [Google Scholar]

3. Кальпе-Бердьель Л., Эскола-Хил Дж. К., Бланко-Вака Ф. 2009. Новое понимание молекулярного действия растительных стеролов и станолов на метаболизм холестерина. Атеросклероз. 203: 18–31. [PubMed] [Академия Google]

4. Де Смет Э., Менсинк Р. П., Плат Дж. 2012. Влияние растительных стеролов и станолов на метаболизм холестерина в кишечнике: предполагаемые механизмы от прошлого к настоящему. Мол. Нутр. Еда Рез. 56: 1058–1072. [PubMed] [Google Scholar]

5. Brufau G., Kuipers F., Lin Y., Trautwein E.A., Groen A.K. 2011. Переоценка механизма, с помощью которого растительные стеролы способствуют потере нейтральных стеролов у мышей. ПЛОС ОДИН. 6: е21576. [Бесплатная статья PMC] [PubMed] [Google Scholar]

6. Plat J., Brufau G., Dallinga-Thie G.M., Dasselaar M., Mensink R.P. 2009 г.. Растительный станоловый йогуртовый напиток сам по себе или в сочетании с низкими дозами статинов снижает сывороточный триацилглицерин и не-ЛПВП-холестерин у пациентов с метаболическим синдромом. Дж. Нутр. 139: 1143–1149. [PubMed] [Google Scholar]

7. Сиалвера Т. Э., Пунис Г. Д., Кутелидакис А. Э., Рихтер Д. Дж., Ифанти Г., Капсокефалу М., Гумас Г., Киотинис Н., Диамантопулос Э., Зампелас А. 2012. Добавка фитостеролов снижает уровни малых и плотных ЛПНП в плазме у пациентов с метаболическим синдромом, находящихся на диете западного типа. Нутр. Метаб. Кардиовас. Дис. 22: 843–848. [PubMed] [Академия Google]

8. Науманн Э., Плат Дж., Кестер А.Д., Менсинк Р.П. 2008. Исходный профиль липопротеинов сыворотки связан с индуцированными растительным станолом изменениями концентраций холестерина липопротеинов сыворотки и триацилглицерина. Варенье. Сб. Нутр. 27: 117–126. [PubMed] [Google Scholar]

9. Демонти И., Рас Р. Т., ван дер Кнаап Х. К., Мейер Л., Зок П. Л., Гелейнсе Дж. М., Траутвайн Э. А. 2013. Влияние растительных стеролов на концентрацию триглицеридов в сыворотке зависит от исходных концентраций: объединенный анализ 12 рандомизированных контролируемых исследований. Евро. Дж. Нутр. 52: 153–160. [Бесплатная статья PMC] [PubMed] [Google Scholar]

10. Райдаут Т. С., Хардинг С. В., Джонс П. Дж. 2010. Потребление растительных стеролов снижает уровень триглицеридов в плазме и печени и модулирует экспрессию генов, регулирующих уровень липидов, и липогенез de novo у мышей C57BL/6J. Мол. Нутр. Еда Рез. 54 (Приложение 1): S7–S13. [PubMed] [Google Scholar]

11. Emerging Risk Collaboration, E. Di Angelantonio, N. Sarwar, P. Perry, S. Kaptoge, K.K. Ray, A. Thompson, AM Wood, S. Lewington, N. Sattar , CJ Packard, R. Collins, SG Thompson и J. Danesh. 2009 г.. Основные липиды, аполипопротеины и риск сосудистых заболеваний. ДЖАМА. 302: 1993–2000 гг. [Бесплатная статья PMC] [PubMed] [Google Scholar]

12. Накадзима К., Накано Т., Токита Ю., Нагамин Т., Иназу А., Кобаяши Дж., Мабучи Х., Стэнхоуп К. Л., Гавел П. Дж., Окадзаки М. и др. 2011. Постпрандиальный метаболизм липопротеинов: ЛПОНП против хиломикронов. клин. Чим. Акта. 412: 1306–1318. [Бесплатная статья PMC] [PubMed] [Google Scholar]

13. Джексон К.Г., Уолден С.М., Мюррей П., Смит А.М., Лавгроув Дж.А., Минихейн А.М., Уильямс С.М. 2012. Последовательная двухразовая провокационная провокация выявляет аномалии постпрандиальных ТАГ, но не глюкозы у мужчин с увеличением числа компонентов метаболического синдрома. Атеросклероз. 220: 237–243. [PubMed] [Академия Google]

14. Нордестгард Б.Г., Бенн М., Шнохр П., Тибьерг-Хансен А. 2007. Триглицериды не натощак и риск инфаркта миокарда, ишемической болезни сердца и смерти у мужчин и женщин. ДЖАМА. 298: 299–308. [PubMed] [Google Scholar]

15. Блай Э. Г., Дайер В. Дж. 1959. Экспресс-метод экстракции и очистки общих липидов. Может. Дж. Биохим. Физиол. 37: 911–917. [PubMed] [Google Scholar]

16. Gautier T., Tietge U. J., Boverhof R., Perton F. G., Le Guern N., Masson D., Rensen P. C., Havekes L. M., Lagrost L., Kuipers F. 2007. Накопление липидов в печени у мышей с дефицитом аполипопротеина C-I усиливается белком-переносчиком эфира холестерина. Дж. Липид Рез. 48: 30–40. [PubMed] [Академия Google]

17. Грефхорст А., Эльзинга Б. М., Вошол П. Дж., Плош Т., Кок Т., Блокс В. В., ван дер Слуйс Ф. Х., Хавекес Л. М., Ромейн Дж. А., Веркаде Х. Дж. и др. 2002. Стимуляция липогенеза путем фармакологической активации Х-рецептора печени приводит к продукции больших, богатых триглицеридами частиц липопротеинов очень низкой плотности. Дж. Биол. хим. 277: 34182–34190. [PubMed] [Google Scholar]

18. Плош Т., Блокс В. В., Баллер Дж. Ф., Хавинга Р., Веркаде Х. Дж., Янсен П. Л., Койперс Ф. 2002. Mdr P-гликопротеины не являются существенными для экскреции с желчью гидрофобного предшественника гема протопорфирина в мышиной модели эритропоэтической протопорфирии, индуцированной гризеофульвином. Гепатология. 35:299–306. [PubMed] [Google Scholar]

19. Стрикер Д. 2008. BrightStat.com: бесплатная статистика онлайн. вычисл. Методы Программы Биомед. 92: 135–143. [PubMed] [Google Scholar]

20. Отман Р. А., Могадасян М. Х. 2011. Помимо эффектов растительных стеролов, снижающих уровень холестерина: клинические и экспериментальные доказательства противовоспалительных свойств. Нутр. преп. 69: 371–382. [PubMed] [Google Scholar]

21. Грефхорст А., Паркс Э. Дж. 2009. Уменьшение инсулин-опосредованного ингибирования секреции ЛПОНП при фармакологической активации Х-рецептора печени у мышей. Дж. Липид Рез. 50: 1374–1383. [Бесплатная статья PMC] [PubMed] [Google Scholar]

22. Ким Д. Х., Чжан Т., Рингквист С., Донг Х. Х. 2011. Ориентация на FoxO1 при гипертриглицеридемии. Курс. Цели для наркотиков. 12: 1245–1255. [PubMed] [Google Scholar]

23. Рахшандеру М., Кнох Б., Мюллер М., Керстен С. 2010. Гены-мишени альфа-рецептора, активируемого пролифератором пероксисом. ППАР рез. 2010 Эп. 26 сентября 2010 г. 10.1155/2010/612089. [Бесплатная статья PMC] [PubMed] [Google Scholar]

24. Plösch T., Kruit J.K., Bloks V.W., Huijkman N.C., Havega R., Duchateau G.S., Lin Y., Kuipers F. 2006. Снижение всасывания холестерина растительными стеролами и станолами в рационе мышей не зависит от транспортера Abcg5/8. Дж. Нутр. 136: 2135–2140. [PubMed] [Академия Google]

25. Кальпе-Бердьель Л., Эскола-Хил Х. К., Рибас В., Наварро-Састре А., Гарсес-Гарсес Х., Бланко-Вака Ф. 2005. Изменения глобальной экспрессии генов кишечника и печени в ответ на диету, обогащенную фитостеролом. Атеросклероз. 181: 75–85. [PubMed] [Google Scholar]

26. Фольгер О. Л., ван дер Бум Х. , де Вит Э. К., ван Дайвенвоорде В., Хорнстра Г., Плат Дж., Хавекес Л. М., Менсинк Р. П., Принсен Х. М. 2001. Диетические эфиры растительных станолов снижают секрецию холестерина ЛПОНП и насыщение желчи у трансгенных мышей с аполипопротеином E*3-Leiden. Артериосклероз. тромб. Васк. биол. 21: 1046–1052. [PubMed] [Академия Google]

27. Остлунд Р. Э. мл. 2002. Фитостеролы в питании человека. Анну. Преподобный Нутр. 22: 533–549. [PubMed] [Google Scholar]

28. Гиббонс Г. Ф., Виггинс Д., Браун А. М., Хеббачи А. М. 2004. Синтез и функция печеночных липопротеинов очень низкой плотности. Биохим. соц. Транс. 32: 59–64. [PubMed] [Google Scholar]

29. Adiels M., Taskinen M.R., Packard C., Caslake M.J., Soro-Paavonen A., Westerbacka J., Vehkavaara S., Hakkinen A., Olofsson S.O., Yki-Jarvinen H. ., и другие. 2006. Перепроизводство крупных частиц ЛПОНП обусловлено повышенным содержанием жира в печени у человека. Диабетология. 49: 755–765. [PubMed] [Google Scholar]

30. Матикайнен Н. , Таскинен М. Р., Стеннабб С., Лундбом Н., Хаккараинен А., Вааралахти К., Райвио Т. 2012. Снижение циркулирующего фактора роста фибробластов 21 после оральной жировой нагрузки связано с постпрандиальными липопротеинами, богатыми триглицеридами, и жиром печени. Евро. Дж. Эндокринол. 166: 487–492. [PubMed] [Google Scholar]

31. Wiegman C. H., Bandsma R. H., Ouwens M., van der Sluijs F. H., Havega R., Boer T., Reijngoud D. J., Romijn J. A., Kuipers F. 2003. Продукция ЛПОНП в печени у мышей ob/ob не стимулируется массивным липогенезом de novo, но менее чувствительна к подавляющему действию инсулина. Диабет. 52: 1081–1089. [PubMed] [Google Scholar]

32. Грефхорст А., Хекстра Дж., Деркс Т. Г., Оуэнс Д. М., Баллер Дж. Ф., Хавинга Р., Хавекес Л. М., Ромейн Дж. А., Куйперс Ф. 2005. Острый стеатоз печени у мышей за счет блокирования бета-окисления не снижает чувствительности к инсулину выработки липопротеинов очень низкой плотности. Являюсь. Дж. Физиол. Гастроинтест. Физиол печени. 289: Г592–Г598. [PubMed] [Google Scholar]

33. van Diepen J. A., Vroegrijk I. O., Berbee J. F., Shoelson S. E., Romijn J. A., Havekes L. M., Rensen P. C., Voshol P. J. 2011. Аспирин снижает гипертриглицеридемию за счет снижения выработки триглицеридов ЛПОНП у мышей, получавших диету с высоким содержанием жиров. Являюсь. Дж. Физиол. Эндокринол. Метаб. 301: Е1099–E1107. [Бесплатная статья PMC] [PubMed] [Google Scholar]

34. Oosterveer M.H., Grefhorst A., Groen A.K., Kuipers F. 2010. Рецептор X печени: контроль гомеостаза клеточных липидов и не только. Значение для дизайна лекарств. прог. Липид Рез. 49: 343–352. [PubMed] [Google Scholar]

35. Basciano H., Miller A., ​​Baker C., Naples M., Adeli K. 2009. Активация LXRальфа нарушает печеночную передачу сигналов инсулина и стимулирует выработку липопротеинов, содержащих аполипопротеин В. Являюсь. Дж. Физиол. Гастроинтест. Физиол печени. 297: Г323–Г332. [PubMed] [Google Scholar]

36. Zhou J., Febbraio M., Wada T. , Zhai Y., Kuruba R., He J., Lee J.H., Khadem S., Ren S., Li S., и другие. 2008. Печеночный переносчик жирных кислот Cd36 является общей мишенью для LXR, PXR и PPARgamma в развитии стеатоза. Гастроэнтерология. 134: 556–567. [PubMed] [Google Scholar]

37. Koonen D. P., Jacobs R. L., Febbraio M., Young M. E., Soltys C. L., Ong H., Vance D. E., Dyck J. R. 2007. Повышенная экспрессия CD36 в печени способствует дислипидемии, связанной с ожирением, вызванным диетой. Диабет. 56: 2863–2871. [PubMed] [Академия Google]

38. VerHague M.A., Cheng D., Weinberg R.B., Shelness G.S. 2013. Экспрессия аполипопротеина A-IV в печени мышей усиливает секрецию триглицеридов и снижает содержание липидов в печени, способствуя расширению частиц липопротеинов очень низкой плотности. Артериосклероз. тромб. Васк. биол. 33: 2501–2508. [PubMed] [Google Scholar]

39. Ван дер Вин Дж. Н., Хавинга Р., Блокс В. В., Гроен А. К., Койперс Ф. 2007. Кормление холестерином сильно снижает выработку триглицеридов ЛПОНП в печени у мышей, у которых отсутствует альфа-рецептор Х печени.