Свойства и типы соответствий — Студопедия
Виды соответствий
Соответствие называется всюду определенным на множестве X, если:
а) , то есть: : у=f(x), или на «языке» полного образа элемента;
б) , или на «языке» графов;
в) из каждого элемента множества X выходит стрелка и приходит в Y.
Соответствие называют сюръективным, если:
а) , то есть : хfу ⇔ у=f(x), или на языке полного прообраза;
б) , или на «языке» графов;
в) в каждый элемент множества Y приходит стрелка из X.
Если f — всюду определенно на X, то f -1 — сюръективное соответствие Y на X, если f — сюрьективно, то f -1 всюду определенно на Y.
Соответствие f называют функциональным, если:
а) R(x) содержит не более одного элемента, то есть ;
б) на языке графов это означает, что из каждого элемента множества 
Соответствие f называется инъективным, если:
а) содержит неболее одного элемента, то есть ;
б) на «языке» графов это означает, что в каждый элемент множества Y приходит не более одной стрелки.
Из этих определений следует, что соответствие, обратное функциональному, — инъективно, а обратное инъективному — функционально.
Если f и g — всюду определенные, функциональные, инъективные и сюръективные соответствия, то — тоже будет обладать всеми этими свойствами.
П р и м е р 1: Соответствие на рисунке
а) не всюду определено;
б) функционально;
в) инъективно;
г) сюръективно.
П р и м е р 2: Пусть X — множество студентов в аудитории. Y — множество стульев. Зададим соответствие x f y «студент x сидит на стуле y».
Это соответствие будет:
а) всюду определенным, если каждый студент будет сидеть;
б) сюрьективным, если все стулья заняты;
в) функциональным, если каждый студент не сидит на двух стульях;
г) инъективным, если на каждом стуле не сидят два студента.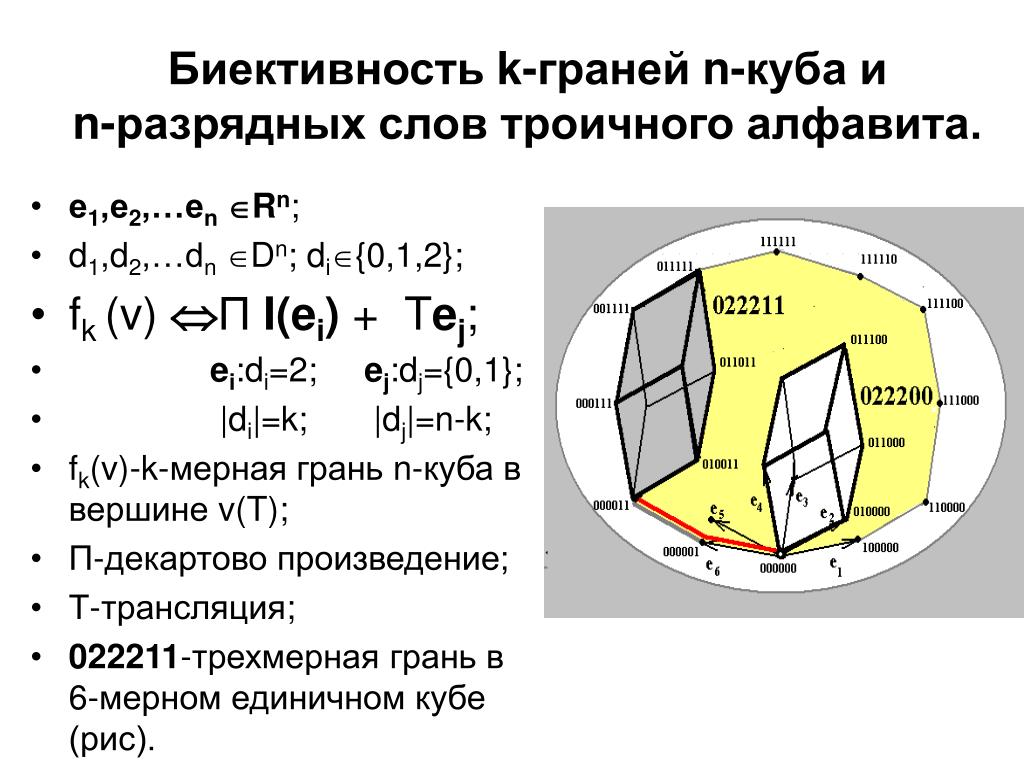
П р и м е р 3: Пусть х f у (у = sin х), X = R, Y = R. Тогда графиком этого соответствия будет синусоида:
Соответствие это будет:
а) всюду определено, так как : (у = sin х) (любая прямая, параллельная оси ОY, пересекает график функции хотя бы в одной точке).
б) функционально, так как состоит из одного элемента (любая прямая, параллельная оси ОУ, пересекает график функции в единственной точке).
в) не инъективно, так как , для которых R -1(у) состоит более чем из одного элемента (существуют прямые, параллельные оси ОХ, которые пересекают график множество раз).
г) не сюръективно, так как , для которых не существует х: у=sinx (существуют прямые, параллельные оси ОХ, которые не пересекают график ни в одной точке).
Рассмотренные выше свойства соответствий (инъективность, сюръективностъ и т.п.) позволяют классифицировать все соответствия на определенные типы.
Приведем классификацию соответствий по свойствам в виде таблицы:
| Функциональность | Всюду определенность | Инъективность | Сюръективность | Название |
| + | Функция типа | |||
| + | + | Отображение из X в Y | ||
| + | + | + | Вложение(инъекция) X в Y | |
| + | + | + | Наложение (сюръекция) X на Y | |
| + | + | + | + | Биекция X на Y |
Из этой таблицы видно, например, что отображение — это всюду определенное функциональное соответствие.
П р и м е р 4: Отображение сюръективно и инъективно, так как: из того, что
и . Следовательно, соответствие — биекция.
Понятие об отображении. Образ и прообраз, биекция
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас.
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Часть 4 Тема 1
Понятие об отображении
Образ и прообраз, биекция
1. Определение отображения
В этом видео
2. Понятие об образе и
прообразе
3. Инъективность,
сюръективность и
биективность
Отображением множества во
множество называется некоторое
правило , при котором каждому
элементу соответствует один и
только один элемент .
Понятие об образе и
прообразе
Образ и прообраз
Свойства образа
Образ и прообраз
Свойства прообраза
Пример отображения
Инъективность, сюръективность и
биективность отображений
Инъекция — отображение , при
котором
Table Y
Table X
1
1
2
4
1
1
2
3
4
5
6
Инъекция — отображение , при
котором
Table f
1
1
2
3
4
1
3
5
6
1
Сюръекция — отображение , при
котором
Table Y
Table X
1
1
2
3
4
1
3
5
1
Сюръекция — отображение f, при
котором
Table f
1
1
2
3
4
1
3
5
5
*
Биекция — отображение
одновременно являющееся
инъекцией и сюръекцией
Table Y
Table X
1
1
2
3
4
1
1
3
6
5
Биекция — отображение
одновременно являющееся
инъекцией и сюръекцией
Table f
1
1
2
3
4
1
3
6
5
1
1.
Сформировано понятие обИтоги
отображении, образе и
прообразе
2. Закреплено понятие о
биекции отображения
Часть 4 Тема 1
Функция и ее предел
Определение и свойства функций
В этом видео
преобразовании и функции
2. Определения предела
функции
3. Виды пределов
Функцией называется множество
упорядоченных пар
, таких,
что пары существуют для всех
элементов множества , и, если
первые элементы пар совпадают, то
совпадают и вторые их элементы.
1. — область задания (определения) функции
2. — область значений функции
3. Множество всех элементов
, называется
множеством значений функции
4. Множество упорядоченных пар
функции
называется также графиком
Оператор — ставит функцию в
соответствие другой функции
Преобразование — оператор,
изменяющий аргумент функции.
Предел функции (по Коши)
Предел функции (по Гейне)
Односторонние пределы —
предел справа и предел слева
Предел на бесконечности —
предел функции при стремлении
аргумента к бесконечности
Бесконечный предел — предел
функции, равный бесконечности
Примеры нахождения пределов
1.
Сформировано определениефункции, отделено от
оператора и преобразования
Итоги
2. Дано два равноправных
определения предела
функции
3. Изучены виды пределов,
разобраны примеры
Часть 4 Тема 3
Свойства функции
Математический анализ функции
1. Описания множеств задания
В этом видео
и значений
2. Особые точки
3. Виды поведения функции
Область задания
(область определения)
Примеры
Область значений
Примеры
Нули функции
Непрерывность
Промежутки знакопостоянства
Монотонность
1)Убывание на
:
1)Невозрастание на
:
Монотонность
3)Неубывание на
:
3)Возрастание на
:
3)Стационарная на
неубывающая на
— невозрастающая и
Четность функции
Нечетность функции
Ограниченность функции
сверху:
снизу:
Периодичность
1. Изучены свойства функций.
2. Даны определения
непрерывности,
монотонности,
периодичности,
знакопостоянства и
ограниченности функции.
English Русский Правила
Математика | Классы (инъективные, сюръективные, биективные) функций
- Написать интервью
- Математика | Введение в теорию множеств
- Математика | Операции над множествами (теория множеств)
- Включение-исключение и их различные приложения
- Математика | Степенной набор и его свойства
- Математика | Частичные порядки и решетки
- Математика | Алгебраическая структура
- Математика | Введение и типы отношений
- Дискретная математика | Представление отношений
- Математика | Представления матриц и графов в отношениях
- Математика | Замыкание отношений и отношений эквивалентности
- Количество возможных отношений эквивалентности на конечном множестве
- Математика | Классы (инъективные, сюръективные, биективные) функций
- Математика | Общее количество возможных функций
- Дискретная математика | Генерирующие функции — введение и предпосылки
- Математика | Генерирующие функции – Набор 2
- Математика | Последовательность, ряд и суммирование
- Математика | Независимые множества, покрытие и сопоставление
- Математика | Введение в доказательства
- Дискретная математика | Диаграммы Хассе
- Введение в преобразование Можетта
- Математика | Кольца, области целостности и поля
Написать статью
Логика высказываний и первого порядка
Теория множеств
Комбинаторика
Теория графов
Линейная алгебра
Вероятность
Исчисление
Практические вопросы по математике
Вопросы по математике GATE
Улучшить статью
Сохранить статью
- Уровень сложности: Easy
- Последнее обновление: 04 апр, 2019
Улучшить статью
Сохранить статью
Функция f из A в B является присвоением ровно одного элемента B каждому элементу A (A и B непустые множества). A называется доменом f, а B называется со-доменом f. Если b — уникальный элемент B, назначенный функцией f элементу a множества A, он записывается как f(a) = b. f отображает A в B. означает, что f является функцией от A до B, она записывается как
Термины, относящиеся к функциям:
- Домен и совместный домен – если f является функцией из набора A в набор B, то A называется доменом, а B называется совместным доменом.
- Диапазон — Диапазон f — это набор всех изображений элементов A. В основном Range — это подмножество ко-домена.
- Изображение и прообраз – b является изображением a, а a является прообразом b, если f(a) = b.
Свойства функции:
- Сложение и умножение: пусть f1 и f2 две функции от A до B, тогда f1 + f2 и f1.f2 определяются как-:
f1+f2(x) = f1(x) + f2(x ). (дополнение)
f1f2(x) = f1(x) f2(x).
(умножение) - Равенство: Две функции равны только тогда, когда они имеют один и тот же домен, один и тот же содомен и одинаковые элементы отображения из домена в содомен.
Типы функций:
- Функция «один к одному» (вводная): Функция называется взаимно однозначной, если для всех элементов a и b в A, если f(a) = f(b), то должно быть так, что a = b. Он никогда не сопоставляет отдельные элементы своего домена с одним и тем же элементом своего содомена .
Мы можем выразить, что f является взаимно однозначным, используя кванторы как или эквивалентно , где вселенная дискурса является доменом функции.
- Онто-функция (сюръективно): Если каждому элементу b в B соответствует элемент a в A такой, что f(a) = b. Не требуется, чтобы a был уникальным; Функция f может отображать один или несколько элементов A в один и тот же элемент B.
- Функция соответствия «один к одному» (биективная/обратимая): Функция является биективной, если она является одновременно взаимно однозначной и на функцию.
- Обратные функции: Функция биекции также известна как обратимая функция, потому что она обладает свойством обратной функции. Обратная биекция f обозначается как f -1 . Это функция, которая присваивает b уникальный элемент a такой, что f(a) = b. следовательно, f -1 (b) = a.
Некоторые полезные функции -:
Строго возрастающие и строго убывающие функции: Функция f строго возрастает, если f(x) > f(y), когда x>y. Функция f строго убывает, если f(x) < f(y), когда x Возрастающие и убывающие функции: Функция f возрастает, если f(x) ≥ f(y), когда x>y. Функция f убывает, если f(x) ≤ f(y) при x Композиция функций: пусть g будет функцией от B до C, а f будет функцией от A до B, композицией f и g, которая обозначается как туман(a)=f(g(a)). Свойства функциональной композиции: Некоторые важные моменты: Статьи по теме Что нового Мы используем файлы cookie, чтобы обеспечить вам максимальное удобство просмотра нашего веб-сайта. Используя наш сайт, вы
подтверждаете, что вы прочитали и поняли наши Политика в отношении файлов cookie & Политика конфиденциальности Прежде чем впадать в панику по поводу «страшности» трех слов, которыми назван этот урок, давайте вспомним, что терминологии нечего бояться — все, что она означает, это то, что у нас есть что-то новое учить! Как вы увидите к концу этого урока, эти три слова на самом деле совсем не страшны. У математиков есть забавный способ приписывать очень причудливые слова не очень глубоким идеям, и это один из таких примеров. Поэтому давайте продолжим и просто узнаем, что означают эти слова. На предыдущем уроке мы узнали о функциях между наборами, что дало нам механизм связи элементов одного набора с элементами другого набора (хотя этот «другой» набор может быть самим набором: например, если , то функция f из A в A такая, что является совершенно хорошей функцией, как и функция g из A в A такая, что Мы помним, что функция является невероятно общим объектом: все, что нужно, это два множества и отношение между ними такой, что в одном из двух наборов есть каждый его элемент связан с ровно одним элементом в другом наборе. Вот и все. Других требований к функциям не было. В частности, если (напомним, что это читается как «если f — функция из множества A в множество B»), то f может быть таким, что оно отправляет каждый элемент в A в 90 251 один и тот же 90 252 элемент в B. Также не было Нет никаких требований к тому, сколько элементов в B должно быть «вызвано» функцией. Функция — это просто правило, которое присваивает каждому элементу A ровно один элемент B, а любое другое свойство, которым обладает функция, — это просто бонус. Однако универсальность функций имеет свою цену. Цена заключается в том, что очень трудно что-то доказать об общей функции просто потому, что ее общность означает, что у нас очень мало структуры для работы. Таким образом, мы хотим сосредоточиться на определенных видах функций. То есть мы хотим ограничиться рассмотрением функций, обладающих определенными свойствами, чтобы мы могли использовать эти новые свойства для доказательства. На самом деле это очень общий шаблон в математике: мы определяем какой-то очень общий объект (множество, функцию или что-то еще), а затем медленно начинаем «добавлять структуру» к нему, чтобы мы могли что-то доказать. Итак, какой тип «специальных функций» мы хотим здесь рассмотреть? Давайте рассмотрим, что такое функция, и спросим, какими «наиболее очевидными» свойствами мы хотели бы обладать у некоторых функций. В оставшейся части этого урока пусть («пусть f будет функцией от множества A до множества B). Во-первых, вспомним, что f может отправить два разных элемента из A в один и тот же элемент из B. Например, если и , то функция, определяемая как , является совершенно хорошей функцией, несмотря на то, что и кошка, и собака отправляются к сыру. Предположим, однако, что f — функция, которая не имеет это свойство ни для каких элементов в A. А именно, предположим, что f не переводит никакие два различных элемента в A в один и тот же элемент B. Пусть A — набор мальчиков, B — набор девочек, и пусть f — функция «школьного танца». А именно, пусть f будет функцией, которая назначает мальчиков из A танцевать с девочками из B. Если бы f была просто какой-то старой функцией, то мог бы быть случай, когда все мальчики танцуют с одной и той же девочкой (конечно, неприятный опыт). ), или может быть так, что пять мальчиков танцуют с одной девочкой, а остальные мальчики танцуют с какой-то другой девочкой (все равно довольно неудобно). Но предположим, что каждому мальчику было назначено разных девочек, чтобы ни одна девушка не танцевала более чем с одним мальчиком. Тогда эта функция была бы инъективной. В этом примере становится очевидным одно важное качество инъективных функций, которое важно для нас при строгом определении инъективной функции. Предположим, вы сказали мне, что функция, которая связывает мальчиков с девочками, является инъективной, и предположим, что вы также сказали мне, что «мальчик 1» танцевал с «девочкой 17» и что «мальчик 56» также танцевал с «девочкой 17». Определение 7.1 Пусть будет функция из множества A в множество B. Тогда f равно инъективный если для любых элементов a и b в A следует, что . // Говоря менее формально, это определение говорит нам, что функция определена как инъективная , если в любой момент два элемента в A передаются одному и тому же элементу в B, они должны фактически быть одними и теми же элементами в A для начинать с! Давайте теперь еще раз вспомним школьный танец. Даже если функция инъективна, не обязательно у каждой девушки есть мальчик, с которым можно танцевать. Обратите внимание, что сюръективность ничего не говорит о сколько мальчиков танцует с определенной девочкой, а только то, что с каждой девочкой хотя бы один танцующий мальчик. Определение 7.2 Пусть . Тогда f называется сюръективным , если для каждого элемента b в B существует некоторый элемент a в A такой, что . // Проще говоря, это просто означает, что мы определяем функцию как сюръективную, если для каждого элемента в ее кодовом домене (помните «кодовой домен» из предыдущего урока?) мы можем найти какой-либо элемент в его домене, который будет отправлен к этому. Может случиться так, что в ее области есть несколько различных элементов, которые мы могли бы найти, но пока мы всегда можем найти один, мы называем функцию сюръективной. Мы заканчиваем этот урок определением, которое мы в конечном итоге изучим намного больше на следующем уроке. Учитывая то, что мы определили до сих пор, на самом деле это очень очевидное определение. Определение 7.3 Пусть . Тогда f называется биективным , если оно одновременно инъективное и сюръективное. // Обратите внимание, что это определение имеет смысл. Другими словами, мы видели, что у нас могут быть функции, которые являются инъективными и не сюръективными (если девочек больше, чем мальчиков), и у нас могут быть функции, которые являются сюръективными, но не инъективными (если мальчиков больше, чем девочек, то мы должны были отправить более одного мальчика хотя бы к одной из девочек). Таким образом, мы дополнительно ограничиваемся рассмотрением биективных функций. То есть класс биективных функций «меньше» класса инъективных функций, а также он меньше класса сюръективных. Более того, класс инъективных функций и класс сюръективных функций меньше, чем класс всех общих функций.
Эта статья предоставлена Nitika Bansal Урок 7: Инъективное, Сюръективное, Биективное
Под «добавлением структуры» я просто подразумеваю, что мы наделяем объект определенными дополнительными свойствами, так что, хотя он и теряет часть своей общности, он приобретает определенную структуру, которая позволяет нам задавать более интересные вопросы о нем. Тогда мы назвали бы эту функцию инъективной . Давайте посмотрим пример. Тогда я бы немедленно знаю, что мальчик 1 и мальчик 56 на самом деле являются одним и тем же человеком (один и тот же элемент множества), потому что я знаю, что никакие два разных мальчика не танцуют с одной и той же девушкой (потому что вы сказали мне, что функция инъективна). Таким образом, инъективная функция — это такая функция, что если a — элемент в A, а b — элемент в A, и (f отправляет их к одному и тому же элементу в B), то a=b! Поэтому давайте сделаем это определение: А именно, девочек может быть больше, чем мальчиков. В этом случае, даже если только одному мальчику будет поручено танцевать с любой данной девушкой, все равно останутся девочки. Ситуация, конечно, хуже, если нескольким мальчикам разрешается танцевать с одной и той же девушкой (т. е. если функция не инъективна). Но предположим, что — это достаточное количество мальчиков, чтобы у каждой девочки был партнер по танцам. Это все еще не обязательно означает, что у каждой девочки будет партнер по танцу, потому что мы могли бы, например, назначить всех мальчиков танцевать с одной и той же девочкой (оставив всех остальных без партнеров). Если, однако, мы распределили мальчиков таким образом, что каждая девочка имела партнера по танцу (возможно, более одного), то функция называется сюръективной . Если бы было 10 мальчиков (обозначенных «мальчик 1», «мальчик 2» и т. д.) и 4 девочки (обозначенных аналогичным образом), то мы могли бы поручить мальчикам 1–7 танцевать с девочкой 1, а затем мальчику 8 танцевать. с девочкой 2, мальчиком 9 с девочкой 3 и мальчиком 10 с девочкой 4. Тогда у каждой девушки есть партнер, несмотря на то, что их у них очень разное количество. Теперь у нас достаточно, чтобы дать следующее определение: