Т критерий стьюдента автоматический расчет. Основные статистики и t-критерий Стьюдента
Наступила осень, а значит, настало время для запуска нового тематического проекта «Статистический анализ с R». В нем мы рассмотрим статистические методы с точки зрения их применения на практике: узнаем какие методы существуют, в каких случаях и каким образом их проводить в . На мой взгляд, Критерий Стьюдента или t-тест (от англ. t-test) идеально подходит в качестве введения в мир статистического анализа. Тест Стьюдента достаточно прост и показателен, а также требует минимум базовых знаний в статистике, с которыми читатель может ознакомиться в ходе прочтения этой статьи.
Примечание_1: здесь и в других статьях Вы не увидите формул и математических объяснений, т.к. информация рассчитана на студентов естественных и гуманитарных специальностей, которые делают лишь первые шаги в стат. анализе.
Что такое t-тест и в каких случаях его стоит применять
В начале следует сказать, что в статистике зачастую действует принцип бритвы Оккамы , который гласит, что нет смысла проводить сложный статистический анализ, если можно применить более простой (не стоит резать хлеб бензопилой, если есть нож).
Любопытно, что создал этот метод Уильямом Госсет — химик, приглашенный работать на фабрику Guinness. Разработанный им тест служил изначально для оценки качества пива. Однако, химикам фабрики запрещалось независимо публиковать научные работы под своим именем. Поэтому в 1908 году Уильям опубликовал свою статью в журнале «Biometrika» под псевдонимом «Стьюдент». Позже, выдающийся математик и статистик Рональд Фишер доработал метод, который затем получил массовое распространение под названием Student»s t-test.
Критерий Стьюдента (t-тест) — это статистический метод, который позволяет сравнивать средние значения двух выборок и на основе результатов теста делать заключение о том, различаются ли они друг от друга статистически или нет. Если Вы хотите узнать, отличается ли средний уровень продолжительности жизни в Вашем регионе от среднего уровня по стране; сравнить урожайность картофеля в разных районах; или изменяется ли кровяное давление до и после употребления нового лекарства, то t-тест может быть Вам полезен. Почему может быть? Потому что для его проведения, необходимо, чтобы данные выборок имели распределение близкое к нормальному.
Для этого существуют методы оценки, которые позволяют сказать, допустимо ли в данном случае полагать, что данные распределены нормально или нет. Поговорим об этом подробнее.
Почему может быть? Потому что для его проведения, необходимо, чтобы данные выборок имели распределение близкое к нормальному.
Для этого существуют методы оценки, которые позволяют сказать, допустимо ли в данном случае полагать, что данные распределены нормально или нет. Поговорим об этом подробнее.
Нормальное распределение данных и методы его оценки qqplot и shapiro.test
Нормальное распределение данных характерно для количественных данных, на распределение которых влияет множество факторов, либо оно случайно. Нормальное распределение характеризуется несколькими особенностями:
- Оно всегда симметрично и имеет форму колокола.
- Значения среднего и медианы совпадают.
- В пределах одного стандартного отклонения в обе стороны лежат 68.2% всех данных, в пределах двух — 95,5%, в пределах трех — 99,7%
Давайте создадим случайную выборку с нормальным распределением на , где общее количество измерений = 100, среднее арифметическое = 5, а стандартное отклонение = 1. Затем отобразим его на графике в виде гистограммы:
Затем отобразим его на графике в виде гистограммы:
mydata Ваш график может слегка отличаться от моего, так как числа сгенерированы случайным образом. Как Вы видите, данные не идеально симметричны, но кажется сохраняют форму нормального распределения. Однако, мы воспользуемся более объективными методами определения нормальности данных.
Одним из наиболее простых тестов нормальности является график квантилей (qqplot) . Суть теста проста: если данные имеют нормальное распределение, то они не должны сильно отклоняться от линии теоретических квантилей и выходить за пределы доверительных интервалов. Давайте проделаем этот тест в R.
пакета «car» в среду R qqPlot(mydata) #запустим тест
Как видно из графика, наши данные не имеют серьезных отклонений от теоретического нормального распределения. Но порой при помощи qqplot невозможно дать однозначный ответ. В этом случае следует использовать тест Шапиро-Уилка , который основан на нулевой гипотезе, что наши данные распределены нормально.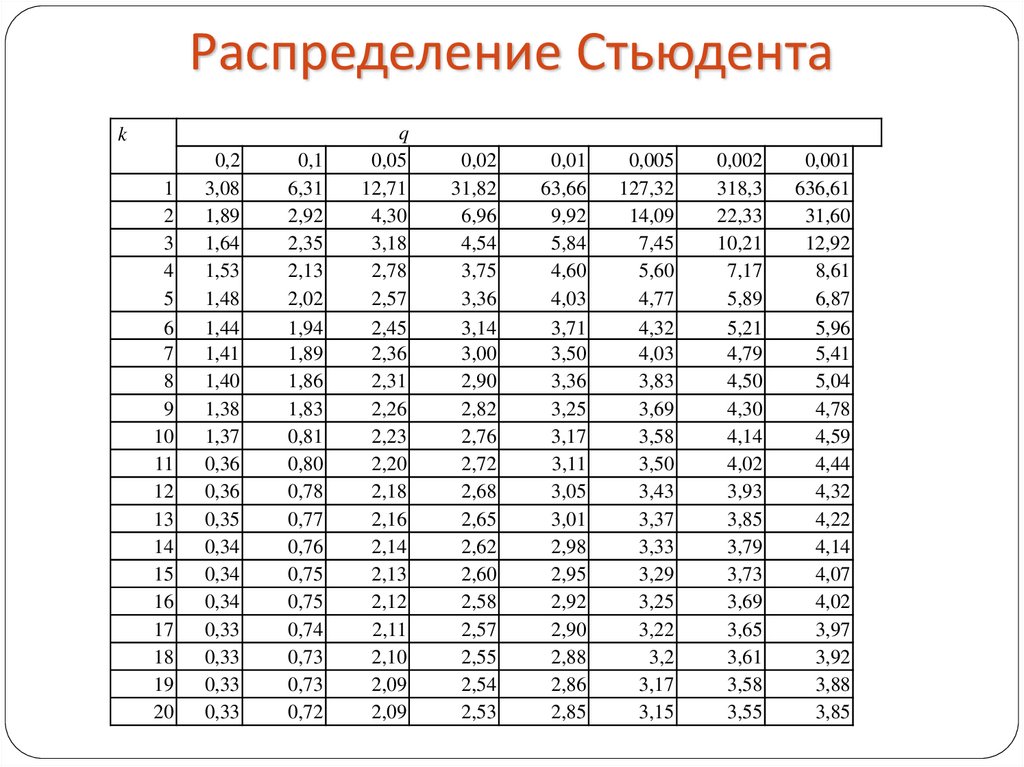 Если же P-значение менее 0.05 (p-value
Если же P-значение менее 0.05 (p-value
Провести тест Шапиро-Уилка в R не составит труда. Для этого нужно всего лишь вызвать функцию shapiro.test, и в скобках вставить имя ваших данных. В нашем случае p-value должен быть значительно больше 0.05, что не позволяет отвергнуть нулевую гипотезу о том, что наши данные распределены нормально.
Запускаем t-тест Стьюдента в среде R
Итак, если данные из выборок имеют нормальное распределение, можно смело приступать к сравнению средних этих выборок. Существует три основных типа t-теста, которые применяются в различных ситуациях. Рассмотрим каждый из них с использованием наглядных примеров.
Одновыборочный критерий Стьюдента (one-sample t-test)
Одновыборочный t-тест следует выбирать, если Вы сравниваете выборку с общеизвестным средним.
Например, отличается ли средний возраст жителей Северо-Кавказского Федерального округа от общего по России. Существует мнение, что климат Кавказа и культурные особенности населяющих его народов способствуют продлению жизни. Для того, чтобы проверить эту гипотезу, мы возьмем данные РосСтата (таблицы среднего ожидаемого продолжительности жизни по регионам России) и применим одновыборочный критерий Стьюдента. Так как критерий Стьюдента основан на проверке статистических гипотез, то за нулевую гипотезу будем принимать то, что различий между средним ожидаемым уровнем продолжительности по России и республикам Северного Кавказа нет. Если различия существуют, то для того, чтобы считать их статистически значимыми p-value должно быть менее 0.05 (логика та же, что и в вышеописанном тесте Шапиро-Уилка).
Для того, чтобы проверить эту гипотезу, мы возьмем данные РосСтата (таблицы среднего ожидаемого продолжительности жизни по регионам России) и применим одновыборочный критерий Стьюдента. Так как критерий Стьюдента основан на проверке статистических гипотез, то за нулевую гипотезу будем принимать то, что различий между средним ожидаемым уровнем продолжительности по России и республикам Северного Кавказа нет. Если различия существуют, то для того, чтобы считать их статистически значимыми p-value должно быть менее 0.05 (логика та же, что и в вышеописанном тесте Шапиро-Уилка).
Загрузим данные в R. Для этого, создадим вектор со средними значениями по республикам Кавказа (включая Адыгею). Затем, запустим одновыборочный t-тест, указав в параметре mu среднее значение ожидаемого возраста жизни по России равное 70.93.
rosstat Несмотря на то, что у нас всего 7 точек в выборке, в целом они проходят тесты нормальности и мы можем на них полагаться, так как эти данные уже были усреднены по региону.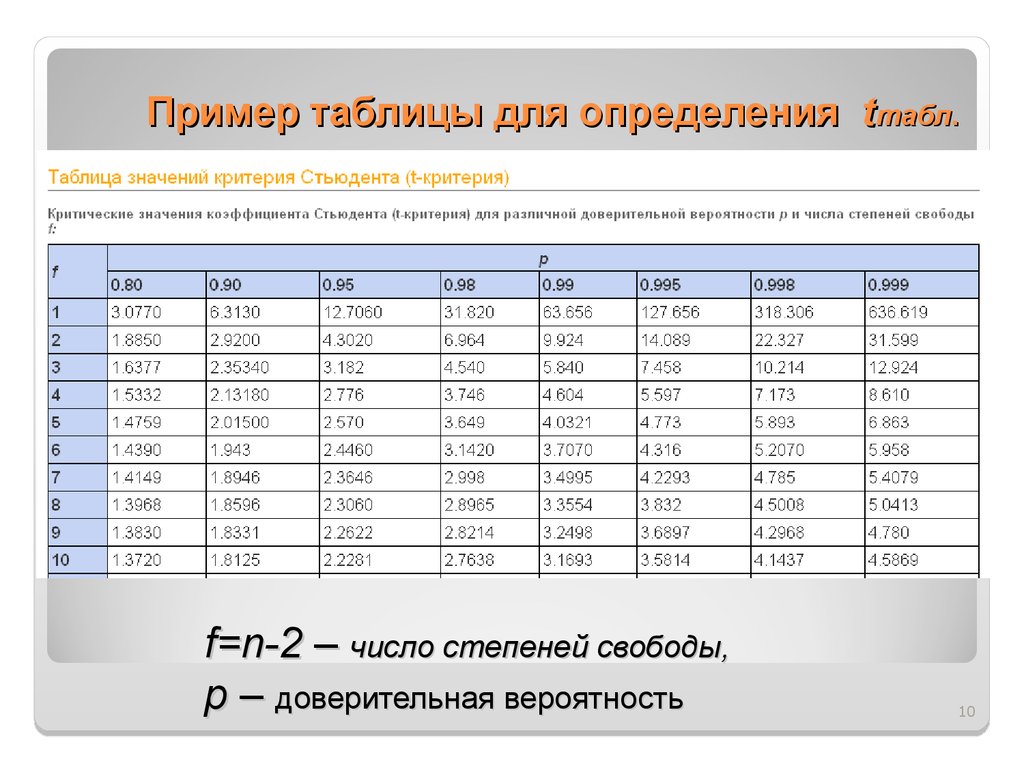
Результаты t-теста говорят о том, что средняя ожидаемая продолжительность жизни у жителей Северного Кавказа (74.6 лет) действительно выше, чем в среднем по России (70.93 лет), а результаты теста являются статистически значимыми (p
Двувыборочный для независимых выборок (independent two-sample t-test)
Двувыборочный t-тест используется, когда Вы сравниваете две независимые выборки . Допустим, мы хотим узнать, отличается ли урожайность картофеля на севере и на юге какого-либо региона. Для этого, мы собрали данные с 40 фермерских хозяйств: 20 из которых располагались на севере и сформировали выборку «North», а остальные 20 — на юге, сформировав выборку «South».
Загрузим данные в среду R. Кроме проверки нормальности данных, будет полезно построить «график с усами», на котором можно видеть медианы и разброс данных для обеих выборок.
North Как видно из графика, медианы выборок не сильно отличаются друг от друга, однако разброс данных гораздо сильнее на севере. Проверим отличаются ли статистически средние значения при помощи функции t.test. Однако в этот раз на место параметра mu мы ставим имя второй выборки. Результаты теста, которые Вы видите на рисунке снизу, говорят о том, что средняя урожайность картофеля на севере статистически не отличается от урожайности на юге (p = 0.6339).
Проверим отличаются ли статистически средние значения при помощи функции t.test. Однако в этот раз на место параметра mu мы ставим имя второй выборки. Результаты теста, которые Вы видите на рисунке снизу, говорят о том, что средняя урожайность картофеля на севере статистически не отличается от урожайности на юге (p = 0.6339).
Двувыборочный для зависимых выборок (dependent two-sample
t -test )Третий вид t-теста используется в том случае, если элементы выборок зависят друг от друга . Он идеально подходит для проверки повторяемости результатов эксперимента: если данные повтора статистически не отличаются от оригинала, то повторяемость данных высокая. Также двувыборочный критерий Стьюдента для зависимых выборок широко применяется в медицинских исследованиях при изучении эффекта лекарства на организм до и после приема.
Для того, чтобы запустить его в R, следует ввести все ту же функцию t.test
. Однако, в скобках, после таблиц данных, следует ввести дополнительный аргумент paired = TRUE
.
t.test(experiment, povtor.experimenta, paired = TRUE) t.test(davlenie.do.priema, davlenie.posle.priema, paired = TRUE)
Также в функции t.test существует два дополнительных аргумента, которые могут улучшить качество результатов теста: var.equal и alternative . Если вы знаете, что вариация между выборками равна, вставьте аргумент var.equal = TRUE . Если же вы хотите проверить гипотезу о том, что разница между средними в выборках значительно меньше или больше 0, то введите аргумент alternative=»less» или alternative=»greater» (по умолчанию альтернативная гипотеза говорит о том, что выборки просто отличаются друг от друга: alternative=»two.sided» ).
Заключение
Статья получилась довольно длинной, зато теперь Вы знаете: что такое критерий Стьюдента и нормальное распределение; как при помощи функций qqplot и shapiro.test
проверять нормальность данных в R; а также разобрали три типа t-тестов и провели их в среде R.
Тема для тех, кто только начинает знакомиться со статистическим анализом — непростая. Поэтому не стесняйтесь, задавайте вопросы, я с удовольствием на них отвечу. Гуру статистики, пожалуйста поправьте меня, если где-нибудь допустил ошибку. В общем, пишите Ваши комментарии, друзья!
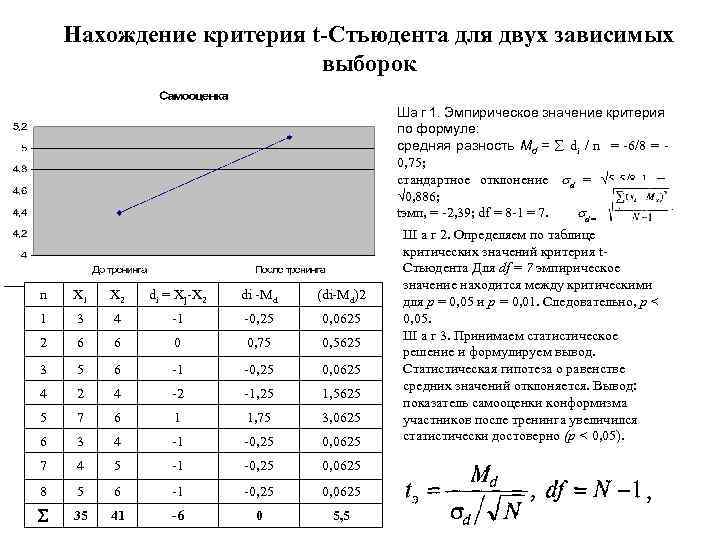
Чаще всего в психологическом исследовании наблюдается задачи на выявление различий между двумя или более группами признаков. Выяснение таких различий на уровне средних арифметических рассмотрено в процедуре анализа первичных статистик. Однако возникает вопрос, насколько эти различия достоверны и можно ли их распространить (экстраполировать) на всю популяцию. Для решения этой задачи чаще всего используют (при условии нормального или близкого к нормальному распределению) t — критерий (критерий Стьюдента), который предназначен для выяснения, насколько достоверно отличаются показатели одной выборки испытуемых от другой (например, когда исследуемые получают в результате тестирования одной группы высшие баллы, чем представители другой).
1) несвязанный (нечетная) t — критерий, предназначенный для того, чтобы выяснить, есть ли различия между оценками, полученными при использовании одного и того же теста для тестирования двух групп, сформированных из разных людей. Например, это может быть сравнение уровня интеллекта или нервно-психической устойчивости, тревожности успевающих и неуспевающих учеников или сравнение по этим признакам учеников разных классов, возрастов, социальных уровней и тому подобное. Могут быть и разнополые, разнонациональные выборки, а также подвыборки в исследуемых выборках, выделены по определенному признаку. Критерий называют «несвязанный», потому что сравниваемые группы сформированы из разных людей;
2) связан (парный) t — критерий, применяемый для сравнения показателей двух групп, между элементами которых существует специфическая связь. Это означает, что каждому элементу первой группы соответствует элемент второй группы, похожий на него по определенным параметром интересующей исследователя. Чаще всего сравнивают параметры одних и тех же лиц до и после определенного события или действия (например, в процессе проведения лонгитюдного исследования или формирующего эксперимента). Поэтому этот критерий используют для сравнения показателей одних и тех же лиц до и после обследования, эксперимента или истечении определенного времени.
Чаще всего сравнивают параметры одних и тех же лиц до и после определенного события или действия (например, в процессе проведения лонгитюдного исследования или формирующего эксперимента). Поэтому этот критерий используют для сравнения показателей одних и тех же лиц до и после обследования, эксперимента или истечении определенного времени.
Если данные не подлежат нормальному закону распределения, используют непараметрические критерии, эквивалентные t — критерия: критерий Манна — Уитни, эквивалентный нечетном t — критерия, и Двухвыборочный критерий Вилкоксона, эквивалентный парном t — критерия.
С помощью t — критериев и их непараметрических эквивалентов можно только сравнивать результаты двух групп, полученные с использованием одного и того же теста. Однако в некоторых случаях возникает необходимость сравнения нескольких групп или оценок нескольких видов. Это можно сделать поэтапно, разбив задачу на несколько пар сравнений (например, если надо сравнить группы А, Б и Y по результатам тестов X и Y, то можно с помощью t — критерия сначала сравнить группы А и Б по результатам теста X, затем А и Б по результатам теста В, А и В по результатам теста Х и т. д.). Однако это очень трудоемкий метод, поэтому прибегают к более сложному методу дисперсионного анализа.
д.). Однако это очень трудоемкий метод, поэтому прибегают к более сложному методу дисперсионного анализа.
Метод оценки достоверности различий средних арифметических по достаточно эффективным параметрическим критерием Стьюдента предназначен для решения одной из задач, чаще всего наблюдаются при обработке данных — выявление достоверности различий между двумя или более рядами значений. Такая оценка часто необходимо при сравнительном анализе полярных групп. их выделяют на основе различной выраженности определенной целевой признаки (характеристики) изучаемого явления. Как правило, анализ начинают с подсчета первичных статистик выделенных групп «, затем оценивают достоверность различий. Критерий Стьюдента вычисляют по формуле:
Значение критерия Стьюдента для трех уровней доверительной (статистической) значимости (р) приводят в справочниках по матстатистику. Количество степеней свободы определяют по формуле:
С уменьшением объемов выборок (n
Решение о достоверности различий принимают в том случае, если исчисленная величина t превышает табличное значение для определенного количества степеней свободы (d (v)). В публикациях или научных отчетах указывают высокий уровень значимости из трех: р
В публикациях или научных отчетах указывают высокий уровень значимости из трех: р
При любом числового значения критерия достоверности различия между средними этот показатель оценивает не степень выявленной различия (ее оценивают по самой разницей между средними), а только его статистическую достоверность, то есть право распространять полученный на основе сопоставления выборок вывод о наличии разницы на все явление (весь процесс) в целом. Низкий исчисленный критерий отличия не может служить доказательством отсутствия различия между двумя признаками (явлениями), потому что его значимость (степень достоверности) зависит не только от величины средних, но и от количества сравниваемых выборок. Он указывает не на отсутствие различия, а на то, что при такой величины выборок она статистически недостоверная: очень большой шанс, что разница в этих условиях случайная, очень мала вероятность ее достоверности.
Таблица 2.17. Доверительные границы для критерия Стьюдента (t-критерий) для f степеней свободы
ния среднего времени выполнения задания во второй попытке (по сравнению с первой пробой) не является достоверным.
Это выражение не равносильно утверждению о статистической однородности двух выборок, которые сопоставляют. Кроме того, применение критерия Стьюдента в случае таких неодинаковых выборок не вполне корректное математически и, безусловно, сказывается на конечном итоге о недостоверности различий Хср = 9,1 и Хср = 8,5. Пользуясь этим критерием, оценивают не степень близости двух средних, а рассматривают отнесения или невод несения случайной (при заданном уровне значимости). .
Excel для Office 365 Excel для Office 365 для Mac Excel 2019 Excel 2016 Excel 2019 для Mac Excel 2013 Excel 2010 Excel 2016 для Mac Excel для Mac 2011 Excel Online Excel для iPad Excel для iPhone Excel для планшетов с Android Excel для телефонов с Android Excel Mobile Excel Starter 2010 Меньше
Возвращает вероятность, соответствующую t-тесту Стьюдента. Функция СТЬЮДЕНТ.ТЕСТ позволяет определить вероятность того, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же среднее.
Синтаксис
СТЬЮДЕНТ.ТЕСТ(массив1;массив2;хвосты;тип)
Аргументы функции СТЬЮДЕНТ.ТЕСТ описаны ниже.
Массив1 Обязательный. Первый набор данных.
Массив2 Обязательный. Второй набор данных.
Хвосты Обязательный. Число хвостов распределения. Если значение «хвосты» = 1, функция СТЬЮДЕНТ.ТЕСТ возвращает одностороннее распределение. Если значение «хвосты» = 2, функция СТЬЮДЕНТ.ТЕСТ возвращает двустороннее распределение.
Тип Обязательный. Вид выполняемого t-теста.
Параметры
Замечания
Если аргументы «массив1» и «массив2» имеют различное число точек данных, а «тип» = 1 (парный), то функция СТЬЮДЕНТ.ТЕСТ возвращает значение ошибки #Н/Д.
Аргументы «хвосты» и «тип» усекаются до целых значений.
Если аргумент «хвосты» или «тип» не является числом, то функция СТЬЮДЕНТ.ТЕСТ возвращает значение ошибки #ЗНАЧ!.
Если аргумент «хвосты» принимает любое значение, отличное от 1 и 2, то функция СТЬЮДЕНТ. ТЕСТ возвращает значение ошибки #ЧИСЛО!.
ТЕСТ возвращает значение ошибки #ЧИСЛО!.
Функция СТЬЮДЕНТ.ТЕСТ использует данные аргументов «массив1» и «массив2» для вычисления неотрицательной t-статистики. Если «хвосты» = 1, СТЬЮДЕНТ.ТЕСТ возвращает вероятность более высокого значения t-статистики, исходя из предположения, что «массив1» и «массив2» являются выборками, принадлежащими к генеральной совокупности с одним и тем же средним. Значение, возвращаемое функцией СТЬЮДЕНТ.ТЕСТ в случае, когда «хвосты» = 2, вдвое больше значения, возвращаемого, когда «хвосты» = 1, и соответствует вероятности более высокого абсолютного значения t-статистики, исходя из предположения, что «массив1» и «массив2» являются выборками, принадлежащими к генеральной совокупности с одним и тем же средним.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.
В каких случаях можно использовать t-критерий Стьюдента?
Для применения t-критерия Стьюдента необходимо, чтобы исходные данные имели нормальное распределение . В случае применения двухвыборочного критерия для независимых выборок также необходимо соблюдение условия равенства (гомоскедастичности) дисперсий .
При несоблюдении этих условий при сравнении выборочных средних должны использоваться аналогичные методы непараметрической статистики , среди которых наиболее известными являются U-критерий Манна — Уитни (в качестве двухвыборочного критерия для независимых выборок), а также критерий знаков и критерий Вилкоксона (используются в случаях зависимых выборок).
Для сравнения средних величин t-критерий Стьюдента рассчитывается по следующей формуле:
где М 1 — средняя арифметическая первой сравниваемой совокупности (группы), М 2 — средняя арифметическая второй сравниваемой совокупности (группы), m 1 — средняя ошибка первой средней арифметической, m 2 — средняя ошибка второй средней арифметической.
Как интерпретировать значение t-критерия Стьюдента?
Полученное значение t-критерия Стьюдента необходимо правильно интерпретировать. Для этого нам необходимо знать количество исследуемых в каждой группе (n 1 и n 2). Находим число степеней свободы f по следующей формуле:
f = (n 1 + n 2) — 2
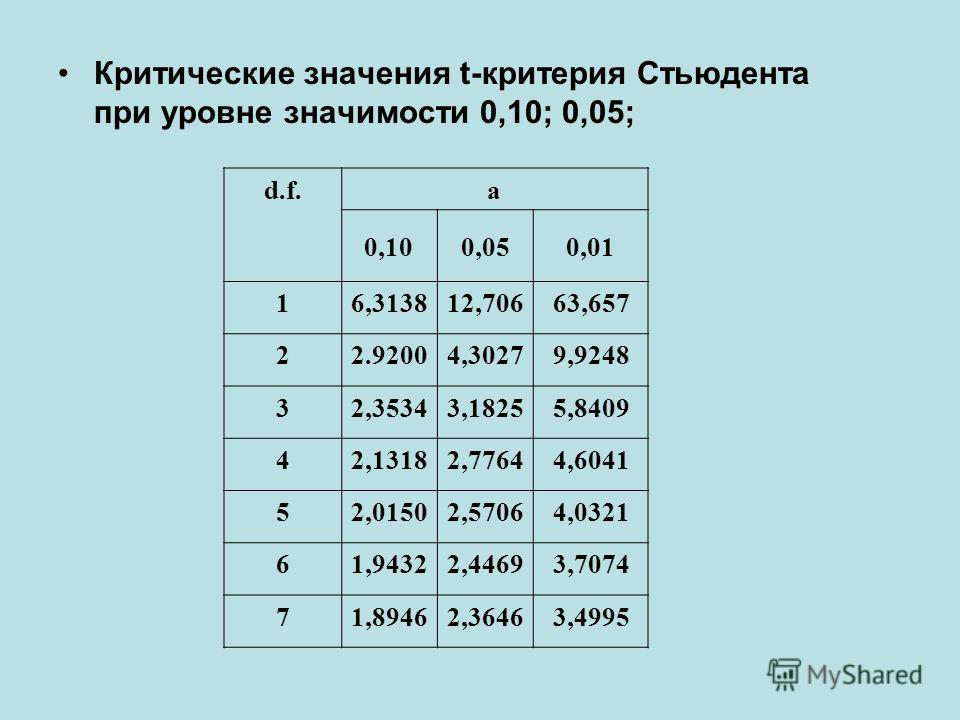
После этого определяем критическое значение t-критерия Стьюдента для требуемого уровня значимости (например, p=0,05) и при данном числе степеней свободы f по таблице (см. ниже ).
Сравниваем критическое и рассчитанное значения критерия:
· Если рассчитанное значение t-критерия Стьюдента равно или больше критического, найденного по таблице, делаем вывод о статистической значимости различий между сравниваемыми величинами.
· Если значение рассчитанного t-критерия Стьюдента меньше табличного, значит различия сравниваемых величин статистически не значимы.
Пример расчета t-критерия Стьюдента
Для изучения эффективности нового препарата железа были выбраны две группы пациентов с анемией. В первой группе пациенты в течение двух недель получали новый препарат, а во второй группе — получали плацебо. После этого было проведено измерение уровня гемоглобина в периферической крови. В первой группе средний уровень гемоглобина составил 115,4±1,2 г/л, а во второй — 103,7±2,3 г/л (данные представлены в формате M±m ), сравниваемые совокупности имеют нормальное распределение. При этом численность первой группы составила 34, а второй — 40 пациентов. Необходимо сделать вывод о статистической значимости полученных различий и эффективности нового препарата железа.
В первой группе пациенты в течение двух недель получали новый препарат, а во второй группе — получали плацебо. После этого было проведено измерение уровня гемоглобина в периферической крови. В первой группе средний уровень гемоглобина составил 115,4±1,2 г/л, а во второй — 103,7±2,3 г/л (данные представлены в формате M±m ), сравниваемые совокупности имеют нормальное распределение. При этом численность первой группы составила 34, а второй — 40 пациентов. Необходимо сделать вывод о статистической значимости полученных различий и эффективности нового препарата железа.
Решение: Для оценки значимости различий используем t-критерий Стьюдента, рассчитываемый как разность средних значений, поделенная на сумму квадратов ошибок:
После выполнения расчетов, значение t-критерия оказалось равным 4,51. Находим число степеней свободы как (34 + 40) — 2 = 72. Сравниваем полученное значение t-критерия Стьюдента 4,51 с критическим при р=0,05 значением, указанным в таблице: 1,993. Так как рассчитанное значение критерия больше критического, делаем вывод о том, что наблюдаемые различия статистически значимы (уровень значимости р
Так как рассчитанное значение критерия больше критического, делаем вывод о том, что наблюдаемые различия статистически значимы (уровень значимости р
Распределение Фишера – это распределение случайной величины
где случайные величины Х 1 и Х 2 независимы и имеют распределения хи – квадрат с числом степеней свободы k 1 и k 2 соответственно. При этом пара (k 1 , k 2) – пара «чисел степеней свободы» распределения Фишера, а именно, k 1 – число степеней свободы числителя, а k 2 – число степеней свободы знаменателя. Распределение случайной величины F названо в честь великого английского статистика Р.Фишера (1890-1962), активно использовавшего его в своих работах.
Распределение Фишера используют при проверке гипотез об адекватности модели в регрессионном анализе, о равенстве дисперсий и в других задачах прикладной статистики.
Таблица критических значений Стьюдента.
Начало формы
| Число степеней свободы, f | Значение t-критерия Стьюдента при p=0. 05 05 |
| 12.706 | |
| 4.303 | |
| 3.182 | |
| 2.776 | |
| 2.571 | |
| 2.447 | |
| 2.365 | |
| 2.306 | |
| 2.262 | |
| 2.228 | |
| 2.201 | |
| 2.179 | |
| 2.160 | |
| 2.145 | |
| 2.131 | |
| 2.120 | |
| 2.110 | |
| 2.101 | |
| 2.093 | |
| 2.086 | |
| 2.080 | |
| 2.074 | |
| 2.069 | |
| 2.064 | |
| 2.060 | |
| 2.056 | |
| 2.052 | |
2. 048 048 | |
| 2.045 | |
| 2.042 | |
| 2.040 | |
| 2.037 | |
| 2.035 | |
| 2.032 | |
| 2.030 | |
| 2.028 | |
| 2.026 | |
| 2.024 | |
| 40-41 | 2.021 |
| 42-43 | 2.018 |
| 44-45 | 2.015 |
| 46-47 | 2.013 |
| 48-49 | 2.011 |
| 50-51 | 2.009 |
| 52-53 | 2.007 |
| 54-55 | 2.005 |
| 56-57 | 2.003 |
| 58-59 | 2.002 |
| 60-61 | 2.000 |
| 62-63 | 1.999 |
| 64-65 | 1.998 |
| 66-67 | 1.997 |
| 68-69 | 1. 995 995 |
| 70-71 | 1.994 |
| 72-73 | 1.993 |
| 74-75 | 1.993 |
| 76-77 | 1.992 |
| 78-79 | 1.991 |
| 80-89 | 1.990 |
| 90-99 | 1.987 |
| 100-119 | 1.984 |
| 120-139 | 1.980 |
| 140-159 | 1.977 |
| 160-179 | 1.975 |
| 180-199 | 1.973 |
| 1.972 | |
| ∞ | 1.960 |
Эквивалентным подходом к интерпретации результатов теста будет следующий: допустив, что нулевая гипотеза верна, мы можем рассчитать, насколько велика вероятность получить t -критерий, равный или превышающий то реальное значение, которое мы рассчитали по имеющимся выборочным данным. Если эта вероятность оказывается меньше, чем заранее принятый уровень значимости (например, Р
Предположим, у нас имеются данные по суточному потреблению энергии, поступающей с пищей (кДж/сутки), для 11 женщин (пример заимствован из книги Altman D. G. (1981) Practical Statistics for Medical Research , Chapman & Hall, London ):
G. (1981) Practical Statistics for Medical Research , Chapman & Hall, London ):
Среднее значение для этих 11 наблюдений составляет:
Вопрос: отличается ли это выборочное среднее значение от установленной нормы в 7725 кДж/сутки? Разница между нашим выборочным значением и этим нормативом довольно прилична: 7725 — 6753.6 = 971.4. Но насколько велика эта разница статистически? Ответить на этот вопрос поможет одновыборочный t -тест. Как и другие варианты t -теста, одновыборочный тест Стьюдента выполняется в R при помощи функции t.test()
:
Вопрос: различаются ли эти средние значения статистически? Проверим гипотезу об отсутствии разницы при помощи t -теста:
Но как в таких случаях оценить наличие эффекта от воздействия статистически? В общем виде критерий Стьюдента можно представить как
Алгоритм расчета t-критерия Стьюдента для независимых выборок измерений
Определить расчетное значение t-критерия по формуле
где f – степень свободы, которая определяется как
- Определить
критическое значение t-критерия
с использованием таблицы 1 приложения,
при заданном уровне значимости и
степени свободы.

Сравнить расчетное и критическое значение t — критерия. Если расчетное значение больше или равно критическому, то гипотеза равенства средних значений в двух выборках изменений отвергается (Но). Во всех других случаях она принимается на заданном уровне значимости.
Пример. Две группы студентов обучались по двум различным методикам. В конце обучения с ними был проведен тест по всему курсу. Необходимо оценить, насколько существенны различия в полученных знаниях. Результаты тестирования представлены в таблице 4.
Таблица 4
25 | 18 | 9 | 13 | 8 | 20 | 25 | 18 | 6 | 12 |
19 | 13 | 12 | 12 | 18 | 9 | 7 | 10 | 18 | 20 |
Рассчитаем выборочное среднее, дисперсию и стандартное отклонение:
Определим значение tp по формуле tp = 0,45
По
таблице 1 (см. приложение) находим
критическое значение tk для уровня значимости р = 0,01
приложение) находим
критическое значение tk для уровня значимости р = 0,01
tk = 2,88
Вывод: так как расчетное значение критерия меньше критического 0,45<2,88 гипотеза Но подтверждается и существенных различий в методиках обучения нет на уровне значимости 0,01.
Алгоритм расчета t-критерия Стьюдента для зависимых выборок измерений
1. Определить расчетное значение t-критерия по формуле
, где
2. Рассчитать степень свободы f
3. Определить критическое значение t-критерия по таблице 1 приложения.
4.
Сравнить расчетное и критическое
значение t-критерия.
Если расчетное значение больше или
равно критическому, то гипотеза равенства
средних значений в двух выборках
изменений отвергается (Но). Во всех
других случаях она принимается на
заданном уровне значимости.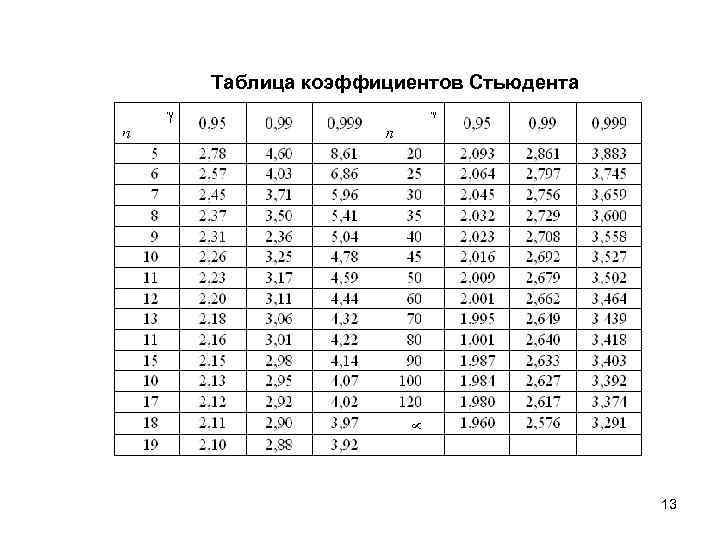
U—критерий Манна—Уитни
Назначение критерия
Критерий предназначен для оценки различий между двумя непараметрическими выборками по уровню какого-либо признака, количественно измеренного. Он позволяет выявлять различия между малыми выборками, когда n < 30.
Описание критерия
Этот метод определяет, достаточно ли мала зона пересекающихся значений между двумя рядами. Чем меньше эта область, тем более вероятно, что различия достоверны. Эмпирическое значение критерия U отражает то, насколько велика зона совпадения между рядами. Поэтому чем меньше U, тем более вероятно, что различия достоверны.
Гипотезы
НО: Уровень признака в группе 2 не ниже уровня признака в группе 1.
HI:
Уровень признака в группе 2 ниже уровня
признака в группе 1.
Алгоритм расчета критерия Манна-Уитни (u)
Перенести все данные испытуемых на индивидуальные карточки.
Пометить карточки испытуемых выборки 1 одним цветом, скажем красным, а все карточки из выборки 2 – другим, например, синим.
Разложить все карточки в единый ряд по степени нарастания признака, не считаясь с тем, к какой выборке они относятся, как если бы мы работали с одной большой выборкой.
Проранжировать значения на карточках, приписывая меньшему значению меньший ранг.
Вновь разложить карточки на две группы, ориентируясь на цветные обозначения: красные карточки в один ряд, синие – в другой.
Подсчитать сумму рангов отдельно на красных карточках (выборка 1) и на синих карточках (выборка 2). Проверить, совпадает ли общая сумма рангов с расчетной.

Определить большую из двух ранговых сумм.
Определить значение U по формуле:
где n1 – количество испытуемых в выборке 1;
n2 – количество испытуемых в выборке 2,
Тх – большая из двух рантовых сумм;
nх – количество испытуемых в группе с большей суммой рангов.
9. Определить критические значения U по таблице 2 (см. приложение).
Если Uэмп.> Uкр0,05, то гипотеза Но принимается. Если Uэмп.≤ Uкр, то отвергается. Чем меньше значения U, тем достоверность различий выше.
Пример. Сравнить эффективность двух методов обучения в двух группах. Результаты испытаний представлены в таблице 5.
Таблица 5
18 | 10 | 7 | 15 | 14 | 11 | 13 | ||||
15 | 20 | 10 | 8 | 16 | 10 | 19 | 7 | 15 | 14 | 29 |
Перенесем
все данные в другую таблицу, выделив
данные второй группы подчеркиванием
и сделаем ранжирование общей выборки
(см. алгоритм ранжирования в методических
указаниях к заданию 3).
алгоритм ранжирования в методических
указаниях к заданию 3).
Значения | 7 | 7 | 8 | 10 | 10 | 10 | 11 | 13 | 14 | 14 | 15 | 15 | 15 | 16 | 18 | 19 | 20 | 29 |
Ранги | 1,5 | 1,5 | 3 | 5 | 5 | 5 | 7 | 8 | 9,5 | 9,5 | 12 | 12 | 12 | 14 | 15 | 16 | 17 | 18 |
Номер | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
Найдем сумму рангов двух выборок и выберем большую из них: Тх = 113
Рассчитаем
эмпирическое значение критерия по
формуле 2: Up = 30.
Определим по таблице 2 приложения критическое значение критерия при уровне значимости р = 0.05 : Uk = 19.
Вывод: так как расчетное значение критерия U больше критического при уровне значимости р = 0.05 и 30 > 19, то гипотеза о равенстве средних принимается и различия в методиках обучения несущественны.
Т-тест Стьюдента: отличный справочник, который вам понравится
Т-тест Стьюдента
В этой статье описывается независимый Т-критерий Стьюдента , который используется для сравнения средних значений двух независимых групп. Этот тест также называется t-критерий Стьюдента , t-критерий Стьюдента и t-критерий равной дисперсии . Например, вы можете сравнить средние веса людей, сгруппированных по полу: мужские и женские группы, которые представляют собой две несвязанные/независимые группы.
Стьюдентный критерий независимых выборок бывает двух разных форм:
- стандартный Стьюдентский критерий , который предполагает, что дисперсии двух групп равны.

- t-критерий Уэлча , который является менее строгим по сравнению с исходным критерием Стьюдента. Этот тест описан в отдельной главе.
Обратите внимание, что t-критерий Уэлча считается более безопасным. Обычно результаты классического t-критерия Стьюдента и t-критерий Велча очень похожи, если только размеры групп и стандартные отклонения не сильно различаются.
В этой статье вы узнаете:
- Формула Стьюдента и предположения
- Как вычислить, интерпретировать и представить t-критерий Стьюдента в R .
- Как проверить предположения t-критерия Стьюдента
Содержимое:
- Предпосылки
- Исследовательские вопросы
- Статистические гипотезы
- Формула
- Предположения и предварительные тесты
- Расчет теста в R
- Демонстрационные данные
- Сводная статистика
- Визуализация
- Вычисление
- d Коэна для t-критерия Стьюдента
- Отчет
- Резюме
Связанная книга
Практическая статистика в R II — Сравнение групп: числовые переменные
Предварительные условия
Убедитесь, что вы установили следующие пакеты R:
-
tidyverseдля обработки данных и визуализации -
ggpubrдля создания готовых к публикации графиков -
rstatix предоставляет удобные функции R для удобного статистического анализа.
-
datarium: содержит необходимые наборы данных для этой главы.
Начните с загрузки следующих необходимых пакетов:
библиотека(tidyverse) библиотека (ggpubr) library(rstatix)
Исследовательские вопросы
Типичный исследовательский вопрос: равно ли среднее значение группы A (\(m_A\)) среднему значению группы B (\(m_B\))?
Формула
Классический критерий Стьюдента является более строгим. Предполагается, что две группы имеют одинаковую дисперсию населения. Если дисперсия двух групп эквивалентна ( гомоскедастичность ), значение t-теста, сравнивая две выборки (A и B), можно рассчитать следующим образом. 92}}{n_A+n_B-2}
\]
со степенями свободы (df): \(df = n_A + n_B — 2\).
Значение p может быть вычислено для соответствующего абсолютного значения t-статистики (|t|).
Если p-значение меньше или равно уровню значимости 0,05, мы можем отклонить нулевую гипотезу и принять альтернативную гипотезу. Другими словами, мы можем заключить, что средние значения групп А и В существенно различаются.
Другими словами, мы можем заключить, что средние значения групп А и В существенно различаются.
Предположения и предварительные тесты
Независимый t-тест для двух выборок предполагает следующие характеристики данных:
- Независимость наблюдений . Каждый предмет должен принадлежать только к одной группе.
- Нет значительных выбросов в двух группах
- Нормальность . данные для каждой группы должны быть примерно нормально распределены.
- Однородность отклонений . дисперсия переменной результата должна быть одинаковой в каждой группе.
Нажмите, чтобы проверить предположения t-критерия Стьюдента.
Расчет теста в Р
Демонстрационные данные
Демонстрационный набор данных: гендерный вес [в пакете datarium], содержащий вес 40 человек (20 женщин и 20 мужчин).
Загрузить данные и показать несколько случайных строк по группам:
# Загрузить данные
данные ("половой вес", пакет = "датариум")
# Показать выборку данных по группам
сет. сид(123)
гендерный вес %>% sample_n_by(group, size = 2)
сид(123)
гендерный вес %>% sample_n_by(group, size = 2) ## # Набор символов: 4 x 3 ## вес группы id ## <фкт> <фкт>## 1 6 Ж 65,0 ## 2 15 F 65,9## 3 29 М 88,9 ## 4 37 M 77.0
Визуализация
Визуализируйте данные с помощью коробчатых диаграмм. Вес участка по группам.
битхр <- ggboxplot( гендерный вес, x = "группа", y = "вес", ylab = "Вес", xlab = "Группы", add = "дрожание" ) bxp
Вычисление
Мы будем использовать удобную для каналов функцию t_test() [пакет rstatix], оболочку базовой функции R t.test() .
Напомним, что по умолчанию R вычисляет t-критерий Уэлча, который является более безопасным. Это тест, в котором вы не предполагаете, что дисперсия одинакова в двух группах, что приводит к дробным степеням свободы. Если вы хотите предположить равенство дисперсий (критерий Стьюдента), укажите параметр var.equal = TRUE :
stat.test <- гендерный вес %>% t_test(вес ~ группа, var.equal = TRUE) %>% add_significance() стат.тест
## # Тиббл: 1 x 9 ## .у. группа1 группа2 n1 n2 статистика df p p.signif #### 1 масса F M 20 20 -20.8 38 2.33e-22 ****
Приведенные выше результаты показывают следующие компоненты:
-
.y.: переменная y, используемая в тесте. -
group1,group2: сравниваемые группы в попарных тестах. -
статистика: Тестовая статистика, используемая для вычисления p-значения. -
df: степени свободы. -
p: p-значение.
Обратите внимание, что вы можете получить подробный результат, указав опцию details = TRUE .
Коэффициент Коэна для t-критерия Стьюдента
Величина эффекта рассчитывается путем деления средней разницы между группами на объединенное стандартное отклонение.
Формула Коэна d:
d = (mean1 - mean2)/pooled. , где: sd
sd
-
pooled.sd— общее стандартное отклонение двух групп.pooled.sd = sqrt([var1*(n1-1) + var2*(n2-1)]/[n1 + n2-2]); -
var1иvar2— это дисперсии (квадраты стандартных отклонений) групп 1 и 2 соответственно. -
n1иn2— число выборок для группы 1 и 2 соответственно. -
означает 1иmean2средние значения каждой группы соответственно.
Расчет:
гендерный вес %>% cohens_d(вес ~ группа, var.equal = TRUE)
## # Таблица: 1 x 7 ## .у. группа1 группа2 effsize n1 n2 величина ## *## 1 вес F M -6,57 20 20 большой
Имеется большой размер эффекта, d = 6,57.
Отчет
Результат можно представить следующим образом:
Средний вес в группе женщин составил 63,5 (SD = 2,03), тогда как средний вес в группе мужчин составил 85,8 (SD = 4,3). Критерий Стьюдента показал, что разница статистически значима, t(38) = -20,8, p < 0,0001, d = 6,57; где t(38) — сокращенное обозначение t-статистики Стьюдента с 38 степенями свободы.
Критерий Стьюдента показал, что разница статистически значима, t(38) = -20,8, p < 0,0001, d = 6,57; где t(38) — сокращенное обозначение t-статистики Стьюдента с 38 степенями свободы.
stat.test <- stat.test %>% add_xy_position(x = "группа") бхп + stat_pvalue_manual (stat.test, tip.length = 0) + labs(subtitle = get_test_label(stat.test, подробный = TRUE))
Резюме
В этой статье описываются формула и основы t-критерия Стьюдента. Приведены примеры R-кодов для расчета теста и размера эффекта, интерпретации и представления результатов.
Версия: Французский
Непарный Т-тест (предыдущий урок)
(следующий урок) Т-тест Велча
Назад к основам Т-теста: определение, формула и расчетУчитель
Альбукадель Кассамбара
Роль: Основатель Datanovia
- Веб-сайт: https://www.datanovia.com/en
- Опыт: >10 лет
- Специалист в области биоинформатики и биологии рака
Подробнее
Что такое множественные формулы и когда их использовать
Что такое Т-тест?
Стьюдент-критерий — это выводная статистика, используемая для определения того, существует ли значительная разница между средними значениями двух групп и тем, как они связаны. T-тесты используются, когда наборы данных следуют нормальному распределению и имеют неизвестные отклонения, например, набор данных, записанный при 100-кратном подбрасывании монеты.
T-тесты используются, когда наборы данных следуют нормальному распределению и имеют неизвестные отклонения, например, набор данных, записанный при 100-кратном подбрасывании монеты.
Стьюдентный тест – это тест, используемый для проверки гипотез в статистике. Он использует t-статистику, значения t-распределения и степени свободы для определения статистической значимости.
Ключевые выводы
- Стьюдент-критерий — это статистический вывод, используемый для определения наличия статистически значимой разницы между средними значениями двух переменных.
- Стьюдентный критерий — это критерий, используемый для проверки гипотез в статистике.
- Для расчета t-критерия требуются три основных значения данных, включая разницу между средними значениями из каждого набора данных, стандартное отклонение каждой группы и количество значений данных.
- Т-тесты могут быть зависимыми или независимыми.
Т-тест
Понимание Т-теста
Стьюдентный тест сравнивает средние значения двух наборов данных и определяет, получены ли они из одной и той же совокупности. В приведенных выше примерах выборка учащихся из класса A и выборка учащихся из класса B, скорее всего, не будут иметь одинаковое среднее значение и стандартное отклонение. Точно так же образцы, взятые из контрольной группы, получавшей плацебо, и образцы, взятые из группы, которой прописали лекарство, должны иметь несколько разные среднее значение и стандартное отклонение.
В приведенных выше примерах выборка учащихся из класса A и выборка учащихся из класса B, скорее всего, не будут иметь одинаковое среднее значение и стандартное отклонение. Точно так же образцы, взятые из контрольной группы, получавшей плацебо, и образцы, взятые из группы, которой прописали лекарство, должны иметь несколько разные среднее значение и стандартное отклонение.
Математически t-критерий берет выборку из каждого из двух наборов и устанавливает постановку задачи. Он предполагает нулевую гипотезу о том, что два средних равны.
С помощью формул рассчитываются значения и сравниваются со стандартными значениями. Предполагаемая нулевая гипотеза соответственно принимается или отвергается. Если нулевая гипотеза может быть отвергнута, это указывает на то, что показания данных сильны и, вероятно, не случайны.
Стьюдент-тест — это лишь один из многих тестов, используемых для этой цели. Статистики используют дополнительные тесты, кроме t-критерия, для изучения большего количества переменных и больших размеров выборки. Для выборки большого размера статистики используют z-критерий. Другие варианты тестирования включают тест хи-квадрат и f-тест.
Для выборки большого размера статистики используют z-критерий. Другие варианты тестирования включают тест хи-квадрат и f-тест.
Использование Т-теста
Предположим, что производитель лекарств тестирует новое лекарство. Следуя стандартной процедуре, препарат дается одной группе пациентов, а плацебо — другой группе, называемой контрольной группой. Плацебо — это вещество, не имеющее терапевтической ценности, и служит эталоном для измерения того, как реагирует другая группа, получающая реальное лекарство.
После испытания препарата члены контрольной группы, получавшей плацебо, сообщили об увеличении средней продолжительности жизни на три года, в то время как члены группы, которым прописали новый препарат, сообщили об увеличении средней продолжительности жизни на четыре года.
Начальное наблюдение указывает на то, что препарат работает. Однако также возможно, что наблюдение может быть обусловлено случайностью. Стьюдентный тест можно использовать, чтобы определить, являются ли результаты правильными и применимыми ко всей популяции.
При использовании t-теста делаются четыре предположения. Собранные данные должны соответствовать непрерывной или порядковой шкале, такой как баллы для теста IQ, данные собираются из случайно выбранной части всего населения, данные будут иметь нормальное распределение в виде колоколообразной кривой, и равная или гомогенная дисперсия существует, когда стандартные вариации равны.
Формула Т-теста
Для расчета t-критерия требуются три значения фундаментальных данных. Они включают разницу между средними значениями из каждого набора данных или среднюю разницу, стандартное отклонение каждой группы и количество значений данных в каждой группе.
Это сравнение помогает определить влияние случайности на разницу, а также определить, находится ли разница за пределами этого диапазона вероятности. Стьюдентный тест ставит вопрос о том, представляет ли разница между группами истинную разницу в исследовании или просто случайную разницу.
На выходе t-критерий выдает два значения: t-значение и степени свободы. Значение t или t-оценка представляет собой отношение разницы между средним значением двух наборов выборок и вариацией, которая существует в наборах выборок.
Значение t или t-оценка представляет собой отношение разницы между средним значением двух наборов выборок и вариацией, которая существует в наборах выборок.
Значение числителя представляет собой разницу между средним значением двух наборов выборок. Знаменатель представляет собой вариацию, существующую в наборах выборок, и является мерой дисперсии или изменчивости.
Это рассчитанное t-значение затем сравнивается со значением, полученным из таблицы критических значений, называемой таблицей T-распределения. Более высокие значения t-показателя указывают на большую разницу между двумя наборами выборок. Чем меньше t-значение, тем больше сходства существует между двумя наборами выборок.
T-Score
Большой t-показатель или t-значение указывает на то, что группы различаются, а маленький t-показатель указывает на то, что группы похожи.
Степени свободы относятся к значениям в исследовании, которые могут варьироваться и необходимы для оценки важности и достоверности нулевой гипотезы. Вычисление этих значений обычно зависит от количества записей данных, доступных в выборке.
Вычисление этих значений обычно зависит от количества записей данных, доступных в выборке.
Парный Т-тест
Коррелированный t-критерий, или парный t-критерий, является зависимым типом теста и выполняется, когда выборки состоят из согласованных пар одинаковых единиц или когда есть случаи повторных измерений. Например, могут быть случаи, когда одни и те же пациенты повторно тестируются до и после получения конкретного лечения. Каждый пациент используется в качестве контрольного образца против себя.
Этот метод также применим к случаям, когда образцы связаны или имеют совпадающие характеристики, например, сравнительный анализ с участием детей, родителей или братьев и сестер.
Формула для вычисления t-значения и степеней свободы для парного t-теста:
Т знак равно иметь в виду 1 − иметь в виду 2 с ( разница ) ( н ) куда: иметь в виду 1 а также иметь в виду 2 знак равно Средние значения каждого из выборочных наборов с ( разница ) знак равно Стандартное отклонение разностей парных значений данных н знак равно Размер выборки (количество парных различий) н − 1 знак равно Степени свободы \begin{align}&T=\frac{\textit{mean}1 - \textit{mean}2}{\frac{s(\text{diff})}{\sqrt{(n)}}}\\& \textbf{где:}\\&\textit{mean}1\text{ и }\textit{mean}2=\text{Средние значения каждого из выборочных наборов}\\&s(\text{diff}) =\text{Стандартное отклонение разностей парных значений данных}\\&n=\text{Размер выборки (количество парных разностей)}\\&n-1=\text{Степени свободы}\end {выровнено} T=(n)s(diff)mean1-mean2где:mean1 и mean2=средние значения каждого набора выборокss(diff)=стандартное отклонение разностей парных значений данных n=размер выборки (количество парных различий)n−1=степени свободы
Равная дисперсия или объединенный Т-тест
Стьюдентный критерий равной дисперсии является независимым t-тестом и используется, когда количество выборок в каждой группе одинаково или дисперсия двух наборов данных аналогична.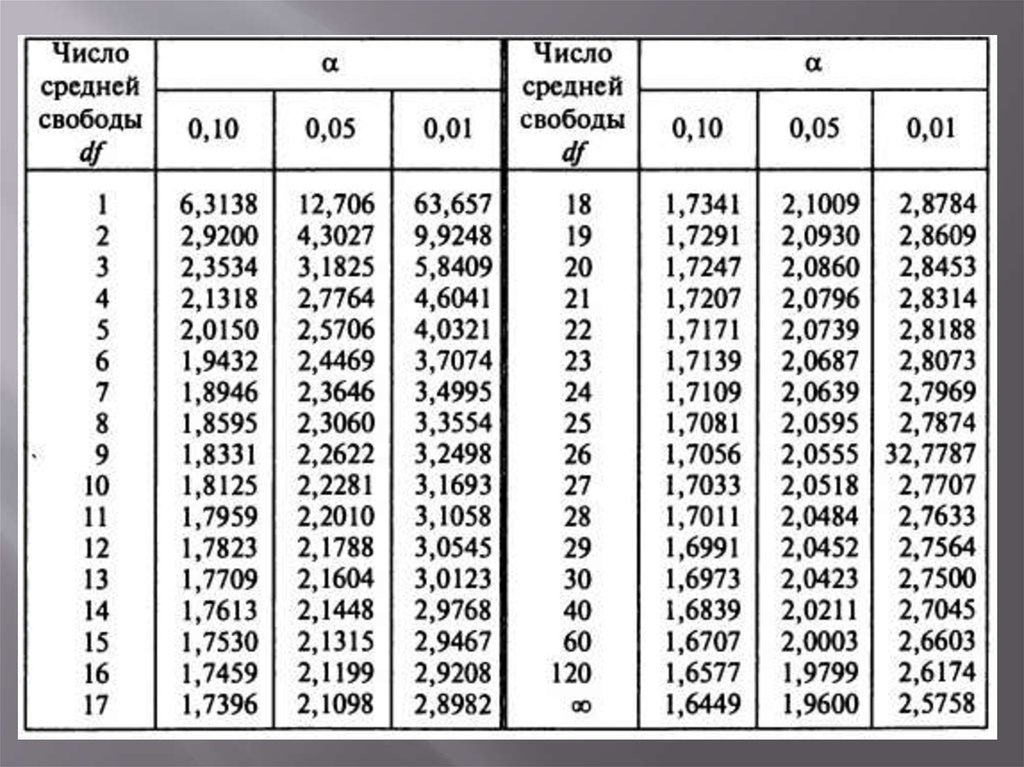 2 }{ n1 + n2 - 2}\times \sqrt{ \frac{1}{n1} + \frac{1}{n2}} } \\&\textbf{где:}\\&mean1 \text{ и } mean2 = \text{ Средние значения каждого} \\&\text{выборочных наборов}\\&var1 \text{ и } var2 = \text{Дисперсия каждого из выборочных наборов}\\&n1 \text{ и } n2 = \text{ Количество записей в каждом наборе образцов} \end{aligned}
T-значение=n1+n2−2(n1−1)×var12+(n2−1)×var22×n11+n21среднее1−среднее2, где:среднее1 и среднее2=средние значения каждого из выборочных наборовvar1 и var2 = дисперсия каждого набора образцов n1 и n2 = количество записей в каждом наборе образцов
2 }{ n1 + n2 - 2}\times \sqrt{ \frac{1}{n1} + \frac{1}{n2}} } \\&\textbf{где:}\\&mean1 \text{ и } mean2 = \text{ Средние значения каждого} \\&\text{выборочных наборов}\\&var1 \text{ и } var2 = \text{Дисперсия каждого из выборочных наборов}\\&n1 \text{ и } n2 = \text{ Количество записей в каждом наборе образцов} \end{aligned}
T-значение=n1+n2−2(n1−1)×var12+(n2−1)×var22×n11+n21среднее1−среднее2, где:среднее1 и среднее2=средние значения каждого из выборочных наборовvar1 и var2 = дисперсия каждого набора образцов n1 и n2 = количество записей в каждом наборе образцов
а также,
Степени свободы знак равно н 1 + н 2 − 2 куда: н 1 а также н 2 знак равно Количество записей в каждом наборе образцов \begin{align} &\text{Степени свободы} = n1 + n2 - 2 \\ &\textbf{где:}\\ &n1 \text{ и } n2 = \text{Количество записей в каждом наборе образцов} \ \ \ конец {выровнено} Степени свободы=n1+n2−2, где: n1 и n2=количество записей в каждом наборе образцов
Т-тест с неравной дисперсией
Стьюдентный критерий неравной дисперсии является независимым t-тестом и используется, когда количество выборок в каждой группе различно, и дисперсия двух наборов данных также различна. Этот тест также называют t-критерием Уэлча.
Этот тест также называют t-критерием Уэлча.
Формула, используемая для расчета t-значения и степеней свободы для t-критерия неравной дисперсии:
Т-значение знак равно м е а н 1 − м е а н 2 ( в а р 1 н 1 + в а р 2 н 2 ) куда: м е а н 1 а также м е а н 2 знак равно Средние значения каждого наборов образцов в а р 1 а также в а р 2 знак равно Дисперсия каждого из наборов образцов н 1 а также н 2 знак равно Количество записей в каждом наборе образцов \begin{align}&\text{T-value}=\frac{mean1-mean2}{\sqrt{\bigg(\frac{var1}{n1}{+\frac{var2}{n2}\bigg)} }}\\&\textbf{где:}\\&mean1 \text{ и } mean2 = \text{Средние значения каждого} \\&\text{набора образцов} \\&var1 \text{ и } var2 = \text{Дисперсия каждого набора образцов} \\&n1 \text{ и } n2 = \text{Количество записей в каждом наборе образцов} \end{выравнивание} T-значение=(n1var1+n2var2)mean1-mean2где:mean1 и mean2=Средние значения каждого из выборочных наборов var1 и var2=дисперсия каждого из выборочных наборов n1 и n2=количество записей в каждом выборочном наборе 92 }{ n2 - 1}} \\ &\textbf{где:}\\ &var1 \text{ и } var2 = \text{Дисперсия каждого из выборочных наборов} \\ &n1 \text{ и } n2 = \text {Количество записей в каждом наборе образцов} \\ \end{aligned} Степени свободы=n1−1(n1var12)2+n2−1(n2var22)2(n1var12+n2var22)2, где: var1 и var2 = дисперсия каждого набора выборки n1 и n2 = число записей в каждом наборе образцов
Какой Т-тест использовать?
Следующая блок-схема может быть использована для определения того, какой t-критерий использовать, исходя из характеристик наборов выборок.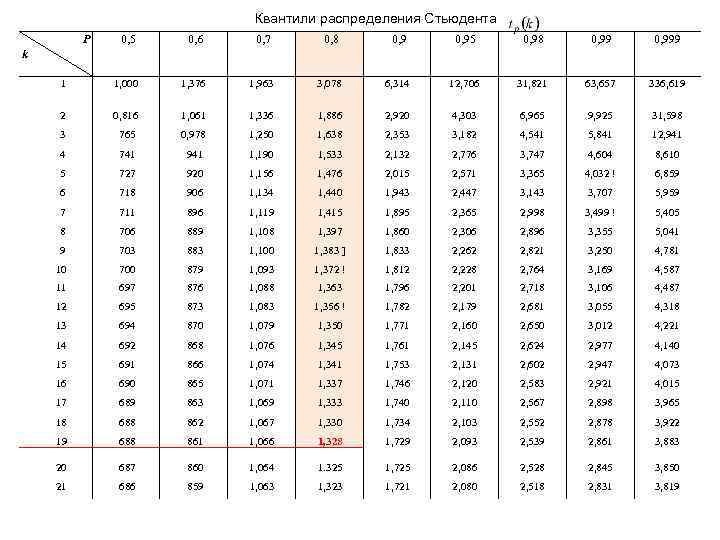 Ключевые элементы, которые следует учитывать, включают сходство записей выборки, количество записей данных в каждой выборке и дисперсию каждой выборки.
Ключевые элементы, которые следует учитывать, включают сходство записей выборки, количество записей данных в каждой выборке и дисперсию каждой выборки.
Изображение Джули Банг © Investopedia 2019
Пример T-критерия неравной дисперсии
Предположим, что берется диагональный размер картин, полученных в художественной галерее. В одну группу образцов входит 10 картин, в другую – 20 картин. Наборы данных с соответствующими средними значениями и значениями дисперсии следующие:
| Комплект 1 | Комплект 2 | |
|---|---|---|
| 19,7 | 28,3 | |
| 20,4 | 26,7 | |
| 19,6 | 20,1 | |
| 17,8 | 23,3 | |
| 18,5 | 25,2 | |
| 18,9 | 22,1 | |
| 18,3 | 17,7 | |
| 18,9 | 27,6 | |
| 19,5 | 20,6 | |
| 21,95 | 13,7 | |
| 23,2 | ||
| 17,5 | ||
| 20,6 | ||
| 18 | ||
| 23,9 | ||
| 21,6 | ||
| 24,3 | ||
| 20,4 | ||
| 23,9 | ||
| 13,3 | ||
| Среднее | 19,4 | 21,6 |
| Разница | 1,4 | 17,1 |
Хотя среднее значение набора 2 выше, чем у набора 1, мы не можем заключить, что совокупность, соответствующая набору 2, имеет более высокое среднее значение, чем население, соответствующее набору 1.
Является ли разница между 19,4 и 21,6 исключительно случайной, или существуют различия в общей совокупности всех картин, полученных в художественной галерее? Мы устанавливаем проблему, принимая нулевую гипотезу о том, что среднее значение одинаково для двух наборов выборок, и проводим t-тест, чтобы проверить, правдоподобна ли гипотеза.
Поскольку количество записей данных различно (n1 = 10 и n2 = 20) и дисперсия также различна, значение t и степени свободы вычисляются для вышеуказанного набора данных с использованием формулы, упомянутой в Т-критерии неравной дисперсии. раздел.
Значение t равно -2,24787. Поскольку знак минус можно игнорировать при сравнении двух t-значений, вычисленное значение равно 2,24787.
Значение степени свободы равно 24,38 и уменьшено до 24 из-за определения формулы, требующей округления значения до наименьшего возможного целого числа.
Можно указать уровень вероятности (альфа-уровень, уровень значимости, p ) в качестве критерия приемлемости. В большинстве случаев можно принять значение 5%.
В большинстве случаев можно принять значение 5%.
Используя значение степени свободы, равное 24, и уровень значимости 5%, просмотр таблицы распределения t-значения дает значение 2,064. Сравнение этого значения с вычисленным значением 2,247 показывает, что рассчитанное значение t больше табличного значения при уровне значимости 5%. Следовательно, можно с уверенностью отвергнуть нулевую гипотезу об отсутствии разницы между средними значениями. Набор населения имеет внутренние различия, и они не случайны.
Как используется таблица Т-распределения?
Таблица Т-распределения доступна в одностороннем и двустороннем форматах. Первый используется для оценки случаев, которые имеют фиксированное значение или диапазон с четким направлением, положительным или отрицательным. Например, какова вероятность того, что выходное значение останется ниже -3 или будет больше семи при броске пары игральных костей? Последний используется для анализа с привязкой к диапазону, например, чтобы узнать, находятся ли координаты в диапазоне от -2 до +2.




 сид(123)
гендерный вес %>% sample_n_by(group, size = 2)
сид(123)
гендерный вес %>% sample_n_by(group, size = 2) 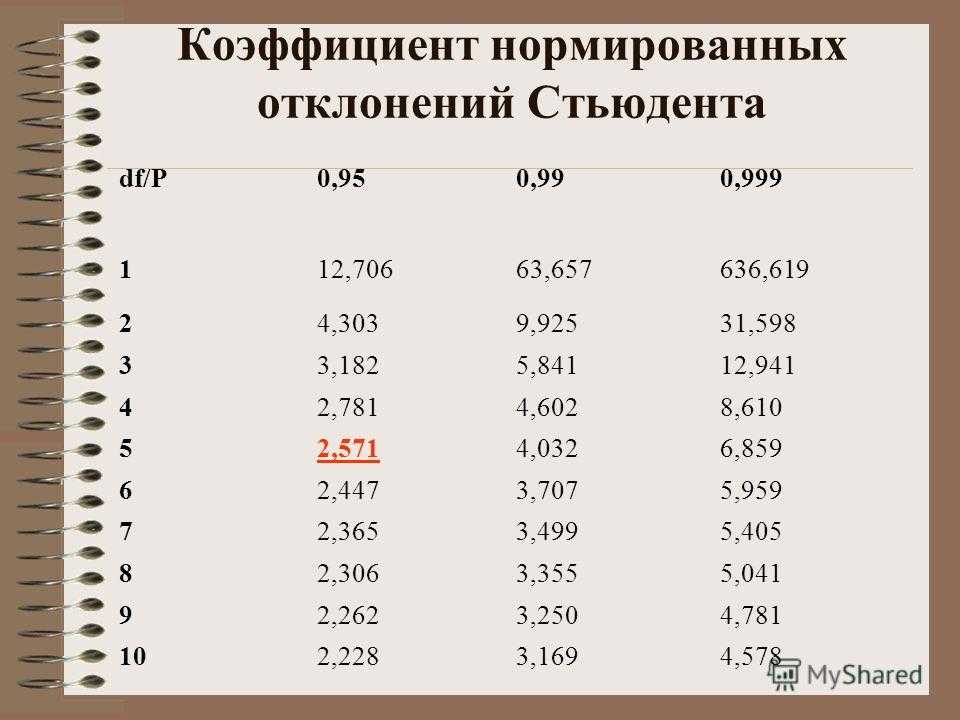 equal = TRUE) %>%
add_significance()
стат.тест
equal = TRUE) %>%
add_significance()
стат.тест