тангенсы, котангенсы, синусы и косинусы с инструкцией.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90,.. градусов. Определение данных величин дают определить значение функций углов в 0 и 90 градусов:
Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.
При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054
При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 200 = 0.9397
Значения tg угла до 900 и cot малого угла, верны и поправок в них нет. К примеру, найти tg 78 0 37мин = 4,967
а ctg 200 13мин = 25,83
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
90000 90001 Table of cosines 90002 90003 cos (0 °) = 1 90004 cos (1 °) = 0.999848 90004 cos (2 °) = 0.999391 90004 cos (3 °) = 0.99863 90004 cos (4 °) = 0.997564 90004 cos (5 °) = 0.996195 90004 cos (6 °) = 0.994522 90004 cos (7 °) = 0.992546 90004 cos (8 °) = 0.990268 90004 cos (9 °) = 0.987688 90004 cos (10 °) = 0.984808 90004 cos (11 °) = 0.981627 90004 cos (12 °) = 0.978148 90004 cos (13 °) = 0.97437 90004 cos (14 °) = 0.970296 90004 cos (15 °) = 0.965926 90004 cos (16 °) = 0.961262 90004 cos (17 °) = 0.956305 90004 cos (18 °) = 0.Дев’ятсот п’ятьдесят одна тисяча п’ятьдесят сім 90004 cos (19 °) = 0.945519 90004 cos (20 °) = 0.939693 90004 cos (21 °) = 0.93358 90004 cos (22 °) = 0.927184 90004 cos (23 °) = 0.920505 90004 cos (24 °) = 0.913545 90004 cos (25 °) = 0.906308 90004 cos (26 °) = 0.898794 90004 cos (27 °) = 0.891007 90004 cos (28 °) = 0.882948 90004 cos (29 °) = 0.87462 90004 cos (30 °) = 0.866025 90004 cos ( 31 °) = 0.857167 90004 cos (32 °) = 0.848048 90004 cos (33 °) = 0.838671 90004 cos (34 °) = 0.829038 90004 cos (35 °) = 0.819152 90004 cos (36 °) = 0.809017 90004 cos (37 ° ) = 0.798636 90004 cos (38 °) = 0.788011 90004 cos (39 °) = 0.777146 90004 cos (40 °) = 0.766044 90004 cos (41 °) = 0.75471 90004 cos (42 °) = 0.743145 90004 cos (43 °) = 0.731354 90004 cos (44 °) = 0.71934 90004 cos (45 °) = 0.707107 90004 90050 90003 cos (46 °) = 0.694658 90004 cos (47 °) = 0.681998 90004 cos (48 °) = 0.669131 90004 cos (49 °) = 0.656059 90004 cos (50 °) = 0.642788 90004 cos (51 °) = 0.62932 90004 cos (52 °) = 0.615661 90004 cos (53 °) = 0.601815 90004 cos (54 °) = 0.587785 90004 cos (55 °) = 0.573576 90004 cos (56 °) = 0.559193 90004 cos ( 57 °) = 0.544639 90004 cos (58 °) = 0.529919 90004 cos (59 °) = 0.515038 90004 cos (60 °) = 0.5 90004 cos (61 °) = 0.48481 90004 cos (62 °) = 0.469472 90004 cos (63 °) = 0.45399 90004 cos (64 °) = 0.438371 90004 cos (65 °) = 0.422618 90004 cos (66 °) = 0.406737 90004 cos (67 °) = 0.390731 90004 cos (68 °) = 0.374607 90004 cos (69 °) = 0.358368 90004 cos ( 70 °) = 0.34202 90004 cos (71 °) = 0.325568 90004 cos (72 °) = 0.309017 90004 cos (73 °) = 0.292372 90004 cos (74 °) = 0.275637 90004 cos (75 °) = 0.258819 90004 cos (76 ° ) = 0.241922 90004 cos (77 °) = 0.224951 90004 cos (78 °) = 0.207912 90004 cos (79 °) = 0.190809 90004 cos (80 °) = 0.173648 90004 cos (81 °) = 0.156434 90004 cos (82 °) = 0.139173 90004 cos (83 °) = 0.121869 90004 cos (84 °) = 0.104528 90004 cos (85 °) = 0.087156 90004 cos (86 °) = 0.069756 90004 cos (87 °) = 0.052336 90004 cos (88 °) = 0.034899 90004 cos (89 °) = 0.017452 90004 cos ( 90 °) = 0 90004 90050 90003 cos (91 °) = -0.017452 90004 cos (92 °) = -0.034899 90004 cos (93 °) = -0.052336 90004 cos (94 °) = -0.069756 90004 cos (95 °) = -0.087156 90004 cos (96 °) = -0.104528 90004 cos (97 °) = -0.121869 90004 cos (98 °) = -0.139173 90004 cos (99 °) = -0.156434 90004 cos (100 °) = -0.173648 90004 cos (101 °) = -0.190809 90004 cos (102 °) = -0.207912 90004 cos (103 °) = -0.224951 90004 cos (104 °) = -0.241922 90004 cos (105 °) = -0.258819 90004 cos (106 °) = -0.275637 90004 cos (107 °) = -0.292372 90004 cos (108 °) = -0.309017 90004 cos (109 °) = -0.325568 90004 cos (110 °) = -0.34202 90004 cos (111 °) = -0.358368 90004 cos (112 °) = -0.374607 90004 cos (113 ° ) = -0.390731 90004 cos (114 °) = -0.406737 90004 cos (115 °) = -0.422618 90004 cos (116 °) = -0.438371 90004 cos (117 °) = -0.45399 90004 cos (118 °) = -0.469472 90004 cos (119 °) = -0.48481 90004 cos (120 °) = -0.5 90004 cos (121 °) = -0.515038 90004 cos (122 °) = -0.529919 90004 cos (123 °) = -0.544639 90004 cos (124 °) = -0.559193 90004 cos (125 °) = -0.573576 90004 cos (126 °) = -0.587785 90004 cos (127 °) = -0.601815 90004 cos (128 °) = -0.615661 90004 cos (129 °) = -0.62932 90004 cos (130 °) = -0.642788 90004 cos (131 °) = -0.656059 90004 cos (132 ° ) = -0.669131 90004 cos (133 °) = -0.681998 90004 cos (134 °) = -0.694658 90004 cos (135 °) = -0.707107 90004 90050 90003 cos (136 °) = -0.71934 90004 cos (137 °) = -0.731354 90004 cos (138 °) = -0.743145 90004 cos (139 °) = -0.75471 90004 cos (140 °) = -0.766044 90004 cos (141 °) = -0.777146 90004 cos (142 °) = -0.788011 90004 cos (143 °) = -0.798636 90004 cos (144 °) = -0.809017 90004 cos (145 °) = -0.819152 90004 cos (146 °) = -0.829038 90004 cos (147 °) = -0.838671 90004 cos (148 °) = -0.848048 90004 cos (149 °) = -0.857167 90004 cos (150 °) = -0.866025 90004 cos ( 151 °) = -0.87462 90004 cos (152 °) = -0.882948 90004 cos (153 °) = -0.891007 90004 cos (154 °) = -0.898794 90004 cos (155 °) = -0.906308 90004 cos (156 °) = -0.913545 90004 cos (157 °) = -0.920505 90004 cos (158 °) = -0.927184 90004 cos (159 °) = -0.93358 90004 cos (160 °) = -0.939693 90004 cos (161 °) = -0.945519 90004 cos (162 °) = -0.951057 90004 cos (163 °) = -0.956305 90004 cos (164 °) = -0.961262 90004 cos (165 °) = -0.965926 90004 cos (166 °) = -0.970296 90004 cos (167 °) = -0.97437 90004 cos (168 °) = -0.978148 90004 cos (169 ° ) = -0.981627 90004 cos (170 °) = -0.984808 90004 cos (171 °) = -0.987688 90004 cos (172 °) = -0.990268 90004 cos (173 °) = -0.992546 90004 cos (174 °) = -0.994522 90004 cos (175 °) = -0.996195 90004 cos (176 °) = -0.997564 90004 cos (177 °) = -0.99863 90004 cos (178 °) = -0.999391 90004 cos (179 °) = -0.999848 90004 cos (180 °) = -1 90004 90050 90192.90000 90001 Table of sine 90002 90003 sin (0 °) = 0 90004 sin (1 °) = 0.017452 90004 sin (2 °) = 0.034899 90004 sin (3 °) = 0.052336 90004 sin (4 °) = 0.069756 90004 sin (5 °) = 0.087156 90004 sin (6 °) = 0.104528 90004 sin (7 °) = 0.121869 90004 sin (8 °) = 0.139173 90004 sin (9 °) = 0.156434 90004 sin (10 °) = 0.173648 90004 sin (11 °) = 0.190809 90004 sin (12 °) = 0.207912 90004 sin (13 °) = 0.224951 90004 sin (14 °) = 0.241922 90004 sin (15 °) = 0.258819 90004 sin (16 °) = 0.275637 90004 sin (17 °) = 0.292372 90004 sin (18 °) = 0.309017 90004 sin (19 °) = 0.325568 90004 sin (20 °) = 0.34202 90004 sin (21 °) = 0.358368 90004 sin (22 °) = 0.374607 90004 sin (23 °) = 0.390731 90004 sin (24 °) = 0.406737 90004 sin (25 °) = 0.422618 90004 sin (26 °) = 0.438371 90004 sin (27 °) = 0.45399 90004 sin (28 °) = 0.469472 90004 sin (29 °) = 0.48481 90004 sin (30 °) = 0.5 90004 sin ( 31 °) = 0.515038 90004 sin (32 °) = 0.529919 90004 sin (33 °) = 0.544639 90004 sin (34 °) = 0.559193 90004 sin (35 °) = 0.573576 90004 sin (36 °) = 0.587785 90004 sin (37 ° ) = 0.601815 90004 sin (38 °) = 0.615661 90004 sin (39 °) = 0.62932 90004 sin (40 °) = 0.642788 90004 sin (41 °) = 0.656059 90004 sin (42 °) = 0.669131 90004 sin (43 °) = 0.681998 90004 sin (44 °) = 0.694658 90004 sin (45 °) = 0.707107 90004 90050 90003 sin (46 °) = 0.71934 90004 sin (47 °) = 0.731354 90004 sin (48 °) = 0.743145 90004 sin (49 °) = 0.75471 90004 sin (50 °) = 0.766044 90004 sin (51 °) = 0.777146 90004 sin (52 °) = 0.788011 90004 sin (53 °) = 0.798636 90004 sin (54 °) = 0.809017 90004 sin (55 °) = 0.819152 90004 sin (56 °) = 0.829038 90004 sin ( 57 °) = 0.838671 90004 sin (58 °) = 0.848048 90004 sin (59 °) = 0.857167 90004 sin (60 °) = 0.866025 90004 sin (61 °) = 0.87462 90004 sin (62 °) = 0.882948 90004 sin (63 °) = 0.891007 90004 sin (64 °) = 0.898794 90004 sin (65 °) = 0.906308 90004 sin (66 °) = 0.913545 90004 sin (67 °) = 0.920505 90004 sin (68 °) = 0.927184 90004 sin (69 °) = 0.93358 90004 sin ( 70 °) = 0.939693 90004 sin (71 °) = 0.945519 90004 sin (72 °) = 0.951057 90004 sin (73 °) = 0.956305 90004 sin (74 °) = 0.961262 90004 sin (75 °) = 0.965926 90004 sin (76 ° ) = 0.970296 90004 sin (77 °) = 0.97437 90004 sin (78 °) = 0.978148 90004 sin (79 °) = 0.981627 90004 sin (80 °) = 0.984808 90004 sin (81 °) = 0.987688 90004 sin (82 °) = 0.990268 90004 sin (83 °) = 0.992546 90004 sin (84 °) = 0.994522 90004 sin (85 °) = 0.996195 90004 sin (86 °) = 0.997564 90004 sin (87 °) = 0.99863 90004 sin (88 °) = 0.999391 90004 sin (89 °) = 0.999848 90004 sin ( 90 °) = 1 90004 90050 90003 sin (91 °) = 0.999848 90004 sin (92 °) = 0.999391 90004 sin (93 °) = 0.99863 90004 sin (94 °) = 0.997564 90004 sin (95 °) = 0.996195 90004 sin ( 96 °) = 0.994522 90004 sin (97 °) = 0.992546 90004 sin (98 °) = 0.990268 90004 sin (99 °) = 0.987688 90004 sin (100 °) = 0.984808 90004 sin (101 °) = 0.981627 90004 sin (102 °) = 0.978148 90004 sin (103 °) = 0.97437 90004 sin (104 °) = 0.970296 90004 sin (105 °) = 0.965926 90004 sin (106 °) = 0.961262 90004 sin (107 °) = 0.956305 90004 sin (108 °) = 0.951057 90004 sin (109 °) = 0.945519 90004 sin ( 110 °) = 0.939693 90004 sin (111 °) = 0.93358 90004 sin (112 °) = 0.927184 90004 sin (113 °) = 0.920505 90004 sin (114 °) = 0.913545 90004 sin (115 °) = 0.906308 90004 sin (116 ° ) = 0.898794 90004 sin (117 °) = 0.891007 90004 sin (118 °) = 0.882948 90004 sin (119 °) = 0.87462 90004 sin (120 °) = 0.866025 90004 sin (121 °) = 0.857167 90004 sin (122 °) = 0.848048 90004 sin (123 °) = 0.838671 90004 sin (124 °) = 0.829038 90004 sin (125 °) = 0.819152 90004 sin (126 °) = 0.809017 90004 sin (127 °) = 0.798636 90004 sin (128 °) = 0.788011 90004 sin ( 129 °) = 0.777146 90004 sin (130 °) = 0.766044 90004 sin (131 °) = 0.75471 90004 sin (132 °) = 0.743145 90004 sin (133 °) = 0.731354 90004 sin (134 °) = 0.71934 90004 sin (135 ° ) = 0.707107 90004 90050 90003 sin (136 °) = 0.694658 90004 sin (137 °) = 0.681998 90004 sin (138 °) = 0.669131 90004 sin (139 °) = 0.656059 90004 sin (140 °) = 0.642788 90004 sin (141 °) = 0.62932 90004 sin (142 °) = 0.615661 90004 sin (143 °) = 0.601815 90004 sin (144 °) = 0.587785 90004 sin (145 °) = 0.573576 90004 sin (146 °) = 0.559193 90004 sin (147 °) = 0.544639 90004 sin (148 °) = 0.529919 90004 sin (149 °) = 0.515038 90004 sin (150 °) = 0.5 90004 sin (151 °) = 0.48481 90004 sin (152 °) = 0.469472 90004 sin (153 °) = 0.45399 90004 sin ( 154 °) = 0.438371 90004 sin (155 °) = 0.422618 90004 sin (156 °) = 0.406737 90004 sin (157 °) = 0.390731 90004 sin (158 °) = 0.374607 90004 sin (159 °) = 0.358368 90004 sin (160 °) = 0.34202 90004 sin (161 °) = 0.325568 90004 sin (162 °) = 0.309017 90004 sin (163 °) = 0.292372 90004 sin (164 °) = 0.275637 90004 sin (165 °) = 0.258819 90004 sin (166 °) = 0.241922 90004 sin ( 167 °) = 0.224951 90004 sin (168 °) = 0.207912 90004 sin (169 °) = 0.190809 90004 sin (170 °) = 0.173648 90004 sin (171 °) = 0.156434 90004 sin (172 °) = 0.139173 90004 sin (173 ° ) = 0.121869 90004 sin (174 °) = 0.104528 90004 sin (175 °) = 0.087156 90004 sin (176 °) = 0.069756 90004 sin (177 °) = 0.052336 90004 sin (178 °) = 0.034899 90004 sin (179 °) = 0.017452 90004 sin (180 °) = 0 90004 90050 90192.2} {2bc} \ right] \) 90005 90004
90007
90008 A = angle A
90008 B = angle B
90008 C = angle C
90008 a = side a
90008 b = side b
90008 c = side c
90008 P = perimeter
90008 s = semi-perimeter
90008 K = area
90008 r = radius of inscribed circle
90008 R = radius of circumscribed circle
90005
90004 * Length units are for your reference-only since the value of the resulting lengths will always be the same no matter what the units are.90005
90022 Calculator Use 90003
90004 Uses the law of cosines to calculate unknown angles or sides of a triangle. In order to calculate the unknown values you must enter 3 known values. 90005
90004 To calculate any angle, A, B or C, enter 3 side lengths a, b and c. This is the same calculation as
Side-Side-Side (SSS) Theorem. To calculate side a for example, enter the opposite angle A and the two other adjacent sides b and c.Using different forms of the law of cosines we can calculate all of the other unknown angles or sides. This is the same calculation as
Side-Angle-Side (SAS) Theorem.
90005
90028
90002 Law of Cosines 90003
90004 If a, b and c are the lengths of the legs of a triangle opposite to the angles A, B and C respectively; then the law of cosines states: 90005
90004 \ (a ^ 2 = b ^ 2 + c ^ 2 — 2bc \ cos A \) 90005
90004 \ (b ^ 2 = a ^ 2 + c ^ 2 — 2ac \ cos B \) 90005
90004 \ (c ^ 2 = a ^ 2 + b ^ 2 — 2ab \ cos C \) 90005
90039 Law of Cosines solving for sides a, b, and c 90040
90004 \ (a = \ sqrt {b ^ 2 + c ^ 2 — 2bc \ cos A} \) 90005
90004 \ (b = \ sqrt {a ^ 2 + c ^ 2 — 2ac \ cos B} \) 90005
90004 \ (c = \ sqrt {a ^ 2 + b ^ 2 — 2ab \ cos C} \) 90005
90039 Law of Cosines solving for angles A, B, and C 90040
90004 \ (A = \ cos ^ {- 1} \ left [\ dfrac {b ^ 2 + c ^ 2-a ^ 2} {2bc} \ right] \) 90005
90004 \ (B = \ cos ^ {- 1} \ left [\ dfrac {a ^ 2 + c ^ 2-b ^ 2} {2ac} \ right] \) 90005
90004 \ (C = \ cos ^ {- 1} \ left [\ dfrac {a ^ 2 + b ^ 2-c ^ 2} {2ab} \ right] \) 90005
90002 Triangle Characteristics 90003
90004 Triangle perimeter, P = a + b + c 90005
90004 Triangle semi-perimeter, s = 0.5 * (a + b + c) 90005
90004 Triangle area, K = √ [s * (s-a) * (s-b) * (s-c)] 90005
90004 Radius of inscribed circle in the triangle, r = √ [(s-a) * (s-b) * (s-c) / s] 90005
90004 Radius of circumscribed circle around triangle, R = (abc) / (4K) 90005
90002 References / Further Reading 90003
90004
Weisstein, Eric W. «Law of Cosines» From
90070 MathWorld 90071 — A Wolfram Web Resource.Law of Cosines. 90005
90004 Zwillinger, Daniel (Editor-in-Chief).
90070 CRC Standard Mathematical Tables and Formulae, 31st Edition 90071 New York, NY: CRC Press, p. 512, 2003.
90005
90004
http://hyperphysics.phy-astr.gsu.edu/hbase/lcos.html
90005
90004
http://hyperphysics.phy-astr.gsu.edu/hbase/lsin.html
90005 .90000 Degrees to Radians conversion 90001 90002 Enter angle in degrees and press the 90003 Convert 90004 button (e.g: 30 °, -60 °): 90005 90002 Radians to degrees converter ► 90005
90008 How to convert degrees to radians 90009
90002 Pi radians are equal to 180 degrees: 90005
90002 π rad = 180 ° 90005
90002 One degree is equal 0.01745329252 radians: 90005
90002 1 ° = π / 180 ° = 0.005555556π = 0.01745329252 rad 90005
90002 The angle α in radians is equal to the angle α in degrees times pi constant divided by 180 degrees: 90005
90002 α 90021 (radians) 90022 = α 90021 (degrees) 90022 × π / 180 ° 90005
90002 or 90005
90002 radians = degrees × π / 180 ° 90005
90030 Example 90031
90002 Convert 30 degrees angle to radians: 90005
90002 α 90021 (radians) 90022 = α 90021 (degrees) 90022 × π / 180 ° = 30 ° × 3.14159/180 ° = 0.5236 rad 90005 90040
90041
90042 Degrees (°) 90043
90042 Radians (rad) 90043
90042 Radians (rad) 90043
90048
90041
90050 0 ° 90051
90050 0 rad 90051
90050 0 rad 90051
90048
90041
90050 30 ° 90051
90050 π / 6 rad 90051
90050 0.5235987756 rad 90051
90048
90041
90050 45 ° 90051
90050 π / 4 rad 90051
90050 0.7853981634 rad 90051
90048
90041
90050 60 ° 90051
90050 π / 3 rad 90051
90050 1.0471975512 rad 90051
90048
90041
90050 90 ° 90051
90050 π / 2 rad 90051
90050 1.5707963268 rad 90051
90048
90041
90050 120 ° 90051
90050 2π / 3 rad 90051
90050 2.0943951024 rad 90051
90048
90041
90050 135 ° 90051
90050 3π / 4 rad 90051
90050 2.3561944902 rad 90051
90048
90041
90050 150 ° 90051
90050 5π / 6 rad 90051
90050 2.6179938780 rad 90051
90048
90041
90050 180 ° 90051
90050 π rad 90051
90050 3.1415926536 rad 90051
90048
90041
90050 270 ° 90051
90050 3π / 2 rad 90051
90050 4.7123889804 rad 90051
90048
90041
90050 360 ° 90051
90050 2π rad 90051
90050 6.2831853072 rad 90051
90048
90137
90002 90005
90002 Radians to degrees conversion ► 90005
90002 90005
90144
90008 See also 90009 .
Как бы не совершенствовалась вычислительная техника, определение синусов, косинусов, тангенсов и котангенсов с помощью таблицы Брадиса будет всегда актуально.
Таблица Брадиса создана выдающимся педагогом-математиком Владимиром Модестовичем Брадисом. Чтобы вы научились пользоваться таблицами Брадиса, которые представлены ниже, рекомендуем сначала прочесть инструкцию.
Таблица брадиса — инструкция
- Возьмите саму таблицу Брадиса. Если у вас нет её в напечатанной виде, то воспользуйтесь нашими таблицами брадиса. Откройте соответствующую главу: тангенсы-котангенсы или синусы-косинусы. Для примера возьмем синус.
- Убедитесь, какой угол нужен Вам для решения задачи. Таблицу Брадиса можно и без проблем применить в том разе, даже когда угол является дробным, то есть его расчет происходит в градусах и минутах. Если величина угла подаётся в радианах, преобразуйте её значения в градусы. Оно будет равняться произведению размера ( считают в радианах) , помноженному на отношение 180-ти градусов на значение π и подаётся общей формулой, а именно : α
- В таблице Брадиса, Вам будут видны некие рядки, которые будут находиться и по горизонтали, и по вертикали. Обратите внимание на самый крайний ряд, находящийся слева. Вверху левого угла находится слово sin, а под ним расположился столбец из цифр с наименованием градуса. Это целая величина градусов. Отыщите число, которое будет напрямую соответствовать величине целых градусов в уже заданном Вами угле. К примеру, вам дан в задании угол равный 27°18′. Обратите внимание, что в крайнем левом столбце имеется число 27. Потом в самой верхней строчку отыщите число 18. На перекрёстке строчки и столбика Вы сможете увидеть нужное для Вас значение.
- Сделайте акцент на то, что градусы в таблице Брадиса идут между собой подряд, а минуты чередуются через шесть. К примеру, 18 минут в таблице подаваться будут, а 19 найти Вы уже не сможете . Чтобы высчитать синус нужного угла, величину минут которого непосредственно не будет кратно 6ти, применяются некие поправки. Они расположились в правой части таблицы. Посчитайте разницу между количеством заданных минут в нужном угле и самом ближайшем угле, где величина минут будет кратна 6ти. Если это различие будет составлять приблизительно 1, 2, 3 минуты, то Вы просто добавьте требуемое значение к конечной цифре величины синуса самого малого угла. Если разность будит близиться к 4 или 5, возьмите величину самого близкого большого угла и вычтите от конечного числа величину первой или второй поправки.
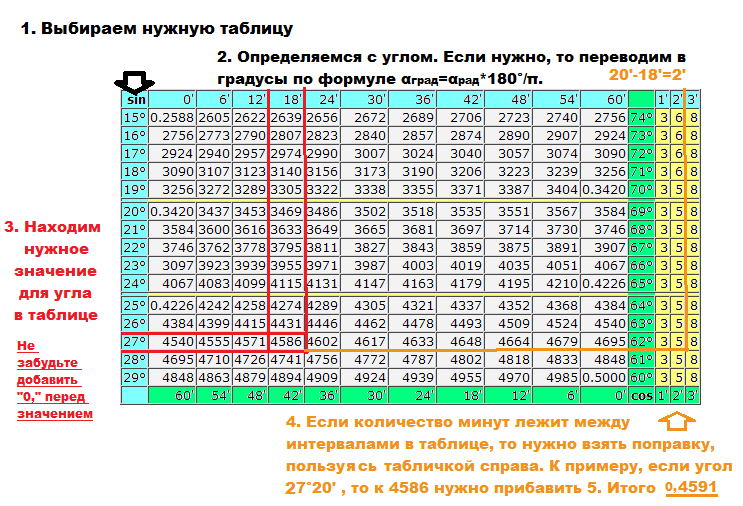
Таблица Брадиса: Косинусы-синусы
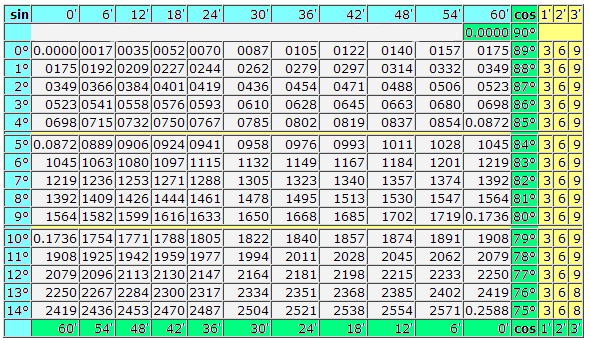
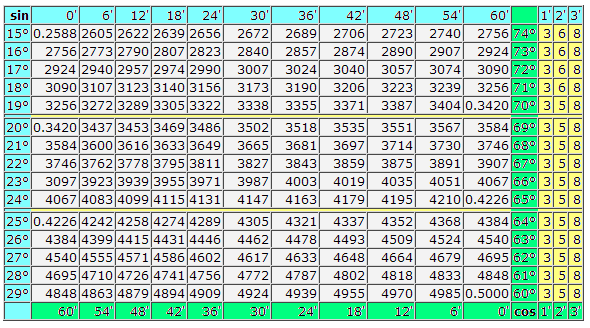
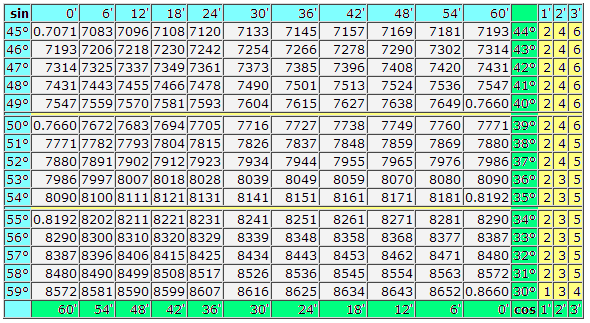
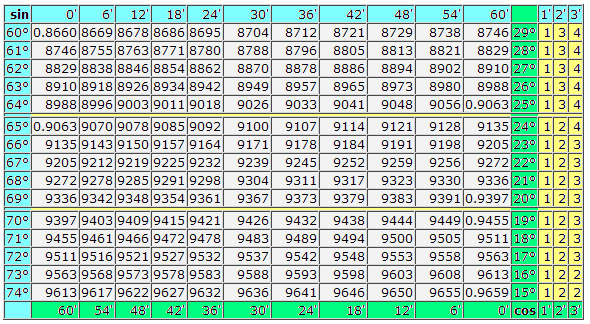
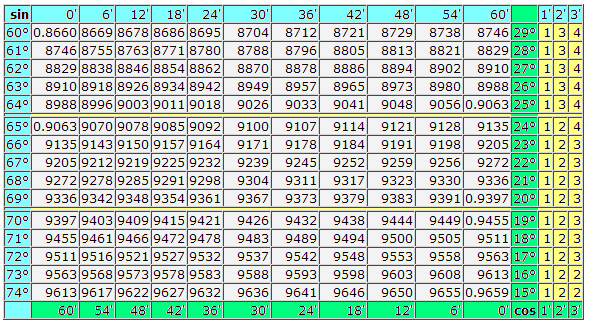
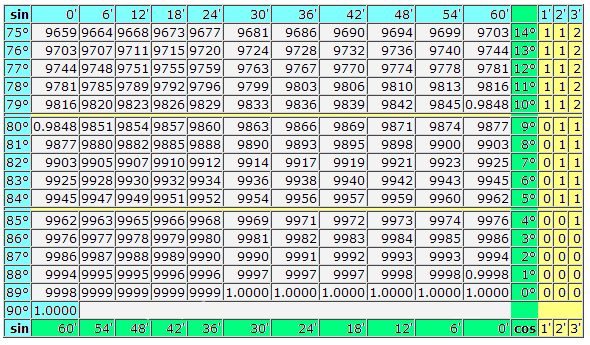
Таблица Брадиса: тангенсы — котангенсы
tg и ctg больших углов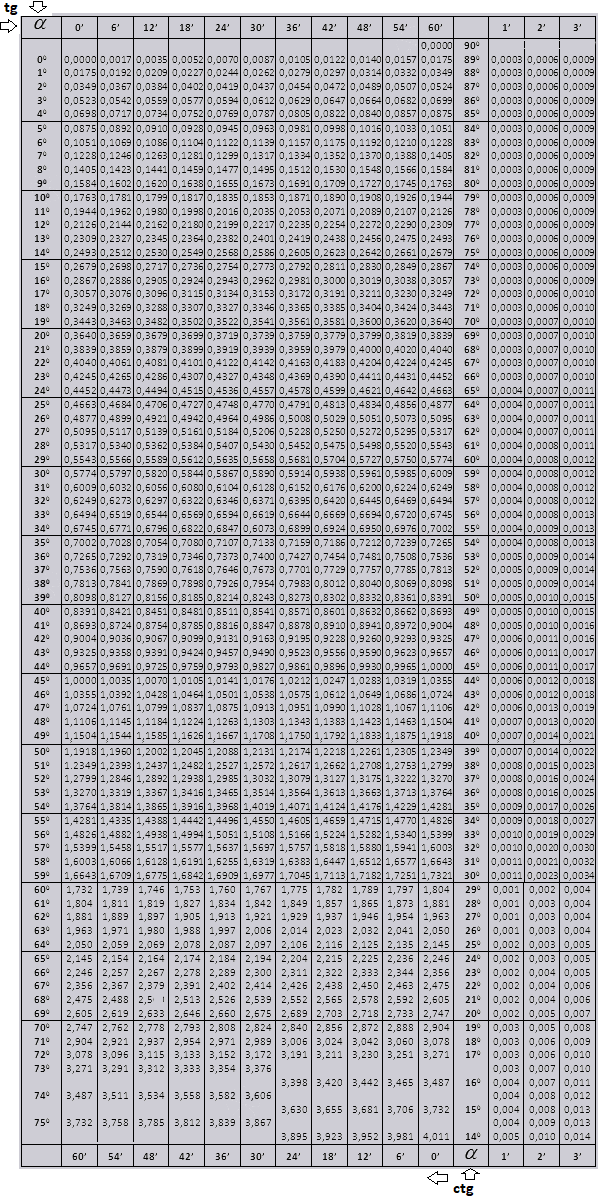
tg и ctg малых углов
Если по пользованию таблицами Брадиса у вас возникли какие то вопросы, то пишите их в комментариях.
Спасибо за пользование нашим сервисом.
Москвичей возможно заинтересует — дистанционное образование в москве. Учиться дистанционно — шикарная возможность стать свободнее уже сейчас.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Тригонометрическая таблица
В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса . Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90,…,360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
sin 00=0, cos 00 = 1. tg 00 = 0, котангенс от 00 будет неопределенным
sin 900 = 1, cos 900 =0, ctg900 = 0,тангенс от 900 будет неопределенным
Если взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим:
sin 300 = 1/2, cos 300 = √3/2, tg 300 = √3/3, ctg 300 = √3
sin 450 = √2/2, cos 450 = √2/2, tg 450= 1, ctg 450 = 1
sin 600 = √3/2, cos 600 = 1/2, tg 600 =√3 , ctg 600 = √3/3
Изобразим все полученные значения в виде тригонометрической таблицы
:Таблица синусов, косинусов, тангенсов и котангенсов!
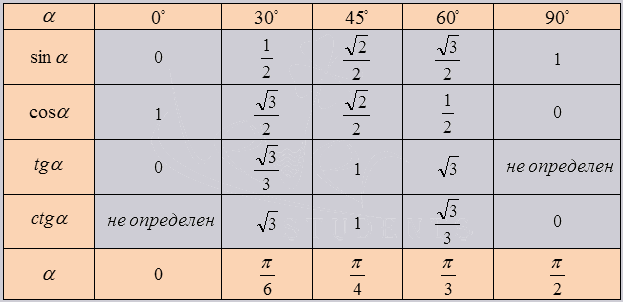
Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как:
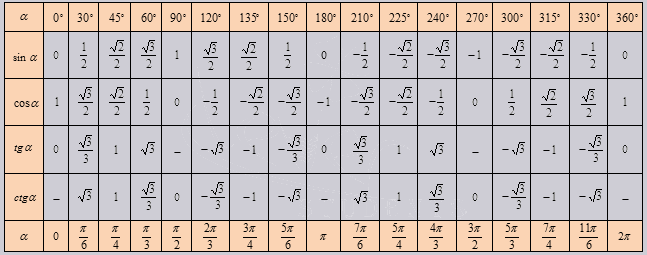
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 00+3600*z …. 3300+3600*z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.
Разберем наглядно как использовать таблицу в решении.
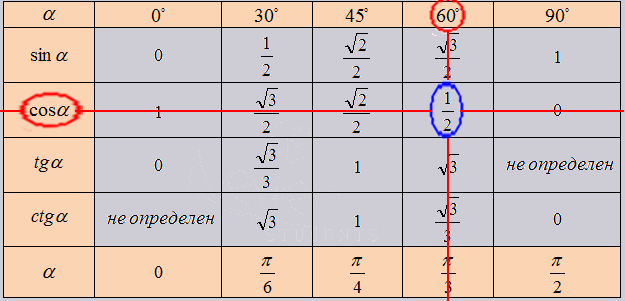
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:
В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 10200 = 3000+3600*2. Найдем по таблице.
Для более поиска тригонометрических значений углов с точностью до минут используются таблицы Брадиса. Подробная инструкция как ими пользоваться на странице по ссылке.
Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.
Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — которая поделена на две части (tg угла до 90 градусов и ctg малых углов).
Синус и косинус
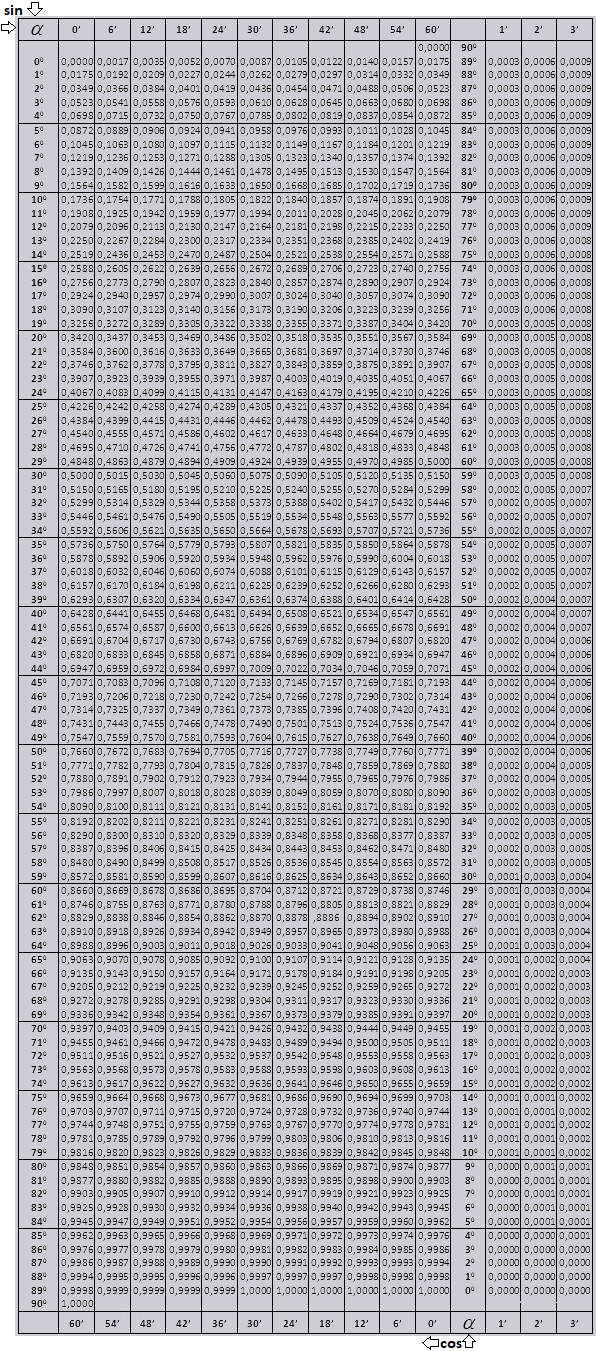
tg угла начиная с 00 заканчивая 760, ctg угла начиная с 140 заканчивая 900.
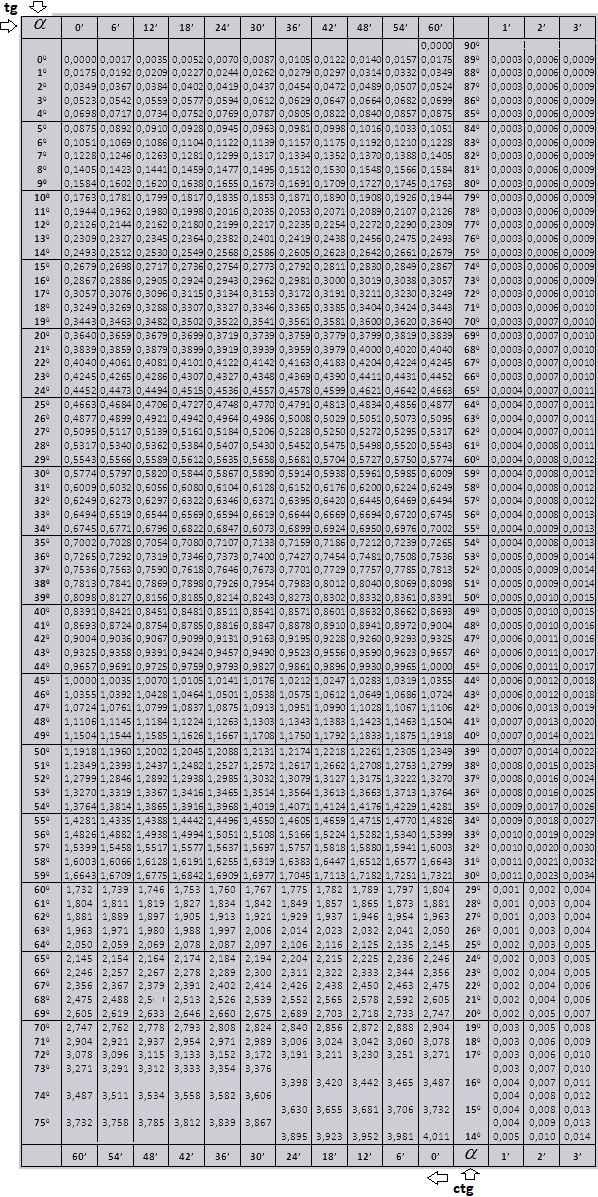
tg до 900 и ctg малых углов.
Разберемся как пользоваться таблицами Брадиса в решении задач.
Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.
Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.
При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054
При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 200 = 0.9397
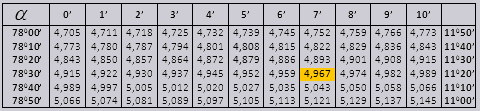
Значения tg угла до 900 и cot малого угла, верны и поправок в них нет. К примеру, найти tg 78 0 37мин = 4,967
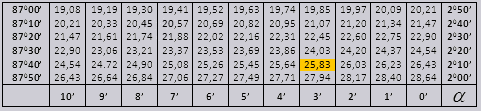
а ctg 200 13мин = 25,83
Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!
Заметка: Стеновые отбойники — отбойная доска для защиты стен (http://www.spi-polymer.ru/otboyniki/)
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Таблица Брадиса, с примерами
Правила пользования таблицами: таблицы дают значения синусов (косинусов) любого острого угла, содержащего целое число градусов и десятых долей градуса, на пересечении строки, имеющей в заголовке слева (справа) соответствующее число градусов, и столбца, имеющего в заголовке сверху (снизу) соответствующее число минут.
Тригонометрические функции sin x и cos x от аргумента в градусах
Таблица Брадиса тригонометрические функции tg x, ctg x от аргумента в градусах
Таблица Брадиса – тангенсы углов, близких к 90°, котангенсы малых углов
Тригонометрические функции от аргумента в радианах
Примеры решения задач
Если же нужно найти значение угла, которого нет в таблице, то выбирается наиболее близкое к нему значение, а на разницу берется поправочное значение из столбца поправок справа (возможная разница – 1′, 2′, 3′).
Замечание. Для косинусов поправка имеет отрицательный знак.
Эти правила справедливы и для нахождения значений тангенсов и котангенсов углов.
| Понравился сайт? Расскажи друзьям! | |||
Синус Косинус — Таблица Брадиса №8 (находить угол)
Таблица Брадиса — синусы и косинусы даёт значение синуса любого острого угла, содержащего целое число градусов и десятых долей градуса, на пересечении строки, имеющей в заголовке (слева) соответствующее число градусов, и столбца, имеющего в заголовке (сверху) соответствующее число минут. Так, sin 70°30’=0,9426. Для получения синусов прочих углов нужна интерполяция, вводящая поправку на разность между данным углом и ближайшим табличным. Эта поправка берётся из соответствующего столбца поправок справа (курсив). Она прибавляется к ближайшему меньшему значению синуса, если данный угол превосходит ближайший меньший табличный на 1, 2, 3 минуты, и отнимается от ближайшего большего табличного синуса в остальных случаях. Например, sin 70°32’=0,9428, так как 9426+2=9428, и sin 70°34’=0,9430, так как 9432-2 = 9430. Эта же таблица Брадиса служит для разыскания косинусов, причём надо пользоваться нумерацией градусов справа, нумерацией минут снизу, и не забывать, что при возрастании острого угла его косинус убывает. Подыскание косинусов можно устранить, заменяя их синусами дополнительных углов.
Таблица Брадиса 8 и таблица брадиса 9 — тангенсы и котангенсы позволяют решать и обратный вопрос, то-есть находить острый угол по данному значению его синуса или тангенса
Читайте также — как пользоваться таблицами Брадиса
Смотрите — все таблицы Брадиса
Таблица Брадиса 8 — cинусы и косинусы
СИНУСЫ | |||||||||||||||
| А | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 0,0000 | 90° | ||||||||||||||
| 0° | 0,0000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89° | 3 | 6 | 9 |
| 1° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88° | 3 | 6 | 9 |
| 2° | 0349 | 0366 | 0384 | 0401 | 0419 | 0436 | 0454 | 0471 | 0488 | 0506 | 0523 | 87° | 3 | 6 | 9 |
| 3° | 0523 | 0541 | 0558 | 0576 | 0593 | 0610 | 0628 | 0645 | 0663 | 0680 | 0698 | 86° | 3 | 6 | 9 |
| 4° | 0698 | 0715 | 0732 | 0750 | 0767 | 0785 | 0802 | 0819 | 0837 | 0854 | 0,0872 | 85° | 3 | 6 | 9 |
| 5° | 0,0872 | 0889 | 0906 | 0924 | 0941 | 0958 | 0976 | 0993 | 1011 | 1028 | 1045 | 84° | 3 | 6 | 9 |
| 6° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 83° | 3 | 6 | 9 |
| 7° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 1392 | 32° | 3 | 6 | 9 |
| 8° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 1564 | 81° | 3 | 6 | 9 |
| 9° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1702 | 1719 | 0,1736 | 80° | 3 | 6 | 9 |
| 10° | 0,1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 1908 | 79° | 3 | 6 | 9 |
| 11° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 78° | 3 | 6 | 9 |
| 12° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 2250 | 77° | 3 | 6 | 9 |
| 13° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 76° | 3 | 6 | 8 |
| 14° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 0,2588 | 75° | 3 | 6 | 8 |
| 15° | 0,2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 2756 | 74° | 3 | 6 | 8 |
| 16° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 2924 | 73° | 3 | 6 | 8 |
| 17° | 2924 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3030 | 72° | 3 | 6 | 8 |
| 18° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3256 | 71° | 3 | 6 | 8 |
| 19° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 0,3420 | 70° | 3 | 5 | 8 |
| 20° | 0,3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 69° | 3 | 5 | 8 |
| 21° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3746 | 68° | 3 | 5 | 8 |
| 22° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 67° | 3 | 5 | 8 |
| 23° | 3907 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 66° | 3 | 5 | 8 |
| 24° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 0,4226 | 65° | 3 | 5 | 8 |
| 25° | 0,4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 64° | 3 | 5 | 8 |
| 26° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 4540 | 63° | 3 | 5 | 8 |
| 27° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 62° | 3 | 5 | 8 |
| 28° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 61° | 3 | 5 | 8 |
| 29° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 0,5000 | 60° | 3 | 5 | 8 |
| 30° | 0,5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 5150 | 59° | 3 | 5 | 8 |
| 31° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 5299 | 58° | 2 | 5 | 7 |
| 32° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 57° | 2 | 5 | 7 |
| 33° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 56° | 2 | 5 | 7 |
| 34° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 0,5736 | 55° | 2 | 5 | 7 |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | А | 1′ | 2′ | 3′ | |
КОСИНУСЫ | |||||||||||||||
| СИНУСЫ | |||||||||||||||
| A | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 35° | 0,5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 0,5878 | 54° | 2 | 5 | 7 |
| 36° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 6018 | 53° | 2 | 5 | 7 |
| 37° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 32° | 2 | 5 | 7 |
| 38° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 6293 | 51° | 2 | 5 | 7 |
| 39° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 0,6428 | 30° | 2 | 4 | 7 |
| 40° | 0,6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 49° | 2 | 4 | 7 |
| 41° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 48° | 2 | 4 | 7 |
| 42° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 6820 | 47° | 2 | 4 | 6 |
| 43° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 6909 | 6921 | 6934 | 6947 | 46° | 2 | 4 | 6 |
| 44° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 0,7071 | 45° | 2 | 4 | 6 |
| 45° | 0,7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 44° | 2 | 4 | 6 |
| 46° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 43° | 2 | 4 | 6 |
| 47° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 7431 | 42° | 2 | 4 | 6 |
| 48° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 7547 | 41° | 2 | 4 | 6 |
| 49° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 0,7660 | 40° | 2 | 4 | 6 |
| 50° | 0,7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 7771 | 39° | 2 | 4 | 6 |
| 51° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 7880 | 38° | 2 | 4 | 5 |
| 52° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 37° | 2 | 4 | 5 |
| 53° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 8090 | 36° | 2 | 3 | 5 |
| 34° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 0,8192 | 35° | 2 | 3 | 5 |
| 55° | 0,8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 8290 | 34° | 2 | 3 | 5 |
| 56° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 33° | 2 | 3 | 5 |
| 57° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 8480 | 32° | 2 | 3 | 5 |
| 58° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 31° | 2 | 3 | 5 |
| 59° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 0,8660 | 30° | 1 | 3 | 4 |
| 60° | 0,8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 29° | 1 | 3 | 4 |
| 61° | 8746 | 8755. | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 28° | 1 | 3 | 4 |
| 62° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 8910 | 27° | 1 | 3 | 4 |
| 63° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 8988 | 26° | 1 | 3 | 4 |
| 64° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 0,9063 | 25° | 1 | 3 | 4 |
| 65° | 0,9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 9135 | 24° | 1 | 2 | 4 |
| 66° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 23° | 1 | 2 | 3 |
| 67° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9265 | 9272 | 22° | I | 2 | 3 |
| 68° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 9336 | 21° | 1 | 2 | 3 |
| 69° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9385 | 9391 | 0,9397 | 20° | 1 | 2 | 3 |
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | А | 1′ | 2′ | 3′ | |
| КОСИНУСЫ | |||||||||||||||
| СИНУСЫ | |||||||||||||||
| А | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
| 70° | 0,9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 0,9455 | 19° | 1 | 2 | 3 |
| 71° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 9511 | 18° | 1 | 2 | 3 |
| 72° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 17° | 1 | 2 | 3 |
| 73° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 16° | 1 | 2 | 2 |
| 74° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 0,9659 | 15° | 1 | 2 | 2 |
| 75° | 0,9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 9703 | 14° | 1 | 1 | 2 |
| 76° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 9744 | 13° | 1 | 1 | 2 |
| 77° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 9781 | 12° | 1 | 1 | 2 |
| 78° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 9816 | 11° | 1 | 1 | 2 |
| 79° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 0,9848 | 10° | 1 | 1 | 2 |
| 80° | 0,9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 9° | 0 | 1 | 1 |
| 81° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 9903 | 8° | 0 | 1 | 1 |
| 82° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 7° | 0 | 1 | 1 |
| 83° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 9945 | 6° | 0 | 1 | 1 |
| 84° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 0,9962 | 5° | 0 | 1 | 1 |
| 85° | 0,9962 | 9963 | 9965 | 9Г66 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 4° | 0 | 0 | 1 |
| 86° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 3° | 0 | 0 | 0 |
| 87° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 9994 | 2° | 0 | 0 | 0 |
| 88° | 9994 | 9995 | 9995 | 9S96 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 0,9998 | 1° | 0 | 0 | 0 |
| 89° | 9998 | 9999 | 9999 | 9999 | 9999 | 0000 | 0000 | 0000 | 0000 | 0000 | 1,0000 | 0° | 0 | 0 | 0 |
| 90° | 1.0000 | ||||||||||||||
| 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | А | 1′ | 2′ | 3′ | |
| КОСИНУСЫ | |||||||||||||||
Ниже вы можете скачать таблицу Брадиса — синусы и косинусы в виде изображений
_______________
Источник информации: Брадис В.М. Четырехзначные математические таблицы: Для средней школы. / В.М. Брадис . — 57-е изд., — М.: Просвещение, 1990.
| Техническая информация тут | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблицы Брадиса. Значения тригонометрических, логарифмических функций. Прочее / / Таблица Брадиса тригонометрические функции sin x, cos x от аргумента в угловых градусах. Таблица Брадиса синусы-косинусы. Значения тригонометрических функций. Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||