Онлайн системы неравенств – Калькулятор онлайн — Решение систем неравенств (линейных, квадратных и дробных) (с подробным решением)

Системы и совокупности неравенств. Видеоурок. Алгебра 11 Класс

В данном уроке мы рассмотрим системы и совокупности различных неравенств, приведем соответствующие примеры.

Тема: Уравнения и неравенства. Системы уравнений и неравенств

Урок: Системы и совокупности неравенств

Рассмотрим систему неравенств:

Мы знаем, как решить каждое из этих неравенств. Найти решение каждого неравенства – значит найти множество всех х, при которых неравенство обращается в верное числовое соотношение. Предположим, мы нашли такое множество для каждого из заданных уравнений системы:

Решить систему – означает найти все х, удовлетворяющие одновременно и первому, и второму неравенству, то есть принадлежащие и множеству А, и множеству В.

Пример 1 – решить систему неравенств:

Покажем решение системы графически:

Рис. 1. Иллюстрация к примеру

Очевиден ответ:

Комментарий: только значения х, находящиеся на выбранном отрезке, удовлетворяют одновременно первому и второму неравенству.

Рассмотрим совокупность двух неравенств:

Предположим, мы нашли решения обоих неравенств:

Решить совокупность – означает найти все х, которые удовлетворяют хотя бы одному неравенству, то есть входят хотя бы в одно из множеств А или В.

Например:

Полученные интервалы проиллюстрированы на рисунке 10.1. Очевиден ответ:

Теперь можем дать строгие определения.

Рис. 2. Пересечение двух множеств

Определение:

Пересечением двух множеств А и В называют такое множество С, которое состоит из всех элементов, входящих одновременно и в множество А, и в множество В.

 

Рис. 3. Объединение двух множеств

Определение:

Объединением двух множеств А и В называют такое множество D, которое состоит из всех элементов, входящих хотя бы в одно из множеств А или В.

 

 

Пример 1 – решить систему и совокупность:

а)

interneturok.ru

Системы линейных неравенств. Решение систем линейных неравенств

Системой линейных неравенств – называют несколько линейных неравенств, которые должны выполняться одновременно

Например:

\begin{cases}x>4\\x\leq7\end{cases} \begin{cases}2x-5\geq11\\3+x>7\end{cases} \begin{cases}2x\leq19\\3x<14\\5x>-1\end{cases}

Примеры не систем линейных неравенств:

\(\begin{cases}3>4\\x\leq7\end{cases}\)		– первое неравенство не линейное, а числовое
\(\begin{cases}2x^{2}-5\geq11\\3+\frac{1}{x}>7\end{cases}\)		– первое неравенство квадратное, второе дробно-рациональное, т.е. оба не линейные
\(\left[ \begin{gathered} 2x\leq19 \\ 3x<14\\ 5x>-1\\ \end{gathered} \right.\)		—  а это совокупность линейных неравенств, а не система

Решение систем линейных неравенств

Чтобы решить систему неравенств мы должны найти значения иксов, которые подойдут всем неравенствам в системе.

Пример: Решим систему \(\begin{cases}x>4\\x\leq7\end{cases}\)
Решение: Первое неравенство становится верным, если икс больше \(4\). То есть, решения первого неравенства – все значения иксов из интервала \((4;\infty)\), или на числовой оси:

Второму неравенству подойдут значения иксов меньшие чем 7, включая саму семерку, то есть любой икс  из интервала \((-\infty;7]\) или на числовой оси:

А какие значения подойдут обоим неравенствам? Те, которые принадлежат обоим промежуткам, то есть где промежутки пересекаются.

Ответ: \((4;7]\)

Как вы могли заметить для пересечения решений неравенств в системе удобно использовать числовые оси.

Если в системе находятся требующие преобразований неравенства, то при решении системы каждое неравенство независимо от других преобразовывается к одному из видов: \(x<c\), \(x>c\), \(x\leq c\), \(x\geq c\). И только после этого ищут общее решение, пересекая решения неравенств на числовой оси.

Пример:  Решить систему \(\begin{cases}x-4\geq0\\x-0,3\geq1\end{cases}\)
Решение:

\(\begin{cases}x-4\geq0\\x-0,3\geq1\end{cases}\)		Перенесем \(-4\) и \(-0,3\) в правую сторону, меняя при этом их знак
\(\begin{cases}x\geq4\\x\geq1,3\end{cases}\)		Отметим решения на числовой оси
		Запишем общее решения неравенств

Ответ: \([4;+\infty)\)

Пример:  Решить систему \(\begin{cases}4(x-1)<3x+1\\-3x+7\geq4(1-x)\end{cases}\)
Решение:

\(\begin{cases}4(x-1)<3x+1\\-3x+7\geq4(1-x)\end{cases}\)		Раскроем в каждом неравенстве скобки
\(\begin{cases}4x-4<3x+1\\-3x+7\geq4-4x\end{cases}\)		Слагаемые с иксом в одну сторону,слагаемые без икса в другую
\(\begin{cases}4x-3x<1+4\\-3x+4x\geq4-7\end{cases}\)		Приведем подобные слагаемые
\(\begin{cases}x<5\\x\geq-3\end{cases}\)		Объединим решения на числовой оси
		Запишем ответ

Ответ: \([-3;5)\)

Заметьте, что для решения первой системы мы использовали две числовые оси, пересекая их пунктиром, а для решения второй и третьей – одну ось. Вы можете сами выбирать сколько осей вам рисовать, оба варианта допустимы. Однако в больших системах (\(3\) или более неравенства) советую для каждого неравенства чертить свою ось.

Системы линейных неравенств и двойные неравенства

Помимо рассмотренных выше примеров, есть особый вид систем линейных неравенств: двойные неравенства. Они притворяются, что совсем не системы, но на самом деле еще какие системы!

Например:  
— неравенство \(3<x-1<7\)  можно записать как  \(\begin{cases}x-1>3\\x-1<7\end{cases}\)
— неравенство \(2x-5<3x+7≤8x\) можно записать как \(\begin{cases}2x-5< 3x+7\\3x+7\leq8x\end{cases}\)

Первое неравенство удобнее решать в виде двойного, из-за того, что в левой и правой части нет

переменных. А вот второе лучше решать как систему из-за того, что иксы есть во всех трех частях неравенства.

Скачать статью

cos-cos.ru

Найти область решений и область допустимых решений системы неравенств — 22 Апреля 2015 — Примеры решений задач

Контрольная работа по дисциплине “Методы оптимальных решений”

Задание 1  Найти область решений и область допустимых решений системы неравенств:

$\left\{\begin{matrix}x_1-x_2\leq 1\\ x_1-2x_2\leq 1\\x_1\leq 0.25\end{matrix}\right..$

Решение.

Построим область решений, т.е. решим графически систему неравенств. Для этого построим каждую прямую и определим полуплоскости, заданные неравенствами (полуплоскости обозначены штрихом).

Построим уравнение x₁-x₂ = 1 по двум точкам.
Для нахождения первой точки приравниваем x₁ = 0. Находим x₂

= -1. Для нахождения второй точки приравниваем x₂ = 0. Находим x₁ = 1. Соединяем точку (0;-1) с (1;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 1 • 0 — 1 • 0 — 1 ≤ 0, т.е. x₁-x₂ — 1≤ 0 в полуплоскости ниже прямой.
Построим уравнение x₁-2x₂ = 1 по двум точкам.
Для нахождения первой точки приравниваем x₁ = 0. Находим x₂ = -0.5. Для нахождения второй точки приравниваем x₂ = 0. Находим x₁ = 1. Соединяем точку (0;-0.5) с (1;0) прямой линией. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 1 • 0 — 2 • 0 — 1 ≤ 0, т.е. x₁-2x₂ — 1≥ 0 в полуплоскости выше прямой.
Построим уравнение x₁ = 0.25.
Эта прямая проходит через точку x₁ = 0.25 параллельно оси OX₂. Определим полуплоскость, задаваемую неравенством. Выбрав точку (0; 0), определим знак неравенства в полуплоскости: 1 • 0 — 0.25 ≤ 0, т.е. x₁ — 0.25≥ 0 в полуплоскости правее прямой.

Пересечением полуплоскостей будет являться область, координаты точек которого удовлетворяют условию неравенствам системы ограничений задачи.

Получаем область решений (ОР), треугольник ABC

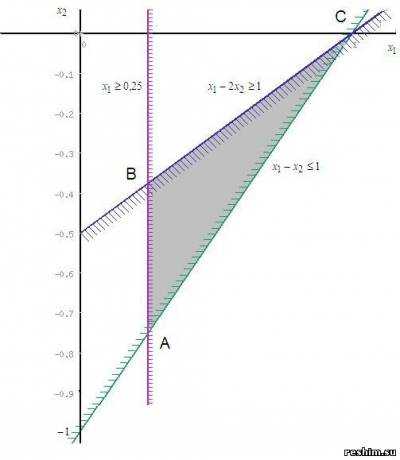
Область решения (ОР) системы, удовлетворяющая условиям неотрицательности (xj ≥ 0, j = 1,n), называется областью неотрицательных, или допустимых, решений (ОДР). Следовательно, задача области допустимых значений (ОДР) не имеет.

 

www.reshim.su

StudyPort.Ru — Система неравенств. Решения системы

Системой неравенств называется совокупность неравенств, для которых нужно найти значения неизвестных, удовлетворяющие одновременно всем неравенствам системы.

Значения неизвестных, удовлетворяющие одновременно всем уравнением системы называются решениями системы.

 

Примеры систем неравенств:

 

Системы неравенств могут состоять из двух и более неравенств и содержать одну и более переменных. Система неравенств может не иметь решений, иметь несколько решений, иметь бесконечное множество решений.

В школьной программе изучаются системы, содержащие одну переменную.

Для решения различных видов систем разработано много различных методов решения, но   в рамках школьного курса рассматривается один самый простой метод. Он заключается в том, что мы решаем каждое неравенство в отдельности, а затем все полученные решения пересекаем на координатной оси.    

 

Примеры решения систем неравенств.

1. Решить систему неравенств 

Решим первое неравенство:

x²-4 < 0;

(x-2)(x+2) < 0.

Решим это неравенство методом интервалов.

Решением этого неравенства будет промежуток (-2;2).

Второе неравенство уже решено — пересекаем решения первого и второго неравенства.

Итак, решением системы неравенств будет промежуток (-2;1).

Ответ: (-2;1).

 2. Решить систему неравенств 

Решим первое неравенство:

 

Решим второе неравенство:

x-12 < 1;

x < 13.

Пересекаем решения первого и второго неравенства.

Итак, решение системы неравенств — промежуток [8;13).

Ответ: [8;13).

studyport.ru

Решение системы неравенств с модулем

Решим систему неравенств с модулем из варианта №50 А. Ларина.

Решим каждое неравенство системы по отдельности, а потом совместим решения обоих неравенств на одной координатной прямой.

1. Решим первое неравенство системы.

Чтобы решить неравенство, содержащее модули, нужно раскрыть модули.

Приравняем каждое подмодульное выражение к нулю и найдем точки, в которых подмодульные выражения меняют знак.

Нанесем эти значения на числовую прямую:

Мы получили три промежутка. Найдем знаки каждого подмодульного выражения на каждом промежутке:

Раскроем модули на каждом промежутке (мы можем граничные точки  и  включать в оба промежутка):

а)

На этом промежутке оба подмодульных выражения отрицательны, поэтому мы раскрываем модули с противоположным знаком:

(1)

Так как исходное неравенство «превращается» в неравенство (1) только при , получим систему неравенств:

.

Решим первое неравенство, и получим систему:

.

Решением системы неравенств является промежуток:

б)

На этом промежутке первое подмодульное выражение положительно, а второе отрицательно, поэтому первый модуль мы раскрываем с тем же знаком, а второй с противоположным.

Получаем неравенство:

(2)

Так как исходное неравенство «превращается» в неравенство (2) только при , получим систему неравенств:

или

Решением системы неравенств является промежуток:

в)

На этом промежутке оба подмодульных выражения положительны, поэтому оба модуля мы раскрываем с тем же знаком.

Получаем неравенство:

(3)

Так как исходное неравенство «превращается» в неравенство (3) только при , получим систему неравенств:

или

Решением системы является промежуток:

Объединим три промежутка и получим решение первого неравенства исходной системы:

2. Решим второе неравенство системы.

Приведем левую часть неравенства к общему основанию. Сначала разложим на множители знаменатель первой дроби:

Решим это неравенство методом интервалов.

Найдем корни числителя и знаменателя и нанесем их на числовую ось.

На самом правом промежутке , поэтому знаки расставим так:

Нас интересуют промежутки со знаком «-«:

следовательно, решение этого неравенства:

Совместим решения первого и второго неравенств исходной системы на одной координатной прямой и найдем их пересечение:

 

Ответ: [-2;1)(2;2,4]

И.В. Фельдман, репетитор по математике.

ege-ok.ru