Часть 1.
(Часть 2 см. здесь)
Примеры решения простейших тригонометрических неравенств
Простейшими тригонометрическими неравенствами называются неравенства вида
 ,
,
 ,
,
 ,
,
 ,
,
где 
 ,
,  .
.Вы должны прежде, конечно, хорошо ориентироваться в тригонометрическом круге и уметь решать простейшие тригонометрические уравнения (часть I, часть II).

Кстати, умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.
Сначала мы рассмотрим простейшие тригонометрические неравенства с синусом и косинусом
. Во второй части статьи – с тангенсом, котангенсом.Пример 1.
Решить неравенство: 
Решение:
Отмечаем на оси косинусов 
Все значения  , меньшие
, меньшие  – левее точки
– левее точки 

Отмечаем все точки (дугу, точнее – серию дуг) тригонометрического круга, косинус которых будет меньше 

Полученную дугу мы проходим против часовой стрелки (!), то есть от точки  до
до 
Обратите внимание, многие, назвав первую точку  вместо второй точки
вместо второй точки  указывают точку
указывают точку  , что неверно!
, что неверно!
Становится видно, что неравенству удовлетворяют следующие значения 

Следите за тем, чтобы «правая/вторая точка» была бы больше «левой/первой».
Не забываем «накидывать» счетчик 
Вот так выглядит графическое решение неравенства не на тригонометрическом круге, а в прямоугольной системе координат:

Пример 2.
Решить неравенство: 
Решение:
Отмечаем на оси косинусов 
Все значения  , большие или равные
, большие или равные  – правее точки
– правее точки  , включая саму точку.
, включая саму точку.
Тогда выделенные красной дугой аргументы 
 .
.

Пример 3.
Решить неравенство: 
Решение:
Отмечаем на оси синусов 
Все значения  , большие или равные
, большие или равные  – выше точки
– выше точки  , включая саму точку.
, включая саму точку.

«Транслируем» выделенные точки на тригонометрический круг:


Пример 4.
Решить неравенство: 
Решение:
Кратко:


или все 

Пример 5.
Решить неравенство: 
Решение:
Неравенство  равносильно уравнению
равносильно уравнению  , так как область значений функции
, так как область значений функции 
![Rendered by QuickLaTeX.com [-1;1].](http://xn----8sbanwvcjzh9e.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)


Пример 6.
Решить неравенство: 
Решение:
Действия – аналогичны применяемым в примерах выше. Но дело мы имеем не с табличным значением синуса.
Здесь, конечно, нужно знать определение арксинуса.


Если не очень понятно, загляните сюда –>+ показать
Согласны с таким вариантом (одним из) названия углов, соответствующих тому, что синус в них равен 

А теперь мы должны позаботиться о том, чтобы правый конец промежутка, являющего собой решение неравенства, был бы больше левого конца.
Поэтому

Тренируемся в решении простейших тригонометрических неравенств
Имейте ввиду, решения (ответы) к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. Например, в задании 2 ответ можно было записать и так: 
1. Решить неравенство: 
Ответ: + показать

2. Решить неравенство: 
Ответ: + показать

3. Решить неравенство: 
Ответ: + показать

4. Решить неравенство: 
Ответ: + показать
![Rendered by QuickLaTeX.com [2\pi n;\pi +2\pi n,\;n\in Z]](http://xn----8sbanwvcjzh9e.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
5. Решить неравенство: 
Ответ: + показать
![Rendered by QuickLaTeX.com [arccos0,2+2\pi n;2\pi-arccos0,2+2\pi n,\;n\in Z]](http://xn----8sbanwvcjzh9e.xn--p1ai/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
Часть 2
Если у вас есть вопросы, – пожалуйста, – спрашивайте!

Тригонометрические уравнения и неравенства
Тригонометрические уравнения и неравенстваРешение простейших тригонометрических уравнений
Простейшими тригонометрическими уравнениями называют уравнения cos x = a, sin x = a, tg x = a, ctg x = a.
Чтобы рассуждения по нахождению корней этих уравнений были более наглядными, воспользуемся графиками соответствующих функций.
Уравнение cos x = a
Примеры решения задач
Уравнение sin x = a
Примеры решения задач
Уравнение tg x = a и ctg x = a
Примеры решения задач
Решение тригонометрических уравнений, отличающихся от простейших
Как правило, решение тригонометрических уравнений сводится к решению простейших уравнений с помощью преобразований тригонометрических выражений, разложения на множители и замены переменных.
Замена переменных при решении тригонометрических уравнений
Если в уравнение, неравенство или тождество переменная входит в одном и том же виде, то удобно соответствующее выражение с переменной обозначить одной буквой (новой переменной).
При поиске плана решения более сложных тригонометрических уравнений можно воспользоваться таким ориентиром:
-
Пробуем привести все тригонометрические функции к одному аргументу.
-
Если удалось привести к одному аргументу, то пробуем все тригонометрические выражения привести к одной функции.
-
Если к одному аргументу удалось привести, а к одной функции — нет, тогда пробуем привести уравнение к однородному.
-
В других случаях переносим все члены в одну сторону и пробуем получить произведение ил используем специальные приемы решения.
Решение тригонометрических уравнений приведением к одной функции
Решение простейших тригонометрических неравенств
Тригонометрические неравенства и их решения
Решение тригонометрических неравенств
Решение тригонометрических неравенств зачастую сводится к решению простейших тригонометрических неравенств вида:
Решаются простейшие тригонометрические неравенства графически или с помощью единичной тригонометрической окружности.
По определению, синусом угла есть ординатой точки единичного круга (рис. 1), а косинусом – абсцисса этой точки. Этот факт используется при решении простейших тригонометрических неравенств с косинусом и синусом с помощью единичного круга.
Рис. 1
Примеры решения тригонометрических неравенств
Тригонометрические неравенства со сложным аргументом
Тригонометрические неравенства со сложным аргументом можно свести к простейшим тригонометрическим неравенствам с помощью замены. После его решения делается обратная замена и выражается исходная неизвестная.
Двойные тригонометрические неравенства
| Понравился сайт? Расскажи друзьям! | |||
Неравенства – это соотношения вида a › b, где a и b – есть выражения, содержащие как минимум одну переменную. Неравенства могут быть строгими — ‹, › и нестрогими — ≥, ≤.
Тригонометрические неравенства представляют собой выражения вида: F(x) › a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a, в которых F(x) представлено одной или несколькими тригонометрическими функциями.
Простейшие тригонометрические неравенства
Примером простейшего тригонометрического неравенства является: sin x ‹ 1/2. Решать подобные задачи принято графически, для этого разработаны два способа.
Способ 1 — Решение неравенств с помощью построения графика функции
Чтобы найти промежуток, удовлетворяющий условиям неравенство sin x ‹ 1/2, необходимо выполнить следующие действия:
- На координатной оси построить синусоиду y = sin x.
- На той же оси начертить график числового аргумента неравенства, т. е. прямую, проходящую через точку ½ ординаты ОY.
- Отметить точки пересечения двух графиков.
- Заштриховать отрезок являющийся, решением примера.

Когда в выражении присутствуют строгие знаки, точки пересечения не являются решениями. Так как наименьший положительный период синусоиды равен 2π, то запишем ответ следующим образом:

Если знаки выражения нестрогие, то интервал решений необходимо заключить в квадратные скобки — [ ]. Ответ задачи можно также записать в виде очередного неравенства: 
Способ 2 — Решение тригонометрических неравенств с помощью единичной окружности
Подобные задачи легко решаются и с помощью тригонометрического круга. Алгоритм поиска ответов очень прост:
- Сначала стоит начертить единичную окружность.
- Затем нужно отметить значение аркфункции аргумента правой части неравенства на дуге круга.
- Нужно провести прямую проходящую через значение аркфункции параллельно оси абсциссы (ОХ).
- После останется только выделить дугу окружности, являющуюся множеством решений тригонометрического неравенства.
- Записать ответ в требуемой форме.
Разберем этапы решения на примере неравенства sin x › 1/2. На круге отмечены точки α и β – значения

Точки дуги, расположенные выше α и β, являются интервалом решения заданного неравенства.

Если нужно решить пример для cos, то дуга ответов будет располагаться симметрично оси OX, а не OY. Рассмотреть разницу между интервалами решений для sin и cos можно на схемах приведенных ниже по тексту.

Графические решения для неравенств тангенса и котангенса будут отличаться и от синуса, и от косинуса. Это обусловлено свойствами функций.

Арктангенс и арккотангенс представляют собой касательные к тригонометрической окружности, а минимальный положительный период для обеих функций равняется π. Чтобы быстро и правильно пользоваться вторым способом, нужно запомнить на какой из оси откладываются значения sin, cos, tg и ctg.
Касательная тангенс проходит параллельно оси OY. Если отложить значение arctg a на единичном круге, то вторая требуемая точка будет расположено в диагональной четверти. Углы
 являются точками разрыва для функции, так как график стремится к ним, но никогда не достигает.
являются точками разрыва для функции, так как график стремится к ним, но никогда не достигает.

В случае с котангенсом касательная проходит параллельно оси OX, а функция прерывается в точках π и 2π.

Сложные тригонометрические неравенства
Если аргумент функции неравенства представлен не просто переменной, а целым выражением содержащим неизвестную, то речь уже идет о сложном неравенстве. Ход и порядок его решения несколько отличаются от способов описанных выше. Допустим необходимо найти решение следующего неравенства:

Графическое решение предусматривает построение обычной синусоиды y = sin x по произвольно выбранным значениям x. Рассчитаем таблицу с координатами для опорных точек графика:

В результате должна получиться красивая кривая.
Для простоты поиска решения заменим сложный аргумент функции



Пересечение двух графиков позволяет определить область искомых значений, при которых выполняется условие неравенства.

Найденный отрезок является решением для переменной t:

Однако, цель задания найти все возможные варианты неизвестной x:

Решить двойное неравенство достаточно просто, нужно перенести π/3 в крайние части уравнения и произвести требуемые вычисления:

Ответ на задание будет выглядеть как интервал для строгого неравенства:

Подобные задачи потребует опыта и сноровки учащихся в обращении с тригонометрическими функциями. Чем больше тренировочных заданий будет решено в процессе подготовке, тем проще и быстрее школьник найдет ответ на вопрос ЕГЭ теста.
Похожие статьи
Рекомендуем почитать:
1. Синус и косинус любого угла (пропедевтика к изучению тригонометрических уравнений)
Пример задания. Найти приближенно углы, косинусы которых равны 0,8.
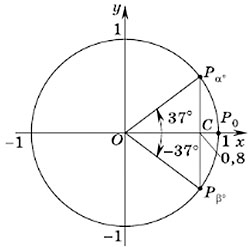
Решение. Косинус — это абсцисса соответствующей точки единичной окружности. Все точки с абсциссами, равными 0,8, принадлежат прямой, параллельной оси ординат и проходящей через точку C(0,8; 0). Эта прямая пересекает единичную окружность в двух точках: Pα° и Pβ°, симметричных относительно оси абсцисс.
С помощью транспортира находим, что угол α° приближенно равен 37°. Значит, общий вид углов поворота с конечной точкой Pα°:
α° ≈ 37° + 360°n, где n — любое целое число.
В силу симметрии относительно оси абсцисс точка Pβ° — конечная точка поворота на угол –37°. Значит, для нее общий вид углов поворота:
β° ≈ –37° + 360°n, где n — любое целое число.
Ответ: 37° + 360°n, –37° + 360°n, где n— любое целое число.
Пример задания. Найти углы, синусы которых равны 0,5.
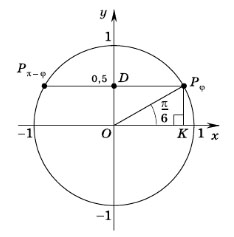
Решение. Синус — это ордината соответствующей точки единичной окружности. Все точки с ординатами, равными 0,5, принадлежат прямой, параллельной оси абсцисс и проходящей через точку D(0; 0,5).
Эта прямая пересекает единичную окружность в двух точках: Pφ и Pπ–φ, симметричных относительно оси ординат. В прямоугольном треугольнике OKPφ катет KPφ равен половине гипотенузы OPφ, значит, 
Общий вид углов поворота с конечной точкой Pφ:
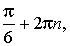
где n — любое целое число. Общий вид углов поворота с конечной точкой Pπ–φ:
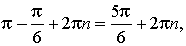
где n — любое целое число.
Ответ: 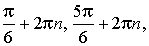 где n — любое целое число.
где n — любое целое число.
2. Тангенс и котангенс любого угла (пропедевтика к изучению тригонометрических уравнений)
Пример 2. Найти общий вид углов, тангенс которых равен –1,2.
Пример задания. Найти общий вид углов, тангенс которых равен –1,2.
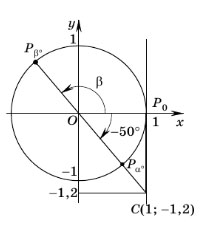
Решение. Отметим на оси тангенсов точку C с ординатой, равной –1,2, и проведем прямую OC. Прямая OC пересекает единичную окружность в точках Pα° и Pβ° — концах одного и того же диаметра. Углы, соответствующие этим точкам, отличаются друг от друга на целое число полуоборотов, т.е. на 180°n (n — целое число). С помощью транспортира находим, что угол Pα° OP0 равен –50°. Значит, общий вид углов, тангенс которых равен –1,2, следующий: –50° + 180°n (n — целое число)
Ответ: –50° + 180°n, n ∈ Z.
По синусу и косинусу углов 30°, 45° и 60° легко найти их тангенсы и котангенсы. Например,
Перечисленные углы довольно часто встречаются в разных задачах, поэтому полезно запомнить значения тангенса и котангенса этих углов.
|
α° |
30° |
45° |
60° |
|
φ рад |
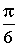
|
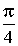
|

|
|
tg φ |
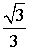
|
1 |

|
|
ctg φ |

|
1 |

|

Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 11 класс. Базовый уровень
Учебник входит в УМК по математике для 10–11 классов, изучающих предмет на базовом уровне. Теоретический материал разделен на обязательный и дополнительный, система заданий дифференцирована по уровню сложности, каждый пункт главы завершается контрольными вопросами и заданиями, а каждая глава — домашней контрольной работой. В учебник включены темы проектов и сделаны ссылки на интернет-ресурсы.
Купить3. Простейшие тригонометрические уравнения
Вводятся обозначения: arcsin α, arccos α, arctg α, arcctg α. Не рекомендуется торопиться с введением объединенной формулы. Две серии корней значительно удобнее записывать, особенно, когда нужно отбирать корни на интервале.
|
tg φ = α, φ = arctg α + πn, n ∊ Z,
т.е. arctg α — угол из промежутка tg (arctg α) = α. |
|
ctg φ = α, φ = arcctg α + πn, n ∊ Z, 0 < arcctg α < π, т.е. arcctg α — угол из промежутка (0; π), котангенс которого равен α, ctg (arcctg α) = α. |
При изучении темы «простейшие тригонометрические уравнения», уравнения чаще всего сводятся к квадратам.
4. Формулы приведения
Формулы приведения являются тождествами, т. е. они верны для любых допустимых значений φ. Анализируя полученную таблицу, можно заметить, что:
1) знак в правой части формулы совпадает со знаком приводимой функции в соответствующей четверти, если считать φ острым углом;
2) название меняют только функции углов  и
и 
|
α |
φ + 2πn |
– φ |
π – φ |
π + φ |
|
sin α |
sin φ |
– sin φ |
sin φ |
– sin φ |
|
cos α |
cos φ |
cos φ |
– cos φ |
– cos φ |
|
tg α |
tg φ |
– tg φ |
– tg φ |
tg φ |
|
ctg α |
ctg φ |
– ctg φ |
– ctg φ |
ctg φ |
|
α |

|
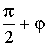
|

|
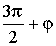
|
|
sin α |
cos φ |
cos φ |
– cos φ |
– cos φ |
|
cos α |
sin φ |
– sin φ |
– sin φ |
sin φ |
|
tg α |
ctg φ |
– ctg φ |
ctg φ |
– ctg φ |
|
ctg α |
tg φ |
— tg φ |
tg φ |
– tg φ |
5. Свойства и график функции y = sin x
Простейшие тригонометрические неравенства решаются либо по графику, либо на окружности. При решении тригонометрического неравенства на окружности важно не перепутать, какую точку указывать первой.
Что ещё почитать?
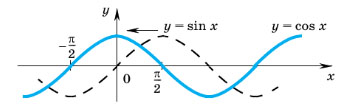
6. Свойства и график функции y = cos x
Задачу построения графика функции y = cos x можно свести к построению графика функции y = sin x. Действительно, поскольку 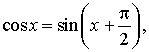 график функции y = cos x можно получить из графика функции y = sin x сдвигом последнего вдоль оси абсцисс влево на
график функции y = cos x можно получить из графика функции y = sin x сдвигом последнего вдоль оси абсцисс влево на 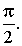
7. Свойства и графики функций y = tg x и y = ctg x
Область определения функции y = tg x включает в себя все числа, кроме чисел вида 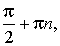 где n ∈ Z. Как и при построении синусоиды, сначала постараемся получить график функции y = tg x на промежутке
где n ∈ Z. Как и при построении синусоиды, сначала постараемся получить график функции y = tg x на промежутке 
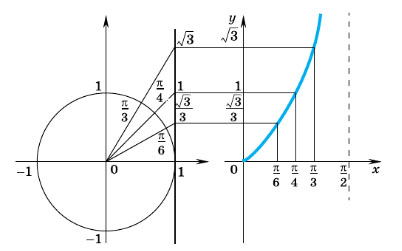
В левом конце этого промежутка тангенс равен нулю, а при приближении к правому концу значения тангенса неограниченно увеличиваются. Графически это выглядит так, как будто график функции y = tg x прижимается к прямой 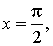 уходя вместе с ней неограниченно вверх.
уходя вместе с ней неограниченно вверх.
8. Зависимости между тригонометрическими функциями одного и того же аргумента
Равенства 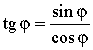 и
и 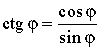 выражают соотношения между тригонометрическими функциями одного и того же аргумента φ. С их помощью, зная синус и косинус некоторого угла, можно найти его тангенс и котангенс. Из этих равенств легко получить, что тангенс и котангенс связаны между собой следующим равенством.
выражают соотношения между тригонометрическими функциями одного и того же аргумента φ. С их помощью, зная синус и косинус некоторого угла, можно найти его тангенс и котангенс. Из этих равенств легко получить, что тангенс и котангенс связаны между собой следующим равенством.
tg φ · ctg φ = 1
Есть и другие зависимости между тригонометрическими функциями.
Уравнение единичной окружности с центром в начале координат x2 + y2 = 1 связывает абсциссу и ординату любой точки этой окружности.
Основное тригонометрическое тождество
cos2 φ + sin2 φ = 1
9. Синус и косинус суммы и разности двух углов
Формула косинуса суммы
cos (α + β) = cos α cos β – sin α sin β
Формула косинуса разности
cos (α – β) = cos α cos β + sin α sin β
Формула синуса разности
sin (α – β) = sin α cos β – cos α sin β
Формула синуса суммы
sin (α + β) = sin α cos β + cos α sin β
10. Тангенс суммы и тангенс разности двух углов
Формула тангенса суммы

Формула тангенса разности


Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 11 класс. Углубленный уровень. Учебник
Учебник входит в УМК по математике для 10–11 классов, изучающих предмет на базовом уровне. Теоретический материал разделен на обязательный и дополнительный, система заданий дифференцирована по уровню сложности, каждый пункт главы завершается контрольными вопросами и заданиями, а каждая глава — домашней контрольной работой. В учебник включены темы проектов и сделаны ссылки на интернет-ресурсы.
Купить11. Тригонометрические функции двойного угла
Формула тангенса двойного угла
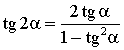
cos2α = 1 – 2sin2α cos2α = 2cos2α – 1
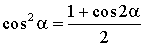
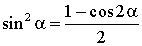
Пример задания. Решить уравнение 
Решение. 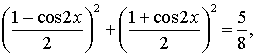
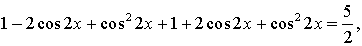
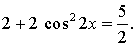
Понизим степень еще раз:
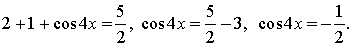


Ответ: 
12. Преобразование произведения тригонометрических функций в сумму. Обратное преобразование
Основные формулы
Переход от суммы к произведению
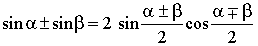
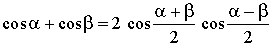
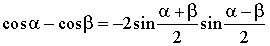
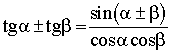
Переход от произведения к сумме

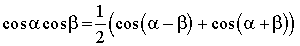
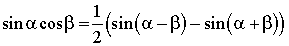
13. Решение тригонометрических уравнений
В большинстве случаев исходное уравнение в процессе решения сводится к простейшим тригонометрическим уравнениям. Однако для тригонометрических уравнений не существует единого метода решения. В каждом конкретном случае успех зависит от знания тригонометрических формул и от умения выбрать из них нужные. При этом обилие различных формул иногда делает этот выбор довольно трудным.
Уравнения, сводящиеся к квадратам
Пример задания. Решить уравнение 2 cos2x + 3 sinx = 0
Решение. С помощью основного тригонометрического тождества это уравнение можно свести к квадратному относительно sinx:
2cos2x + 3sinx = 0, 2(1 – sin2x) + 3sinx = 0,
2 – 2sin2x + 3sinx = 0, 2sin2x – 3sinx – 2 = 0
Введем новую переменную y = sin x, тогда уравнение примет вид: 2y2 – 3y – 2 = 0.
Корни этого уравнения y1 = 2, y2 = –0,5.
Возвращаемся к переменной x и получаем простейшие тригонометрические уравнения:
1) sin x = 2 – это уравнение не имеет корней, так как sin x < 2 при любом значении x;
2) sin x = –0,5, 
Ответ: 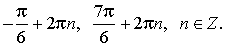
Однородные тригонометрические уравнения
Пример задания. Решить уравнение 2sin2x – 3sinxcosx – 5cos2x = 0.
Решение. Рассмотрим два случая:
1) cosx = 0 и 2) cosx ≠ 0.
Случай 1. Если cos x = 0, то уравнение принимает вид 2sin2x = 0, откуда sinx = 0. Но это равенство не удовлетворяет условию cosx = 0, так как ни при каком x косинус и синус одновременно в нуль не обращаются.
Случай 2. Если cos x ≠ 0, то можно разделить уравнение на cos2x и получить 2tg2x – 3tgx – 5 = 0. Вводя новую переменную y = tg x, получаем квадратное уравнение 2y2 – 3y — 5 = 0.
Корни этого уравнения y1 = –1, y2 = 2,5.
Возвращаемся к переменной x.
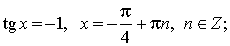
tg x = 2,5,
x = arctg 2,5 + πn, n ∈ Z.
Ответ: 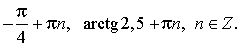
Уравнение, левая часть которого — многочлен, каждый член которого имеет вторую степень, а правая — нуль, называют однородным уравнением второй степени относительно переменных u и v.
Обозначив в исходном уравнении sin x буквой u, а cos x буквой v, получим уравнение вида au2 + buv + cv2 = 0.
Делением на v2 такое уравнение сводится к квадратному относительно 
Напоминаем, что апробировать учебник «Алгебра и начало математического анализа. 10 класс», как и многие другие издания, можно на платформе LECTA. Для этого воспользуйтесь предложением «5 учеников бесплатно».
#ADVERTISING_INSERT#
– Переходим к более сложным тригонометрическим неравенствам,
решение которых будет сводиться к решению простейших тригонометрических неравенств. Рассмотрим примеры.
(Решение неравенств на доске под руководством учителя).
№1. cos22x – 2cos2x 0.
(Вспомним прием решения тригонометрических уравнений вынесением общего множителя за скобку).
cos2x(cos2x – 2) 0.
Замена: cos2x = t, 1; t(t – 2) 0; Второе неравенство не удовлетворяет условию 1.
cos2x 0. (Решить неравенство самостоятельно. Проверить ответ).
Ответ: + p n< х< + p n, n Z.
№2. 6sin2x – 5sinx + 1 0.
(Вспомним прием решения тригонометрических уравнений заменой переменной. У доски решает ученик с комментариями).
Замена sinx = t, 1. 6t2 – 5t +1 0, 6(t – )(t – ),
Ответ: + 2p n х + 2p n, -p -arcsin+ 2p k х arcsin+ 2p k, n, k Z.
№3. sinx + cos2x> 1.
(Обсуждаем варианты решения. Вспоминаем фомулу косинуса двойного угла. Класс решает самостоятельно, один ученик – на индивидуальной доске с последующей проверкой).
sinx + cos2x – 1> 0, sinx – 2sin2x> 0, sinx(1 – 2sinx) > 0,
Ответ:
2p n< x< + 2p n, + 2p n< x< p + 2p n, n Z.
Проанализировать ситуации, когда ответ к решению квадратного неравенства записываем в виде совокупности двух неравенств, а когда – в виде системы. Полезна следующая схема:
00025165926425165824000000000012516582401
№4. coscosx – sinsinx< -.
(Обсуждение. К доске вызываются по одному ученику на каждый шаг решения, комментируются этапы. Учитель проверяет запись у учеников, работающих на месте).
cos(x + ) < -, cost< -.
+ 2p n< t< + 2p n, n Z,
+ 2p n< x + < + 2p n, n Z,
+ 2p n< x< + 2p n, n Z.
Ответ:
+ 2p n < x < + 2p n, n Z.
№5. Определите все а, при каждом из которых неравенство
4sinx + 3cosx а имеет хотя бы одно решение.
(Вспомнить алгоритм решения тригонометрического уравнения с нормирующим множителем. Решение записано на кодоскопной ленте. Открываю его поэтапно по мере рассуждений. Дифференцированная работа).
4sinx + 3cosx а, М = = 5. Разделим обе части неравенства на 5: sinx + cosx . Так как ()2 + ()2 = 1, то существует такой угол , что cos = , а sin = . Перепишем предыдущее неравенство в виде: sin(x + ) . Последнее неравенство, а, значит, и исходное неравенство имеет хотя бы одно решение при каждома таком, что -1, то есть при каждом а -5. Ответ: а -5.
Этот математический калькулятор онлайн поможет вам решить тригонометрическое неравенство. Программа для решения тригонометрического неравенства не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения результата.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Вы можете посмотреть теорию решения тригонометрических неравенств и некоторые методы решения тригонометрических неравенств.
Примеры подробного решения >>
Введите тригонометрическое неравенство
Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.
Сообщение отправлено. Спасибо.
Тригонометрические неравенства
Неравенства вида \( \sin x > a \) и \( \sin x
Пусть дано простейшее неравенство \( \sin x > a \).
1) При \(-1

Из данного рисунка видно, что в этом случае решение неравенства будет таким:
$$ x \in (\arcsin a + 2\pi k; \;\; \pi — \arcsin a + 2\pi k), k \in \mathbb{Z} $$
2) При \(а \geq 1 \) неравенство не имеет решений: \( x \in \emptyset \)
3) При \(а
4) При \(а = -1 \) решением неравенства является любое действительное число, отличное от \( -\frac{\pi}{2} + 2\pi k, \; k \in \mathbb{Z} \)
Пусть дано простейшее неравенство \( \sin x
1) При \(-1

Из данного рисунка видно, что в этом случае решение неравенства будет таким:
$$ x \in (\pi — \arcsin a + 2\pi k; \;\; 2\pi + \arcsin a + 2\pi k), k \in \mathbb{Z} $$
2) При \(а > 1 \) решением неравенства является любое действительное число: \( x \in \mathbb{R} \)
3) При \(а = 1 \) решением неравенства является любое действительное число, отличное от \( \frac{\pi}{2} + 2\pi k, \; k \in \mathbb{Z} \)
4) При \(а \leq -1 \) неравенство не имеет решений.
Неравенства вида \( \cos x > a \) и \( \cos x
Пусть дано простейшее неравенство \( \cos x > a \).
1) При \(-1

Из данного рисунка видно, что в этом случае решение неравенства будет таким:
$$ x \in (-\arccos(a) + 2\pi k; \;\; \arccos a + 2\pi k), \; k \in \mathbb{Z} $$
2) При \( a \geq 1\) неравенство не имеет решений.
3) При \(а
4) При \(а = -1\) решением неравенства является любое действительное число, отличное от \( \pi + 2\pi k, \; k \in \mathbb{Z} \)
Пусть дано простейшее неравенство \( \cos x
1) При \(-1

Из данного рисунка видно, что в этом случае решение неравенства будет таким:
$$ x \in (\arccos a + 2\pi k; \;\; 2\pi — \arccos a + 2\pi k), \; k \in \mathbb{Z} $$
2) При \(a > 1\) решением неравенства является любое действительное число: \( x \in \mathbb{R} \)
3) При \(a \leq -1\) неравенство не имеет решений.
4) При \(a = 1\) решением неравенства является любое действительное число, отличное от \( 2\pi k, \; k \in \mathbb{Z} \)
Неравенства вида \( tg \;x > a \) и \( tg \;x
Пусть дано простейшее неравенство \( tg \;x > a \).
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом \(a \in \mathbb{R} \) решение неравенства будет таким:
$$ x \in \left(arctg \;a + \pi k; \;\; \frac{\pi}{2} + \pi k \right), \; k \in \mathbb{Z} $$
Пусть дано простейшее неравенство \( tg \;x
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом \(a \in \mathbb{R} \) решение неравенства будет таким:
$$ x \in \left(-\frac{\pi}{2} + \pi k; \;\; arctg \;a + \pi k\right), \; k \in \mathbb{Z} $$
Неравенства вида \( ctg \;x > a \) и \( ctg \;x
Пусть дано простейшее неравенство \( ctg \;x > a \).
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом \(a \in \mathbb{R} \) решение неравенства будет таким:
$$ x \in ( \pi k; \;\; arcctg \;a + \pi k ), \; k \in \mathbb{Z} $$
Пусть дано простейшее неравенство \( ctg \;x
Множество всех решений данного тригонометрического неравенства будем искать с помощью тригонометрического круга.

Из данного рисунка видно, что при любом \(a \in \mathbb{R} \) решение неравенства будет таким:
$$ x \in ( arcctg \; a + \pi k; \;\; \pi + \pi k ), \; k \in \mathbb{Z} $$
Решение тригонометрических неравенств
ПРИМЕР 1. Решим неравенство \( \sin x > \frac{1}{2} \).Так как \( -1 $$ x \in \left( \arcsin \frac{1}{2} + 2\pi k; \;\; \pi — \arcsin \frac{1}{2} + 2\pi k \right), \; k \in \mathbb{Z} $$
Так как \( \arcsin \frac{1}{2} = \frac{\pi}{6} \), то решение можно переписать в виде
$$ x \in \left(\frac{\pi}{6} + 2\pi k; \;\; \frac{5\pi}{6} + 2\pi k \right), \; k \in \mathbb{Z} $$
ПРИМЕР 2. Решим неравенство \( \sin \;x
Так как \( -1
$$ x \in \left(\pi — \arcsin \left( -\frac{2}{3} \right) + 2\pi k; \;\; 2\pi + \arcsin \left( -\frac{2}{3} \right) + 2\pi k \right), \; k \in \mathbb{Z} $$
Воспользовавшись равенством \( \arcsin(-a) = -\arcsin a \), перепишем решение в виде
$$ x \in \left(\pi + \arcsin \frac{2}{3} + 2\pi k; \;\; 2\pi — \arcsin \frac{2}{3} + 2\pi k \right), \; k \in \mathbb{Z} $$
ПРИМЕР 3. Решим неравенство \( \cos x > \frac{1}{2} \).
Так как \( -1
$$ x \in \left(-\frac{\pi}{3} + 2\pi k; \;\; \frac{\pi}{3} + 2\pi k \right), \; k \in \mathbb{Z} $$
ПРИМЕР 4. Решим неравенство \( \cos x
Так как \( -1
$$ x \in (\arccos(-0{,}3) + 2\pi k; \;\; 2\pi — \arccos(-0{,}3) + 2\pi k), k \in \mathbb{Z} $$
Воспользовавшись равенством \( \arccos(-a) = \pi — \arccos a \), перепишем решение в виде
$$ x \in (\pi-\arccos 0{,}3 + 2\pi k; \;\; \pi + \arccos 0{,}3 + 2\pi k), \; k \in \mathbb{Z} $$
ПРИМЕР 5. Решим неравенство \( tg \;x > 1 \).
Очевидно, что решение неравенства будет таким:
$$ x \in \left(\frac{\pi}{4} + \pi k; \;\; \frac{\pi}{2} + \pi k\right), \; k \in \mathbb{Z} $$
ПРИМЕР 6. Решим неравенство \( tg \;x
Очевидно, что решение неравенства будет таким:
$$ x \in \left(-\frac{\pi}{2} + \pi k; \;\; arctg \left( -\frac{1}{2} \right) + \pi k\right), \; k \in \mathbb{Z} $$
Воспользовавшись равенством \( arctg(-a) = -arctg \; a \), перепишем решение в виде
$$ x \in \left(-\frac{\pi}{2} + \pi k; \;\; -arctg \frac{1}{2} + \pi k\right), \; k \in \mathbb{Z} $$
ПРИМЕР 7. Решим неравенство \( ctg \;x > \frac{\sqrt{3}}{3} \).
Очевидно, что решение неравенства будет таким:
$$ x \in \left( \pi k; \;\; \frac{\pi}{3} + \pi k \right), \; k \in \mathbb{Z} $$
ПРИМЕР 8. Решим неравенство \( ctg \;x
Очевидно, что решение неравенства будет таким:
$$ x \in \left( arcctg \left( -\frac{5}{4} \right) + \pi k; \;\; \pi + \pi k \right), \; k \in \mathbb{Z} $$
Воспользовавшись равенством \( arcctg(-a) = \pi — arcctg \;a \), перепишем решение в виде
$$ x \in \left( \pi — arcctg \frac{5}{4} + \pi k; \;\; \pi + \pi k \right), \; k \in \mathbb{Z} $$
или в виде
$$ x \in \left( — arcctg \frac{5}{4} + \pi n; \;\; \pi n \right), \; n \in \mathbb{Z} $$

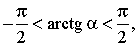
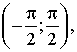 тангенс которого равен α,
тангенс которого равен α,