Лекция 1.Множества. Операции над множествами
Дискретная математика — область математики, в которой изучаются свойства структур конечного характера, а также бесконечных структур, предполагающих скачкообразность происходящих в них процессов или отделимость составляющих их элементов.
Список литературы:
Яблонский С.В. — Введение в дискретную математику
Белоусов А.И. — Дискретная математика
Капитонова Ю.В. и др. – Лекции по дискретной математике
Судоплатов С.В., Овчинникова Е.В. — Элементы дискретной математики
Хаггарти Р. Дискретная математика для программистов
Зайцева С.С. Дискретная математика
К разделам дискретной математики обычно относятся: теория множеств, комбинаторика, общая алгебра, теория графов, математическая логика, теория алгоритмов, теория автоматов, теория кодирования и т.д.
1. Множества. Операции над множествами.
1.1. Множество. Способы задания множеств.
Дискретная математика изучает в основном конечные множества и операции на них.
В 1872 г. Георг Кантор, создатель теории множеств, дал следующие определения для множества:
Множество – это объединение в одно общее объектов, хорошо различаемых нашей интуицией или нашей мыслью.
Множество – это определенная совокупность объектов. Эти объекты называются элементами множества.
Множества обозначаются прописными буквами латинского алфавита: A, B, X, Y, A1, A2, …, элементы множеств – строчными буквами: a, b, x, y, a1, a2, … .
Числовые множества:
N — множество всех натуральных чисел;
N0 — множество неотрицательных целых чисел
Z -множество целых чисел;
Q — множество рациональных чисел;
I — множество иррациональных чисел;
R — множество действительных чисел;
C — множество комплексных чисел;
Символ обозначает принадлежность.
Запись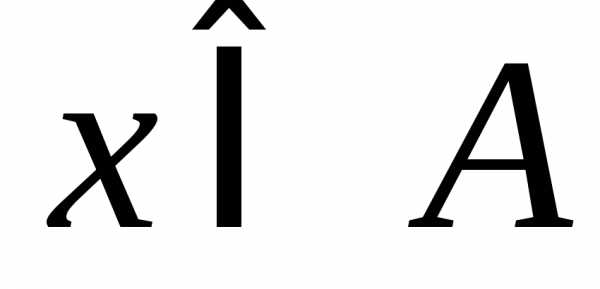 
означает, что элементx принадлежит множеству A.
Если элемент
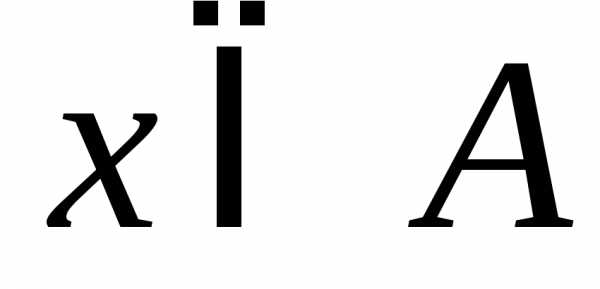.Множества бывают:
конечные; частный случай – единичное (одноэлементное) множество, например, множество преподавателей в этой аудитории, или множество десятичных цифр;
бесконечные; пример – множество натуральных чисел;
пустое (Ø).
Пустым множеством называют множество, не содержащее ни одного элемента.
Способы задания (описания) множеств:
1) Множество A определяется непосредственным перечислением всех своих элементов a1, a2, …, an , т.е. записывается в виде: A=a1, a2, …, an. При задании множества перечислением обозначения элементов обычно заключают в фигурных скобках и разделяют запятыми.
Перечислением можно задавать только конечные множества.
2) Множество A определяется как совокупность тех и только тех элементов из некоторого основного множества T, которые обладают общим свойством P(x). В этом случае используется обозначение , т.е. элементы множества задаетсяхарактеристическим предикатом (условием).
Характеристическим предикатом можно задать как конечные, так и бесконечные множества.
3) Множество A можно задать порождающей процедурой (рекурсивное задание, задание алгоритмом). Используется обозначение .
Пример .. – множество натуральных чисел от 1 до 4. Множество заданоперечислением всех своих элементов. Причем, элемент 3A, а 5A.
Пример .. M=C, C++, Java, C# – множество языков программирования, имеющих С-подобный синтексис. Задано перечислением.
Пример .. Множество A из примера 1.1. можно задать характеристическим предикатом .
Пример .. Зададим рекурсивно множество X алгоритмом:
1) 3X; 2)
если xX,
то элемент 
и (1x)
принадлежат X;
3) других элементов в X нет.
Заметим, что это множество – конечное, и его можно было задать выписыванием его элементов
.
Частным случаем рекурсивного задания множества является способ задания, основанный на процедуре, называемой математической индукцией. Рассмотрим его на примере задания множества натуральных чисел.
Пример .. Множество N задается следующими правилами:
1) задается базис индукции (исходный элемент):
1N;
2) указывается индуктивный переход:
если nN, то (n+1)N;
3) устанавливается правило замыкания:
других элементов, кроме построенных правилами 1 и 2, в N нет.
Задача: Определить различными способами множество М2n-1 всех нечетных чисел, не превышающих 10.
1.2. Подмножество. Равенство множеств.
Универсум. Булеан.
Определение 1.1. Множество A называется подмножеством множества B (обозначается AB), если каждый элемент A есть элемент B, т.е. если xA, то xB.
Символ обозначает отношение включение между множествами.
Пример
.. Пусть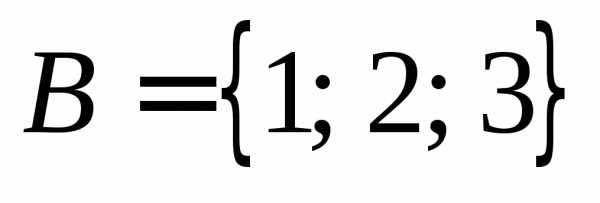
и.
ТогдаBA.Но .
В частности, каждое множество есть подмножество самого себя, т.е. AA.
Определение 1.2. Пусть A и B – некоторые множества. Говорят, что A равно B, и пишут A=B, если для любого x имеем: xA тогда и только тогда, когда xB.
Иначе говоря, A=B тогда и только тогда, когда AB и BA.
Если AB и AB, то это записывается AB, и говорят, что A есть собственное подмножество B. Пустое множество есть подмножество любого данного множества A, т.е. A.
1) Доказать, что A есть подмножество B.
2) Доказать, что B есть подмножество A.
Определение 1.3. Универсальное множество U (или универсум) есть множество, обладающее таким свойством, что все рассматриваемые множества являются его подмножествами.
В теории чисел универсальное множество обычно совпадает с множеством всех целых или натуральных чисел. В математическом анализе универсальное множество может быть множество всех действительных чисел или множество всех точек n-мерного пространства.
Следует отметить, что универсальное множество U, хотя, и названо универсальным, однозначно не определено, если точно не указана область рассмотрения (предметная область). Конечно, любое множество, содержащее U, может быть использовано как универсальное множество.
По определению, каждое множество есть подмножество универсального множества.
Пример .. Так, для множества за универсум можно взять множество натуральных чисел, т.е.U=N.
Определение 1.4. Булеаном множества A (обозначается (A)) называется множество, состоящее из всех подмножеств множества A.
Пример .. Пусть 
.
Следовательно, булеан множества A есть множество (A)=.
Множество A из примера 1.8. содержит три элемента, а булеан (A
По этой причине (A) часто обозначают через 2A.
1.3. Операции над множествами.
Множество часто задают графически с помощью диаграмм Эйлера Л. Эйлер (1707-1783) – швейцарский математик, механик и физик.
Например, задание множеств M1=a, b, c, d и M2=a, c, e, f приведено на рисунке, где замкнутые линия, называемые кругами Эйлера, ограничивают элементы одного множества.
В дальнейшем графическое изображение множеств было плодотворно исследовано Дж. Венном (1834-1923), создавшим диаграммную теорию изучения множеств различной природы.
Диаграммы, задающие множества, принято называть диаграммы Эйлера-Венна.
Если имеются некоторые множества, то из них можно получать новые с помощью определенных операций. Для наглядного изображения операций над множествами воспользуемся диаграммами Эйлера-Венна.
Определение 1.5. Объединением множеств A и B называется множество, (которое обозначается AВ) состоящее из всех элементов, которые принадлежат хотя бы одному из множеств А или В.
Пример .9. Пусть , .
Тогда .
Определение 1.6. Пересечением множеств А и В называется множество, (которое обозначается АВ) которое состоит из общих элементов этих множеств.
Пример .10. Пусть ,. Тогда.
Определение 1.7. Разностью множеств А и В называется множество, (которое обозначается А\В) всех тех и только тех элементов множества А, которые не принадлежат В.
Определение 1.8. Симметрическая разность множеств А и В (обозначается А∆В) есть множество (А\В)(В\А).
Пример .11. Пусть ,.
Тогда ,,
.
Определение
1.9. Дополнением
множества А (обозначается 
)
–это
множество элементов универсума, которые
не принадлежат А, т.е.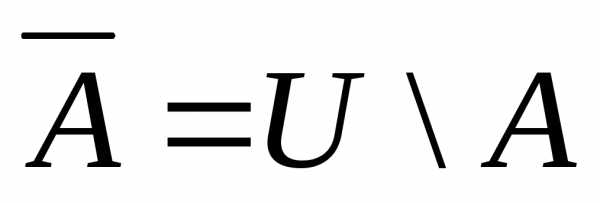 
.
Пример .12. Пусть.
Тогда,
если
,
то
.
Операции пересечения и объединения допускают следующее обобщение.
Пусть задано семейство множеств , где. Тогда
Операции над множествами обладают рядом важных свойств.
Теорема 1.1. Пусть задан универсум U. Тогда A, B, C U выполняются следующие свойства:
1. Свойства коммутативности: АВ=ВА
АВ=ВА
2. Свойства ассоциативности: А(ВС)=(АВ)С
А(ВС)=(АВ)С
3. Свойства дистрибутивности: А(ВС)=(АВ)(АС)
А(ВС)=(АВ)(АС)
4. Свойства тождества: А=А А=
АU=U АU=А
5. Законы идемпотентности: АA=A
АA=A
6. Свойства поглощения: А(АВ)=А
А(АВ)=А
7. Двойное дополнение: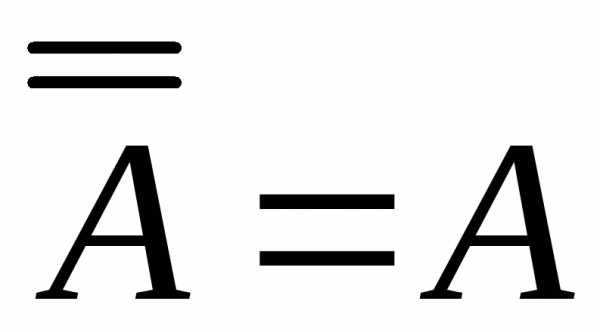 
8.
Свойства дополнения: А
=U
А
=
9. Законы
де Моргана: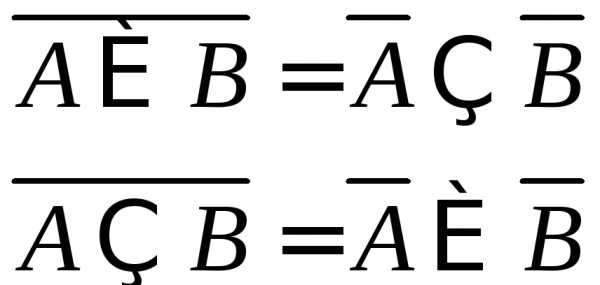 
Кроме того, .
Докажем свойство дистрибутивности относительно :
А(ВС)=(АВ)(АС).
Доказательство.
Пусть M= А(ВС) и K=(АВ)(АС).
1) Докажем, что MK.
Пусть элемент xM, тогда либо xA, либо x(ВС).
Если xA, то x(АВ) и x(АС). Значит x(АВ)(АС), т.е. xK.
Если x(ВС)., то xВ и xС. Значит x(АВ) и x(АС). Т.о. x(АВ)(АС), т.е. xK.
Значит, MK.
2) Докажем, что KM.
Пусть элемент xK, тогда x(АВ)(АС).
Это возможно только тогда, когда и x(АВ) и x(АС).
Здесь возможны 2 варианта.
xA. Но тогда получаем, что xА(ВС), т.е. xM.
xA. Но тогда получаем, что и xВ и xС. Т.е. x(ВС). Но это значит, что xА(ВС), т.е. xM.
Значит, KM.
3) Так как MK и KM, то M=K, то есть А(ВС)=(АВ)(АС).
Остальные тождества доказываются аналогично.
Определение
1.10. Покрытием множества A называется набор подмножеств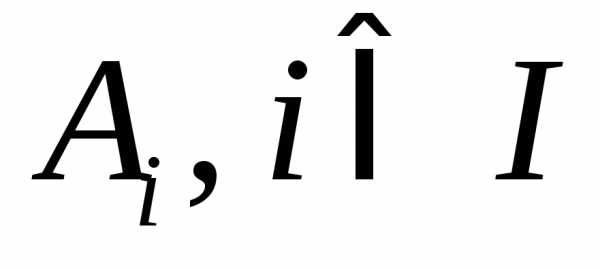 
,
гдеI – некоторое множество индексов, если
каждый элемент A принадлежит хотя бы одному из Ai.
Пример .3. Пусть A=, , , .
Тогда , , , , , является покрытием множества A.
Определение
1.11. Разбиением множества A называется набор его попарно
непересекающихся подмножеств 
,
гдеI – некоторое множество индексов.
— разбиение множества A, если выполняются два условия:
1) ;
2) 
,
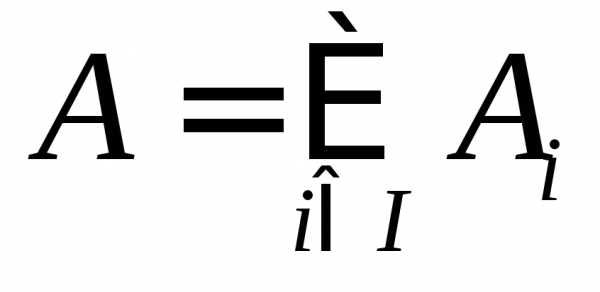т.е.aA тогда и только тогда, когда aAi для некоторого iI.
Пример .. Пусть A=, , , .
Тогда множество A=, , , является разбиением множества A.
Всего возможны 17 вариантов разбиения множества A.
studfiles.net
ВЫСШАЯ МАТЕМАТИКА 2 семестр. Лекция N1 МАТЕМАТИЧЕСКИЙ АНАЛИЗ. Элементы теории множеств. Понятие множества. Операции над множествами
Эквивалентные множества
Эквивалентные множества Теоретические вопросы. Множества конечные и бесконечные.. Сравнение множеств.. Счетные множества..4 Свойства счетных множеств..5 Эквивалентные множества..6 Несчетные множества..7
ПодробнееФУНКЦИЯ ПЕРЕМЕННАЯ ВЕЛИЧИНА
ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА понятия, которые можно описать, но нельзя строго определить, так как любая попытка дать строгое определение неизбежно сведётся к замене определяемого понятия ему
ПодробнееМатематический анализ
Математический анализ Попова Татьяна Михайловна, ауд 433п 2 часа лекции, 3 часа практических занятий ЭКЗАМЕН Содержание 1 семестра: теория пределов, непрерывность функции, основные понятия теории дифференциального
Подробнее3. Множества (продолжение)
3. Множества (продолжение) Несчетность множества действительных чисел имеет следующее более или менее конкретное приложение. Определение 3.1. Число R называется алгебраическим, если оно является корнем
ПодробнееГлава 1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Глава ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА ВАЖНЕЙШИЕ КЛАССЫ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ В элементарной математике изучаются действительные (вещественные) числа Сначала в процессе счета возникли натуральные числа 3 для которых
ПодробнееПределы и непрерывность
Пределы и непрерывность. Предел функции Пусть функция = f ) определена в некоторой окрестности точки = a. При этом в самой точке a функция не обязательно определена. Определение. Число b называется пределом
ПодробнееПредложение 1. Предложение 2.
2. ПРЯМОЕ ВВЕДЕНИЕ ПОРЯДКА В СИСТЕМЕ ПЕАНО В конце XIX века было завершено построение содержательных аксиоматических теорий двух важнейших областей математики — арифметики и евклидовой геометрии (Гильберт).
ПодробнееДискретная математика
Дискретная математика Часть 1 ВЕ Алексеев 2014 Глава 1 Множества 11 Понятие множества Под множеством математики понимают соединение каких-либо объектов в одно целое Создатель теории множеств немецкий математик
ПодробнееЛекция 1. Метрические пространства
Лекция 1. Метрические пространства В математике очень важную роль играет понятие пространства, т. е. множества, между элементами которого аксиоматически заданы некоторые соотношения. В таком случае говорят,
ПодробнееВводный курс математики
Высшее профессиональное образование БАКАЛАВРИАТ И. Л. Тимофеева, И. Е. Сергеева, Е. В. Лукьянова Вводный курс математики Под редакцией академика В. Л. Матросова Рекомендовано Учебно-методическим объединением
ПодробнееГЛАВА 5 МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
ГЛАВА 5 МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ Из способов введения множества R действительных чисел рассмотрим два: индуктивный (индуктивно-аксиоматический), когда множество R строится путём последовательных
ПодробнееВВЕДЕНИЕ В ТЕОРИЮ МНОЖЕСТВ
ВВЕДЕНИЕ В ТЕОРИЮ МНОЖЕСТВ 1 Понятие множества. Операции над множествами В математике встречаются самые разнообразные множества. Можно говорить о множестве граней многогранника, множестве точек на прямой,
ПодробнееДискретная математика
Дискретная математика ЛИТЕРАТУРА. Яблонский С.В. Введение в дискретную математику. — М.: Наука, 979. 2. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженеров. М.: Энергоатомиздат, 988.
ПодробнееМатематический анализ. Введение [1,3,4]
I Краткие исторические сведения Математический анализ Введение [1,3,4] Математический анализ часть математики, в которой изучаются функции и их обобщения методами теории пределов Поскольку понятие предела
ПодробнееМатематический анализ и топология
Математический анализ и топология Д. Вельтищев ЛЭШ-2006 Предисловие Это краткий конспект курса анализа для ЛЭШ-2006. Он включает в себя основы анализа и топологии, изложенные так, чтобы их можно было перенести
ПодробнееТ. В. Родина, Е. С. Трифанова
Т В Родина, Е С Трифанова КУРС ЛЕКЦИЙ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ I для напр «Прикладная математика и информатика» Учебное пособие под редакцией проф И Ю Попова Санкт Петербург МИНИСТЕРСТВО ОБРАЗОВАНИЯ
ПодробнееЛекции 8,9. Глава 5. Непрерывность функции
Лекции 89 Глава 5 Непрерывность функции 5 Непрерывность функции в точке Понятие непрерывности функции является одним из основных понятий высшей математики Очевидно графиком непрерывной функции является
Подробнее{ z } { 1 2 3, 4,…, ( 1) n = ; ,, n,…}
Тема Теория пределов Как мы понимаем слово «предел»? В повседневной жизни мы часто употребляем термин «предел», не углубляясь в его сущность В нашем представлении чаще всего предел отождествляется с понятием
ПодробнееМатематическая логика
Математическая логика Лектор: Подымов Владислав Васильевич e-mail: [email protected] 2017, весенний семестр Лекция 13 Наивная теория множеств Кардинальные числа в наивной теории множеств Выразительные возможности
ПодробнееЯзык теории множеств Цермело Френкеля (ZF)
1 Язык теории множеств Цермело Френкеля (ZF) Алфавит Переменные (по множествам) : a,b,… Предикатные символы:, = Логические связки:, ª, #,, Кванторы: Á, Ú Скобки: (, ) Формулы Атомарные: x y, x=y (где
ПодробнееМАТЕМАТИЧЕСКИЙ АНАЛИЗ 1 семестр. 1. Числа 1.1. Числовые множества. Множество натуральных чисел
МАТЕМАТИЧЕСКИЙ АНАЛИЗ 1 семестр 1. Числа 1.1. Числовые множества. Множество натуральных чисел множество целых чисел N = {0, 1, 2, 3,…, }, Z = {0, ±1, ±2, ±3,…, } множество рациональных чисел { m }
ПодробнееЛЕКЦИЯ 1 НЕКОТОРЫЕ ЭЛЕМЕНТЫ ТЕОРИИ ЧИСЕЛ
ЛЕКЦИЯ 1 НЕКОТОРЫЕ ЭЛЕМЕНТЫ ТЕОРИИ ЧИСЕЛ В пособии не излагается теория чисел а дан минимальный инструментарий из этой теории который в дальнейшем потребуется для изучения криптографических систем используемых
ПодробнееЛекция 2. МНОЖЕСТВА И ОТНОШЕНИЯ
Лекция 2. МНОЖЕСТВА И ОТНОШЕНИЯ Цель лекции: изучить основы теории множеств, необходимые для введения фундаментального понятия «отношение», на котором строится дальнейшее изучение реляционной модели данных.
ПодробнееМножества и отображения
Глава 1 Множества и отображения 11 Множества Когда мы даем определение какому-либо понятию, мы связываем его с другими понятиями Те, в свою очередь, мы можем определить через другие понятия и т д Рано
ПодробнееВВЕДЕНИЕ В СПЕЦИАЛЬНОСТЬ «МАТЕМАТИКА»
А.К. Цих Н.А. Бушуева О.В. Знаменская ВВЕДЕНИЕ В СПЕЦИАЛЬНОСТЬ «МАТЕМАТИКА» Организационно-методические указания по освоению дисциплины Красноярск 2008 1. Общие сведения 3 2. Общая характеристика дисциплины
Подробнее18. Отображения, отношения и лемма Цорна
18. Отображения, отношения и лемма Цорна Вернемся еще раз к теории множеств будем надеяться, что последний раз в курсе анализа. Вы уже знакомы с понятием отображения множеств. Именно, отображение f : X
ПодробнееЛекция 1 Топологические пространства 1
Лекция 1 Топологические пространства 1 Ключевые слова: топология, открытое множество, топологическое пространство, окрестность, внутренние и внешние точки, замкнутое множество, база топологии, отображения
ПодробнееПоследовательность. n n
Последовательность. Определение. Если каждому натуральному числу ( N ) по некоторому закону приведено в соответствие число { }, то этим определена числовая последовательность,,,… (или просто последовательность).
ПодробнееОсновные понятия теории множеств
Министерство образования и науки РФ Уральский государственный экономический университет Ю. Б. Мельников Основные понятия теории множеств Раздел электронного учебника для сопровождения лекции Изд. 4-е,
Подробнее1 Фундированные множества.
ФИВТ МФТИ, весна 2013. Краткие заметки по курсу математическая логика. Часть первая: трансфинитная индукция (4 лекции). (А.Е. Ромащенко). Заметки написаны для студентов, слушавших лекции курса и посещавших
ПодробнееПонятие множества. РЕПОЗИТОРИЙ БГПУ
Понятие множества. Вопросы для изучения 1. Понятие множества. 2. Отношения между множествами. 3. Диаграммы Эйлера Венна. 4. Операции над множествами. «Множество есть многое, мыслимое нами как единое» основатель
ПодробнееЛекция 6 ( ) 1. Теория Γ Q
Лекция 6 (11.10.2014) 1. Теория Γ Q Утверждение. Теория Γ Q полна. Доказательство. Пусть M 1 и M 2 две не эквивалентные модели теории Γ Q, то есть M 1 ϕ и M 2 ϕ для некоторого предложения ϕ. Ни одна из
Подробнее14. Компактные топологические пространства
63 4. Компактные топологические пространства Известно что многие факты математического анализа основаны на одном свойстве отрезка числовой прямой которое называется леммой Гейне — Бореля -Лебега и заключается
ПодробнееФОНД ОЦЕНОЧНЫХ СРЕДСТВ
МИНОБРНАУКИ РОССИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» БОРИСОГЛЕБСКИЙ ФИЛИАЛ (БФ ФГБОУ ВО «ВГУ») УТВЕРЖДАЮ Заведующий
ПодробнееВопросы к экзамену по курсу 1-2 модулей
На устном экзамене студент получает два вопроса и две задачи. Вопросы к экзамену по курсу 1- модулей 1. Расскажите о числах: натуральных, целых, рациональных и иррациональных. Расскажите о числовой прямой
Подробнее1. Топологические пространства
Топологические пространства Топологическое пространство Пусть — произвольное множество и τ = { I} U ; — некоторое семейство его подмножеств Определение Будем говорить, что семейство τ задаёт (определяет)
Подробнее23. Полнота (продолжение)
23. Полнота (продолжение) Завершим доказательство теоремы 22.5. Именно, покажем, что i(x) плотно в X. Так как пространства, о которых идет речь, метрические, нам достаточно проверить, что всякий элемент
ПодробнееВведение в математическую логику
Введение в математическую логику Лекция 11 В следующем разделе мы будем рассуждать в терминах содержательной теории множеств, а не в терминах формальной теории ZF. Полный порядок (содержательная теория
ПодробнееЛекция 1. Мера Лебега плоских множеств
Лекция 1. Мера Лебега плоских множеств Корпусов Максим Олегович, Панин Александр Анатольевич Курс лекций по линейному функциональному анализу 5 сентября 2012 г. Введение Функция Дирихле не интегрируема
Подробнеесайты:
Федеральное агентство по образованию Уральский государственный экономический университет Ю. Б. Мельников Основные понятия теории множеств Раздел электронного учебника для сопровождения лекции Изд. 3-е,
Подробнееdocplayer.ru
Методическая разработка для спецкурса по математике в 9 классе
Методическая разработка для спецкурса по математике в 9-м классе на тему: «Использование элементов теории множеств в решении задач»
Цели:
формировать у учащихся знания основ теории множеств;
познакомить учащихся с различными случаями применения теории множеств при решении задач;
формировать у учащихся умения применять элементы теории множеств в решении задач;
развивать общую математическую культуру, интерес к предмету;
воспитывать у учащихся ответственное отношение к учебному труду.
Оборудование: плакаты с изображением основных отношений и операций между множествами.
Содержание:
1. Основные понятия множества.
2. Отношения между множествами.
3. Операции над множествами.
4. Решение задач.
5. Контрольные вопросы
1. ОСНОВНЫЕ ПОНЯТИЯ МНОЖЕСТВА
Одно из основных понятий современной математики — множество. Это понятие обычно принимается за первичное и поэтому не определяется через другие.
Когда в математике говорят о множестве (чисел, точек, функций и т. д.), то объединяют эти объекты в одно целое — множество, состоящее из этих объектов (чисел, точек, функций и т. д.). Основатель теории множеств, немецкий математик Георг Кантор (1845–1918) выразил эту мысль следующим образом: “Множество есть многое, мыслимое как единое, целое”.
Множество — это совокупность объектов, объединённых между собой по какому-либо признаку.
Слово “множество” в обычном смысле всегда связывается с большим числом предметов. Например, мы говорим, что в лесу множество деревьев, но если перед домом два дерева, в обычной речи не говорят, что перед домом “множество деревьев”.
Математическое же понятие множества не связывается обязательно с большим числом предметов. В математике удобно рассматривать и “множества”, содержащие 3; 2 или 1 предмет и даже “множество”, не содержащее ни одного предмета (пустое множество). Например, мы говорим о множестве решений уравнения, до того как узнаем, сколько оно имеет решений (множество вещественных решений уравнения х2+1 = 0 — пустое множество).
Произвольные множества обозначают большими латинскими буквами А, В, С, … Пустое множество, т.е. множество, которое не имеет элементов, обозначается символом .
О предметах, составляющих множество, говорят, что они принадлежат этому множеству, или являются его элементами. Элементы множества обозначают малыми латинскими буквами a, b, c, … или одной какой-нибудь буквой с индексом, например а1, а2, … ,аn.
Предложение “предмет а принадлежит множеству А”, или “предмет а — элемент множества А”, обозначают символом а А.
Способы задания множеств:
1) Множество может быть задано непосредственным перечислением всех его элементов (в произвольном порядке). В таком случае названия всех элементов множества записываются в строчку, отделяются между собой запятыми и заключаются в фигурные скобки.
Например: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}— множество цифр десятичной системы счисления,
Необходимо различать объекты, обозначаемые символами a и {a}. Символом a означается предмет, символом {a} — множество, состоящее из одного элемента а (единичное множество). Перечислением всех элементов можно задать лишь конечное множество. Такие множества, как, например, множество всех натуральных (N) или всех целых чисел (Z), нельзя задать таким способом, т.к. мы не можем перечислить все N и все Z — таких чисел бесконечное множество.
2) Имеется другой, универсальный, способ задания множества в том смысле, что этим способом может быть задано не только конечное, но и бесконечное множество. Множество может быть задано указанием характеристического свойства, т. е. такого свойства, которым обладают все элементы этого множества и не обладает ни один предмет, не являющийся его элементом.
Например: а) А = { х | sin x = 0}, б) А = {0, 1, 2, 3, 4}— множество всевозможных остатков от деления любого натурального числа на 5.
2. ОТНОШЕНИЯ МЕЖДУ МНОЖЕСТВАМИ
Множество В включается в множество А, если каждый элемент множества В является также элементом множества А. Множество В является подмножеством или частью множества А. Символическая запись: .
Отношение включения обозначается символом , т. е. предложение “множество В включается во множество А” записывается: ВА.
Поскольку множество можно изобразить в виде геометрических фигур, логические рассуждения тоже изображаются геометрически.
Метод геометрической иллюстрации логических рассуждений был предложен великим математиком 18 века петербургским академиком Леонардом Эйлером (1707–1783) и широко применялся английским математиком Джоном Венном (1834–1923), т.е. для наглядности множества и логические рассуждения изображаются в виде кругов, которые называются кругами Эйлера или диаграммами Эйлера-Венна.
Например:
1) N Z QRC.
2) Множество прямоугольников во множество параллелограммов множество четырёхугольников.
Частным случаем включения является равенство.
Два множества, состоящие из одних и тех же элементов называются равными (А = В).
Символическая запись:
Как показывают приведённые выше примеры, если ВА, то возможны два случая:
1) Существует хотя бы один элемент множества А, не принадлежащий множеству В. В таком случае говорят, что В — собственная часть (или собственное подмножество) А, или что В строго включается в А. Отношение строгого включения обозначается : В А.
2) Не существует ни одного элемента множества А, не принадлежащего В. Этот случай равносилен отношению , т. е. равенству А = В.
3. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Объединением АВ двух множеств А и В называется множество, состоящее из общих элементов этих множеств; т. е. множество, состоящее из всех тех и только тех элементов, которые принадлежат множеству А или множеству В.
Символическая запись: .
Например:
Пересечением АВ двух множеств называется множество, состоящее из всех элементов этих множеств, и не содержащее элементов других множеств; т. е. множество, состоящее из всех тех и только тех элементов, которые принадлежат и множеству А и множеству В.
Символическая запись:
Разностью А \ В двух множеств А и В называется множество, состоящее из всех элементов множества А и не содержащее элементов множества В.
Символическая запись:
Симметрической разностью АВ двух множеств А и В называется множество
Пусть даны два множества А и В, В А, разность А \ В двух множеств А и В называется дополнением множества В до множества А (относительно множества А).
Сумма двух множеств является частным случаем объединения множеств.
Под парой будем всегда понимать упорядоченную пару элементов, т. е. два элемента, расположенных в определённом порядке. Элемент, занимающий первое место, называетсяпервой координатой пары, элемент, занимающий второе место, называется второй координатой пары.
Обозначают пару элементов круглыми скобками: (a,b).
Прямым произведением двух множеств называется множество всевозможных пар (a,b), таких, что: a А, b В. Символическая запись: .
4. РЕШЕНИЕ ЗАДАЧ
А. Задачи на прямое произведение множеств.
Задача №1
Задача №2
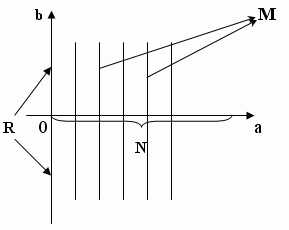
Изобразить на координатной плоскости множество М :
M = N R, где N — множество натуральных чисел, R — множество действительных чисел.
По определению прямого произведения: АВ = {(a,b) : aА, bВ}
М = {(1, х), (2, х), …| 1, 2, … N и х R}
Изобразим это на графике:
B. Задачи на доказательство, решаемые с помощью диаграмм Эйлера-Венна.
Задача №1
Доказать: (АВ)\А =
Доказательство:
,
что и требовалось доказать.
Задача №2
Доказать: А\(ВС) = (А\В)(А\С)
Доказательство:
,
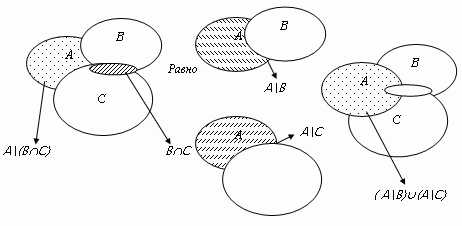что и требовалось доказать.
Задача №3
Доказать: В(А\В) = АВ
Доказательство:
,
что и требовалось доказать.
C. Логические задачи, решаемые с помощью диаграмм Эйлера-Венна.
Задача №1
В отделе научно-исследовательского института работают несколько человек, причём каждый из них знает хотя бы один иностранный язык: 6 человек — английский язык, 7 человек — немецкий язык, 4 человека — оба языка. Сколько человек работает в отделе? Сколько из них знают только английский язык? Только немецкий? Сколько человек знает только один язык?
Решение:
Пусть М1 — работники, знающие английский язык, М2 — работники, знающие немецкий язык.
1) | М1М2| = |М1| + |М2| — |М1М2| = 6 + 7 — 4 = 9 (человек) — работает в отделе.
2) |М1| — |М1М2| = 6 – 4 = 2 (человека) — знают только английский язык.
3) |М2| — |М1М2| = 7 – 4 = 3 (человека) — знают только немецкий язык.
4) 2 + 3 = 5 (человек) — знают только один язык.
Ответ: 9 человек, 2 человека, 3 человека, 5 человек.
Резервная задача
На пикник поехали 92 человека.
48 человек взяли бутерброды с колбасой,
38 человек взяли бутерброды с сыром,
42 человек взяли бутерброды с ветчиной,
28 человек взяли бутерброды с колбасой и с сыром,
21 человек взяли бутерброды с колбасой и с ветчиной,
26 человек взяли бутерброды с сыром и с ветчиной,
25 человек взяли бутерброды трёх видов.
А несколько человек взяли пирожки. Сколько человек взяли пирожки?
(Ответ: 14 человек взяли пирожки.)
5. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Назовите основателя теории множеств.
2. С чем связывают в обычном смысле слово “множество”?
3. Из чего состоит множество?
4. Как обозначают множества, элементы множества?
5. Что называю пустым множеством?
6. Перечислите способы задания множества.
7. Расскажите об отношениях между множествами. Приведите примеры.
8. Расскажите об операциях, которые можно осуществлять между двумя множествами. Приведите примеры.
9. Как для наглядности изображаются множества и логические рассуждения?
10*(для желающих). Составьте несколько задач и решите их, используя элементы теории множеств.
infourok.ru
Лекция № 2
1.Понятие множества 1
2.Способы задания множества 3
3.Отношения между множествами 5
4.Основные операции над множествами 7
5.Свойства объединения и пересечения множеств 10
6.Разбиение множества на классы. Классификация 11
7.Число элементов объединения и разности двух конечных множеств 12
8.Примеры решения задач 13
Понятие множества
Одно из основных понятий современной математики — понятие множества. Оно является первичным, т. е. не поддается определению через другие, более простые понятия. С понятием множества мы встречаемся довольно часто: множество студентов нашего института, множество преподавателей, множество изучаемых дисциплин и т. д.
Хотя в силу первичности понятия множества нельзя дать ему строгое определение, но можно воспользоваться описательным определением, предложенным одним из создателей теории множеств – немецким математиком Георгом Кантором (1845-1918). Он сказал: «Множество есть многое, мыслимое нами как единое».
Приведенные примеры обладают одним существенным свойством: все эти множества состоят из определенного конечного числа объектов, которые мы будем называть элементами множества. При этом каждый из объектов данного вида либо принадлежит, либо не принадлежит рассматриваемому множеству. Например, если мы рассмотрим множество студентов некоторой учебной группы, то, обратившись к списку этой группы, мы можем утверждать, что студент Иванов принадлежит этому множеству, а студент Петров уже не принадлежит в связи с отчислением.
Множества, включающие только такие объекты, принадлежность или не принадлежность которых к тому или иному множеству не вызывает сомнения, называются четкими множествами. Поскольку каждый рассматриваемый объект либо принадлежит, либо не принадлежит к рассматриваемому четкому множеству, эти множества всегда имеют ясно очерченные границы. Четким множествам противопоставлены нечеткие или «лингвистические» множества, включающие такие объекты, которые могут быть отнесены к тому или иному множеству лишь с определенной степенью достоверности. Понятие нечетких множеств (fuzzy sets) было впервые введено в 1965 году американским математиком Л. Заде.
Понятие нечеткого множества можно проиллюстрировать на примере применения прилагательных детский, юношеский, молодой, среднего возраста, пожилой, старый. Разные люди вкладывают в эти понятия разные возрастные рамки. Например, период от 16 до 21 года может считаться либо как юношеский, либо как относящийся к молодому возрасту. Таким образом, каждое из рассмотренных определений представляет собой нечеткое подмножество с размытыми краями. Объекты, попадающие на эти размытые края, относятся к указанным множествам лишь с известной долей достоверности. Так, например, девятнадцатилетний мужчина может быть с достоверностью 50% отнесен к множеству юношей, и с той же достоверностью — к множеству молодых людей.
Аппарат нечетких множеств может применяться для описания процессов мышления, лингвистических явлений и вообще для моделирования человеческого поведения, при котором допускаются частичные истины, а строгий математический формализм не является категорически необходимым.
Множества, которые состоят из конечного числа элементов, называются конечными множествами. К числу конечных множеств относится также и пустое множество, т.е. множество, не содержащее ни одного элемента. Введение понятия пустого множества связано с тем, что, определяя тем или иным способом множество, мы не можем знать заранее, содержит ли оно хотя бы один элемент. Например, множество отличников в какой-либо учебной группе.
Множества, рассматриваемые при решении практических задач, чаще всего имеет дело с конечными множествами объектов. В качестве примеров бесконечных множеств можно привести множества, рассматриваемые в математике: множество всех натуральных чисел (N) и множество всех целых чисел (Z).
studfiles.net
Сборник задач и упражнений с решениями по разделу математики Дискретная математика.doc
x|x{
A 2
};Nn,n2
………………………..
.
A k
}Nn,kn
x|x{
.
Определить мощность множества
C
kA
1k
№ 1.47. Является ли множество {(1, 2), (3, 4), (5, 6), (7, 8)} бинарным
отношением. Почему?
№ 1.48. Выписать элементы множества {0, 1, 2}{a,b}. Найти область
определения и область значений этого отношения, построить его график.
№ 1.49. Показать на примере, что операция образования декартового
произведения не является ни коммутативной, ни ассоциативной.
№ 1.50. Доказать, что декартово произведение дистрибутивно
относительно операции объединения, т.е. что для любых множеств А, В и
С
)CA(C)BA(
)CB(
.
№ 1.51. Пусть отношение “есть брат”, отношение “есть сестра”.
Описать отношения
\
;
;
.
№ 1.52. Является ли отношение “быть рядом” транзитивным?
симметричным,
№ 1.53. Задано бинарное отношение на множестве М={1,2,3,4}. Является
ли оно рефлексивным,
антисимметричным,
транзитивным? Почему? Найдите область определения R, область зна
чений R, обратное отношение R1, пересечение и объединение R и R1.
а) R={(1,1), (1,2), (1,3), (2,3), (3,3), (4,1), (4,4)};
б) R={(1,1), (1,2), (2,1), (2,3), (3,2), (3,3), (4,4)};
в) R={(1,1), (1,4), (2,3), (3,2), (4,1)};
г) R={(1,1), (1,2), (1,4), (2,2), (2,3), (3,3), (4,4)};
д) R={(1,1), (1,3), (2,2), (3,3), (4,1), (4,4)};
е) R={(1,1), (1,2), (3,1), (3,2), (3,3), (4,4)};
ж) R={(1,1), (1,2), (2,2), (2,3), (3,4), (4,4)};
з) R={(1,2), (1,3), (2,2), (2,3), (3,3), (4,3)};
и) R={(1,4), (2,3), (3,2), (3,4), (4,1), (4,3)};
к) R={(2,1), (3,1), (3,2), (3,3), (3,4), (4,1)}.
№ 1.54 Найти область определения, область значений, построить график
каждого из следующих отношений:
а)
б)
x|RR)y,x{(
};1|y|2|x||RR)y,x{(
2
};y
2
znanio.ru