Основные формулы интегрирования
(табличные интегралы)
Непосредственное интегрирование это такой способ, при котором интеграл путем тождественных преобразований подынтегральной функции и свойств неопределённого интеграла производится к одному или нескольким табличным интегралам.
Пример №1
Пример №2
Пример №3
Пример №4
Пример №5
Интегрирование методом подстановки.
Сущность
этого метода заключается в том, что
путём введения новой переменной удаётся
ввести данный интеграл к новому интегралу,
который сравнительно легко берется
непосредственно. Для интегрирования
методом подстановки можно использовать
такую схему.
1. Часть подынтегральной функции надо заменить новой переменной;
Найти дифференциал от обеих частей замены;
Всё подынтегральное выражение выразить через новую переменную
Найти полученный табличный интеграл.
Сделать обратную замену.
Примеры:
1. пусть тогда
или подставим
пусть , тогда или получим
пусть тогда или получим
пусть тогда или подставляем в интеграл
Вопросы для самопроверки:
Какое действие называется интегрированием.
Какая функция называется первообразной?
Дайте определение неопределённого интеграла.
Вспомните свойства неопределённого интеграла
Каким действием можно проверить интегрирование.

Напишите основные формулы интегрирования.
Найдите интегралы:
Ответы:
а) а)
б) б)
в) в)
г) г)
Определённый интеграл.
Напомним, что приращением аргумента x при его изменении от до называется разность , а приращением функции при изменении аргумента от до называется разность .
Если — первообразная функции, для , то приращение первообразных функций при изменении аргумента x от x=a до x=b называется определённым интегралом и обозначается символом , т.е. и читается так: “определённый интеграл от а до в эф от икс дэ икс ”
Формула называется формулой Ньютона – Лейбница свойства определённого интеграла:
Определённый интеграл с одинаковыми пределами равен нулю:
При перестановке пределов интегрирования знак интеграла меняется на противоположный:
Постоянный множитель можно выносить за знак интеграла
Отрезок интегрирования можно разбить на части:
, где
Интеграл от алгебрaичeской суммы функций равен такой же алгебраической сумме интегралов от всех слагаемых:
Порядок вычисления определённого интеграла:
Найти неопределённый интеграл от данной функции;
В полученную первообразную подставить вместо аргумента сначала верхний, затем нижний предел интегрирования.

Из результата подстановки верхнего предела вычесть результат подстановки нижнего предела.
Пример №1
Пример №2
Пример №3
Вычисление определённого интеграла методом подстановки.
Состоит в следующем:
Часть подынтегральной функции заменить новой переменной.
Найти новые пределы определённого интеграла
Найти дифференциал от обеих частей замены
Все подынтегральное выражение выразить через новую переменную
Вычислить полученный определённый интеграл
Пример №1
Вычислить
Решение: Пусть , тогда , т.е.
Если , ; , значит,
Пример №2
Решение.
значит
Пример №3
значит
Пример №4
значит.
Вычисление
площадей фигур с помощью определённого
интеграла.
Задачи на вычисление площадей плоских фигур удобно решать по следующему плану:
По условию задачи делают чертёж.
Представляют искомую площадь как сумму или разность площадей криволинейных трапеций.
Определяют пределы интегрирования.
Записывают каждую функцию в виде
Вычисляют площади каждой криволинейной трапеции и площадь искомой фигуры.
Пример 1
Вычислить площадь фигуры, ограниченной параболой
, прямыми и осью абсцисс.
Y Решение:
-1 2 x
Пример 2
и
Построим прямую
;
Построим прямую
Найдём точку пересечения прямых для этого решим систему
x-2y+4=0
D(0;5)
y
-3y+9=0 x+y-5=0
т. е
M(2;3)
е
M(2;3)
М
C(5;0)
A(-4;0) 0 N(2;0)
Найдём площади треугольников AMN и NMC
Пример 3
точки пересечения параболы с осью ох; и
y
На отрезке график 0 x
функции расположен
ниже оси ох. Следовательно
Вопросы и упражнения для самопроверки.
Дайте определение определённого интеграла.
Перечислите основные свойства определённого интеграла.
Напишите формулы для определения площади плоской фигуры с помощью определённого интеграла.

Вычислите определённые интегралы:
; ; ;
Вычислите площадь фигуры, ограниченной линиями:
а) ; ; ;
б) и
в) и
Тема урока: Свойства неопределённого интеграла.
Предмет: информатика
Преподаватель: Амирханова А. К.
Тема урока: Свойства неопределённого интеграла.
Теперь не очень хорошая новость.
В отличие от дифференцирования, общих стандартных правил интегрирования, справедливых на все случаи жизни, в математике нету. Это фантастика!
Например, вы все прекрасно знаете (надеюсь!), что любое произведение любых двух функций f(x)·g(x) дифференцируется вот так:
(f(x)·g(x))’ = f’(x)·g(x) + f(x)·g’(x).
Любое частное дифференцируется вот так:
А любая сложная функция, какой бы накрученной она ни была, дифференцируется вот так:
И какие бы функции ни скрывались под буквами f и g, общие правила всё равно сработают и производная, так или иначе, будет найдена.
А вот с интегралами такой номер уже не пройдёт: для произведения, частного (дроби), а также сложной функции общих формул интегрирования не существует! Нету никаких стандартных правил! Вернее, они есть. Это я зря математику обидел.) Но, во-первых, их гораздо меньше, чем общих правил для дифференцирования. А во-вторых, большинство методов интегрирования, о которых мы будем разговаривать в следующих уроках, очень и очень специфические. И справедливы лишь для определённого, очень ограниченного класса функций. Скажем, только для дробно-рациональных функций. Или каких-то ещё.
А какие-то интегралы, хоть и существуют в природе, но вообще никак не выражаются через элементарные «школьные» функции! Да-да, и таких интегралов полно! 🙂
Именно поэтому интегрирование — гораздо более трудоёмкое и кропотливое занятие, чем дифференцирование. Но в этом есть и своя изюминка. Занятие это творческое и очень увлекательное.) И, если вы хорошо усвоите таблицу интегралов и освоите хотя бы два базовых приёма, о которых мы поговорим далее (замена переменной и интегрирование по частям), то интегрирование вам очень понравится.
А теперь познакомимся, собственно, со свойствами неопределённого интеграла. Их всего ничего. Вот они.
Первые два свойства полностью аналогичны таким же свойствам для производных и называются свойствами линейности неопределённого интеграла. Тут всё просто и логично: интеграл от суммы/разности равен сумме/разности интегралов, а постоянный множитель можно вынести за знак интеграла.
А вот следующие три свойства для нас принципиально новые. Разберём их поподробнее. Звучат по-русски они следующим образом.
Третье свойство
Всё просто, как в сказке. Если проинтегрировать функцию, а потом обратно найти производную от результата, то… получится исходная подынтегральная функция. 🙂 Этим свойством всегда можно (и нужно) пользоваться для проверки окончательного результата интегрирования. Вычислили интеграл — продифференцируйте ответ! Получили подынтегральную функцию — ОК. Не получили — значит, где-то накосячили. Ищите ошибку.)
Вычислили интеграл — продифференцируйте ответ! Получили подынтегральную функцию — ОК. Не получили — значит, где-то накосячили. Ищите ошибку.)
Конечно же, в ответе могут получаться настолько зверские и громоздкие функции, что и обратно дифференцировать их неохота, да. Но лучше, по возможности, стараться себя проверять. Хотя бы в тех примерах, где это несложно.)
Идём дальше, по порядочку.
Четвёртое свойство
Дифференциал от интеграла равен подынтегральному выражению.
Тут ничего особенного. Суть та же самая, только dx на конце появляется. Согласно предыдущему свойству и правилам раскрытия дифференциала.
Пятое свойство
Интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной.
Тоже очень простое свойство. Им мы тоже будем регулярно пользоваться в процессе решения интегралов. Особенно — в методе подведения функции под знак дифференциала и замены переменной.
Им мы тоже будем регулярно пользоваться в процессе решения интегралов. Особенно — в методе подведения функции под знак дифференциала и замены переменной.
Вот такие вот полезные свойства. Занудствовать с их строгими доказательствами я здесь не собираюсь. Желающим предлагаю это сделать самостоятельно. Прямо по смыслу производной и дифференциала. Докажу лишь последнее, пятое свойство, ибо оно менее очевидно.
Итак, у нас есть утверждение:
Вытаскиваем «начинку» нашего интеграла и раскрываем, согласно определению дифференциала:
На всякий случай, напоминаю, что, согласно нашим обозначениям производной и первообразной, F’(x) = f(x).
Вставляем теперь наш результат обратно внутрь интеграла:
Получено в точности определение неопределённого интеграла (да простит меня русский язык)! 🙂
Вот и вс
Просмотр содержимого документа
«Тема урока: Свойства неопределённого интеграла.
 »
»
Свойства неопределённого интеграла.
Теперь не очень хорошая новость.
В отличие от дифференцирования, общих стандартных правил интегрирования, справедливых на все случаи жизни, в математике нету. Это фантастика!
Например, вы все прекрасно знаете (надеюсь!), что любое произведение любых двух функций f(x)·g(x) дифференцируется вот так:
(f(x)·g(x))’ = f’(x)·g(x) + f(x)·g’(x).
Любое частное дифференцируется вот так:
А любая сложная функция, какой бы накрученной она ни была, дифференцируется вот так:
И какие бы функции ни скрывались под буквами f и g, общие правила всё равно сработают и производная, так или иначе, будет найдена.
А вот с интегралами такой номер уже не пройдёт: для произведения, частного (дроби), а также сложной функции общих формул интегрирования не существует! Нету никаких стандартных правил! Вернее, они есть.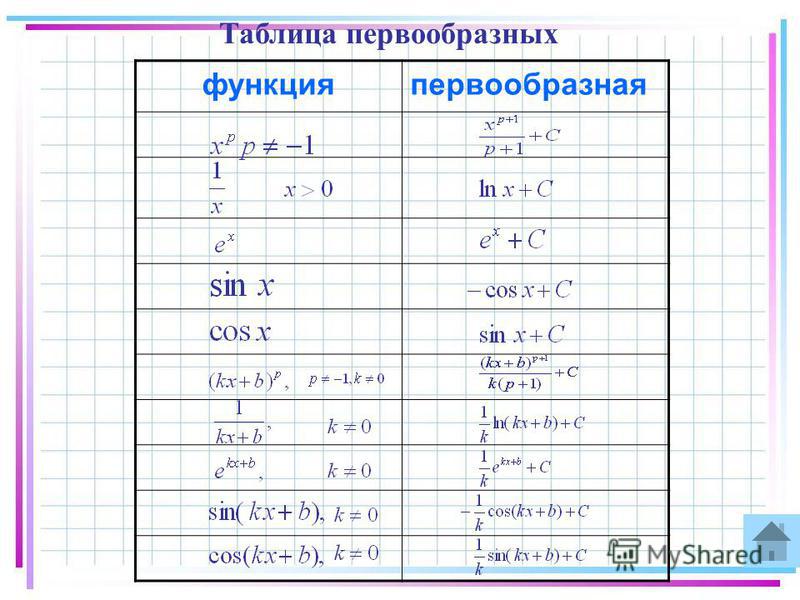 Это я зря математику обидел.) Но, во-первых, их гораздо меньше, чем общих правил для дифференцирования. А во-вторых, большинство методов интегрирования, о которых мы будем разговаривать в следующих уроках, очень и очень специфические. И справедливы лишь для определённого, очень ограниченного класса функций. Скажем, только для дробно-рациональных функций. Или каких-то ещё.
Это я зря математику обидел.) Но, во-первых, их гораздо меньше, чем общих правил для дифференцирования. А во-вторых, большинство методов интегрирования, о которых мы будем разговаривать в следующих уроках, очень и очень специфические. И справедливы лишь для определённого, очень ограниченного класса функций. Скажем, только для дробно-рациональных функций. Или каких-то ещё.
А какие-то интегралы, хоть и существуют в природе, но вообще никак не выражаются через элементарные «школьные» функции! Да-да, и таких интегралов полно! 🙂
Именно поэтому интегрирование — гораздо более трудоёмкое и кропотливое занятие, чем дифференцирование. Но в этом есть и своя изюминка. Занятие это творческое и очень увлекательное.) И, если вы хорошо усвоите таблицу интегралов и освоите хотя бы два базовых приёма, о которых мы поговорим далее (замена переменной и интегрирование по частям), то интегрирование вам очень понравится. 🙂
А теперь познакомимся, собственно, со свойствами неопределённого интеграла. Их всего ничего. Вот они.
Их всего ничего. Вот они.
Первые два свойства полностью аналогичны таким же свойствам для производных и называются свойствами линейности неопределённого интеграла. Тут всё просто и логично: интеграл от суммы/разности равен сумме/разности интегралов, а постоянный множитель можно вынести за знак интеграла.
А вот следующие три свойства для нас принципиально новые. Разберём их поподробнее. Звучат по-русски они следующим образом.
Третье свойство
Производная от интеграла равна подынтегральной функции
Всё просто, как в сказке. Если проинтегрировать функцию, а потом обратно найти производную от результата, то… получится исходная подынтегральная функция. 🙂 Этим свойством всегда можно (и нужно) пользоваться для проверки окончательного результата интегрирования. Вычислили интеграл — продифференцируйте ответ! Получили подынтегральную функцию — ОК. Не получили — значит, где-то накосячили. Ищите ошибку.)
Не получили — значит, где-то накосячили. Ищите ошибку.)
Конечно же, в ответе могут получаться настолько зверские и громоздкие функции, что и обратно дифференцировать их неохота, да. Но лучше, по возможности, стараться себя проверять. Хотя бы в тех примерах, где это несложно.)
Идём дальше, по порядочку.
Четвёртое свойство
Дифференциал от интеграла равен подынтегральному выражению.
Тут ничего особенного. Суть та же самая, только dx на конце появляется. Согласно предыдущему свойству и правилам раскрытия дифференциала.
Пятое свойство
Интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной.
Тоже очень простое свойство. Им мы тоже будем регулярно пользоваться в процессе решения интегралов. Особенно — в методе подведения функции под знак дифференциала и замены переменной.
Вот такие вот полезные свойства. Занудствовать с их строгими доказательствами я здесь не собираюсь. Желающим предлагаю это сделать самостоятельно. Прямо по смыслу производной и дифференциала. Докажу лишь последнее, пятое свойство, ибо оно менее очевидно.
Итак, у нас есть утверждение:
Вытаскиваем «начинку» нашего интеграла и раскрываем, согласно определению дифференциала:
На всякий случай, напоминаю, что, согласно нашим обозначениям производной и первообразной, F’(x) = f(x).
Вставляем теперь наш результат обратно внутрь интеграла:
Получено в точности определение неопределённого интеграла (да простит меня русский язык)! 🙂
Вот и вс
Table of Integrals, Series, and Products
Select country/regionUnited States of AmericaUnited KingdomAfghanistanÅland IslandsAlbaniaAlgeriaAmerican SamoaAndorraAngolaAnguillaAntigua and BarbudaArgentinaArmeniaArubaAustraliaAustriaAzerbaijanBahamasBahrainBangladeshBarbadosBelgiumBelizeBeninBermudaBhutanBoliviaBonaire, Sint Eustatius and SabaBosnia and HerzegovinaBotswanaBrazilBritish Indian Ocean TerritoryBritish Virgin IslandsBruneiBulgariaBurkina FasoBurundiCambodiaCameroonCanadaCanary IslandsCape VerdeCayman IslandsCentral African RepublicChadChileChinaChristmas IslandCocos (Keeling) IslandsColombiaComorosCongoCook IslandsCosta RicaCroatiaCubaCuraçaoCyprusCzech RepublicDemocratic Republic of the CongoDenmarkDjiboutiDominicaDominican RepublicEcuadorEgyptEl SalvadorEquatorial GuineaEritreaEstoniaEthiopiaFalkland Islands (Malvinas)Faroe IslandsFederated States of MicronesiaFijiFinlandFranceFrench GuianaFrench PolynesiaGabonGambiaGeorgiaGermanyGhanaGibraltarGreeceGreenlandGrenadaGuadeloupeGuamGuatemalaGuernseyGuineaGuinea-BissauGuyanaHaitiHondurasHong KongHungaryIcelandIndiaIndonesiaIranIraqIrelandIsle of ManIsraelItalyJamaicaJapanJerseyJordanKazakhstanKenyaKiribatiKuwaitKyrgyzstanLaoLatviaLesothoLiberiaLibyaLiechtensteinLuxembourgMacaoMacedoniaMadagascarMalawiMalaysiaMaldivesMaliMaltaMarshall IslandsMartiniqueMauritaniaMauritiusMayotteMexicoMoldovaMonacoMongoliaMontenegroMontserratMoroccoMozambiqueMyanmarNamibiaNepalNetherlandsNew CaledoniaNew ZealandNicaraguaNigerNiueNorfolk IslandNorth KoreaNorthern Mariana IslandsNorwayOmanPakistanPalauPanamaPapua New GuineaParaguayPeruPhilippinesPitcairnPolandPortugalPuerto RicoQatarRéunionRomaniaRwandaSaint BarthélemySaint HelenaSaint Kitts and NevisSaint LuciaSaint Martin (French part)Saint Pierre and MiquelonSaint Vincent and the GrenadinesSamoaSan MarinoSao Tome and PrincipeSaudi ArabiaSenegalSerbiaSeychellesSierra LeoneSingaporeSint Maarten (Dutch part)SlovakiaSloveniaSolomon IslandsSomaliaSouth AfricaSouth Georgia and the South Sandwich IslandsSouth KoreaSouth SudanSpainSri LankaSudanSurinameSvalbard and Jan MayenSwazilandSwedenSwitzerlandSyriaTaiwanTajikistanTanzaniaThailandTimor LesteTogoTokelauTongaTrinidad and TobagoTunisiaTurkeyTurkmenistanTurks and Caicos IslandsTuvaluUgandaUkraineUnited Arab EmiratesUruguayUS Virgin IslandsUzbekistanVanuatuVatican CityVenezuelaVietnamWallis and FutunaWestern SaharaYemenZambiaZimbabwe
Варианты покупкиПечать — Hardcover $ 99,95Vailable
Ebook $ 78,99
Налог с продаж будет рассчитана при выборе
Бесплатная мировая доставка
NO MINOMUME
ОПИСАНИЕ
ЭК -eddition of Gradsh представляет собой обновленное, полностью переработанное издание того, что повсеместно признано пользователями математических и прикладных наук в качестве ключевого справочника по интегралам и специальным функциям. Книга ценится пользователями предыдущих изданий работы как за всесторонний охват интегралов и специальных функций, так и за ее точность и ценные обновления. Начиная с первого издания, вышедшего в 1965, математическое содержание этой книги значительно увеличилось за счет добавления нового материала, хотя объем книги остался почти неизменным. Новое 8-е издание содержит совершенно новые результаты и поправки к вспомогательным условиям, сопровождающим интегралы, и везде, где это возможно, большинство статей содержат ценные ссылки на их источник.
Книга ценится пользователями предыдущих изданий работы как за всесторонний охват интегралов и специальных функций, так и за ее точность и ценные обновления. Начиная с первого издания, вышедшего в 1965, математическое содержание этой книги значительно увеличилось за счет добавления нового материала, хотя объем книги остался почти неизменным. Новое 8-е издание содержит совершенно новые результаты и поправки к вспомогательным условиям, сопровождающим интегралы, и везде, где это возможно, большинство статей содержат ценные ссылки на их источник.
Основные функции
- Более 10 000 математических записей
- Самый последний список интегралов, рядов и произведений (специальные функции)
- Обеспечивает точность и эффективность в отраслевой работе
- 25 % новых материалов, не включая изменения ограничений на результаты, которые пересматривают диапазон достоверности результатов, что дает приблизительно 35 % новых обновлений
Читательская аудитория
Инженеры, чистые и прикладные математики, ученые, физики и аспиранты
Содержание
- Предисловие к восьмому изданию
- Благодарности
- Порядок представления формул
- Использование таблиц*
- Полиномы и числа Бернулли и Эйлера
- Эллиптические функции и эллиптические интегралы
- The Jacobi Zeta Functions 902 Функции
- Экспоненциальные и родственные интегралы
- Ортогональные многочлены Эрмита и Чебышева
- Функции Бесселя
- Функции параболического цилиндра и функции Уиттекера
- Mathieu Functions
- Индекс специальных функций
- Обозначение
- ПРИМЕЧАНИЕ О библиографических ссылках
- 0.
 ВВЕДЕНИЕ
ВВЕДЕНИЕ- 0,1 Сумма
- 0.2 Series Series и Infinite Series
- Series
- Series
- Series
- .
- Series
- .
- Series
- .
- Series
- .
- Series. из дифференциального исчисления
- 1. Элементарные функции
- 1.1 Степени биномов
- 1.2 Показательная функция
- 1.3–1.4 Trigonometric and Hyperbolic Functions
- 1.5 The Logarithm
- 1.6 The Inverse Trigonometric and Hyperbolic Functions
- 2. Indefinite Integrals of Elementary Functions
- 2.0 Introduction
- 2.1 Rational Functions
- 2.2 Algebraic functions
- 2.3 Показательная функция
- 2.4 Гиперболические функции
- 2.5–2.6 Тригонометрические функции
- 2.7 Логарифмы и обратные гиперболические функции
- 2.8 Обратные тригонометрические функции
- 3-4. Определенные интегралы элементарных функций
- 3.
 0 ВВЕДЕНИЕ
0 ВВЕДЕНИЕ - 3.1-3.2 Функции мощности и алгебраии
- 3,3–3,4 Экспоненциальные функции
- 3,5 Гиперболические функции
- 3,6–4,1 Тригонометрические функции
- 3.
- 3,6–4,1 Функции
- 3,6–4,1 Функции 240024 240024 240024 240024 240024 240024 240024 240024 240024 240024
- 3,6–4,1. 4.11–4.12 Комбинации с участием тригонометрических и гиперболических функций и степеней
- 4.13 Combinations of trigonometric and hyperbolic functions and exponentials
- 4.14 Combinations of trigonometric and hyperbolic functions, exponentials, and powers
- 4.2–4.4 Logarithmic Functions
- 4.5 Inverse Trigonometric Functions
- 4.6 Multiple Integrals
- 5.1 Эллиптические интегралы и функции
- 5.13 Эллиптические функции Якоби
- 5.14 Weierstrass elliptic functions
- 5.
 2 The Exponential Integral function
2 The Exponential Integral function - 5.3 The Sine Integral and the Cosine Integral
- 5.4 The Probability Integral and Fresnel Integrals
- 5.5 Bessel Functions
- 5.6 Orthogonal Polynomials
- 5.7 Hypergeometric Functions
- 6.1 Эллиптические интегралы и функции
- 6.2–6.3 Экспоненциальная интегральная функция и функции, ею порожденные
- 6.22–6,23 Экспоненциальная интегральная функция
- 6.24–6,26 Интегральные и косинусные интегральные функции
- 6.27. Интегральная интегральная и гиперболическая интегральная функция
- 6.28–6.31. Скорее Гамма-функция и функции, порожденные ею
- 6.46–6.47 Функция ψ ( x )
- 6.5–6.7 Функции Бесселя
- 6.8 Функции, порожденные функциями Бесселя
- 6.9 Mathieu Functions
- 7.
 1-7.2 Associated Legendre Functions
1-7.2 Associated Legendre Functions - 7.3–7.4 Orthogonal Polynomials
- 7.325* Complete System of Orthogonal Step Functions
- 7.33 Combinations of the polynomials Cnv( x) и функции Бесселя. Интегрирование функций Гегенбауэра по индексу
- 7.34 Комбинации полиномов Чебышева и степеней
- 7.35 Combinations of Chebyshev polynomials and elementary functions
- 7.36 Combinations of Chebyshev polynomials and Bessel functions
- 7.37−7.38 Hermite polynomials
- 7.39 Jacobi polynomials
- 7.41–7.42 Laguerre polynomials
- 7.5 Hypergeometric Functions
- 7.53 Hypergeometric and trigonometric functions
- 7.54 Комбинации гипергеометрических функций и функций Бесселя
- 7.6 Вырожденные гипергеометрические функции
- 7.68 Combinations of confluent hypergeometric functions and other special functions
- 7.69 Integration of confluent hypergeometric functions with respect to the index
- 7.
 7 Parabolic Cylinder Functions
7 Parabolic Cylinder Functions - 7.8 Meijer’s and MacRobert’s Functions ( G and E )
- 8.1 Эллиптические интегралы и функции
- 8.2 Экспоненциальная интегральная функция и функции, ею порожденные
- 8.3 Интегралы Эйлера первых и вторых видов и функций, сгенерированных ими
- 8.4–8,5 Функции и функции Бесселя, связанные с ними
- 9.1 Гипергеометрические функции
- 9.1 Гипергеометрические функции
- 9.1. Мейера G — Функция
- 9.4 МакРоберта E — Функция
- 9.5 Дзета-функции Римана ζ ( z , Q ) и ζ ( Z ) и функции φ ( Z , S , V ) и ξ ( S ) и ξ ( S ) и ξ ( S ) и ξ ( S ) и ξ (). Числа, функции v( x ), v( x , α), µ(x, β), µ(x, β, α), λ( x , y ) и многочлены Эйлера
- 9.
 7 Константы
7 Константы
- 10. Теория векторного поля
- 10.1–10.8 Векторы, векторные операторы и интегральные теоремы
- 11. Integral Inequalities
- 11.11 Mean Value Theorems
- 11.21 Differentiation of Definite Integral Containing a Parameter
- 11.31 Integral Inequalities
- 11.41 Convexity and Jensen’s Inequality
- 11.51 Fourier Series and Related Inequalities
- 12. Преобразования Фурье, Лапласа и Меллина
- 12.1–12.4 Интегральные преобразования
- Библиографические ссылки
- Дополнительные ссылки
- Индекс функций и константов
- Индекс концепций
Де 18, 2014
О редакторе
Daniel Zwillinger0375
Доктор Даниэль Цвиллингер — старший главный системный инженер компании Raytheon. Он был ответственным за системные требования для корабля-заменителя Cobra Judy (CJR), а также был руководителем требований и испытаний для отслеживания на неклассифицированных радарах раннего предупреждения (UEWR). Он улучшил процесс аккредитации программного обеспечения эсминца Zumwalt и руководил испытаниями радара с активной решеткой с электронным сканированием (AESA). Дэн является экспертом в предметной области (SME) в области дизайна для Six Sigma (DFSS) и является DFSS SME в области оптимизации тестирования, управления программами критической цепи и голоса клиента. В настоящее время он возглавляет проект по созданию Trust in Autonomous Systems. В компании Raytheon он дважды получал награду президента за лучший проект года «Шесть сигм»: за преобразование пакетов планирования в рабочие пакеты для ракеты Patriot и за пересмотр системы учета рабочего времени Raytheon. Он руководил программой обучения белых поясов «Шесть сигм».
До прихода в Raytheon Дэн работал в Sandia Labs, JPL, Exxon, MITRE, IDA, BBN и The Mathworks (где он разработал раннюю версию их Statistics Toolbox).
Он был ответственным за системные требования для корабля-заменителя Cobra Judy (CJR), а также был руководителем требований и испытаний для отслеживания на неклассифицированных радарах раннего предупреждения (UEWR). Он улучшил процесс аккредитации программного обеспечения эсминца Zumwalt и руководил испытаниями радара с активной решеткой с электронным сканированием (AESA). Дэн является экспертом в предметной области (SME) в области дизайна для Six Sigma (DFSS) и является DFSS SME в области оптимизации тестирования, управления программами критической цепи и голоса клиента. В настоящее время он возглавляет проект по созданию Trust in Autonomous Systems. В компании Raytheon он дважды получал награду президента за лучший проект года «Шесть сигм»: за преобразование пакетов планирования в рабочие пакеты для ракеты Patriot и за пересмотр системы учета рабочего времени Raytheon. Он руководил программой обучения белых поясов «Шесть сигм».
До прихода в Raytheon Дэн работал в Sandia Labs, JPL, Exxon, MITRE, IDA, BBN и The Mathworks (где он разработал раннюю версию их Statistics Toolbox).
В течение десяти лет Цвиллингер был владельцем и президентом корпорации Aztec. Будучи малым предприятием, Aztec выиграла несколько контрактов на исследования в сфере инноваций для малого бизнеса (SBIR). Компания также создала несколько программных пакетов для издательских компаний. До прихода в Aztec Цвиллингер был профессором математического факультета Политехнического института Ренсселера.
Дэн написал несколько книг по математике на темы дифференциальных уравнений, интегрирования, статистики и общей математики. Он является главным редактором «Стандартных математических таблиц и формул» компании Chemical Rubber Company (CRC) и входит в состав редакционного совета «Справочника по химии и физике» CRC.
Цвиллингер имеет степень бакалавра математики Массачусетского технологического института (MIT). Он получил докторскую степень по прикладной математике в Калифорнийском технологическом институте (Калифорнийский технологический институт). Цвиллингер является сертифицированным экспертом Raytheon Six Sigma и черным поясом Six Sigma, сертифицированным ASQ. Он также имеет лицензию пилота.
Он также имеет лицензию пилота.
Партнерство и экспертиза
Политехнический институт Ренсселера, Трой, Нью -Йорк, США
Рейтинги и обзоры
Напишите обзор
Последние обзоры
(Всего рейтинго Пн. 09.09.2019
Восьмое издание «Классики» Градштейна и Рыжика
Это крупное обновление классики, заслуживающее места на большинстве книжных полок математиков, физиков и других ученых.
кадр данных — значения интеграла в последней строке таблицы в R
спросил
Изменено 1 год, 11 месяцев назад
Просмотрено 251 раз
Часть R Language Collective Collective
Можно ли вычислять интегралы из фрейма данных в R?
Пример.
t <- data.frame(x1 = c(200),
х2 = с(2),
х3 = с(1:500))
Если t является таблицей, можно ли создать новый столбец с интегральными результатами, как и в других операциях?
Я пытался использовать этот код, но это не сработало.
Func <- function(z) {(t$x1+t$x2+t$x3)*z}
t$new <- интегрировать (Func, нижний = 1, верхний = 2)
- r
- кадр данных
- dplyr
- интеграл
2
С dplyr :
библиотека (dplyr)
Func <- function(z,t) {t*z}
t %>% построчно %>%
мутировать (новый = интегрировать (функция (z) Func (z, x1 + x2 + x3), нижний = 1, верхний = 2) $ значение)
# Таблетка: 500 x 4
# По строкам:
х1 х2 х3 новый
1 200 2 1 305.
2 200 2 2 306.
3 200 2 3 308.
4 200 2 4 309
5 200 2 5 310.
6 200 2 6 312
7 200 2 7 314.
8 200 2 8 315
9200 2 9 316.
10 200 2 10 318
# . .. еще 490 строк
.. еще 490 строк
1
Вот способ.
Перепишите функцию так, чтобы она принимала дополнительный аргумент, трехмерный вектор X , соответствующий каждой строке таблицы t . Затем вычислите интегралы в цикле apply по строкам t .
Func <- function(z, X) {
х1 <- Х[[1]]
х2 <- Х[[2]]
х3 <- Х[[3]]
(x1 + x2 + x3)*z
}
t $ новый <- применить (т, 1, функция (х) {
интегрировать (Функция, нижняя = 1, верхняя = 2, X = x) $ значение
})
голова (т)
# x1 x2 x3 новый
#1 200 2 1 304,5
#2 200 2 2 306,0
#3 200 2 3 307,5
#4 200 2 4 309.0
#5 200 2 5 310,5
#6 200 2 6 312,0
Если вам не очень удобно *нанесите петель, вот эквивалент для петель.
t$новый <- NA
for(i in seq_len(nrow(t))){
t$new[i] <- интегрировать(Func, нижний = 1, верхний = 2, X = t[i, 1:3, drop = TRUE])$value
}
Вывод такой же, как указано выше.
Аналогичный подход @Waldi, но с восстановлением всей информации из вызова .0449 интегрировать объект в список (поскольку нет встроенной версии).
as.list.integrate <- function(x) {
список(
значение=х$значение,
абс.ошибка=x$абс.ошибка,
подразделения=x$подразделения,
сообщение=x$сообщение,
вызов = х $ вызов
)
}
Теперь выполните интеграцию.
т %>%
построчно() %>%
мутировать (новый = список (как. список (интегрировать (функция (z) {(x1 + x2 + x3) * z}, 1, 2)))) %>%
unnest_wider (новое, упрощение = ИСТИНА)
# Таблетка: 500 x 8
x1 x2 x3 значение абс.ошибка подразделения сообщение вызов 1 200 2 1 305. 3.38e-12 1 OK <язык> 2 200 2 2 306. 3.40e-12 1 OK <язык> 3 200 2 3 308. 3.41e-12 1 OK <язык> 4 200 2 4 3093.43e-12 1 ОК <язык> 5 200 2 5 310. 3.45e-12 1 OK <язык> 6 200 2 6 312 3.46e-12 1 OK <язык> 7 200 2 7 314. 3.48e-12 1 OK <язык> 8 200 2 8 315 3.



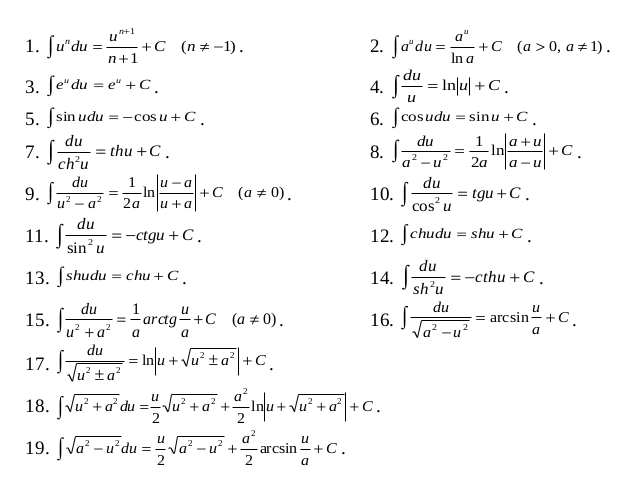
 ВВЕДЕНИЕ
ВВЕДЕНИЕ 0 ВВЕДЕНИЕ
0 ВВЕДЕНИЕ 2 The Exponential Integral function
2 The Exponential Integral function 1-7.2 Associated Legendre Functions
1-7.2 Associated Legendre Functions 7 Parabolic Cylinder Functions
7 Parabolic Cylinder Functions 7 Константы
7 Константы