ОглавлениеВВЕДЕНИЕЧасть первая.  Глава I. ДЕЙСТВИТЕЛЬНЫЕ И КОМПЛЕКСНЫЕ ЧИСЛА 2. Простые и составные числа. Признаки делимости. 3. Наибольший общий делитель и наименьшее общее кратное. 4. Целые числа. Рациональные числа. 5. Десятичные дроби. Представление рациональных чисел десятичными дробями. 6. Иррациональные числа. Действительные числа. 7. Действия с приближенными числами. 8. Числовая ось. Координаты точки на плоскости. § 2. Степени и корни 9. Степени с натуральными показателями. 10. Степени с целыми показателями. 11. Корни. 12. Степени с рациональными показателями. Степени с действительными показателями. 13. Алгоритм извлечения квадратного корня. § 3. Комплексные числа 14. Основные понятия и определения. 15. Рациональные действия с комплексными числами. 16. Геометрическое изображение комплексных чисел. Тригонометрическая форма комплексного числа. 17. Действия с комплексными числами, заданными в тригонометрической форме. 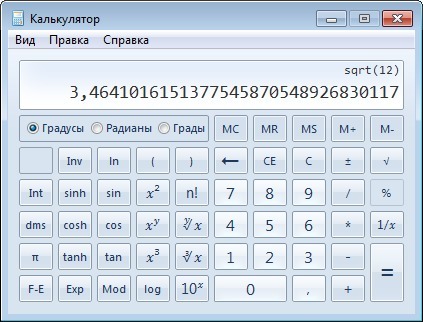 Формула Муавра. Формула Муавра.18. Извлечение корня из комплексного числа. Глава II. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ 19. Алгебраические выражения. Одночлены и многочлены. 20. Формулы сокращенного умножения. 21. Бином Ньютона. 22. Разложение многочлена на множители. 23. Дробные алгебраические выражения. § 2. Иррациональные алгебраические выражения 24. Радикалы из алгебраических выражений. 25. Освобождение от иррациональности в знаменателе дроби. Глава III. ЛОГАРИФМЫ 26. Определение и свойства логарифмов. 27. Логарифмы по различным основаниям. Модуль перехода. § 2. Десятичные логарифмы 28. Характеристика и мантисса десятичного логарифма. 29. Применение десятичных логарифмов к вычислениям. Глава IV. ФУНКЦИИ И ГРАФИКИ 30. Величина. Числовые множества. 31. Определение функции. 32. График функции. Способы задания функций. 34. Сложная функция. 35. Обратная функция. 36.  n. n.41. Обратная пропорциональная зависимость. Степенная функция с рациональным показателем степени. 42. Показательная функция. 43. Логарифмическая функция. § 3. Преобразование графиков 44. Параллельный сдвиг графика. 45. График квадратного трех члена. 46. График дробно-линейной функции. 47. Преобразование симметрии. Сжатие и растяжение графика. 48. Построение графиков функций. 49. Сложение графиков. § 4. Некоторые сведения о рациональных функциях 50. Целые и дробные рациональные функции. Деление многочленов. 51. Схема Горнера. Теорема Безу. 52. Нули многочлена. Разложение многочлена на множители. Глава V. УРАВНЕНИЯ 53. Уравнение. Корни уравнения. 54. Равносильные уравнения. 55. Системы уравнений. 56. Графическое решение уравнений. §. 2. Алгебраические уравнения с одной неизвестной 57. Число и кратность корней. 58. Уравнения первой степени (линейные уравнения). 59. Уравнения второй степени (квадратные уравнения). 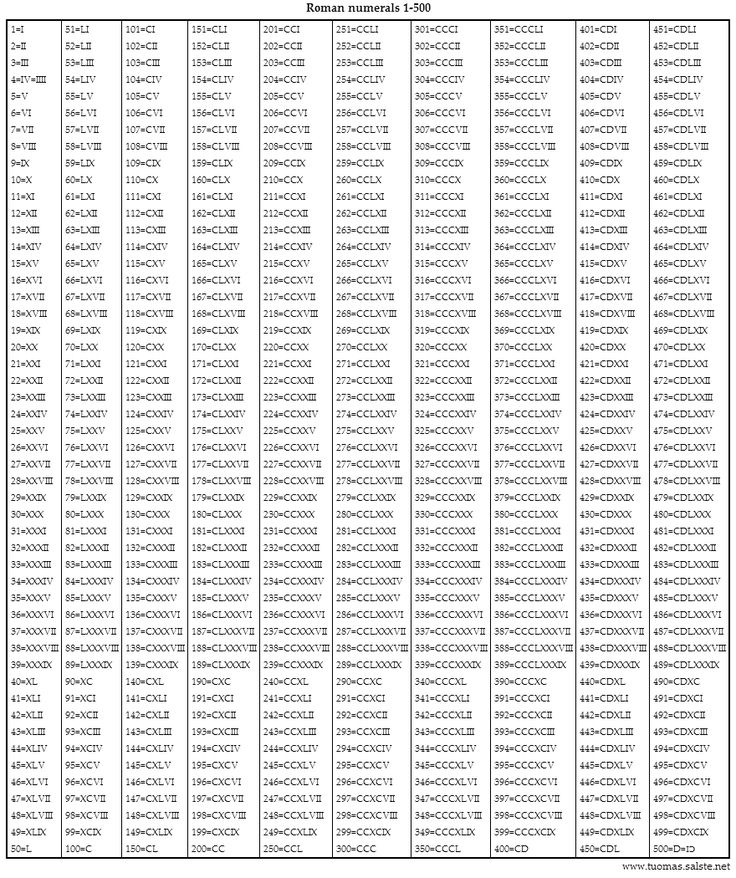 60. Формулы Виета. Разложение квадратного трехчлена на множители. 61. Исследование квадратного уравнения. 62. Уравнения высших степеней. Целые корни. 63. Двучленные уравнения. 64. Уравнения, сводящиеся к квадратным. 65. Возвратные уравнения. § 3. Системы алгебраических уравнений 66. Линейные системы. 67. Определители второго порядка. Исследование линейных систем двух уравнений с двумя неизвестными. 68. Системы, состоящие из уравнения второй степени и линейного уравнения. 69. Примеры систем двух уравнений второй степени. Системы уравнений высших степеней. 70. Иррациональные уравнения. 71. Показательные уравнения. 72. Логарифмические уравнения. 73. Разные уравнения. Системы уравнений. Глава VI. НЕРАВЕНСТВА 74. Свойства неравенств. Действия над неравенствами. 75. Алгебраические неравенства. § 2. Решение неравенств 76. Множество решений неравенства.  Равносильные неравенства. Равносильные неравенства.77. Графическое решение неравенств. 79. Квадратные неравенства. 80. Неравенства высших степеней. Неравенства, содержащие дробные рациональные функции от х. 81. Иррациональные, показательные и логарифмические неравенства. 82. Неравенства с двумя неизвестными. Глава VII. ПОСЛЕДОВАТЕЛЬНОСТИ 83. Числовая последовательность. 84. Предел числовой последовательности. 85. Бесконечно малые. Правила предельного перехода. § 2. Арифметическая прогрессия 86. Арифметическая прогрессия. Формула общего члена. 87. Свойства арифметической прогрессии. 88. Формула для суммы n членов арифметической прогрессии. § 3. Геометрическая прогрессия 89. Геометрическая прогрессия. Формула общего члена. 90. Свойства геометрической прогрессии. 91. Формулы для суммы n членов геометрической прогрессии. 92. Бесконечно убывающая геометрическая прогрессия. Глава VIII. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА (ДУГИ) 93. Вектор, проекция вектора.  94. Положительные углы и дуги, меньшие 360°. 95. Углы и дуги, большие 360°. 96. Отрицательные углы. Сложение и вычитание углов. § 2. Тригонометрические функции произвольного угла 97. Определение основных тригонометрических функций. § 3. Соотношения между тригонометрическими функциями одного и того же угла 99. Основные тригонометрические тождества. 100. Вычисление значений тригонометрических функций по значению одной из них. 101. Значения тригонометрических функций некоторых углов. § 4. Четность, нечетность и периодичность тригонометрических функций 102. Четность и нечетность. 103. Понятие периодической функции. 104. Периодичность тригонометрических функций. § 5. Формулы приведения 105. Зависимость между тригонометрическими функциями дополнительных углов. 106. Формулы приведения. Глава IX. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА И ИХ ГРАФИКИ § 1. 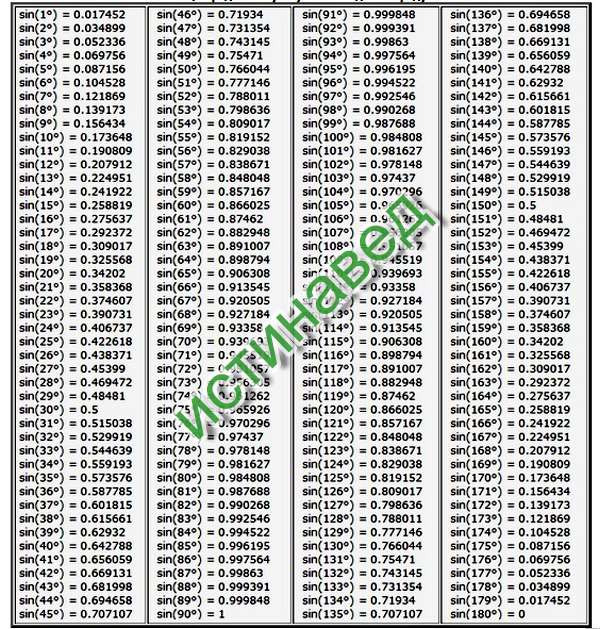 Тригонометрические функции числового аргумента Тригонометрические функции числового аргумента108. Области определения и области изменения значений тригонометрических функций. 109. Некоторые неравенства и их следствия. § 2. Графики тригонометрических функций 110. Первоначальные сведения о таблицах тригонометрических функций. 111. Основные графики. 112. Примеры построения графиков некоторых других тригонометрических функций. 113. Дальнейшие примеры построения графиков функций. Глава X. ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ 114. Расстояние между двумя точками на плоскости. 115. Косинус суммы и разности двух аргументов. 116. Синус суммы и разности двух аргументов. 117. Тангенс суммы и разности двух аргументов. 118. О формулах сложения для нескольких аргументов. § 2. Формулы для двойного и половинного аргумента. Выражение sin na и cos na через степени sin a и cos a 119. Тригонометрические функции двойного аргумента. 120. Выражение sin na и cos na через степени sin a и cos a при натуральном числе n.  121. Тригонометрические функции половинного аргумента. 122. Выражение основных тригонометрических функций аргумента а через tg(a/2). § 3. Преобразование в сумму выражений вида sina•cosb, cosa•cosb и sinа•sinb § 4. Преобразование в произведение сумм вида § 5. Преобразование некоторых выражений в произведения с помощью введения вспомогательного аргумента 127. Преобразование в произведение выражения a•sina + b•cosa. 128. Преобразование в произведение выражений a•sina+b и a•cosa+b 129. Преобразование в произведение выражения a•tga+b. Глава XI. ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ИХ ГРАФИКИ 130. Функция у = arcsin x (арксинус). 131. Функция y = arccos x (арккосинус). 132. Функция y = arctg x (арктангенс). 133. Функция y = arcctg x (арккотангенс). 134. Пример. § 2. Операции над обратными тригонометрическими функциями 135. Тригонометрические операции. 136. Операции сложения (вычитания). § 3. Обратные тригонометрические операции над тригонометрическими функциями 137.  Функция у = arcsin (sin x). Функция у = arcsin (sin x).138. Функция y = arctg (tg x). Глава XII. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА 139. Уравнение sin х = а. 140. Уравнение cos х = a. 141. Уравнение tg x = a. 142. Уравнение ctg x = a. 143. Некоторые дополнения. § 2. Способ приведения к одной функции одного и того же аргумента 145. Некоторые типы уравнений, приводящихся к уравнениям относительно функции одного аргумента. 146. Способ разложения на множители. 147. Решение рациональных тригонометрических уравнений с помощью универсальной тригонометрической подстановки tg(x/2) = t. § 3. Некоторые частные приемы решения тригонометрических уравнений и систем 148. Введение вспомогательного аргумента. 149. Преобразование произведения в сумму или разность. 151. Решение уравнения типа… 152. Применение подстановок sinx ± соsx = y. § 4. Решение тригонометрических неравенств 154. Простейшие тригонометрические неравенства.  155. Примеры тригонометрических неравенств, сводящихся к простейшим. Часть вторая. ГЕОМЕТРИЯ 156. Точка. Прямая. Луч. Отрезок. 157. Плоскость. Фигуры и тела. 160. Равенство фигур. Движение. 161. Равенство тел. § 2. Измерение геометрических величин 162. Сложение отрезков. Длина отрезка. 163. Общая мера двух отрезков. 164. Сравнительная длина отрезков и ломаных. 165. Измерение углов. 166. Радианная мера угла. 167. Измерение площадей. 168. Площадь прямоугольника. Объем прямоугольного параллелепипеда. Глава XIV. ПЕРПЕНДИКУЛЯРНЫЕ И ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ. ЗАДАЧИ НА ПОСТРОЕНИЕ 169. Перпендикуляр и наклонные. 170. Свойство перпендикуляра, проведенного к отрезку в его середине. 171. Параллельные прямые. 172. Углы, образованные двумя параллельными прямыми и секущей. 173. Углы с параллельными или перпендикулярными сторонами. § 2. Геометрические места точек. Окружность 174. Геометрическое место точек. 175. Свойство биссектрисы угла.  176. Окружность. 177. Взаимное расположение прямой и окружности. Касательная и секущая. 178. Хорда и диаметр. Сектор и сегмент. 179. Взаимное расположение двух окружностей. § 3. Основные задачи на построение 181. Деление отрезка пополам. Построение перпендикуляров. 182. Построение углов. 183. Другие задачи на построение. Глава XV. ТРЕУГОЛЬНИКИ, ЧЕТЫРЕХУГОЛЬНИКИ 184. Стороны и углы треугольника. 185. Биссектрисы треугольника. Вписанная окружность. 186. Оси симметрии сторон треугольника. Описанная окружность. 187. Медианы и выcоты треугольника. 188. Равенство треугольников. 189. Построение треугольников. 190. Равнобедренные треугольники. 191. Прямоугольные треугольники. § 2. Параллелограммы 192. Четырехугольники. 193. Параллелограмм и его свойства. 194. Прямоугольник. § 3. Трапеция 196. Трапеция. 197. Средняя линия треугольника. 198. Средняя линия трапеции. 199. Деление отрезка на равные части.  § 4. Площади треугольников и четырехугольников 200. Площадь параллелограмма. 201. Площадь треугольника. 202. Площадь трапеции. Глава XVI. ПОДОБИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР 203. Пропорциональные отрезки. 204. Свойства биссектрис внутреннего и внешнего углов треугольника. § 2. Подобное преобразование фигур (гомотетия) 205. Определение гомотетичных фигур. 206. Свойства преобразования подобия. § 3. Общее подобное соответствие фигур 207. Подобные фигуры. 208. Периметры и площади подобных треугольников. 209. Применение подобия к решению задач на построение. Глава XVII. МЕТРИЧЕСКИЕ СООТНОШЕНИЯ В ТРЕУГОЛЬНИКЕ И КРУГЕ 210. Углы с вершиной на окружности. 211. Углы с вершиной внутри и вне круга. 212. Угол, под которым виден данный отрезок. 213. Четырехугольники, вписанные в окружность. 214. Пропорциональные отрезки в круге. 215. Задачи на построение. § 2. Метрические соотношения в треугольнике 216. Пропорциональные отрезки в прямоугольном треугольнике.  Теорема Пифагора. Теорема Пифагора.218. Теорема синусов. Формула Герона. 217. Квадрат стороны, лежащей против острого или тупого утла и треугольнике. Теорема косинусов. 218. Теорема синусов. Формула Герона. 219. Радиусы вписанной и описанной окружностей. § 3. Решение треугольников 220. Таблицы функций. 221. Решение треугольников. Сводка основных формул. 222. Решение прямоугольных треугольников. 223. Решение косоугольных треугольников. Глава XVIII. ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ. ДЛИНА окружности И ПЛОЩАДЬ КРУГА 224. Выпуклые многоугольники. 225. Правильные многоугольники. 226. Соотношения между стороной, радиусом и апофемой. 227. Периметр и площадь правильного n-угольника. 228. Удвоение числа сторон правильного многоугольника. § 2. Длина окружности. Площадь круга и его частей 229. Длина окружности. 230. Площадь круга и его частей. Глава XIX. ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ 231. Взаимное расположение двух прямых в пространстве.  232. Взаимное расположение прямой линии и плоскости. 233. Взаимное расположение двух плоскостей. 234. Свойства параллельных прямых и плоскостей. 235. Построения в стереометрии. § 2. Перпендикулярность прямых и плоскостей 236. Перпендикуляр к плоскости. 237. Перпендикуляр и наклонные. 238. Угол между прямой и плоскостью. 239. Связь между перпендикулярностью и параллельностью прямых и плоскостей. 240. Общий перпендикуляр двух скрещивающихся прямых. § 3. Двугранные и многогранные углы 241. Двугранный угол. 242. Взаимно перпендикулярные плоскости. 243. Трехгранные углы. 244. Многогранные углы. § 4. Многогранники 245. Многогранники. 246. Правильные многогранники. Глава XX. МНОГОГРАННИКИ И КРУГЛЫЕ ТЕЛА 247. Цилиндры и призмы. 248. Параллелепипеды. 249. Объемы призм и цилиндров. 250. Площадь боковой поверхности призмы. 251. Площадь поверхности цилиндра. § 2. Пирамида. Конус 252. Свойства пирамиды и конуса. 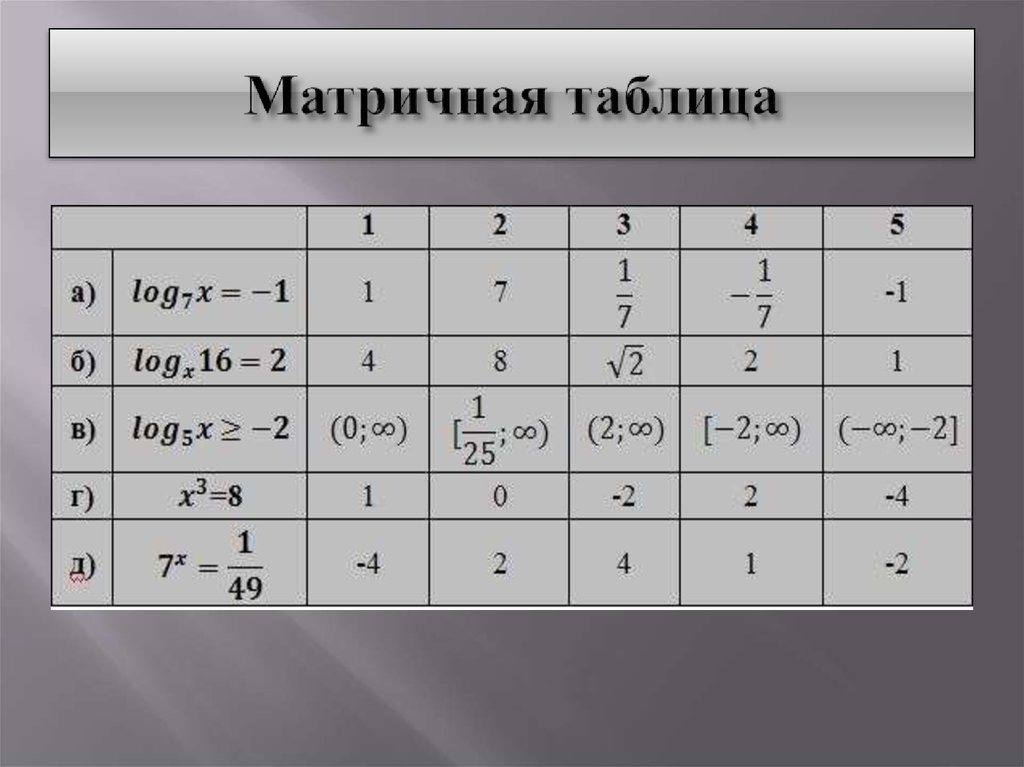 253. Объем пирамиды и конуса. 254. Площадь боковой поверхности правильной пирамиды и конуса. 255. Усеченный конус и усеченная пирамида. § 3. Шаровая поверхность. Шар 256. Шар и шаровая поверхность. 257. Объем шара и его частей. 258. Площадь поверхности шара и ее частей. 259. Понятие телесного угла. Ответы к упражнениям Приложения |
Внеклассное мероприятие в рамках недели математики по теме «Таблица логарифмов»
Цели:
- Образовательная цель: Ознакомление учащихся с историей возникновения и историей применения таблицы логарифмов, а также использование её в наши дни. Повторение свойств логарифмов, основных навыков решения логарифмических уравнений и неравенств, а также построения логарифмической функции.
- Развивающая цель : Развитие у учащихся познавательного интереса, внимания, наблюдательности, накопление определенного запаса математических фактов и сведений, дополняющих и углубляющих знания, приобретаемые в основном курсе математики.
- Воспитательная цель : Воспитание устойчивого интереса к предмету и ответственности за конечный результат.

Оборудование: мультимедийный проектор, компьютер (Приложение 1), карточки с заданиями (Приложение 2).
Ход мероприятия
“Изобретение логарифмов, сократив работу
астронома, продлило ему жизнь”.
П. С. Лаплас
Первый ведущий: Здравствуйте, начинаем конкурс между двумя командами. Давайте поприветствуем команду (название 1ой команды) и ее капитана (фамилия), а также команду (название 2ой команды) и ее капитана (фамилия).
Второй ведущий: А оценивать работу команд и их болельщиков будет жюри: (фамилии).
Первый ведущий: Тема нашего мероприятия “Таблица логарифмов”. И
сегодня именно о ней вы узнаете много интересной и занимательной информации. Участникам команд для победы в конкурсе нужно будет вспомнить основные свойства
логарифмов, как решать логарифмические уравнения и строить графики функций. А у
их болельщиков тоже будет возможность заработать для своих команд дополнительные
баллы.
Участникам команд для победы в конкурсе нужно будет вспомнить основные свойства
логарифмов, как решать логарифмические уравнения и строить графики функций. А у
их болельщиков тоже будет возможность заработать для своих команд дополнительные
баллы.
Первый конкурс.
Второй ведущий: Итак, начнем. В далеком 1614 году (ровно 400 лет назад) знаменитый шотландский математик Джон Непер опубликовал сочинение под названием “Описание удивительной таблицы логарифмов”. Там было краткое описание логарифмов и их свойств, а также 8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1′(минута).
Первый ведущий: Кто же такой Непер? Джон Непер родился в 1550 г в
дворянской семье, был потомком воинственного шотландского рода. В 1563 году
поступил в Сент-Эндрюсский университет, после окончания которого совершил
путешествие по странам Европы. Вернувшись в 1571 в Мерчистон в близи Эдинбурга,
больше уже не покидал свой родной край. Математика не была его основным видом
деятельности, а лишь увлечением. Он , как мог, пытался упростить громозкие
вычисления, подчинив их определенным правилам. Поиск новых формул его увлёк и
принёс свои плоды. Математика стала для него интересной и красивой наукой: “ Я
всегда старался, насколько позволяли мои силы и способности, освободить людей от
трудности и скуки вычислений, докучливость которых обыкновенно отпугивает очень
многих от изучения математики”.
Математика не была его основным видом
деятельности, а лишь увлечением. Он , как мог, пытался упростить громозкие
вычисления, подчинив их определенным правилам. Поиск новых формул его увлёк и
принёс свои плоды. Математика стала для него интересной и красивой наукой: “ Я
всегда старался, насколько позволяли мои силы и способности, освободить людей от
трудности и скуки вычислений, докучливость которых обыкновенно отпугивает очень
многих от изучения математики”.
Второй ведущий: Не будучи математиком, именно он ввел название
логарифм (от греческих слов “логос” – отношение, “арифмос” – число) и именного
его идея определения логарифма оказалась наиболее прогрессивной и оригинальной.
Он близко подошел к понятию логарифмической зависимости и созданию натуральных
логарифмов и потому число е часто называют числом Непера. К сожалению, его
работа имела погрешности. Непер это понимал и, не задолго до своей смерти в 1617
г, приступил к разработке десятичных логарифмов, более удобных для вычисления,
вместе со своим другом профессором Лондонского университета. Уже после его
смерти вышло в свет их совместное сочинение: “Устройство чудесных таблиц
логарифмов”.
Уже после его
смерти вышло в свет их совместное сочинение: “Устройство чудесных таблиц
логарифмов”.
Первый ведущий: А теперь вопрос к командам: “Кто продолжил работу Непера по созданию таблиц логарифмов?”. Для ответа на этот вопрос игроки команды должны вычислить логарифмические выражения и с помощью ключа назвать фамилию этого человека. Капитаны команд, получите карточки с заданиями. На выполнение заданий отводится (на усмотрение учителя) минут. Время пошло. А пока команды выполняют задание, их болельщики им будут помогать зарабатывать дополнительные баллы. Проверим, как вы выполнили домашнее задание. Назовите пословицы, поговорки, в которых присутствуют числа. Победителей определит жюри.
Второй конкурс.
Второй ведущий: Итак, время вышло. Сдаем работы. Правильный ответ –
Бригс. Генри Бригс – профессор математики в Грешем-колледже (Лондон), затем в
Оксфорде. Развивая идеи Джона Непера, составил и опубликовал первые таблицы
десятичных логарифмов и потому десятичные логарифмы называли еще бригсовыми.
Первый ведущий: В основе идеи создания логарифма лежало желание облегчить расчеты, в которых буквально утопали астрономы тех лет. Известно высказывание Пьера Лапласа: “Изобретение логарифмов, сократив работу астронома, продлило ему жизнь”. Годы жизни Непера и Бригса принадлежат той эпохе, когда Англия захватывала пути заокеанской морской торговли. Английские мореплаватели предъявляли большой спрос на астрономические таблицы. К тому же мореплаватели продолжали открывать новые земли. Так в 1614 году был обнаружен заброшенный гористый остров голландским китобойным капитаном и назван в его честь Ян-Майен. В наши дни остров относится к территории Норвегии. На нём находится самый северный активный вулкан земли – Бееренберг.
Второй ведущий: А вопрос командам будет следующим: “Укажите
географические координаты острова Ян-Майен”. Для ответа на этот вопрос игроки
команды должны решить два логарифмических уравнения, корни которых и являются
соответствующими координатами. Капитаны команд, получите карточки с заданиями.
На выполнение заданий отводится (на усмотрение учителя) минут. Время пошло. А
пока команды выполняют задание, их болельщики продолжат помогать своим командам.
Проверим ваши творческие способности. Попробуйте сочинить стих по нашей теме со
следующими рифмами: логарифмы – рифмы, Непер – пример, таблицы – молодцы.
Капитаны команд, получите карточки с заданиями.
На выполнение заданий отводится (на усмотрение учителя) минут. Время пошло. А
пока команды выполняют задание, их болельщики продолжат помогать своим командам.
Проверим ваши творческие способности. Попробуйте сочинить стих по нашей теме со
следующими рифмами: логарифмы – рифмы, Непер – пример, таблицы – молодцы.
Третий конкурс.
Первый ведущий: Время вышло. Сдаем работы. Правильный ответ: географические координаты: 71°00′с.ш., 8°00′з.д. Ян-Майен – остров между Гренландским и Норвежским морями, примерно в 600 километрах к северу от Исландии, в 500 километрах к востоку от Гренландии и в 1000 километрах к западу от Норвегии.
Второй ведущий: Работа, начатая Бригсом, была закончена голландцем
Андрианом Влакком. Именно его таблицы вошли во всеобщее употребление в Европе и
легли в основу создания таблиц логарифмов в России, изданные в начале ХVIII века
под названием: “Таблицы логарифмов и синусов, тангенсов и секансов тщанием и за
освидетельствованием математических и навигацких школ учителей Андрея
Фархвардсона, Стефана Гвина и Леонтия Магницкого”. Леонтий Филиппович Магницкий
известен как автор первой в России учебной энциклопедии по математике и
преподаватель математики в
Школе математических и навигацких наук в
Москве. (Уроженец
города Осташков.)
Леонтий Филиппович Магницкий
известен как автор первой в России учебной энциклопедии по математике и
преподаватель математики в
Школе математических и навигацких наук в
Москве. (Уроженец
города Осташков.)
Первый ведущий: В прошлом веке наибольшую известность имели
четырёхзначные таблицы Брадиса, издаваемые с 1921 года. Их изучение и применение
входило в школьную программу. Таблицы Брадиса были основным инструментом для
вычислений любого советского инженера, чьи вычисления не требовали большой
точности, но с приходом в нашу жизнь компьютеров и калькуляторов, к сожалению,
оказались забытыми. Известно, что Брадис родился 23 декабря 1890 года в городе
Пскове в семье учителей. Будучи гимназистом, подвергся аресту за распространение
нелегальной литературы и исключён из гимназии, после чего был сослан в Сибирь.
Отбыв ссылку, поступил в Петербургский университет. С 1920 года по 1959 год
Владимир Модестович работал в Тверском институте народного образования (ныне
Тверской государственный университет). Скончался Брадис в 1975 году в Калинине
(сейчас Тверь), похоронен там же.
Скончался Брадис в 1975 году в Калинине
(сейчас Тверь), похоронен там же.
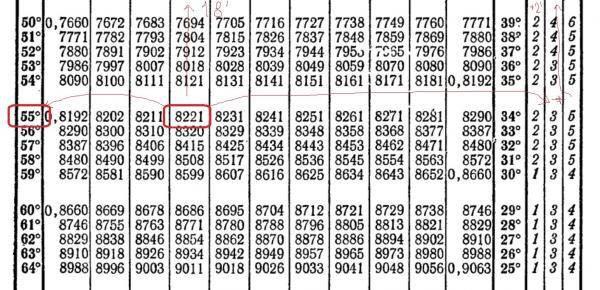
Второй ведущий: А теперь мы предлагаем командам с помощью таблиц Брадиса вычислить логарифмическое выражение. Капитаны команд, получите карточки с заданиями. На выполнение задания отводится (на усмотрение учителя) минут. Время пошло. А их болельщикам мы предлагаем решить кроссворд (см. приложение 2).
Четвёртый конкурс.
Второй ведущий: Время вышло. Сдаем работы членам жюри. Правильный
ответ: 5. Таблицы – не единственный технический инструмент для вычисления. Они
были трансформированы в компактное устройство, чрезвычайно ускоряющее процесс
вычисления – логарифмическая линейка. Решающий вклад в изобретение удобной в
применении логарифмической линейки внес Уильям Отред. Он предложил использовать
две одинаковые шкалы, скользящие одна вдоль другой. И в таком виде
логарифмическая линейка верно прослужила подручным инструментом для вычисления
многим инженерам и математикам более 300 лет, пока её место не занял электронный
калькулятор.
Первый ведущий: Непер же придумал в 1617 году (год его смерти) другой – не логарифмический способ перемножения чисел. Инструмент получил название «палочки Непера», но широкого распространения не получили.
Второй ведущий: В наши дни продолжает использоваться навигационная линейка (НЛ-10М). Она представляет собой навигационный расчётчик, построенный по принципу логарифмической линейки и адаптированный для решения задач самолётовождения и навигации. Мы предлагаем командам побывать в роли штурманов авиации, построить график полёта вертолета по кусочно-заданной функции. Капитаны команд, получите карточки с заданиями. На выполнение задания отводится (на усмотрение учителя) минут. Время пошло. А болельщики команд продолжат в это время разгадывать кроссворд.
Пятый конкурс.
Второй ведущий: Итак, время вышло. Сдаем работы. Правильный ответ: (Приложение 1)
Рис. 1
1
Первый ведущий: В начале XXI века логарифмические линейки получили второе рождение в наручных часах. Появился спрос на подручное вычислительное устройство. Производители дорогих и престижных марок часов разработали модели со встроенной логарифмической линейкой. Она выполнена в виде вращающихся колец со шкалами вокруг циферблата. Производители обычно называют такие устройства “навигационная линейка”, с помощью которой, в отличие от микрокалькулятора, можно получить сразу таблицу (например, расхода топлива на пройденное расстояние, перевода миль в километры и тому подобное).
Второй ведущий: А теперь проведем заключительный конкурс. Конкурс капитанов. Блиц – опрос. Каждому из них будут заданы 10 вопросов, на которые они попробуют дать правильные ответы.
Подведение итогов.
Баллада о Логарифме.
Стихи слагались про любовь,
О жизни смерти и несчастьях,
И про дождливые ненастья
Немало спето песен вновь!
Но не нашлось для логарифма
Любой, пусть простенькой – но рифмы.
Что логарифм? Ядро науки,
Чтоб школьники не знали скуки.
Чтоб экспоненту вычислять –
Но почему нельзя сказать,
Что: “Логарифм, как ты прекрасен…”
Иль: “Логарифм – ты безучастен
К моим попыткам ночи к ряду
Твое значенье посчитать!”
Ядро физических процессов
И информатики эксцессы…
Все в логарифме! Он готов
На все вопросы дать ответы.
Пространством-временем, шутя,
Играет логарифм не зря!
Источники информации:
- http://ru.wikipedia.org,
- консультации с лётчиками.
Список литературы:
- Брадис В. М. Четырёхзначные математические таблицы для средней школы. – М.: Просвещение. – 1976.
- Гиршвальд Л. Я. История открытия логарифмов. – Харьков:
издательство Харьковского государственного университета имени А. М.
 Горького. – 1952.
Горького. – 1952.
Статья о логарифмических+таблицах от The Free Dictionary
Логарифмические+таблицы | Статья о логарифмических+таблицах от The Free DictionaryЛогарифмические+таблицы | Статья о логарифмических+таблицах The Free Dictionary
Слово, не найденное в Словаре и Энциклопедии.
Возможно, Вы имели в виду:
Пожалуйста, попробуйте слова по отдельности:
логарифмический столы
Некоторые статьи, соответствующие вашему запросу:
Не можете найти то, что ищете? Попробуйте выполнить поиск по сайту Google или помогите нам улучшить его, отправив свое определение.Полный браузер ?
- ▲
- логарифмическая шкала
- Логарифмические весы
- Логарифмические весы
- Логарифмические весы
- Логарифмические весы
- Логарифмические весы
- логарифмический ряд
- Распределение логарифмического ряда
- Логарифмический синус
- Логарифмический синус
- Логарифмический синус
- Логарифмическое неравенство Соболева
- Логарифмический программный ввод Программный вывод
- Логарифмическая спираль
- Логарифмическая спираль
- Логарифмическая спираль
- Логарифмические спиральные пляжи
- логарифмические спирали
- логарифмические спирали
- Логарифмическое стандартное отклонение
- Логарифмические таблицы
- Логарифмический тангенс
- Логарифмический тангенс
- Логарифмический тангенс
- Логарифмическое время
- Логарифмическая шкала времени
- Логарифмическое преобразование
- логарифмическая тригонометрическая функция
- Логарифмические единицы
- логарифмический профиль скорости
- логарифмический + таблицы
- логарифмический
- логарифмический
- логарифмический
- логарифмически
- логарифмически
- логарифмически
- логарифмически
- Цифровой фильтр с логарифмической архитектурой
- Логарифмически вогнутая функция
- Логарифмически вогнутая мера
- Логарифмически выпуклый
- Логарифмически выпуклая функция
- Логарифмически выпуклая функция
- логарифмомантия
- Логарифмы
- Логарифмы
- Логарифмы
- Логарифмы апостериорных отношений вероятностей
- двойной логарифм
- ЛОГАСРЕК
- ЛОГАССЕСРЕП
- логастения
- логастения
- логастения
- Логата
- ЛОГАТАК
- ЛОГАТАКМ
- Логатек
- Логатримы
- Логатримы
- ▼
Сайт: Следовать:
Делиться:
Открыть / Закрыть
Добро пожаловать в онлайн-калькулятор логарифмов. Для чего нужен этот калькулятор? Ну, во-первых, для проверки своими письменными или умственными расчетами. Калькулятор логарифмов (реальных) — этот калькулятор находит логарифм по заданному основанию онлайн.
Понятие вещественного логарифма: Существует множество различных определений логарифма. Во-первых, неплохо бы знать, что логарифм — это своего рода алгебраическая запись, обозначаемая как log a b, где a — основание, b — число. И эта запись читается так: Логарифм по основанию а числа b. Иногда используется обозначение log b.
А операция, обратная логарифму, — это потенцирование. |


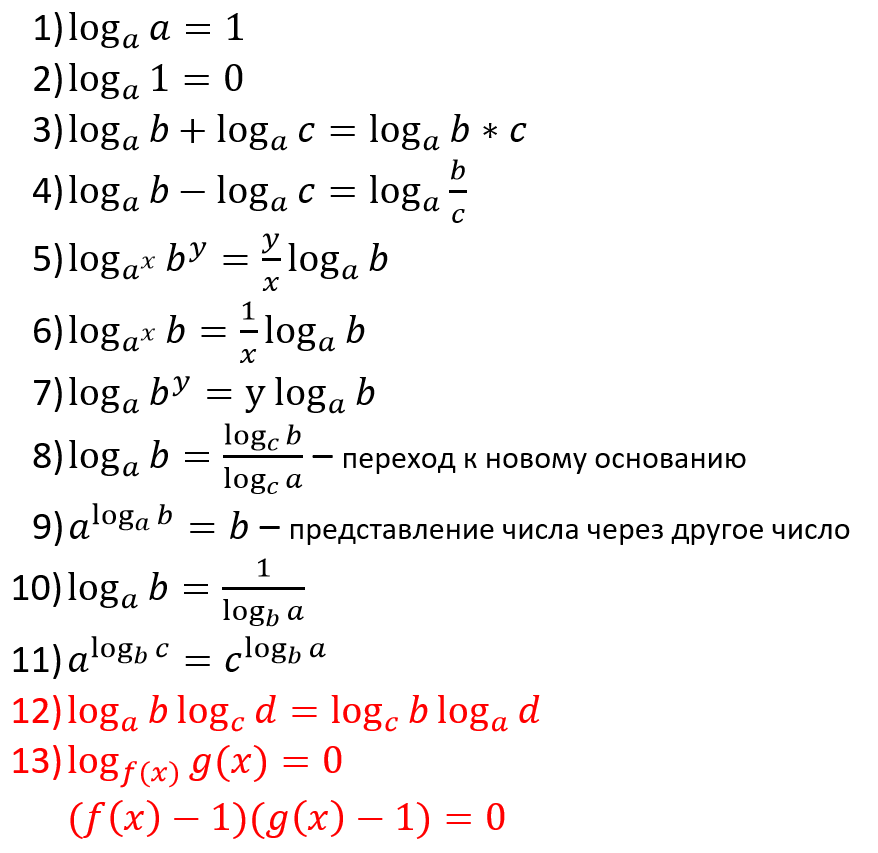 Горького. – 1952.
Горького. – 1952. Логарифм
Логарифм Для более простого понимания поставим задачу так: сколько раз нужно умножить двойку саму на себя, чтобы в результате получилось 16? Очевидно, что 4, поэтому корень этого уравнения равен x = 4.
Для более простого понимания поставим задачу так: сколько раз нужно умножить двойку саму на себя, чтобы в результате получилось 16? Очевидно, что 4, поэтому корень этого уравнения равен x = 4.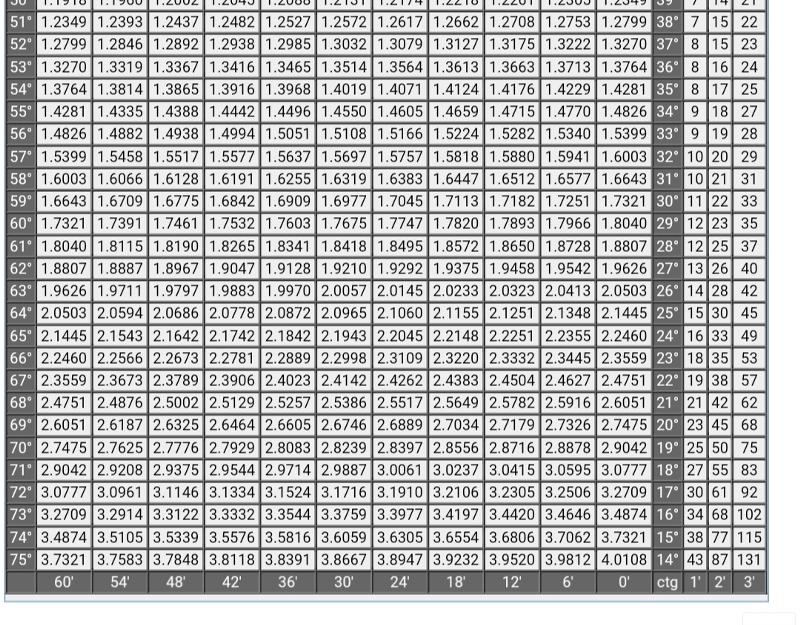 Например, для уравнений:
Например, для уравнений: Число e = 2,718281828 — константа, естественно возникающая при описании процессов непрерывного роста. Как бы ни было важно число пи для геометрии, число е играет важную роль в моделировании временных процессов.
Число e = 2,718281828 — константа, естественно возникающая при описании процессов непрерывного роста. Как бы ни было важно число пи для геометрии, число е играет важную роль в моделировании временных процессов. Великий физик и астроном Пьер-Симон Лаплас говорил, что «изобретение логарифмов сократило работу астронома и удвоило его жизнь». С развитием математического аппарата были созданы целые логарифмические таблицы, с помощью которых ученые могли оперировать огромными числами, а свойства функций позволяют преобразовывать выражения, оперирующие иррациональными числами, в целочисленные выражения. Также логарифмическая запись позволяет представлять слишком маленькие и слишком большие числа в компактной форме.
Великий физик и астроном Пьер-Симон Лаплас говорил, что «изобретение логарифмов сократило работу астронома и удвоило его жизнь». С развитием математического аппарата были созданы целые логарифмические таблицы, с помощью которых ученые могли оперировать огромными числами, а свойства функций позволяют преобразовывать выражения, оперирующие иррациональными числами, в целочисленные выражения. Также логарифмическая запись позволяет представлять слишком маленькие и слишком большие числа в компактной форме. Десятичная функция используется для нахождения необходимого количества десятичных знаков, а естественная функция — это время, необходимое для достижения заданного уровня.
Десятичная функция используется для нахождения необходимого количества десятичных знаков, а естественная функция — это время, необходимое для достижения заданного уровня.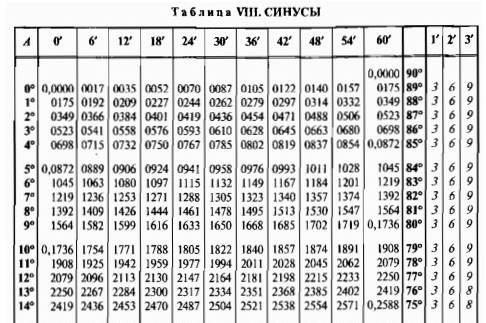
 С логарифмами (в российских школах) можно столкнуться уже в 10 классе. И эта тема считается достаточно сложной. Решать логарифмы, особенно с большими или дробными числами, знаете ли, непросто. Лучше перестраховаться и воспользоваться калькулятором. При заполнении будьте внимательны, не перепутайте базу с цифрой. Калькулятор логарифмов чем-то похож на калькулятор факториалов, который автоматически генерирует несколько решений.
С логарифмами (в российских школах) можно столкнуться уже в 10 классе. И эта тема считается достаточно сложной. Решать логарифмы, особенно с большими или дробными числами, знаете ли, непросто. Лучше перестраховаться и воспользоваться калькулятором. При заполнении будьте внимательны, не перепутайте базу с цифрой. Калькулятор логарифмов чем-то похож на калькулятор факториалов, который автоматически генерирует несколько решений. 
 Кстати, не только база должна быть в положительном виде. Число (аргумент) также должно быть положительным. В противном случае калькулятор логарифмов поднимет неприятную тревогу. Логарифм — это операция нахождения логарифма по основанию. Эта операция обратна возведению в степень с соответствующим основанием. Сравните:
Кстати, не только база должна быть в положительном виде. Число (аргумент) также должно быть положительным. В противном случае калькулятор логарифмов поднимет неприятную тревогу. Логарифм — это операция нахождения логарифма по основанию. Эта операция обратна возведению в степень с соответствующим основанием. Сравните:  Похоже на орфографическую ошибку или даже опечатку, в которой отсутствует латинская буква «о».
Похоже на орфографическую ошибку или даже опечатку, в которой отсутствует латинская буква «о».  А именно, десятичные логарифмы характерны исключительно для положительных чисел. Десятичные логарифмы чисел больше единицы положительны, а чисел меньше единицы отрицательны; из двух неотрицательных чисел больший десятичный логарифм эквивалентен большему и т. д. Кроме того, десятичные логарифмы имеют отличительные черты и особенности, которые объясняют, почему удобно предпочесть число десять в качестве основы логарифмов.
А именно, десятичные логарифмы характерны исключительно для положительных чисел. Десятичные логарифмы чисел больше единицы положительны, а чисел меньше единицы отрицательны; из двух неотрицательных чисел больший десятичный логарифм эквивалентен большему и т. д. Кроме того, десятичные логарифмы имеют отличительные черты и особенности, которые объясняют, почему удобно предпочесть число десять в качестве основы логарифмов.
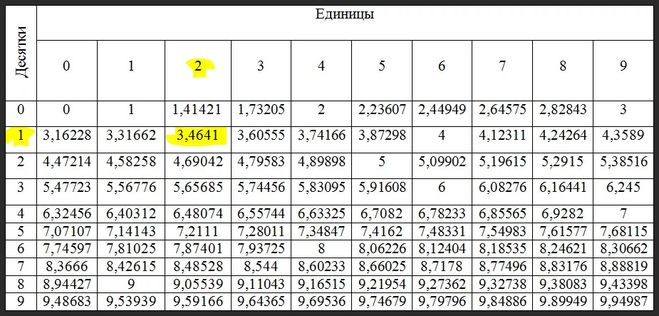
 Наиболее распространенные и популярные из них:
Наиболее распространенные и популярные из них: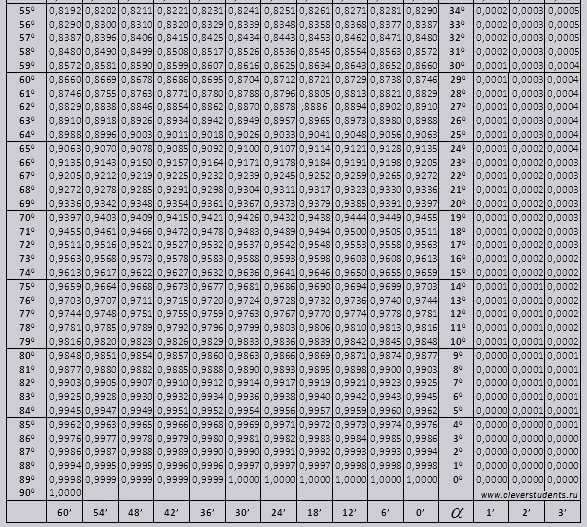 В противном случае «а» трансформируется в «у» и имеет трансцендентные и иррациональные черты. Также стоит отметить, что натуральное значение рассчитывается по специальному уравнению, где доказательством становится теория, изучаемая вне школьной программы.
В противном случае «а» трансформируется в «у» и имеет трансцендентные и иррациональные черты. Также стоит отметить, что натуральное значение рассчитывается по специальному уравнению, где доказательством становится теория, изучаемая вне школьной программы.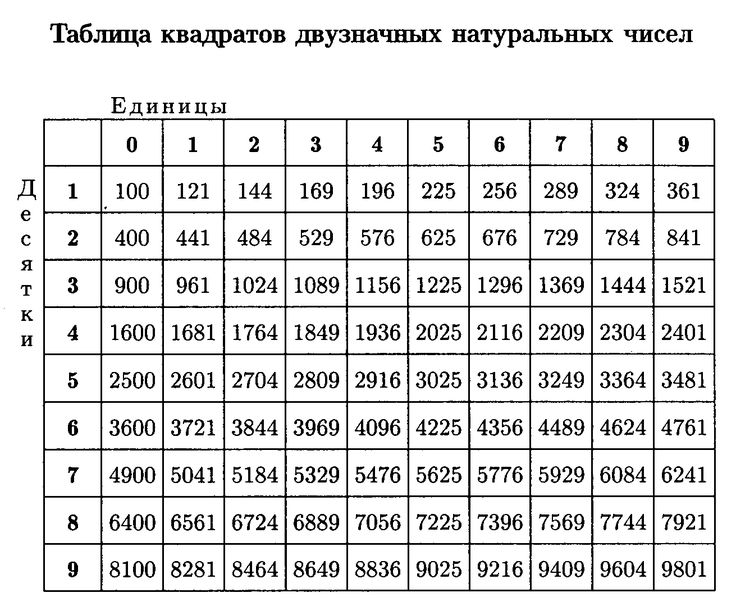 Показательное уравнение является почти точной копией логарифмических вычислений, если смотреть со стороны правильности решения. Просто первый вариант включает в себя специализированный номер, помогающий быстро понять условие, а второй заменяет log на обычную степень. В этом случае расчеты по последней формуле должны включать переменное значение.
Показательное уравнение является почти точной копией логарифмических вычислений, если смотреть со стороны правильности решения. Просто первый вариант включает в себя специализированный номер, помогающий быстро понять условие, а второй заменяет log на обычную степень. В этом случае расчеты по последней формуле должны включать переменное значение.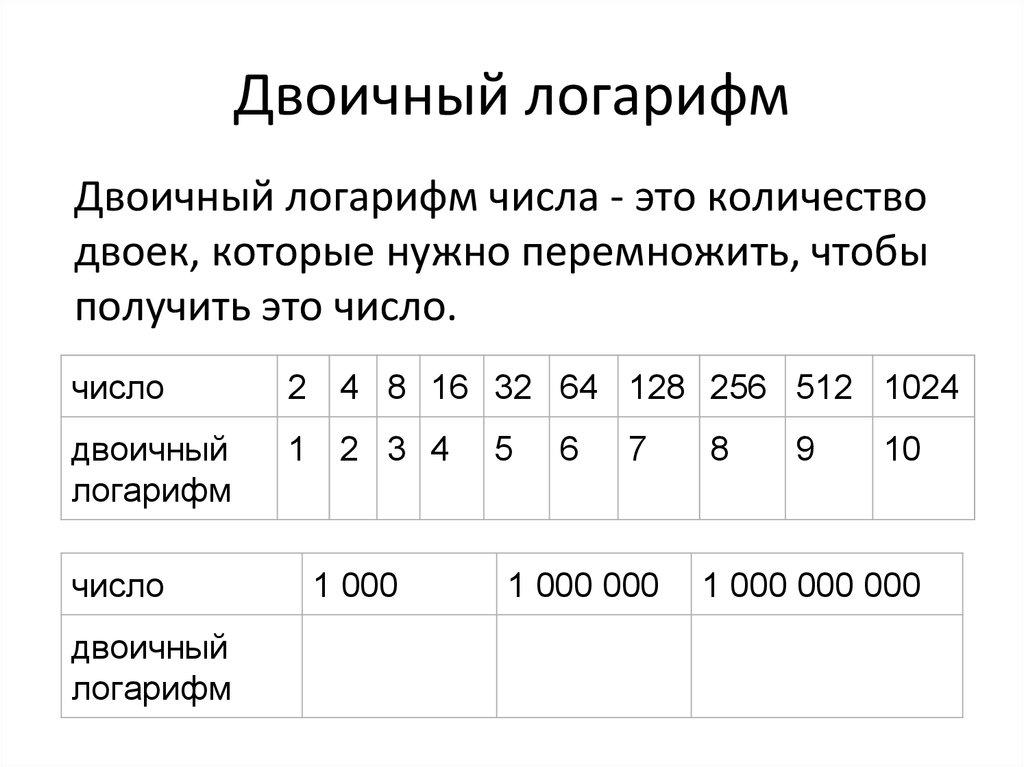 Есть и самый сложный вариант с базовым показателем 64, который попадает под систематизированное управление адаптивного типа, вычисляющее конечный результат с геометрической точностью.
Есть и самый сложный вариант с базовым показателем 64, который попадает под систематизированное управление адаптивного типа, вычисляющее конечный результат с геометрической точностью.
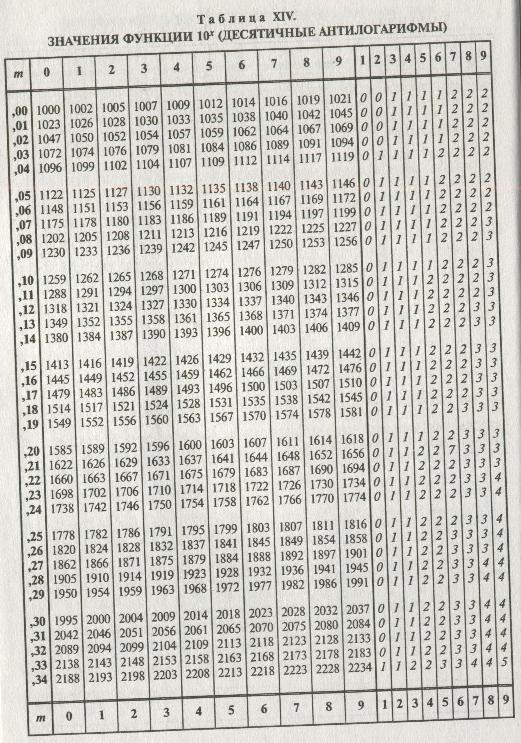 В этом случае все основные расчеты должны были опираться на последнее значение. Точно так же ученые интегрировали и вычитание.
В этом случае все основные расчеты должны были опираться на последнее значение. Точно так же ученые интегрировали и вычитание.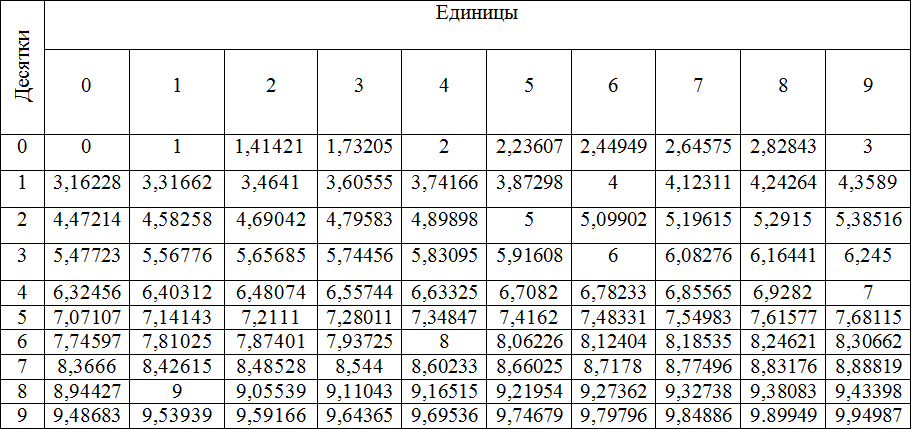 В середине века формула была продемонстрирована как окончательный вариант. Кроме того, Эйлер опубликовал производную десятичного логарифма и составил первые графики.
В середине века формула была продемонстрирована как окончательный вариант. Кроме того, Эйлер опубликовал производную десятичного логарифма и составил первые графики.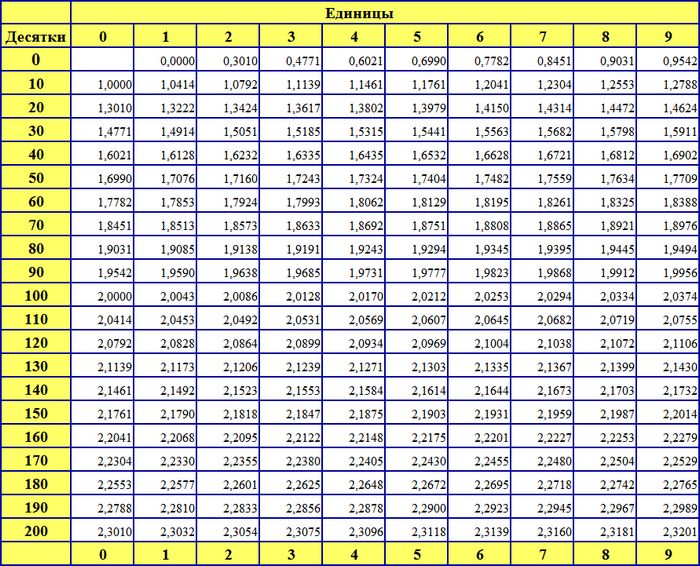 Также это может быть программный калькулятор из стандартного набора ОС Windows. Самый простой способ запустить его — нажать комбинацию клавиш WIN+R, ввести команду calc и нажать кнопку «ОК». Другой способ – открыть меню на кнопке «Пуск» и выбрать в нем «Все программы». Затем нужно открыть раздел «Стандартные» и перейти в подраздел «Утилиты», чтобы нажать там ссылку «Калькулятор». Если вы используете Windows 7, вы можете нажать клавишу WIN и ввести «Калькулятор» в поле поиска, а затем щелкнуть соответствующую ссылку в результатах поиска.
Также это может быть программный калькулятор из стандартного набора ОС Windows. Самый простой способ запустить его — нажать комбинацию клавиш WIN+R, ввести команду calc и нажать кнопку «ОК». Другой способ – открыть меню на кнопке «Пуск» и выбрать в нем «Все программы». Затем нужно открыть раздел «Стандартные» и перейти в подраздел «Утилиты», чтобы нажать там ссылку «Калькулятор». Если вы используете Windows 7, вы можете нажать клавишу WIN и ввести «Калькулятор» в поле поиска, а затем щелкнуть соответствующую ссылку в результатах поиска.