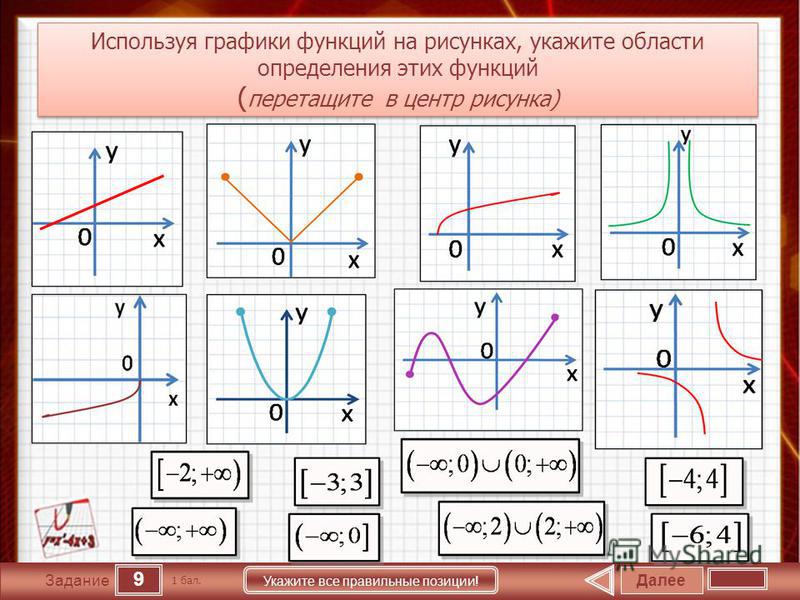
Функции и ее графики — презентация онлайн
Похожие презентации:
Функции и их графики. Определение графика функции
Функция. Графики функций
Функция. Графики функций
Готовимся к ГИА. Элементарные функции
Функции и графики
Функции. Область определения и множество значений; график функции; построение графиков функций, заданных различными способами
Касательная к графику функции
Функция у=х2 и её график
Функция и её свойства
Функция у=кх², ее свойства и график
1. Функция
Графики функций2. Виды функций
ЛинейнаяПрямая пропорциональность
Обратная пропорциональность
Квадратичная
Кубическая
Квадратный корень
Модуль
Преобразование графиков
3. Линейная функция
у = kх + bу = 2х +1
график – прямая
у
х 0 1
у 1 3
0
х
4. Прямая пропорциональность
у = kх график – прямая, проходящаячерез (0;0)
у
у = 3х
х 0 1
у 0 3
0
х
5.
 Обратная пропорциональностьk
Обратная пропорциональностьkу= x
4
у= x
x=0
х 4 2 1 -4 -2 -1
у 1 2 4 -1 -2 -4
График — гипербола
у
0
х
6. Квадратичная функция
у = ах2у=
а=0
х2
график – парабола
у
х -2 -1 0 1 2
у 4 1 0 1 4
0
х
Преобразование симметрии
относительно оси x:
f(x) ―>- f(x)
y=x²
7
8. Кубическая функция
у = ах3 а = 0 график – кубическаяпарабола
у
3
у=х
х -2 -1 0 1 2
у -8 -1 0 1 8
0
х
9. Квадратный корень
у= хграфик – ветвь параболы
в первой четверти
у
х 0 4 9
у 0 2 3
0
х
10. Модуль
у= х{
х =
x, если х > 0
-x, если х < 0
у
х 0 3 -3
у 0 3 3
0
х
Построение графика
у
у = 2х + 5
7
Построить график
функции
5
у = 2х + 5
Линейная функция
График – прямая
3
1
-6 -5 -4 -3 -2 -1-1 0
-3
1 2
3 4
х
х
у
5 6
0
5
-4
-3
-5
содержание
7
у = -2х + 3
у
у = 1,5х -2
7
5
5
3
3
1
1
х
у
х
-6 -5 -4 -3 -2 -1-1 0 1 2 3 4 5 6 -6 -5 -4 -3 -2 -1-1 0 1 2 3 4 5 6
(0; 3)
-3
-3
-5
-5
(0; -2)
График функции у = kх + b проходит через точку …(0;
b)
k – угловой коэффициент
содержание
4
3
2
20:08
13
Построение графиков функций
y = f (x) и y = f (x + a)
Сдвиг вдоль оси абсцисс
y=(x+3)²
y=x²
y=(x-3)²
14
Построение графиков функций
y = f (x) и y = f (x) +n
Сдвиг вдоль оси ординат
y=x²
y=x²+3
y=x²-3
15
Преобразование графиков
Вершина параболы:
20:08
17
20:08
18
20:08
19
20.
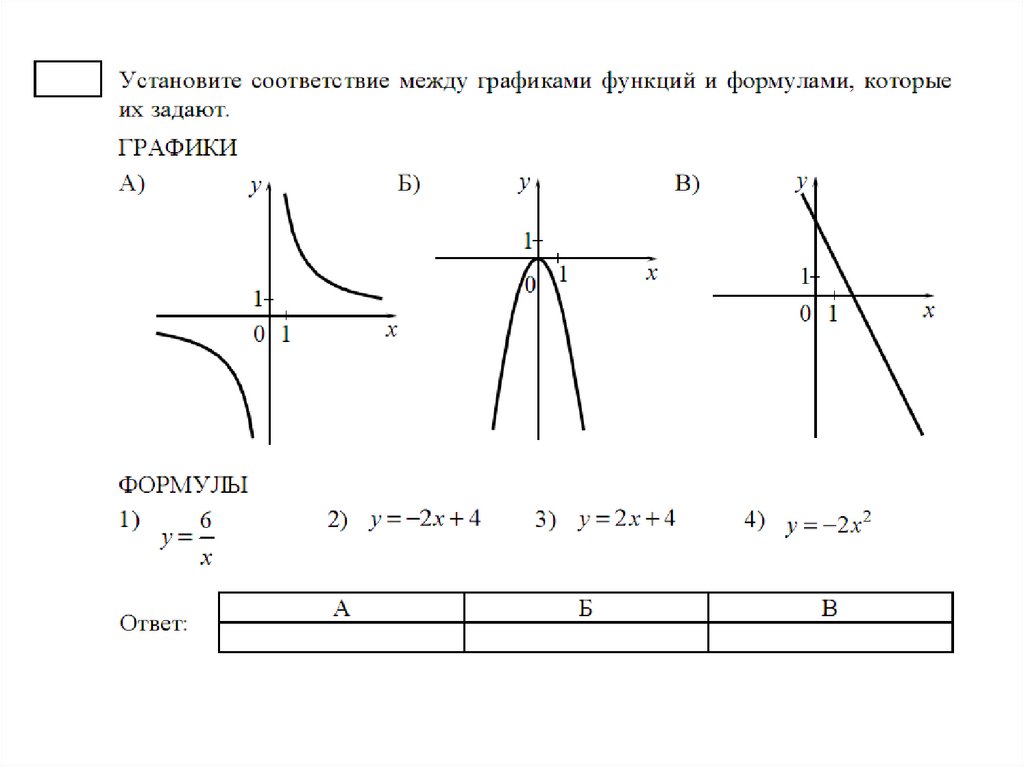
 Установите соответствие между формулой и названием графикаА) Прямая;
Установите соответствие между формулой и названием графикаА) Прямая;Б) Ветвь параболы;
В) Гипербола;
Г) Парабола;
Д) Прямая,
проходящая через
начало координат
Запишите название каждой функции
21. Самопроверка
1) Квадратичнаяфункция
2) Прямая
пропорциональност
ь;
3) Обратная
пропорциональност
ь;
4) Линейная функция;
5) Квадратный корень
из х;
6) Линейная функция
23. Домашнее задание: Тест по теме «Функции и их графики»
English Русский Правила
Раздел 3. Функции и графики (справочник)
Материалы для подготовки к ЕГЭ. Справочник по математике.
Раздел 3 «Функции и графики» (параграфы 5 — 10). Свойства и виды функций. Преобразование графиков
ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА
Раздел III. Функции и графики
§ 11. Свойства функций.
89.
90. Аналитическое задание функции.
91. Табличное задание функции.
92. Графическое задание функции.
93. График функции, заданной аналитически.
94. Четные и нечетные функции.
95. Графики четной и нечетной функций.
96. Периодические функции.
97. Возрастающие и убывающие функции.
§ 12. Виды функций.
98. Постоянная функция.
99. Прямая пропорциональность.
100. Линейная функция.
101. Взаимное расположение графиков линейных функций.
102. Обратная пропорциональность.
103. Функция у = х2.
104. Функция у = х3.
105. Степенная функция с натуральным показателем.
106. Степенная функция с целым отрицательным показателем.
107. Функция у = √x
108. Функция y = 3√x
109. Функция y = n√x.
110. Степенная функция с положительным дробным показателем.
111. Степенная функция с отрицательным дробным показателем.
112. Функция у = [х].
113. Функция у = {х}.
114. Показательная функция.
115. Обратная функция. График обратной функции.
116. Логарифмическая функция.
117. Число е. Функция у = ех. Функция у = In x.
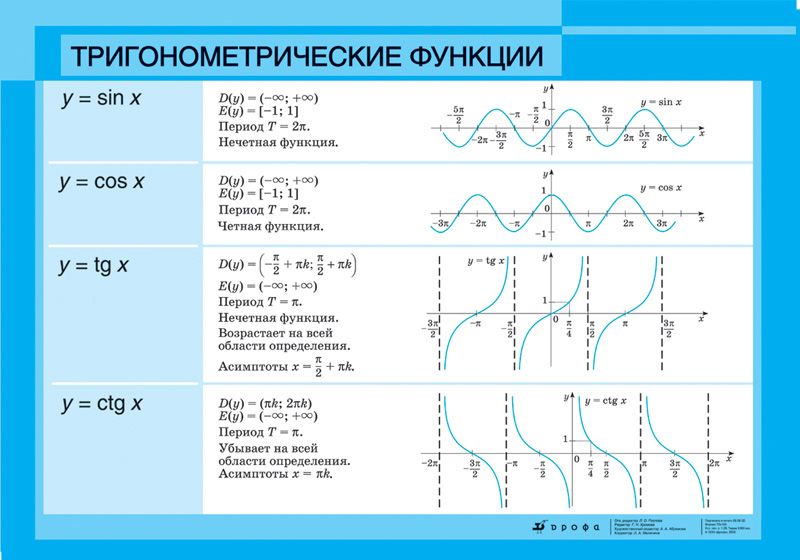
118. Определение тригонометрических функций.
119. Знаки тригонометрических функций по четвертям.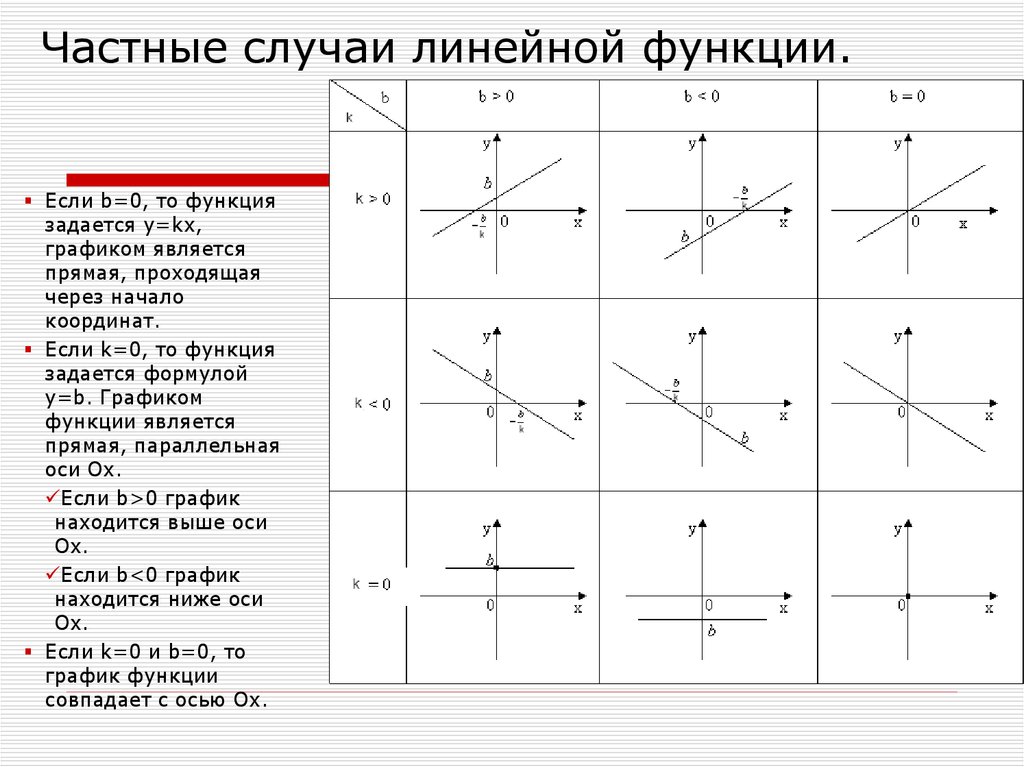
120. Исследование тригонометрических функций на четность, нечетность.
121. Периодичность тригонометрических функций.
122. Свойства и график функции у = sin х.
123. Свойства и график функции у = cos х.
124. Свойства и график функции у = tg х.
125. Свойства и график функции у = ctg х.
126. Функция у = arcsin x.
127. Функция у = arccos х.
128. Функции у = arctg х, у = arcctg х.
129. Арксинус, арккосинус, арктангенс и арккотангенс.
§ 13. Преобразования графиков.
130. Построение графика функции у = mf(х).
131. Графики функций у = ах2, у = ах3.
132. Построение графика функции у = f(х — а) + b.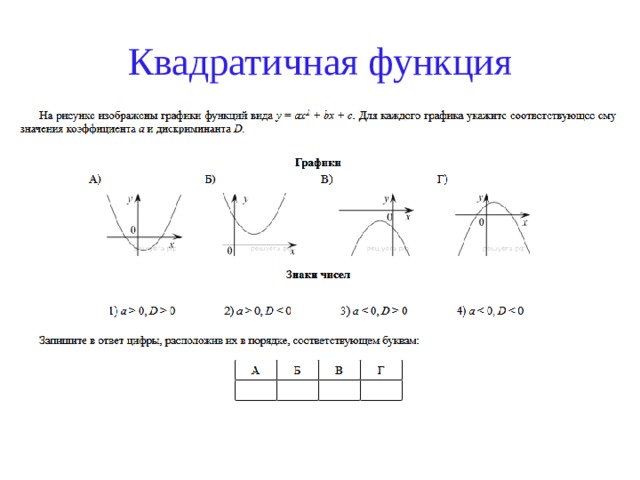
133. График квадратичной функции.
134. Способы построения графика квадратичной функции.
135. Построение графика функции у = f(kx).
136. Сжатие и растяжение графиков тригонометрических функций.
137. График гармонического колебания у = Asin (ωx + а).
ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА
§ 11. Свойства функций.89. Определение функции.
90. Аналитическое задание функции.
91. Табличное задание функции.
92. Графическое задание функции.
93. График функции, заданной аналитически.
94. Четные и нечетные функции.
95. Графики четной и нечетной функций.
96. Периодические функции.
97. Возрастающие и убывающие функции.
ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА
§ 12. Виды функций.98.
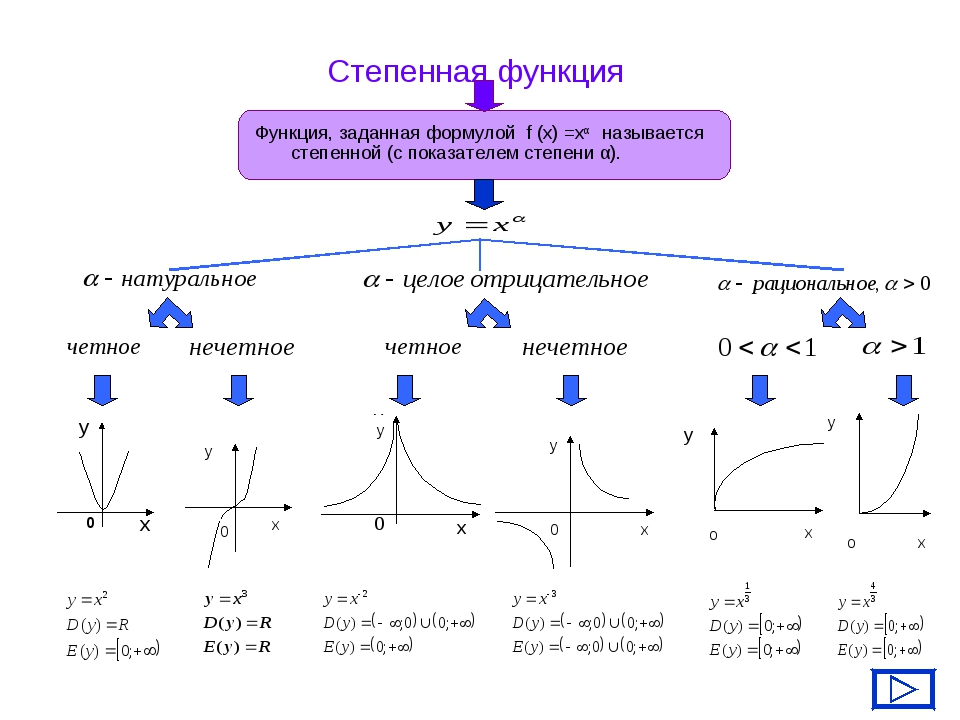 Постоянная функция.
Постоянная функция.99. Прямая пропорциональность.
100. Линейная функция.
101. Взаимное расположение графиков линейных функций.
102. Обратная пропорциональность.
103. Функция у = х
2.104. Функция у = х
3.105. Степенная функция с натуральным показателем.
106. Степенная функция с целым отрицательным показателем.
107. Функция у = √x
108. Функция y =
3√x109. Функция y =
n√x.110. Степенная функция с положительным дробным показателем.
111. Степенная функция с отрицательным дробным показателем.
112. Функция у = [х].
113. Функция у = {х}.
114. Показательная функция.
115. Обратная функция. График обратной функции.
116. Логарифмическая функция.
117.
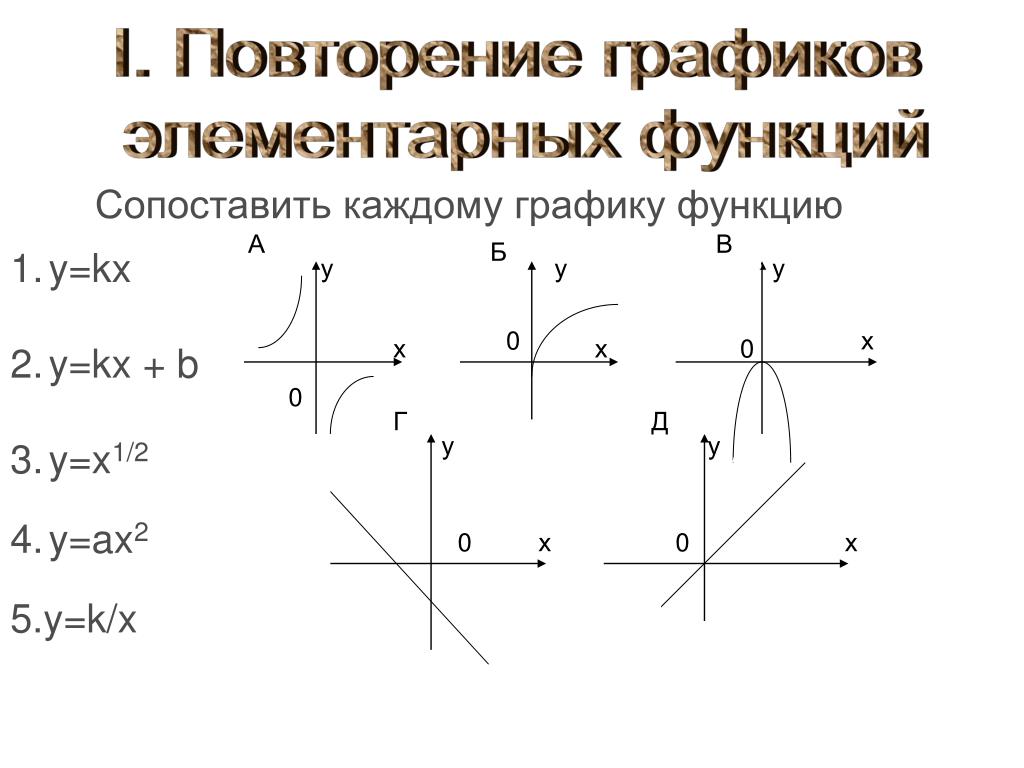 Число е. Функция у = ех. Функция у = In x.
Число е. Функция у = ех. Функция у = In x.118. Определение тригонометрических функций.
119. Знаки тригонометрических функций по четвертям.
120. Исследование тригонометрических функций на четность, нечетность.
121. Периодичность тригонометрических функций.
122. Свойства и график функции у = sin х.
123. Свойства и график функции у = cos х.
124. Свойства и график функции у = tg х.
125. Свойства и график функции у = ctg х.
126. Функция у = arcsin x.
127. Функция у = arccos х.
128. Функции у = arctg х, у = arcctg х.
129. Арксинус, арккосинус, арктангенс и арккотангенс.
ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА
§ 13. Преобразования графиков.130. Построение графика функции у = mf(х).
131. Графики функций
у = ах2, у = ах3.
132. Построение графика функции
у = f(х — а) + b.133. График квадратичной функции.
134. Способы построения графика квадратичной функции.
135. Построение графика функции
у = f(kx).136. Сжатие и растяжение графиков тригонометрических функций.
137. График гармонического колебания
у = Asin (ωx + а).ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА
Материалы для подготовки к ЕГЭ. Справочник по математике.
Раздел 3 «Функции и графики» (параграфы 5 — 10). Свойства и виды функций. Преобразование графиков
Просмотров: 3 896
Метки: Справочники
Типы функций и их графики
Вы можете определить функцию, взглянув на ее график. На этом уроке мы исследуем различные типы функций и их графики.
Необходимые условия для изучения этой статьи перечислены ниже.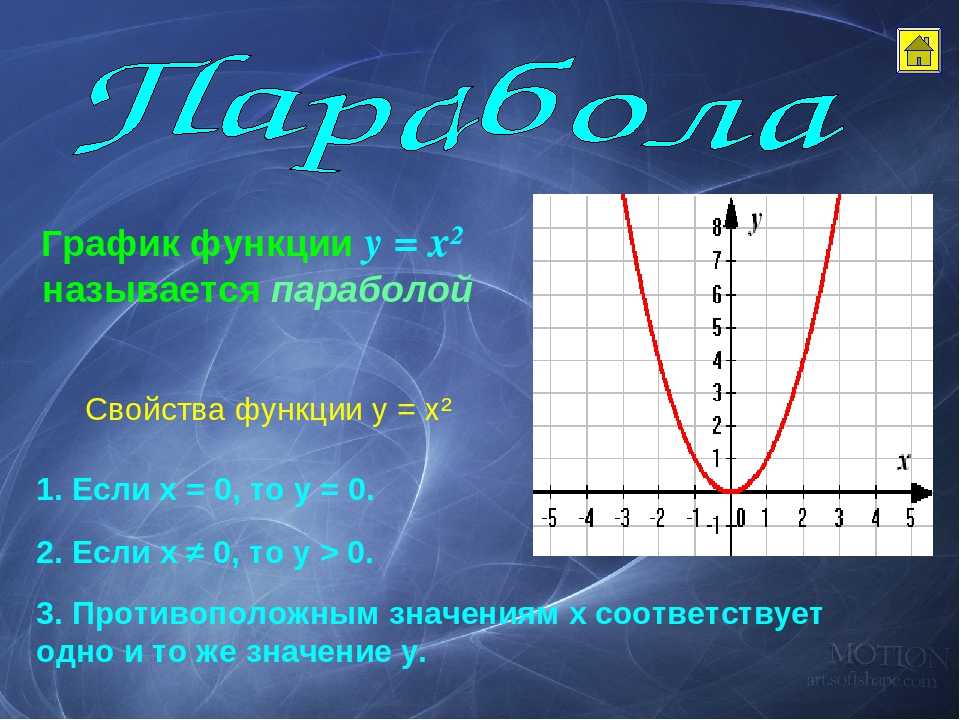
- Функции
- График функции
- Возрастающие, убывающие и постоянные функции.
- Четные и нечетные функции
Существует связь между функцией и ее графиком. С помощью графика функции можно обнаружить многие свойства, которых нет в алгебраической форме.
График функций помогает визуализировать функцию, заданную в алгебраической форме. Глядя на уравнение, вы можете сказать, что график будет нечетным или четным, возрастающим или убывающим, или даже уравнение вообще представляет собой график.
- Линейная функция
- Функция возведения в квадрат
- Кубическая функция
- Функция извлечения квадратного корня
- Обратная функция
- Ступенчатая функция
- Кусочная функция
Содержание
Линейные функции
Линейные функции представляют собой прямые линии. Прочтите следующую статью, чтобы узнать больше о линейной функции.
Линейные уравнения
Функции возведения в квадрат
График функции возведения в квадрат широко известен как парабола, представляющая собой U-образную кривую. Диаграмма функции возведения в квадрат приведена ниже.
Диаграмма функции возведения в квадрат приведена ниже.
Свойства функции возведения в квадрат
Свойства функции возведения в квадрат — область определения и диапазон, точки пересечения и т. д.
- Область определения множества функций возведения в квадрат всех действительных чисел, соответствующих оси x.
- Диапазон функции возведения в квадрат — все неотрицательные действительные числа, поскольку график имеет U-образную форму.
- Функция является четной, поскольку она симметрична относительно оси Y.
- Точка пересечения функции возведения в квадрат находится в точке (0, 0).
- График функции возведения в квадрат имеет относительный минимум в точке (0, 0).
- График функции возведения в квадрат уменьшается между интервалами . 93
точка -2 -8 (-2, -8) -1 -1 (-1, -1) 0 0 (0, 0) 1 1 (1, 1) 2 8 (2, 8) График кубической функции выглядит следующим образом.
График кубической функции
Свойства кубической функции
Кубическая функция обладает следующими свойствами.
- Кубическая функция является нечетной функцией.
- Кубическая функция симметрична относительно начала координат.
- Область определения кубической функции состоит из всех действительных чисел.
- Диапазон кубической функции состоит из всех действительных чисел, поскольку функция имеет интервал между .
- Точка пересечения графика находится в точке (0, 0).
- Функция всегда возрастает между интервалом – .
График функции извлечения квадратного корня
График функции, где значение приводит к .
f(x) = x
Построим график функции квадратного корня, получив несколько точек. Мы использовали калькулятор для вычисления некоторых значений.
х точка 4 2 (4, 2) 3 1,73 (3, 1,73) 2 1,41 (2, 1.  41)
41)1 1 (1, 1) 0 0 (0, 0) Ниже приведен график функции возведения в квадрат.
График функции возведения в квадратКак вы можете видеть, график имеет только положительную сторону для обоих и .
Свойства функции возведения в квадрат
График функции возведения в квадрат приведен ниже.
- Домен представляет собой набор неотрицательных действительных чисел.
- Диапазон представляет собой набор неотрицательных действительных чисел.
- Точка пересечения графика находится в точке .
- Увеличивается между интервалом .
График обратной функции
Пусть функция, тогда
f(x) = 1x
называется обратной функцией.
Чтобы построить график обратной функции, сначала найдем все точки.
х f(x) = 1/x точка -3 -1/3 (-3, -1/3) -2 -1/2 (-2, -1/2) -1 -1 (-1, -1) 0 не определено не определено 1 1 (1, 1) 2 1/2 (2, 1/2) 3 1/3 (3, 1/3) График обратной зависимости показан ниже.

Свойства графика обратной функции
Обратная функция симметрична относительно начала координат, но никогда не касается самого начала координат. Свойства обратной функции приведены ниже.
- Это нечетная функция, поскольку она симметрична относительно начала координат.
- Нет перехватов.
- Область обратной функции находится между .
- Диапазон обратной функции .
- Убывает в интервале .
- и увеличивается в интервале .
График ступенчатой функции
График ступенчатой функции на самом деле выглядит как лестница со ступенями.
Пусть , будет ступенчатой функцией, где
[[x]] означает найти значение ‘ больше или равно x ‘.
Нужно найти точки для построения графика ступенчатой функции.
х f(x) = [[x]] + 1 точки -2 -1 (-2, 1) -1 0 (-1, 0) 0 1 (0, 1) 1 2 (1, 2) 2 3 (2, 3) График ступенчатой функции показан ниже.
График ступенчатой функции
Свойства ступенчатой функции
Свойства ступенчатой функции приведены ниже.
- Домен состоит из всех действительных чисел.
- Диапазон функции состоит из всех целых чисел.
- Точка пересечения по оси Y равна (0,0), а точка пересечения по оси X равна [0, 1).
- График является постоянным между каждой парой целых чисел.
- График перемещается по вертикали на одну единицу для каждого значения y.
График кусочной функции
График кусочной функции уже обсуждался в предыдущих уроках.
Графики функций
Если вы помните эти основные графики функций, используемые в алгебре, то вам будет легче выучить более высокие и сложные графики. Позже, когда вы изучите исчисление, визуализировать концепции будет намного проще с графиком функции.
Связанные статьи:-
- График уравнений.

- Перехваты и симметрия графов.
- Возрастающие и убывающие функции.
- Нечетные и четные функции.
Типы функций — типы, определение, примеры
Типы функций определяются на основе домена, диапазона и функционального выражения. Выражение, используемое для записи функции, является основным определяющим фактором для функции. Наряду с выражением отношение между элементами набора доменов и набора диапазонов также определяет тип функции. Классификация функций помогает легко понять и изучить различные типы функций.
Каждое математическое выражение, имеющее входное значение и результирующий ответ, может быть удобно представлено в виде функции. Здесь мы узнаем о типах функций и их определении, примерах.
1. Какие существуют типы функций? 2. Представление функций 3. 
Список типов функций 4. Типы функций — на основе элементов набора 5. Типы функций — на основе уравнения 6. Типы функций — на основе диапазона 7. Типы функций — на основе домена 8. Часто задаваемые вопросы о типах функций Какие бывают типы функций?
Функция y = f(x) подразделяется на различные типы функций на основе таких факторов, как область определения и диапазон функции, а также выражение функции. Функции имеют значение домена x , которое называется входным. Значением домена может быть число, угол, десятичная дробь, дробь. Точно так же значение y или значение f(x) (обычно это числовое значение) является диапазоном. Типы функций были классифицированы на следующие четыре типа.
- На основе элементов набора
- На основе уравнения
- На основе диапазона
- На основе домена
Представление функций
Существуют три различных формы представления функций.
 Функции должны быть представлены для демонстрации значений предметной области и значений диапазона, а также отношений между ними. Функции могут быть представлены с помощью диаграмм Венна, графических форматов и реестровых форм. Детали каждой из форм представительства заключаются в следующем.
Функции должны быть представлены для демонстрации значений предметной области и значений диапазона, а также отношений между ними. Функции могут быть представлены с помощью диаграмм Венна, графических форматов и реестровых форм. Детали каждой из форм представительства заключаются в следующем.Диаграмма Венна: Диаграмма Венна является важным форматом для представления функции. Диаграммы Венна обычно представляются в виде двух окружностей со стрелками, соединяющими элементы в каждой из окружностей. Домен представлен в одном круге, а значения диапазона представлены в другом круге. И функция определяет стрелки и то, как стрелки соединяют разные элементы в двух кругах.
Графическая форма: Функции легко понять, если они представлены в графической форме с помощью осей координат. Представление функции в графической форме помогает нам понять изменение поведения функций, если функция увеличивается или уменьшается. Домен функции — значение x представлено вдоль оси x, а диапазон или значение f(x) функции нанесено относительно оси y.

Реестровая форма: Реестровая нотация набора представляет собой простое математическое представление набора в математической форме. Домен и диапазон функции представлены в цветочных скобках, где первый элемент пары представляет домен, а второй элемент представляет диапазон. Попробуем разобраться в этом на простом примере. Для функции вида f(x) = x 2 функция представляется как {(1, 1), (2, 4), (3, 9), (4, 16)}. Здесь первый элемент — это домен или значение x, а второй элемент — это диапазон или значение f(x) функции.
Список типов функций
Типы функций классифицируются далее для облегчения понимания и изучения. Типы функций были дополнительно классифицированы на четыре различных типа и представлены следующим образом.
На основе элементов - Один Один Функция
- Много одна функция
- На работу
- Один раз и вперед, функция
- В действие
- Постоянная функция
На основе уравнения - Функция идентификации
- Линейная функция
- Квадратичная функция
- Кубическая функция
- Полиномиальные функции
На основе диапазона - Функция модуля
- Рациональная функция
- Функция Сигнум
- Четные и нечетные функции
- Периодические функции
- Функция наибольшего целого числа
- Обратная функция
- Составные функции
На основе домена - Алгебраические функции
- Тригонометрические функции
- Логарифмические функции
Типы функций — на основе элементов набора
Эти типы функций классифицируются на основе количества взаимосвязей между элементами домена и кодового домена.
Функция One One Различные типы функций, основанные на элементах множества, следующие.
Различные типы функций, основанные на элементах множества, следующие.Взаимно-однозначная функция определяется выражением f: A → B таким образом, что каждый элемент множества A связан с отдельным элементом множества B. Взаимно-однозначная функция также называется инъективной функцией. Здесь каждый элемент домена имеет отдельный образ или элемент домена для данной функции.
Функция «многие к одному»Функция «многие к одному» определяется функцией f: A → B, так что более одного элемента множества A соединены с одним и тем же элементом множества B. одной функции более одного элемента имеют один и тот же домен или изображение. Если функция «многие к одному» в домене кода представляет собой одно значение или все элементы домена связаны с одним элементом, то это называется константной функцией.
На функциюВ функции on каждый элемент кодовой области связан с элементом доменной области.
Функция One One и Onto (биекция) Для функции, определяемой f: A → B, такой, что каждый элемент множества B имеет прообраз множества A. Онто-функция также называется субъективной функцией.
Для функции, определяемой f: A → B, такой, что каждый элемент множества B имеет прообраз множества A. Онто-функция также называется субъективной функцией.Функция, которая одновременно является и единицей, и функцией onto, называется биективной функцией. Здесь каждый элемент домена связан с отдельным элементом в домене кода, и каждый элемент домена кода имеет прообраз. Иными словами, каждый элемент множества А связан с отдельным элементом множества В, и в множестве В нет ни одного неучтенного элемента.
ВфункцияВфункция полностью противоположна по свойствам онтофункции. Здесь есть определенные элементы в со-области, которые не имеют никакого прообраза. Элементы множества B избыточны и не связаны ни с одним элементом множества A.
Постоянная функцияПостоянная функция — это важная форма функции «многие к одному». В постоянной функции все элементы домена имеют одно изображение.
 Постоянная функция имеет вид f(x) = K, где K — действительное число. Для разных значений домена (значение x) для постоянной функции получается одно и то же значение диапазона K.
Постоянная функция имеет вид f(x) = K, где K — действительное число. Для разных значений домена (значение x) для постоянной функции получается одно и то же значение диапазона K.Типы функций — на основе уравнения
Алгебраические выражения также являются функциями и основаны на степени многочлена. Функции, основанные на уравнениях, классифицируются в следующие уравнения в зависимости от степени переменной «x».
- Полиномиальная функция нулевой степени называется постоянной функцией.
- Полиномиальная функция первой степени называется линейной функцией.
- Полиномиальная функция второй степени называется квадратичной функцией.
- Полиномиальная функция третьей степени является кубической функцией.
Давайте подробно разберем каждую из этих функций.
Функция идентификацииФункция идентификации имеет тот же домен и диапазон. Уравнение функции тождества имеет вид f(x) = x или y = x.
 Область определения и область значений функции тождества имеют вид {(1, 1), (2, 2), (3, 3), (4, 4)…..(n, n)}.
Область определения и область значений функции тождества имеют вид {(1, 1), (2, 2), (3, 3), (4, 4)…..(n, n)}.График функции тождества представляет собой прямую, одинаково наклоненную к осям координат и проходящую через начало координат. Функция тождества может принимать как положительные, так и отрицательные значения, поэтому она присутствует в первом и третьем квадрантах координатной оси.
Линейная функцияПолиномиальная функция, имеющая уравнение первой степени, является линейной функцией. Область определения и диапазон линейной функции – это действительное число, и она имеет прямолинейный график. Такие уравнения, как y = x + 2, y = 3x, y = 2x — 1, являются примерами линейных функций. Функция тождества y = x также может считаться линейной функцией.
Общая форма линейной функции f(x) = ax + b используется для представления целевых функций в задачах линейного программирования. Здесь x, y — переменные, а a, b — действительные числа.
Квадратичная функция Графически линейная функция может быть представлена уравнением линии y = mx + c, где m – наклон линии, а c – точка пересечения линии по оси y.
Графически линейная функция может быть представлена уравнением линии y = mx + c, где m – наклон линии, а c – точка пересечения линии по оси y.Квадратичная функция имеет квадратное уравнение второй степени и имеет график в виде кривой. Общая форма квадратичной функции такова: f(x) = ax 2 + bx + c, где a ≠ 0, a, b, c — константы, а x — переменная. Область определения и область значений квадратичной функции R.
График квадратного уравнения представляет собой нелинейный график и имеет параболическую форму. Примеры квадратичных функций: f(x) = 3x 2 + 5, f(x) = x 2 — 3x + 2.
Кубическая функцияКубическая функция имеет уравнение третьей степени. Общая форма кубической функции такова: f(x) = ax 3 + bx 2 + cx +d, где a ≠ 0, a, b, c и d — действительные числа, а x — переменная. Область определения и область значений кубической функции R.

График кубической функции более изогнут, чем график квадратичной функции. Примером кубической функции является f(x) = 8x 3 + 5x 9.0564 2 + 3.
Полиномиальная функцияОбщая форма полиномиальной функции: н-2 х н-2 + ….. топор + б. Здесь n — целое неотрицательное число, а x — переменная. Область определения и область значений полиномиальной функции равны R. В зависимости от мощности полиномиальной функции функции можно классифицировать как квадратичные, кубические и т. д.
Типы функций — на основе диапазона
Здесь типы функций классифицированы на основе диапазона, который получается из заданных функций. Различные типы функций, основанные на диапазоне, следующие.
Функция модуляФункция модуля дает абсолютное значение функции, независимо от знака входного значения домена. Функция модуля представлена как f(x) = |x|. Входное значение ‘x’ может быть положительным или отрицательным выражением.
Рациональная функция График модульной функции лежит в первом и втором квадрантах, поскольку координаты точек на графике имеют вид (x, y), (-x, y).
График модульной функции лежит в первом и втором квадрантах, поскольку координаты точек на графике имеют вид (x, y), (-x, y).Функция, состоящая из двух функций и выраженная в виде дроби, является рациональной функцией. Рациональная дробь имеет вид f(x)/g(x) и g(x) ≠ 0. Функции, используемые в этой рациональной функции, могут быть алгебраическими или любыми другими функциями. Графическое представление этих рациональных функций подобно асимптотам, так как не касается осевых линий.
Функция SignumФункция signum помогает нам узнать знак функции и не дает числовое значение или какие-либо другие значения для диапазона. Диапазон знаковой функции ограничен {-1, 0, 1}. Для положительного значения домена сигнум-функция дает ответ 1, для отрицательных значений сигнум-функция дает ответ -1, а для нулевого значения домена изображение равно 0. Сигнум-функция имеет широкое применение. в программировании программного обеспечения.
Четная и нечетная функция
Четные и нечетные функции основаны на соотношении между входными и выходными значениями функции. Для отрицательного значения домена, если диапазон представляет собой отрицательное значение диапазона исходной функции, функция является нечетной. А для отрицательного значения домена, если диапазон такой же, как у исходной функции, то функция является четной функцией.
Если f(-x) = f(x) для всех значений x, то функция является четной функцией, а если f(-x) = -f(x) для всех значений x, то функция нечетная. Примером четных функций являются x 2 , Cosx, Secx и пример нечетных функций: x 3 , Sinx, Tanx.
Периодическая функцияФункция считается периодической, если один и тот же диапазон появляется для разных значений домена и последовательно. Тригонометрические функции можно считать периодическими функциями. Например, функция f(x) = Sinx имеет диапазон [-1, 1] для различных значений домена x = nπ + (-1) 90 564 n 90 565 x.
Обратная функция Точно так же мы можем написать область определения и диапазон тригонометрических функций и доказать, что диапазон проявляется периодически.
Точно так же мы можем написать область определения и диапазон тригонометрических функций и доказать, что диапазон проявляется периодически.Обратная функция f(x) обозначается f -1 (x). Для обратной функции область определения и область значений данной функции изменяются как область значений и область определения обратной функции. Обратную функцию можно увидеть в алгебраических функциях и обратных тригонометрических функциях. Домен Sinx равен R, а его диапазон равен [-1, 1], а для Sin -1 x домен равен [-1, 1], а диапазон равен R. Обратная функция существует, если она биективная функция.
Если функция f(x) = x 2 , то обратной функцией является f -1 (x) = \(\sqrt x\).
Функция наибольшего целого числаФункция наибольшего целого числа также известна как ступенчатая функция. Функция наибольшего целого числа округляет число до ближайшего целого числа, меньшего или равного заданному числу.
 Ясно, что входная переменная x может принимать любое действительное значение. Однако на выходе всегда будет целое число. Кроме того, все целые числа будут встречаться в выходном наборе. Таким образом, областью определения этой функции являются действительные числа R, а область значений — целые числа (Z).
Ясно, что входная переменная x может принимать любое действительное значение. Однако на выходе всегда будет целое число. Кроме того, все целые числа будут встречаться в выходном наборе. Таким образом, областью определения этой функции являются действительные числа R, а область значений — целые числа (Z).График наибольшей целочисленной функции известен как ступенчатая кривая из-за ступенчатой структуры кривой. Наибольшая интегральная функция обозначается как f(x) = ⌊x⌋. Для функции, принимающей значения из [1, 2], значение f(x) равно 1.
Составная функцияСоставные функции имеют вид gof(x), туман(x), h( g(f(x))) и состоит из отдельных функций f(x), g(x), h(x). Составные функции, состоящие из двух функций, имеют диапазон одной функции, образующий область определения для другой функции. Рассмотрим составную функцию туман(х), состоящую из двух функций f(х) и g(х).
Здесь мы пишем туман(х) = f(g(x)). Диапазон g(x) образует область определения функции f(x).
 Его можно рассматривать как последовательность двух функций. Если f (x) = 2x + 3 и g (x) = x + 1, мы имеем туман (x) = f (g (x)) = f (x + 1) = 2 (x + 1) + 3 = 2x + 5.
Его можно рассматривать как последовательность двух функций. Если f (x) = 2x + 3 и g (x) = x + 1, мы имеем туман (x) = f (g (x)) = f (x + 1) = 2 (x + 1) + 3 = 2x + 5.Типы функций — на основе домена
Функции используются во всех других разделах математики. Функции были классифицированы на основе типов уравнений, используемых для определения функций. Уравнения функций обычно имеют алгебраические выражения, тригонометрические функции, логарифмы, показатели степени и, следовательно, называются на основе этих значений домена. Ниже приведены три основных типа функций, основанных на значении домена.
Алгебраическая функцияАлгебраическая функция полезна для определения различных операций алгебры. Алгебраическая функция имеет переменную, коэффициент, постоянный член и различные арифметические операторы, такие как сложение, вычитание, умножение, деление. Алгебраическая функция обычно имеет вид f(x) = a n x n + a n — 1 x n — 1 + a n-2 x n-2 + .
 …… топор + ц.
…… топор + ц.Алгебраическая функция также может быть представлена графически. Алгебраическая функция также называется линейной функцией, квадратичной функцией, кубической функцией, полиномиальной функцией в зависимости от степени алгебраического уравнения.
Тригонометрические функцииТригонометрические функции также имеют область определения и диапазон, как и любые другие функции. Шесть тригонометрических функций: f(θ) = sinθ, f(θ) = cosθ, f(θ) = tanθ, f(θ) = secθ, f(θ) = cosecθ. Здесь значение домена θ представляет собой угол и выражается в градусах или в радианах. Эти тригонометрические функции были взяты на основе отношения сторон прямоугольного треугольника и основаны на теореме Пифагора.
Помимо этих тригонометрических функций, были также получены обратные тригонометрические функции. Область определения обратной тригонометрической функции представляет собой действительное числовое значение, а ее область значений представляет собой угол.
Логарифмические функции Тригонометрические функции и обратные тригонометрические функции также иногда называют периодическими функциями, поскольку главные значения повторяются.
Тригонометрические функции и обратные тригонометрические функции также иногда называют периодическими функциями, поскольку главные значения повторяются.Логарифмические функции были получены из экспоненциальных функций. Логарифмические функции рассматриваются как обратные показательным функциям. Логарифмические функции имеют «лог» в функции, и у него есть база. Логарифмическая функция имеет вид y = \(\log_ax \). Здесь значение домена является входным значением «x» и рассчитывается с использованием логарифмической таблицы Нейпира. Логарифмическая функция дает число экспоненциальных умножений, до которого было возведено основание, чтобы получить значение x. Та же логарифмическая функция может быть выражена как экспоненциальная функция как x = a и .
Связанная тема
Следующая тема поможет лучше понять типы функций.
- Функции
- Что такое функции?
- Отношения и функции
- Графические функции
- Домен и область действия
- Составные функции
Часто задаваемые вопросы о типах функций
Какие существуют типы функций в математике?
Типы функций можно разделить на четыре типа.

- Основано на Элементе: Функция один к одному, функция многие к одному, на функцию, один на один и на функцию, в функцию.
- На основе предметной области: алгебраические функции, тригонометрические функции, логарифмические функции.
- На основе диапазона: функция модуля, рациональная функция, сигнум-функция, четная и нечетная функция, функция наибольшего целого числа.
- На основе уравнений: функция тождества, линейная функция, квадратичная функция, кубическая функция, полиномиальная функция.
Как вы определяете типы функций?
Типы функций можно определить на основе домена, диапазона и функционального уравнения. Дальнейшая классификация функций по типам функций помогает сгруппировать и легко понять каждый из типов функций. Все тригонометрические функции можно сгруппировать под периодическими функциями. Такие функции, как тождественная функция, линейная функция, квадратичная, кубическая функция, могут быть сгруппированы под полиномиальными функциями.
 Таким образом, уравнение функции y = f(x) помогает определить тип функции.
Таким образом, уравнение функции y = f(x) помогает определить тип функции.Какой тип функций всегда непрерывен?
Функции, которые имеют диапазон для каждого входного значения домена, можно назвать непрерывной функцией. Простейшим примером непрерывной функции является функция тождества, которая имеет одинаковые значения домена и диапазона. Другими примерами непрерывных функций являются тригонометрическая функция синуса и функция косинуса.
Какие существуют формы представления функций?
Функции обычно представляются в виде уравнения y = f(x), где x — область определения, а y или f(x) — диапазон функции. Функции с элементами домена и диапазона также представлены в виде диаграмм Венна или в виде реестра. В форме реестра домен и диапазон функции представлены как {\((x_1, f(x_1)), (x_2, f(x_2)), (x_3, f(x_3))\)}.
Каковы другие математические приложения типов функций?
Типы функций имеют огромное применение в алгебре, тригонометрии, логарифмах, экспонентах.
 Все алгебраические выражения можно рассматривать как функции, поскольку они имеют значение входной области x и выходной диапазон, который является ответом алгебраической функции. Тригонометрические функции также имеют значение угла в качестве значения домена и диапазона.
Все алгебраические выражения можно рассматривать как функции, поскольку они имеют значение входной области x и выходной диапазон, который является ответом алгебраической функции. Тригонометрические функции также имеют значение угла в качестве значения домена и диапазона.Можно ли любое математическое уравнение считать функцией?
Да. Математическое уравнение, не равное нулю, можно рассматривать как функцию. В качестве альтернативы, математическое уравнение с двумя переменными, где одна переменная может быть взята в качестве домена, а другая переменная может быть взята в качестве диапазона, может быть названа функцией.
Каковы приложения типов функций?
Типы функций имеют множество приложений в физике, технике, компьютерных науках, искусственном интеллекте. Все эти поля предназначены для подключения одного набора точек данных (домен) к другому набору точек данных (диапазон). Кроме того, функции помогают представить огромный набор точек данных в простом математическом выражении формального выражения y = f(x).



 41)
41)



 Функции должны быть представлены для демонстрации значений предметной области и значений диапазона, а также отношений между ними. Функции могут быть представлены с помощью диаграмм Венна, графических форматов и реестровых форм. Детали каждой из форм представительства заключаются в следующем.
Функции должны быть представлены для демонстрации значений предметной области и значений диапазона, а также отношений между ними. Функции могут быть представлены с помощью диаграмм Венна, графических форматов и реестровых форм. Детали каждой из форм представительства заключаются в следующем.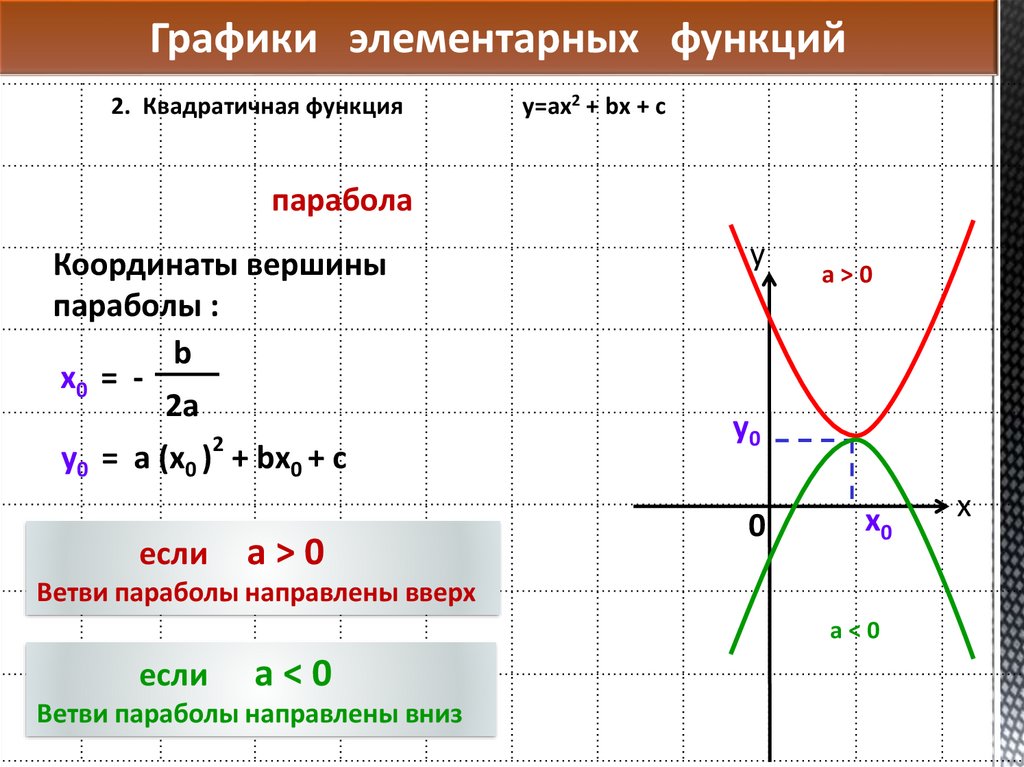
 Различные типы функций, основанные на элементах множества, следующие.
Различные типы функций, основанные на элементах множества, следующие. Для функции, определяемой f: A → B, такой, что каждый элемент множества B имеет прообраз множества A. Онто-функция также называется субъективной функцией.
Для функции, определяемой f: A → B, такой, что каждый элемент множества B имеет прообраз множества A. Онто-функция также называется субъективной функцией. Постоянная функция имеет вид f(x) = K, где K — действительное число. Для разных значений домена (значение x) для постоянной функции получается одно и то же значение диапазона K.
Постоянная функция имеет вид f(x) = K, где K — действительное число. Для разных значений домена (значение x) для постоянной функции получается одно и то же значение диапазона K. Область определения и область значений функции тождества имеют вид {(1, 1), (2, 2), (3, 3), (4, 4)…..(n, n)}.
Область определения и область значений функции тождества имеют вид {(1, 1), (2, 2), (3, 3), (4, 4)…..(n, n)}.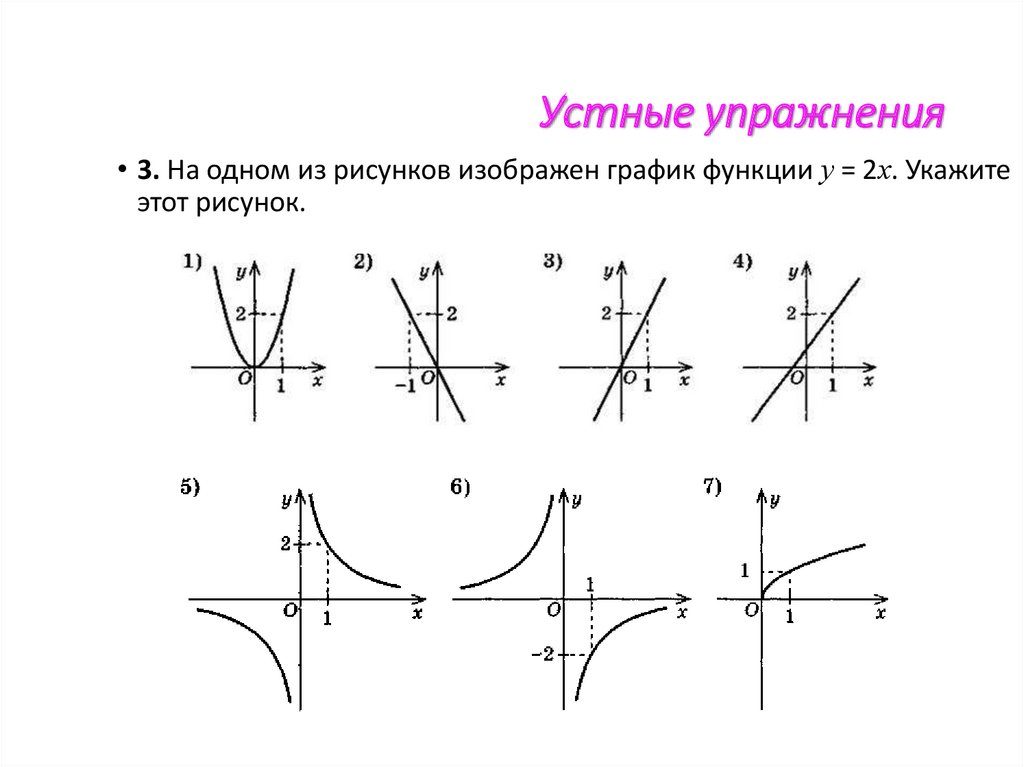 Графически линейная функция может быть представлена уравнением линии y = mx + c, где m – наклон линии, а c – точка пересечения линии по оси y.
Графически линейная функция может быть представлена уравнением линии y = mx + c, где m – наклон линии, а c – точка пересечения линии по оси y.

 Точно так же мы можем написать область определения и диапазон тригонометрических функций и доказать, что диапазон проявляется периодически.
Точно так же мы можем написать область определения и диапазон тригонометрических функций и доказать, что диапазон проявляется периодически. Ясно, что входная переменная x может принимать любое действительное значение. Однако на выходе всегда будет целое число. Кроме того, все целые числа будут встречаться в выходном наборе. Таким образом, областью определения этой функции являются действительные числа R, а область значений — целые числа (Z).
Ясно, что входная переменная x может принимать любое действительное значение. Однако на выходе всегда будет целое число. Кроме того, все целые числа будут встречаться в выходном наборе. Таким образом, областью определения этой функции являются действительные числа R, а область значений — целые числа (Z).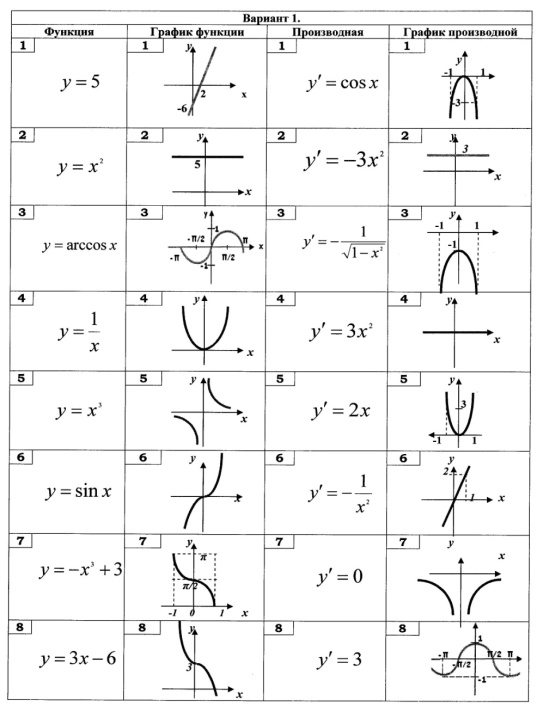 Его можно рассматривать как последовательность двух функций. Если f (x) = 2x + 3 и g (x) = x + 1, мы имеем туман (x) = f (g (x)) = f (x + 1) = 2 (x + 1) + 3 = 2x + 5.
Его можно рассматривать как последовательность двух функций. Если f (x) = 2x + 3 и g (x) = x + 1, мы имеем туман (x) = f (g (x)) = f (x + 1) = 2 (x + 1) + 3 = 2x + 5. …… топор + ц.
…… топор + ц.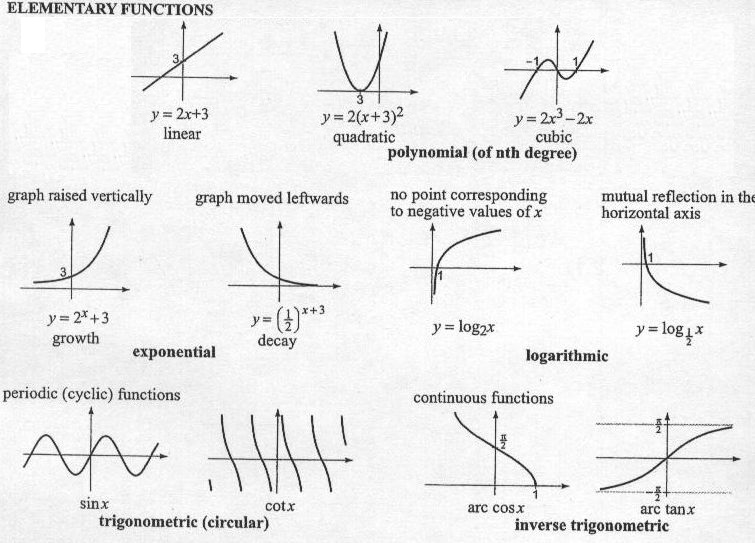 Тригонометрические функции и обратные тригонометрические функции также иногда называют периодическими функциями, поскольку главные значения повторяются.
Тригонометрические функции и обратные тригонометрические функции также иногда называют периодическими функциями, поскольку главные значения повторяются.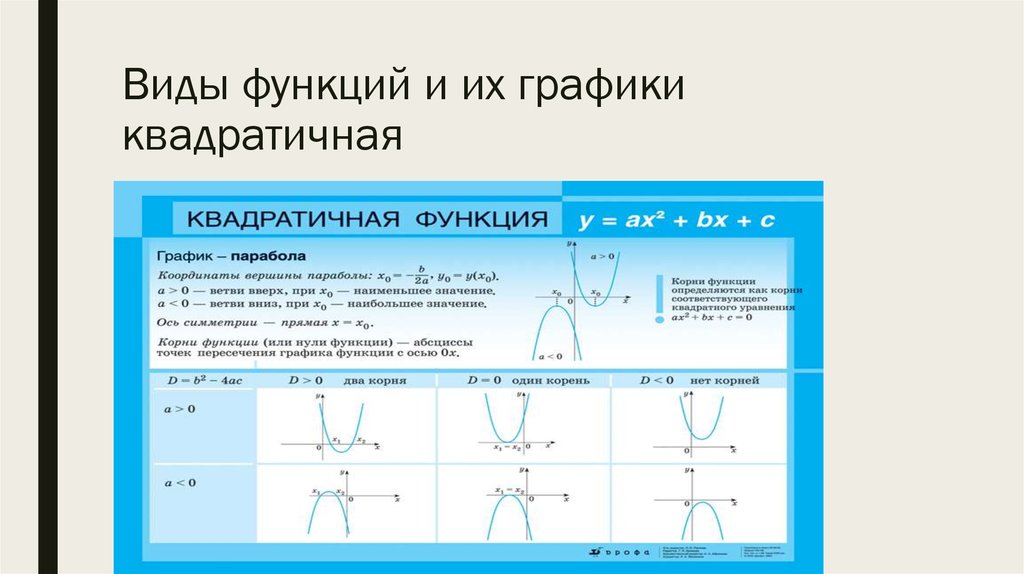
 Таким образом, уравнение функции y = f(x) помогает определить тип функции.
Таким образом, уравнение функции y = f(x) помогает определить тип функции. Все алгебраические выражения можно рассматривать как функции, поскольку они имеют значение входной области x и выходной диапазон, который является ответом алгебраической функции. Тригонометрические функции также имеют значение угла в качестве значения домена и диапазона.
Все алгебраические выражения можно рассматривать как функции, поскольку они имеют значение входной области x и выходной диапазон, который является ответом алгебраической функции. Тригонометрические функции также имеют значение угла в качестве значения домена и диапазона.