Таблица Sin Cos Tan — формулы, значения, примеры и часто задаваемые вопросы
Таблица Sin Cos TanТригонометрические функции sin, cos и tan являются основными функциями, которые мы рассматриваем при решении тригонометрических задач. «Таблица sin cos tan» состоит из значений sin, cos и tan стандартных углов 0°, 30°, 45°, 60° и 90°, а иногда и других углов, таких как 180°, 270° и 360°.
Формула Sin Cos TanТри отношения sin, cos и tan имеют свои индивидуальные формулы. Предположим, что ABC — прямоугольный треугольник с прямым углом в точке B, как показано на рисунке ниже:
Три стороны прямоугольного треугольника приведены ниже:
AB = сторона, прилежащая к углу θ
BC = сторона, противоположная углу θ
CA = гипотенуза к углу θ формулы cos и tan, имеем:
sin θ = Противоположная сторона / Гипотенуза = BC / CA
cos θ = Прилежащая сторона / Гипотенуза = AB / CA
tan θ = Противоположная сторона / Прилежащая сторона = CB / AB
Диаграмма Sin Cos Tan (таблица) Посмотрим таблицу, в которой значения sin, cos и tan приведены для стандартных углов 0°, 30° (π/6), 45° (π/4), 60° (π/3) и 90° (π/2).
Чтобы найти значения sin, cos, tan, выполните следующие действия:
- Создайте таблицу и укажите первую строку с углами 0°, 30°, 45°, 60°, 90° и напишите тригонометрическую функцию. имя в первом столбце, например грех.
- Теперь определим значения sin. Напишите числа 0, 1, 2, 3, 4 под углами 0°, 30°, 45°, 60°, 90° соответственно.
- Теперь разделите числа на 4 и найдите квадратный корень. Мы получим √(0/4), √(¼), √(2/4), √(¾) и √(4/4).
- Упростив это, мы получим значения синуса для этих 5 углов.
- Теперь для оставшихся трех углов используйте следующие формулы:
sin (180° − x) = sin x
sin (180° + x) = – (sin x)
sin (360° − x) = – (sin x)
Это означает,
sin 180° = sin (180° − 0°) = sin 0° = 0
sin 270° = sin (180° +90°) = – (sin 90°) = -1
Sin 360° = sin (360 ° − 0°) = – (sin 0°) = 0
- Теперь определим значения cos по формуле cos x = sin (90° – x).
Например, cos 60° = sin (90° – 30°) = sin 30° = ½. Аналогично можно узнать и другие значения.
Например, cos 60° = sin (90° – 30°) = sin 30° = ½. Аналогично можно узнать и другие значения.- Чтобы определить значения tan, мы используем формулу tan x = (sin x/cos x).
Например, значение tan 30° = (sin 30°/cos 30°) = (½) /(√3/2) = (1/√3). Точно так же мы можем сгенерировать другие значения.
Значение тригонометрических функций для углов от 0° до 360° приведено в следующей тригонометрической таблице.
Примеры1. Каково значение sin 270°?
Мы знаем, что sin 270° = sin (180° + 90°)
Кроме того, sin (180° + x) = – (sin x)
Следовательно, sin (180° + 90°) = – sin 90° = – 1
Следовательно, sin 270° = – 1
2. Используя таблицу тригонометрии, запишите значения:
(a) sin(π/4) (b) cos(π/3) ) (c) tan (π/2)
Таблица тригонометрии помогает нам быстро найти эти значения. Имеем:
(a) sin(π/4) = sin 45º = (1/√2)
(b) cos(π/3) = cos 60º = (1/2)
(c) tan (π/2) = tan 90º = ∞
Все, что нужно знать о тригонометрии Таблица
Тригонометрия является одной из наиболее важных областей математики, которая имеет широкий спектр приложений.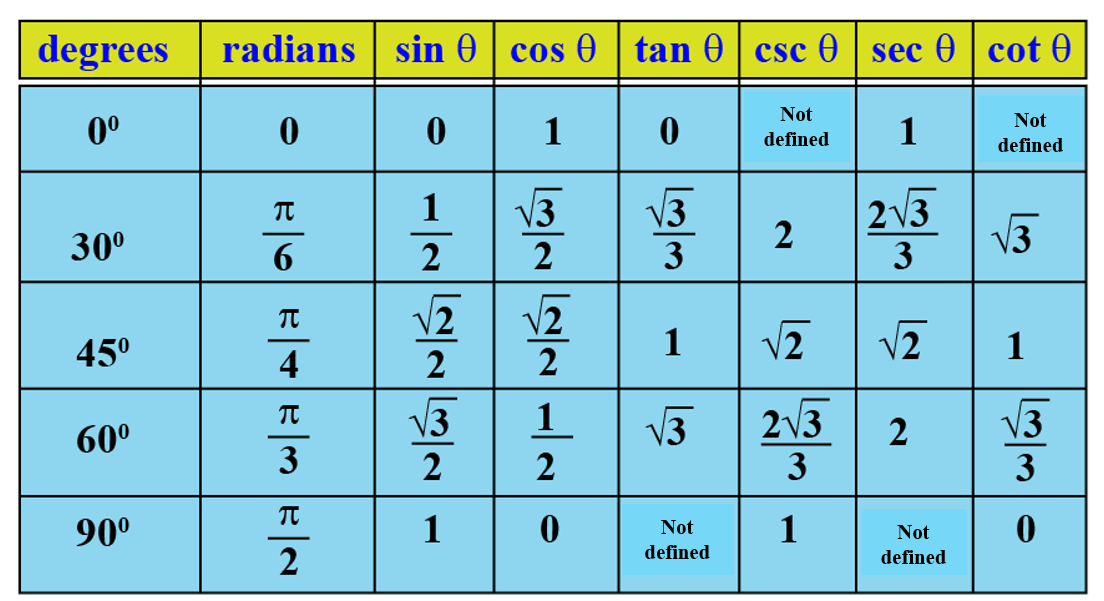
Тригонометрия — это дисциплина математики, изучающая взаимосвязь между длинами и углами прямоугольного треугольника.
В результате с помощью тригонометрических формул, функций или тождеств можно найти недостающие или неизвестные углы или стороны прямоугольного треугольника. 0°, 30°, 45°, 60° и 90° — одни из наиболее часто используемых тригонометрических углов в расчетах.
Тригонометрия далее делится на две ветви. Ниже приведены два типа тригонометрии:
Таблица тригонометрии:
Значения стандартных тригонометрических углов, таких как 0°, 30°, 45°, 60° и 90°, можно найти с помощью таблицы тригонометрических соотношений. Тригонометрическими отношениями являются синус, косинус, тангенс, косеканс, секанс и котангенс. Sin, cos, tan, cosec, sec и cot являются сокращенными формами этих соотношений.
Для решения задач по тригонометрии требуются значения тригонометрических отношений стандартных углов. В результате значение тригонометрических отношений таких стандартных углов необходимо запомнить.
В таблице указаны типичные углы, которые можно использовать для решения многочисленных задач на тригонометрические соотношения.
УГОЛКИ | 0 ̊ | 30 ̊ | 45 ̊ | 60 ̊ | 90 ̊ |
Грех ϴ | 0 | ½ | 1/√2 | √3/2 | 1 |
Кос ϴ | 1 | √3/2 | 1/√2 | ½ | 0 |
Тан ϴ | 0 | 1/√3 | 1 | √3 | ∞ |
Косек ϴ | ∞ | 2 | √2 | 2/√3 | 1 |
сек ϴ | 1 | 2/√3 | √2 | 2 | ∞ |
Детская кроватка ϴ | ∞ | √3 | 1 | 2/3 | 0 |
Точно так же мы можем определить значения тригонометрического отношения для углов, отличных от 90°, например 180°, 270° и 360°.
Единичный круг:
Мы можем использовать тригонометрические функции для любого угла, даже больше 90°, используя единичный круг. Периодичность тригонометрических функций демонстрируется единичным кругом, который показывает, что они производят набор чисел через равные промежутки времени.
Поскольку центр круга находится в начале координат, а радиус равен 1, идея единичного круга позволяет нам точно измерить углы cos, sin и tan. Предположим, что тета — это угол.
Предположим, что длина перпендикуляра равна y, а длина основания равна x. Гипотенуза имеет ту же длину, что и радиус единичного круга, который также равен 1. В результате тригонометрические отношения можно записать как;
Sin ϴ | y/1 = y |
Cos ϴ | x/1 = x |
| г/х |
Тригонометрические тождества:
Тождества геометрически связаны с определенными тригонометрическими функциями (такими как синус, косинус и тангенс) одного или даже нескольких углов.
Основными функциями тригонометрии являются синус, косинус и тангенс, а остальные 3 функции – котангенс, секанс и косеканс.
Только прямоугольный треугольник имеет тригонометрические тождества. Стороны прямоугольного треугольника, такие как смежная, противолежащая сторона и сторона гипотенузы, используются для определения всех этих тригонометрических соотношений.
Список тригонометрических тождеств:
В тригонометрии для решения множества тригонометрических задач используются многочисленные тождества. Сложные тригонометрические задачи можно быстро решить с помощью этих тригонометрических тождеств или формул. Давайте рассмотрим все основные тригонометрические тождества.
Взаимные тождества в тригонометрии
Ниже приведены взаимные тригонометрические тождества:
Sinϴ = 1/cosecϴ
cosϴ = 1/секϴ
tanϴ = 1/cotϴ
Тригонометрические тождества Пифагора
В тригонометрии существует 3 тригонометрических тождества Пифагора, основанных на теореме прямоугольного треугольника, также называемой теоремой Пифагора.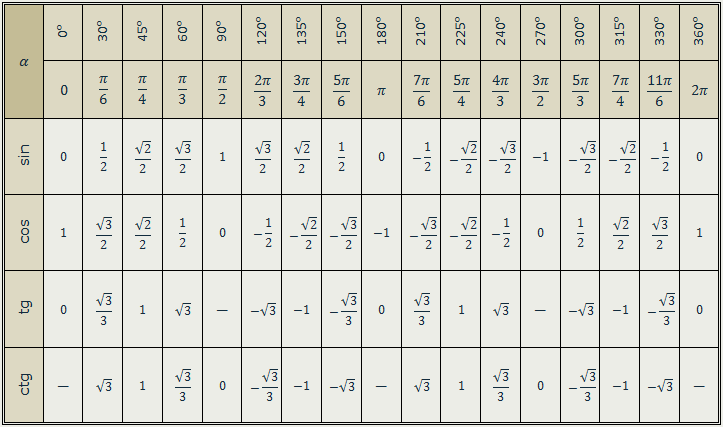
Тождества противоположных углов в тригонометрии
Ниже приведены примеры тригонометрических тождеств противоположных углов:
Sin (-ϴ) = – Sin ϴ
Cos (-ϴ) = Cos ϴ
Тан (-ϴ) = – Тан ϴ
Детская кроватка (-ϴ) = – Детская кроватка ϴ
сек (-ϴ) = сек ϴ
Тригонометрические тождества дополнительных углов
Два угла называются дополнительными в геометрии, если их сумма равна 90°. Точно так же здесь можно изучить тригонометрические тождества для дополнительных углов.
Sin (90° – ϴ) = Cos ϴ
Cos (90° – ϴ) = Sin ϴ
Tan (90° – ϴ) = Cot ϴ
Cot (90° – ϴ) = Tan ϴ
- сек (90° – ϴ) = cosec ϴ
Косек (90° – ϴ) = ϴ сек
Тригонометрические тождества дополнительных углов
Если сумма двух углов равна 90 градусам, они являются дополнительными.
Точно так же здесь можно изучить тригонометрические тождества для дополнительных углов.
sinϴ = sin (180°-θ)
-cos θ = cos (180°- θ)
косек θ = косек (180°-θ)
-сек θ = сек (180°- θ)
-тангенс θ = тангенс (180°- θ)
— детская кроватка θ = детская кроватка (180°- θ)
Тождества с двойным углом
Тригонометрические тождества для sin, cos и tan при удвоении углов:
2 sinϴ cosϴ = sin 2ϴ
2 cos2ϴ – 1 = 1 – 2sin2 ϴ = cos 2ϴ = cos2ϴ – sin2 ϴ
(2tanϴ)/ (1 – tan2ϴ) = tan 2ϴ
Тождества произведения-суммы в тригонометрии
Сумма и разность синусов или косинусов преобразуются в произведение синусов и косинусов с использованием тригонометрических тождеств произведения-суммы.