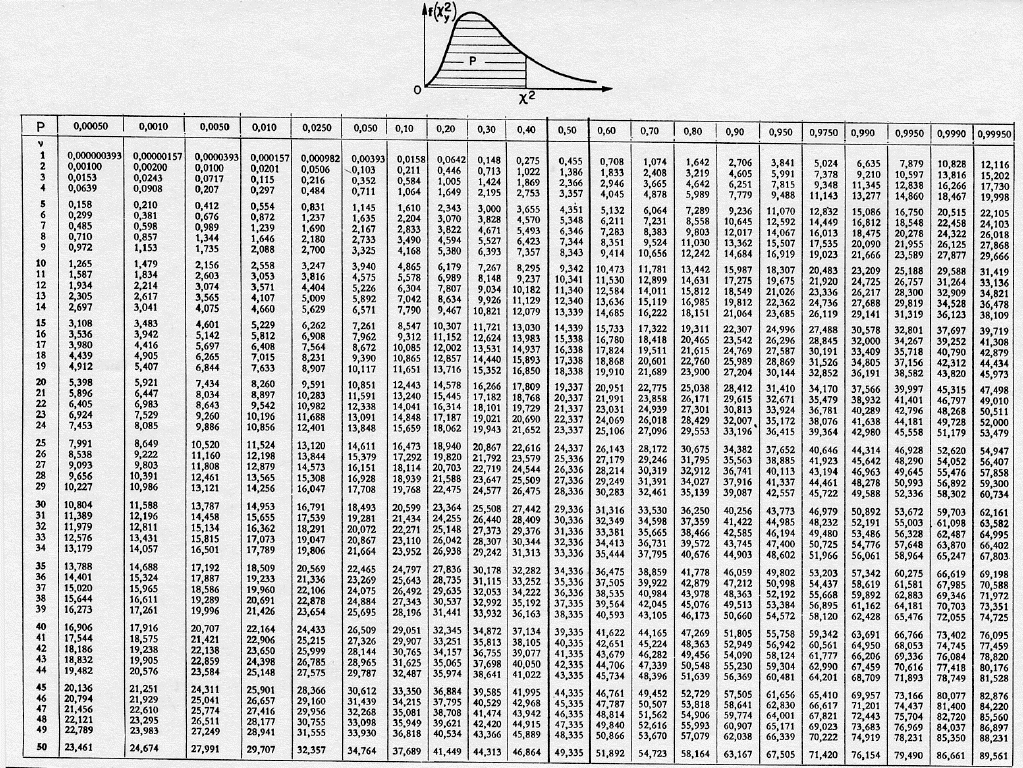
5. Интегральная теорема Лапласа.
Вновь будем предполагать, что производится испытаний, в каждом из которых вероятность появления событияпостоянна и равна. Как вычислить вероятностьтого, что событиепоявится виспытаниях не менееи не болеераз (для краткости будем говорить “отдораз”) ? На этот вопрос отвечает интегральная теорема Лапласа.
Теорема 3.2. Если вероятность наступления событияв каждом испытании постоянна и отлична от нуля и единицы, то вероятностьтого, что событиепоявится виспытаниях отдораз, приближенно равна определенному интегралу
,
где и .
При решении задач,
требующих применения интегральной
теоремы Лапласа, пользуются специальными
таблицами, так как неопределенный
интеграл
не выражается через элементарные
функции. Таблица для интегралаприведена в приложении 2. В таблице даны
значения функциидля положительных значений,
дляпользуются той же таблицей (функциянечетна т.
Итак, вероятность того, что событие появится внезависимых испытаниях отдораз, приближенно равна
,
где и.
Пример 4. Вероятность того, что деталь изготовлена с нарушениями стандартов, равна . Найти вероятность того, что средислучайно отобранных деталей окажется нестандартных отдодеталей.
Решение. По условию ,,,,. Воспользуемся интегральной теоремой Лапласа:
.
Вычислим нижний предел интегрирования:
.
Вычислим верхний предел интегрирования:
.
Таким образом, имеем
.
По таблице (приложение 2) находим
, .
Искомая вероятность равна
.
6. Использование интегральной теоремы Лапласа.
Если число (число появлений событияпринезависимых испытаниях) будет изменяться отдо, то дробьбудет изменяться отдо. Следовательно, интегральную теорему Лапласа можно записать и так:
. (3.6)
Поставим своей задачей найти вероятность того, что отклонение относительной частоты от постоянной вероятностипо абсолютной величине не превышает заданного числа. Другими словами, найдем вероятность осуществления неравенства, или, что то же самое,. Эту вероятность будем обозначать так:. С учетом формулы (3.6) для данной вероятности получаем (выкладки опускаем виду их громоздкости):
. (3.7)
Пример 5. Вероятность того, что деталь нестандартна, равна . Найти вероятность того, что среди случайно отобранныхдеталей относительная частота появления нестандартных деталей отклонится от вероятностипо абсолютной величине не более, чем на.
Решение. По условию
,,,. Требуется найти вероятность.
Пользуясь формулой (3.7), будем иметь:
Требуется найти вероятность.
Пользуясь формулой (3.7), будем иметь:
.
По таблице (приложение 2) находим , следовательно,. Итак, искомая вероятность приближенно равна. Смысл полученного результата таков: если взять достаточно большое число проб подеталей в каждой, то примерно в% этих проб отклонение относительной частоты от постоянной вероятности по абсолютной величине не превысит.
7. Формула Пуассона для маловероятных событий.
Если вероятность наступления события в отдельном испытании близка к нулю, то даже при большом числе испытаний, но при небольшой величине произведенияполучаемые по формуле Лапласа значения вероятностейоказываются недостаточно точными и возникает потребность в другой приближенной формуле.
Теорема 3.3. Если вероятность наступления событияв каждом испытании постоянна, но мала, число независимых испытанийдостаточно велико, но произведениеостается небольшим (не больше десяти), то вероятностьтого, что в этих испытаниях событиенаступитраз
.
Для упрощения расчетов, связанных с применением формулы Пуассона, составлена таблица значений функции Пуассона (приложение 3).
Пример 6. Пусть вероятность изготовления нестандартной детали равна . Найти вероятность того, что средидеталей окажетсянестандартных.
Решение. Здесь ,, а. Все три числа удовлетворяют требованиям теоремы 3.3, поэтому для нахождения вероятности искомого событияприменяем формулу Пуассона. По таблице значений функции Пуассона (приложение 3) прииполучаем.
Найдем вероятность того же события по формуле Лапласа. Для этого сначала вычисляем значение , соответствующее:
.
Поэтому приближенное значение искомой вероятности согласно формуле Лапласа таково:
,
а точное значение ее, которое дает формула Бернулли, такое:
.
Таким образом,
относительная ошибка вычисления
вероятностей
по приближенной формуле Лапласа
составляет,
или%,
а по формуле Пуассона —
,
или%,
т. е. во много раз меньше.
е. во много раз меньше.
ЗАДАЧИ
1. Наблюдениями установлено, что в некоторой местности в сентябре бывает дождливых дней. Какова вероятность того, что из случайно взятых в этом месяце восьми дней три дня окажутся дождливыми ?
Ответ: .
2. Что вероятнее выиграть у равносильного противника (ничейный исход партии исключен): три партии из четырех или пять из восьми ?
Ответ: вероятнее выиграть три партии из четырех.
3. Изделия некоторого производства содержат % брака. Найдите вероятность того, что среди пяти взятых наугад изделий: а) нет ни одного испорченного; б) будут два испорченных.
Ответ: а) ; б).
4. Всхожесть семян данного сорта растений оценивается с вероятностью, равной . Какова вероятность того, что из пяти посеянных семян взойдут не менее четырех ?
Ответ: .
5. Вероятность рождения мальчика равна , а девочки -. В некоторой семье шестеро детей. Найти вероятность того, что среди них не больше двух девочек.
Ответ:
6. Вероятность того, что любой абонент позвонит на коммутатор в течение часа, равна . Телефонная станция обслуживаетабонентов. Какова вероятность, что в течение часа позвонят пять абонентов ?
Ответ: .
7. Имеется общество из человек. Найти вероятность того, что у двух человек день рождения придется на Новый год. Считать, что вероятность рождения в фиксированный день равна.
Ответ: .
8. Вероятность появления успеха в каждом испытании равна . Какова вероятность, что прииспытаниях успех наступит: а) ровнораз ? б) ровнораз ?
Ответ: а) ; б).
9. Какова вероятность того, что в столбике из ста наугад отобранных монет число монет, расположенных “гербом” вверх, будет отдо?
Ответ: .
10. Производство дает % брака. Какова вероятность того, что из взятых на исследование изделий бракованных будет не больше?
Ответ: .
Локальная и интегральная теоремы Лапласа. Решение задач
Если количество независимых испытаний достаточно большое применения формулы Бернулли становится трудоемким. Для упрощения вычислений применяют локальную и интегральную теоремы Лапласа, которые дают близкий к формуле Бернулли результат при большом количестве испытаний и не требуют больших вычислений.
ЛОКАЛЬНАЯ ТЕОРЕМА ЛАПЛАСА
Вероятность того, что в независимых испытаниях с вероятностью появления события равной событие наступит ровно раз (безразлично в какой последовательности) определяется по приближенной формуле
где
– Функция Гаусса,
– аргумент функции Гаусса;
– вероятность противоположного события .
Формулу называют локальной формулой Лапласа.
Функция обладает следующими свойствами:
1) она является четной функцией ;
2) для значений аргумента больше четырех она сколь угодно мала
Теорему Лапласа рекомендуется применять при значениях произведения больше девяти
ИНТЕГРАЛЬНАЯ ТЕОРЕМА МУАВРА-ЛАПЛАСА
Вероятность, что в независимых испытаниях событие с вероятностью появления наступит не менее раз и не более (независимо от последовательности появления) приближенно определяется зависимостью
где – интегральная функция Лапласа;
– аргументы интегральной функции распределения;
– вероятность невыполнения события .
Функция обладает следующими свойствами:
1) она является нечетной функцией
2) для аргументов больше пяти она равна 0,5
Значение обеих функций находят из таблиц в которых функции с достаточной точностью протабульовани.
———————————
Рассмотрим задачи на применение каждой из теорем.
Пример 1. Есть 100 лунок по которым случайным образом разбрасывают 30 шариков. Каждый шарик с равной вероятностью может попасть в любую лунку (в одну лунку попадает не более одного шарика). Найти вероятность того, что в выбранную лунку попадет ровно один шарик.
Решение. Проводится независимых бросков шариков с одинаковой вероятностью попадания при каждом броске
Вероятность попадания в лунку ровно одного шарика определим по локальной формулой Лапласа:
Для этого определяем составляющие
и подставим в зависимость
———————————
Пример 2. Проводится 200 независимых опытов с вероятностью успеха в каждом 24%. Какова вероятность успешного проведения 50 опытов?
Какова вероятность успешного проведения 50 опытов?
Решение. По условию
находим составляющие формулы Лапласа
Подставляя в формулу, находим
———————————
Пример 3. Вероятность выхода из строя за смену одного станка равна 0,1. Определить вероятность выхода из строя от 2 до 13 станков при наличии 100 станков.
Решение. Записываем входные данные
Для подобных примеров применяем интегральную формулу Муавра-Лапласа и находим вероятность
———————————
Решение задач по приведенным теоремам позволяет при большом количестве испытаний находить приближенное значение вероятности. Локальная теорема необходима при определении конкретного количества появления событий, интегральная теорема Муавра-Лапласа — в случаях, когда задан диапазон возможного количества появлений события. Таблицы табулирования функций, применяемых в формулах можно найти в сборниках по теории вероятностей и интернете.
14.3: Первая теорема интегрирования
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5503
- Джереми Татум
- Университет Виктории
Выражение в скобках равно нулю в обоих пределах, и, следовательно, теорема доказана.
Эта страница под названием 14.3: Первая теорема об интеграции распространяется под лицензией CC BY-NC 4.0 и была создана, изменена и/или курирована Джереми Татумом посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Джереми Татум
- Лицензия
- CC BY-NC
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Теги
- Первая теорема интегрирования
- обратное преобразование Лапласа
- источник@http://orca.
 phys.uvic.ca/~tatum/elmag.html
phys.uvic.ca/~tatum/elmag.html
Внутренняя структура и свойства интегральных преобразований типа Лапласа
На этой странице
АннотацияВведениеЗаключениеКонфликты интересовБлагодарностиСсылкиАвторское правоСтатьи по теме
Мы хотели бы установить внутреннюю структуру и свойства интегральных преобразований типа Лапласа. Методология этой статьи основана на рассмотрении общей структуры ядер интегрального преобразования типа Лапласа, а -преобразование, обобщенное интегральное преобразование типа Лапласа, предлагается с признаком инклюзивности. Предложенное -преобразование может обеспечить адекватное преобразование в ряде инженерных задач.
1. Введение
Основная мотивация для изучения теорий интегральных преобразований заключается в том, что они дают простой инструмент, который представлен алгебраической задачей в процессе решения дифференциальных уравнений [1]. В большинстве теорий интегральных преобразований важную роль играет ядро, которое преобразует одно пространство в другое для решения задачи. Основная причина преобразования заключается в том, что нелегко решить уравнение в заданном пространстве или легко найти характеристику для специальной цели. Например, в компьютерной томографии (КТ) или магнитно-резонансной томографии (МРТ) мы получаем проекционные данные с помощью интегрального преобразования и создаем изображение с обратным преобразованием. Это сильная сторона интегрального преобразования.
В большинстве теорий интегральных преобразований важную роль играет ядро, которое преобразует одно пространство в другое для решения задачи. Основная причина преобразования заключается в том, что нелегко решить уравнение в заданном пространстве или легко найти характеристику для специальной цели. Например, в компьютерной томографии (КТ) или магнитно-резонансной томографии (МРТ) мы получаем проекционные данные с помощью интегрального преобразования и создаем изображение с обратным преобразованием. Это сильная сторона интегрального преобразования.
Для начала рассмотрим внутреннюю структуру интегральных преобразований типа Лапласа. Конечно, структура зависит от ядра, и форма ядра в интегральных преобразованиях типа Лапласа выглядит следующим образом. Преобразование Лапласа определяется Сумуду и Эльзаки. Поскольку преобразование Лапласа можно переписать как для , мы можем естественно считать, что форма интегрального преобразования типа Лапласа предназначена для подходящего целого числа : например, если для .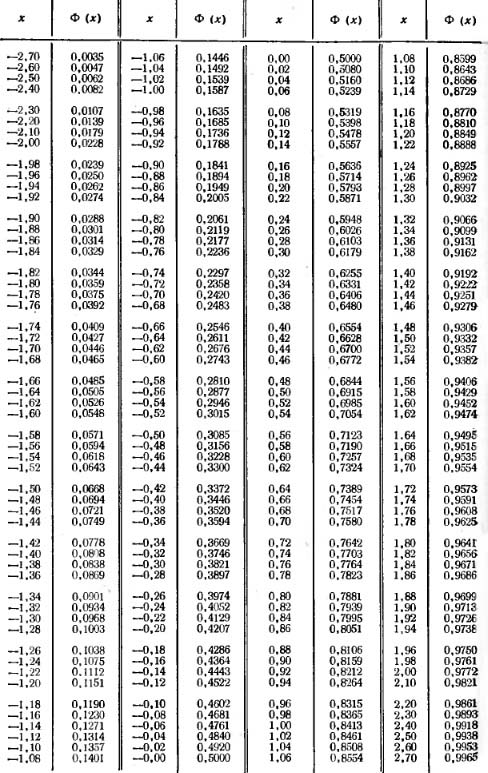
Обычно интегральные преобразования основаны на экспоненциальной функции, и они согласуются с тем, как интегрировать от до, чтобы использовать свойство к или сходится к при приближении к . Преобразование Сумуду/Эльзаки является своего рода модифицированным преобразованием Лапласа, введенным Ватугалой [2] в 1993/Эльзаки и др. [3] в 2012 г. для решения начальных задач в инженерных задачах [4]. Белгасем и др. [5, 6] упоминают, что преобразование Сумуду () обладает свойствами сохранения масштаба и единицы измерения, и его можно использовать для решения задач, не прибегая к новой частотной области. Эльзаки и др. [3, 7, 8] настаивает на том, что преобразование Эльзаки () должно легко применяться к задачам с начальными значениями с меньшими вычислительными затратами и решать различные примеры, которые не решаются преобразованием Лапласа или Сумуду. В качестве заявки Agwa et al. [9] имеют дело с преобразованием Сумуду во временных масштабах и его приложениями, Эльтайеб и Киликман [10] проверили некоторые приложения преобразования Сумуду, а Эльтайеб и др. подчеркивают важность дробных операторов интегрального преобразования и их приложений в [11]. Задачи со сдвигом данных, теоремы о сдвиге и формы решений ОДУ с переменными коэффициентами можно найти в [4, 12, 13].
подчеркивают важность дробных операторов интегрального преобразования и их приложений в [11]. Задачи со сдвигом данных, теоремы о сдвиге и формы решений ОДУ с переменными коэффициентами можно найти в [4, 12, 13].
С другой стороны, Крейзиг [1] говорит, что преобразование Лапласа () имеет сильную сторону в преобразованиях производных; т. е. дифференцированию функции соответствует умножение ее преобразования на . С другой точки зрения, если нам нужен обратный случай, когда преобразование дает простой инструмент для преобразования интегралов, то мы можем выбрать подходящую форму интегрального преобразования, такую как Это означает, что целое число применимо к . Как мы проверили выше, необходимо всеобъемлющее преобразование в преобразованиях типа Лапласа, и поэтому мы хотели бы предложить -преобразование, обобщенное интегральное преобразование типа Лапласа, которое является более полным и внутренним, чем существующие преобразования.
Эта внутренняя структура интегральных преобразований типа Лапласа имеет значение, которое можно непосредственно применить к любой ситуации, выбрав соответствующее целое число . Основная цель данной статьи состоит в построении обобщенного вида интегральных преобразований типа Лапласа и установлении его свойств, и, насколько известно автору, предложенное -преобразование является первой попыткой обобщения интегральных преобразований типа Лапласа. Наконец, мы хотели бы отметить, что преобразование Лапласа дало много соображений этой статье.
Основная цель данной статьи состоит в построении обобщенного вида интегральных преобразований типа Лапласа и установлении его свойств, и, насколько известно автору, предложенное -преобразование является первой попыткой обобщения интегральных преобразований типа Лапласа. Наконец, мы хотели бы отметить, что преобразование Лапласа дало много соображений этой статье.
2. Свойства интегральных преобразований типа Лапласа
2.1. Определение и таблица обобщенного интегрального преобразования , Теоремы о сдвиге
Как упоминалось ранее, давайте перепишем определение интегрального преобразования типа Лапласа, и мы хотели бы назвать его -преобразованием.
Определение 1. Если интегрируемая функция определена для всех , ее обобщенное интегральное преобразование есть интеграл времен от до . Это функция, скажем, и обозначается ; таким образом
Сначала проверим теоремы о сдвиге.
Теорема 2. (1) (-сдвиг) Если имеет преобразование , то имеет преобразование То есть, (2) (-сдвиг) Если имеет преобразование , то сдвинутая функция имеет преобразование . В формуле для есть функция Хевисайда (мы пишем, так как нужно обозначать -пространство). Кроме того, держит.
В формуле для есть функция Хевисайда (мы пишем, так как нужно обозначать -пространство). Кроме того, держит.
Доказательство. Из получаем результат.
(2)Подставив , получим для is функцию Хевисайда.
Аналогичным образом у нас есть функция Хевисайда.
Используя для преобразования Лапласа , мы можем получить таблицу обобщенного интегрального преобразования, как показано в Таблице 1. В таблице мы рассматриваем интегральное преобразование типа Лапласа как преобразование. Однако мы можем выбрать подходящую константу в соответствии с каждой ситуацией. Например, выбор имеет значение в преобразованиях производных и имеет сильную сторону в преобразованиях интегралов.
Если определено и кусочно непрерывно на и удовлетворяет для всех , то существует для всех . Так как утверждение верно.
2.2. Преобразования производных и интегралов
Теорема 3. Пусть функция является -й дифференцируемой. Тогда преобразования первой, второй и -й производных удовлетворяют (1) (2) (3) для произвольное целое число. (4) Пусть кусочно непрерывна для и интегрируема. Тогда выполняется для .
(4) Пусть кусочно непрерывна для и интегрируема. Тогда выполняется для .
Доказательство. Интегрированием по частям и, аналогично, следует.
Продолжая этот процесс путем подстановки, как описано выше, и используя индукцию, следует (3). Давайте подробно установим справедливость утверждения (3) по математической индукции. Для , это ясно следует. Далее, мы предполагаем, что и мы показываем, что может быть выражено In утверждение , доказательство утверждения следует, применяя к .
Наконец, следует следующее.
Показать, что верно для . Используя теорему 3 и полагая , Более того, очевидно, удовлетворяет ограничению роста.
Проверим пример из [1] с помощью -преобразования.
Пример 4. Решить , , и .
Решение . Выполняя -преобразование с обеих сторон, имеем Организуя это равенство, имеем Упрощение дает Так как из таблицы 1 имеем решение для гиперболической функции. Из подстановки выше в точности решение данного уравнения. Конечно, простым вычислением приведенный выше ответ равен решению [1], которое равно .
Конечно, простым вычислением приведенный выше ответ равен решению [1], которое равно .
2.3. Свертка и интегральные уравнения для -преобразования
Хорошо известно, что и for является сверткой и . Это означает, что свертка связана с умножением преобразований в преобразовании Лапласа. Здесь мы исследуем изменение в -transform. Если две функции и интегрируемы, то имеет место следующая теорема.
Лемма 5 (теорема Лебега об мажорируемой сходимости (LDCT) [14]). Позвольте быть пространством с мерой и предположим, что это последовательность расширенных измеримых функций с действительным знаком, определенных на таком, что (a) существует -a.e. (b) существует интегрируемая функция такая, что для каждого , -п.в. Тогда интегрируема и
Заметим, что из приведенной выше леммы справедливо следующее равенство: for — неубывающая последовательность.
Теорема 6.
Доказательство. Положим и положим Тогда положим , где сначала константа. Тогда и так мы получаем Поскольку функция интегрируема, мы можем изменить порядок интегрирования, используя теорему Лебега о мажорируемой сходимости. Следовательно, и когда изменяется на , изменяется на . Отсюда общеизвестный факт, что свертка помогает нам решать интегральные уравнения определенного типа, в основном интегральное уравнение Вольтерра. Следовательно, мы хотели бы проверить теорему с помощью некоторых примеров, использующих -преобразование.
Тогда и так мы получаем Поскольку функция интегрируема, мы можем изменить порядок интегрирования, используя теорему Лебега о мажорируемой сходимости. Следовательно, и когда изменяется на , изменяется на . Отсюда общеизвестный факт, что свертка помогает нам решать интегральные уравнения определенного типа, в основном интегральное уравнение Вольтерра. Следовательно, мы хотели бы проверить теорему с помощью некоторых примеров, использующих -преобразование.
Пример 7. Решить интегральное уравнение Вольтерра второго рода
Решение . Это переписывается как свертка: выполнив -преобразование с обеих сторон и применив теорему 6, мы имеем для . Решение есть и дает ответ по таблице 1.
Пример 8. Решить интегральное уравнение Вольтерра второго рода
Решение . Как и в примере 7, данное уравнение такое же, как . Взяв -преобразование, мы имеем, следовательно, Упрощение дает, и поэтому мы получаем ответ по таблице 1.
Пример 9.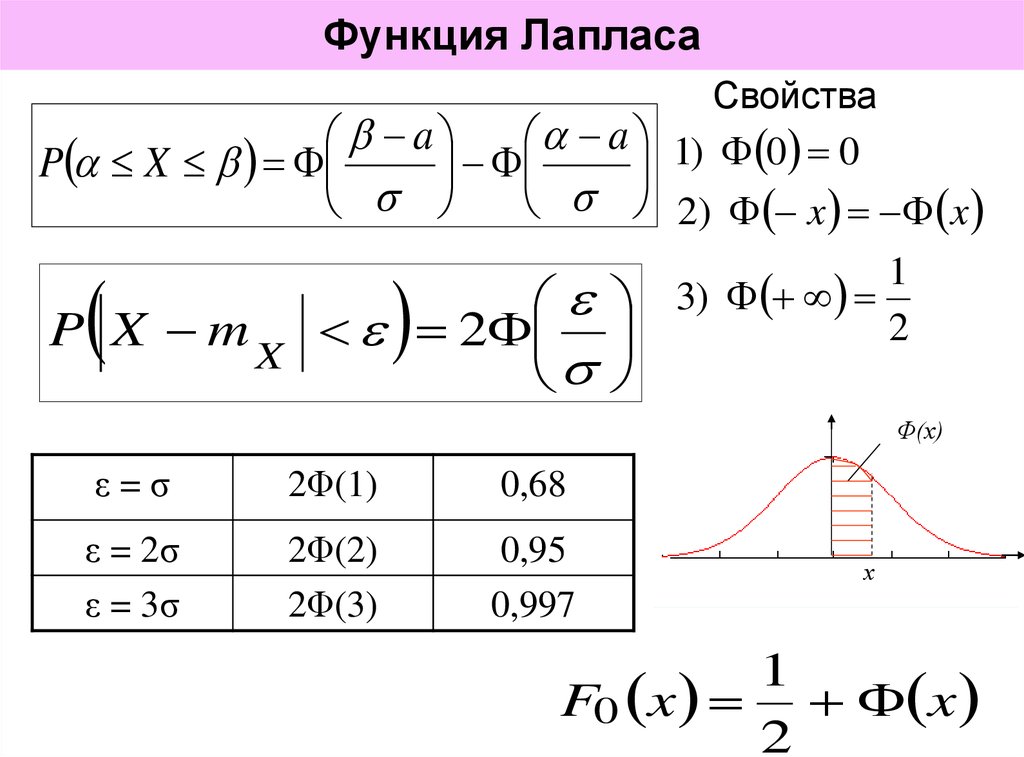 Найдите решение
Найдите решение
Решение . Так как это уравнение , принимая -преобразование с обеих сторон, мы имеем для . Таким образом, мы получаем решение.
Проверим это прямым вычислением. Расширяя данное уравнение, имеем Дифференцируя обе части дважды по , имеем . Таким образом, из и, полученного путем вычисления курса, имеем решение .
Точно так же мы можем легко получить решение интегральных уравнений, используя . Например, давайте рассмотрим с помощью -transform, у нас есть и, следовательно, у нас есть решение для . Конечно, этот результат такой же, как и при использовании свертки, и результат прямого вычисления такой же. Точно так же, поскольку решение . Здесь мы отмечаем, что -transform предназначен для .
3. Дифференцирование и интегрирование преобразований: ОДУ с переменными коэффициентами
Теорема 10. Положим . Затем (1) , (2) , (3) , (4) , , (5) .
Доказательство. (1) Поскольку для .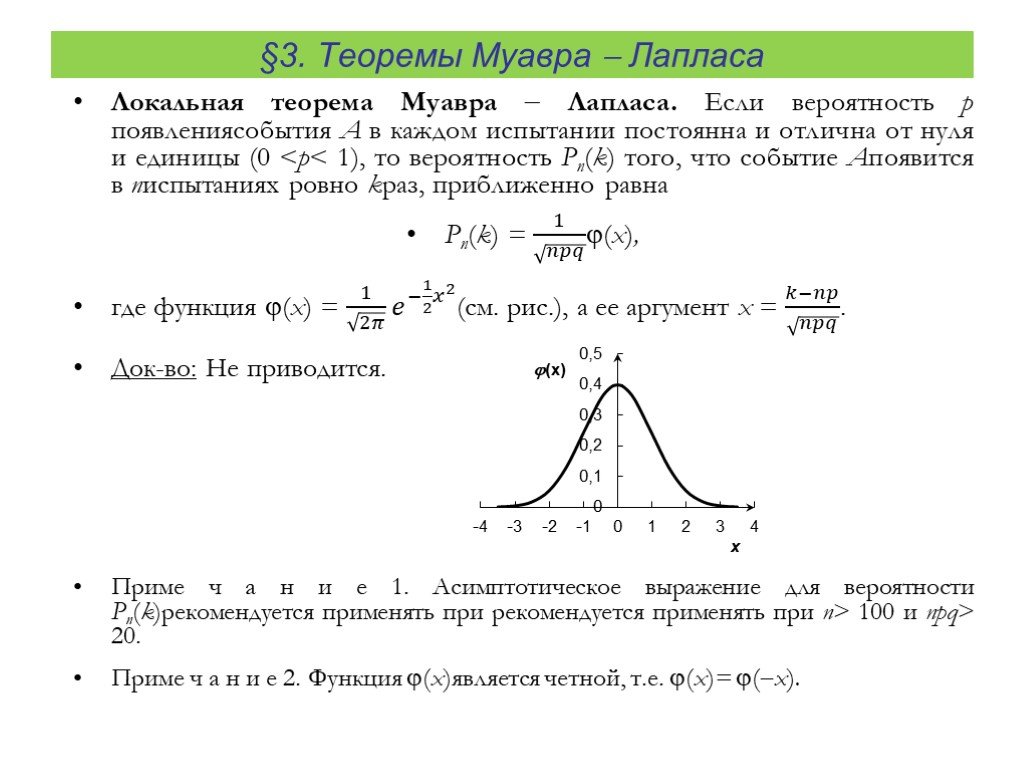
(2) Так как мы имеем Организуя это равенство, мы имеем (3) благодаря теореме Лебега о мажорируемой сходимости.
(4) В определение положим . Тогда Так как это то же самое, что и для .
В приведенной выше теореме отметим, что ее можно представить в виде (5) Из (4) утверждение выполняется для произвольного целого числа .
4. Преобразования функции Хевисайда и дельта-функции Дирака: задачи со сдвинутыми данными
4.1. Функция Хевисайда
, где функция Хевисайда.
4.2. Дельта-функция Дирака
Рассмотрим функцию тогда и иначе. Выполняя -преобразование, имеем Если обозначить предел как , то
4.3. Проблемы со сдвинутыми данными
Для заданных дифференциальных уравнений , , и , где и и являются постоянными, можно установить . Затем дает и так мы имеем для ввода. Выполнив преобразование, мы можем получить результат.
5. Решение полубесконечной строки с помощью -преобразования
Проверим решение полубесконечной строки с помощью -преобразования на типичном примере, приведенном в [1].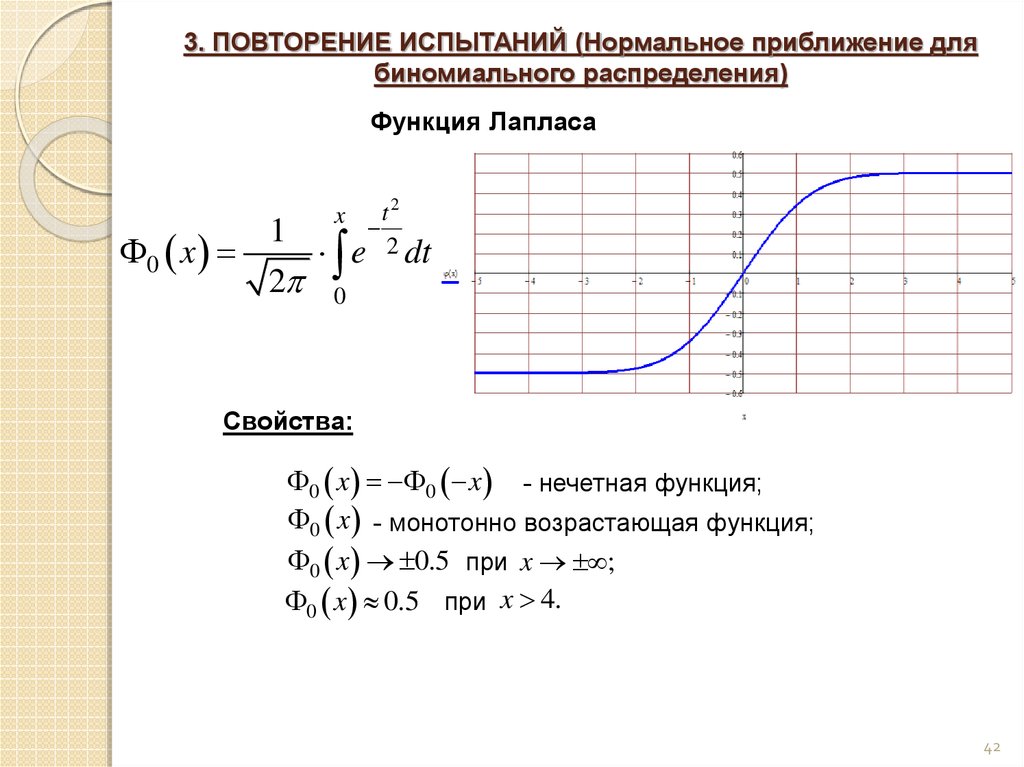
Пример 11 (полубесконечная строка). Найдите перемещение упругой струны при следующих условиях: (а) Струна изначально покоится на -оси от до . (б) При , левый конец струны перемещается заданным образом, а именно, согласно к одной синусоиде , если и ноль в противном случае. (c) Кроме того, как и для .
Конечно, бесконечной струны не существует, но наша модель описывает длинную струну или веревку (пренебрежимо малого веса), правый конец которой закреплен далеко на -оси [1].
Решение . Хорошо известно, что уравнение полубесконечной струны может быть выражено с учетом , as , и . Выполняя -преобразование относительно и по теореме 3, имеем для . С другой стороны, Таким образом, уравнение принимает вид Поскольку это уравнение можно рассматривать как ОДУ для рассматриваемой функции от , его общее решение можно представить в виде Из начальных условий имеем . В [15, 16] мы рассмотрели справедливость взаимозаменяемости интеграла и предела в процессе решения УЧП с помощью теоремы о мажорируемой сходимости.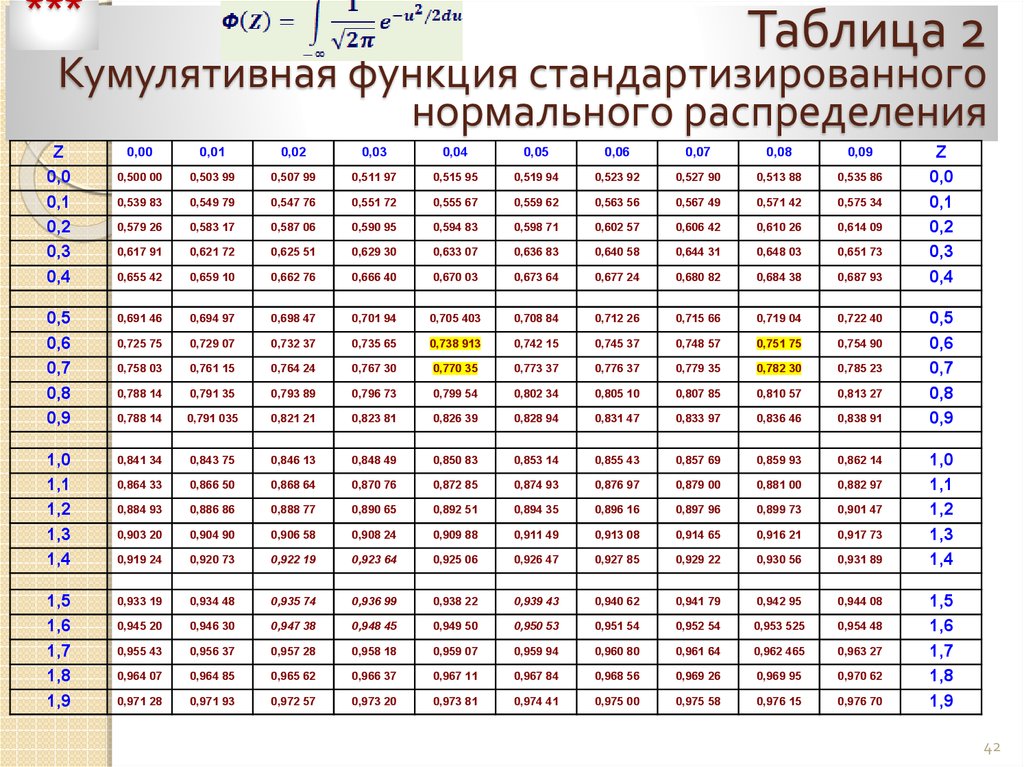 Следовательно, мы имеем в виду, что и так. Таким образом, По теореме -сдвига (теорема 2) получаем обратное преобразование для и нуль в противном случае, где — функция Хевисайда.
Следовательно, мы имеем в виду, что и так. Таким образом, По теореме -сдвига (теорема 2) получаем обратное преобразование для и нуль в противном случае, где — функция Хевисайда.
6. Заключение
В этой статье построена обобщенная форма интегральных преобразований типа Лапласа и установлены свойства обобщенного интегрального преобразования типа Лапласа, -преобразования. Преобразование является всеобъемлющей формой, и оно было хорошо адаптировано в ряде ситуаций инженерных задач путем выбора адекватных значений в ядре, и мы вновь представили значение, подходящее для преобразований интегралов. И дальнейшая работа заключается в том, чтобы найти другие значения, подходящие для каждой ситуации. Сильной стороной данной статьи является высокая применимость к инженерным задачам.
Конфликт интересов
Автор заявляет об отсутствии конфликта интересов в связи с публикацией этой статьи.
Благодарности
Это исследование было поддержано Исследовательским грантом Университета Кёндон.
Ссылки
E. Kreyszig, Advanced Engineering Mathematics , Wiley, Singapore, 2013.
G.K. Watugala, «Преобразование Сумуду — новое интегральное преобразование для решения дифференциальных уравнений и инженерных задач управления»0162 Международный журнал математического образования в области науки и технологий , том. 24, нет. 1, стр. 35–43, 1993.
Посмотреть по адресу:
Сайт издателя | ученый Google | MathSciNet
Т. М. Эльзаки, С. М. Эльзаки и Э. М. А. Хилал, «Преобразования Эльзаки и Сумуду для решения некоторых дифференциальных уравнений», Global Journal of Pure & Applied Mathematics , vol. 8, нет. 2, стр. 167–173, 2012.
Посмотреть по адресу:
Google Scholar
ХДж. Ким, «Теорема о сдвиге во времени и свертка для преобразования Эльзаки», Global Journal of Pure and Applied Mathematics , vol.
 87, стр. 261–271, 2013.
87, стр. 261–271, 2013.Просмотр по адресу:
Google Scholar
Ф. Б. Белгасем и С. Сивасундарам, «Новые разработки в вычислительных методах и приложения теории преобразования к нелинейным дробным и стохастическим дифференциальным уравнениям и системам, Нелинейные исследования. Международный журнал , том. 22, нет. 4, стр. 561–563, 2015.
Посмотреть по адресу:
Google Scholar | MathSciNet
Ф. Б. М. Белгасем и А. Карабалли, «Исследования и приложения фундаментальных свойств преобразования Сумуду», , Журнал прикладной математики и стохастического анализа, , том. 2006 г., ID статьи 91083, 23 страницы, 2006 г.
Посмотреть по адресу:
Сайт издателя | ученый Google | MathSciNet
Т. М. Эльзаки и Дж.
 Биазар, «Гомотопический метод возмущения и преобразование Эльзаки для решения системы нелинейных дифференциальных уравнений в частных производных», Всемирный журнал прикладных наук , том. 24, нет. 7, стр. 944–948, 2013 г.
Биазар, «Гомотопический метод возмущения и преобразование Эльзаки для решения системы нелинейных дифференциальных уравнений в частных производных», Всемирный журнал прикладных наук , том. 24, нет. 7, стр. 944–948, 2013 г.Посмотреть по адресу:
Сайт издателя | Google Scholar. 9, нет. 21–24, стр. 1065–1071, 2015.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Агва Х.А., Али Ф.М. и Киличман А. Новое интегральное преобразование во временных масштабах и его приложения, стр. 9.0162 Успехи в разностных уравнениях , vol. 60, стр. 1–14, 2012 г.
Посмотреть по адресу:
Сайт издателя | ученый Google | MathSciNet
H. Eltayeb и A. Kilicman, «О некоторых применениях нового интегрального преобразования», International Journal of Mathematical Analysis , vol.
 4, нет. 1–4, стр. 123–132, 2010 г.
4, нет. 1–4, стр. 123–132, 2010 г.Посмотреть по адресу:
Google Scholar | MathSciNet
Х. Эльтайеб, А. Киликман и М. Б. Джлели, «Преобразование дробного интеграла и его применение», Реферативный и прикладной анализ , vol. 2015 г., ID статьи 150863, 1 стр., 2015 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Ким Х., «Форма решения ОДУ с переменными коэффициентами с помощью интеграла и преобразования Лапласа», Global Journal of Pure and Applied Mathematics , vol. 12, pp. 2901–2904, 2016.
Просмотр по адресу:
Google Scholar
Ким Х., «Задачи со сдвигом данных с использованием преобразования производных», Прикладные математические науки , том. 8, нет. 149–152, стр. 7529–7534, 2014.

Посмотреть по адресу:
Сайт издателя | Google Scholar
D. L. Cohn, Measure Theory , Birkhäauser, Boston, Mass, USA, 1980. интеграла и предела в процессе решения УЧП», International Journal of Mathematical Analysis , том. 8, нет. 22, стр. 1089–1092, 2014.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Дж. Ян и Х. Ким, «Применение теоремы о монотонной сходимости в анализе частных чисел и анализе Фурье», Дальневосточный журнал математических наук, , том. 98, нет. 5, стр. 665–669, 2015.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Copyright
Copyright © 2017 Hwajoon Kim. Эта статья находится в открытом доступе и распространяется в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.

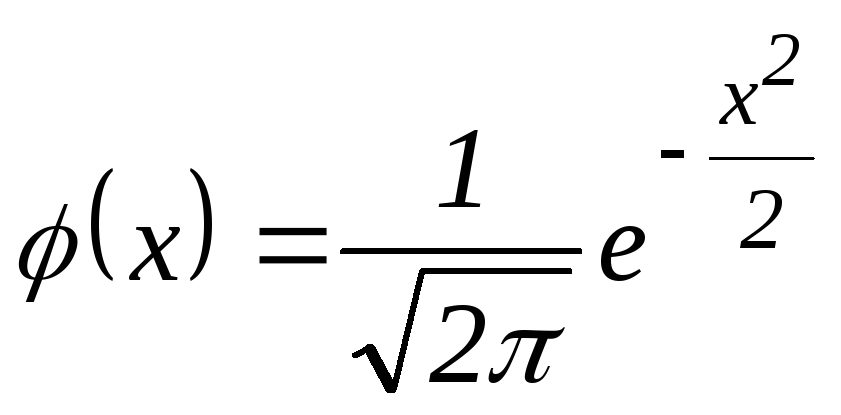 phys.uvic.ca/~tatum/elmag.html
phys.uvic.ca/~tatum/elmag.html