Метод зейделя онлайн: Метод Зейделя онлайн

Решить систему методом зейделя онлайн. Метод зейделя решения слау

1. Преобразовать систему к виду одним из описанных способов.

2. Задать начальное приближение решения произвольно или положить , а также малое положительное число (точность). Положить .

3. Произвести расчеты по формуле (1)или (2) и найти .

(1)

4. Если выполнено условие окончания , процесс завершить и в качестве приближенного решения задачи принять . Иначе положить и перейти к пункту 3.

Решение систем нелинейных уравнений (СНУ).

Запишем систему n нелинейных уравнений с n неизвестными (СНУ) в общем виде:

f 1 (x 1 , x 2 , …, x n) = 0

f 2 (x 1 , x 2 , …, x n) = 0 (5.1)

f n (x 1 , x 2 , …, x n) = 0

Эту систему можно записать в компактной, операторной форме:

вектор-функция

вектор неизвестных

Решением системы называется набор значений ,(векторX *), при которых все функции f i равны 0 (система (5. 1) обращается в тождество.)

СНУ могут иметь единственное решение, множество решений или вообще не иметь его. Поэтому численное решение СНУ проводят в два этапа:

1 этап – отделение решений.

2 этап – уточнение всех или только нужных решений.

Отделить решения – значит установить количество решений, определить приближенные значения каждого из них или указать область, в которой решение существует и является единственным.

Задача отделения решений достаточно просто решается только для системы двух уравнений с двумя неизвестными.

f 1 (x 1 , x 2) = 0

f 2 (x 1 , x 2) = 0

Для этого необходимо в координатах (x 1 , x 2) построить кривые

f 1 (x 1 ,х 2) = 0, f 2 (x 1 ,х 2) = 0.

Точки пересечения этих кривых являются решениями системы . Так как координаты точек пересечения определяются приближенно, целесообразно говорить об области существования решения D. Эта область задается интервалами по каждой координате, внутри которых находятся искомые значения неизвестных.

Имеется два решения.

D 1 – область существования первого решения.

D 1 = {a 1

Графическое отделение решений СНУ.

Для систем с большим числом неизвестных (n  3) удовлетворительных общих методов определения области существования решения нет. Поэтому при решении СНУ эта область обычно определяется при анализе решаемой задачи, например, исходя из физического смысла неизвестных.

Отделение решений позволяет:

Выявить число решений и область существования каждого из них.

Проанализировать возможность применения выбранного метода решения СНУ в каждой области.

Выбрать начальное приближение решения X (0) из области его существования, так что X (0) D.

При отсутствии информации об области существования решения СНУ выбор начального приближения X (0) проводиться методом проб и ошибок (методом “тыка”).

Постановка задачи.

Требуется решить систему нелинейных уравнений . В координатном виде эту задачу можно записать так: , где 1 ≤ k ≤ n .

Убедиться в существовании решения и количестве корней, а также выбрать нулевое приближение в случае системы двух уравнений с двумя неизвестными можно, построив графики функций в удобных координатах. В случае сложных функций можно посмотреть поведение аппроксимирующих их полиномов. Для трех и более неизвестных, а также для комплексных корней, удовлетворительных способов подбора начального приближения нет.

Метод простых итераций.

Как и в случае одного уравнения, метод простых итераций заключается в замене исходной системы уравнений

f 1 (x 1 , x 2 , …, x n) = 0

f 2 (x 1 , x 2 , …, x n) = 0

f n (x 1 , x 2 , …, x n) = 0 (5.1)

эквивалентной системой X=Φ(X) –(5.3) и построении итерационной последовательности

(5.4)-X (k) = Φ(X (k -1)) , где k=1,2,3,… — номер итерации,которая при k→∞ сходится к точному решению.

Здесь — итерирующая вектор-функция, X (0) D – начальное приближение решения.

В развернутом виде формула итерационного процесса (выражение для вычисления очередного k-го приближения решения) имеет вид:

x i. (k) = φ i (x 1 (k-1) , x 2 (k-1) , … , x n (k-1)), .(5.5)

Условие окончания расчета

δ≤ε (5.6)

где ε  заданная точность решения;

δ = (5.7)

Итерационный процесс (5.5) сходиться к точному решению, если в окрестности решения соблюдаются условия сходимости:

Таким образом, для уточнения решения СНУ методом простых итераций нужно найти такое эквивалентное преобразование (5.1) в (5.3), чтобы в области существования решения выполнялись условия (5.9) или (5.10).

В простейшем случае эквивалентную систему можно получать как.

Метод Зейделя (второе название — Гаусса-Зейделя) — это классический интернациональный метод, при помощи которого можно решать различные системы Сейчас мы расскажем об этом более детально.

Суть работы

Данный способ является своеобразной упрощенной модификацией метода Якоби. Инновация состоит в том, что новое значение (і) используется сразу же после получения, а не после очередной итерации. Помимо этого, четко определены условия сходимости и окончания, нарушение которых приведет к неправильному ответу уравнения. Метод Зейделя, пример которого мы предоставили на картинке, не только упрощает процесс решения, но также ускоряет его. Поэтому он активно используется программистами для создания и решения сложных систем.

Метод Зейделя. «Паскаль»

Ни одна программист не обходится без математических формул и уравнений. А это значит, что метод Зейделя активно используется в программе «Паскаль» для получения опыта роботы с базовыми элементами. Выглядит все довольно-таки просто: в листе программы создается новый документ, с самого начала вводится условие уравнения и его границы, затем объясняются дополнительные сменные элементы (при условии их наличия), после этого прописывается проверка на совместимость. Если она положительна, то выводится сам алгоритм решения, а уже потом вывод могут включать несколько этапов решения, каждая часть которого имеет свой алгоритм, обязательные составные, сменные элементы и базовые формулы. Все это записывается исключительно на английском языке, без возможных аналогов. Решение уравнения будет выводиться в виде готовой формулы или числа после сохранения всех данных.

«С++»

Метод Зейделя также широко используется в программе «С++», но здесь все совсем иначе, чем в «Паскале». Уравнение в «С++» начинается не с условия всей задачи, а с условия окончания, которое прописывается в три-четыре этапа с конечным выводом результата. Далее прописывается сам ход решения при помощи данного метода, детально описывая все неизвестные, после чего выводится формула для того, чтобы доказать равенство между двумя результатами уравнения. Условием есть то, что каждое значение предыдущего является необходимым для решения последующего. Учетные записи здесь также ведутся на английском языке, который заменить невозможно. «С++» значительно сложнее «Паскаля», поэтому, не имея базовых знаний, ее не следует использовать изначально.

Подведем итоги

Итак, метод Зейделя — это специальный способ, благодаря которому можно решать системы линейных уравнений любой сложности. Чаще всего он является базовым для таких программ, как «Паскаль» и «С++». Это своеобразная улучшенная модификация метода Якоби, которая исключает вариант использования дополнительных формул, но при этом имеет четкие условия сходимости и окончания. Строго установленные критерии упрощают весь процесс работы, так как в случае невыполнения одного из условий программа, будь то или «Паскаль», или «С++», просто-напросто откажется от дальнейшего решения задачи.

Одним из самых распространенных итерационных методов, отличающийся простотой и легкостью программирования, является метод Гаусса –Зейделя .

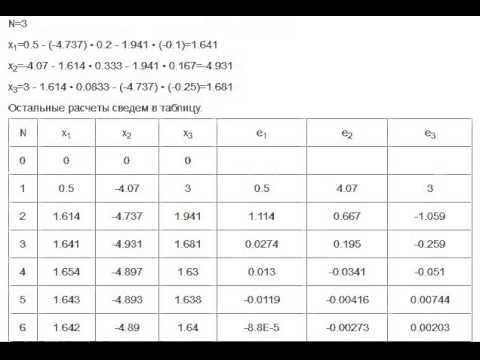
Проиллюстрируем сначала этот метод па примере решения системы

Предположим, что диагональные элементы а 11, а 22, а 33отличны от нуля (в противном случае можно переставить уравнения). Выразим неизвестные х 1, х 2и х 3 соответственно из первого, второго и третьего уравнений системы (2.27):

(2.28)

(2.29)

(2. 30)

Зададим некоторые начальные (нулевые) приближения значений неизвестных: Подставляя эти значения в правую часть выражения (2.28), получаем новое (первое) приближение для х 1:

Используя это значение для x 1 и приближение для х3 , находим из (2.29) первое приближение для

х2 :

И наконец, используя вычисленные значения находим с помощью выражения (2.30) первое приближение для х 3:

На этом заканчивается первая итерация решения системы (2.28) — (2.30). Теперь с помощью значений х 1(1), х 2(1)и х 3(1)можно таким же способом провести вторую итерацию, в результате которой будут найдены вторые приближения к решению: х 1 = х 1 (2), х 2 = х 2(2)и х 3 = х 3(2)и т.д.

Приближение с номером k можно вычислить, зная приближение с номером k – 1, как

Итерационный процесс продолжается до тех пор, пока значения х 1(k), х 2(k)и х 3(k)не станут близкими с заданной погрешностью к значениям х 1(k-1), х 2(k-1)и х 3(k-1).

Пример. Решить с помощью метода Гаусса – Зейделя следующую систему уравнений:

Легко проверить, что решение данной системы следующее: х 1 = х 2 = х 3 = 1.

Решение . Выразим неизвестные х 1, х 2и х 3соответственно из первого, второго и третьего уравнений:

В качестве начального приближения (как это обычно делается) примем х 1= 0, х 2 = 0, х 3 = 0. Найдем новые приближения неизвестных:

Аналогично вычислим следующие приближения:

Итерационный процесс можно продолжать до получения малой разности между значениями неизвестных в двух последовательных итерациях.

Рассмотрим теперь систему п линейных уравнений с п неизвестными. Запишем ее в виде

Здесь также будем предполагать, что все диагональные элементы отличны от нуля. Тогда в соответствии с методом Гаусса – Зейделя k -e приближение к решению можно представить в виде

Итерационный процесс продолжается до тех пор, пока все значения не станут близкими к , т.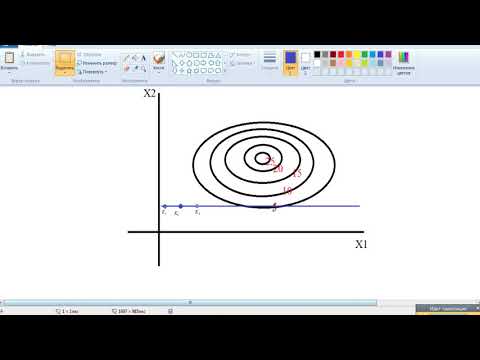

е. критерием завершения итераций является одно из условий (2.21) – (2.24).

Для сходимости итерационного процесса (2.31) достаточно, чтобы модули диагональных коэффициентов для каждого уравнения системы были не меньше сумм модулей всех остальных коэффициентов (преобладание диагональных элементов):

(2.32)

При этом хотя бы для одного уравнения неравенство должно выполняться строго. Эти условия являются достаточными для сходимости метода, но они не являются необходимыми, т.е. для некоторых систем итерации сходятся и при нарушении условий (2.32).

Алгоритм решения системы п линейных уравнений методом Гаусса – Зейделя представлен на рис.2.6. В качестве исходных данных вводят п, коэффициенты и правые части уравнений системы, погрешность ε, максимально допустимое число итераций М, а также начальные приближения переменных

xi (i =1,2,…,n ).Отметим, что начальные приближения можно не вводить в компьютер, а полагать их равными некоторым значениям (например, нулю). Критерием завершения итераций выбрано условие (2.22), в котором через δ обозначена максимальная абсолютная величина разности и :

Для удобства чтения структурограммы объясним другие обозначения: k — порядковый номер итерации; i – номер уравнения, а также переменного, которое вычисляется в соответствующем цикле; j – номер члена вида или в правой части соотношения (2.31). Итерационный процесс прекращается либо при δ , либо при k = М. В последнем случае итерации не сходятся, о чем выдается сообщение. Для завершения цикла, реализующего итерационный процесс, используется переменная l , которая принимает значения 0, 1 и 2, соответственно, при продолжении итераций, при выполнении условия

δ и при выполнении условия k = М .

Рис. 2.6. Алгоритм решения системы n линейных уравнений методом Гаусса–Зейделя

Отчет по

ЧИСЛЕНННЫМ МЕТОДАМ

Выполнил: студент

Сулейманова Д. И.

Проверила: доцент каф. хим.

кибернетики Кошкина Л.Ю.

Казань, 2012

Тема 1. «Численное решение систем линейных алгебраических уравнений». 3

Постановка задачи. 3

Прямые (точные) методы.. 3-4

Итерационные методы.. 5

Листинг программ. 4

Результаты.. 5

Выводы.. 5

Список литературы.. 5

ТЕМА 2. «ЧИСЛЕННОЕ РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ»

Постановка задачи

Решить систему линейных алгебраических уравнений:

0,5	1,7	0,3		-0,24
1,6	1,5	-2,3		4,3
3,7	-2,5	3,2		6,5

0,5х 1 +1,7х 2 +0,3х 3 =-0,24

1,6х 1 +1,5х 2 -2,3х 3 =4,3

3,7х 1 -2,5х 2 +3,2х 3 =6,5

Для решения уравнения использовали следующие методы:

1. метод обратной матрицы,

2. метод Крамера,

3. метод Гаусса,

4. метод простых итераций,

5. метод Гаусса-Зейделя.

Решение:

Прямые (точные) методы

1) Метод обратной матрицы: (х=А -1 *В – формула данного метода, где В-вектор свободных членов, А -1 -обратная функция)

А) Для реализации данного метода в электронных таблицах воспользовались математической функцией =МОБР(А1:С3) для определения коэффициента А:

0,3

4,3 1,5 -2,3 6,5 -2,5 3,2 0,5 -0,24
Ввод n, a, b FOR k=1 TO n-1 FOR i=k+1 TO n m=a ik /a kk FOR j=k+1 TO n a ij =a ij -m*a kj b i =b i -m*b k x n =b n /a nn FOR i=n-1 TO 1 шаг — 1 FOR j=i+1 TO n S=∑a ij *x i x i =(b i -s)/a ii Печать x i

Прямой ход

Обратный ход

Выбор главного элемента и перестановка уравнений

1) Метод простых итераций:

А) Выразим х 1 , х 2 , х 3 из уравнений главного определителя, тогда получим:

x 1 =(b 1 -a 12 x 2 -a 13 x 3)/a 11

x 2 =(b 2 -a 21 x 1 -a 23 x 3)/a 22

x 3 =(b 3 -a 31 x 1 -a 32 x 2)/a 33

Б) Зададим начальное (нулевое) приближение x 1 (0) , x 2 (0) , x 3 (0) . Подставляя их, получаем новое приближение.

В) Обозначим k-номер итерации, тогда для n уравнений итерационные формулы можно записать так:

x i (k) = (k-1))

Итерации проводятся до тех пор, пока не будет выполнено условие

|x i (k)-x i (k-1) |

2) Метод Гаусса-Зейделя:

Этот метод представляет собой модификацию метода простых итераций, когда на k-той итерации при j

x i (k) = (k) — (k-1))

Итерационный процесс продолжается до тех пор, пока не будет выполнено условие

|x i (k)-x i (k-1) |

Если условие не выполняется, итерации повторяются, приняв x i (k-1) = x i (k)

Алгоритм метода Гаусса-Зейделя

n-количество уравнений; e-точность; a(n,n)-массив коэффициентов; b(n)-массив свободных членов; x(n)-массив решения. Вводится начальное приближение x(n).

Листинг программ

Sub metod_g()

Dim a(1 To 3, 1 To 3)

a(i, j) = Worksheets(«Лист2»).Cells(i, j). Value

b(i) = Worksheets(«Лист2»).Cells(i, 5).Value

For k = 1 To n — 1

For i = k + 1 To n

If Abs(a(i, k)) > Abs(a(g, k)) Then g = i

z = a(g, j): a(g, j) = a(k, j): a(k, j) = z

z = b(g): b(g) = b(k): b(k) = z

For i = k + 1 To n

m = a(i, k) / a(k, k)

For j = k + 1 To n

a(i, j) = a(i, j) — m * a(k, j)

b(i) = b(i) — m * b(k)

x(n) = b(n) / a(n, n)

For i = n — 1 To 1 Step -1

For j = i + 1 To n

s = s + a(i, j) * x(j)

x(i) = (b(i) — s) / a(i, i)

Worksheets(«Лист2»).Cells(i, 9).Value = x(i)

Sub MPI_SLAY()

Dim a(1 To 3, 1 To 3)

x2 = (b(2) — a(2, 1) * x10 — a(2, 3) * x30) / a(2, 2)

x3 = (b(3) — a(3, 1) * x10 — a(3, 2) * x20) / a(3, 3)

Loop While c > e

With Worksheets(«Лист2»)

Range(«J1»).Value = x1

Range(«J2»).Value = x2

Range(«J3»).Value = x3

Range(«J5»).Value = k

Sub GausZeid()

Dim a(1 To 3, 1 To 3)

a(i, j) = Worksheets(«Лист3»). Cells(i, j).Value

b(i) = Worksheets(«Лист3»).Cells(i, 5).Value

x10 = 0: x20 = 0: x30 = 0

x1 = (b(1) — a(1, 2) * x20 — a(1, 3) * x30) / a(1, 1)

x2 = (b(2) — a(2, 1) * x1 — a(2, 3) * x30) / a(2, 2)

x3 = (b(3) — a(3, 1) * x1 — a(3, 2) * x2) / a(3, 3)

c = Abs(x1 — x10) + Abs(x2 — x20) + Abs(x3 — x30)

Loop While c > e

With Worksheets(«Лист2»)

Range(«K1»).Value = x1

Range(«K2»).Value = x2

Range(«K3»).Value = x3

Range(«K5»).Value = k

Для запуска программ нажать на кнопку или на Run .

Полученный результат находится на Листе 2.

Результаты

Выводы

Системы линейных алгебраических уравнений можно решать как с помощью прямых, так и итерационных методов. Для систем уравнений средней размерности чаще используют прямые методы.

Итерационные методы применяют главным образом для решения задач большой размерности, когда использование прямых методов невозможно из-за ограничений в доступной оперативной памяти ЭВМ или из-за необходимости выполнения чрезмерно большого числа арифметических операций.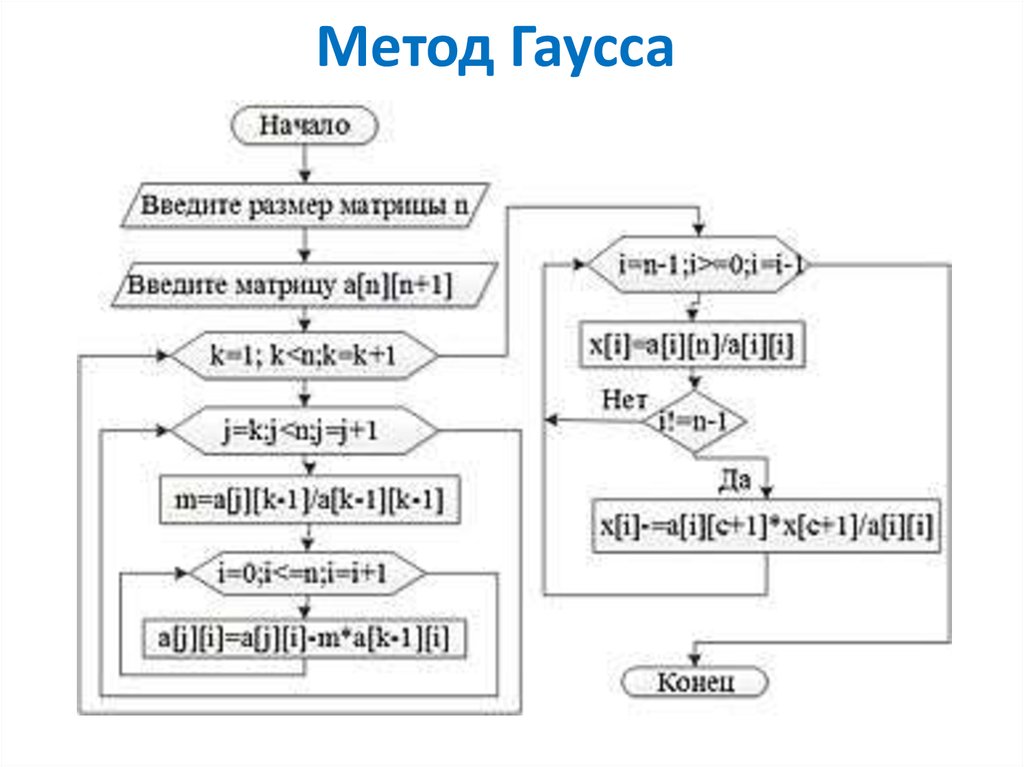

В данной работе мы рассмотрели 5 методов решения линейных алгебраических уравнений: метод обратной матрицы, Крамера, Гаусса, простой итерации и Гаусса-Зейделя. Первые 3 метода составляют группу прямых методов. Это аналитические методы, в них отсутствует погрешность метода, но погрешность вычислений неизбежна. Тем не менее, методы обратной матрицы и Крамера достаточно просты в алгоритме, тем более нами было найдено решение трехмерной матрицы (небольшая размерность), значения неизвестных сошлись. Что касается метода Гаусса, алгоритм данного метода достаточно громоздкий. Каждая следующая формула вычисления коэффициентов при преобразовании матрицы содержит результат предыдущей формулы, а значит и ее ошибку при вычислении. Наибольшее влияние на эту ошибку оказывает величина знаменателя (коэффициенты главной диагонали) – она не должна быть равна 0 и малой по абсолютной величине. В нашем случае таких предпосылок нет, метод Гаусса был осуществлен с выбором главного элемента, что дает малые невязки.

Можей Н.П. преподавание методов оптимизации с применением электронных обучающих материалов

УДК 378:51

Преподавание методов оптимизации с применением электронных обучающих материалов

Можей Н.П.

Белорусский государственный университет информатики и радиоэлектроники, Минск, Республика Беларусь, Этот e-mail адрес защищен от спам-ботов, для его просмотра у Вас должен быть включен Javascript

Применение электронных обучающих материалов обусловлено возможностью предоставления образовательных услуг независимо от времени и места, управления темпом обучения, быстрой актуализации учебных материалов, оперативного контроля успеваемости. Целью работы является анализ особенностей дистанционного обучения методам оптимизации и возможностей реализации целей и задач преподавания дисциплины при подготовке электронных материалов.

Для дистанционной работы требуется обеспечить студентов учебно-методическим комплексом [1] (УМК), созданным на основе мультимедийных технологий. Электронный учебно-методический комплекс по дисциплине (ЭУМКД) – это программный комплекс, включающий учебные, научные и методические материалы, методику изучения дисциплины средствами информационно- коммуникационных технологий и обеспечивающий условия для осуществления учебной деятельности. Основными принципами формирования элементов ЭУМКД являются: дискретизация (модульность), наглядность, иерархическая структура и ветвление, регулирование, адаптивность, компьютерная поддержка, универсальность, совместимость. ЭУМКД выполнен с использованием web-технологий, предусмотрена навигация по материалам ЭУМКД, обеспечивающая возможность быстрого поиска информации, переход из одного раздела в другой, использование гиперссылок. Материалы для наполнения УМК проходят предварительную апробацию с участием обучаемых как очно, так и дистанционно, что позволяет дифференцировать сложность материала с учётом индивидуальных возможностей учащихся.

Основными элементами ЭУМКД являются: титульный экран, рабочая учебная программа дисциплины, теоретический раздел, практический раздел, блок контроля знаний. Базовым принципом реализации такой модели обучения является модульность. Курс разбивается на ряд законченных модулей, информация структурируется в виде графа, вершины которого соответствуют тематическим разделам, а ребра – отношениям между ними, т.е. закладывается последовательность, этапность и системность обучения. Представление материала в виде графа позволяет связывать новые понятия с существующими, что улучшает понимание, и обеспечивать индивидуальный темп обучения. Наличие модулей глубины и полноты изложения материала позволяет индивидуализировать работу и предоставить студенту большую самостоятельность в изучении материала. Теоретический раздел состоит из логически завершенных учебных модулей – единиц ЭУМКД, содержащих необходимую и достаточную информацию для изучения отдельного раздела дисциплины. Наиболее важный материал выделяется, его знание позволяет осваивать другие блоки курса, а также другие предметы, использующие наработанный аппарат. Четкое разграничение материала по уровням трудности и выделение обязательного поля знаний является мощным стимулом и дополнительной мотивацией к обучению не только для хорошо успевающих студентов, но и для тех, кому трудно усваивать достаточно абстрактный материал по методам оптимизации.

Теоретический раздел представлен в виде электронного конспекта лекций, иллюстрирован вставками, наглядно представляющими и объясняющими излагаемый материал. Практический раздел содержит примеры практического решения задач, предназначенные для овладения умениями и навыками, повторения и закрепления пройденного материала. Подраздел «Лабораторный практикум» включает методические материалы к лабораторным работам –методические указания по выполнению, снабжённые иллюстрациями и объясняющие основные этапы подготовки к выполнению, непосредственного практического выполнения и анализа полученных результатов. Как и обычное аудиторное занятие, лабораторное занятие, содержащееся в ЭУМКД, начинается с контрольных вопросов. Если обучаемый испытывает затруднения в ответе на них, он возвращается к теоретической части курса. Кроме того, в практической части ЭУМКД содержатся индивидуальные задания по всем основным разделам изучаемого курса. Студент, изучив некоторую тему по теоретическому материалу и закрепив полученные знания практическими занятиями, может пройти тест. Контролирующие задания касаются основных узловых проблем дисциплины. Подраздел «Контрольные работы» включает перечни заданий для контроля и рекомендации по выполнению заданий. В учебно-методических пособиях приведены алгоритмы выполнения заданий контрольной работы, примеры их выполнения, вопросы для самопроверки. Весь блок контроля знаний ЭУМКД содержит комплекс тестирующих и контролирующих средств: тесты, контрольные вопросы, контрольные задания, обеспечивающие возможность студенту оценить уровень освоения тем, разделов и дисциплины в целом, а также задания текущей и итоговой аттестации.

Поскольку современные техника, наука, экономика, финансы существенно используют экстремальные свойства процессов и систем, большое внимание уделяется созданию автоматизированных систем планирования, проектирования и управления в различных областях народного хозяйства. На первый план выдвигаются вопросы качества принимаемых решений, в связи с чем возрастает роль методов и алгоритмов решения оптимизационных задач в математическом обеспечении систем различного уровня и назначения. Поэтому достижения в теории оптимизации — в математическом программировании, теории управления — находят различные области применения. Целью преподавания дисциплины «Методы оптимизации» является изучение математического аппарата и методов решения экстремальных задач, возникающих в практической деятельности, задач оптимального управления, распределения ресурсов, организации производства, сетевого планирования, теории игр и др.; подготовка специалистов, владеющих систематизированными знаниями, имеющих определенный уровень математической подготовки и обладающих необходимыми навыками по методам оптимизации. Задачами изучения методов оптимизации являются: выработка навыков по применению методов оптимизации и алгоритмов решения прикладных задач на профессиональном уровне; подготовка студентов к их внедрению; приобретение знаний по линейной оптимизации, включая задачи распределения ресурсов, элементы теории двойственности, оптимизации поставок, размещения и концентрации производства; по применению методов оптимизации в теории игр, в сетевом планировании и управлении; приобретение знаний по нелинейной оптимизации и ее приложениям, в том числе по поисковым методам одномерной и многомерной, локальной и глобальной, условной и безусловной оптимизации; овладение элементами многокритериальной оптимизации и динамического программирования. В результате изучения дисциплины студент должен научиться моделировать оптимизационные задачи; проводить анализ результатов; корректировать результат при изменении исходных данных; овладеть навыками выбора подходящих методов оптимизации и их применения.

Обучение дистанционно, с применением электронных обучающих материалов, – не синоним заочной формы обучения, ибо здесь предусматривается постоянный контакт с преподавателем, с другими студентами, имитация очного обучения, но специфичными формами. Предлагаемый студентам для такого обучения материал призван помочь им в изучении основных методов решения оптимизационных задач, а также при выполнении индивидуальных заданий по курсу «Методы оптимизации». В современной литературе описано большое число методов решения оптимизационных задач, все их изложить невозможно. Поэтому в ЭУМКД включены основные из наиболее эффективных и важных с методологической точки зрения методов. Сначала приводятся классические методы решения оптимизационных задач, основанные на использовании дифференциального исчисления для нахождения точек экстремумов функций. Далее рассматривается одна из оптимизационных задач, обладающих единым методом решения – задача с линейной целевой функцией и линейными ограничениями. Эта глава посвящена основам линейного программирования. Здесь же подробно описан и процесс построения математической модели. На примере задачи с двумя переменными описано графическое решение задачи линейного программирования. Большое внимание в данной главе уделено практическим вопросам — изучению алгоритмов решения и решению конкретных задач линейного программирования с использованием компьютера. В частности, имеются весьма эффективные средства поиска оптимальных решений в Microsoft Excel и других пакетах. Далее глава посвящена разбору транспортной задачи, начиная с самых общих вопросов и заканчивая такими, как несбалансированные, многопродуктовые, двухэтапные транспортные задачи с различными ограничениями. Также вводятся задачи о назначениях и методы их решения. Рассматривается применение линейного программирования в теории игр, в сетевом планировании и управлении. Следующие разделы посвящены методам одномерной минимизации, широко применяемым на практике в качестве составной части методов поиска экстремумов функций многих переменных. Отдельно рассматриваются численные методы безусловной оптимизации и численные методы условной оптимизации (алгоритм равномерного поиска, деления пополам, Фибоначчи, золотого сечения, метод квадратичной аппроксимации, метод Пауэлла, методы на основе поиска стационарной точки критерия оптимальности, метод перебора, одномерный метод Монте-Карло, метод выделения интервалов унимодальности, метод аппроксимирующих моделей). Также разбирается многомерная локальная безусловная оптимизация. Отдельно выделены детерминированные прямые методы (метод Гаусса-Зейделя, Хука-Дживса, Метод Розенброка, сопряженных направлений, симплекс-метод, метод деформируемого многогранника Нелдера-Мида), детерминированные методы первого и второго порядков (метод наискорейшего спуска, дробления шага, метод оптимизации Ньютона) и методы случайного поиска (метод с возвратом при неудачном шаге, метод наилучшей пробы, метод комплексов, метод повторяющегося случайного поиска, случайного поиска с постоянным радиусом поиска и случайными направлениями) и др. При изучении многомерной локальной условной оптимизации разбираются методы последовательной безусловной оптимизации, скользящего допуска, модифицированный метод комплексов, метод линейной аппроксимации, метод проекции градиента. Например, комбинацию метода проекции градиента и градиентного метода с дроблением шага иллюстрирует рисунок 1, на котором показан фрагмент линий уровня функции Химмельблау.

Многомерная глобальная условная оптимизация включает методы сведения к совокупности вложенных задач глобальной одномерной минимизации, сведения к задаче одномерной глобальной оптимизации с помощью развертки Пеано, метод Монте-Карло. Например, комбинацию метода сведения к совокупности вложенных одномерных задач с методом случайного поиска для двумерной задачи иллюстрирует рисунок 2, где принято, что X* — точка минимума функции Ф(X) в области D после (r – 1)-ой итерации.

Также рассматриваются задачи многокритериальной оптимизации и методы их решения (метод весовых множителей решения задачи многокритериальной оптимизации, эпсилон-ограничений решения задачи многокритериальной оптимизации, справедливого компромисса, приближения к идеальному решению, последовательных уступок для решения задач многокритериальной оптимизации). Отдельная глава посвящена задачам оптимального управления и методам их решения, в частности, рассматриваются принцип максимума Понтрягина, метод динамического программирования Беллмана с примерами применения. В каждом разделе даны краткая характеристика рассматриваемых методов, основные рабочие формулы и алгоритмы решения оптимизационных задач, применение алгоритмов иллюстрируется примерами, тестовые же задания снабжены ответами. Текущий контроль осуществляется также в форме контрольных работ, представляемых студентом и принимаемых преподавателем дистанционно. Опыт проведения текущего контроля и сессий выявил определенное различие в степени проработанности отдельных разделов в электронной форме, однако полученные по результатам тестирования результаты сопоставимы с получаемыми студентами очно. Таким образом, электронный обучающий комплекс разработан так, чтобы помочь быстро и эффективно изучить методы оптимизации.

Для повышения эффективности дистанционного обучения в БГУИР внедрена система дистанционного обучения (СДО), созданная на платформе Microsoft Office, позволяющая легко найти требуемую информацию и людей, а, в случае, если пользователь находится онлайн, тут же обратиться к нему как с текстовым сообщением, так и организовав сеанс аудио- или видео-связи [2]. Система позволяет преподавателю отслеживать статистику посещаемости курса, можно просматривать статистическую информацию о времени, которое пользователь проводит в курсе, и детальный отчет по статистике для каждого раздела курса. Извещения предназначены для передачи информации, при необходимости создается извещение, которое увидят остальные участники курса, оно содержит, кроме текста, ключевые слова, дату начала и срок действия. Календарь курса представляет собой органайзер, планируется график консультаций, зачётов, экзаменов. Информация отображается на домашней странице. Почтовый ящик позволяет посылать и получать сообщения по электронной почте. СДО также включает систему тестирования, позволяющую организовать уникальную выборку вопросов с вариантами ответов, что обеспечивает интерактивный подход к обучению. Вопросы наряду с текстом содержат изображения (область допустимых планов, градиент, линии уровня, фрагменты вычислительных таблиц). Важным аспектом является периодичность контроля знаний. Опыт преподавания на дневной форме обучения показывает, что трёх контрольных точек в течение семестра вполне достаточно для составления объективной оценки об уровне знаний студента по методам оптимизации. Раздел «документы» — хранилище файлов, которые учащиеся могут просматривать или сохранять. Раздел «форум» предназначен для того чтобы пользователи могли обмениваться сообщениями, обсуждать различные темы и оставлять комментарии, предназначен только для курса «Методы оптимизации». Преподаватель может просматривать, отвечать и редактировать обсуждения форума. Форум позволяет отслеживать информацию о темах, обсуждаемых пользователем, обсуждениях, в которых пользователь принимает участие, ответах, которые добавляет пользователь и т.д. В целях общения между учениками и учителем создан чат (в частности, для проведения онлайн консультаций). Преимуществами СДО являются, во-первых, разработка на платформе Microsoft, что дает возможность использования дополнительных опций этой платформы. Во-вторых, полная интеграция со всеми продуктами Microsoft, что позволяет избежать конфликтов с дополнительным программным обеспечением. В-третьих, наличие встроенного модуля для проведения online конференций, вебинаров. Все необходимые инструменты для создания и редактирования контента также встроены в СДО. Планирование и мониторинг учебного процесса (встроенные инструменты СДО) позволяют создавать структурированную систему представления учебного материала, получать наглядные отчеты по успеваемости пользователей. СДО позволяет автоматизировать процесс, создать единую базу электронных учебных материалов, доставить учебный материал обучающимся, эффективно управлять им, автоматизировать процесс формирования и сбора отчетов. Специфика применения этой системы в образовательном процессе в том, что наибольшая методическая нагрузка преподавателя появляется на подготовительной стадии, когда требуется лекции и лабораторные занятия перевести в электронную форму, адаптированную под программы дистанционного обучения [3, 4]. Опыт использования дистанционной формы обучения выявил возможности повышения эффективности образовательного процесса: использование ЭУМКД, получение учебных материалов в электронном виде, проведение консультаций посредством электронной почты, чатов, форумов, представление студентами результатов обучения по электронной почте.

Поддержание учебно-методического обеспечения на современном уровне интенсифицирует образовательный процесс, позволяет улучшить качество и повысить эффективность обучения, оптимизировать организацию учебного процесса.

Список литературы

1. Григорьев, С.Г. Разработка концепции образовательных электронных изданий и ресурсов/ С.Г. Григорьев [и др.] // Открытое и дистанционное образование, 2002. — № 3.

2. Батура М.П., Никульшин Б.В., Цветков В.Ю. Высококачественная видеоконференц-связь в системе дистанционного обучения БГУИР // Университетское образование: сборник статей XV Международной научно-методической конференции (г. Пенза, 6–7 апреля 2011 г.) / под ред. В. И. Волчихина, Р. М. Печерской. – Пенза: Изд-во ПГУ, 2011. – 486 с.

3. Демкин, В.П. Принципы и технологии создания электронных учебников / В.П.Демкин, В.М. Вымятин. — Томск: Издательство ТГУ, 2002. — 84 с.

4. Краснова, Г.А. Технологии создания электронных обучающих средств / Г. А.Краснова, М.И. Беляев, А.В. Соловов. — М.: МГИУ, 2001. — 224 с.

Калькулятор метода Гаусса-Зейделя с решением

Используйте этот онлайн-калькулятор метода Гаусса-Зейделя, который позволяет решить систему линейных одновременных уравнений. Вы также можете вычислить значения, относящиеся к задачам метода Гаусса-Зейделя, используя наш онлайн-калькулятор метода мощности за доли секунды.

Что такое метод Гаусса-Зейделя?

«Метод, в котором первая заданная система линейных уравнений приводится в диагонально доминирующую форму, называется методом Гаусса-Зейделя» 9-1(b-Uxk)

Где

• L* = нижняя треугольная матрица
• U = верхняя треугольная матрица

Нижняя треугольная матрица:

«Если все элементы выше главной диагонали равны нулю, это называется нижней треугольной матрицей»

A = \left[\begin{array}{ccc} 2 & 0 & 0 \ \ 1 & 5 & 0 \\ 1 & -1 & -2 \end{array}\right]

Верхняя треугольная матрица:

A = \left[\begin{array}{ccc} 2 & -1 & 3 \\ 0 & 5 & 2\\ 0 & 0 & -2 \end{array}\right]

Итеративный алгоритм Гаусса-Зейделя Алгоритм метода:

Давайте обсудим алгоритм итеративного метода Гаусса-Зейделя относительно коэффициента переменных. Ниже приведены шаги, чтобы вычислить его легко.

• Сначала запустите процесс
• После этого нужно привести заданную систему линейных уравнений в диагонально доминирующую форму.
• После прочтения проверить ошибку (e).
• Преобразование первого уравнения в терминах первой переменной, второго уравнения в терминах второй переменной и так далее.
• После преобразования переменных установите начальные предположения для x_0, y_0, z_0 и т. д.
• Подставьте значение y_0, z_0 … из шага 5 в первое уравнение, полученное из шага 4, чтобы оценить новое значение x1_. Используйте x_1, z_0, u_0…. во втором уравнении, полученном на шаге 4, для вычисления нового значения y1. Точно так же используйте x_1, y_1, u_0…, чтобы найти новый z_1 и так далее.
• Если| х0 – х1| > е и | у0 – у1| > е и | z0 – z1| > e
  и т. д., затем перейдите к шагу 9.
• Установите x_0=x_1, y_0=y_1, z0=z1 и т. д. и перейдите к шагу 6. ​​
• Вывести значение x_1, y_1, z_1 и т.  д.
• Наконец, остановите процесс и получите результаты.

Кроме того, наш онлайн-калькулятор метода Гаусса-Зейделя также поддерживает алгоритм итеративного метода Гаусса-Зейделя, и вы можете рассчитать его за пару секунд.

Метод Гаусса-Зейделя Пример: 9-1b

$$ \begin{bmatrix}783061,99 \\ -696054,33 \\\end{bmatrix} $$

x_1 = 783061,99
x_2 = -696054,33

\bmatrix $

{

{ 0 & 2 \\ 0 & 0 \\\end{bmatrix} $$

Нижняя треугольная компонента T

$$ \begin{bmatrix} 1 & 0 \\ 8 & 9 \\\end{bmatrix} $$

Инверсия L*-1

$$ \begin{bmatrix} 1 & 0 \\ -0,89 & 0,11 \\\end{bmatrix} $$

Расчет T 9{(19)}= \begin{bmatrix} 0 & -2 \\ 0 & 1,78 \\\end{bmatrix} \times \begin{bmatrix} 440469,308 \\ -391527,496 \\\end{bmatrix} + \begin{ bmatrix}7 \\ -5,44 \\\end{bmatrix} = \begin{bmatrix} 783061,991 \\ -696054,326 \\\end{bmatrix} $$

рассчитать значения метода Гуасса-Зейделя за доли секунды.

Как работает калькулятор метода Гаусса-Зейделя?

Этот онлайн-калькулятор метода мощности позволяет выполнять расчеты, просто вводя следующие данные:
Ввод:

• Сначала введите количество уравнений (2 или 3)
• После этого введите значения коэффициентов для уравнений
• Просто нажмите кнопку «Рассчитать»

Выходы:

Калькулятор метода Гаусса-Зейделя вычисляет следующие результаты:

• Обратный L-1*
• Расчет Т
• Расчет C
• Применить алгоритм Гаусса-Зейделя

Вы также можете рассчитать разрешающие системы уравнений с помощью калькулятора исключения Гаусса.

Часто задаваемые вопросы:

Является ли метод Гаусса-Якоби итерационным методом?

Да, Гаусс-Якоби или метод Якоби обычно представляют собой итерационный метод, который используется для решения уравнений диагонально доминирующей системы линейных уравнений. И вы можете рассчитать значения метода Гаусса-Зейделя по отношению к итеративному методу, используя этот калькулятор метода Гаусса-Зейделя

В чем разница между методами Якоби и Гаусса-Зейделя?

Разница между методами Якоби и Гаусса-Зейделя заключается в том, что в методе Якоби значения переменных не изменяются до следующей итерации. В то время как в методе Гаусса-Зейделя значения переменных изменяются, как только рассматривается новое значение. Вы можете рассчитать значения метода Гаусса-Зейделя с помощью нашего калькулятора метода Гаусса-Зейделя

Какой итерационный метод более эффективен: метод Якоби или метод Гаусса-Зейделя?

Метод Гаусса-Зейделя более эффективен по сравнению с методом Якоби, поскольку метод Гаусса-Зейделя требует меньшего количества итераций для объединения фактического решения с определенной степенью точности. Мы предоставляем вам онлайн-калькулятор метода Гаусса-Зейделя, чтобы быстро выполнять расчеты, связанные с методом Гаусса-Зейделя.

В чем недостаток метода Якоби?

Недостаток метода Якоби состоит в том, что после оценки измененного значения переменной на текущей итерации оно не используется до следующей итерации. Проще говоря, значение всех переменных, используемых в текущей итерации, взято из предыдущей итерации, что увеличивает количество итераций для достижения точного решения.

В чем разница между методом исключения Гаусса и методом Гаусса-Зейделя?

Исключение Гаусса — это прямой метод, а метод Гаусса-Зейделя — итерационный метод. Эти два метода отличаются друг от друга и обычно используются для разных целей.

Когда применим метод Гаусса-Зейделя?

Метод Гаусса-Зейделя применим, если он следует строго диагонально доминирующим или симметрично определенным матрицам.

Заключение:

Метод Гаусса-Зейделя обычно используется для нахождения уравнений линейной системы. Этот метод дан и назван немецкими учеными Карлом Фридрихом Гауссом и Филиппом Людвигом Зиделем. В общем случае метод Гаусса-Зейделя применим, если итерациями необходимо решить n линейных уравнений с неизвестными переменными. Этот метод очень прост и вычисляет значения с помощью нашего онлайн-калькулятора метода Гаусса-Зейделя за пару шагов.

Ссылки:

Из Википедии: Метод Гаусса-Зейделя, Алгоритм, Примеры
Из источника sciencedirect.com: Итерационные методы решения, Решение системы линейных алгебраических уравнений

Метод Гаусса-Зейделя, Якоби Метод — Обмен файлами

Теперь вы подписаны на эту отправку

• Вы будете видеть обновления в ленте отслеживаемого контента
• Вы можете получать электронные письма, в зависимости от ваших предпочтений в общении

Версия 1.0.0.0 (29,4 КБ) от Бхартенду

Итерационные методы Якоби и Гаусса-Зейделя

9,4 тыс. загрузок За все время: 9 387″ data-original-title=»Загрузки» aria-describedby=»popover506129″>

Обновлено 29 мая 2017 г.

Посмотреть лицензию

• Обзор
• Функции
• Примеры
• История версий
• Отзывы (21)
• Обсуждения (6)

См.: https://www3.nd.edu/~zxu2/acms40390F12/Lec-7.3.pdf
Метод Якоби:
Итерационный метод Якоби представляет собой алгоритм нахождения решений диагонально доминирующей системы линейных уравнений. Выполняется поиск каждого диагонального элемента и подставляется приблизительное значение. Затем процесс повторяется до тех пор, пока не сойдется.

Метод Гаусса–Зейделя:
Метод Гаусса-Зейделя, также известный как метод Либмана или метод последовательного смещения, представляет собой итерационный метод, используемый для решения линейной системы уравнений.

Цитировать как

Бхартенду (2023). Метод Гаусса-Зейделя, метод Якоби (https://www.mathworks.com/matlabcentral/fileexchange/63167-gauss-seidel-method-jacobi-method), центральный файловый обмен MATLAB. Проверено 26 января 2023 г. .

Совместимость версий MATLAB

Создано с помощью R2014a

Совместимость с любой версией

Совместимость с платформами

Windows macOS Linux

Категории

• МАТЛАБ > Математика > Линейная алгебра >

Метки Добавить теги

метод гаусса-зайделя-якоби линейная алгебра живой сценарий система линейных …

Community Treasure Hunt

Найдите сокровища в MATLAB Central и узнайте, как сообщество может вам помочь!

На охоту!

Версия	Опубликовано	Примечания к выпуску
1. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт