|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Основы обеспечения единства измерений: Обеспечение единства измерений — деятельность метрологических служб, направленная на достижение… Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие… Интересное: Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны… Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления… Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом. Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
Стр 1 из 2Следующая ⇒ Определение гиперболических синусов, косинусов, тангенсов и котангенсов Графики гиперболических функций Свойства 3. Чётность Разность квадратов Формулы суммы и разности аргументов Формулы произведений гиперболического синуса и косинуса Формулы суммы и разности гиперболических функций Формулы производных Формулы интегралов Формулы неравенства Формулы разложения в степенные ряды Появление названия «гиперболическая функция» Применение гиперболических функций.
Гиперболи́ческие фу́нкции — семейство элементарных функций, выражающихся через экспоненту и тесно связанных с тригонометрическими функциями. Гиперболические функции были введены Винченцо Риккати (Vincenzo Riccati) в 1757 году («Opusculorum», том I). Он получил их из рассмотрения единичной гиперболы. Цель данной работы – изучить гиперболические функции и их применение.
Определения гиперболических синусов, косинусов, тангенсов и котангенсов Гиперболическим синусом называется функция:
Гиперболическим тангенсом называется функция: Гиперболическим котангенсом называется функция: Гиперболическим секансом и косекансом называется функции: , .
Свойства 3.1) Связь (сумма) sin iz = i sh z ; cos iz = ch z Применяя эти формулы к тригонометрическим функциям, получаем формулы, связывающие гиперболические функции. Чётность sh(–x) = – sh x; ch(–x) = ch x. Функция ch(x) – четная. Функции sh(x), th(x), cth(x) – нечетные. Разность квадратов ch2 x – sh2 x = 1. Формулы производных
Формулы интегралов Формулы неравенства Для всех выполняется: Определение гиперболических синусов, косинусов, тангенсов и котангенсов 12Следующая ⇒ Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни. Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)… |
Формулы приведения как пользоваться. Изменение синуса, косинуса и тангенса при возрастании угла
С центром в точке A .
α — угол, выраженный в радианах.
Определение
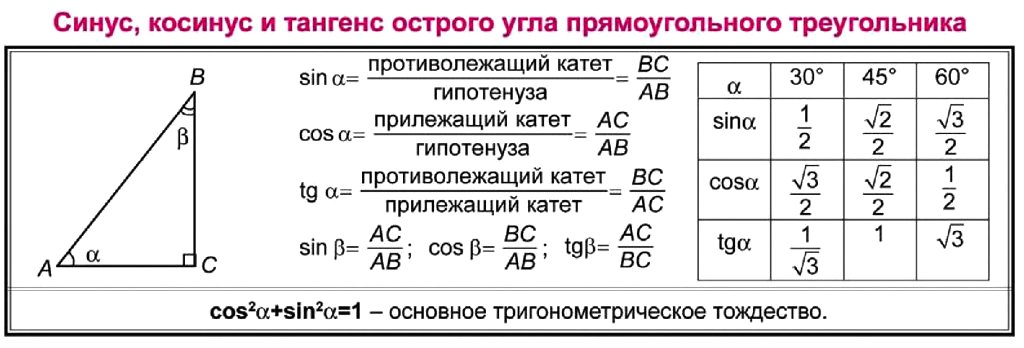
Синус (sin α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус — нечетная. Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| — ∞ | — ∞ | |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
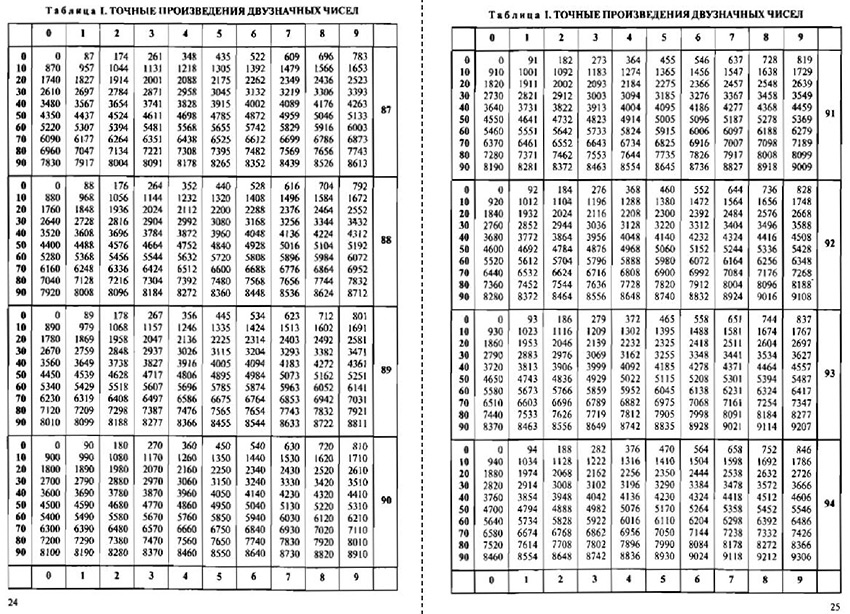
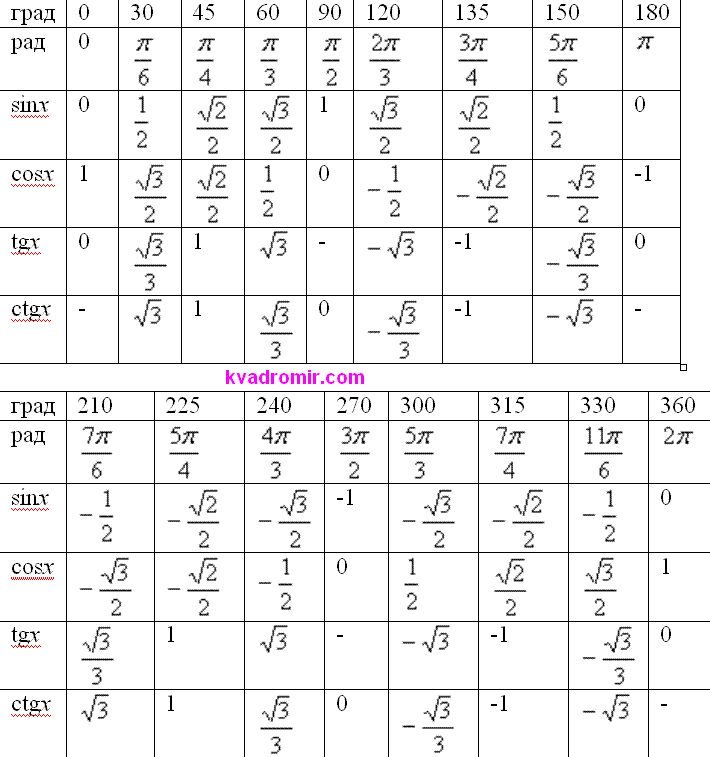
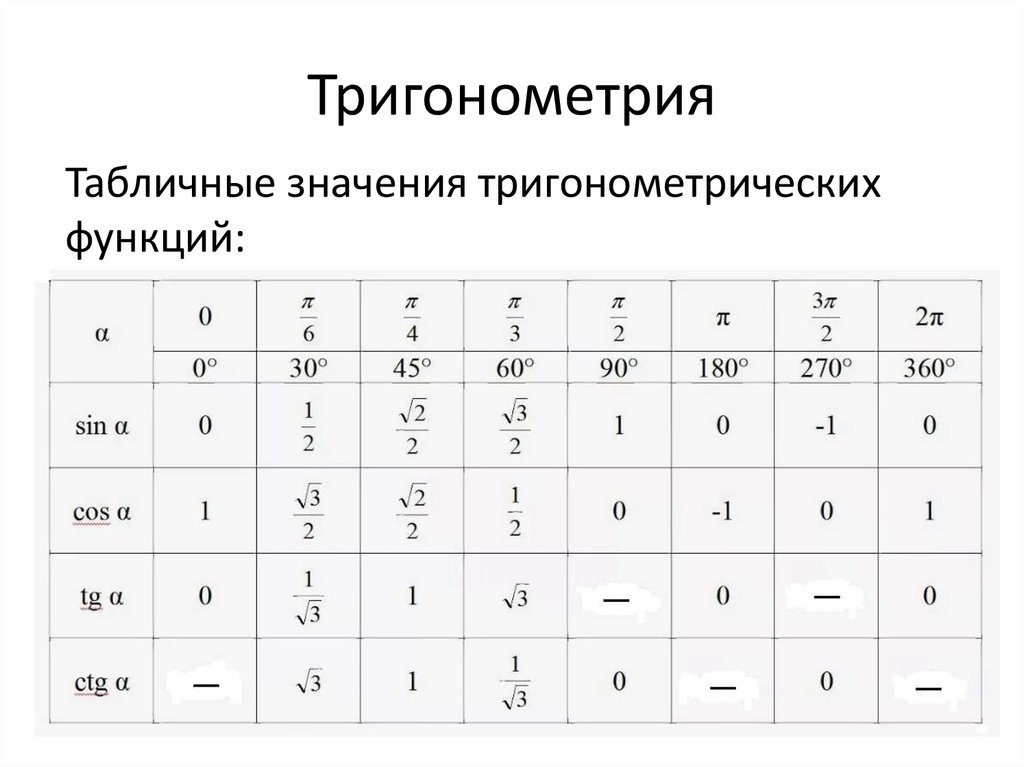
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Тригонометрия.Формулы приведения.
Формулы приведения не нужно учить их нужно понять. Понять алгоритм их вывода. Это очень легко!
Понять алгоритм их вывода. Это очень легко!
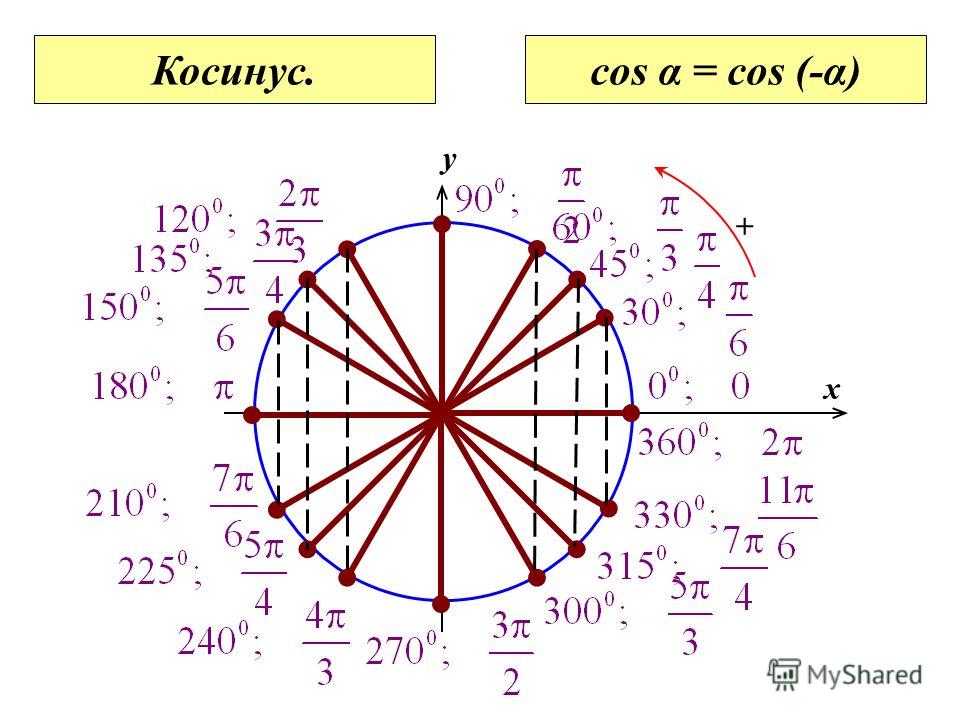
Возьмем единичную окружность и расставим все градусные меры (0°; 90°; 180°; 270°; 360°) на ней.
Разберем в каждой четверти функции sin(a) и cos(a).
Запомним, что функцию sin(a) смотрим по оси Y, а функцию cos(a) по оси X.
В первой четверти видно, что функция sin(a)>0
И функция cos(a)>0
Первую четверть можно описать через градусную меру, как (90-α) или (360+α).
Во второй четверти видно, что функция sin(a)>0 , потому что ось Y положительна в этой четверти.
А функция cos(a) , потому что ось X отрицательна в этой четверти.
Вторую четверть можно описать через градусную меру, как (90+α) или (180-α).
В третьей четверти видно, что функции sin(a) Третья четверть можно описать через градусную меру, как (180+α) или (270-α).
В четвертой четверти видно, что функция sin(a) , потому что ось Y отрицательна в этой четверти.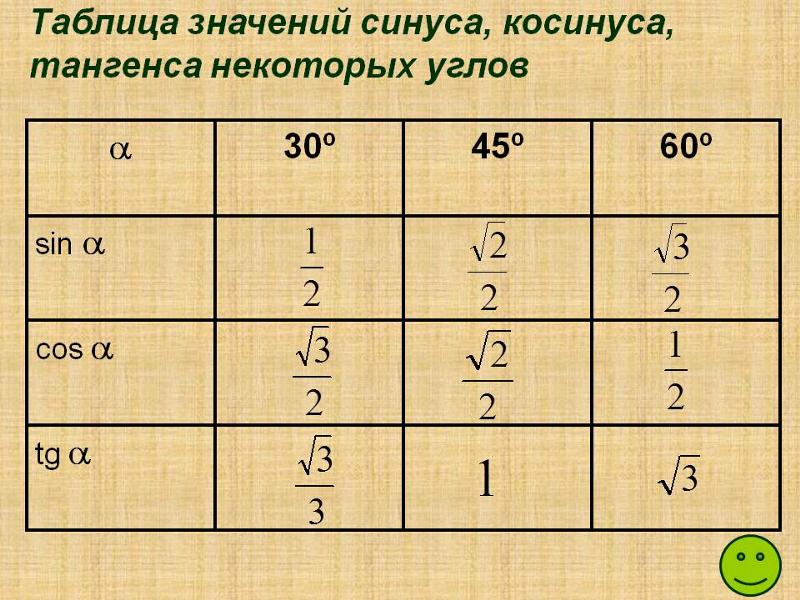
А функция cos(a)>0 , потому что ось X положительна в этой четверти.
Четвертую четверть можно описать через градусную меру, как (270+α) или (360-α).
Теперь рассмотрим сами формулы приведения.
Запомним простой алгоритм :
1. Четверть. (Всегда смотрите в какой вы четверти находитесь).
2. Знак. (Относительно четверти смотрите положительны или отрицательный функции косинуса или синуса).
3. Если у вас есть в скобочках (90° или π/2) и (270° или 3π/2), то функция меняется .
И так начнем разбирать по четвертям данный алгоритм.
Выясни чему будет равно выражение cos(90-α)
Рассуждаем по алгоритму:
1. Четверть первая.
Будет cos(90-α) = sin(α)
Выясни чему будет равно выражение sin(90-α)
Рассуждаем по алгоритму:
1. Четверть первая.
Будет sin(90-α) = cos(α)
Выясни чему будет равно выражение cos(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.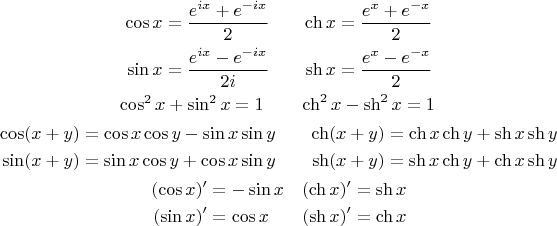
2. В первой четверти знак у функции косинуса положительный.
Будет cos(360+α) = cos(α)
Выясни чему будет равно выражение sin(360+α)
Рассуждаем по алгоритму:
1. Четверть первая.
2. В первой четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(360+α) = sin(α)
Выясни чему будет равно выражение cos(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.
3. В скобочках есть (90° или π/2), то функция меняется с косинуса на синус.
Будет cos(90+α) = -sin(α)
Выясни чему будет равно выражение sin(90+α)
Рассуждаем по алгоритму:
1. Четверть вторая.
3. В скобочках есть (90° или π/2), то функция меняется с синуса на косинус.
Будет sin(90+α) = cos(α)
Выясни чему будет равно выражение cos(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции косинуса отрицательный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет cos(180-α) = cos(α)
Выясни чему будет равно выражение sin(180-α)
Рассуждаем по алгоритму:
1. Четверть вторая.
2. Во второй четверти знак у функции синуса положительный.
3. В скобочках нет (90° или π/2) и (270° или 3π/2), то функция не меняется.
Будет sin(180-α) = sin(α)
Рассуждаю про третью и четвертую четверть подобным образом составим таблицу:
Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.
Они относятся к разделу «тригонометрия» в математике. Суть их заключается в приведении тригонометрических функций углов к более «простому» виду. О важности их знания написать можно много. Этих формул аж 32 штуки!
Не пугайтесь, учить их не надо, как и многие другие формулы в курсе математики. Лишней информацией голову забивать не нужно, необходимо запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить!!!» – это значит, что действительно, это необходимо именно выучить.
Кстати, когда я пишу в статьях «… нужно выучить!!!» – это значит, что действительно, это необходимо именно выучить.
Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.
Перечислю лишь некоторые задачи, которые будут на ЕГЭ по математике, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:
– задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.
– задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.
– задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.
– стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.
И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.
Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?
Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от 0 до 450 градусов:
угол альфа лежит пределах от 0 до 90 градусов
* * *
Итак, необходимо уяснить «закон», который здесь работает:
1. Определите знак функции в соответствующей четверти.
Напомню их:
2. Запомните следующее:
функция изменяется на кофункцию
функция на кофункцию не изменяется
Что означает понятие — функция изменяется на кофункцию?
Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.
Вот и всё!
Теперь по представленному закону запишем несколько формул приведения самостоятельно:
Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:
Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:
Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов, значит:
Вот вам ещё дополнительное подтверждение того, что синусы смежных углов равны:
Угол лежит во второй четверти, синус во второй четверти положителен. Не меняем функцию на кофункцию, так как у нас 180 градусов, значит:
Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.
***
В статье на решение был отмечен такой факт – синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём.
Тема урока
- Изменение синуса, косинуса и тангенса при возрастании угла.
Цели урока
- Познакомиться с новыми определениями и вспомнить некоторые уже изученные.
- Познакомится с закономерностью изменений значений синуса косинуса и тангенса при возрастании угла.

- Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
- Воспитательные — посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.
Задачи урока
- Проверить знания учащихся.
План урока
- Повторение ранее изученного материала.
- Задачи на повторение.
- Изменение синуса, косинуса и тангенса при возрастании угла.
- Практическое применение.
Повторение ранее изученного материала
Начнем с самого начала и вспомним то что будет полезно освежить в памяти. Что же такое синус, косинус и тангенс и к какому разделу геометрии относятся эти понятия.
Тригонометрия — это такое сложное греческое слово: тригонон — треугольник, метро — мерять. Стало быть по-гречески это означает: мерятся треугольниками.
Предмети > Математика > Математика 8 класс
Урок и презентация на тему: «Применение формул приведения при решении задач»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса
1С: Школа. Интерактивные задания на построение для 7-10 классов
1С: Школа. Решаем задачи по геометрии. Интерактивные задания на построение в пространстве для 10–11 классов
Что будем изучать:
1. Немного повторим.
2. Правила для формул приведения.
3. Таблица преобразований для формул приведения.
4. Примеры.
Повторение тригонометрических функций
Ребята, с формулами привидения вы уже сталкивались, но так их еще не называли. Как думаете: где?
Посмотрите на наши рисунки. Правильно, когда вводили определения тригонометрических функций.
Правило для формул приведения
Давайте введем основное правило: Если под знаком тригонометрической функции содержится число вида π×n/2 + t, где n – любое целое число, то нашу тригонометрическую функцию можно привести к более простому виду, которая будет содержать только аргумент t. Такие формулы и называют формулами привидения.
Такие формулы и называют формулами привидения.
Вспомним некоторые формулы:
- sin(t + 2π*k) = sin(t)
- cos(t + 2π*k) = cos(t)
- sin(t + π) = -sin(t)
- cos(t + π) = -cos(t)
- sin(t + π/2) = cos(t)
- cos(t + π/2) = -sin(t)
- tg(t + π*k) = tg(x)
- ctg(t + π*k) = ctg(x)
формул привидения очень много, давайте составим правило по которому будем определять наши тригонометрические функции при использовании формул привидения :
- Если под знаком тригонометрической функции содержатся числа вида: π + t, π — t, 2π + t и 2π — t, то функция не изменится, то есть, например, синус останется синусом, котангенс останется котангенсом.
- Если под знаком тригонометрической функции содержатся числа вида: π/2 + t, π/2 — t,
3π/2 + t и 3π/2 — t, то функция изменится на родственную, т. е. синус станет косинусом, котангенс станет тангенсом. - Перед получившийся функцией, надо поставить тот знак, который имела бы преобразуемая функция при условии 0
Эти правила применимы и когда аргумент функции задан в градусах!
Так же мы можем составить таблицу преобразований тригонометрических функций:
Примеры применения формул приведения
1. Преобразуем cos(π + t). Наименование функции остается, т.е. получим cos(t). Далее предположим, что π/2
Преобразуем cos(π + t). Наименование функции остается, т.е. получим cos(t). Далее предположим, что π/2
2. Преобразуем sin(π/2 + t). Наименование функции изменяется, т.е. получим cos(t). Далее предположим что 0 sin(t + π/2) = cos(t)
3. Преобразуем tg(π + t). Наименование функции остается, т.е. получим tg(t). Далее предположим, что 0
4. Преобразуем ctg(270 0 + t). Наименование функции изменяется, то есть получим tg(t). Далее предположим что 0
Задачи с формулами приведения для самостоятельного решения
Ребята, преобразуйте самостоятельно, используя наши правила:
1) tg(π + t),
2) tg(2π — t),
3) ctg(π — t),
4) tg(π/2 — t),
5) ctg(3π + t),
6) sin(2π + t),
7) sin(π/2 + 5t),
8) sin(π/2 — t),
9) sin(2π — t),
10) cos(2π — t),
11) cos(3π/2 + 8t),
12) cos(3π/2 — t),
13) cos(π — t).
перевод на английский, синонимы, антонимы, примеры предложений, значение, словосочетания
Согласно нему квадратный корень носа равен сумме синусов больше семи. | It states that the square root of the proboscis equals the sum of the sinuses over seven. |
Это было самое раннее известное использование угла падения и самое раннее практическое применение закона синусов . | This was the earliest known use of dip angle and the earliest practical use of the law of sines. |
Лимфа поступает в выпуклую сторону лимфатического узла через многочисленные афферентные лимфатические сосуды и оттуда перетекает в ряд синусов . | Lymph enters the convex side of a lymph node through multiple afferent lymphatic vessels and from here flows into a series of sinuses. |
Но некоторые ученые не верят, что таблица синусов Арьябхаты имеет какое-либо отношение к таблице аккордов Гиппарха, которая не существует сегодня. | But some scholars do not believe Āryabhaṭa’s sine table has anything to do with Hipparchus’s chord table which does not exist today. |
Закон синусов может быть обобщен на более высокие размеры на поверхностях с постоянной кривизной. | The law of sines can be generalized to higher dimensions on surfaces with constant curvature. |
Ниже приведены примеры того, как решить задачу с помощью закона синусов . | The following are examples of how to solve a problem using the law of sines. |
Закон синусов принимает подобную форму при наличии кривизны. | The law of sines takes on a similar form in the presence of curvature. |
В гиперболической геометрии, когда кривизна равна -1, закон синусов становится. | In hyperbolic geometry when the curvature is −1, the law of sines becomes. |
Согласно Убиратану Д’Амброзио и Хелен Селин, сферический закон синусов был открыт в 10 веке. | According to Ubiratàn D’Ambrosio and Helaine Selin, the spherical law of sines was discovered in the 10th century. |
Книга ибн Мудада Аль-Джаяни неизвестные дуги сферы в XI веке содержит общий закон синусов . | Ibn Muʿādh al — Jayyānī’s The book of unknown arcs of a sphere in the 11th century contains the general law of sines. |
Закон синусов является одним из двух тригонометрических уравнений, обычно применяемых для нахождения длин и углов в скалярных треугольниках, а другим является закон косинусов. | The law of sines is one of two trigonometric equations commonly applied to find lengths and angles in scalene triangles, with the other being the law of cosines. |
Подставляя K = 0, K = 1 и K = -1, получаем соответственно евклидов, сферический и гиперболический случаи закона синусов , описанные выше. | By substituting K = 0, K = 1, and K = −1, one obtains respectively the Euclidean, spherical, and hyperbolic cases of the law of sines described above. |
Все шесть тригонометрических функций, используемых в настоящее время, были известны в Исламской математике к IX веку, как и закон синусов , используемый при решении треугольников. | All six trigonometric functions in current use were known in Islamic mathematics by the 9th century, as was the law of sines, used in solving triangles. |
В качестве альтернативы использованию тождества для суммы или разности двух синусов можно привести тригонометрическое тождество. | As an alternative to using the identity for the sum or difference of two sines, one may cite the trigonometric identity. |
Закон синусов может быть использован для вычисления оставшихся сторон треугольника, когда известны два угла и сторона-метод, известный как триангуляция. | The law of sines can be used to compute the remaining sides of a triangle when two angles and a side are known—a technique known as triangulation. |
В своей работе о секторе он изложил закон синусов для плоских и сферических треугольников и привел доказательства этого закона. | In his On the Sector Figure, he stated the law of sines for plane and spherical triangles, and provided proofs for this law. |
Закон синусов полезен для вычисления длин неизвестных сторон треугольника, если известны два угла и одна сторона. | The law of sines is useful for computing the lengths of the unknown sides in a triangle if two angles and one side are known. |
Таблица синусов и косинусов Региомонтана была опубликована в 1533 году. | Regiomontanus’s table of sines and cosines was published in 1533. |
Предлагаемые системы стадирования учитывают протяженность полипов, видимых при эндоскопическом исследовании, и количество синусов , пораженных при компьютерной томографии. | Proposed staging systems take into account the extent of polyps seen on endoscopic exam and the number of sinuses affected on CT imaging. |
Две пары синусов образуются во время пренатального развития и две пары-после рождения. | Two pairs of sinuses form during prenatal development and two pairs form after birth. |
Череп жирафа освещен множеством синусов . | A giraffe’s skull is lightened by multiple sinuses. |
Кавернозный синус — это один из дуральных венозных синусов головы. | The cavernous sinus is one of the dural venous sinuses of the head. |
При тромбозе церебральных венозных синусов сгустки крови обычно образуются как в венах головного мозга, так и в венозных синусах . | In cerebral venous sinus thrombosis, blood clots usually form both in the veins of the brain and the venous sinuses. |
Большинство случаев тромбоза церебральных венозных синусов обусловлено гиперкоагуляцией. | Most cases of cerebral venous sinus thrombosis are due to hypercoagulability. |
Тромбоз церебральных венозных синусов встречается редко, по оценкам, в среднем 3-4 случая на миллион в год у взрослых. | Cerebral venous sinus thrombosis is rare, with an estimated 3 — 4 cases per million annual incidence in adults. |
Верхний петросальный синус — это один из дуральных венозных синусов , расположенных под головным мозгом. | The superior petrosal sinus is one of the dural venous sinuses located beneath the brain. |
Это было самое раннее известное использование угла падения и самое раннее практическое применение закона синусов . | This was the earliest known use of dip angle and the earliest practical use of the law of sines. |
Эти ощущения могут способствовать сохранению образа синусов как эффективных резонаторов. | These sensations might support the preservation of the image of the sinuses as effective resonators. |
Это использование синусов в сочетании с углеродными квантовыми точками привело к созданию солнечного элемента, который достиг 9,10% PCE. | This use of SiNWs in conjunction with carbon quantum dots resulted in a solar cell that reached 9.10% PCE. |
Наиболее часто выполняемая операция заключается в хирургическом иссечении комплекса пилонидальных синусов , причем рана часто остается открытой для заживления. | The most commonly performed surgery is for the pilonidal sinus complex to be surgically excised with the wound often left open to heal. |
Две пары синусов образуются во время пренатального развития и две пары-после рождения. | Gillespie spoke about the Baháʼí Faith frequently on his trips abroad. |
Вскрыл мозговую оболочку и обнажил общий у них венозный синус . | I’ve opened the dura and revealed the venous sinus that they share. |
Экг, нормальный синус , нормальные интервалы. | Ekg, normal sinus, normal intervals. |
Доктор Рэмзи добралась до менингиомы через сагиттальный синус . | Dr. Ramsey’s got a meningioma invading the sagittal sinus. |
А этот синус кавернозный это опасно? | This cavernous sinus thing, is it dangerous? |
Слив вниз наоборот поперечный синус и вниз сигмовидной к внутренней яремной? | Is draining down the opposite transverse sinus and down the sigmoid to the internal jugular? |
Плюс одна пятая a… на синус два ax. (Заряд батареи…) | Plus one over five a… sine two eight X. ‘Your battery… ‘ |
И здесь всё становится ещё интереснее, потому что sin это ещё и синус . | And this is where it gets interesting, because sin is also an abbreviation for sine. |
Которая будет использована как новый сагиттальный синус . | Which will be used as the new sagittal sinus. |
Сейчас я разделяю сагиттальный синус . | I’m now separating the sagittal sinus. |
Что такое затылочный венозный синус ? | What’s the sagittal sinus? |
Проблема в том, что прут давит на затылочный венозный синус . | The problem is it’s pressing against the sagittal sinus. |
Просто небольшой ушиб, но реберно-диафрагмальный синус в норме. | It’s just a mild contusion, but the costophrenic angle is clear. |
Один общий сагиттальный синус снабжает мозг кровью. | There is one shared sagittal sinus supplying blood to the brain. |
Синус угла A равен отношению BC к AB и равен отношению перпендикуляра к гипотенузе. | Sine A equals B — C over A — B. |
Затемнённый синус и и повреждение решётчатой пластины. | Sinus opacification. And invasion through the cribriform plate. |
В худшем случае прут может разорвать синус , и он умрет за одну секунду. | If his sagittal sinus tears, he’ll die in seconds. |
Окончательный урогенитальный синус состоит из каудальной цефальной части и промежуточного узкого канала-тазовой части. | The definitive urogenital sinus consists of a caudal cephalic portion and an intermediate narrow channel, the pelvic portion. |
Установлено, что атрезия влагалища возникает тогда, когда урогенитальный синус не способствует формированию нижней части влагалища. | Vaginal atresia is found to occur when the urogenital sinus does not contribute to the formation of the lower portion of the vagina. |
x86 также включает в себя ряд трансцендентных функций, включая синус , Косинус, тангенс, арктангенс, возведение в степень с основанием 2 и логарифмы к основаниям 2, 10 или e. | x86 also includes a number of transcendental functions, including sine, cosine, tangent, arctangent, exponentiation with the base 2 and logarithms to bases 2, 10, or e. |
В дифференциальных уравнениях функция eix часто используется для упрощения решений, даже если конечным ответом является реальная функция, включающая синус и косинус. | In differential equations, the function eix is often used to simplify solutions, even if the final answer is a real function involving sine and cosine. |
Синус между основаниями боковых чашелистиков загибается внутрь и имеет небольшую выемку в центре. | The sinus between the bases of the lateral sepals curves inward and has a small notch in the centre. |
От головы до хвоста это инфундибулум, бульбус Кордис, примитивный желудочек, примитивное предсердие и синус венозный. | From head to tail, these are the infundibulum, bulbus cordis, primitive ventricle, primitive atrium, and the sinus venosus. |
Первоначально вся венозная кровь поступает в венозный синус и движется от хвоста к голове к артериальному стволу. | Initially, all venous blood flows into the sinus venosus, and is propelled from tail to head to the truncus arteriosus. |
Кавернозный синус находится в полости черепа, между слоями мозговых оболочек и является главным каналом венозного дренажа из головного мозга. | The cavernous sinus lies within the cranial cavity, between layers of the meninges and is a major conduit of venous drainage from the brain. |
Если кавернозный синус заражен, это может привести к свертыванию крови внутри синуса , что приведет к тромбозу кавернозного синуса . | If the cavernous sinus is infected, it can cause the blood within the sinus to clot resulting in a cavernous sinus thrombosis. |
Амиопатический ДМ, также называемый ДМ синус миозит, был назван в 2002 году. | Amyopathic DM, also called DM sine myositis, was named in 2002. |
Синус этого угла можно записать как длину его противоположного отрезка, разделенного гипотенузой прямоугольного треугольника. | The sine of this angle can be written as the length of its opposite segment, divided by the hypotenuse of the right triangle. |
Использование компьютерной томографии в сложных случаях также помогает хирургу идентифицировать и избежать жизненно важных структур, таких как Нижний альвеолярный нерв и синус . | The use of CT scanning in complex cases also helps the surgeon identify and avoid vital structures such as the inferior alveolar nerve and the sinus. |
Для угла целого числа градусов синус и косинус могут быть выражены через квадратные корни и кубический корень нереального комплексного числа. | For an angle of an integer number of degrees, the sine and the cosine may be expressed in terms of square roots and the cube root of a non — real complex number. |
Hyperbolic Trig Identities — Список функций гиперболической тригонометрии
Hyperbolic Trig Identities похож на тригонометрических тождеств , но может отличаться от них в определенных терминах. Фундаментальные гиперболические функции представляют собой гиперболы с синусом и гиперболы с косинусом , из которых выводятся остальные тригонометрические функции . Вы можете легко изучить многие другие Trig Identities на этом сайте.
Итак, здесь мы дали диаграмму гиперболы вдоль этих линий, чтобы вы подумали о местах синуса, косинуса и так далее.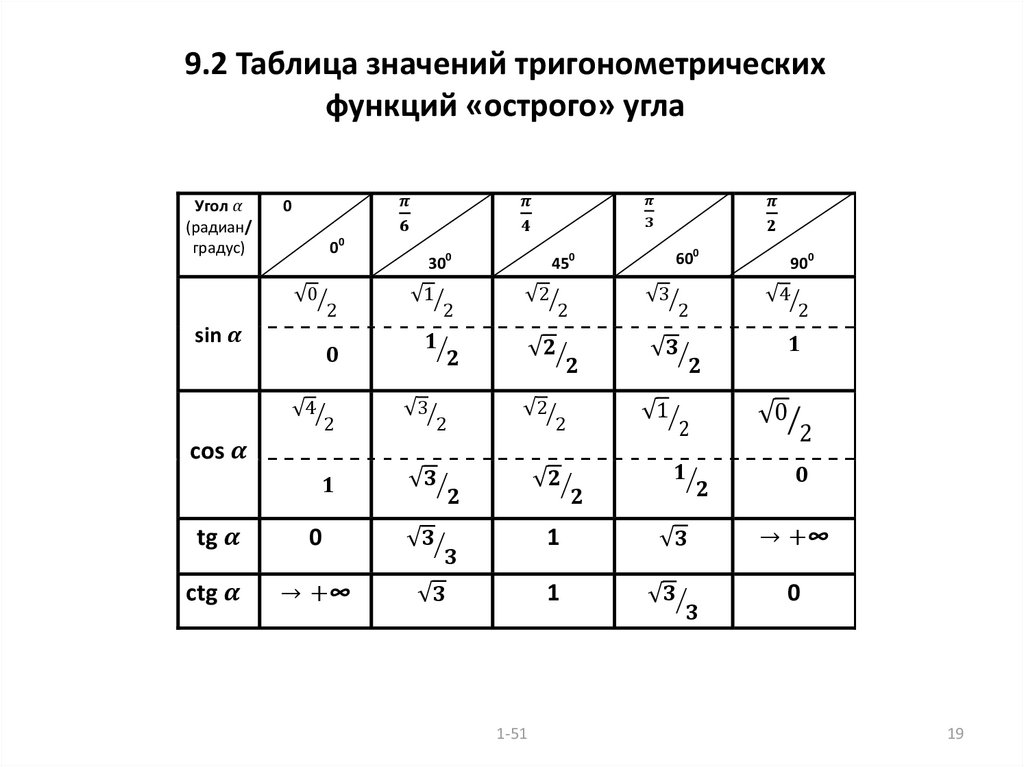
Различные основные гиперболические идентификаторы триггеров
Введение
- x и y являются независимыми переменными.
- e является основанием натурального логарифма.
- d — дифференциальный оператор.
- int — целочисленный символ.
- C — постоянная интегрирования.
Идентификаторы гиперболических триггеров | |
| sh x = ( e x – e – x )/2 | Уравнение 1 |
| cosh x = ( e x + e – x )/2 | Уравнение 2 |
| сек х = 1/ш х | Уравнение 3 |
| csch x = 1/sinh x | Уравнение 4 |
| tanh x = sh x /cosh x | Уравнение 5 |
| coth x = 1/th x | Уравнение 6 |
| coш 2 x – sin 2 x = 1 | Уравнение 7 |
| танх 2 x + сек 2 x = 1 | Уравнение 8 |
| coth 2 x – csch 2 x = 1 | Уравнение 9 |
sinh ( x + y ) = sinh x ch y + ch x sinh9 y | Уравнение 10 |
| sinh ( x – y ) = sh x ch y – ch x sinh 9 y | Уравнение 11 |
| ch ( x + y ) = ch x ch y + sh x sinh 9 y | Уравнение 12 |
| чеш ( x – y ) = чеш x ch y – sinh x sinh y | Уравнение 13 |
| sinh 2 x = [-1 + ch (2 x )]/2 | Уравнение 14 |
| sin (2 x ) = 2 sin x ch x | Уравнение 15 |
| кош 2 x = [1 + кош (2 x )]/2 | Уравнение 16 |
| ch (2 x ) = ch 2 x + sin 2 x | Уравнение 17 |
| arcsinh x = ln [ x + ( x 2 + 1) 1/2 ] | Уравнение 18 |
| arccosh x = ln [ x + ( x 2 – 1) 1/2 ] | Уравнение 19 |
| arctg x = (1/2) ln [(1 + x )/(1 – x )] | Уравнение 20 |
| arccoth x = (1/2) ln [( x + 1)/( x – 1)] | Уравнение 21 |
| arcsech x = ln [[1 + (1 – x 2 ) 1/2 ]/ x ] | Уравнение 22 |
| arccsch x = ln [[1 + (1 + x 2 ) 1/2 ]/| х |] | Уравнение 23 |
| танх (2 x ) = 2 танх x / (1 + танх 2 x ) | Уравнение 24 |
| сч х – танх х = 2 сщ (2 х ) | Уравнение 25 |
| ткань x + tanh x = 2 coth (2 x ) | Уравнение 26 |
| (d/d x ) sin x = ch x | Уравнение 27 |
| (d/d x ) cosh x = sinh x | Уравнение 28 |
| (d/d x ) tanh x = sech 2 x | Уравнение 29 |
| (d/d x ) coth x = -csch 2 x | Уравнение 30 |
| (d/d x ) sech x = -sech x tanh x | Уравнение 31 |
| (d/d x ) csch x = -csch x coth x | Уравнение 32 |
| (д/д x ) arcsinh x = 1/( x 2 + 1) 1/2 | Уравнение 33 |
| (d/d x ) arccosh x = 1/( x 2 – 1) 1/2 | Уравнение 34 |
| (d/d x ) arctanh x = 1/(1 – x 2 ) | Уравнение 35 |
| (д/д х ) arccoth x = 1/(1 – x 2 ) | Уравнение 36 |
| (d/d x ) arcsech x = -1/[x (1 – x 2 ) 1/2 ] | Уравнение 37 |
| (d/d x ) arccsch x = -1/[|x| (1 + x 2 ) 1/2 ] | Уравнение 38 |
Интегралы. | |
| инт x d x = sinh x + C | Уравнение 39 |
| int sinh x d x = cosh x + C | Уравнение 40 |
| int sech 2 x d x = tanh x + C | Уравнение 41 |
| int csch 2 x d x = -coth x + C | Уравнение 42 |
| int sech x tanh x d x = -sech x + C | Уравнение 43 |
| int csch x coth x d x = -csch x + C | Уравнение 44 |
| внутр. д x /( x 2 + 1) 1/2 = arcsinh x + C | Уравнение 45 |
| int d x /( x 2 – 1) 1/2 = arccosh x + C | 9Уравнение 46 |
| int d x /(1 – x 2 ) = arctanh x + C | Уравнение 47 |
| инт д x /(1 – x 2 ) = arccoth x + C | Уравнение 48 |
| int d x /[ x (1 – x 2 ) 1/2 ] = -arcsech x 0 8 + | Уравнение 49 |
интервал d x /[| х | (1 + x 2 ) 1/2 ] = -arccsch x + C 92x = 1$Функции отрицательных аргументовsin(-x) = -sinx кош(-х) = кош х танх(-х) = -танхх csch(-x) = -csch x сек(-х) = сек х спот(-х) = -спот х Дополнительные формулы$\text{sinh}(x \pm y) = \text{sinh}\ x \ \text{cosh}\ y \pm \text{cosh}\ x\ \text{sinh}\ y$ $\text{cosh}(x \pm y) = \text{cosh}\ x\ \text{cosh}\ y \pm \text{sinh}\ x\ \text{sinh}\ y$ 94 x = \frac{3}{8} + \frac12 \text{cosh}\ 2x + \frac18 \text{cosh}\ 4x$Сумма, разница и произведение$\text{sinh}\ x + \text{sinh}\ y = 2 \text{sinh}\ \frac12(x + y)\ \text{cosh}\ \frac12(x — y)$ $\text{sinh}\ x — \text{sinh}\ y = 2 \text{cosh}\ \frac12(x + y)\ \text{sinh} \frac12(x — y)$ $\text{cosh}\ x + \text{cosh}\ y = 2 \text{cosh}\ \frac12(x + y)\ \text{cosh}\ \frac12(x — y)$ $\text{cosh}\ x — \text{cosh}\ y = 2 \text{sinh}\ \frac12(x + y)\ \text{sinh}\ \frac12(x — y)$ $\text{sinh}\ x\ \text{sinh}\ y = \frac12(\text{cosh}(x + y) — \text{cosh} (x — y))$ $\text{cosh}\ x\ \text{cosh}\ y = \frac12(\text{cosh}(x + y) + \text{cosh} (x — y))$ $\text{sinh}\ x\ \text{cosh}\ y = \frac12(\text{sinh}(x + y) + \text{sinh} (x — y))$ Выражение гиперболических функций через другие функции Далее предполагается, что x > 0. | $u$ |
Графики гиперболических функций
у = шп х
у = ш х
у = танх х
у = кат х
у = сек х
у = сщ х
Обратные гиперболические функции
Если x = sin y, , тогда y = sin -1 a называется обратным гиперболическим синусом от x. Аналогично определим другие обратные гиперболические функции. Обратные гиперболические функции многозначны, и, как и в случае обратных тригонометрических функций, мы ограничиваемся главными значениями, при которых их можно считать однозначными.
В следующем списке показаны главные значения [если не указано иное] обратных гиперболических функций, выраженных в терминах логарифмических функций, которые принимаются в качестве действительных значений. 92} + 1})$ $x \neq 0$
Связь между обратными гиперболическими функциями
csch -1 x = sin -1 (1/x)
сек -1 х = кош -1 (1/х)
coth -1 x = tanh -1 (1/x)
sin -1 (- x ) = -sin -1 x
танх -1 (- х )= -танх -1 х
coth -1 (-x) = -coth -1 x
csch -1 (- x) = -csch -1 x
Графики обратных гиперболических функций
y = sin -1 x
у = -1 х
г = танх -1 x
г = -1 х
у = сек -1 х
у = сщ -1 х
Связь между гиперболическими и тригонометрическими функциями
| $\sin(ix) = i \text{sinh}\ x$ | $\cos(ix) = \text{cos}\ x$ | $\tan(ix) = i \text{tanh}\ x$ |
| $\csc(ix) = -i \text{csch}\ x$ | $\sec(ix) = \text{sech}\ x$ | $\cot(ix) = -i \text{coth}\ x$ |
| $\text{sinh}(ix) = i \sinx$ | $\text{cosh}(ix) = \cos x$ | $\text{tanh}(ix) = i \tanx$ |
| $\text{csch}(ix) = -i \csc x$ | $\text{sech}(ix) = \sec x$ | $\text{coth}(ix) = -i \cot x$ |
Периодичность гиперболических функций
Далее $k$ — любое целое число.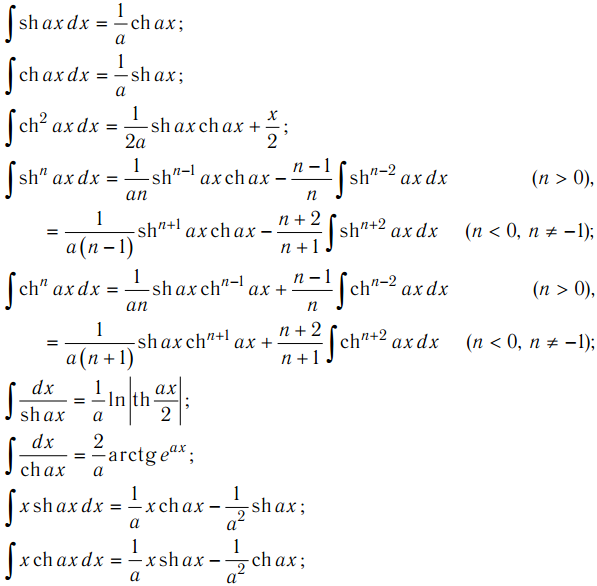
$\text{sinh} (x + 2k \pi i) = \text{sinh}\ x$ $\text{csch} (x + 2k\pi i) = \text{csch} x$
$\text{cosh} (x + 2k \pi i) = \text{cosh}\ x$ $\text{sech} (x + 2k\pi i) = \text{sech} x$
$\text{tanh} (x + k\pi i) = \text{tanh}\ x$ $\text{coth} (x + k\pi i) =\text{coth} x$
Связь между обратной гиперболической и обратной тригонометрической функциями
| sin -1 (ix) = isinh -1 x | sin -1 (ix) = i sin -1 x |
| cos -1 x = ±i cosh -1 x | cos -1 x = ±i cos -1 x |
| tan -1 (ix) = i tanh -1 x | танх -1 (ix) = я тан -1 х |
| детская кроватка -1 (ix) = -i детская -1 x | детская кроватка -1 (ix) = -i детская кроватка -1 x |
| сек -1 x = ±i сек -1 x | с -1 x = ±i с -1 x |
| csc -1 (ix) = -i csch -1 x | csch -1 (ix) = -i csc -1 x |
7.
 3: Гиперболические функции — Математика LibreTexts
3: Гиперболические функции — Математика LibreTexts- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 5493
Гиперболические функции довольно часто встречаются в приложениях и во многих отношениях очень похожи на тригонометрические функции. Это немного удивительно, учитывая наши первоначальные определения. 92 -1})\) является действительным числом, а \(y =\cosh x\), поэтому \(y\) находится в диапазоне \(\cosh(x)\).
\(\square\)
Определение 4.11.3: Гиперболический тангенс и котангенс
Другими гиперболическими функциями являются
\[\eqalign{\tanh x &= {\sinx x\over\cosh x}\cr \coth x &= {\cosh x\over\sinh x}\cr \text{sech} x &= {1\over\cosh x}\cr \text{csch} x &= {1\over\sinh x }\cr} \]
Область определения \(\coth\) и \(\text{csch}\) равна \(x\neq 0\), тогда как областью определения других гиперболических функций являются все действительные числа. Графики показаны на рисунке \(\PageIndex{1}\) 92x-1}=\pm\sinh t\). Итак, для некоторых подходящих \(t\), \(\ch t\) и \(\sinh t\) являются координатами типичной точки гиперболы. Фактически получается, что \(t\) в два раза больше площади, показанной на первом графике рисунка \(\PageIndex{2}\). Даже это аналогично тригонометрии; \(\cos t\) и \(\sin t\) — координаты типичной точки на единичной окружности, а \(t\) — удвоенная площадь, показанная на втором графике рисунка \(\PageIndex{2 }\).
Графики показаны на рисунке \(\PageIndex{1}\) 92x-1}=\pm\sinh t\). Итак, для некоторых подходящих \(t\), \(\ch t\) и \(\sinh t\) являются координатами типичной точки гиперболы. Фактически получается, что \(t\) в два раза больше площади, показанной на первом графике рисунка \(\PageIndex{2}\). Даже это аналогично тригонометрии; \(\cos t\) и \(\sin t\) — координаты типичной точки на единичной окружности, а \(t\) — удвоенная площадь, показанная на втором графике рисунка \(\PageIndex{2 }\).
Рисунок \(\PageIndex{2}\): 9{-x }\over 2} =\cosh x.\]
\(\square\)
Поскольку \(\cosh x > 0\), \(\sinh x\) является возрастающим и, следовательно, инъективным, поэтому \(\sinh x\) имеет обратный, \(\text{arcsinh} x\). Кроме того, \(\sinh x > 0\), когда \(x>0\), поэтому \(\cosh x\) инъективен на \([0,\infty)\) и имеет (частичный) обратный, \ (\текст{арккош} х\). Другие гиперболические функции также имеют инверсию, хотя \(\text{arcsech} x\) является лишь частичной инверсией.


 1. Связь (сумма)
1. Связь (сумма) Винсент Риккати (итал. Vincenzo de Riccati; 11 января 1707, Кастель-Франко — 17 января 1775, Тревизо) — итальянский математик, иностранный почётный член Петербургской Академии Наук с 17 января 1760 года. Известен как создатель гиперболических функций. Отец Винсента Якопо Франческо Риккати (в честь которого названо уравнение Риккати) был одним из крупных итальянских математиков того времени. Винсент Риккати унаследовал интересы отца в области дифференциальных уравнений, которые естественно возникали при решении геометрических задач. Это привело его к изучению конических сечений в декартовых координатах и к заинтересованности в изучении гиперболы 1.
Винсент Риккати (итал. Vincenzo de Riccati; 11 января 1707, Кастель-Франко — 17 января 1775, Тревизо) — итальянский математик, иностранный почётный член Петербургской Академии Наук с 17 января 1760 года. Известен как создатель гиперболических функций. Отец Винсента Якопо Франческо Риккати (в честь которого названо уравнение Риккати) был одним из крупных итальянских математиков того времени. Винсент Риккати унаследовал интересы отца в области дифференциальных уравнений, которые естественно возникали при решении геометрических задач. Это привело его к изучению конических сечений в декартовых координатах и к заинтересованности в изучении гиперболы 1.  Риккати не только рассмотрел эти новые функции, но и на основе связанных с ними интегральных формул и с помощью геометрических методов получил интегральную формулу для тригонометрических функций. Его книга «Institutiones» признана как первый обширный трактат по интегральному исчислению. Работы Эйлера и Ламберта изданы позже. Саладини и Риккати также рассматривали другие геометрические проблемы, в том числе трактрису, строфоиду. Риккати применял для гиперболических функций обозначения и в дальнейшем в обозначениях гиперболических функций утвердился некоторый разнобой.
Риккати не только рассмотрел эти новые функции, но и на основе связанных с ними интегральных формул и с помощью геометрических методов получил интегральную формулу для тригонометрических функций. Его книга «Institutiones» признана как первый обширный трактат по интегральному исчислению. Работы Эйлера и Ламберта изданы позже. Саладини и Риккати также рассматривали другие геометрические проблемы, в том числе трактрису, строфоиду. Риккати применял для гиперболических функций обозначения и в дальнейшем в обозначениях гиперболических функций утвердился некоторый разнобой.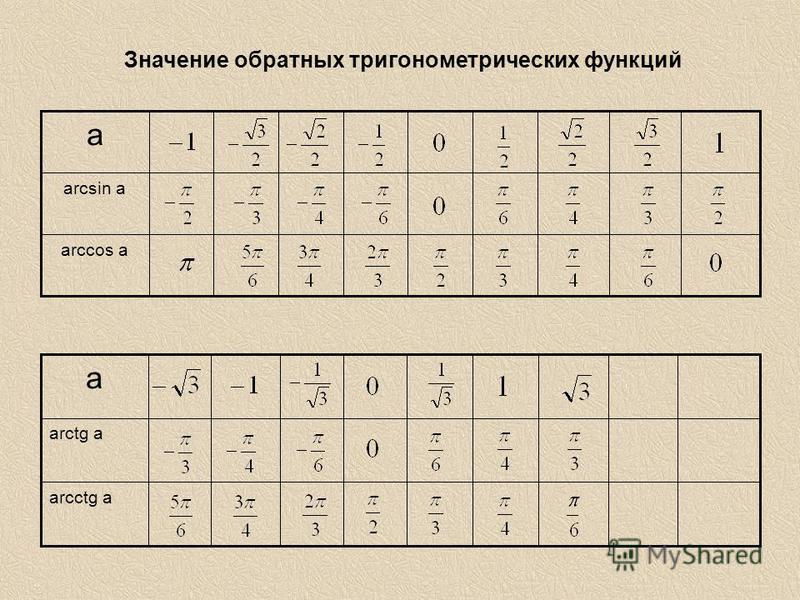
 ..
..




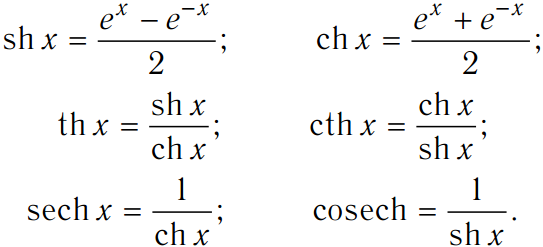


 .. equals the perpendicular over the hypotenuse.
.. equals the perpendicular over the hypotenuse.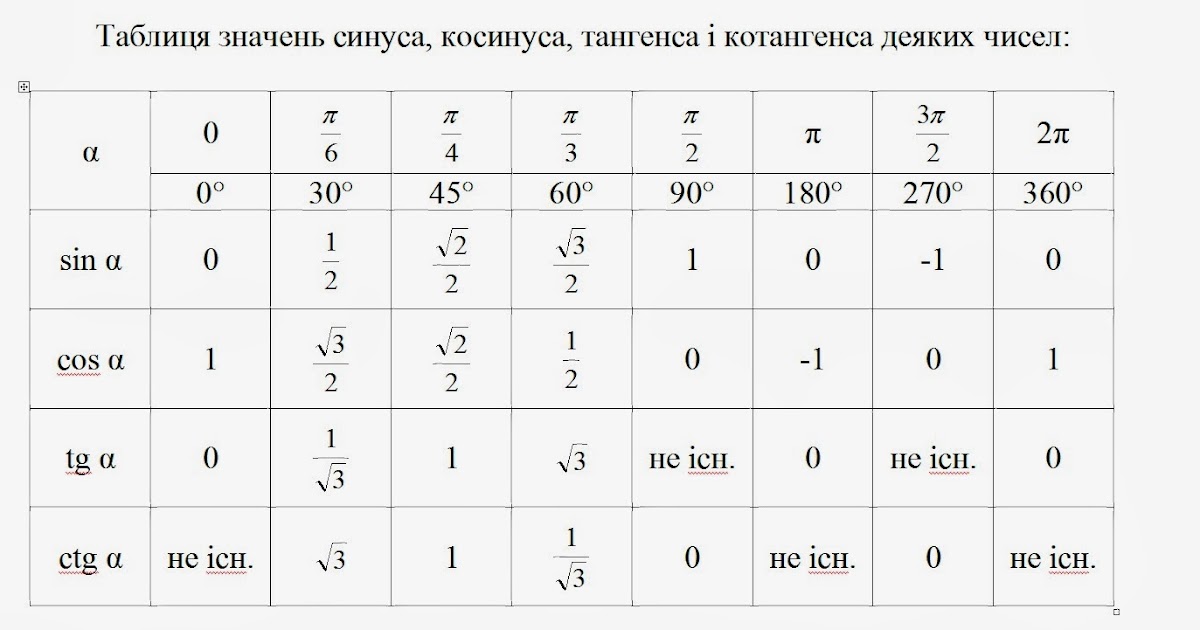



 Если x < 0, используйте соответствующий знак, как указано в формулах в разделе «Функции отрицательных аргументов» 92}}$
Если x < 0, используйте соответствующий знак, как указано в формулах в разделе «Функции отрицательных аргументов» 92}}$