Нулевая матрица пример: Виды матриц.

Виды матриц.

Виды матриц.

Навигация по странице:

• Квадратная матрица
• Нулевая матрица
• Вектор строка
• Вектор столбец
• Диагональная матрица
• Единичная матрица
• Верхняя треугольная матрица
• Нижняя треугольная матрица
• Ступенчастая матрица

Онлайн калькуляторы с матрицами.

Упражнения с матрицами.

Определение.

Квадратной матрицей называется матрица, у которой количество строк равно количеству столбцов (размера n×n), число n называется порядком матрицы.

Пример.

	4	1	-7		— квадратная матрица размера 3×3
	-1	0	2
	4	6	7

Определение.

Нулевой матрицей называется матрица, все элементы которой равны нулю, т.е. a_ij = 0, ∀i, j.

Пример.

	0	0	0		— нулевая матрица
	0	0	0

Определение.

Вектор-строкой называется матрица, состоящая из одной строки.

Пример.

1

4

-5

— вектор-строка

Определение.

Вектор-столбцом называется матрица, состоящая из одного столбца.

Пример.

	8		— вектор-столбец
	-7
	3

Определение.

Диагональной матрицей называется квадратная матрица, все элементы которой, стоящие вне главной диагонали, равны нулю.

Пример диагональной матрицы.

	4	0	0		— диагональные элементы произвольныене диагональные элементы равны нулю
	0	5	0
	0	0	0

Определение.

Единичной матрицей называется диагональная матрица, диагональные элементы которой равны 1.

Обозначение.

Единичную матрицу обычно обозначают символом E.

Пример единичной матрицы.

E =		1	0	0		— диагональные элементы равны 1не диагональные элементы равны нулю
		0	1	0
		0	0	1

Определение.

Верхней треугольной матрицей называется матрица, все элементы которой ниже главной диагонали равны нулю.

Пример верхней треугольной матрицы.

	7	-6	0
	0	1	6
	0	0	0

Определение.

Нижней треугольной матрицей называется матрица, все элементы которой выше главной диагонали равны нулю.

Пример нижней треугольной матрицы.

	7	0	0
	6	1	0
	-2	0	5

N.B. Диагональная матрица — матрица, которая одновременно является верхней треугольной и нижней треугольной.

Определение.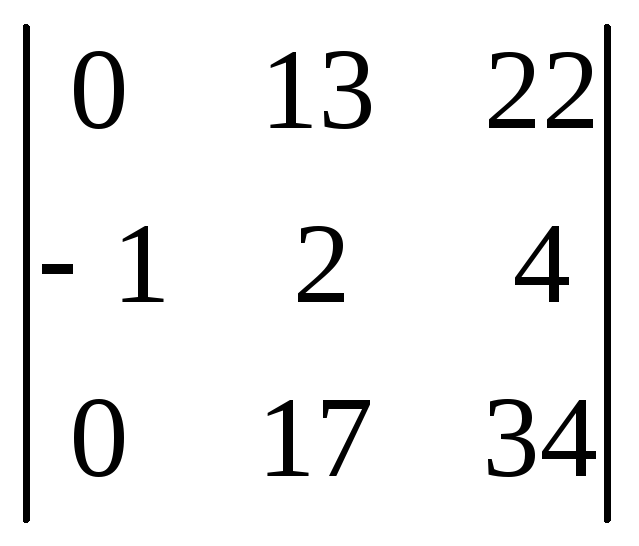

Ступенчатой матрицей называется матрица, удовлетворяющая следующим условиям:

• если матрица содержит нулевую строку, то все строки, расположенные под нею, также нулевые;
• если первый ненулевой элемент некоторой строки расположен в столбце с номером i, и следующая строка не нулевая, то первый ненулевой элемент следующей строки должен находиться в столбце с номером большим, чем i.

Примеры ступенчатых матриц.

7   0   8   0   0   4

7   0   8   8   8   0   0   1   3   5   0   0   0   -3   5   0   0   0   0   0   0   0   0   0   0

Онлайн калькуляторы с матрицами.

Упражнения с матрицами.

Описание основных видов матриц, определения и их примеры

Поможем решить контрольную, написать реферат, курсовую и диплом от 800р

Содержание:

• Диагональные матрицы
• Треугольные матрицы
• Ступенчатая матрица

Определение

Матрица размера $n \times n$ называется квадратной, число $n$ называется порядком матрицы.

Пример

$A_{2 \times 2}=\left(\begin{array}{rr} 1 & -3 \\ 7 & 2 \end{array}\right)$ — квадратная матрица порядка 2 или матрица второго порядка.

Определение

Матрица $\Theta$ называется нулевой, если все её элементы равны нулю, т.е. $a_{i j}=0, \forall i, j$.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

$$\Theta=\left(\begin{array}{ll} 0 & 0 \\ 0 & 0 \\ 0 & 0 \end{array}\right)$$

Определение

Матрица, состоящая из одной строки, называется вектор-строкой, а матрица, состоящая из одного столбца, — вектор-столбцом.

Пример

$B=(1 3 7)$ — вектор-строка; $B=\left(\begin{array}{l} 1 \\ 3 \\ 7 \end{array}\right)$ — вектор-столбец.

Диагональные матрицы

Определение

Квадратная матрица $D$ называется диагональной, если все ее элементы, стоящие вне главной диагонали, равны нулю.

Замечание. Диагональные элементы матрицы (т.е. элементы, стоящие на главной диагонали) могут также равняться нулю.

Пример

$$D=\left(\begin{array}{lll} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 3 \end{array}\right)=\operatorname{diag}(1 ; 0 ; 3)$$

Определение

Скалярной называется диагональная матрица $S$, у которой все диагональные элементы равны между собой.

Замечание. Если нулевая матрица является квадратной, то она также является и скалярной.

Пример

$$S=\left(\begin{array}{rr} -1 & 0 \\ 0 & -1 \end{array}\right)$$

Определение

Единичной матрицей $E_{n}$ называется скалярная матрица порядка $n$, диагональные элементы которой равны 1.

Замечание. Для сокращения записи порядок единичной матрицы можно не писать, тогда единичная матрица обозначается просто $E$.

Пример

$E_{2}=\left(\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right)$ — единичная матрица второго порядка.

Треугольные матрицы

Определение

Матрица называется верхней треугольной матрицей, если все элементы ниже главной диагонали равны нулю.

Матрица называется

нижней треугольной матрицей, если все элементы выше главной диагонали равны нулю.

Замечание. Диагональная матрица — это пример матрицы, которая является одновременно верхне- и нижнетреугольной.

Пример

$C=\left(\begin{array}{lll} 2 & 5 & 0 \\ 0 & 4 & 1 \\ 0 & 0 & 3 \end{array}\right)$ — верхнетреугольная матрица.

Ступенчатая матрица

Определение

Ступенчатой называется матрица, удовлетворяющая следующим условиям:

1. если эта матрица содержит нулевую строку (т. е. строку, все элементы которой равны нулю), то все строки, расположенные под нею, также нулевые;
2. если первый ненулевой элемент некоторой строки расположен в столбце с номером $i$, то первый ненулевой элемент следующей строки должен находиться в столбце с номером большим, чем $i$.

Другое определение ступенчатой матрицы.

Определение

Ступенчатой называется матрица, которая содержит $m$ строк и у которой первые $r \leq m$ диагональных элементов ненулевые, а элементы, лежащие ниже главной диагонали и элементы последних $m-r$ строк равны нулю, то есть это матрица вида:

$$A=\left(\begin{array}{ccccccc} a_{11} & a_{12} & a_{13} & \ldots & a_{1 r} & \ldots & a_{1 n} \\ 0 & a_{22} & a_{23} & \ldots & a_{2 r} & \ldots & a_{2 n} \\ 0 & 0 & a_{33} & \ldots & a_{3 r} & \ldots & a_{3 n} \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & 0 & \ldots & a_{r r} & \ldots & a_{r n} \\ 0 & 0 & 0 & \ldots & 0 & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & 0 & \ldots & 0 & \ldots & 0 \end{array}\right)$$

Определение

Главным элементом некоторой строки матрицы $A$ называется ее первый ненулевой элемент.

Пример

Задание. Найти главные элементы каждой строки матрицы $A=\left(\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 0 & 1 \end{array}\right)$

Решение. Главный элемент первой строки — это первый ненулевой элемент этой строки, а поэтому $a_{11}=1$ — главный элемент строки под номером 1; аналогично $a_{23}=1$ — главный элемент второй строки.

Другое определение ступенчатой матрицы.

Определение

Матрица $A$ называется ступенчатой, если:

1. все ее нулевые строки стоят после ненулевых;
2. в каждой ненулевой строке, начиная со второго, ее главный элемент стоит правее (в столбце с большим номером) главного элемента предыдущей строки.

По определению к ступенчатым матрицам будем относить нулевую матрицу $\Theta$, а также матрицу, которая содержит одну строку.

Пример

Примеры ступенчатых матриц:

$A=\left(\begin{array}{ll} 0 & 0 \\ 0 & 0 \end{array}\right)$, $B=(1 2 3 4)$, $C=\left(\begin{array}{lll} 1 & 2 & 3 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array}\right)$, $D=\left(\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 2 \\ 0 & 0 & 8 \\ 0 & 0 & 0 \end{array}\right)$, $F=\left(\begin{array}{rrr} 1 & 2 & 3 \\ 0 & 1 & 1 \\ 0 & 0 & -7 \end{array}\right)$

Примеры матриц, которые не являются ступенчатыми:

$A=\left(\begin{array}{ll} 0 & 0 \\ 1 & 0 \end{array}\right)$, $B=\left(\begin{array}{lll} 1 & 2 & 3 \\ 0 & 0 & 1 \\ 0 & 0 & -3 \end{array}\right)$, $D=\left(\begin{array}{rrr} 1 & 0 & -1 \\ 0 & 1 & 2 \\ 0 & 5 & 8 \\ 0 & 0 & 3 \end{array}\right)$

Пример

Задание.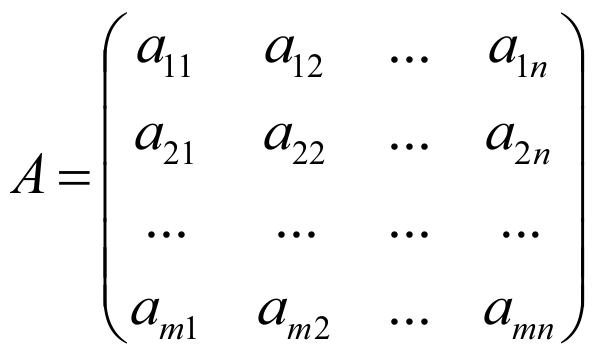 Выяснить, является ли матрица $A=\left(\begin{array}{llllll} 0 & 1 & 2 & 0 & 3 & 1 \\ 0 & 0 & 3 & 2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 2 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right)$ ступенчатой.

Решение. Проверяем выполнение условий из определения:

1. все строки под первой нулевой строкой матрицы (четвертая строка) являются нулевыми;
2. первый ненулевой элемент строки № 1 находится во втором столбце, значит, первый ненулевой элемент второй строки должен находиться, по крайней мере, в третьем столбце — выполняется, т.к. первый ненулевой элемент второй строки $a_{23} = 3 \neq 0$ находится в третьем столбце; аналогично, первый ненулевой элемент третьей строки находится в шестом столбце, а первый ненулевой элемент предыдущей, второй, строки, находится в столбце с номером 3 и 3

Итак, заданная матрица $A$ является ступенчатой.

Читать дальше: операции над матрицами.

Матрицы. Виды матриц

Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.

Матрица порядка m × n записывается в форме:

или (i=1,2,…m; j=1,2,…n).

Числа a_ij входящие в состав данной матрицы называются ее элементами. В записи a_ij первый индекс i означает номер строки, а второй индекс j— номер столбца.

Матрица строка

Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:

Матрица столбец

Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например

Нулевая матрица

Если все элементы матрицы равны нулю,то матрица называется нулевой матрицей . Например

Квадратная матрица

Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:

Главная диагональ матрицы

Элементы расположенные на местах a₁₁, a₂₂ ,…, a_nn образуют главную диагональ матрицы. Например:

В случае m×n -матриц элементы a_ii ( i=1,2,…,min(m,n)) также образуют главную диагональ. Например:

Элементы расположенные на главной диагонали называются главными диагональными элементами или просто диагональными элементами .

Побочная диагональ матрицы

Элементы расположенные на местах a_1n, a_2n-1 ,…, a_n1 образуют побочную диагональ матрицы. Например:

Диагональная матрица

Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:

Единичная матрица

Квадратную матрицу n-го порядка, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю, называется единичной матрицей и обозначается через E или E ⁿ, где n — порядок матрицы. Единичная матрица порядка 3 имеет следующий вид:

След матрицы

Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:

Верхняя треугольная матрица

Квадратная матрица порядка n×n называется верхней треугольной матрицей, если равны нулю все элементы матрицы, расположенные под главной диагональю, т. е. a_ij=0, при всех i>j . Например:

Нижняя треугольная матрица

Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. a_ij=0, при всех i<j. Например:

Cтроки матрицы A образуют пространство строк матрицы и обозначаются через R(A^T).

Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).

Ядро или нуль пространство матрицы

Множесто всех решений уравнения Ax=0, где A- mxn-матрица, x— вектор длины n — образует нуль пространство или ядро матрицы A и обозначается через Ker(A) или N(A).

 Противоположная матрица

Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0.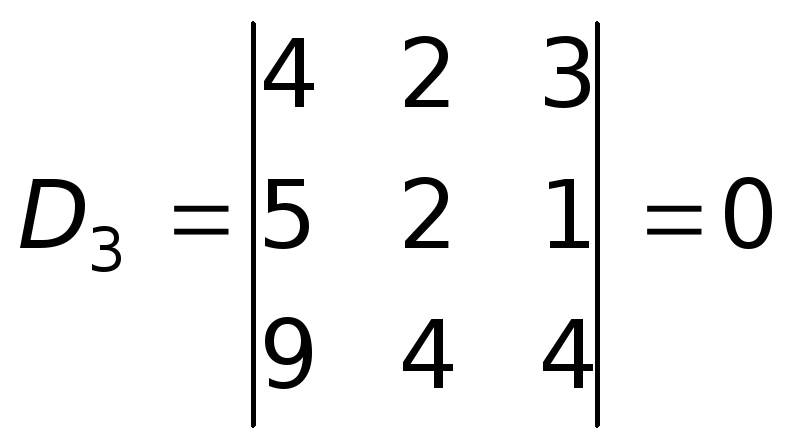 Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.

 Кососимметричная (Кососимметрическая) матрица

Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:

A^T=−A.

В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.

Пример кососимметрической матрицы:

 Разность матриц

Разностью C двух матриц A и B одинакового размера определяется равенством

C=A+(-1)B.

Для обозначения разности двух матриц используется запись:

C=A-B.

 Степень матрицы

Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:

A⁰=E,

где E-единичная матрица.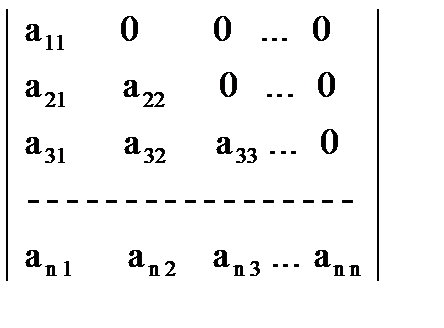

Из сочетательного свойства умножения следует:

где p,q— произвольные целые неотрицательные числа.

  Симметричная (Симметрическая) матрица

Матрица, удовлетворяющая условию A=A^T называется симметричной матрицей.

Для симметричных матриц имеет место равенство:

a_ij=a_ji ;   i=1,2,…n,   j=1,2,…n

Нулевая матрица (нулевая матрица) — определение, формула, свойства, примеры

LearnPracticeDownload

Нулевая матрица — это матрица, каждый из элементов которой равен нулю. Нулевая матрица также называется нулевой матрицей, и она может иметь разное количество строк и столбцов. Добавление нулевой матрицы к любой матрице приводит к той же самой матрице, и, следовательно, нулевая матрица также называется аддитивной идентичностью данной матрицы.

Давайте узнаем больше о свойствах нулевой матрицы, с примерами, часто задаваемыми вопросами.

1.	Что такое нулевая матрица?
2.	Свойства нулевой матрицы
3.	Примеры на нулевой матрице
4.	Практические вопросы
5.	Часто задаваемые вопросы о нулевой матрице

Что такое нулевая матрица (нулевая матрица)?

Нулевая матрица — это квадратная матрица, все элементы которой равны нулю. Поскольку нулевая матрица имеет все нули в качестве своих элементов, нулевая матрица также называется нулевой матрицей . Нулевая матрица — это аддитивная идентичность любой матрицы. Порядок нулевой матрицы равен m x n, и она может иметь неравное количество строк и столбцов. Вот несколько примеров нулевой матрицы или нулевой матрицы.

\(\begin{bmatrix}0&0\\0&0\end{bmatrix}\)

\(\begin{bmatrix}0&0&0\\0&0&0\end{bmatrix}\)

\(\begin{bmatrix}0&0&0\\0&0&0\\0&0&0\end{bmatrix}\)

Добавление нулевой матрицы к любой другой матрице того же порядка не меняет матрицу и, следовательно, нулевая матрица также называется аддитивной идентичностью.

\(\begin{bmatrix}a&b\\c&d\end{bmatrix}\) + \(\begin{bmatrix}0&0\\0&0\end{bmatrix}\) = \(\begin{bmatrix}a&b\\ c&d\end{bmatrix}\)

Свойства нулевой матрицы (нулевой матрицы)

Ниже перечислены некоторые важные свойства нулевой матрицы.

• Нулевая матрица является квадратной матрицей.
• Нулевая матрица может иметь неравное количество строк и столбцов.
• Добавление нулевой матрицы к любой матрице не изменяет матрицу.
• Умножение нулевой матрицы на любую другую матрицу превращает матрицу в нулевую матрицу.
• Определитель нулевой матрицы равен нулю.
• Нулевая матрица является сингулярной матрицей.

Связанные темы

Следующие темы помогают лучше понять нулевую матрицу.

• Идемпотентная матрица
• Определитель матрицы
• Матрица столбцов
• Матрица строк

 

Примеры нулевой матрицы

1. Пример 1: Приведите пример нулевой матрицы с двумя строками и тремя столбцами.

   Решение:

   Нулевая матрица с двумя строками и тремя столбцами имеет порядок 2 x 3 и все элементы равны нулю.

   \(\begin{bmatrix}0&0&0\\0&0&0\end{bmatrix}\)

   Следовательно, у нас есть требуемая нулевая матрица.

2. Пример 2: Докажите, что аддитивная идентичность \(\begin{bmatrix}4&2&6\\3&1&5\end{bmatrix}\) является нулевой матрицей.

   Решение:

   Данная матрица имеет вид \(\begin{bmatrix}4&2&6\\3&1&5\end{bmatrix}\)

   Нулевая матрица того же порядка, что и данная матрица, имеет вид \(\begin{bmatrix}0&0&0\\0&0&0 \end{bmatrix}\).

   \(\begin{bmatrix}4&2&6\\3&1&5\end{bmatrix}\) + \(\begin{bmatrix}0&0&0\\0&0&0\end{bmatrix}\) = \(\begin{bmatrix}4&2&6\\ 3&1&5\end{bmatrix}\)

   Таким образом, добавление нулевой матрицы к данной матрице также возвращает ту же матрицу.

   Таким образом, нулевая матрица является аддитивной единицей данной матрицы.

перейти к слайдуперейти к слайду

Есть вопросы по основным математическим понятиям?

Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, зачем нужна математика, с нашими сертифицированными экспертами

Запишитесь на бесплатный пробный урок

Практические вопросы по нулевой матрице

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о нулевой матрице

Что такое нулевая матрица?

Нулевая матрица — это матрица, все элементы которой равны нулю. Нулевая матрица также называется нулевой матрицей, так как все ее элементы равны нулю. Добавление нулевой матрицы к любой матрице не меняет значения матрицы, поэтому нулевую матрицу также называют аддитивной идентичностью.

В чем разница между нулевой матрицей и нулевой матрицей?

Нулевая матрица или нулевая матрица относятся к одной и той же матрице, и обе матрицы содержат нуль в качестве своих элементов.

Каков порядок нулевой матрицы?

Порядок нулевой или нулевой матрицы равен m x n, и она может иметь разное количество строк и столбцов. Следовательно, нулевая матрица может быть квадратной или прямоугольной матрицей.

Какая польза от нулевой матрицы?

Нулевая матрица полезна, поскольку она является аддитивной идентичностью любой матрицы. Добавление нулевой матрицы к любой матрице не меняет значения матрицы, поэтому нулевую матрицу также называют аддитивной идентичностью.

Рабочие листы по математике и
наглядный учебный план

Нулевое пространство и недействительность матрицы

Ненулевое пространство и недействительность — это концепции линейной алгебры, которые используются для определения линейной взаимосвязи между атрибутами.

Пустое пространство:

Пустое пространство любой матрицы A состоит из всех векторов B, таких что AB = 0 и B не равен нулю. Его также можно рассматривать как решение, полученное из AB = 0,, где A — известная матрица размера м x n , а B — находимая матрица размера 9.0194 н х к . Размер нулевого пространства матрицы дает нам количество линейных отношений между атрибутами.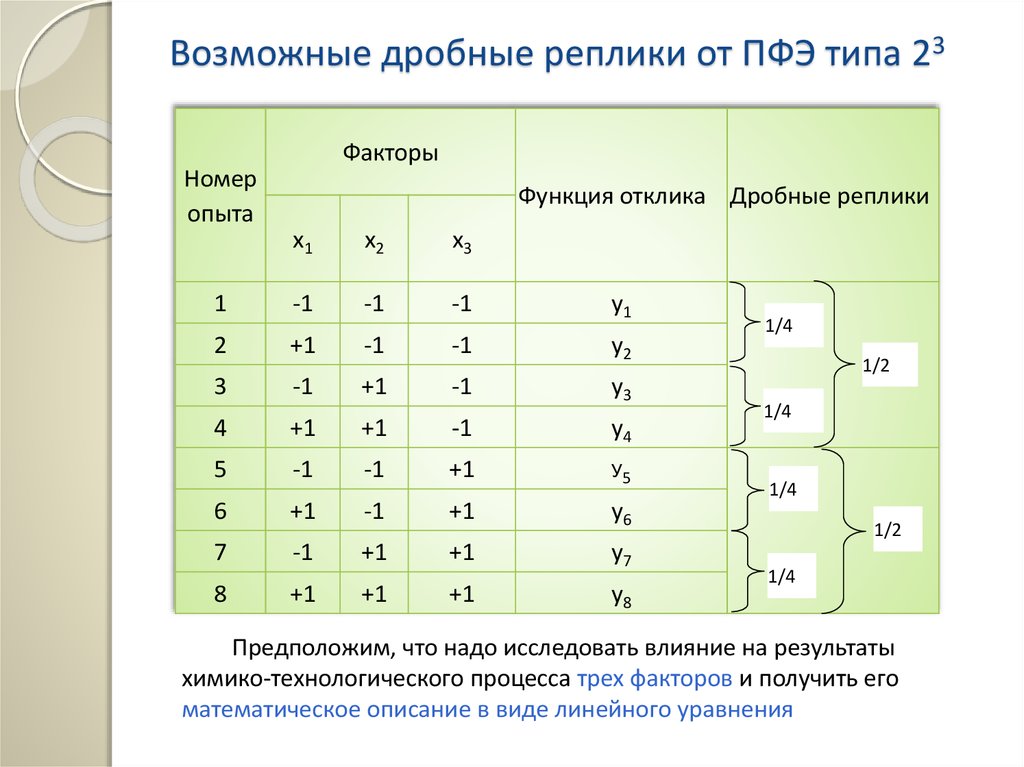

Обобщенное описание:

Пусть матрица

и в нуль-пространстве A есть один вектор, т.е. 1. AB = 0 означает, что каждая строка A при умножении на B обращается в нуль.
2. Значения переменных в каждом образце (представленном строкой) ведут себя одинаково.
3. Это помогает в определении линейных отношений в атрибутах.
4. Каждый нулевой пространственный вектор соответствует одному линейному отношению.

Недействительность:

Недействительность можно определить как количество векторов, присутствующих в пустом пространстве данной матрицы. Другими словами, размерность нулевого пространства матрицы A называется недействительностью матрицы A. Количество линейных отношений между атрибутами определяется размером нулевого пространства. Векторы нулевого пространства B можно использовать для определения этих линейных отношений.

Теорема о недействительности ранга:
Теорема о недействительности ранга помогает нам связать недействительность матрицы данных с рангом и количеством атрибутов в данных. Теорема ранга-недействительности задается формулой –

Недействительность A + Ранг A = Общее количество атрибутов A (т.е. общее количество столбцов в A)

Ранг:
Ранг матрицы ссылается к числу линейно независимых строк или столбцов матрицы.

Пример доказательства ранговой теоремы о недействительности:

Рассмотрим матрицу A с атрибутами {X1, X2, X3}
    1 2 0
А = 2 4 0
    3 6 1
тогда,
Количество столбцов в A = 3

R1 и R3 линейно независимы.
Ранг матрицы  A , которая является
количество ненулевых строк в его эшелонированной форме равно 2.
у нас есть,
АВ = 0

Тогда мы получаем,
б1 + 2*б2 = 0
б3 = 0
Нулевой вектор, который мы можем получить, равен

Количеством параметров в общем решении является размерность
нулевого пространства (которое в этом примере равно 1). Таким образом, сумма
ранг и ничтожность   равно 2 + 1, что
равно количеству столбцов A. 
 

Это отношение ранга и недействительности верно для любой матрицы.

Python Example to find null space of a Matrix:

from sympy import Matrix     A = [[ 1 , 2 , 0 ], [ 2 , 4 , 0 ], [ 3 , 6 , 1 ]]   A = Matrix(A)     NullSpace = A. nullspace()       NullSpace = Matrix(NullSpace)   print ( "Null Space : " , NullSpace)     print (A * NullSpace)

Выход:

Пустое пространство: матрица ([[-2], [1], [0]])
Матрица([[0], [0], [0]])
 

Пример Python для определения недействительности матрицы:

from sympy import Matrix     A = [[ 1 , 2 , 0 ], [ 2 , 4 , 0 ], [ 3 , 6 , 1 ]]      A = Matrix(A)     NoC = A. shape[ 1 ]     rank = A.rank()     nullity = NoC - rank     print ( "Недействительность : " , недействительность)

Вывод:

Недействительность : 1
 

Определение, свойства, ранг и примеры решения

Матрица может быть определена как прямоугольный массив строк, чисел, выражений или символов. Матрица, в которой все элементы равны нулю, называется нулевой матрицей . Существуют различные типы матриц, а именно квадратная матрица, симметричная матрица, диагональная матрица, единичная матрица, треугольная матрица и ортогональная матрица.

Размер матрицы можно определить по количеству строк и столбцов в ней. Нулевая матрица может быть прямоугольной матрицей 2×3, которая обозначает 2 строки и 3 столбца, а также может быть квадратной матрицей 3×3 с 3 строками и 3 столбцами.

В этой статье мы узнаем об определении нулевой матрицы, свойствах нулевой матрицы, сложении и скалярном умножении нулевой матрицы с некоторыми решенными примерами.

Нулевая матрица Определение

Нулевая матрица — это матрица, в которой каждый из элементов равен 0. Нулевая матрица, часто называемая нулевой матрицей, имеет переменное количество строк и столбцов. Поскольку добавление нулевой матрицы к любой другой матрице дает тот же результат, нулевая матрица также известна как аддитивная идентичность предоставленной матрицы. Квадратная матрица с нулевыми элементами также считается нулевая матрица .

\(\begin{bmatrix}0&0&0\\0&0&0\\0&0&0\end{bmatrix}\)

Узнайте больше о тригонометрических тождествах здесь

Ранг нулевой матрицы независимые строки и столбцы. Ранг нулевой матрицы должен быть меньше или равен количеству строк или столбцов, присутствующих в матрице.

Если в матрице нет элементов, пространство столбца заполняется нулями. Нулевое пространство определяется как пространство, которое содержит только нулевое значение и не содержит других чисел. Если это условие выполняется, то ранг становится равным нулю. Нулевые матрицы — это единственная матрица, ранг которой равен 9.0005 0 .

Термин «недействительность» относится к количеству нулей, присутствующих в матрице. Поскольку все значения, текущие в нулевой матрице, равны «0», недействительность нулевой матрицы становится числом элементов, присутствующих в ней, то есть размером матрицы.

Свойства нулевой матрицы

Вот некоторые свойства нулевой матрицы , которые помогают понять основные операции, связанные с нулевой матрицей.

• Квадратная и прямоугольная матрица может быть в виде нулевой матрицы.
• Нулевая матрица может иметь любое количество строк и столбцов.
• Добавление нулевой матрицы никоим образом не меняет структуру матрицы. Это называется аддитивной идентичностью.
• При умножении нулевой матрицы на другую матрицу получается нулевая матрица.
• Нулевые матрицы являются сингулярными, когда бы они ни создавались.

Вас может заинтересовать Окружность круга

Добавление нулевой матрицы

В нулевой матрице все элементы установлены на 0. Например, рассмотрим квадратную матрицу 3 × 3 «A» с элементами, идентичными 4, и нулевую матрицу «B».

\( A=\begin{bmatrix}4 & 4 & 4\\4 & 4 & 4 \\ 4 & 4 & 4\end{bmatrix}\)

\( B=\begin{bmatrix}0 & 0 & 0\\0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}\)

Теперь, если мы сложим матрицу ‘A’ и матрицу ‘B’ (т.е. A+B), мы получим результат, как показано ниже.

\(\begin{bmatrix}4 & 4 & 4\\4 & 4 & 4 \\ 4 & 4 & 4\end{bmatrix} + \begin{bmatrix}0 & 0 & 0\\0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}= \begin{bmatrix}4+0 & 4+0 & 4+0\\4+0 & 4+0 & 4+0 \\ 4+0 & 4 +0 и 4+0\end{bmatrix} = \begin{bmatrix}4&4&4\\4&4&4\\4&4&4\end{bmatrix}\)

Скалярное умножение нулевой матрицы

Мультипликативное свойство — мультипликативное свойство нулевых состояний: «Любое число, умноженное на ноль, дает ноль в произведении». Следовательно, умножение нулевой матрицы на любую другую матрицу дает матрицу произведения, в которой все элементы равны нулю, то есть нулевая матрица.

\(6\cdot\begin{bmatrix}0 & 0 \\0 & 0 \end{bmatrix}=\begin{bmatrix}6\left(0\right) & 6\left(0\right) \\ 6\влево(0\вправо) и 6\влево(0\вправо) \end{bmatrix} = \begin{bmatrix}0 & 0 \\0 & 0 \end{bmatrix}\)

Кроме того, читайте больше о параболе здесь

Является ли нулевая матрица диагональной матрицей?

Квадратная матрица становится диагональной, если все ее недиагональные элементы равны нулю. В нулевой или нулевой матрице все элементы равны нулю. Таким образом, мы можем сказать, что нулевая матрица может быть диагональной матрицей. Вот несколько примеров диагональной матрицы:

\(B= \begin{bmatrix}4 & 0 & 0\\0 & 7 & 0 \\ 0 & 0 & 9 \end{bmatrix}\)

\ (M= \begin{bmatrix}0 & 0 & 7\\0 & 1 & 0 \\ 5 & 0 & 0 \end{bmatrix}\)

Является ли нулевая матрица верхнетреугольной матрицей?

Матрица, в которой все элементы ниже главной диагонали равны нулю, называется верхнетреугольной матрицей. В нулевой матрице все элементы равны нулю, поэтому нулевая матрица также может быть верхней треугольной матрицей. Вот пример верхней треугольной матрицы.

Решенные примеры на нулевой матрице

Для лучшего понимания мы показали несколько решенных примеров на нулевой матрице.

Показать результат вычитания из нулевой матрицы 2×3 матрицы ‘B’ с элементами b11 = 1, b12 = 2, b13 = 7, b21 = -5, b22 = 4 и b23 = -10 «А».

Решение:

Рассмотрим нулевую матрицу 2×3 «A» и другую матрицу 2×3 «B» с другими элементами, как показано ниже.

Теперь, вычитая матрицу B из матрицы A (т.е. A-B), мы получаем результат, как показано ниже:

Показать скалярное умножение нулевой матрицы.

Решение:

Что получится, если матрица 3×3 с элементами a11=2, a12=4, a13=6, a21=6, a22=3, a23=4, a31=5, a32=7, a33=4 добавляется с нулевой матрицей 3×3?

Решение:

Проверим добавление нулевой матрицы. См. сложение нулевой матрицы 3×3 с другой матрицей 3×3 ниже:

\begin{bmatrix}2 & 4 & 6\\6 & 3 & 4 \\ 5 & 7 & 4\end{bmatrix} + \ begin{bmatrix}0 & 0 & 0\\0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix}= \begin{bmatrix}2+0 & 4+0 & 6+0\\6+0 & 3+0 & 4+0 \\ 5+0 & 7+0 & 4+0 \end{bmatrix} = \begin{bmatrix}2 & 4 & 6\\6 & 3 & 4 \\ 5 & 7 & 4\конец{bматрица}

Учащиеся могут воспользоваться преимуществами онлайн-курсов Testbook и серии экзаменов, а также других образовательных ресурсов, охватывающих широкий спектр тем от математики до физики.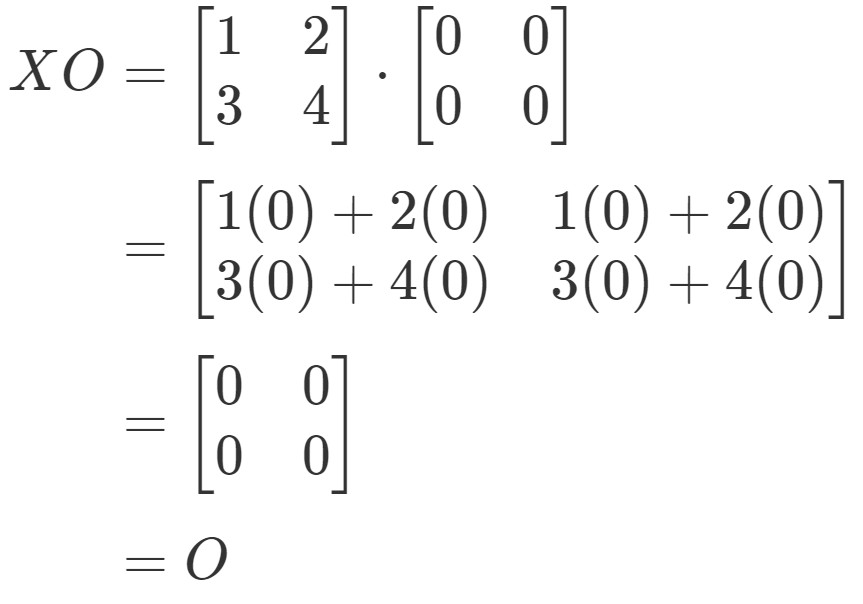 Подготовьтесь к экзамену, скачав приложение Testbook прямо сейчас.

 

Часто задаваемые вопросы о нулевой матрице

В.1 Что такое нулевая матрица и как она обозначается?

Ответ 1 Из-за свойства аддитивной идентичности нулевая матрица допустима. Добавление нулевой матрицы к любой матрице не влияет на ее значение. В результате всякий раз, когда операция должна быть выполнена без изменения важности матрицы, наилучшим выбором являются нулевые матрицы. Нулевая матрица обозначается O или 0 (ноль).

Q.2 Каков ранг нулевой матрицы?

Ответ 2 Размер линейно независимых строк и столбцов нулевой матрицы определяется ее рангом. В нулевых матрицах нет ненулевых строк. В результате он имеет свою строку или столбец. Итак, ранг нулевой матрицы равен нулю.

Q.3 Что такое определитель нулевой матрицы?

Ответ 3 Определитель нулевой матрицы равен нулю.