(курс 68 ч.) §11. Логические выражения
Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, углубленный уровень)
Главная | Информатика и информационно-коммуникационные технологии | Планирование уроков и материалы к урокам | 9 классы | Планирование уроков на учебный год (по учебнику К.Ю. Полякова, Е.А. Еремина, углубленный уровень) | §11. Логические выражения
Содержание урока
Формализация
Таблицы истинности
Составление условий
Логические схемы
Выводы
Вопросы и задания
Любую логическую функцию можно задать с помощью таблицы истинности, которая показывает, чему равно значение логического выражения при всех возможных комбинациях значений исходных переменных. Построим таблицу истинности для выражения
X = А и не В или не А и B,
которое можно также записать в виде
X = А • B + А • В.
Сколько строк в таблице истинности выражения с двумя переменными?
Будем вычислять выражение по частям: добавим в таблицу истинности дополнительные столбцы А • B и А • В, а потом выполним операцию ИЛИ с этими значениями (рис. 2.18).
Рис. 2.18
Из этой таблицы истинности видно, что при некоторых значениях переменных значение X истинно, а при некоторых — ложно. Такие выражения называют вычислимыми.
Высказывание «Вася — школьник или он не учится в школе» всегда истинно (для любого Васи). Выражение, истинное при любых значениях переменных, называется тождественно истинным или тавтологией.
Высказывание «Сегодня безветрие, и дует сильный ветер» никогда не может быть истинным. Соответствующее логическое выражение всегда ложно, оно называется тождественно ложным или противоречием.
Выполните формализацию высказываний, о которых шла речь в последних двух абзацах. Запишите формулы для упрощения каждого из них.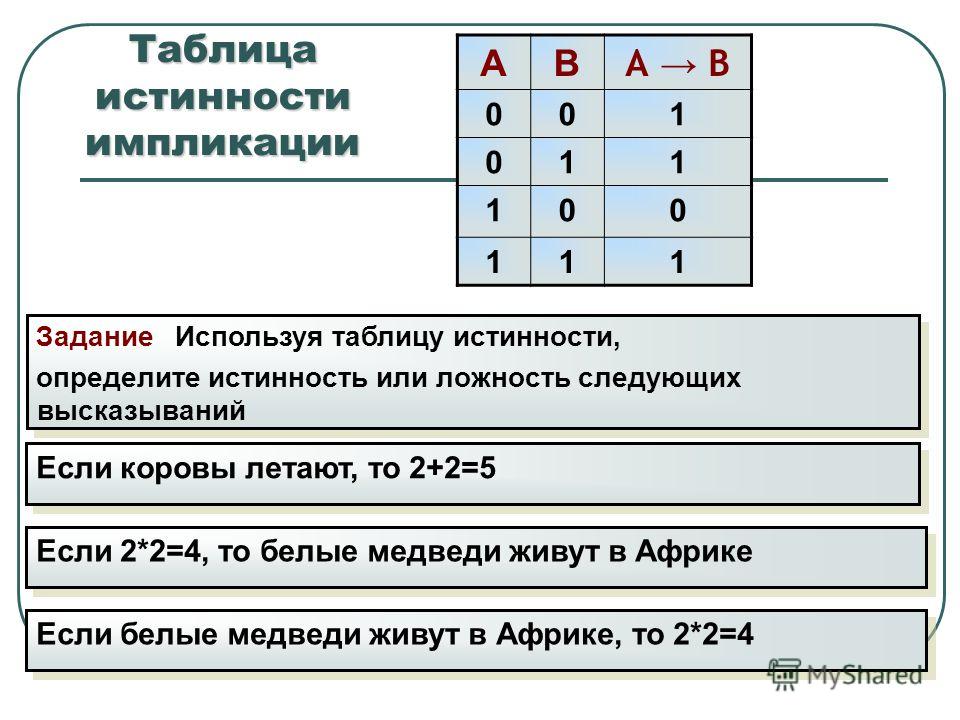
Постройте самостоятельна таблицу истинности логического выражения X = (А + В) • (A + B). Сравните её с таблицей на рис. 2.18. Истинно ли высказывание «Разные логические выражения могут определять одну и ту же логическую функцию»?
Если два выражения принимают одинаковые значения при всех значениях переменных, они называются равносильными или тождественно равными. Равносильные выражения определяют одну и ту же логическую функцию, т. е. при одинаковых исходных данных приводят к одинаковым результатам.
Сколько строк в таблице истинности выражения с тремя переменными?
Постройте таблицу истинности логического выражения
Х = А • В + А • С + В • С.
Предположим, что нам известна только часть таблицы истинности для функции трёх переменных (рис. 2.19).
Рис. 2.19
Как вы думаете, можно ли по такой части таблицы истинности определить логическую функцию? Почему?
Всего в таблице истинности функции от трёх переменных 23 = 8 строк, для каждой из них нужно знать, чему равно значение функции.
Сколько различных значений можно закодировать с помощью 5 бит?
Как вы нашли это значение?
Итак, таблице на рис. 2.19 могут соответствовать 32 различные логические функции. Проверим, подходят ли следующие варианты:
а) А + В + C;
б) A • С + В;
в) А + B • С;
г) А • В • C;
д) A • B + C.
Прежде всего, заметим, что в столбце значений функции два нуля и одна единица. Следовательно, вариант а) не подходит, потому что цепочка операций ИЛИ со всеми переменными (или их инверсиями, обратными значениями) даст только один ноль — в случае, когда все слагаемые равны нулю.
Проверяем вариант б), подставляя значения переменных А, В и С сначала из первой строки таблицы, потом из второй и третьей. В первой строке получаем A • С + В = 1 • 1 + 0 = 1, этот результат совпадает со значением функции в этой строке.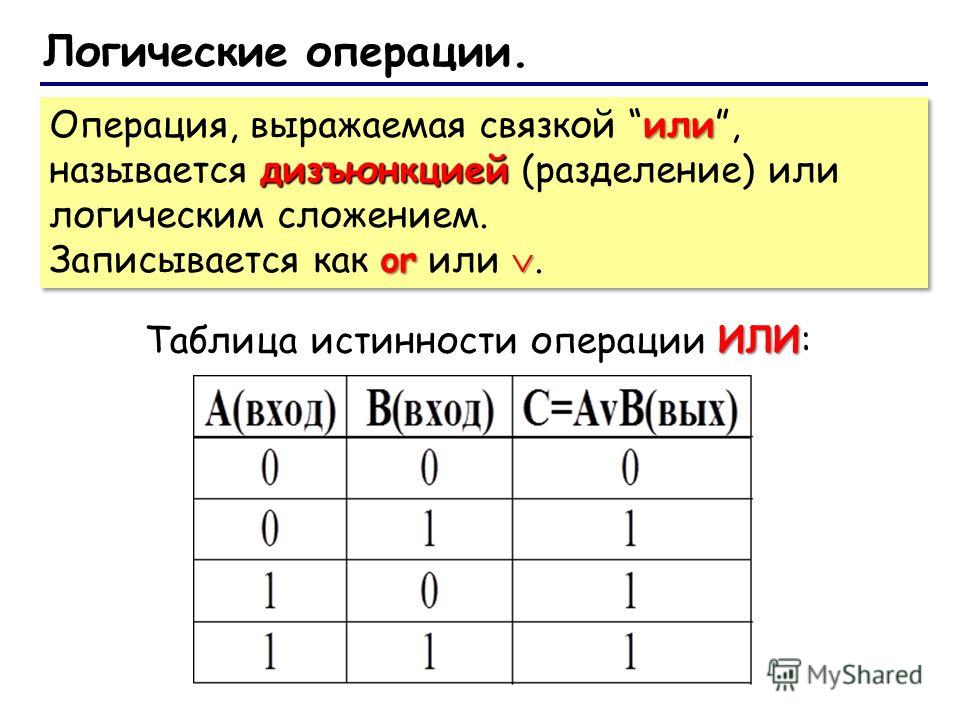
Проверьте самостоятельно, подходят ли остальные варианты.
Скажите без вычислений, сколько нулей и сколько единиц должно быть в последнем столбце таблицы истинности функций с тремя переменными:
а) А + B + C;
б) A • С • В;
в) А • B • C;
г) A + В + С;
д) A + B + C.
Теперь предположим, что нам известна часть таблицы какой-то логической функции, причём с пропусками (рис. 2.20).
Рис. 2.20
Выясним, какие из следующих функций могут соответствовать этой таблице:
а) A + В + C;
б) A • С • В;
в) А + B + C;
г) А • B • С;
д) А + В + C.
Во-первых, обратим внимание, что в столбце значений функции две единицы, поэтому сразу делаем вывод, что это не могут быть цепочки двух операций И (ответы б) и г) неверные).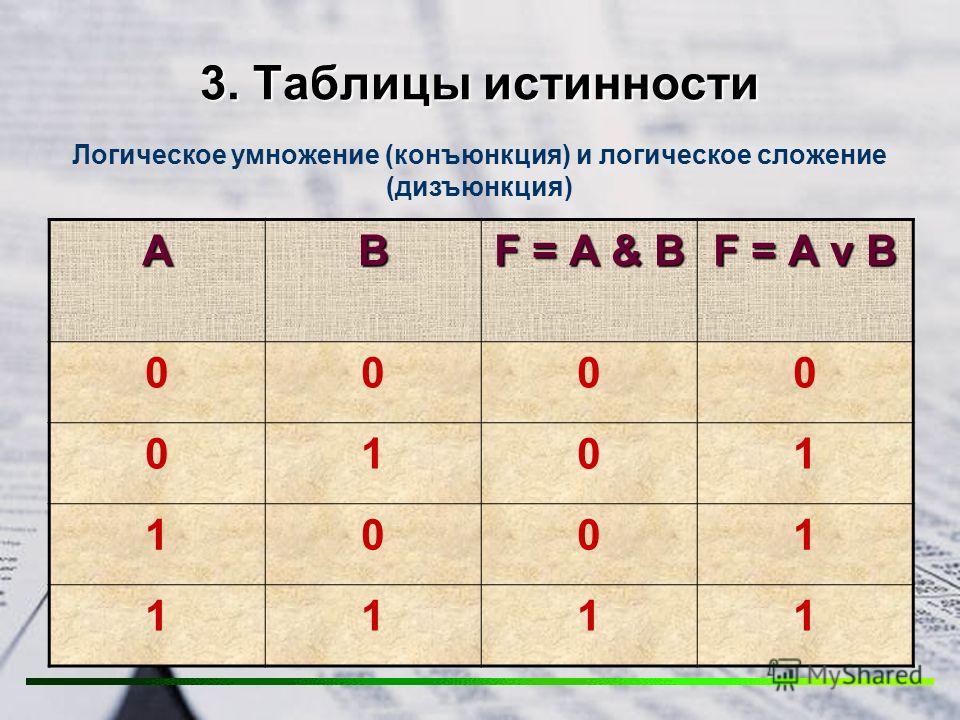 Остались три цепочки из операций ИЛИ, причём для верхней строки (при А = 0 и С = 1) мы должны получить 0 при каком-то выборе неизвестного значения В. Подставляем А = 0 и С = 1 в формулы-кандидаты:
Остались три цепочки из операций ИЛИ, причём для верхней строки (при А = 0 и С = 1) мы должны получить 0 при каком-то выборе неизвестного значения В. Подставляем А = 0 и С = 1 в формулы-кандидаты:
а) 1 + В + 0;
в) 0 + B + 0;
д) 0 + В + 0.
Видим, что в случае а) сумма не может быть равна нулю, это неверный ответ. А варианты в) и д) подходят: в первом из них нужно в первой строке поставить в пустую ячейку 1, а во втором — 0.
Кратко решение можно записать так:
1) поскольку в столбце значений функции один ноль, это не может быть цепочка операций И; остаются только цепочки операций ИЛИ;
2) для того чтобы получить нулевое значение функции в первой строке таблицы, нужно, чтобы переменная А (равная 0 в этой строке) входила в логическую сумму без инверсии (к ней не должна применяться операция НЕ) а переменная С (равная 1) — с инверсией;
3) этим условиям удовлетворяют функции в) и д).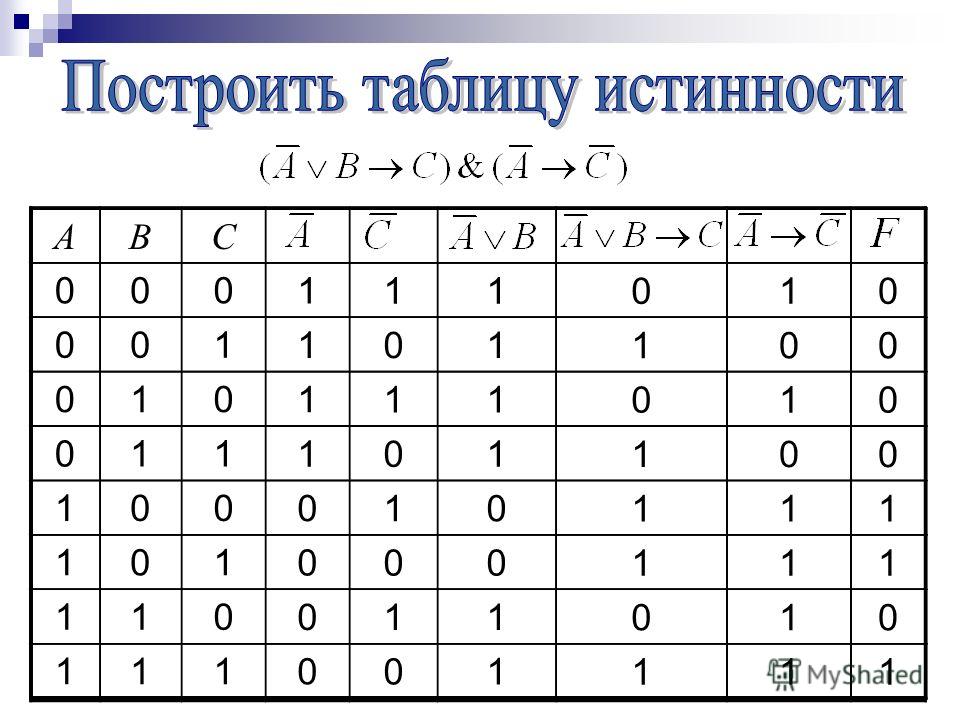
Известна часть таблицы какой-то логической функции с пропусками (рис. 2.21).
Рис. 2.21
Выясните, какие из следующих функций могут соответствовать этой таблице:
а) А • B + C;
б) A • С • В;
в) А + B + C;
г) А • B • С;
д) А + B + C.
Следующая страница Составление условий
Cкачать материалы урока
Таблица истинности логических выражений с примерами решения
Содержание:
- Свойства логических операций
- Законы алгебры логики могут быть доказаны с помощью таблиц истинности
- Примеры с решением
Построение таблиц истинности для логических выражений
Для логического выражения можно построить таблицу истинности, показывающую, какие значения принимает выражение при всех наборах значений входящих в него переменных.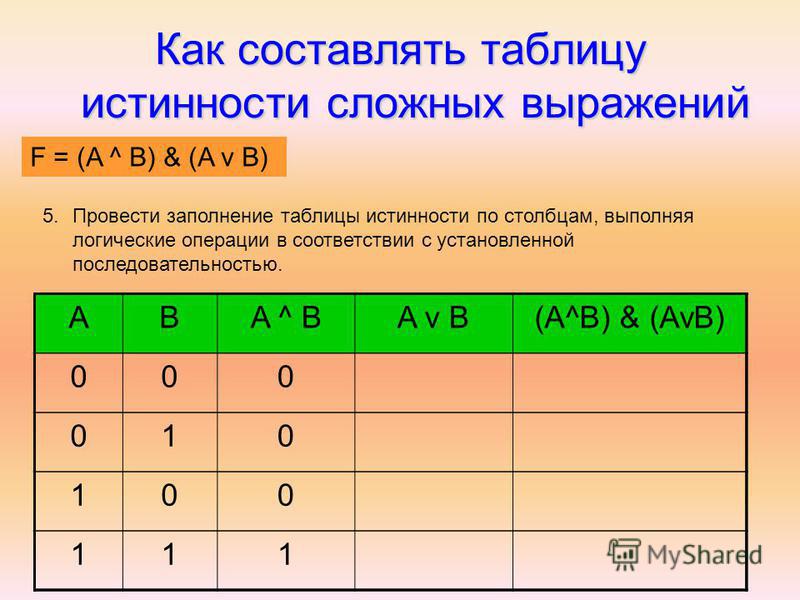 Для построения таблицы истинности следует:
Для построения таблицы истинности следует:
- подсчитать п — число переменных в выражении;
- подсчитать общее число логических операций в выражении;
- установить последовательность выполнения логических операций с учётом скобок и приоритетов;
- определить число столбцов в таблице: число переменных + число операций;
- заполнить шапку таблицы, включив в неё переменные и операции в соответствии с последовательностью, установленной в п. 3;
- определить число строк в таблице (не считая шапки таблицы): ;
- выписать наборы входных переменных с учётом того, что они представляют собой ряд целых п-разрядных двоичных чисел от 0 до ;
- провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью.
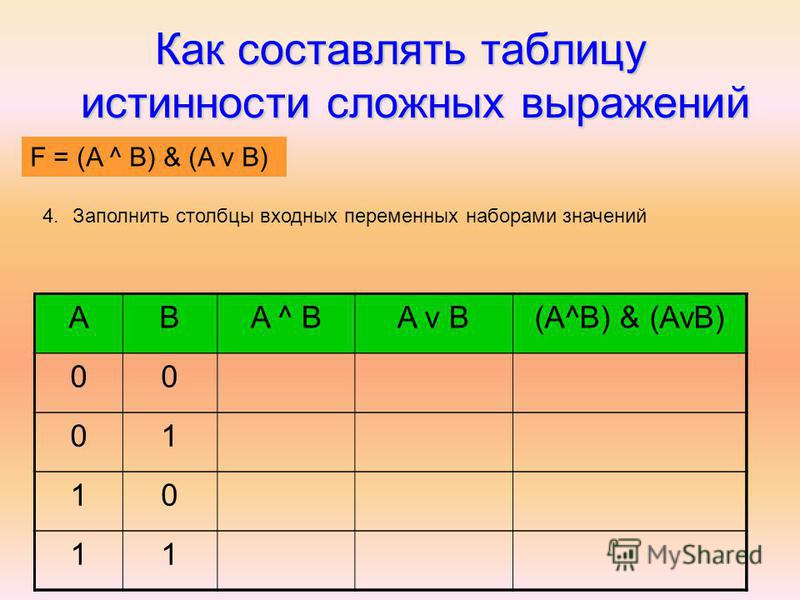
Построим таблицу истинности для логического выражения нём две переменные, две операции, причём сначала выполняется конъюнкция, а затем — дизъюнкция. Всего в таблице будет четыре столбца:
- Наборы входных переменных — это целые числа от 0 до 3, представленные в двухразрядном двоичном коде: 00, 01, 10, 11.

По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Заполненная таблица истинности имеет вид:
Обратите внимание, что последний столбец (результат) совпал со столбцом А. В таком случае говорят, что логическое выражение равносильно логической переменной А.
Возможно вам будут полезны данные страницы:
Интервал сходимости степенного ряда |
Примеры решений пределов с корнями |
Найти производную функции |
Уравнения касательной и нормали |
Свойства логических операций
Рассмотрим основные свойства логических операций, называемые также законами алгебры логики.
1. Переместительный (коммутативный) закон:
• для логического умножения:
• для логического сложения:
2. Сочетательный (ассоциативный) закон:
• для логического умножения:
• для логического сложения:
При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.
3. Распределительный (дистрибутивный) закон:
• для логического умножения:
• для логического сложения:
4. Закон двойного отрицания:
Двойное отрицание исключает отрицание.
5. Закон исключённого третьего:
• для логического умножения:
• для логического сложения:
Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
6. Закон повторения:
• для логического умножения:
• для логического сложения:
7. Законы операций с 0 и 1:
• для логического умножения:
• для логического сложения:
8. Законы общей инверсии:
Законы общей инверсии:
• для логического умножения:
• для логического сложения:
Законы алгебры логики могут быть доказаны с помощью таблиц истинности
Докажем распределительный закон для логического сложения:
Совпадение значений в столбцах, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.
Примеры с решением
Пример 1.
Найдём значение логического выражения для числа X = 0.
Решение:
При X = 0 получаем следующее логическое выражение: . Так как логические выражения 0 < 3, 0 < 2 истинны, то, подставив их значения в логическое выражение, получаем:
Для решения задач вам понадобится знание таблиц истинности логических операций:
А также, вы должны знать:
Порядок выполнения логических операций задается круглыми скобками
Сначала выполняется операция отрицания НЕ
затем И
после И выполняется ИЛИ
затем следование
и в последнюю очередь — эквивалентность.
Задача 1
Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
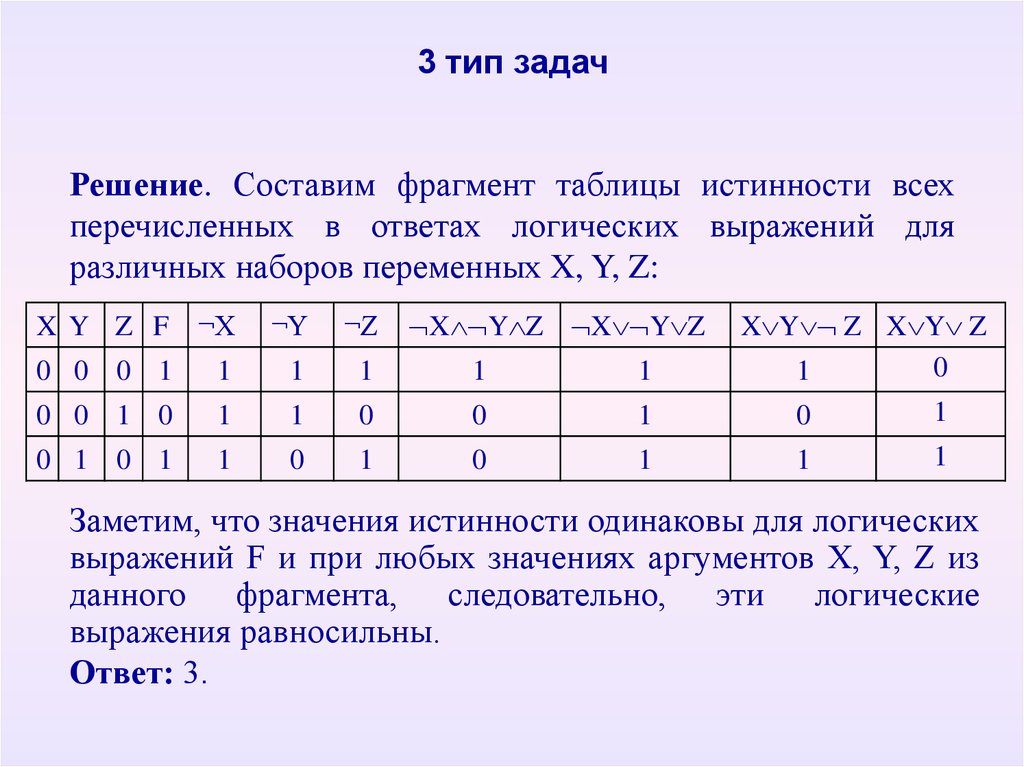
Решение:
Чтобы определить верное выражение, надо значения А,В,С каждой из строк таблицы подставить в очередное выражение, определить его результат выполнения и сравнить со значением F соответствующей строки.
То выражение, значения которого совпадут со значениями столбца F, и будет искомым. Решение:
Ответ: 4
Задача 2
Дан фрагмент таблицы истинности выражения F:
Каким выражением может быть F?
Решение:
Обратите внимание:
1) В каждом из приведенных выражений логические переменные связывает только один тип логической операции. В 1 и 3 вариантах это операция И (), во 2 и 4 вариантах это операция ИЛИ ().
2) По столбцу F видно, что выражение для двух комбинаций данных истинно, а для одной — ложно. Следовательно, выражение не может быть логическим умножением (И), так как логическое умножение истинно только для одной комбинации данных, а в таблице две истины. Следовательно, искомое выражение является логическим сложением (ИЛИ) значений логических переменных.
Следовательно, искомое выражение является логическим сложением (ИЛИ) значений логических переменных.
Поэтому, в качестве ответа может быть 2 или 4 вариант. Рассмотрим их.
1) 2-й вариант: В первой строке таблицы истинности отображены только значения х1, хЗ, х5, и все они равны 0. Но в формуле 2го варианта у нас х5 отрицается, то есть значение х5 будет изменено на 1, и в результате всё выражение должно быть истинным. Что не соответствует заданной таблице. Остаётся 4-й вариант.
2) Как мы видим, переменные х1, хЗ и х5 в 4-м варианте ответа не отрицаются, что соответствует первой строке заданной таблицы.
Ответ: 4
Задача 4
Какое из приведенных имен сказочных героев удовлетворяет логическому условию:
1) АРТЕМОН
2) БАЗИЛИО
3) БУРАТИНО
4) МАЛЬВИНА
Решение:
Составим для каждого из предложенных ответов схему соответственно заданной логической формуле. Ищем истинное значение.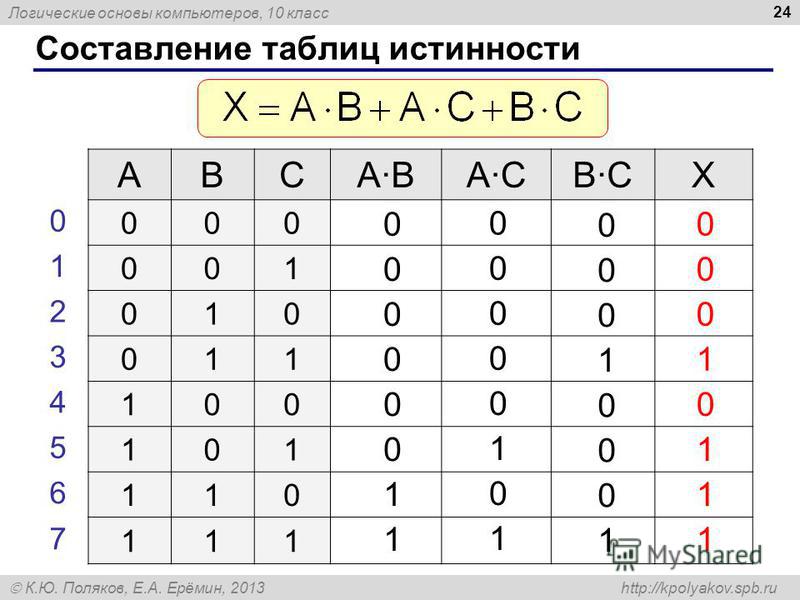
1) АРТЕМОН
Первая буква согласная — НЕТ (0)
Вторая буква не А — ДА (1)
Последняя буква гласная — НЕТ (0) \ / \ у
Предпоследняя буква гласная — ДА (1) X» ‘»X X»
Подставляем полученные значения в формулу и решаем ее: н 0 ->1 ) л 0 -> 1 ),= О
И так с каждым вариантом ответа, пока не найдете истину.
Задача 5
Логическая функция F задаётся выражением
Определите, какому столбцу таблицы истинности функции F соответствует каждая из
переменных X, Y, Z
Решение 1:
Последней операцией выполнения является операция . Поэтому выражение имеет значение ИСТИНА, когда
Рассмотрим все случаи, когда F = 1 (это значения в строках 1 и 3): — не рассматриваем, т.к. в табл, нет строки, где все значения логических переменных = 1.
Рассматриваем только 1 и 3 строки таблицы:
- две единицы в 3-м столбце => это значения X
- два нуля в 1-м столбце => это значения Y
- ноль единица во 2-м столбце => это значения Z
Ответ: YZX
Решение 2:
Последней операцией выполнения является операция .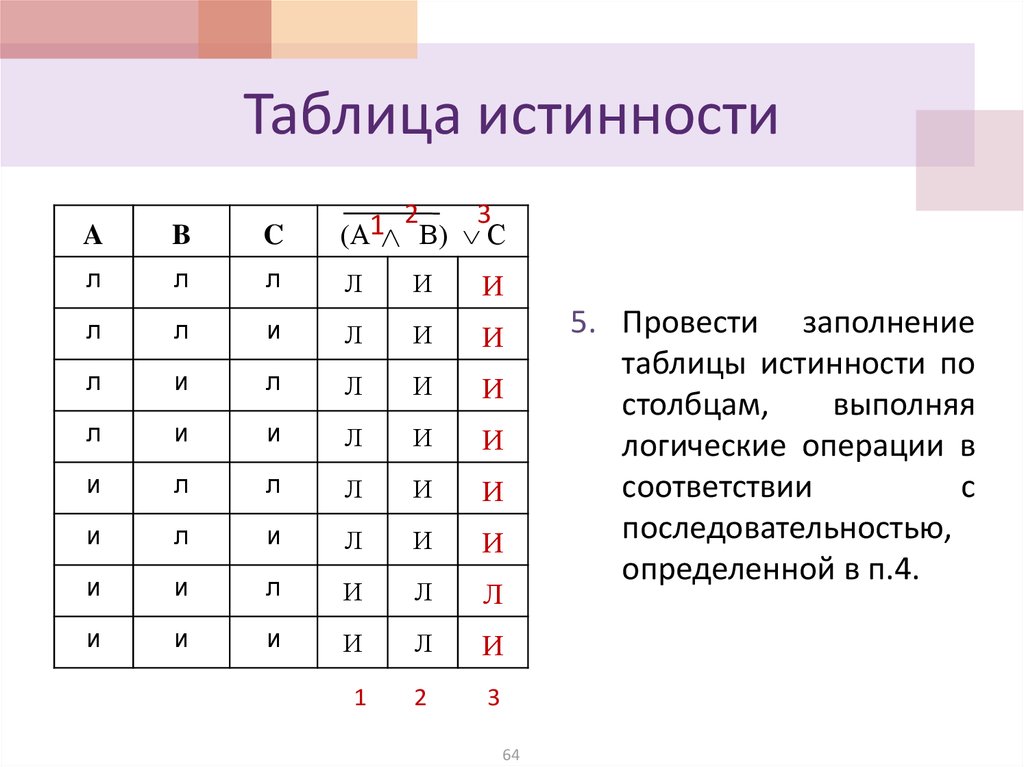 Поэтому выражение
Поэтому выражение
имеет значение ИСТИНА, когда
Выражение F равно 1 в 1й и Зй строках, в этих же строках только “Перем.3”=1, следовательно, значение X находится в 3-м столбце.
Теперь рассмотрим построчно значения 1-х двух столбцов:
(помним, что 1 -> 0 = 0, в остальных комбинациях =1)
1 строка: 0 и О, Y = Z. Поэтому Y и Z для столбцов не определить.
2 строка: 0 и 1. Независимо будет ли Y=0 Z=1 или Y=1 Z=0, функция F=0 т.к. уже
Х=0. Поэтому Y и Z для столбцов не определить.
3 строка: 0 и 1. В этой строке функция F=1, значит Комбинация
невозможна, иначе F будет = 0. Комбинация то, что надо. Следовательно, значение Y находится в 1-м столбце а значение Z во 2-м.
Ответ: YZX
Алгоритм построения таблицы истинности
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
⇐ ПредыдущаяСтр 3 из 11Следующая ⇒ При построении таблицы истинности целесообразно руководствоваться определенной последовательностью действий. 1. Определите количество строк в таблице. Если количество логических переменных равно n, то количество строк = 2n. 2. Определите количество столбцов, которое будет равно количеству переменных + количество логических операций. 3. Постройте таблицу, заполните шапку и внесите возможные наборы значений исходных логических переменных. 4. Заполните таблицу истинности по столбцам, выполняя базовые логические операции в необходимой последовательности. Пример 1. Для формулы A & (B V C) построить таблицу истинности. Количество логических переменных 3, следовательно, количество строк – 23 = 8. Количество логических операций в формуле – 2. Количество столбцов равно 2 + 3 = 5. Далее строим таблицу истинности по заданному алгоритму.
Таблица 13 -Таблица истинности
Исходные данные 1. Таблица 14 -Фрагмент таблицы истинности выражения F
Какое выражение соответствует F: a) X V Y V Z; b) X & Y & Z; c) X & Y & Z; d) X V Y V Z.
Для того чтобы определить, какое выражение соответствует F, необходимо составить фрагменты таблиц истинности для всех приведенных вариантов. 2. По заданному преподавателем варианту из таблицы 15 составить таблицу истинности для заданной формулы. При каких значениях A, B. Таблица 15- Выбор исходных данных
Содержание отчета 1. Номер, название темы практического занятия. 2. Цель практического занятия. 3. Результаты выполнения работы: построение таблиц истинности. 4. Выводы по работе. Контрольные вопросы 1. Перечислите основные логические операции. 2. Заполните таблицы истинности для следующих логических операций: логического отрицания, дизъюнкции, конъюнкции. 3. Поясните, в каком случае строится таблица истинности. 4. Скажите, чему равно количество строк в таблице истинности. 5. Скажите, чему равно количество столбцов в таблице истинности. 6. Сформулируйте алгоритм заполнения таблицы истинности для сложной логической формулы. Практическая работа 4 «Построение логических схем по заданным выражениям» Цель: изучить основные логические элементы, научиться строить логические схемы по заданным логическим выражениям. Теоретические сведения Основой всех компьютерных устройств, построенных по цифровому принципу, являются логические элементы – преобразователи. Логические элементы (преобразователи) могут, получая сигналы об истинности отдельных простых высказываний, обработать их и в результате выдать значение логического произведения или логической суммы, или отрицания. Из логических элементов (вентилей) составляют более сложные схемы, которые позволяют выполнять арифметические операции и хранить информацию. Процесс разработки общей логической схемы устройства (в том числе и компьютера в целом), становится иерархическим, причем на каждом следующем уровне в качестве «кирпичиков» используются логические схемы, созданные на предыдущем этапе. Логический элемент И реализует конъюнкцию двух или более логических значений (табл. 16).
Таблица 16 -Логический элемент И
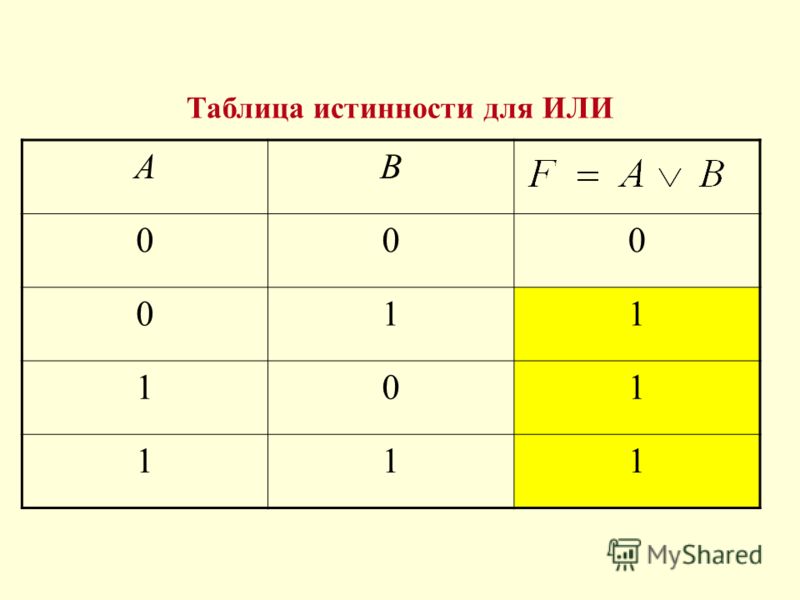
Логический элемент ИЛИ реализует дизъюнкцию двух или более логических значений (табл.
Таблица 17-Логический элемент ИЛИ
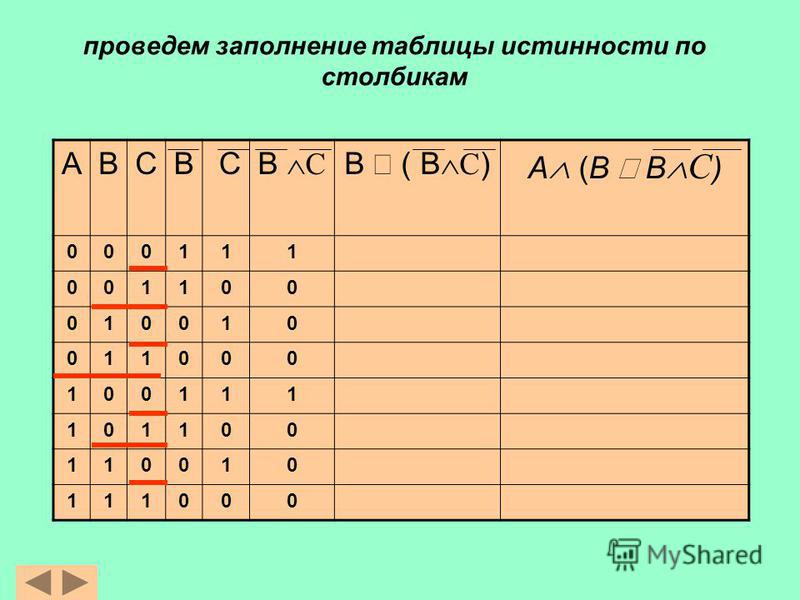
Логический элемент НЕ реализует логическую функцию «инверсия» (табл. 18). Таблица 18 -Логический элемент НЕ
|
Как составить таблицу истинности
Как составить таблицу истинности
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Домашняя страница > Логика > Символическая логика > Таблицы истинности | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Философия 103: Введение в логику Как составить таблицу истинности Аннотация: Объясняются и иллюстрируются общие принципы построения таблиц истинности.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Отправляйте исправления или предложения по адресу webmaster@philosophy.lander.edu | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Аргументы | Язык | Заблуждения | Предложения | Силлогизмы | Перевод | Символический | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Как составить таблицу истинности за девять простых шагов
Как составить таблицу истинности за девять простых шаговФилософия 4: Логика и Критика Думая
Сьерра-колледж
Осень 2004 г.
Инструктор: Аль Чинелли
Шаг 1. Выясните, сколько отдельных переменные утверждения находятся в аргументе или составном утверждении, которое вы будете анализировать, т.е. сколько человек письма, представляющие пункты формулы .
Пример 1. Вот аргумент: A -> (B v C)
~B
~C / ~А
Аргумент содержит три переменные индивидуального требования : A, B, C.
Шаг 2. Каждая переменная утверждения имеет две истины значения: Истина или Ложь.
Вот полезная формула чтобы узнать, сколько строк вам понадобится для таблицы истинности:
Возьмите общее количество независимых переменные претензии, которые вам нужно построить, и сделать это показателем степени 2. Значение для этого показателя — количество необходимых строк.
Один переменная требования: P = две строки, 2 1 .
Два переменные: P, Q = четыре строки, 2 2 .
Три переменные: P, Q, R = восемь строк, 2 3 .
Четыре переменные: P, Q, R, S = шестнадцать строк, 2 4 и так далее.
Пример 2. Аргумент в примере 1 имеет три отдельные переменные заявки.
Следовательно его таблица истинности будет состоять из восьми строк.
Шаг 3. Создайте столбец для каждого отдельного
утверждение и составное утверждение в утверждении или аргументе, который вы анализируете.
Создайте столбец для каждого отдельного
утверждение и составное утверждение в утверждении или аргументе, который вы анализируете.
Сделать отдельные столбцы для: i) отдельные требования, представленные буквами переменных требований, ii) скобочные претензии (претензии внутри претензии), iii) все помещения и iv) заключение рассуждения.
Пример 3. Аргумент в примере у одного есть восемь отдельных утверждений: A, B, C, (B v C), A -> (B v C), ~ B, ~ C и ~А.
Шаг 4. Ваша таблица истинности должна содержать полные возможности истинности для всех утверждений. Для этого нужно перечислить возможности истинности для каждой переменной утверждения.
Возьмите первую переменную претензии, назначьте это значение T для верхней половины строк и F для нижней половины.
Затем возьмите вторую переменную претензии и присвойте ему значение T для первой и третьей четвертей строк.
Для третьей переменной претензии присвоить
Значения T и F для чередующихся восьмых строк и чередующихся шестнадцатых
для четвертой переменной, чередуя тридцать секунд и шестьдесят четвертых для
переменные пятого и шестого индивидуальных требований.
Продолжайте назначать значения истинности попеременно соответствующими показателями двух для каждой дополнительной индивидуальной переменной претензии.
Пример 4. Присвоения значений истинности для отдельных переменных утверждения для аргумента в пример 1.
А | Б | С | Б против С | А -> (Б против С) | ~Б | ~С | ~А |
Т | Т | Т |
|
|
|
|
|
Т | Т | Ф |
|
|
|
|
|
Т | Ф | Т |
|
|
|
|
|
Т | Ф | Ф |
|
|
|
|
|
Ф | Т | Т |
|
|
|
|
|
Ф | Т | Ф |
|
|
|
|
|
Ф | Ф | Т |
|
|
|
|
|
Ф | Ф | Ф |
|
|
|
|
|
Шаг 5. Назначьте соответствующие значения истинности
к составным утверждениям, основанным на: а) значениях истинности отдельного утверждения
переменные и б) логическая связь между более простыми утверждениями в
Претензия к компонентам. Работайте от самых простых составных утверждений к самым сложным.
Назначьте соответствующие значения истинности
к составным утверждениям, основанным на: а) значениях истинности отдельного утверждения
переменные и б) логическая связь между более простыми утверждениями в
Претензия к компонентам. Работайте от самых простых составных утверждений к самым сложным.
Пример 5. Присвоение значения истинности для всех переменных утверждений для аргумента в примере 1.
А | Б | С | Б против С | А -> (Б против С) | ~Б | ~С | ~А |
Т | Т | Т | Т | Т | Ф | Ф | Ф |
Т | Т | Ф | Т | Т | Ф | Т | Ф |
Т | Ф | Т | Т | Т | Т | Ф | Ф |
Т | Ф | Ф | Ф | Ф | Т | Т | Ф |
Ф | Т | Т | Т | Т | Ф | Ф | Т |
Ф | Т | Ф | Т | Т | Ф | Т | Т |
Ф | Ф | Т | Т | Т | Т | Ф | Т |
Ф | Ф | Ф | Ф | Т | Т | Т | Т |
Шаг 6. Если вы строите график одного соединения
утверждение в таблице истинности, сравните его с другими утверждениями, которые вы построили. Если
значения истинности утверждения эквивалентны для одних и тех же назначений истинности
переменные индивидуального утверждения, то два составных утверждения эквивалентны.
Если вы строите график одного соединения
утверждение в таблице истинности, сравните его с другими утверждениями, которые вы построили. Если
значения истинности утверждения эквивалентны для одних и тех же назначений истинности
переменные индивидуального утверждения, то два составных утверждения эквивалентны.
Шаг 7. Чтобы определить действительность аргумент, установить возможные значения истинности для всех отдельных аргументов переменные претензии, составные претензии, предпосылки и вывод. Вычеркнуть все строки в котором вывод верен. Затем вычеркните все строки, в которых есть какие-либо или все посылки ложны. Если строк не осталось, то аргумент является действительным. Если есть одна или несколько строк, содержащих все назначенные помещения значение T, в то время как заключение ложно, аргумент недействителен.
Пример 7а. Удалите строки, в которых вывод верный.
А | Б | С | Б против С | P1: А -> (Б против С) | Ч2: ~В | Р3: ~С | Конц. |
Т | Т | Т | Т | Т | Ф | Ф | Ф |
Т | Т | Ф | Т | Т | Ф | Т | Ф |
Т | Ф | Т | Т | Т | Т | Ф | Ф |
Т | Ф | Ф | Ф | Ф | Т | Т | Ф |
Пример 7б.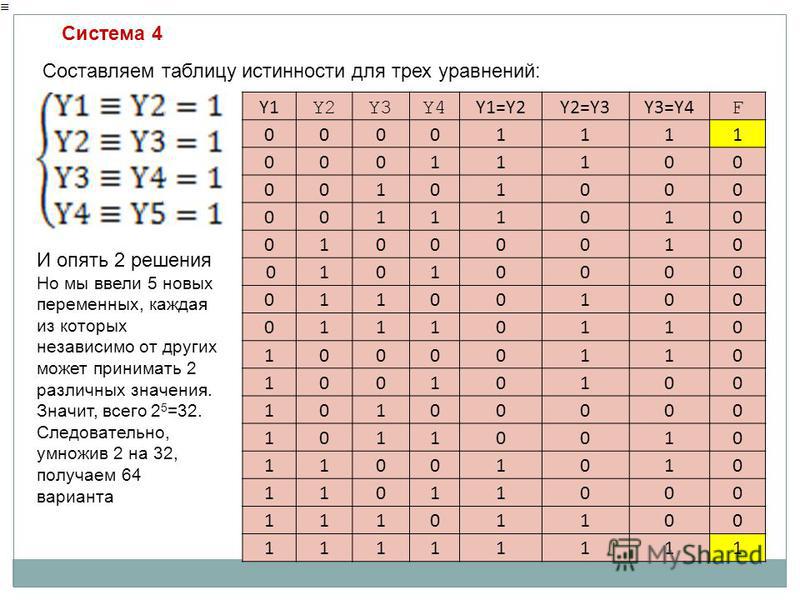 Исключите ряды, в которых одно или все помещения
являются ложными.
Исключите ряды, в которых одно или все помещения
являются ложными.
| P1: А -> (Б против С) | Р2: ~В | Р3: ~С | Конц.: ~A |
х | Т | Ф | Ф | Ф |
х | Т | Ф | Т | Ф |
х | Т | Т | Ф | Ф |
х | Ф | Т | Т | Ф |
Все остальные строки
содержат хотя бы одну ложную посылку, следовательно, аргумент верен.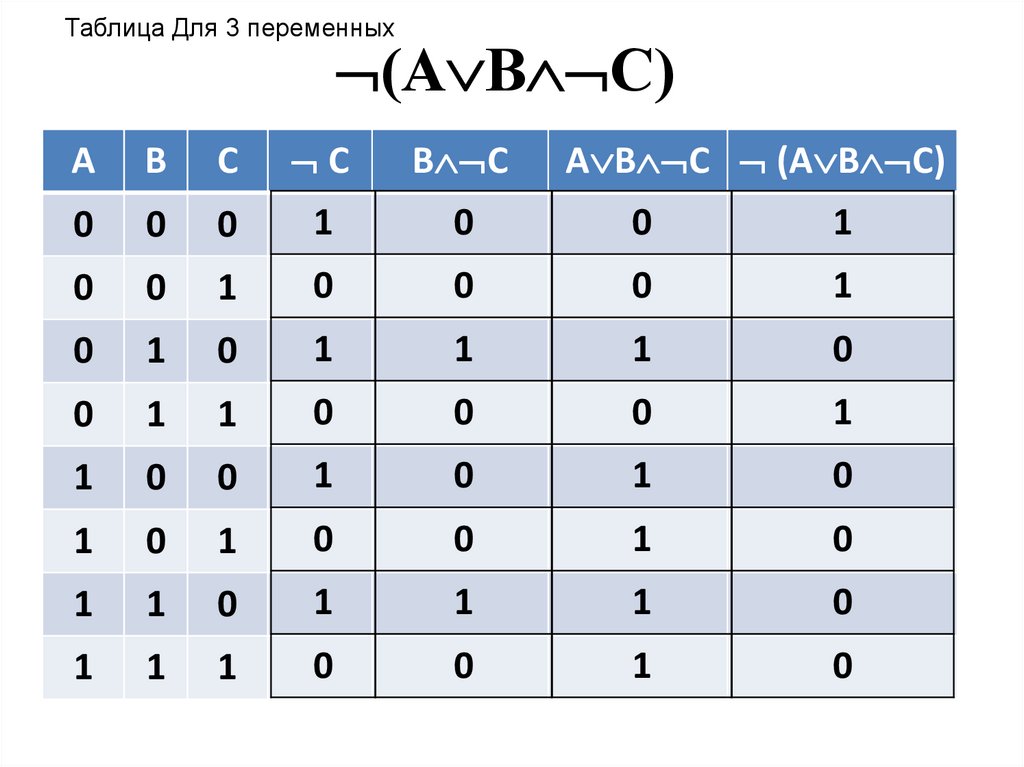
Шаг 8. Для определения достоверности с помощью Версия таблиц истинности с «короткой таблицей», отображающая все столбцы обычной истины. таблицу, затем создайте одну или две строки, где вы назначаете вывод об истине значение F и присвоить всем посылкам значение T.
Пример 8. Два ряды с ложным выводом.
А | Б | С | Б против С | P1: А -> (Б против С) | Ч2: ~В | Р3: ~С | Конц.: ~A |
|
|
|
| Т | Т | Т | Ф |
Шаг 9.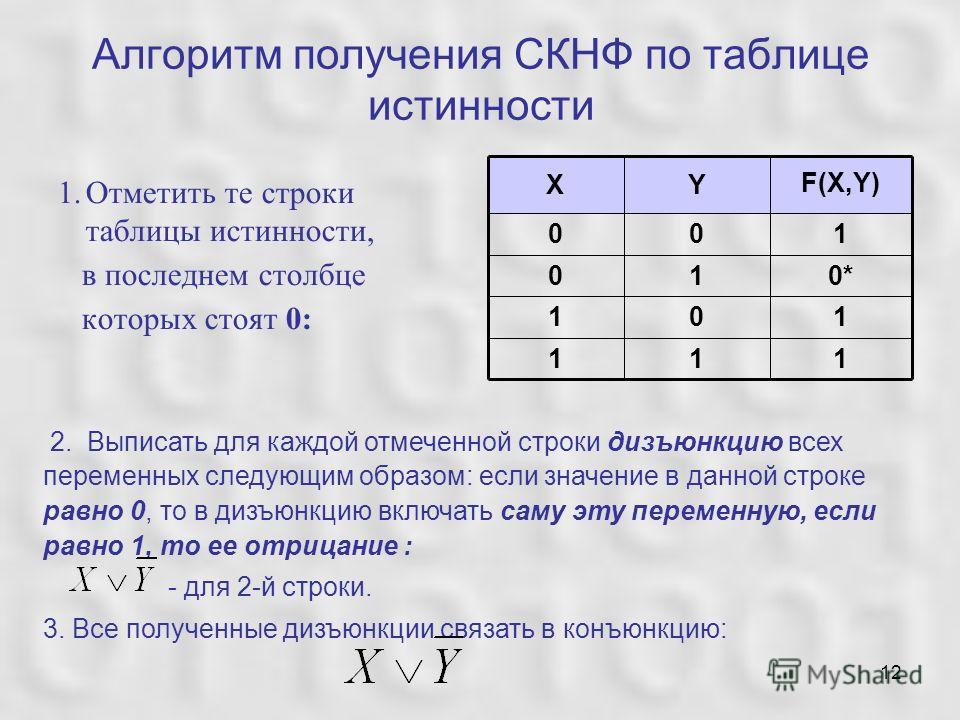 Работайте в обратном направлении от заключения и посылок.
Работайте в обратном направлении от заключения и посылок.
Можете ли вы присвоить значения истинности составные претензии и переменные индивидуальных претензий, которые согласуются с значения истинности, присвоенные посылкам и заключению?
Если сможете, продемонстрируйте, что аргумент неверный. Если вы не можете, это означает, что аргумент действителен.
Некоторые пробы и ошибки здесь может понадобиться.
Пример 9. Если вы знаете, что ~A неверно, что еще можно вывести? Присвойте истинностное значение T помещениям. Будут эта работа?
А | Б | С | Б против С | P1: А -> (Б против С) | Р2: ~В | Р3: ~С | Конц. |
Т | Ф | Ф | хххх | Т | Т | Т | Ф |
(B v C) должно быть правдой чтобы P:1 было правдой. (B v C) не может быть истинным, если B и C оба ложны.
2.8: Таблицы истинности — K12 LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 2146
Пока мы знаем эти символы для логики:
- \(\sim\) не (отрицание)
- \(\стрелка вправо\) если-то
- \(\поэтому\) поэтому
Еще два символа:
- \(\клин\) и
- \(\лор\) или
Мы бы написали «\(p\) и \(q\)» как \(p\клин q\) и «\(p\) или \(q\)» как \(p\lor q\) .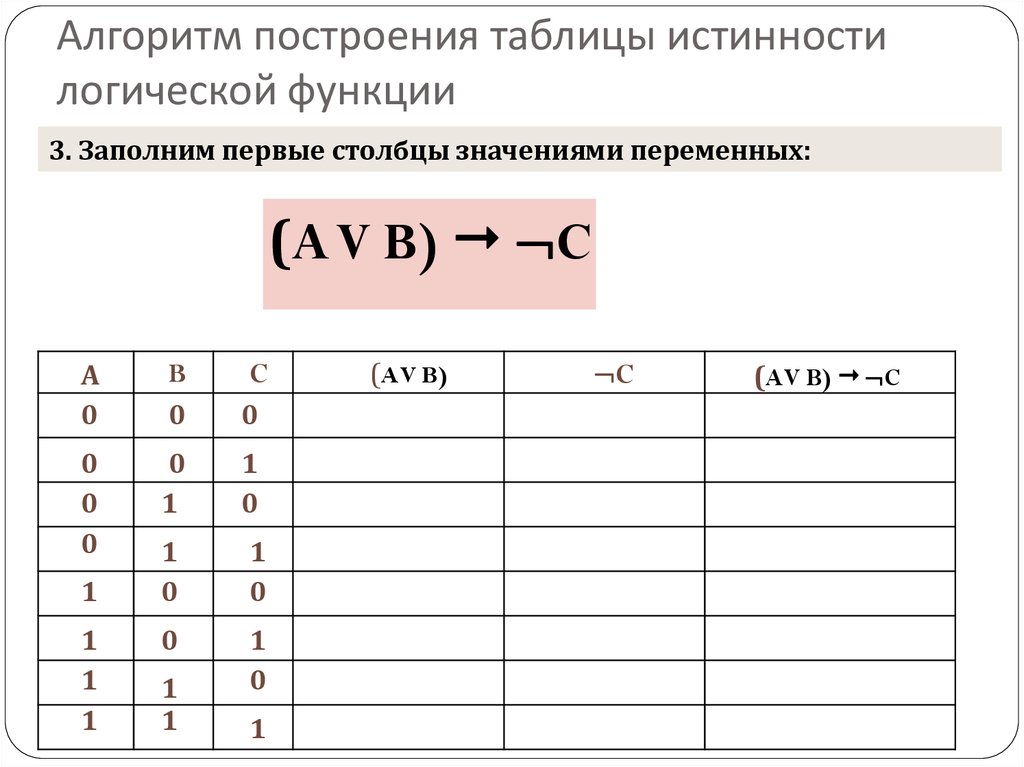
Таблицы истинности используют эти символы и представляют собой еще один способ анализа логики. Во-первых, давайте свяжем p и \sim p. Чтобы было проще, установите p как: Четное число. Следовательно, \sim p равно Нечетное число . Составьте таблицу истинности, чтобы узнать, верны ли они оба. Начните со всех «истин» p, истинных (T) или ложных (F).
Далее мы записываем соответствующие значения истинности для \(\sim p\). \(\sim p\) имеет значения истинности, противоположные \(p\). Итак, если \(p\) истинно, то \(\sim p\) ложно, и наоборот.
| стр | \sim p |
|---|---|
| Т | Ф |
| Ф | Т |
Резюме:
- Начать таблицы истинности со всеми возможными комбинациями истин.
 Для 2 переменных есть 4 комбинации, для 3 переменных есть 8. Вы всегда начинаете таблицу истинности таким образом.
Для 2 переменных есть 4 комбинации, для 3 переменных есть 8. Вы всегда начинаете таблицу истинности таким образом. - Выполните отрицание любой из переменных.
- Любые комбинации в скобках.
- Завершите выполнение того, о чем просила проблема.
Составление таблицы истинности
1. Нарисуйте таблицу истинности для \(p\), \(q\) и \(p \клин q\).
Сначала создайте столбцы для p и q. Заполните столбцы всеми возможными истинными и ложными комбинациями для этих двух.
| р | к | |
|---|---|---|
| Т | Т | |
| Т | Ф | |
| Ф | Т | |
| Ф | Ф |
Обратите внимание на все комбинации p и q. Каждый раз, когда у нас есть таблицы истинности с двумя переменными, это всегда , как мы заполняем первые два столбца.
Каждый раз, когда у нас есть таблицы истинности с двумя переменными, это всегда , как мы заполняем первые два столбца.
Далее нам нужно выяснить, когда \(p\wedge q\) истинно, основываясь на первых двух столбцах. p \wedge q может быть истинным только в том случае, если ОБА p и q истинны. Итак, заполненная таблица выглядит так:
Рисунок \(\PageIndex{1}\)Так всегда заполняется таблица истинности с двумя переменными и их столбцом «и».
2. Нарисуйте таблицу истинности для \(p\), \(q\) и \(p \lor q\).
Сначала создайте столбцы для \(p \lor q\) и \(q\), как в примере A.
| стр | к | |
|---|---|---|
| Т | Т | |
| Т | Ф | |
| Ф | Т | |
| Ф | Ф |
Далее нам нужно выяснить, когда \(p \или q\) истинно, основываясь на первых двух столбцах. \(p \lor q\) истинно, если \(p\) ИЛИ \(q\) истинны, или оба истинны. Итак, заполненная таблица выглядит так:
\(p \lor q\) истинно, если \(p\) ИЛИ \(q\) истинны, или оба истинны. Итак, заполненная таблица выглядит так:
Разница между \(p \wedge q\) и \(p \lor q\) во второй и третьей строках. Для «и» оба \(p\) и \(q\) должны быть истинными, но для «или» только одно должно быть истинным.
Определение истинности переменных
Определите истинность для \(p \клин(\sim q \lor r)\).
Во-первых, есть три переменных, поэтому нам понадобятся все комбинации их истинности. Для трех переменных всегда есть 8 возможных комбинаций.
| \(р\) | \(к\) | \(р\) | |||
|---|---|---|---|---|---|
| Т | Т | Т | |||
| Т | Т | Ф | |||
| Т | Ф | Т | |||
| Т | Ф | Ф | |||
| Ф | Т | Т | |||
| Ф | Т | Ф | |||
| Ф | Ф | Т | |||
| Ф | Ф | Ф |
Далее адрес \(\sim q\).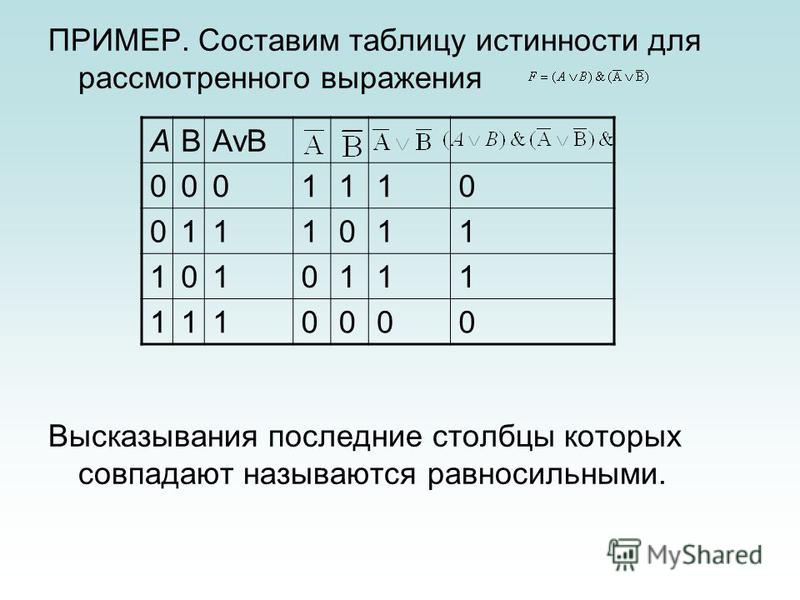 Это будут просто противоположности столбца \(q\).
Это будут просто противоположности столбца \(q\).
| \(р\) | \(к\) | \(р\) | \(\sim q\) | ||
|---|---|---|---|---|---|
| Т | Т | Т | Ф | ||
| Т | Т | Ф | Ф | ||
| Т | Ф | Т | Т | ||
| Т | Ф | Ф | Т | ||
| Ф | Т | Т | Ф | ||
| Ф | Т | Ф | Ф | ||
| Ф | Ф | Т | Т | ||
| Ф | Ф | Ф | Т |
Теперь давайте сделаем то, что указано в скобках, \(\sim q\lor r\). Помните, что для «или» должно быть верно только \(\sim q\) OR \(r\). Используйте только столбцы \(\sim q\) и \(r\) для определения значений в этом столбце.
Помните, что для «или» должно быть верно только \(\sim q\) OR \(r\). Используйте только столбцы \(\sim q\) и \(r\) для определения значений в этом столбце.
| \(р\) | \(к\) | \(р\) | \(\sim q\) | \(\sim q\lor r\) | |
|---|---|---|---|---|---|
| Т | Т | Т | Ф | Т | |
| Т | Т | Ф | Ф | Ф | |
| Т | Ф | Т | Т | Т | |
| Т | Ф | Ф | Т | Т | |
| Ф | Т | Т | Ф | Т | |
| Ф | Т | Ф | Ф | Ф | |
| Ф | Ф | Т | Т | Т | |
| Ф | Ф | Ф | Т | Т |
Наконец, мы можем решить всю проблему, \(p \wedge(\sim q \lor r)\). Используйте \(p\) и \(\sim q\lor r\) для определения значений. Помните, что для «и» оба \(p\) и \(\sim q\lor r\) должны быть истинными.
Используйте \(p\) и \(\sim q\lor r\) для определения значений. Помните, что для «и» оба \(p\) и \(\sim q\lor r\) должны быть истинными.
| \(р\) | \(к\) | \(р\) | \(\sim q\) | \(\sim q\lor r\) | \(p \клин(\sim q \lor r)\) |
|---|---|---|---|---|---|
| Т | Т | Т | Ф | Т | Т |
| Т | Т | Ф | Ф | Ф | Ф |
| Т | Ф | Т | Т | Т | Т |
| Т | Ф | Ф | Т | Т | Т |
| Ф | Т | Т | Ф | Т | Ф |
| Ф | Т | Ф | Ф | Ф | Ф |
| Ф | Ф | Т | Т | Т | Ф |
| Ф | Ф | Ф | Т | Т | Ф |
Напишите таблицу истинности для следующих переменных.
Пример \(\PageIndex{1}\)
\(p \wedge \sim p\)
Решение
Сначала создайте столбцы для \(p\), затем добавьте \(\sim p \) и, наконец, оценить \(p \клин \sim p\).
| \(п\) | \(\сим п\) | \(п \клин \сим п\) |
|---|---|---|
| Т | Ф | Ф |
| Ф | Т | Ф |
Пример \(\PageIndex{2}\)
\(\sim p \lor \sim q\)
Решение
Сначала создайте столбцы для \(p\) и \(q\ ), затем добавьте \(\sim p\) и \(\sim q\). Наконец, оцените \(\sim p \lor \sim q\).
Наконец, оцените \(\sim p \lor \sim q\).
| \(р\) | \(к\) | \(\сим п\) | \(\sim q\) | \(\sim p \lor \sim q\) |
|---|---|---|---|---|
| \(p \lor \sim q\) | Т | Ф | Ф | Ф |
| Т | Ф | Ф | Т | Т |
| Ф | Т | Т | Ф | Т |
| Ф | Ф | Т | Т | Т |
Пример \(\PageIndex{3}\)
\(p \wedge (q\lor \sim q)\)
Решение
Сначала создайте столбцы для p и q, затем добавьте \(\sim q\) и \(q\lor \sim q\).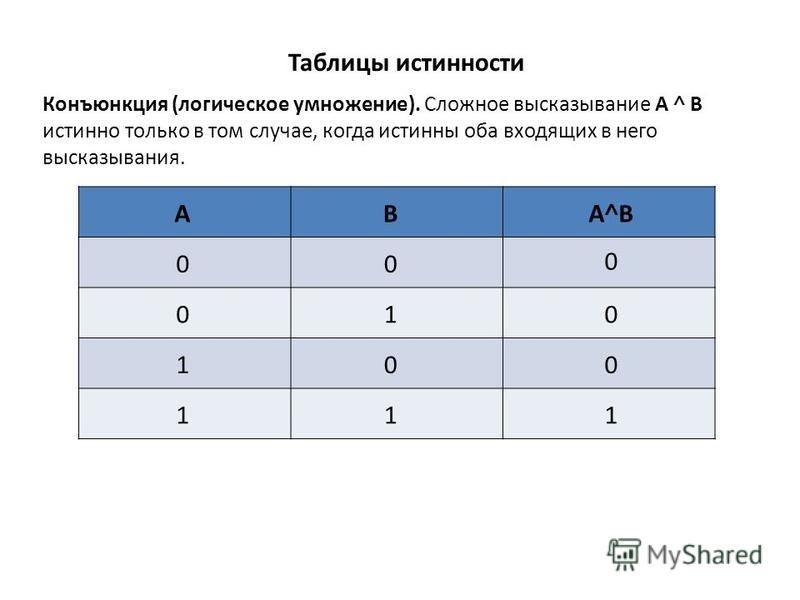 Наконец, оцените \(p\клин (q\lor \sim q)\).
Наконец, оцените \(p\клин (q\lor \sim q)\).
| \(р\) | \(к\) | \(\sim q\) | \(q\lor \sim q\) | \(p\клин (q\lor \sim q)\) |
|---|---|---|---|---|
| Т | Т | Ф | Т | Т |
| Т | Ф | Т | Т | Т |
| Ф | Т | Ф | Т | Ф |
| Ф | Ф | Т | Т | Ф |
Обзор
Напишите таблицу истинности для следующих переменных.
- \((p \клин q)\lor \sim r\)
- \(p \lor ( \sim q \lor r)\)
- \(p \клин (q \lor \sim r)\)
- Единственная разница между #1 и #3 заключается в размещении скобки. Чем отличаются таблицы истинности?
- Когда верно \(p \lor q \lor r\)?
- \(р \лор д \лор г\)
- \((p \lor q) \lor \sim r\)
- \(( \sim p \клин \sim q) \клин r\)
- \(( \sim p \lor \sim q) \клин г\)
Является ли следующий аргумент допустимым? Если да, то какой закон используется? СОВЕТ: Заявления могут быть не по порядку.
\(p \rightarrow q\)
\(r \rightarrow p\)
\(\следовательно r \rightarrow q\)
\(p \rightarrow q\)
\(r \rightarrow q\)
\(\следовательно p \rightarrow r\)
\(p \rightarrow \sim r\)
\(r \)
\(\следовательно \sim p\)
\(\sim q \rightarrow r\)
\(q \)
\(\следовательно \sim r\)
\(p \rightarrow (r \rightarrow s)\)
\(p \)
\(\следовательно r \rightarrow s\)
\(r \rightarrow q\)
\(r \rightarrow s \)
\(\следовательно q \rightarrow s\)
Дополнительные ресурсы
Видео: Таблицы истинности Принципы
Практика: Таблицы истинности 90
Эта страница под названием 2.


 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
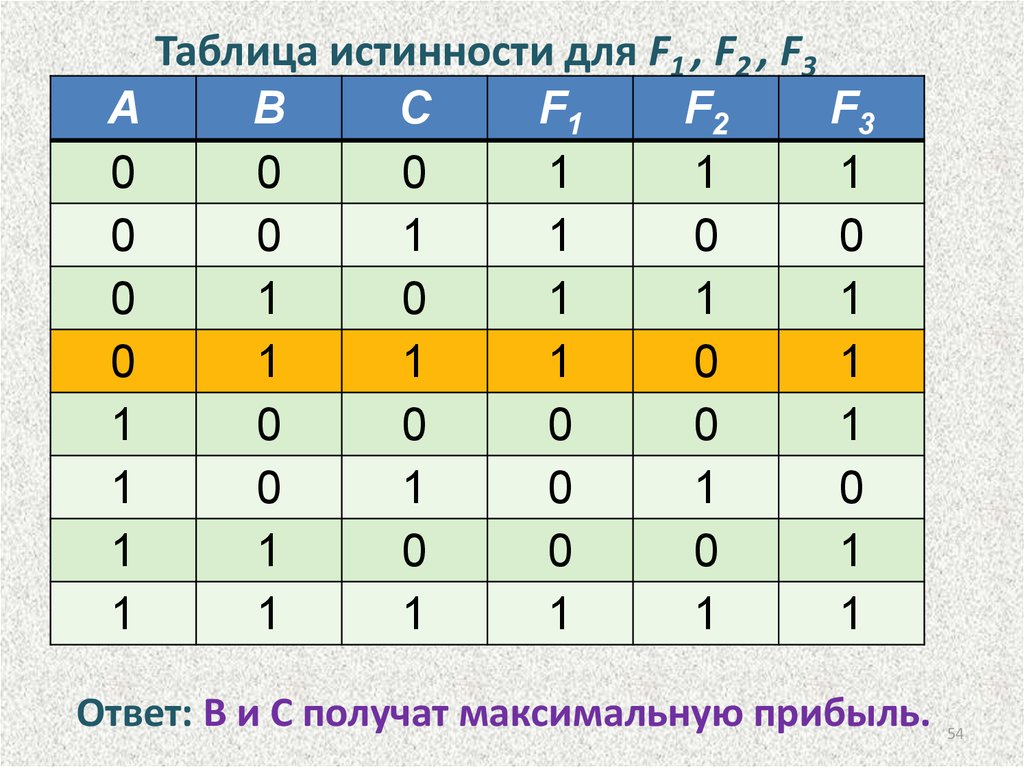
 Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (табл. 14).
Символом F обозначено одно из указанных ниже логических выражений от трех аргументов: X, Y, Z. Дан фрагмент таблицы истинности выражения F (табл. 14).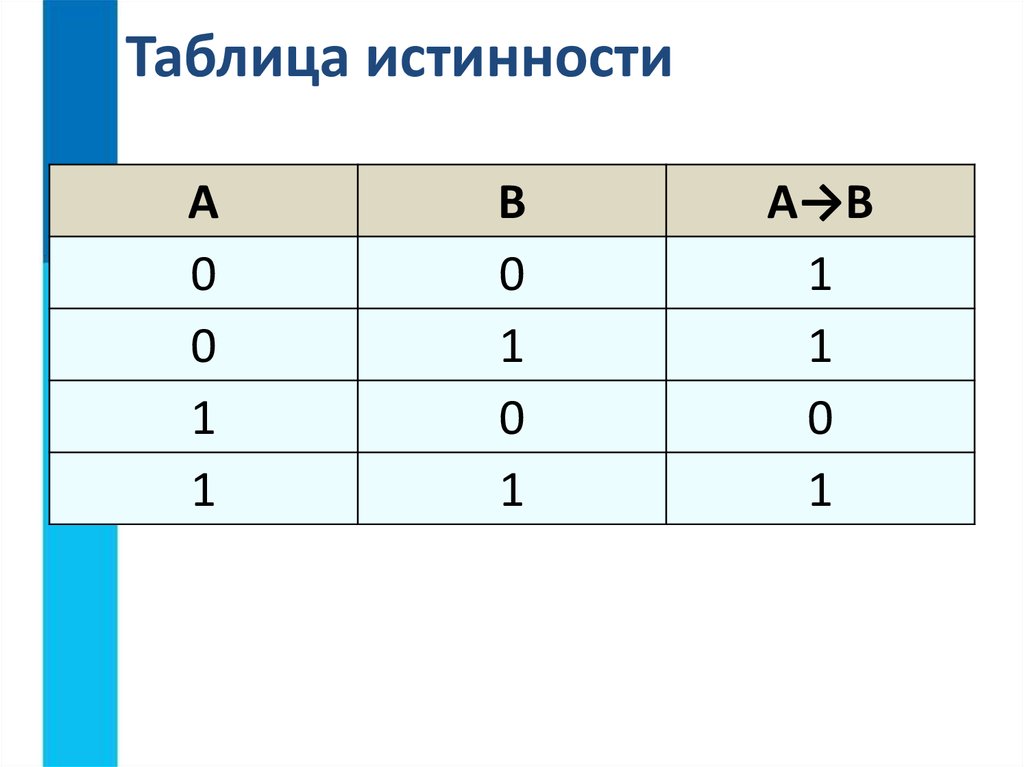 C логическое выражение будет истинным?
C логическое выражение будет истинным?
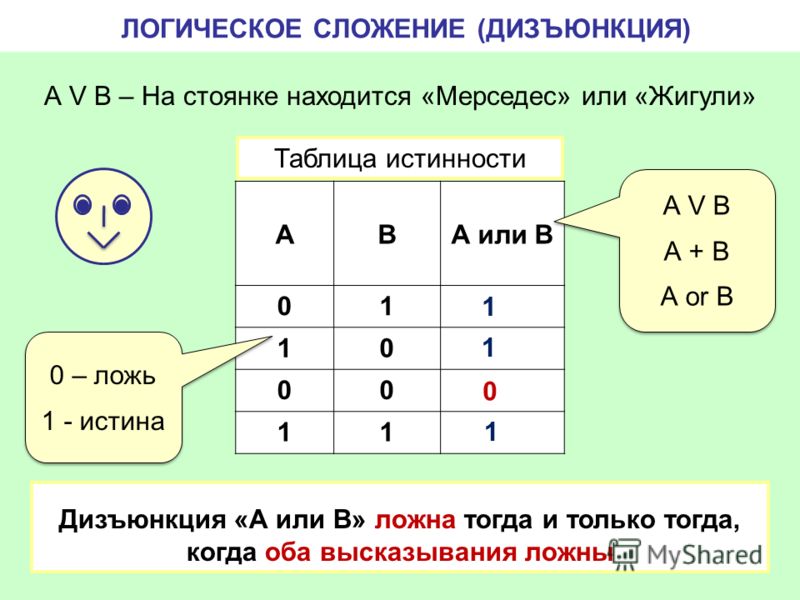 Логический элемент – это электронное устройство, выполняющее соответствующую логическую функцию.
Логический элемент – это электронное устройство, выполняющее соответствующую логическую функцию.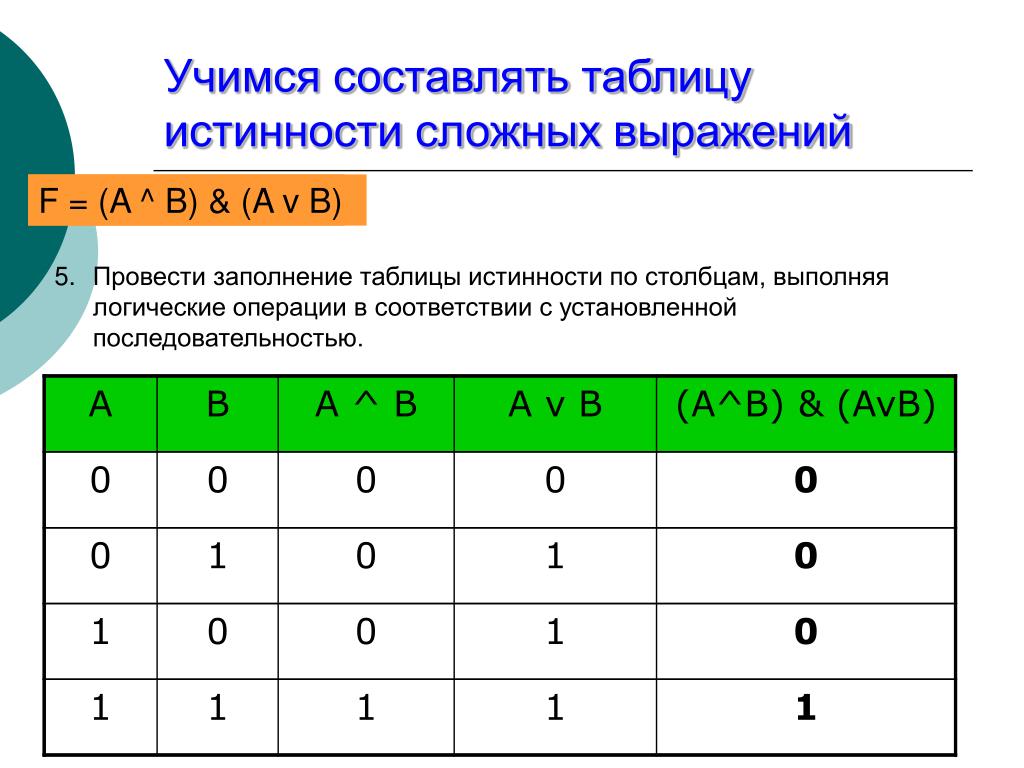 17).
17). su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.006 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.006 с.)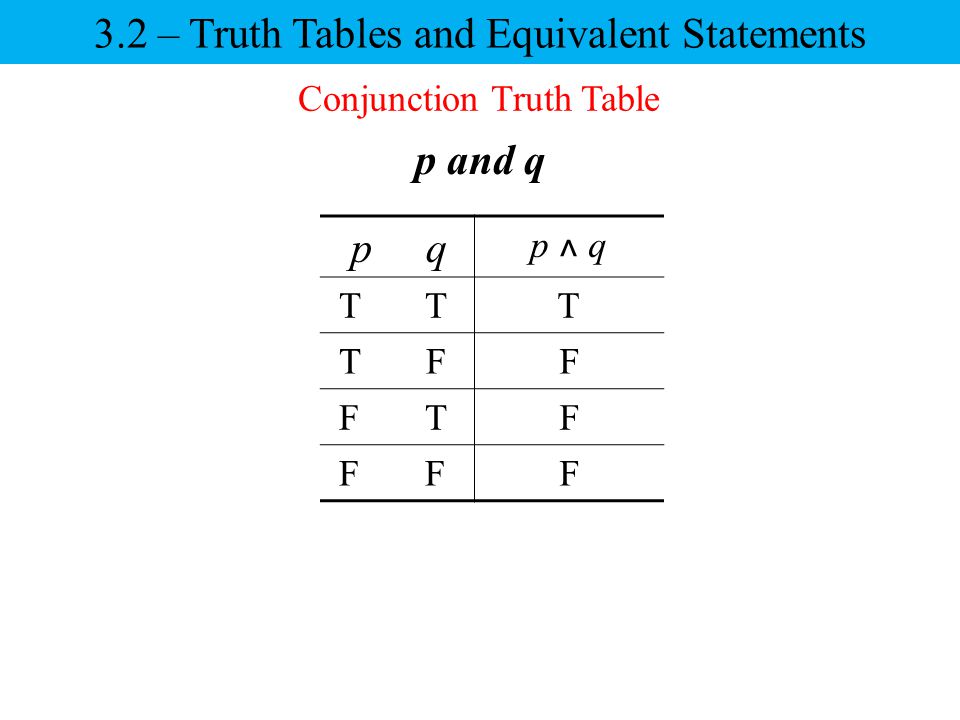
 : ~A
: ~A Для 2 переменных есть 4 комбинации, для 3 переменных есть 8. Вы всегда начинаете таблицу истинности таким образом.
Для 2 переменных есть 4 комбинации, для 3 переменных есть 8. Вы всегда начинаете таблицу истинности таким образом.