Что такое таблица истинности? Таблица, описывающая логическую функцию, называется таблицей истинности. В таблице истинности перечислены все возможные наборы входных переменных. В последнем столбце таблицы истинности выводится число, соответствующее значению функции, по которой строилась данная таблица истинности.
Рассмотрим пример: Допустим, у нас есть две булевых переменных x1 и x2. От этих переменных зависит логическая функция f(x1,x2) Для примера возьмем f(x1,x2)=x1∧x2∨x1. Так как x1, x2 булевы, то они принимают значния 0 или Все возможные варианты входных переменных x1 и x2 можно представить в таблице:
Подставим значения переменных x1 и x2 в каждой строчке в функцию f(x1,x2). f(0,0)= 0∧0∨0=0 f(0,1)= 0∧1∨0=0 f(1,0)= 1∧0∨1=1 f(1,1)= 1∧1∨1=1
Получившиеся значения запишем в последний столбец нашей таблицы:
Мы получили таблицу истинности функции f(x1,x2)=x1∧x2∨x1.
На нашем сайте вы можете построить таблицу истинности online. Для этого вам всего лишь нужно ввести функцию в поле и нажать вычислить.
Таблицы истинности
Унарные функции:
Бинарные функции
| |||||||||||||||||||||||||||||||
Что такое таблица истинности? Приведите примеры
Вы можете изучить и скачать доклад-презентацию на тему Что такое таблица истинности? Приведите примеры. Презентация на заданную тему содержит 21 слайдов. Для просмотра воспользуйтесь проигрывателем, если материал оказался полезным для Вас — поделитесь им с друзьями с помощью социальных кнопок и добавьте наш сайт презентаций в закладки!
Презентации» Образование» Что такое таблица истинности? Приведите примеры
Слайды и текст этой презентации
Слайд 1
Описание слайда:
Что такое таблица истинности? Приведите примеры Что такое таблица истинности? Приведите примеры
Слайд 2
Описание слайда:
Пример:
Слайд 3
Описание слайда:
Логические схемы и выражения
Раздел 9.
1А: Архитектура компьютера
Слайд 4
Описание слайда:
Цели обучения 9.4.2.1 строить логические схемы и логические выражения
Слайд 5
Описание слайда:
Слайд 6
Описание слайда:
Слайд 7
Описание слайда:
Слайд 8
Описание слайда:
Слайд 9
Описание слайда:
Обозначьте своё мнение по изучению темы в свои индивидуальные листы
Слайд 10
Описание слайда:
Цели обучения
9.
Слайд 11
Описание слайда:
Слайд 12
Описание слайда:
Слайд 13
Описание слайда:
Логические схемы и выражения Раздел 9.1А: Архитектура компьютера
Слайд 14
Описание слайда:
Цели обучения 9.4.2.1 строить логические схемы и логические выражения
Слайд 15
Описание слайда:
Повторение тем 5 (мин)
Слайд 16
Знакомство с рубрикой 2 мин
Слайд 17
Описание слайда:
СОР «Архитектура компьютера» 20 мин
Слайд 18
Описание слайда:
(И) Поиграйте в игру Logic Gate Puzzler в онлайн режиме, составляя логические схемы и изучая логические операции
https://goo.
gl/iWsPqA
Слайд 19
Описание слайда:
Обозначьте своё мнение по изучению темы в свои индивидуальные листы
Слайд 20
Описание слайда:Цели обучения 9.4.2.1 строить логические схемы и логические выражения
Слайд 21
Описание слайда:
Подведение итогов урока
Tags Что такое таблица истинности? Приведите примеры
Похожие презентации
Презентация успешно отправлена!
Ошибка! Введите корректный Email!
таблиц правды – критическое мышление
В этой главе представлен способ оценки предложений и аргументов SL.
Хотя метод таблицы истинности может быть трудоемким, он представляет собой чисто механическую процедуру, не требующую интуиции или особого понимания.
Любое неатомарное предложение SL состоит из атомарных предложений с сентенциальными связками. Истинностное значение сложного предложения зависит только от истинностного значения составляющих его атомарных предложений. Чтобы узнать истинное значение (
В этой главе мы воспользуемся тем фактом, что все логические операторы в SL функциональны истинностью — это позволяет строить таблицы истинности для определения логических свойств предложений. Однако вы должны понимать, что это возможно не для всех языков. В английском языке из любого более простого предложения можно составить новое предложение X , говоря: «Возможно, что X ».
Истинностное значение этого нового предложения не зависит напрямую от истинностного значения X . Даже если X ложно, возможно, в каком-то смысле X могло бы быть истинным — тогда новое предложение было бы истинным. Некоторые формальные языки, называемые модальной логикой , имеют оператор возможности. В модальной логике мы могли бы перевести «Возможно, что X » как ◊ X . Однако за возможность переводить такие предложения приходится платить: оператор ◊ не является функционалом истинности, поэтому модальная логика не поддается таблицам истинности.
Значение истинности предложений, содержащих только одну связку, определяется характеристической таблицей истинности для этой связки. В предыдущей главе мы написали характеристические таблицы истинности, где «T» означает «истина», а «F» — ложь. Однако важно отметить, что речь идет не об истине в каком-либо глубоком или космическом смысле. Поэты и философы могут долго спорить о природе и значении 
Чтобы подчеркнуть это, в этой главе мы будем писать «1» и «0» вместо «T» и «F». Хотя мы интерпретируем «1» как значение «истинно», а «0» — как «ложно», компьютеры можно запрограммировать на заполнение таблиц истинности чисто механическим способом. В машине «1» может означать, что регистр включен, а «0» — что регистр выключен. Математически это всего лишь два возможных значения, которые может иметь предложение SL. Таблицы истинности для связок SL, записанных в единицах и нулях, приведены в таблице 5.1.
Характеристическая таблица истинности для союза, например, дает условия истинности для любого предложения формы ( A и B ). Даже если союзы А и В являются длинными сложными предложениями, союз истинен тогда и только тогда, когда оба А и В истинны. Рассмотрим предложение ( H & I ) → H . Мы рассматриваем все возможные комбинации истинного и ложного для H и I , что дает нам четыре строки.
Затем мы копируем значения истинности для букв предложения и пишем их под буквами в предложении.
Теперь рассмотрим подпредложение H & I . Это соединение A и B с H как A и с I как B . H и I верны в первой строке. Поскольку конъюнкция истинна, когда оба конъюнкта истинны, мы пишем 1 под символом конъюнкции. Продолжаем остальные три ряда и получаем вот это:
Все предложение является условным A → B с ( H и I ) как A и с H как B . Например, во второй строке ( H и I ) ложно, а H истинно. Поскольку условие истинно, когда антецедент ложен, мы пишем 1 во второй строке под условным символом. Продолжаем для остальных трех строк и получаем:
Столбец с единицами под условным предложением говорит нам, что предложение ( H & I ) → I истинно независимо от значений истинности H и I .
Они могут быть истинными или ложными в любой комбинации, и составное предложение все равно будет истинным. Крайне важно, чтобы мы рассмотрели все возможные комбинации. Если бы у нас была только двухстрочная таблица истинности, мы не могли бы быть уверены, что предложение не является ложным для какой-либо другой комбинации значений истинности.
В этом примере мы не повторили все записи в каждой последующей таблице. Однако при написании таблиц истинности на бумаге нецелесообразно стирать целые столбцы или переписывать всю таблицу для каждого шага. Хотя таблица истинности более объемная, ее можно записать следующим образом:
Большинство столбцов под предложением предназначены только для бухгалтерских целей. Когда вы станете лучше разбираться в таблицах истинности, вам, вероятно, больше не потребуется копировать столбцы для каждой буквы предложения. В любом случае истинностное значение предложения в каждой строке — это просто столбец под основным логическим оператором предложения; в этом случае столбец под условным.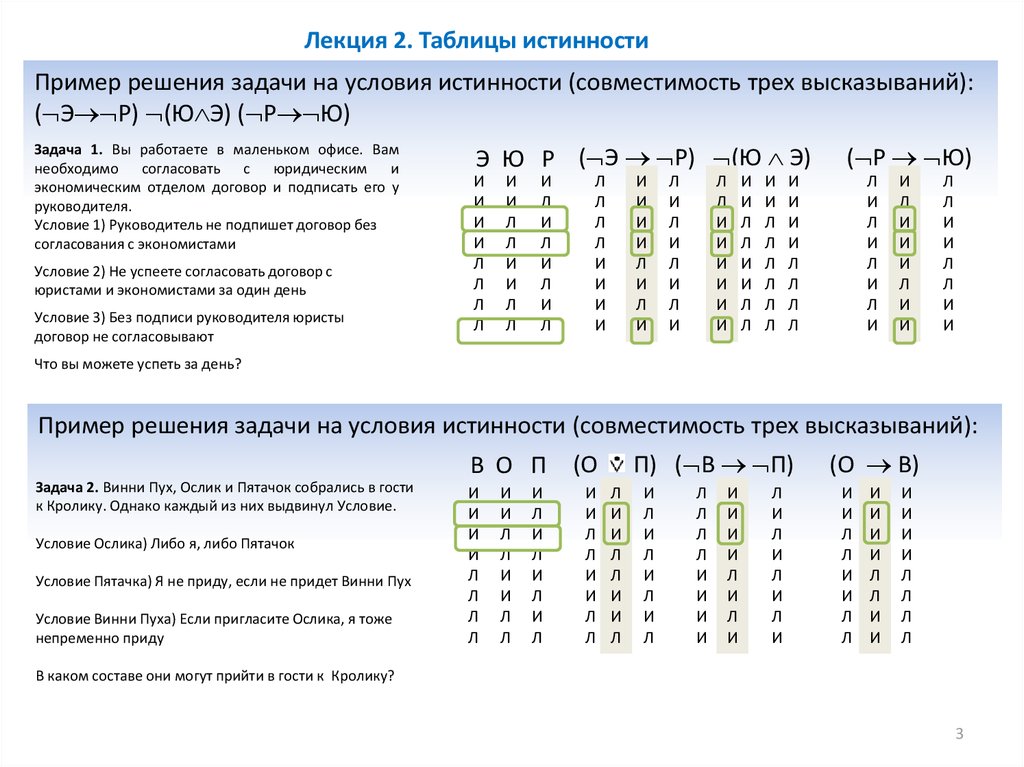
В ПОЛНОЙ ТАБЛИЦЕ ИСТИННОСТИ есть строка для всех возможных комбинаций 1 и 0 для всех букв предложения. Размер полной таблицы истинности зависит от количества различных букв предложения в таблице. Предложение, содержащее только одну букву предложения, требует только двух строк, как в характеристической таблице истинности для отрицания. Это верно, даже если одна и та же буква повторяется много раз, как в предложении [( C ↔ C ) → C ] & ¬ ( C → C ). Полная таблица истинности требует всего две строки, потому что есть только две возможности: C может быть истинным или ложным. Одна буква предложения никогда не может быть отмечена как 1, так и 0 в одной и той же строке. Таблица истинности для этого предложения выглядит так:
Глядя на столбец под главной связкой, мы видим, что предложение ложно в обеих строках таблицы; т. е. ложно независимо от того, является ли C истинным или ложным.
Предложение, содержащее две буквы предложения, требует четырех строк для полной таблицы истинности, как в таблицах характеристической истинности и таблице для ( H и I ) → I .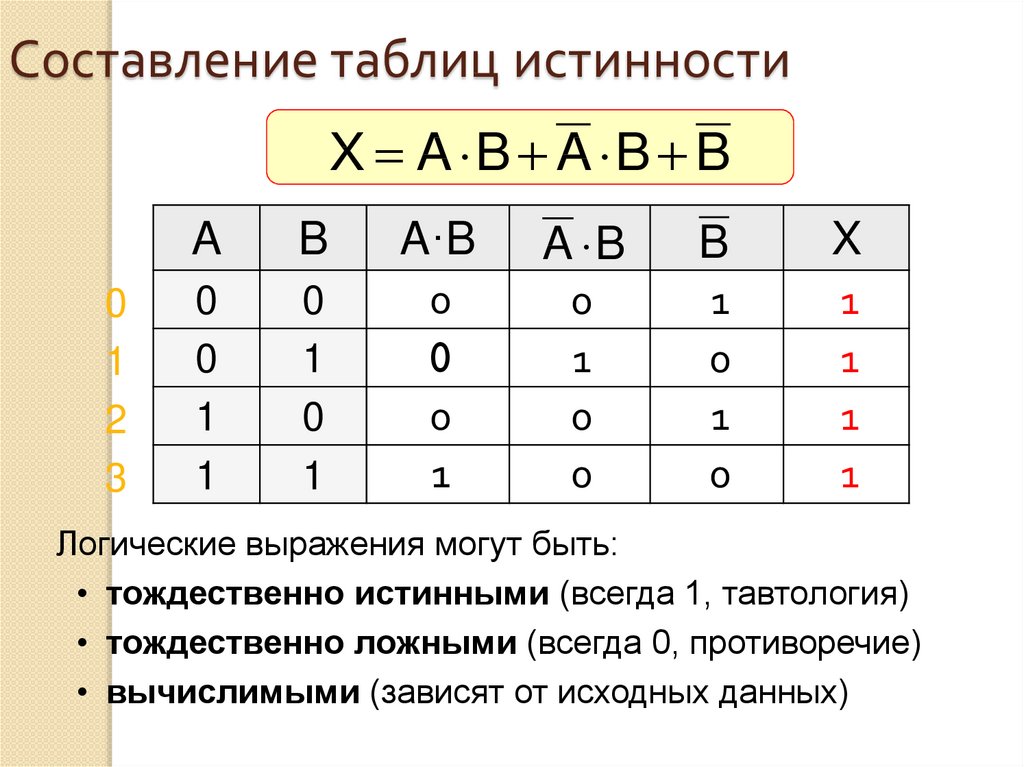
Предложение, содержащее три буквы предложения, занимает восемь строк. Например:
Из этой таблицы мы знаем, что предложение M & ( N ∨ P ) может быть истинным или ложным, в зависимости от значений истинности M , N и . Р .
Полная таблица истинности предложения, состоящего из четырех разных букв, занимает 16 строк. Пять букв, 32 строки. Шесть букв, 64 строки. И так далее. Чтобы быть совершенно общим: если полная таблица истинности имеет n различных букв предложения, то он должен иметь 2 n строк.
Чтобы заполнить столбцы полной таблицы истинности, начните с самой правой буквы предложения и чередуйте 1 и 0. В следующем столбце слева напишите две единицы, напишите два нуля и повторите. В третьем предложении напишите четыре единицы, а затем четыре нуля. Это дает восьмистрочную таблицу истинности, подобную приведенной выше.
Для 16-строчной таблицы истинности в следующем столбце букв предложения должно быть восемь единиц, за которыми следуют восемь нулей.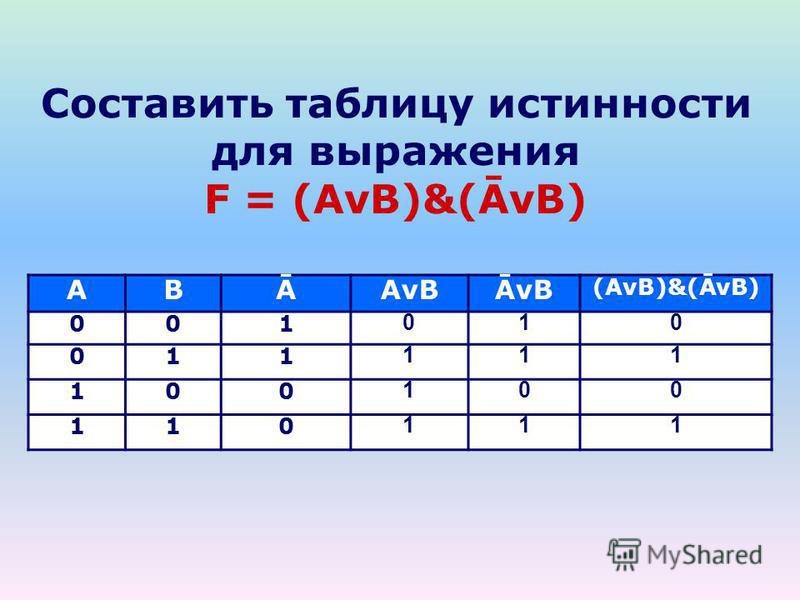
Для 32-строчной таблицы в следующем столбце будет 16 единиц, за которыми следуют 16 нулей. И так далее.
Напомним, что английское предложение является тавтологией, если оно должно быть истинным с точки зрения логики. Имея полную таблицу истинности, мы рассматриваем все способы, которыми может быть мир. Если предложение истинно в каждой строке полной таблицы истинности, то оно истинно с точки зрения логики, независимо от того, на что похож мир.
Таким образом, предложение является ТАВТОЛОГИЕЙ В SL, если столбец под его основной связкой равен 1 в каждой строке полной таблицы истинности.
И наоборот, предложение является ПРОТИВОРЕЧИЕМ В SL, если столбец под его основной связкой равен 0 в каждой строке полной таблицы истинности.
Предложение является УСЛОВНЫМ В SL, если оно не является ни тавтологией, ни противоречием; то есть если это 1 хотя бы в одной строке и 0 хотя бы в одной строке.
Из таблиц истинности в предыдущем разделе мы знаем, что ( H & I ) → H является тавтологией, что [( C ↔ C ) → C ] & ¬( C → C ) является противоречием, и что M & ( N ∨ P ) является случайным.
Логическая эквивалентностьДва предложения в английском языке являются логически эквивалентными, если они имеют такое же истинностное значение, как и логика материи. Опять же, таблицы истинности позволяют нам определить аналогичную концепцию для SL: два предложения ЛОГИЧЕСКИ ЭКВИВАЛЕНТНЫ в SL, если они имеют одно и то же значение истинности в каждой строке полной таблицы истинности.
Рассмотрим предложения ¬( A ∨ B ) и ¬ A и ¬ B . Являются ли они логически эквивалентными? Чтобы это выяснить, составим таблицу истинности.
Посмотрите на столбцы основных связок; отрицание в первом предложении, союз во втором.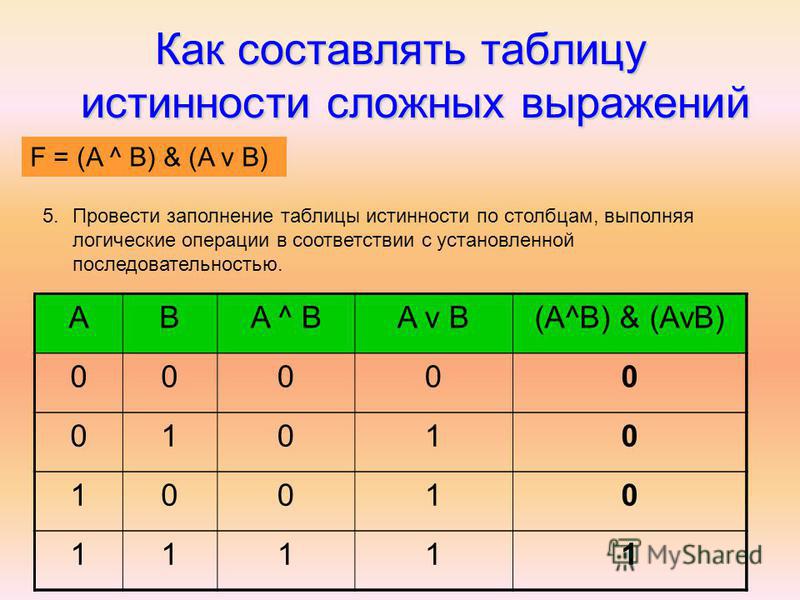
В первых трех строках оба равны 0. В последней строке оба равны 1. Поскольку они совпадают в каждой строке, два предложения логически эквивалентны.
Набор предложений на английском языке является непротиворечивым, если логически возможно, чтобы все они одновременно были истинными. Набор предложений ЛОГИЧЕСКИ СООТВЕТСТВЕНЕН В SL, если есть хотя бы одна строка полной таблицы истинности, в которой все предложения истинны. В противном случае НЕСООТВЕТСТВУЕТ.
ДостоверностьАргумент на английском языке действителен, если логически невозможно, чтобы посылки были истинными, а вывод был ложным одновременно. Аргумент является ДЕЙСТВИТЕЛЬНЫМ В SL, если нет строки полной таблицы истинности, в которой все посылки равны 1, а заключение равно 0; аргумент INVALID IN SL, если есть такая строка.
Рассмотрим этот аргумент:
Действительно ли это? Чтобы это выяснить, составим таблицу истинности.
Да, аргумент правильный. Единственная строка, в которой обе посылки равны 1, — это вторая строка, и в этой строке заключение также равно 1.
Чтобы показать, что предложение является тавтологией, нам нужно показать, что оно равно 1 в каждой строке. Итак, нам нужна полная таблица истинности. Однако, чтобы показать, что предложение , а не , является тавтологией, нам нужна только одна строка: строка, на которой предложение равно 0. Следовательно, чтобы показать, что что-то не является тавтологией, достаточно указать одну- строка таблица частичной истинности — независимо от того, сколько букв в предложении может быть в нем.
Рассмотрим, например, предложение ( U и T ) → ( S и W ). Мы хотим показать, что , а не — тавтология, предоставив частичную таблицу истинности. Мы заполняем 0 для всего предложения. Главной связкой предложения является условная.
Чтобы условие было ложным, антецедент должен быть истинным (1), а консеквент должен быть ложным (0). Итак, мы заполняем это на столе:
Чтобы ( U и T ) были истинными, оба U и T должны быть истинными.
Теперь нам просто нужно сделать ( S & W ) ложным. Для этого нам нужно сделать хотя бы одно из S и W ложным. Мы можем сделать как S , так и W ложными, если захотим. Важно только то, что в этой строке все предложение оказывается ложным. Приняв произвольное решение, заканчиваем таблицу таким образом:
Чтобы показать, что что-то является противоречием, требуется полная таблица истинности. Чтобы показать, что что-то равно , а не , противоречие требует только однострочной таблицы частичной истинности, где предложение истинно в этой одной строке.
Предложение условно, если оно не является ни тавтологией, ни противоречием. Таким образом, чтобы показать, что предложение условно, требуется двухстрочная таблица частичной истинности: предложение должно быть истинным в одной строке и ложным в другой.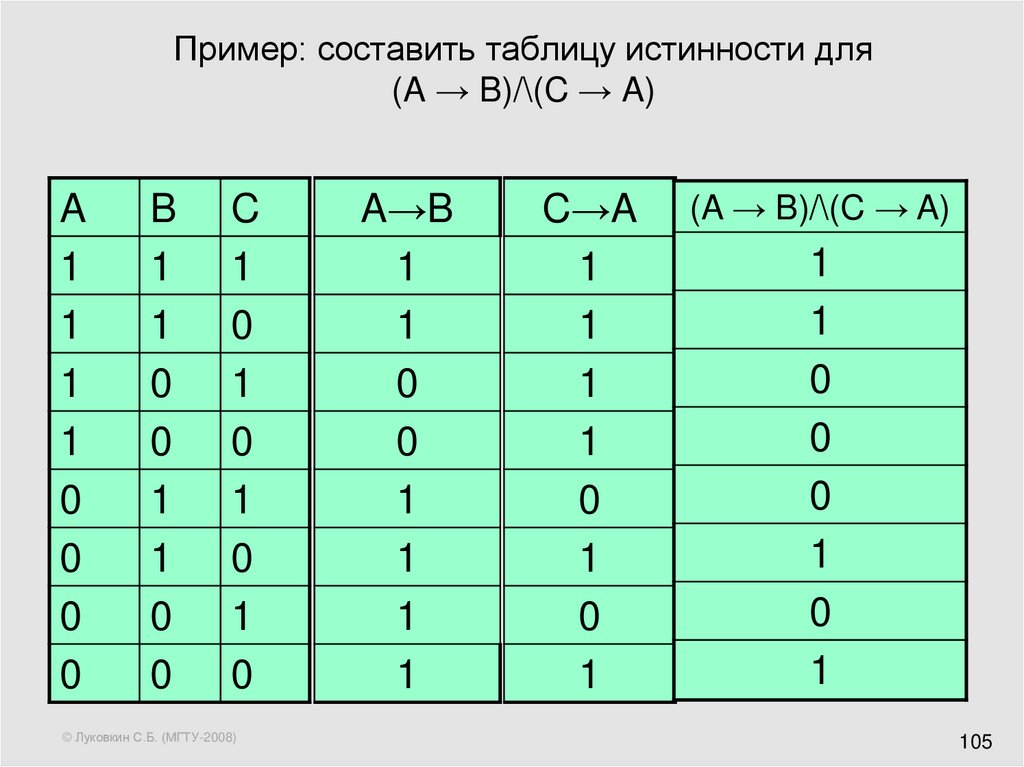
Например, мы можем показать, что приведенное выше предложение зависит от этой таблицы истинности:
Обратите внимание, что есть много комбинаций значений истинности, которые сделали бы предложение истинным, поэтому есть много способов, которыми мы могли бы написать вторую строку.
Чтобы показать, что предложение является , а не контингентным, требуется предоставить полную таблицу истинности, потому что это требует показать, что предложение является тавтологией или что оно является противоречием. Если вы не знаете, является ли конкретное предложение контингентным, то вы не знаете, нужна ли вам полная или частичная таблица истинности. Вы всегда можете начать работу над полной таблицей истинности. Если вы закончите ряды, которые показывают, что предложение является условным, вы можете остановиться. Если нет, то заполните таблицу истинности.
Хотя две тщательно отобранные строки покажут, что условное предложение является условным, нет ничего плохого в том, чтобы заполнить больше строк.
Чтобы показать, что два предложения логически эквивалентны, необходимо предоставить полную таблицу истинности. Чтобы показать, что два предложения , а не логически эквивалентны, требуется только однострочная таблица частичной истинности: Составьте таблицу так, чтобы одно предложение было истинным, а другое — ложным.
Чтобы показать, что набор предложений непротиворечив, необходимо предоставить одну строку таблицы истинности, в которой все предложения истинны. Остальная часть таблицы не имеет значения, поэтому подойдет однострочная таблица частичной истинности. С другой стороны, чтобы показать, что набор предложений несовместим, требуется полная таблица истинности: вы должны показать, что в каждой строке таблицы хотя бы одно из предложений ложно.
Для демонстрации правильности аргумента требуется полная таблица истинности.
Чтобы показать, что аргумент недействителен , требуется предоставить только однострочную таблицу истинности: если вы можете вывести строку, в которой все посылки верны, а заключение ложно, то аргумент недействителен.
В таблице 5.2 показано, когда требуется полная таблица истинности, а когда — частичная.
V. Практические упражнения
Если вам нужна дополнительная практика, вы можете построить таблицы истинности для любых предложений и аргументов в упражнениях к предыдущей главе.
* Часть A Определите, является ли каждое предложение тавтологией, противоречием или условным предложением. Обоснуйте свой ответ полной или частичной таблицей истинности, где это уместно.
* Часть B Определите, является ли каждая пара предложений логически эквивалентной. Обоснуйте свой ответ полной или частичной таблицей истинности, где это уместно.
* Часть C Определите, является ли каждый набор предложений последовательным или непоследовательным.
Обоснуйте свой ответ полной или частичной таблицей истинности, где это уместно.
* Часть D Определите, является ли каждый аргумент допустимым или недопустимым. Обоснуйте свой ответ полной или частичной таблицей истинности, где это уместно.
* Ответьте на вопросы Части E .
Часть F Мы могли бы исключить из языка бикондиционал (↔). Если бы мы сделали это, мы все еще могли бы написать ‘ A ↔ B ’, чтобы предложения было легче читать, но это было бы сокращением для ( A → B ) и ( B → A ). Результирующий язык будет формально эквивалентен SL, поскольку A ↔ B и ( A → B ) & ( B → A ) логически эквивалентны в SL. Если бы мы предпочитали формальную простоту выразительному богатству, мы могли бы заменить больше связок условными обозначениями и по-прежнему иметь язык, эквивалентный SL.
Существует ряд эквивалентных языков только с двумя связками. Достаточно было бы только отрицания и материальной условности. Покажите это, написав предложения, которые логически эквивалентны каждому из следующих, используя только круглые скобки, буквы предложения, отрицание (¬) и материальное условное предложение (→).
Мы могли бы иметь язык, который эквивалентен SL только с отрицанием и дизъюнкцией в качестве связок. Покажите это: используя только круглые скобки, буквы предложений, отрицание (¬) и дизъюнктуру (∨), напишите предложения, которые логически эквивалентны каждому из следующих.
Штрих Шеффера является логической связкой со следующей характеристикой истинности:
7. Составьте предложение, используя связки SL, которое логически эквивалентно ( A | B ).
Каждое предложение, написанное с использованием связки SL, может быть переписано как логически эквивалентное предложение с использованием одного или нескольких штрихов Шеффера.
Используя только штрих Шеффера, напишите предложения, эквивалентные каждому из следующих.
Математика за минуту: Таблицы истинности
Поделиться этой страницей
Представлено Marianne 4 июля 2018 г.
В стандартной математической логике каждое утверждение — «кот белый», «собака чёрная», «я голоден» — считается либо истинным, либо ложным. Имея два оператора P и Q , вы можете сделать более сложные операторы, используя логические связки, такие как И и ИЛИ.
Например, выписка P И Q (например, «кот белый, а собака черная») считается истинным, только если оба P и Q верны, в противном случае оно ложно. This can be summarised in a truth table:
| P | Q | P AND Q |
| T | T | T |
| T | F | Ф |
| Ф | Т | F |
| F | F | F |
В таблице перечислены каждая комбинация значений истины для P и Q , а затем рассказывает вам о том, что соответствует значению истины для P и Q , а затем рассказывает вам о том, что соответствует значению истины для P и .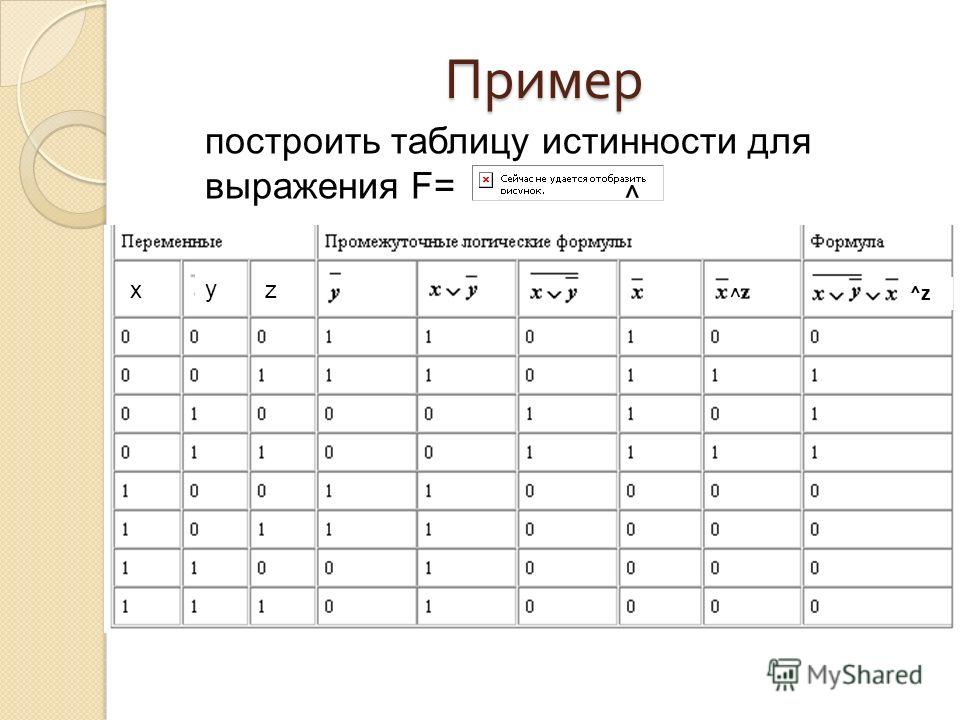
является.
Аналогично, связка ИЛИ определяется следующей таблицей:
| P | Q | P | 6 05 05 050456 T | T | T |
| T | F | T | |||
| F | T | T | |||
| F | F | F |
There is also a truth таблица, определяющая NOT P , отрицание утверждения P (если P означает «кот белый», то NOT P означает «кот не белый»). Неудивительно, что НЕ P истинно, когда P является ложным и наоборот:
| P | НЕ P | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| T | F | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
. Выведите закон исключенной средней , в котором говорится, что P или нет P всегда верно:
Если вам понравилось это делать, вы также можете определить свои собственные логические связки, используя таблицы истинности. |
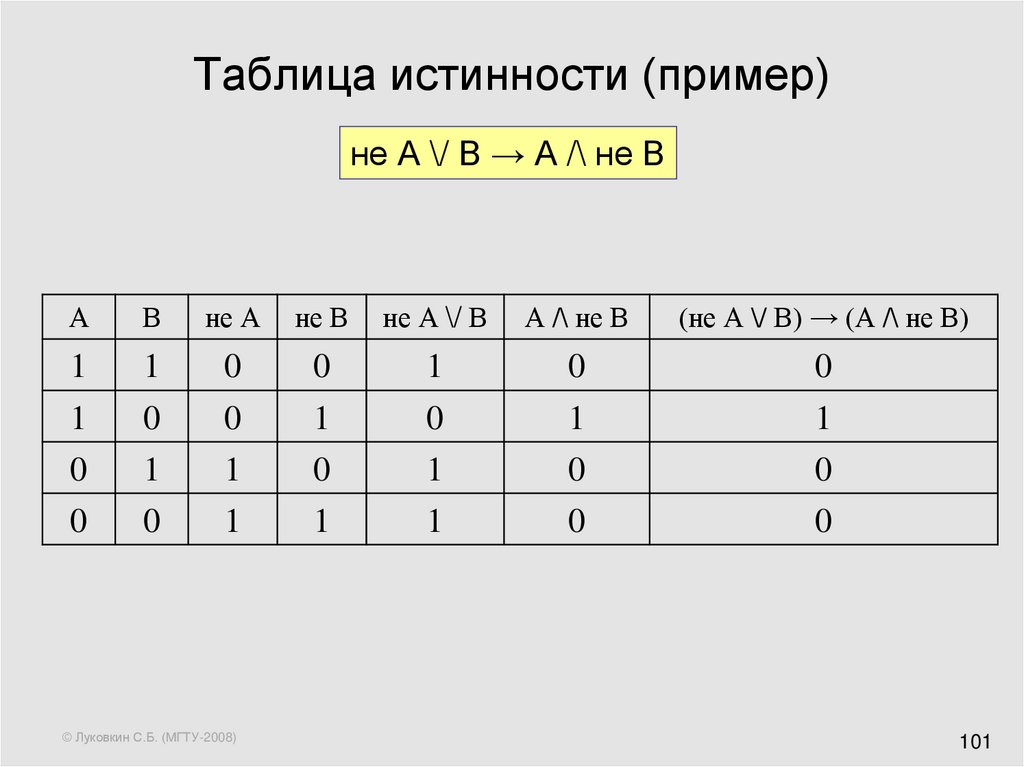P И ( Q ИЛИ НЕ R)