6 ctg
6 ctgВы искали 6 ctg? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и cos 0 sin, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «6 ctg».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как 6 ctg,cos 0 sin,cos 0 sin 0,cos sin 0,cos sin tg ctg таблица,cos sin tg углов таблица,cos sin таблица,cos sin таблица значений,cos и sin таблица,cos таблица брадиса,ctg 0 чему равен,ctg 180,ctg 30,ctg 30 градусов,ctg 40,ctg 44,ctg 45,ctg 45 градусов,ctg 5,ctg 5 2,ctg 6,ctg 6 pi,ctg 60,ctg 60 градусов,ctg п 2,ctg таблица,ctg30,sin 0 cos,sin cos 0,sin cos tg ctg таблица,sin cos tg ctg таблица значений,sin cos tg ctg таблица значения,sin cos tg таблица,sin cos tg углов таблица,sin cos таблица,sin и cos таблица,tg и ctg таблица,брадиса таблица cos,значение тангенса и котангенса таблица,значения cos и sin таблица,значения sin,значения sin cos,значения sin cos tg ctg таблица,значения sin и cos таблица,значения синуса косинуса тангенса таблица,значения синусов и косинусов таблица,значения синусов косинусов тангенсов котангенсов таблица,кос син табл,косинус и синус таблица,косинус синус и тангенс таблица,косинус синус таблица,косинусы синусы таблица,косинусы синусы тангенсы котангенсы таблица,котангенс 10,котангенс 15,котангенс 15 градусов,котангенс 225,котангенс 30,котангенс 35,котангенс 360,котангенс 4,котангенс 40,котангенс 45,котангенс 5,котангенс 60 градусов,котангенс 75,котангенс таблица,полная таблица sin cos tg ctg,полная таблица косинусов и синусов,полная таблица косинусов синусов,полная таблица синусов и косинусов,полная таблица синусов косинусов,син кос табл,син кос таблица,син кос танг таблица,син кос тг ктг таблица,синус и косинус 20 градусов,синус и косинус тангенс таблица,синус косинус и тангенс таблица,синусы косинусы таблица,синусы косинусы таблица значений,синусы косинусы тангенсы котангенсы таблица брадиса,табл кос и син,табл кос син,табл син и кос,табл син кос,таблица cos sin,таблица cos sin tg,таблица cos sin tg ctg,таблица cos sin tg ctg полная,таблица cos sin углов,таблица cos брадиса,таблица cos и sin,таблица ctg,таблица sin cos,таблица sin cos tg,таблица sin cos tg ctg,таблица sin cos tg ctg значения,таблица sin cos tg ctg полная,таблица sin и cos,таблица брадиса косинусы синусы тангенсы котангенсы,таблица брадиса котангенс,таблица брадиса синусы и косинусы тангенсы котангенсы,таблица брадиса синусы косинусы тангенсы котангенсы,таблица всех синусов косинусов тангенсов и котангенсов,таблица градусов,таблица градусов синус косинус тангенс котангенс,таблица градусов тангенсов синусов косинусов тангенсов,таблица значений cos sin,таблица значений cos sin tg,таблица значений sin cos,таблица значений sin cos tg,таблица значений sin cos tg ctg,таблица значений sin cos tg ctg таблица,таблица значений tg cos sin,таблица значений tg sin cos,таблица значений косинус синус,таблица значений косинусов синусов тангенсов,таблица значений котангенса,таблица значений синус косинус тангенс,таблица значений синуса и косинуса,таблица значений синусов и косинусов,таблица значений синусов косинусов,таблица значений синусов косинусов тангенсов,таблица значений синусов косинусов тангенсов котангенсов,таблица значений синусы косинусы,таблица значений тангенса и котангенса,таблица значения cos sin tg ctg,таблица значения cos и sin,таблица значения sin cos tg ctg,таблица значения sin и cos,таблица значения углов,таблица кос син,таблица кос син тг ктг,таблица кос тг син,таблица косинус синус,таблица косинуса и синуса и тангенса,таблица косинуса синуса,таблица косинуса синуса и тангенса,таблица косинуса синуса тангенса котангенса,таблица косинусов и синусов в радианах,таблица косинусов и синусов тангенсов,таблица косинусов и синусов тангенсов котангенсов,таблица косинусов и синусов тангенсов котангенсов в радианах,таблица косинусов и тангенсов,таблица косинусов синусов и тангенсов,таблица косинусов синусов полная,таблица косинусов синусов тангенсов,таблица косинусов синусов тангенсов и котангенсов в радианах,таблица косинусов синусов тангенсов котангенсов,таблица косинусов синусов тангенсов котангенсов полная,таблица косинусов тангенсов,таблица косинусы синусы,таблица котангенса,таблица котангенсов,таблица котангенсов углов от 0 до 90,таблица син кос,таблица син кос тан катан,таблица син кос танг,таблица син кос тг ктг,таблица синус косинус,таблица синус косинус и тангенс,таблица синус косинус тангенс,таблица синус косинус тангенс и котангенс таблица,таблица синуса и косинуса и тангенса,таблица синуса косинуса,таблица синуса косинуса и тангенса,таблица синуса косинуса тангенса и котангенса,таблица синуса косинуса тангенса котангенса,таблица синуса тангенса и косинуса,таблица синусов и косинусов в радианах,таблица синусов и косинусов всех углов,таблица синусов и косинусов полная,таблица синусов и косинусов тангенсов,таблица синусов и косинусов тангенсов котангенсов,таблица синусов и косинусов тангенсов котангенсов в радианах,таблица синусов косинусов,таблица синусов косинусов и тангенсов,таблица синусов косинусов полная,таблица синусов косинусов тангенсов,таблица синусов косинусов тангенсов и котангенсов,таблица синусов косинусов тангенсов и котангенсов от 0 до 360 и,таблица синусов косинусов тангенсов котангенсов,таблица синусов косинусов тангенсов котангенсов от 0 до 360,таблица синусов косинусов тангенсов котангенсов полная,таблица синусов косинусов тангенсов котангенсов полная таблица,таблица синусов тангенсов,таблица синусы косинусы,таблица тангенса синуса и косинуса,таблица тангенсов и косинусов,таблица тангенсов и котангенсов синусов и косинусов,таблица тангенсов котангенсов косинусов синусов в радианах,таблица тангенсов котангенсов синусов косинусов в радианах,таблица тангенсов синусов,таблица тангенсов синусов и косинусов,таблица тг ктг син кос,таблица тригонометрии,таблица тригонометрическая углов,таблица тригонометрические,таблица тригонометрических значений с градусами,таблица углов,таблица углов cos sin,таблица углов sin cos tg,таблица углов косинусов синусов,таблица углов синусов и косинусов,таблицу синусов и косинусов,таблицы косинусов синусов,таблицы синусов косинусов,таблицы синусов косинусов тангенсов и котангенсов,таблицы синусов косинусов тангенсов котангенсов,таблицы тригонометрических функций,таблиця кутів,табличные значения синусов косинусов,табличные значения синусов косинусов тангенсов котангенсов,тангенс синус и косинус таблица,тригонометрическая таблица,тригонометрическая таблица косинусов синусов,тригонометрическая таблица синусов косинусов,тригонометрические таблица,тригонометрические таблицы,тригонометрия таблица косинусов и синусов.
Решить задачу 6 ctg вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.
Формулы приведения в тригонометрии тригонометрических функций
Формулы приведения относятся к тригонометрической функции, которая использует периодичность для преобразования тригонометрической функции с относительно большим углом в тригонометрическую функцию с относительно небольшим углом.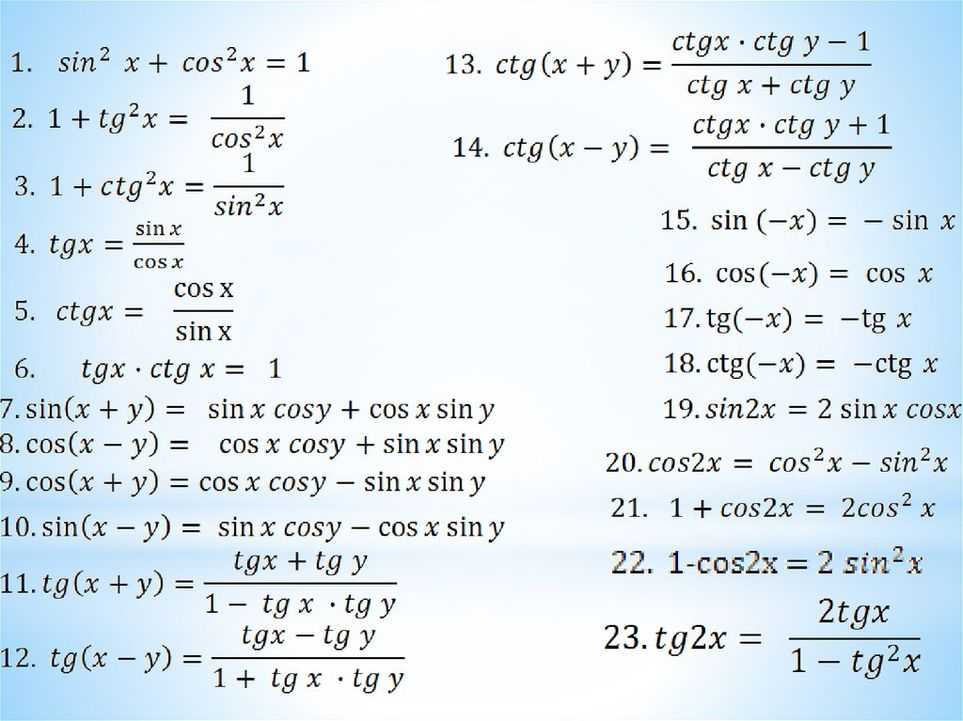
Содержание
Формулы взаимосвязи между углами противоположными на 360 градусов или круг
Эти формулы устанавливают связь между углами противоположными на 360 градусов или круг. Значение одной и той же тригонометрической функции для того же угла на противоположной стороне равно.
Пусть α — любой острый угол, выражение угла в радианной системе:
В градусной мере тригонометрическая функция угла будет выражаться формулами:
.
.
.
.
.
.
Формулы тригонометрической функции π + α, связанные с значением тригонометрической функции α
Эта группа устанавливает связь между значением тригонометрической функции π + α и значением тригонометрической функции α.
Пусть α — любой угол, выражение угла в радианной системе:
sin (π+α)=-sinα.
cos (π+α)=-cosα.
tg (π+α)=tgα.
ctg (π+α)=ctgα.
sec (π+α)=-secα.
cosec (π+α)=-cosecα.
В градусной мере:
sin (180°+α)=-sinα.
cos (180°+α)=-cosα.
tg (180°+α)=tgα.
ctg (180°+α)=ctgα.
sec (180°+α)=-secα.
cosec (180°+α)=-cosecα.
Связь между значением тригонометрической функции любого угла α и -α
Приведем формулы приведения, в которых устанавливается связь между значением тригонометрической функции любого угла α и угла -α:
sin (-α) = — sinα.
cos (-α) = cosα.
tg (-α) = — tgα.
ctg (-α)=ctgα.
sec (-α) = secα.
cosec (-α) = — cosecα.
Связь между значениями тригонометрических функций π-α и α
Эти формулы могут быть получены по формулам связи между значениями тригонометрических функций углов α и -α и между значением тригонометрической функции π + α и значением тригонометрической функции α :
Представление угла в радианной мере:
sin (π - α) = sinα.
cos (π - α) = — cosα.
tg (π - α) = — tgα.
ctg (π - α) = — ctgα.
sec (π - α) = — secα.
cosec (π - α) = cosecα.
Представление угла в градусной мере:
sin (180 ° -α) = sinα.
cos (180 ° -α) = — cosα.
tg (180 ° -α) = — tgα.
ctg (180 ° -α) = — ctgα.
sec(180 ° -α) = — secα.
cosec (180 ° -α) = cosecα.
Связь между значением тригонометрической функции 2π-α и α
Эти формулы могут быть получены по формулам связи тригонометрических функций аргументов противоположных на круг и угла α и угла -α :
Представление угла в радианной мере:
sin (2π - α) = — sinα.
cos (2π - α) = cosα.
tg (2π - α) = — tgα.
ctg (2π - α) = — ctgα.
sec (2π - α) = secα.
cosec (2π - α) = — cosecα.
Представление в градусной мере:
sin (360 ° -α) = — sinα.
cos (360 ° -α) = cosα.
tg (360 ° -α) = -tgα.
ctg (360 ° -α) = — ctgα.
sec(360 ° -α) = secα.
cosec (360 ° -α) = — cosecα.
Связь между значениями тригонометрических функций π/2 ± α и 3π/2 ± α и α
Связь между π / 2 + α и значением тригонометрической функции α
Представление угла в радианной мере:
sin (π / 2 + α) = cosα.
cos (π / 2 + α) = — sinα.
tg (π / 2 + α) = — ctgα.
ctg (π / 2 + α) = — tgα.
sec (π / 2 + α) = — cosecα.
cosec (π / 2 + α) = secα.
Представление угла в градусах:
sin (90 ° + α) = cosα.
cos (90 ° + α) = — sinα.
tg (90 ° + α) = -ctgα.
ctg (90 ° + α) = -tgα.
sec (90 ° + α) = -cosecα.
cosec (90 ° + α) = secα.
Связь между π / 2-α и значением тригонометрической функции α
Представление угла в радианной системе:
sin (π / 2 - α) = cosα.
cos (π / 2 - α) = sinα.
tg (π / 2 - α) = ctgα.
ctg (π / 2 - α) =tgα.
sec (π / 2 - α) = cosecα.
cosec (π / 2 - α) = secα.
Представление угла в градусах:
sin (90 ° -α) = cosα.
cos (90 ° -α) = sinα.
tg (90 ° -α) = ctgα.
ctg (90 ° -α) = tgα.
sec (90 ° -α) = cosecα.
cosec (90 ° -α) = secα.
Связь между 3π / 2 + α и значением тригонометрической функции α
Представление угла в радианах:
sin (3π / 2 + α) = — cosα.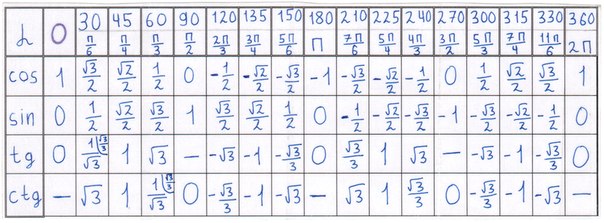
cos (3π / 2 + α) = sinα.
tg (3π / 2 + α) = — ctgα.
ctg (3π / 2 + α) = -tgα.
sec (3π / 2 + α) = cosecα.
cosec (3π / 2 + α) = — secα.
Представление угла в градусах:
sin (270 ° + α) = — cosα.
cos (270 ° + α) = sinα.
tg (270 ° + α) = -ctgα.
ctg(270 ° + α) = -tgα.
sec (270 ° + α) = cosecα.
cosec (270 ° + α) = — secα.
Связь между 3π / 2 - α и значением тригонометрической функции α
Представление угла в радианах:
sin (3π / 2- α) = — cosα.
cos (3π / 2 -α) = — sinα.
tg (3π / 2 - α) =ctgα.
ctg (3π / 2 — α) =tgα.
sec (3π / 2 - α) = -cosecα.
cosec (3π / 2 - α) = — secα.
Представление угла в градусах:
sin (270 ° -α) = — cosα.
cos (270 ° -α) = — sinα.
tg(270 ° -α) = tgα.
ctg(270 ° -α) =tgα.
sec (270 ° -α) = -cosecα.
cosec (270 ° -α) = — secα.
Правило определения приведенной функции
Приведенные выше формулы приведения можно резюмировать так: для значения тригонометрической функции kπ / 2 ± α (k∈Z),
- Когда k — четное число, значение приведенной функции будет с тем же именем, что и приводимая функция, но для α (острый угол), то есть имя функции не изменяется
- Когда k — нечетное число, мы возьмем ко-функцию, но уже для α (острый угол), а именно sin (kπ / 2 ± α) → cosα; cos (kπ / 2 ± α) → sinα; tg (kπ / 2 ± α) → ctgα, ctg (kπ / 2 ± α) → tgα.

Запомни
Перед приведенной функцией мы должны добавить знак приводимой функции.
То есть мы получим:
(1)
(2)
Правило лошади в тригонометрии
Математики придумывают все новые и новые способы заставить ученика выучить это несложное правило, что придумали даже «кивающую лошадь». А правило, которое с ее помощью легче запомнить — это как раз вторая часть правила, когда k — нечетное число. В этом случае угол отсчитывается по вертикали. И тогда воображаемая лошадь кивает головой и функция меняется на ко-функцию. На наш взгляд абсолютно лишняя информация. Но если вам удобно — пользуйтесь.
Правило лошади в тригонометрии
Например:
sin (2π-α) = sin (4 · π/2-α), k = 4 — четное число, поэтому берется та же функция sinα.
Когда α — острый угол, 2π-α∈ (270°, 360°), sin (2π-α)
Итак, sin (2π-α) = — sinα.
sin (α+ π) = — sinα
youtube.com/embed/Luv3mlOkdOg?feature=oembed» frameborder=»0″ allow=»accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Углы, фигурирующие во всех формулах приведения тригонометрических функций, сначала рассматриваются как острые углы, α + π — это угол в третьей четверти, а синус в третьей четверти отрицательный, поэтому конечный результат отрицательный, а π является четным кратным π/2, поэтому функция остается неизменной.
Чтобы определить знак приводимой функции, нарисуйте тригонометрический круг и вспомните знаки тригонометрических функций в координатных четвертях.
Знаки тригонометрических функций
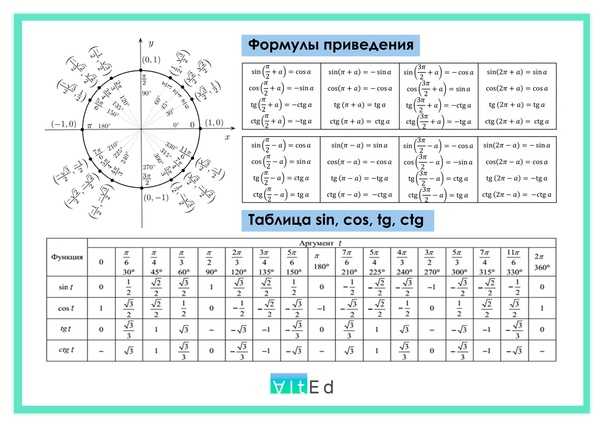
Формулы приведения в тригонометрии таблица
Все формулы приведения тригонометрических функций можно собрать в одну таблицу.
| Угол | Функция | |||
| sinх | cosх | tgх | ctgх | |
| α | sinα | cosα | tgα | ctgα |
| -α | -sinα | cosα | -tgα | -ctgα |
| π / 2 — α | cosα | sinα | ctgα | tgα |
| π / 2 + α | cosα | -sinα | -ctgα | -tgα |
| π-α | sinα | -cosα | -tgα | -ctgα |
| π + α | -sinα | -cosα | tgα | ctgα |
| 3π / 2 -α | -cosα | -sinα | ctgα | tgα |
| 3π / 2+α | -cosα | sinα | -ctgα | -tgα |
| 2π-α | -sinα | cosα | -tgα | -ctgα |
| 2π+α | sinα | cosα | tgα | ctgα |
Формулы и правило приведения тригонометрических функций часто используются при решении тригонометрических уравнений и неравенств.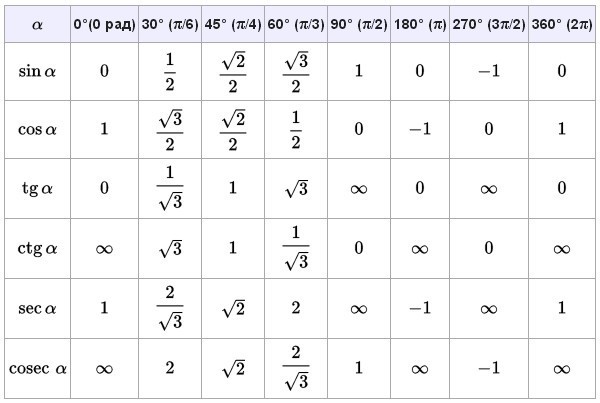
Примеры применения формул приведения
Пример 1
Вычислите .
Решение: Выделим целое количество тригонометрических кругов, каждый из которых . Получим: По формуле приведения из таблицы находим:
, подставляем .
Пример 2
Вычислите .
Решение: Представим, .
Для решения воспользуемся правилом, так как у нас получается нечетное число k и функция поменяется на ко-функцию, то есть был косинус, станет синус. Определимся со знаком, посмотрим, в какую четверть попадает — это вторая четверть, косинус во второй четверти отрицательный, значит перед синусом поставим знак минус (ставим знак приводимой функции, а приводим мы косинус):
.
Пример 3
Вычислите .
Решение: Проведем преобразования и применим правило приведения тригонометрических функций .
Пример 4
Используя формулы приведения, вычислить:
.
Решение:
Представим
Тогда,
Ответ: .
Пример 5
Упростите выражение:
.
Решение:
Приведем тригонометрические функции согласно правилу приведения, получим:
.
Ответ:
Таким образом, чтобы правильно выполнить приведение тригонометрической функции большого угла к тригонометрической функции меньшего угла вы можете использовать формулы приведения, которые нужно будет выучить наизусть, а их свыше 50, можно облегчить себе запоминание — выучив таблицу. Или же воспользоваться простым правилом (рекомендуется). Удачи на экзаменах.
Читайте также:
Тригонометрические таблицы
Тригонометрические таблицы| Дом | Учитель | Родители | Глоссарий | О нас | |||||
|
|
PI = 3,141592. радианы = градусы x PI / 180 (преобразование градусов в рад) градусы = радианы x 180 / PI (преобразование рад в градус)
 Они включены исключительно для демонстрации шаблона. Они включены исключительно для демонстрации шаблона. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
© 2000-2005 Math.com. Все права защищены. Юридический Уведомления. Пожалуйста, ознакомьтесь с нашей Конфиденциальностью Политика. |
Тригонометрическая таблица от 0 до 360 (cos-sin-cot-tan-sec-cosec)
Тригонометрические отношения являются важным модулем в математике. Здесь, в этом посте, я приведу тригонометрическую таблицу от 0 до 360 (cos-sin-cot-tan-sec-cosec), а также простой и удобный способ ее запомнить.
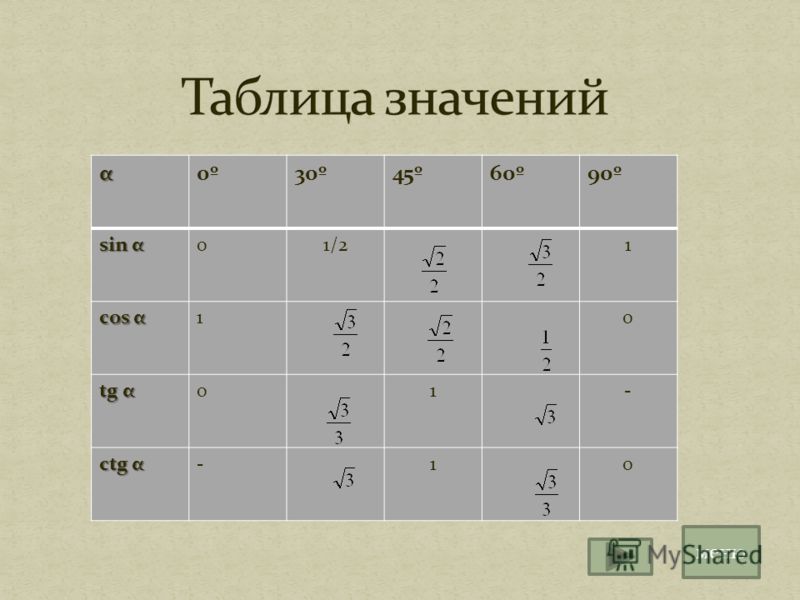
Тригонометрическая таблица для чисел от 0 до 90 представлена как
И это можно легко запомнить с помощью приведенного ниже метода
Как легко запомнить таблицу тригонометрических соотношений задано
Теперь, чтобы вспомнить тригонометрическую таблицу для чисел от 120 до 360, нам просто нужно запомнить знак функций в четырех квадрантах.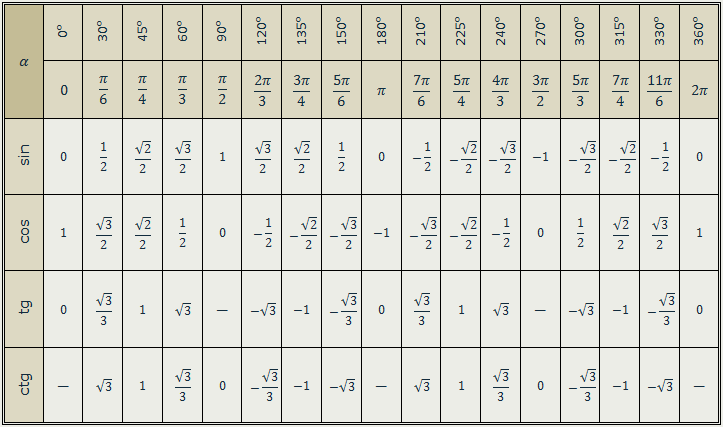 Мы можем использовать приведенную ниже фразу, чтобы запомнить
Мы можем использовать приведенную ниже фразу, чтобы запомнить
Все чашки серебряного чая
A LL — Все тригонометрические функции положительны в IST Quadrant
S Ilver — SIN и COSEC FUNCAND, положительные в REST в REST в REST II в REST в REST в REST II в REST II в REST II в REST II CADANT in II. EA – функции tan и cot положительные, остальные отрицательные в III квадранте
C UPS – функции cos и sec положительные, остальные отрицательные в IV квадранте
Теперь мы можем использовать формулу в таблице ниже для расчета отношений от 120 до 360
Эту таблицу очень легко запомнить, поскольку все они соответствуют одной и той же функции. Знак определяется соответствующим знаком тригонометрической функции угла в квадранте
Например,
a. $ \cos 120 = \cos (180 -60) = – \cos 60$ . Его легко запомнить, а знак определяется угловым квадрантом. Поскольку 120 лежит во II квадранте, cos отрицательно
b. $\sin 120 = \cos (180 -60) = \sin 60$. Здесь, поскольку sin положителен во II квадранте, мы ставим положительный знак
$\sin 120 = \cos (180 -60) = \sin 60$. Здесь, поскольку sin положителен во II квадранте, мы ставим положительный знак
г. $\tan 120 = \tan (180 -60) = – \tan 60$. Здесь, поскольку тангенс отрицателен во II квадранте, мы ставим знак минус
. Теперь тригонометрическая таблица для чисел от 120 до 180 дается как
и рассчитывается как
$\sin (120) = \sin (180 -60) =\sin 60= \frac {\sqrt {3}}{2}$
$\cos (120) = \cos (180 -60) =- \cos 60= – \frac {1}{2}$
$\tan 120 = \frac {\sin 120}{\cos 120} = -\sqrt {3}$
$\sin (135) = \sin (180 -45) = \sin 45= \frac {1}{\sqrt {2}}$
$\cos (135) = \cos (180 -45) =- \cos 45= -\frac {1}{\sqrt {2}}$
$\tan 135 = \frac {\sin 135} { \cos 135} = -1$
$\sin (180) = \sin (180 -0) =sin 0= 0$
$\cos (180) = \cos (180 -0) =-cos 0= -1$
$\tan 180 = \frac {\sin 180}{\cos 180} = 0$
$\csc 120 = \frac {1}{\sin 120} = \frac {2} {\sqrt 3}$
$\sec 120 = \frac {1}{\cos 120} = -2$
$\cot 120 = \frac {1}{\tan 120} = — \frac {1 }{\sqrt 3}$
$\csc 135 = \frac {1}{\sin 135} = \sqrt 2$
$\sec 135 = \frac {1}{\cos 135} = -\sqrt 2$
$\cot 135 = \frac {1}{\tan 135} = – 1$
Теперь Тригонометрическая таблица от 210 до 270 дается как
И рассчитывается как
$\sin (210) = \sin (180 +30) =- \sin 30= -\frac {1}{2}$
$ \cos (210) = \cos (180 +30) =- \cos 30=-\frac {\sqrt {3}}{2}$
$\tan (210) = \frac {\sin 210}{ \cos 210} = \frac {1}{\sqrt {3}}$
$\sin (225) = \sin (180 +45) =- \sin 45= -\frac {1}{\sqrt { 2}}$
$\cos (225) = \cos (180+45) =- \cos 45= -\frac {1}{\sqrt {2}}$
$\tan 225 = \frac {\sin 225} {\cos 225} = 1$
$\sin (270) = \sin (180 +90) =- \sin 90= -1$
$\cos (270) = \cos (180+90) = — \cos 90= 0$
$\tan 270 = \frac {\sin 270}{\cos 270} = -\frac {1}{0}$ Неопределенное значение
$\csc (210) = \frac {1}{\sin (210)} = -2$
$\sec (210) = \frac {1}{\cos (210)}=-\frac {2}{\sqrt 3}$
$\cot (210) = \frac {1}{\tan (210)} = \sqrt {3}$
$\csc (225) = \frac {1}{\sin 225}= -\sqrt {2}$
$\sec (225) = \frac {1}{\cos 225}= -\sqrt {2}$
$\cot 225 = \frac {1}{\tan 225} = 1$
Теперь тригонометрическая таблица для чисел от 300 до 360 задается как
$\sin (300) = \sin ( 360 -60) =- \sin 60=-\frac {\sqrt {3}}{2}$
$\cos (300) = \cos (360-60) =\cos 60=\frac {1} {2}$
$\tan (300) = \frac {\sin 300}{\cos 300} = -{\sqrt {3}}$
$\sin (315) = \sin (360 -45 ) =- \sin 45= -\frac {1}{\sqrt {2}}$
$\cos (315) = \cos (360-45) =\cos 45= \frac {1}{\sqrt {2}}$
$\tan 315 = \frac {\sin 315}{\ cos 315} =- 1$
$\sin (360) = \sin (360 -0) =- \sin 0=0$
$\cos (360) = \cos (360-0) =\cos 0=1$
$\tan (360) = \frac {\sin 360}{\cos 360} = 0$
$\csc (300) = \frac {1}{\sin (300)}= -\frac {2}{\sqrt 3}$
$\sec (300) = \frac {1}{\cos (300)}=2$
$\cot (300) = \frac {1} {\tan 300} = -\frac {1}{\sqrt {3}}$
Как вычислить тригонометрические отношения отрицательных углов от 0 до 360
Это довольно просто.



 0175
0175  0698
0698 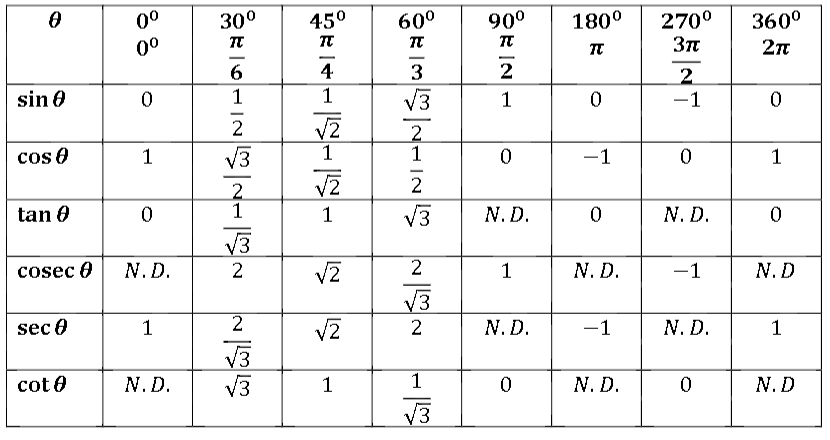 1222
1222 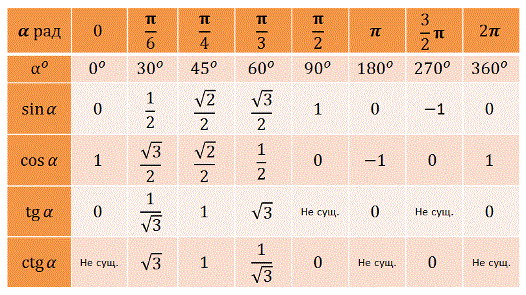 4137
4137 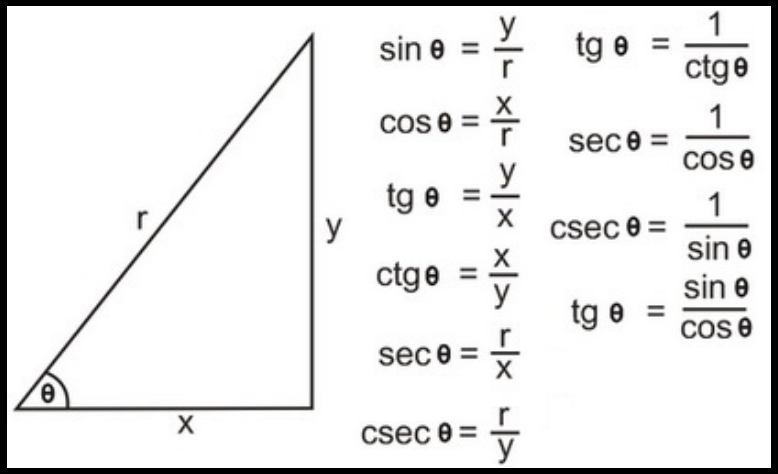 0223
0223 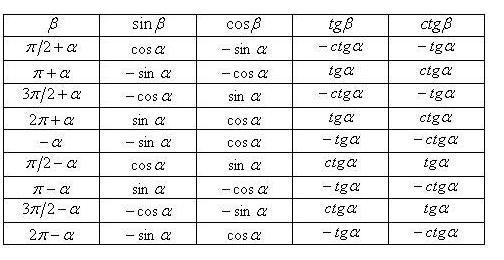 9659
9659  3142
3142 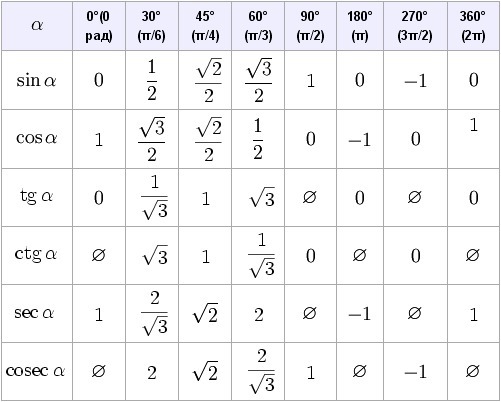 2217
2217 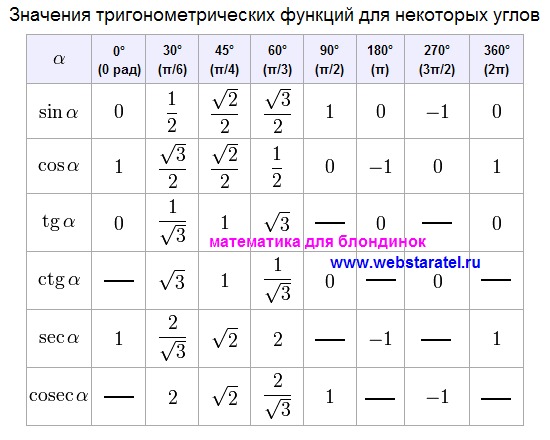 1694
1694 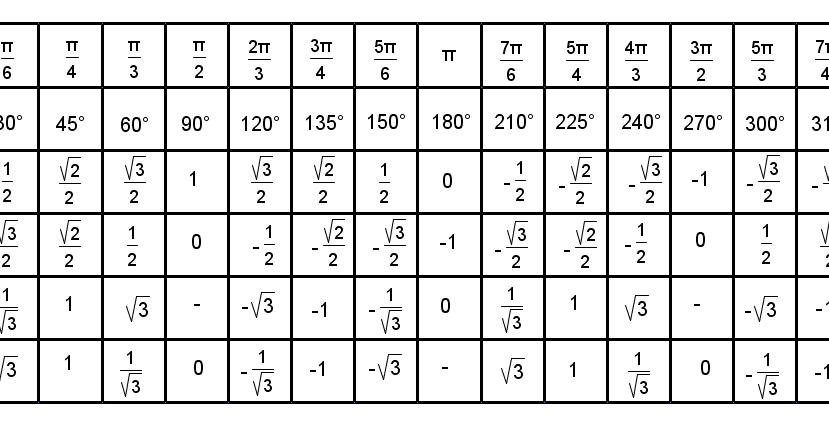 1126
1126 8746
8746  5585
5585  9774
9774  2521
2521 7660
7660 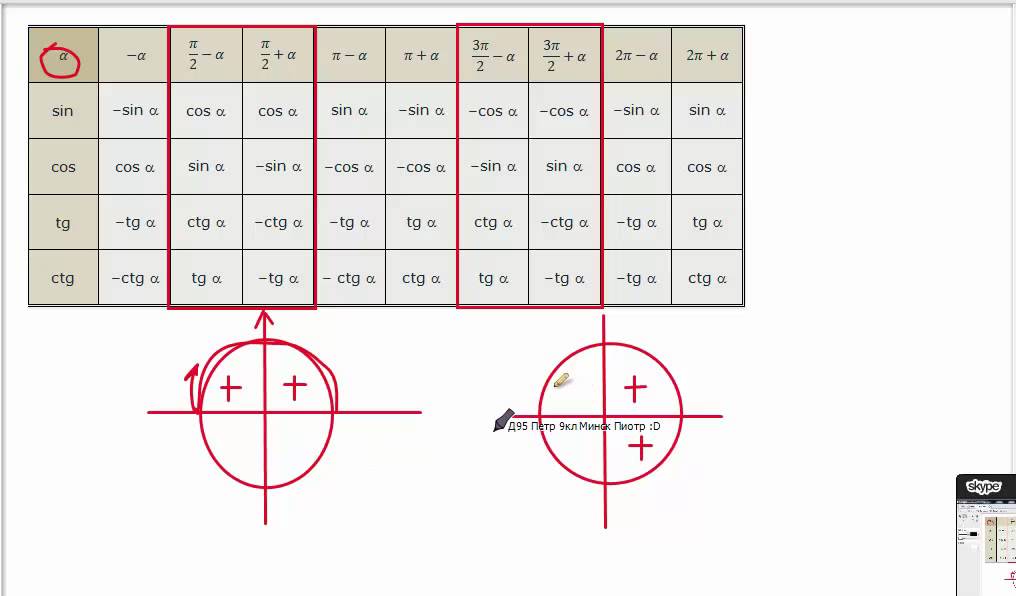 7505
7505  7854
7854