Аналитическая геометрия
Аналитическая геометрия
ОглавлениеВВЕДЕНИЕЧАСТЬ ПЕРВАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ ГЛАВА I. МЕТОД КООРДИНАТ § 2. Координаты на прямой линии. § 3. Расстояние между двумя точками на прямой линии. § 4. Прямоугольные координаты на плоскости. § 5. Расстояние между двумя точками на плоскости. § 6. Деление отрезка в данном отношении. § 7. Угол между двумя осями. § 8. Основные положения теории проекций.  § 9. Проекции направленного отрезка на оси координат. § 10. Площадь треугольника. § 11. Полярные координаты. Упражнения ГЛАВА II. ЛИНИИ И ИХ УРАВНЕНИЯ § 1. Составление уравнений заданных линий. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Пересечение двух линий. § 5. Параметрические уравнения линий. § 6. Уравнения линий в полярных координатах. ГЛАВА III. ПРЯМАЯ ЛИНИЯ § 1. Угловой коэффициент прямой. § 2. Уравнение прямой линии с угловым коэффициентом. § 3. Геометрический смысл уравнения первой степени между двумя переменными. § 4. Исследование общего уравнения первой степени Ах + Ву + С = 0. § 5. Уравнение прямой линии в отрезках. § 6. Построение прямой линии по ее уравнению. § 7. Угол между двумя прямыми. § 8. Условия параллельности и перпендикулярности двух прямых. § 9. Уравнение прямой, проходящей через данную точку в данном направлении. § 10. Взаимное расположение двух прямых на плоскости.  § 11. Уравнение пучка прямых. § 12. Уравнение прямой, проходящей через две данные точки. § 13. Условие, при котором три данные точки лежат на одной прямой. § 14. Нормальное уравнение прямой линии. § 15. Приведение общего уравнения первой степени к нормальному виду. § 16. Расстояние от дайной точки до данной прямой. § 17. Уравнение прямой в полярной системе координат. Упражнения ГЛАВА IV. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ КОНИЧЕСКИХ СЕЧЕНИЙ § 2. Окружность. § 3. Эллипс. § 4. Гипербола и ее асимптоты. § 5. Парабола. § 6. Построение точек эллипса, гиперболы и параболы посредством циркуля и линейки. § 7. Эллипс, гипербола и парабола как конические сечения. § 8. Эксцентриситет и директрисы эллипса. § 9. Эксцентриситет и директрисы гиперболы. § 10. Эксцентриситет и директриса параболы. § 12. Диаметры зллипса. Сопряженные диаметры. § 13. Диаметры гиперболы. Сопряженные диаметры. 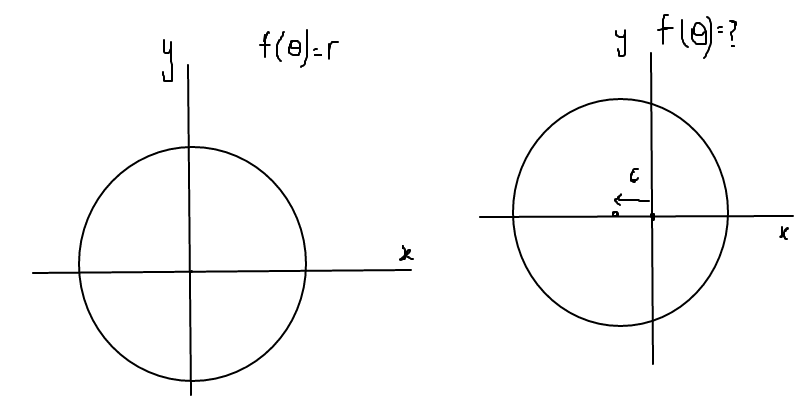 § 14. Диаметры параболы. § 15. Касательная. § 16. Эллипс как проекция окружности. § 17. Параметрические уравнения эллипса. Упражнения ГЛАВА V. ПРЕОБРАЗОВАНИЕ КООРДИНАТ. КЛАССИФИКАЦИЯ ЛИНИЙ § 2. Перенос начала координат. § 3. Поворот осей координат. § 4. Общий случай. § 5. Некоторые приложения формул преобразования координат. § 6. Преобразование общего уравнения второй степени, не содержащего произведения переменных. § 7. Преобразование общего уравнения второй степени. § 8. Классификация линий. Упражнения ГЛАВА VI. ОПРЕДЕЛИТЕЛИ 2-го и 3-го ПОРЯДКА § 2. Однородная система двух уравнений с тремя неизвестными. § 3. Определители 3-го порядка. § 4. Основные свойства определителей 3-го порядка. § 5. Система трех уравнений первой степени с тремя неизвестными. § 6. Однородная система. § 7. Общее исследование системы трех уравнений первой степени с тремя неизвестными. § 8. Некоторые приложения определителей к аналитической геометрии.  Упражнения ЧАСТЬ ВТОРАЯ. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ ГЛАВА I. МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ § 2. Основные задачи. § 3. Основные положения теории проекций в пространстве. § 4. Вычисление угла между двумя осями в пространстве. Упражнения ГЛАВА II. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ § 2. Сложение векторов. § 3. Вычитание векторов. § 4. Умножение вектора на число. § 5. Проекции вектора. § 6. Действия над векторами, заданными своими проекциями. § 7. Скалярное произведение векторов. § 8. Основные свойства скалярного произведения. § 10. Направление вектора. § 11. Векторное произведение. § 12. Основные свойства векторного произведения. § 13. Векторное произведение векторов, заданных проекциями. § 14. Векторно-скалярное произведение. § 15. Векторно-скалярное произведение в проекциях. § 16. Двойное векторное произведение. Упражнения ГЛАВА III. 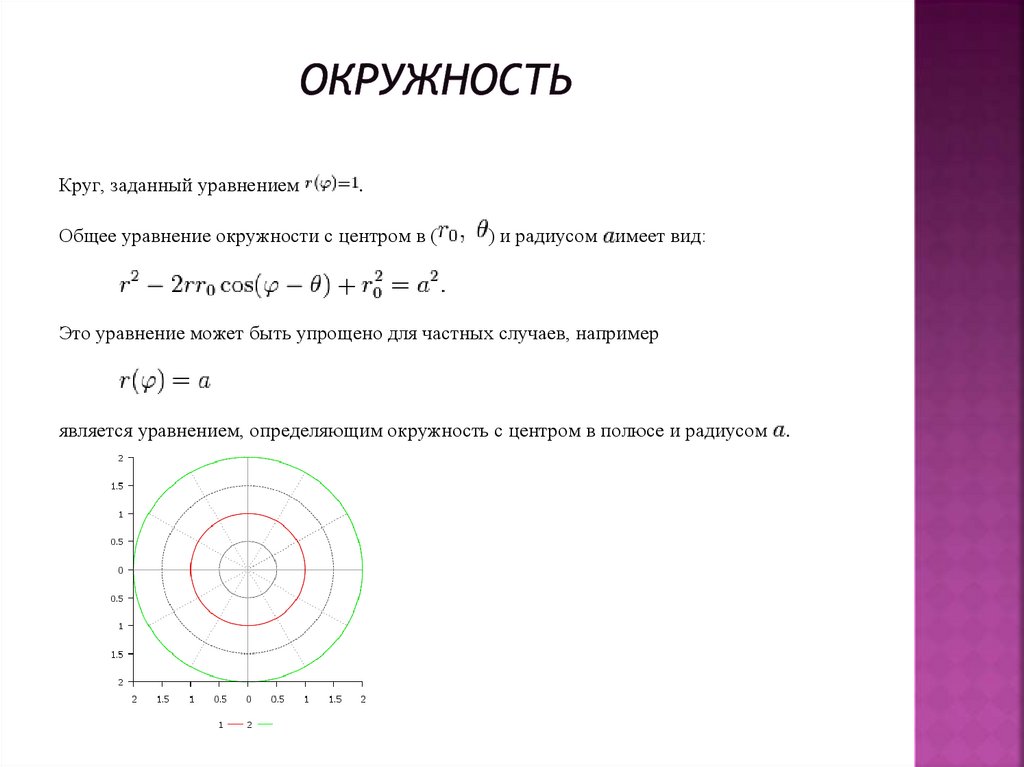 ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ ГЕОМЕТРИЧЕСКОЕ ЗНАЧЕНИЕ УРАВНЕНИЙ§ 1. Уравнение поверхности. § 2. Геометрический смысл уравнений. § 3. Две основные задачи. § 4. Сфера. § 5. Цилиндрические поверхности. § 6. Уравнения линии в пространстве. § 7. Пересечение трех поверхностей. Упражнения ГЛАВА IV. ПЛОСКОСТЬ § 1. Нормальное уравнение плоскости. § 2. Геометрический смысл уравнения первой степени между тремя переменными. Приведение общего уравнения первой степени к нормальному виду. § 3. Исследование общего уравнения плоскости. § 4. Уравнение плоскости в отрезках. § 5. Уравнение плоскости, проходящей через данную точку. § 6. Уравнение плоскости, проходящей через три данные точки. § 7. Угол между двумя плоскостями. § 8. Условия параллельности и перпендикулярности двух плоскостей. § 9. Точка пересечения трех плоскостей. § 10. Расстояние от точки до плоскости. Упражнения ГЛАВА V. ПРЯМАЯ ЛИНИЯ § 1. Уравнения прямой линии. § 2. Прямая как линия пересечения двух плоскостей.  Общие уравнения прямой. Общие уравнения прямой.§ 3. Угол между двумя прямыми линиями. § 4. Условия параллельности и перпендикулярности двух прямых. § 5. Уравнения прямой, проходящей через две данные точки. § 6. Угол между прямой и плоскостью. § 7. Условия параллельности и перпендикулярности прямой и плоскости. § 8. Уравнение пучка плоскостей. § 10. Условие, при котором две прямые лежат в одной плоскости. Упражнения ГЛАВА VI. ЦИЛИНДРИЧЕСКИЕ И КОНИЧЕСКИЕ ПОВЕРХНОСТИ. ПОВЕРХНОСТИ ВРАЩЕНИЯ. ПОВЕРХНОСТИ 2-го ПОРЯДКА § 1. Классификация поверхностей. § 2. Цилиндрические поверхности (общий случай). § 3. Конические поверхности. § 4. Поверхности вращения. § 5. Эллипсоид. § 6. Однополостный гиперболоид. § 7. Двуполостный гиперболоид. § 8. Эллиптический параболоид. § 9. Гиперболический параболоид. § 10. Конус 2-го порядка. § 11. Цилиндры 2-го порядка. § 12. Прямолинейные образующие поверхностей 2-го порядка.  Конструкции В. Г. Шухова. Конструкции В. Г. Шухова.Упражнения Ответы |
Уравнение линии в полярных координатах. Простейшие примеры
По существу, уравнение линии в полярной системе координат представляет собой функцию полярного радиуса от полярного угла (аргумента). При этом полярный угол учитывается в радианах (!) и непрерывно принимает значения от до (иногда следует рассмотреть до бесконечности, или же в ряде задач для удобства от до ). Каждому значению угла «фи», которое входит в область определения функции , соответствует единственное значение полярного радиуса.
Полярную функцию можно сравнить со своеобразным радаром – когда луч света, исходящий из полюса, вращается против часовой стрелки и «прорисовывает» линию.
«Дежурным» примером полярной кривой является Архимедова спираль . На
следующем рисунке изображен её
На
следующем рисунке изображен её
Далее, пересекая полярную ось в точке , спираль продолжит раскручиваться, бесконечно далеко удаляясь от полюса. Но подобные случаи на
практике встречаются довольно редко; более типичная ситуация, когда на всех последующих оборотах мы «пройдёмся по той же самой линии», которая
получена в диапазоне .
В первом же примере мы сталкиваемся и с понятием области определения полярной функции: поскольку полярный радиус неотрицателен , то отрицательные углы у функции рассматривать нельзя.
! Примечание: в ряде случаев принято использовать обобщённые полярные координаты, где радиус может быть отрицательным, и такой подход мы вкратце изучим чуть позже
Кроме спирали Архимеда, есть множество других известных кривых, но искусством, как говорится, сыт не будешь, поэтому я подобрал примеры, которые
очень часто встречаются в реальных практических заданиях.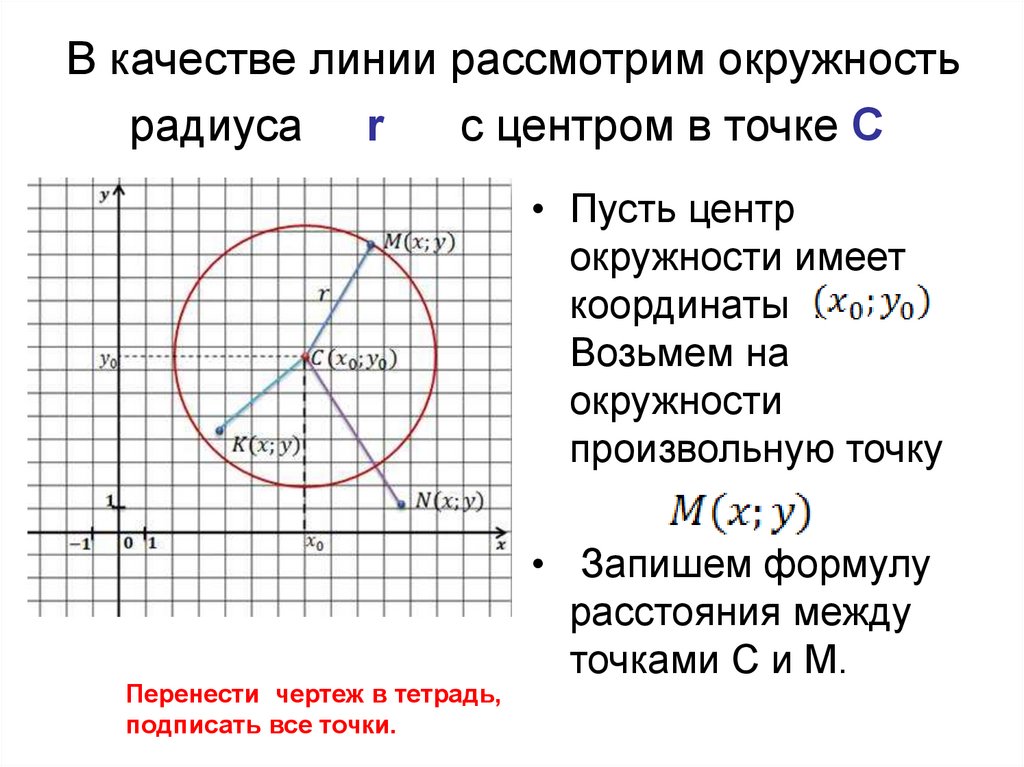
Сначала простейшие уравнения и простейшие линии:
Уравнение вида задаёт луч, исходящий из полюса. Действительно, вдумайтесь, если значение угла всегда (каким бы ни было «эр») постоянно, то какая это линия?
Примечание: в обобщённой полярной системе координат данное уравнение задаёт прямую, проходящую через полюс.
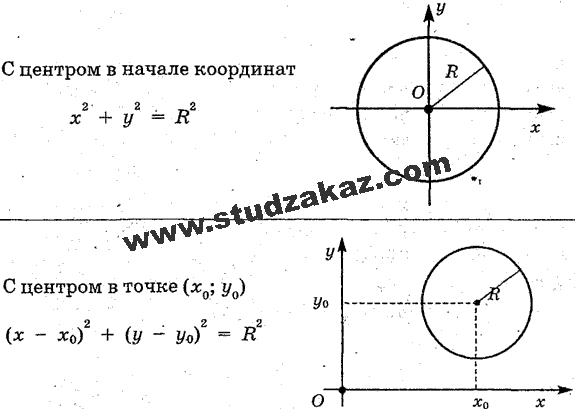
Уравнение вида определяет… догадайтесь с первого раза – если для любого угла «фи» радиус остаётся постоянным? Фактически это определение окружности с центром в полюсе радиуса .
Например, . Для наглядности найдём уравнение этой линии в прямоугольной
системе координат. Используя полученную ранее формулу , проведём замену:
Возведём обе части в квадрат:
– уравнение окружности с центром в начале координат радиуса 2, что и
требовалось проверить.
А теперь оценИте удобство – с окружностью значительно выгоднее работать именно в полярных координатах по причине предельной простоты уравнения .
Рассмотрим более содержательные задачи на построение:
Задача 116
Построить линию
Решение: в первую очередь найдём область определения. Так как полярный радиус неотрицателен, то должно выполняться
неравенство . Можно вспомнить школьные правила решения тригонометрических
неравенств, но в простых случаях как этот,
я советую более быстрый графический метод решения:
– Посмотрим на график функции (см. Приложение
Тригонометрия). Что означает неравенство ? Оно
означает, что нас устраивает тот кусок графика, который не ниже оси абсцисс , а именно, его часть на отрезке . И,
соответственно, интервал не подходит. Таким образом, область определения нашей
функции: , то есть график расположен справа от полюса (по терминологии декартовой системы – в правой полуплоскости).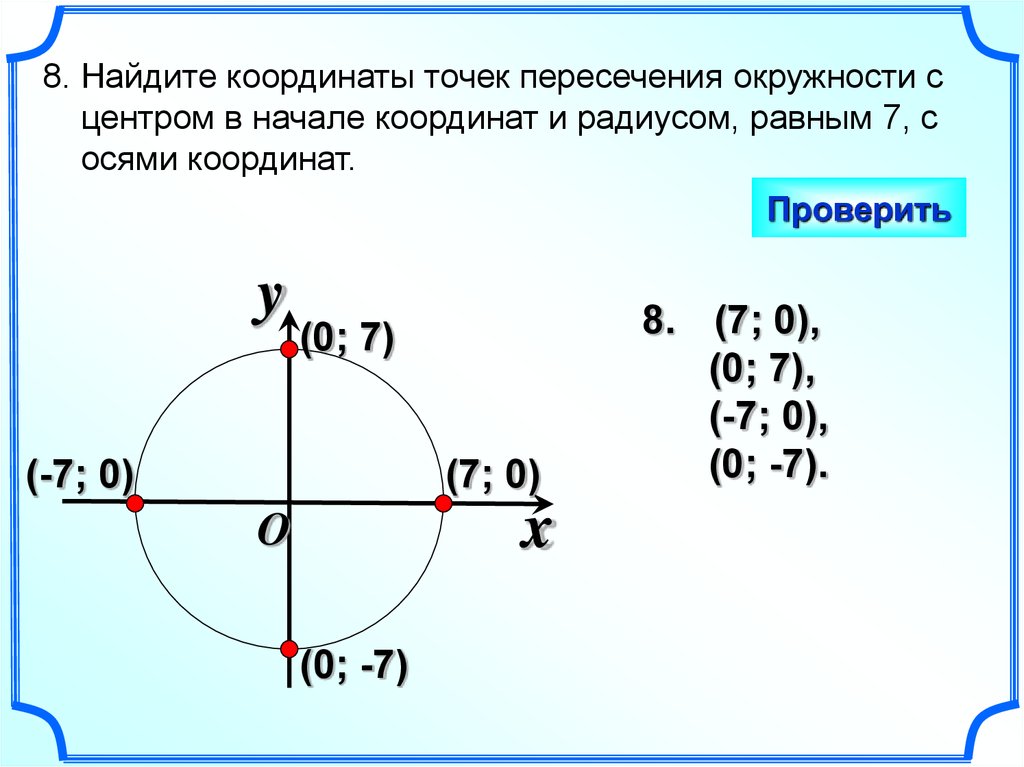
В полярных координатах часто бывает смутное представление о том, какую линию определяет то или уравнение, поэтому чтобы её построить, необходимо найти принадлежащие ей точки – и чем больше, тем лучше. Обычно ограничиваются десятком-другим (а то и меньшим количеством). Проще всего, конечно же, взять табличные значения угла.
Для бОльшей ясности к отрицательным значениям угла я буду «прикручивать» один оборот (левая колонка), и в силу чётности косинуса соответствующие положительные значения можно заново не считать (справа):
Изобразим полярную систему координат и отложим найденные точки, при этом одинаковые значения «эр» удобно откладывать за один раз, делая парные
засечки циркулем по рассмотренной ранее технологии:
В принципе, линия отчётливо прорисовывается, но чтобы
стопроцентно подтвердить догадку, давайте найдём её уравнение в декартовой системе координат. Можно применить недавно выведенные формулы , но я расскажу вам о более хитром приёме.
Можно применить недавно выведенные формулы , но я расскажу вам о более хитром приёме.
Обе части уравнения искусственно домножаем на «эр»: и используем более компактные формулы перехода:
Выделяя полный квадрат, приводим уравнение к понятному виду:
– уравнение окружности с центром в
точке , радиуса 2.
Коль скоро по условию требовалось просто выполнить построение и всё, плавно соединяем найденные точки линией. Ничего страшного, если получится немного неровно, вы же не обязаны были знать, что это окружность 😉
Почему мы не рассмотрели значения угла вне промежутка ?
Ответ прост: нет смысла. Ввиду периодичности функции нас ждёт бесконечный «бег» по построенной окружности.
Несложно провести нехитрый анализ и прийти к выводу, что уравнение вида задаёт окружность диаметра с центром в точке .
Образно говоря, все такие окружности «сидят» на полярной оси и обязательно проходят через полюс. Если же , то весёлая компания перекочует налево – на продолжение полярной оси (подумайте, почему).
Если же , то весёлая компания перекочует налево – на продолжение полярной оси (подумайте, почему).
Похожая задача для самостоятельного решения:
Задача 117
Построить линию и найти её уравнение в декартовой системе координат.
Систематизируем порядок решения задачи:
Находим область определения функции, для этого удобно посмотреть на синусоиду (Приложение Тригонометрия), чтобы сразу же понять, где синус неотрицателен.
На втором шаге рассчитываем полярные координаты точек, используя табличные значения углов; проанализируйте, нельзя ли сократить количество вычислений?
На третьем шаге откладываем точки в полярной системе координат и аккуратно соединяем их линией.
И, наконец, находим уравнение линии в декартовой системе координат.
Примерный образец решения в конце книги.
Общий алгоритм и технику построения в полярных координатах мы детализируем и существенно ускорим совсем скоро, но перед этим познакомимся ещё с одной распространённой линией:
4. 5. Полярная роза
5. Полярная роза
4.3. Взаимосвязь прямоугольной и полярной системы координат
| Оглавление |
Автор: Aлeксaндр Eмeлин
8.2: Полярные координаты — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 13876
- Дэвид Липпман и Мелони Расмуссен
- The OpenTextBookStore
Система координат, с которой мы лучше всего знакомы, называется декартовой системой координат, прямоугольной плоскостью, разделенной на четыре квадранта горизонтальной и вертикальной осями.
В предыдущих главах мы часто находили декартовы координаты точки на окружности под заданным углом от положительной горизонтальной оси. Иногда этот угол, наряду с расстоянием точки от начала координат, обеспечивает более полезный способ описания местоположения точки, чем обычные декартовы координаты.
Иногда этот угол, наряду с расстоянием точки от начала координат, обеспечивает более полезный способ описания местоположения точки, чем обычные декартовы координаты.
ПОЛЯРНЫЕ КООРДИНАТЫ
Полярные координаты точки состоят из упорядоченной пары (\(r\),\(\theta\)), где \(r\) — расстояние от точки до начала координат, а \( \theta\) — угол, измеренный в стандартном положении.
Обратите внимание, что если бы мы «разметили» плоскость в полярных координатах, это выглядело бы как график справа, с кругами с возрастающими радиусами и лучами, нарисованными с возрастающими углами.
Пример \(\PageIndex{1}\)
Постройте полярную точку (\(3, \dfrac{5\pi}{6}\)).
Решение
Эта точка будет находиться на расстоянии 3 от начала координат под углом \(\dfrac{5\pi}{6}\). Построение этого
Пример \(\PageIndex{2}\)
Постройте полярную точку (\(-2, \dfrac{\pi}{4}\)).
Решение
Обычно мы используем положительные значения \(r\), но иногда мы сталкиваемся со случаями, когда \(r\) отрицательно.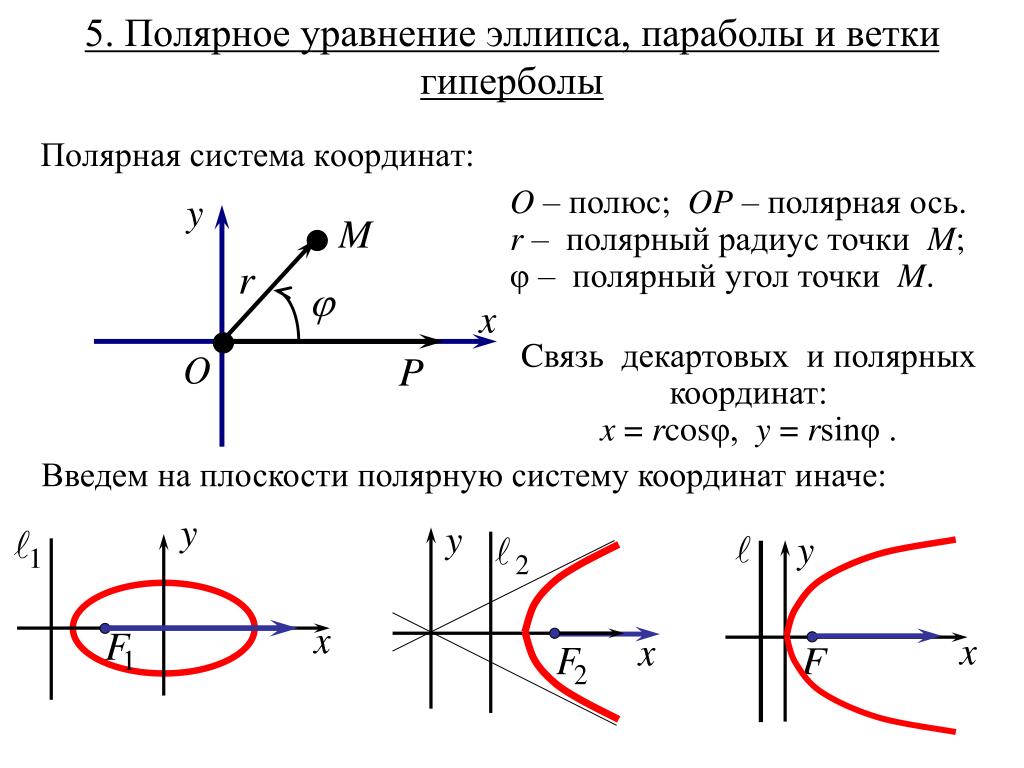 На обычной числовой прямой мы измеряем положительные значения справа и отрицательные значения слева. Аналогично нанесем эту точку. Для начала мы поворачиваем на угол \(\dfrac{\pi}{4}\).
На обычной числовой прямой мы измеряем положительные значения справа и отрицательные значения слева. Аналогично нанесем эту точку. Для начала мы поворачиваем на угол \(\dfrac{\pi}{4}\).
Перемещение в этом направлении в первый квадрант даст положительные значения r . Для отрицательных значений r мы перемещаемся в противоположном направлении, в третий квадрант. График этого:
Обратите внимание, что результирующая точка совпадает с полярной точкой (\(2, \dfrac{5\pi}{4}\)). На самом деле, любую декартову точку можно представить бесконечным числом различных полярных координат, добавляя или вычитая из этих точек полные обороты. Например, одна и та же точка может быть представлена как (\(2, \dfrac{13\pi}{4}\)).
Упражнение \(\PageIndex{1}\)
Нанесите следующие точки, заданные в полярных координатах, и подпишите их.
а. \(A = (3, \dfrac{\pi}{6})\)
б. \(B = (-2, \dfrac{\pi}{3})\)
c. \(C = (4, \dfrac{3\pi}{4})\)
- Ответ
Конверсионные точки
Чтобы преобразовать полярные координаты в декартовы координаты, мы вспоминаем отношения, которые мы разработали еще в главе 5. 9{2}\]
9{2}\]
Исходя из этих соотношений и наших знаний об единичной окружности, если \(r = 1\) и \(\theta = \dfrac{\pi}{3}\), полярные координаты будут \((r, \theta ) = (1, \dfrac{\pi}{3})\), и соответствующие декартовы координаты \((x, y) = (\dfrac{1}{2}, \dfrac{\sqrt{3}} {2})\).
Запоминание значений единичного круга очень пригодится при преобразовании между декартовыми и полярными координатами.
Пример \(\PageIndex{3}\)
Найдите декартовы координаты точки с полярными координатами \((r, \theta) = (5, \dfrac{2\pi}{3})\).
Решение
Чтобы найти \(x\) и \(y\) координаты точки,
\[x = r\text{cos} (\theta) = 5 \cos (\dfrac{ 2\pi}{3}) = 5(-\dfrac{1}{2}) = -\dfrac{5}{2}\nonumber\]
\[y = r\text{sin} (\theta ) = 5 \ sin (\ dfrac {2 \ pi} {3}) = 5 (- \ dfrac {\ sqrt {3}} {2}) = — \ dfrac {5 \ sqrt {3}} {2} \ nonumber\]
Декартовы координаты: (\(-\dfrac{5}{2}, \dfrac{5\sqrt{3}}{2}\)).
Пример \(\PageIndex{4}\)
Найдите полярные координаты точки с декартовыми координатами (−3,−4) .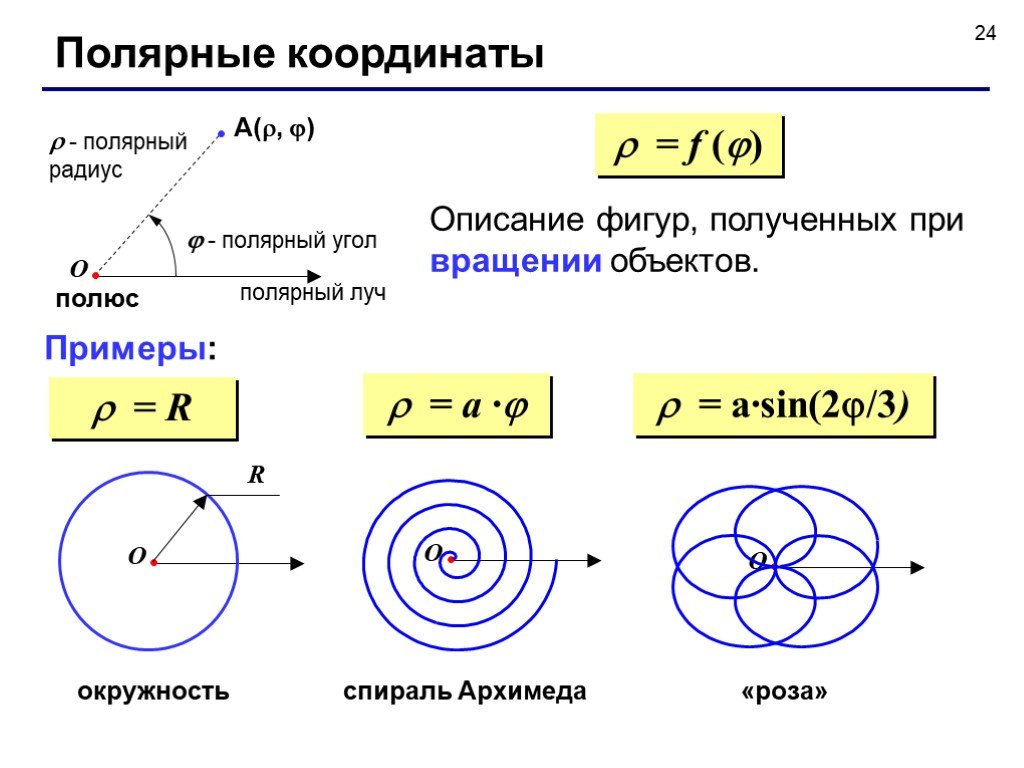 9{\text{rd}}\) квадранта, мы можем определить, что второй угол и есть тот, который нам нужен. Полярные координаты этой точки равны \((r, \theta) = (5, 4,069)\).
9{\text{rd}}\) квадранта, мы можем определить, что второй угол и есть тот, который нам нужен. Полярные координаты этой точки равны \((r, \theta) = (5, 4,069)\).
Упражнение \(\PageIndex{2}\)
Преобразуйте следующее.
а. Преобразуйте полярные координаты \((r, \theta) = (2, \pi)\) в (\(x, y)\).
б. Преобразуйте декартовы координаты \((x, y) = (0, -4)\) в \((r, \theta)\).
- Ответить
а. \((r, \theta) = (2, \pi)\) преобразуется в \((x, y) = (2\cos(\pi), 2\sin(\pi)) = (-2, 0 )\) 92\) описывает связь между значениями \(x\) и \(y\) на декартовой сетке, можно написать полярное уравнение, описывающее связь между значениями \(r\) и \(\theta\) на полярной сетка.
Пример \(\PageIndex{5}\)
Нарисуйте график полярного уравнения \(r = \theta\).
Решение
Уравнение \(r = \theta\) описывает все точки, для которых радиус \(r\) равен углу. Чтобы визуализировать эту связь, мы можем создать таблицу значений.

\(\тета\) 0 \(\пи/4\) \(\пи/2\) \(3\пи/4\) \(\пи\) \(5\пи/4\) \(3\пи/2\) \(7\пи/4\) \(2\пи\) \(р\) 0 \(\пи/4\) \(\пи/2\) \(3\пи/4\) \(\пи\) \(5\пи/4\) \(3\пи/2\) \(7\пи/4\) \(2\пи\) Мы можем нанести эти точки на плоскость, а затем нарисовать кривую, соответствующую этим точкам. Полученный график представляет собой спираль.
Обратите внимание, что результирующий график не может быть результатом функции вида \(y = f(x)\), так как он не проходит тест на вертикальную линию, даже если он является результатом функции, дающей \(r\ ) в терминах \(\тета\).

Хотя приятно видеть полярные уравнения на полярных сетках, полярные графики чаще изображаются в декартовой системе координат, поэтому остальные полярные уравнения будут отображаться соответственно.
Здесь показан приведенный выше спиральный график на декартовой сетке.
Пример \(\PageIndex{6}\)
Нарисуйте график полярного уравнения \(r = 3\).
Решение
Напомним, что когда переменная не появляется в уравнении, это означает, что не имеет значения, какое значение имеет эта переменная; результат уравнения останется прежним. Например, декартово уравнение \(y = 3\) описывает все точки, где \(y = 3\), независимо от значений x, образуя горизонтальную линию.
Аналогично, это полярное уравнение описывает все точки на расстоянии 3 от начала координат, независимо от угла, создавая график окружности .
Обычные настройки графических калькуляторов и графических программ в декартовой системе координат, где \(y\) является функцией \(x\), где графическая утилита запрашивает \(f(x)\), или просто \( у =\).

Для построения полярных уравнений может потребоваться изменить режим калькулятора на полярный. Вы будете знать, что вам удалось изменить режим, если теперь у вас есть \(r\) как функция \(\theta\), где графическая утилита запрашивает \(r(\theta)\), или просто \ (г =\).
Пример \(\PageIndex{7}\)
Нарисуйте график полярного уравнения \(r = 4 \cos(\theta)\) и найдите интервал, на котором оно завершает один цикл.
Решение
Хотя мы могли бы снова создать таблицу, нанести на нее соответствующие точки и соединить точки, мы также можем обратиться к технологии, чтобы построить ее напрямую. Используя технологию, мы производим показанный здесь график, окружность, проходящую через начало координат.
Поскольку этот график замыкает цикл и повторяется, мы можем спросить, какой интервал значений \(\theta\) дает весь график. В \(\theta = 0\), \(r = 4\cos(0) = 4\), что дает точку (4, 0). Нам нужно следующее значение \(\theta\), когда график вернется к точке (4, 0).
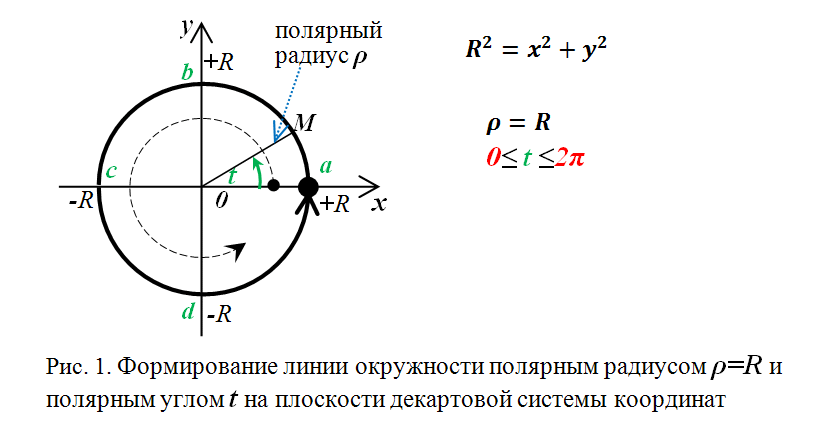
 Решение для случая \(x = 4\) эквивалентно решению \(r\cos(\theta) = 4\). 9{2}(\theta)= 1\nonumber\]У этого есть решения, когда
Решение для случая \(x = 4\) эквивалентно решению \(r\cos(\theta) = 4\). 9{2}(\theta)= 1\nonumber\]У этого есть решения, когда
\[\cos(\theta) = 1\text{ или }\cos(\theta) = -1\nonumber\]Решение этих решений дает решения
\[\theta = 0\text{ или }\theta = \pi\nonumber\]Это показывает нам, что при 0 радианах мы находимся в точке (0, 4), и снова при \(\pi\) радианах мы находимся в точке (0, 4), совершив один полный оборот.
Этот интервал \(0 \le \theta < \pi\) дает одну полную итерацию окружности.
Упражнение \(\PageIndex{3}\)
Нарисуйте график полярного уравнения \(r = 3 \sin (\theta)\) и найдите интервал, на котором оно совершает один цикл.
- Ответить
\[3 \sin(\theta) = 0\text{ at }\theta = 0\text{ и }\theta = \pi\nonumber\]
Он завершает один цикл на интервале \(0 \le \theta < \pi\).
Последние несколько примеров были кругами. Далее мы рассмотрим два других «именных» полярных уравнения, лимасон и розы .

Пример \(\PageIndex{8}\)
Нарисуйте график полярного уравнения \(r = 4\sin(\theta) + 2\). Какой интервал значений \(\theta\) соответствует внутреннему циклу?
Решение
Этот тип графика называется limaçon .
Используя технологию, мы можем нарисовать график. Внутренний цикл начинается и заканчивается в начале координат, где \(r = 0\). Мы можем найти значения \(\theta\), для которых \(r = 0\).\[0 = 4\sin(\theta) + 2\nonnumber\]
\[-2 = 4\sin(\theta)\nonnumber\]
\[\sin(\theta) = -\dfrac{ 1}{2}\nonumber\]
\[\theta = \dfrac{7\pi}{6}\text{ или }\theta = \dfrac{11\pi}{6}\nonumber\]Это говорит нам, что \(r = 0\), поэтому график дважды проходит через начало координат на интервале \([0, 2\pi)\).
Внутренний цикл возникает из интервала \(\dfrac{7\pi}{6} \le \theta \le \dfrac{11\pi}{6}\).
Это соответствует тому, где функция \(r = 4 \sin(\theta) + 2\) принимает отрицательные значения, как мы могли бы видеть, если бы построили график функции в плоскости \(r \theta\).

Пример \(\PageIndex{9}\)
Нарисуйте график полярного уравнения \(r = \cos(3\theta)\). Какой интервал значений \(\theta\) описывает одну маленькую петлю графика?
Решение
Этот тип графика называется трехлистной розой .
Мы можем использовать технологию для создания графика. Интервал \([0, \pi)\) дает один цикл этой функции. Как и в последней задаче, мы можем заметить, что существует интервал, на котором одна петля этого графа начинается и заканчивается в начале координат, где \(r = 0\). Решение для \(\тета\),
\[0 = \cos(3\theta)\nonumber\]Подстановка \(u = 3\theta\)
\[0 = \cos(u)\nonumber\]
\[u = \dfrac{\ pi}{2}\text{ или }u = \dfrac{3\pi}{2}\text{ или }u = \dfrac{5\pi}{2}\nonumber\]Отменить замену,
\[3 \theta = \dfrac{\pi}{2}\text{ или}3 \theta = \dfrac{3\pi}{2}\text{ или}3 \theta = \dfrac{5\pi }{2}\nonumber\]
\[\theta = \dfrac{\pi}{6}\text{ или }\theta = \dfrac{\pi}{2}\text{ или }\theta = \ dfrac{5\pi}{6}\nonumber\]
Есть 3 решения на \(0 \le \theta < \pi\), которые соответствуют 3 раза, когда график возвращается в начало координат, но первые два решения мы решили выше, достаточно, чтобы сделать вывод, что
одна петля соответствует интервалу \(\dfrac{\pi}{6} \le \theta < \dfrac{\pi}{2}\).

Если бы мы хотели получить представление о том, как компьютер нарисовал этот график, рассмотрим, когда \(\theta = 0\).
\(r = \cos(3\theta) = \cos(0) = 1\), поэтому график начинается с (1, 0). Как мы обнаружили выше, при \(\theta = \dfrac{\pi}{6}\) и \(\theta = \dfrac{\pi}{2}\) график находится в начале координат. Глядя на уравнение, обратите внимание, что любой угол между \(\dfrac{\pi}{6}\) и \(\dfrac{\pi}{2}\), например, при \(\theta = \dfrac{ \pi}{3}\), дает отрицательное значение \(r\): \[r = \cos(3 \cdot \dfrac{\pi}{3}) = \cos(\pi) = -1\nonumber \]
Обратите внимание, что при отрицательном значении \(r\) и угле с конечной стороной в первом квадранте соответствующая декартова точка будет в третьем квадранте. Поскольку \(r = \cos(3\theta)\) отрицательно на \(\dfrac{\pi}{6} \le \theta < \dfrac{\pi}{2}\), этот интервал соответствует петля графика в третьем квадранте.
Упражнение \(\PageIndex{4}\)
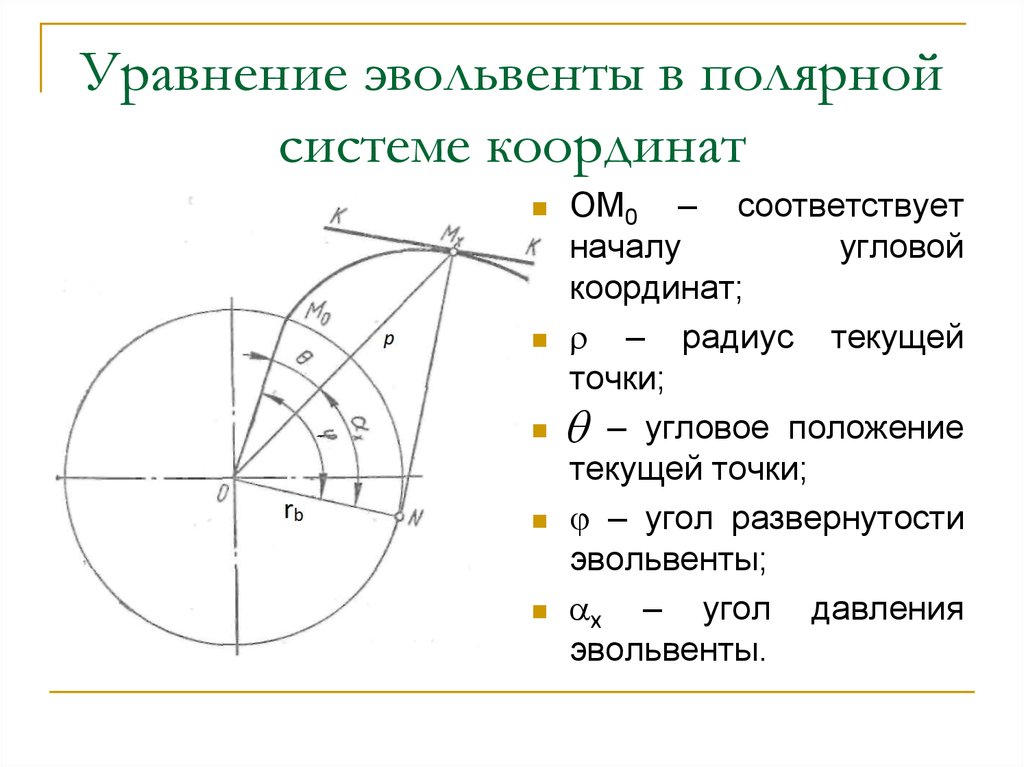
Нарисуйте график полярного уравнения \(r = \sin(2\theta)\).
 Вы бы назвали эту функцию limaçon 9?0049 или роза ?
Вы бы назвали эту функцию limaçon 9?0049 или роза ?- Ответить
Роза с 4 лепестками.
Преобразование уравнений
Хотя многие полярные уравнения невозможно красиво выразить в декартовой форме (и наоборот), может быть полезно преобразовать эти две формы, когда это возможно. Для этого мы используем те же отношения, которые мы использовали для преобразования точек между системами координат.
92 — 6r\sin(\theta) = 0\nonnumber\]Множитель
\[r (r — 6\sin(\theta)) = 0\nonnumber\] Используйте теорему о нулевом множителе
\[r = 6\sin (\theta)\text{ или }r = 0\nonumber\] Поскольку \(r = 0\) — это всего лишь точка, мы отвергаем это решение.Решение \(r = 6\sin(\theta)\) очень похоже на то, что мы изобразили в примере 7. Фактически, это уравнение описывает окружность с низом в начале координат и вершиной в точке (0, 6).

Пример \(\PageIndex{11}\)
Перепишите декартово уравнение \(y = 3x + 2\) как полярное уравнение.
Решение
\[y = 3x + 2\nonnumber\]Используйте \(y = r\sin(\theta)\) и \(x = r\cos(\theta)\)
\[r \sin(\theta) = 3r\cos(\theta) + 2\nonumber\] Переместить все термины с \(r\) в одну сторону
\[r\sin(\theta) — 3r\cos(\theta) = 2\nonumber\] Вынести на множители \(r\)
\[r(\sin(\theta) — 3\cos(\theta)) = 2\nonumber\] Разделить
\[r = \dfrac{2} {\sin(\theta) — 3\cos(\theta)}\nonumber\]В этом случае полярное уравнение является более громоздким, чем декартово уравнение, но все же бывают случаи, когда это уравнение может быть полезным.
Пример \(\PageIndex{12}\)
Перепишите полярное уравнение \(r = \dfrac{3}{1- 2\cos(\theta)}\) как декартово уравнение.
Решение
Мы хотим исключить \(\theta\) и \(r\) и ввести \(x\) и \(y\). Обычно проще всего начать с очистки дроби и поиска подстановочных значений, которые исключат \(\theta\).

\[r = \dfrac{3}{1 — 2\cos(\theta)}\nonumber\]Очистить дробь
\[r(1 — 2\cos(\theta)) = 3\nonumber\] Используйте \(\cos(\theta) = \dfrac{x}{r}\), чтобы исключить \(\theta\) 9{2/3}\номер\]- Декартова система координат
- Полярная система координат
- Нанесение точек в полярных координатах
- Преобразование координат между системами
- Полярные уравнения: спирали, круги, лимасоны и розы Преобразование уравнений между системами
Эта страница под заголовком 8.2: Полярные координаты публикуется в соответствии с лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Дэвидом Липпманом и Мелони Расмуссен (The OpenTextBookStore) посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами. платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Дэвид Липпман и Мелони Расмуссен
- Лицензия
- СС BY-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- полярные координаты
- источник@http://www.
 opentextbookstore.com/details.php?id=30
opentextbookstore.com/details.php?id=30
Полярные координаты
Полярные координаты
Определение полярных координат
Напомним, что мы определяем точку (x,y) на плоскости как x единиц вправо от начала координат и у единиц слева от начала координат. Это отлично работает для линий и парабол, но у окружностей есть несколько запутанные уравнения. Как в качестве альтернативы мы определяем новую систему координат, где первая координата r — расстояние от начала координат до точки и вторая координата q это угол, который луч из начала координат в точку составляет с положительная ось x. Из тригонометрии имеем
x = rcosq y = rsinq
В вашем калькуляторе есть специальный режим для полярных координат. Мы используем
калькулятор для построения графика
Мы используем
калькулятор для построения графикаr = 5cosq
иг = потому что ( )
кругов
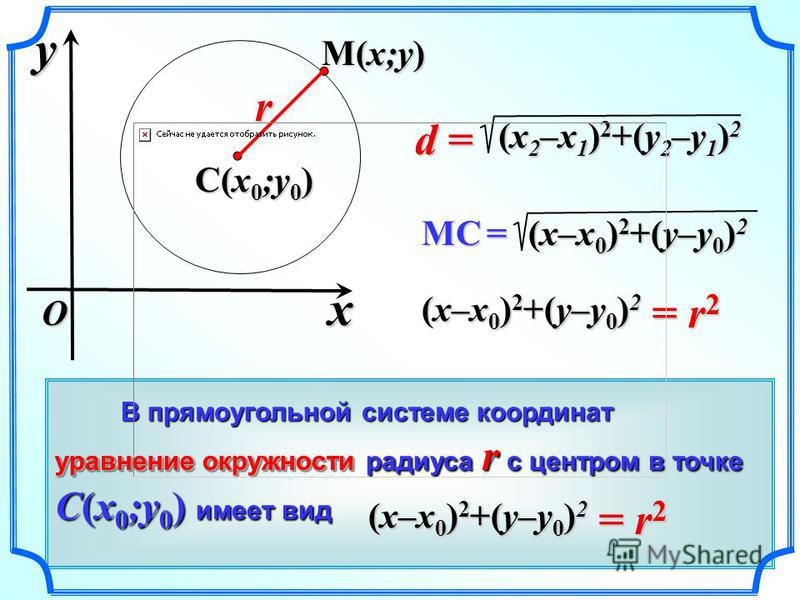
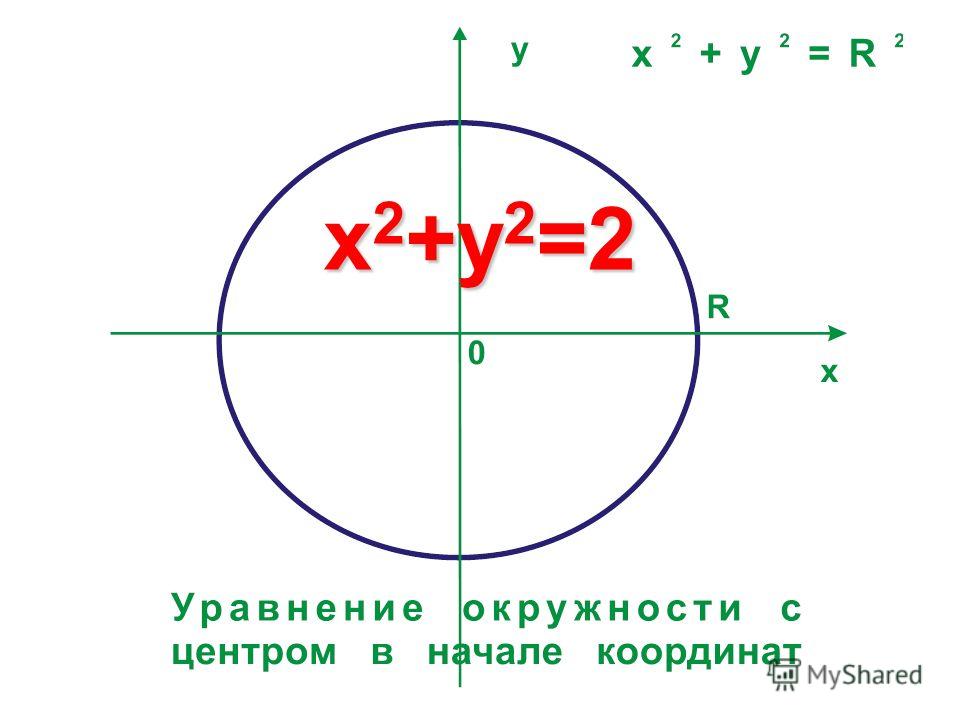
Окружность с центром в начале координат имеет уравнение
x 2 + y 2 = R 2
В полярной форме имеемг = р
Например, круг радиуса 3 с центром в (0,0) имеет полярное уравнениег = 3
Линии
Если
у = мх + б
мы можем написатьг грех (д) = m r cos q + b
илиб
r =
sin q — m cos q
Конические сечения
Напомним, что коническое сечение определяется следующим образом:
по
Пусть f (называемая фокусом ) будет фиксированной точкой на плоскости, м (так называемый директриса ) быть фиксированной линией, а e (называется эксцентриситет ) положительная постоянная. Затем
множество точек P на плоскости с
Затем
множество точек P на плоскости с|ПФ|
= е
|Пм|
является коническим сечением. Если e < 1, то сечение представляет собой эллипс, если e = 1, то это a парабола,
и если e = 0, то это гипербола.Примечание. Если F – исходная точка, m х = d, тогда
|ПФ| = r, |Pm| = д — r cos q
так что уравнение становитсяг = е (d — rcos (q)) = ed — рекос(к)
илиизд.
r =
1 + e cosq
Производные в полярных координатах
Теорема
Пусть r = r(q) представляет собой полярную кривую, тогда
ды dy/dq r’ sinq + г cosq
«=» =
дх дх/дк r ‘cosq — г синкdy r’ sinq + г cosq
=
дх r ‘cosq — г синк
Доказательство:Так как
x = r cosq, и y = r sinq,
мы можем подставить r = r(q), чтобы получить
x = r cosq
Взяв производную,
x’ = r’ cosq — r sinq
и
y’ = r’ sinq + р коскв.





 Решение для случая \(x = 4\) эквивалентно решению \(r\cos(\theta) = 4\). 9{2}(\theta)= 1\nonumber\]У этого есть решения, когда
Решение для случая \(x = 4\) эквивалентно решению \(r\cos(\theta) = 4\). 9{2}(\theta)= 1\nonumber\]У этого есть решения, когда 
 Вы бы назвали эту функцию limaçon 9?0049 или роза ?
Вы бы назвали эту функцию limaçon 9?0049 или роза ?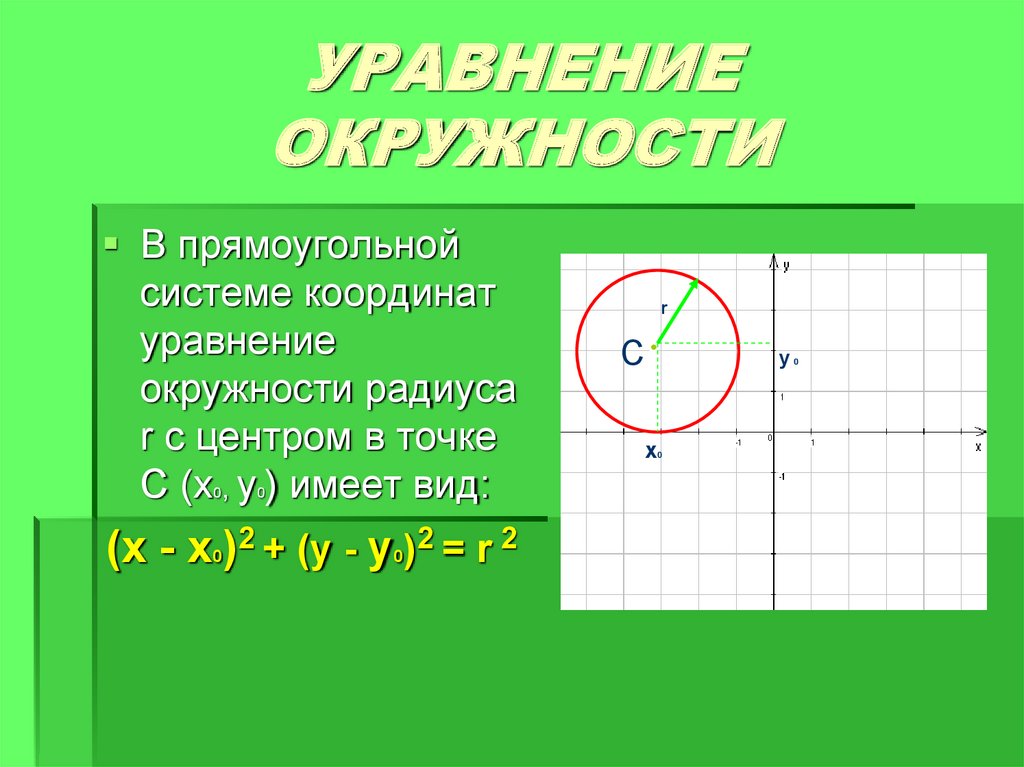

 opentextbookstore.com/details.php?id=30
opentextbookstore.com/details.php?id=30 Мы используем
калькулятор для построения графика
Мы используем
калькулятор для построения графика Затем
множество точек P на плоскости с
Затем
множество точек P на плоскости с