тройные неравенства. Кто поможет? (Алгебра 9 класс Макарычев ) – Рамблер/класс
1006 — тройные неравенства. Кто поможет? (Алгебра 9 класс Макарычев ) – Рамблер/классИнтересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Решите систему трех неравенств:
ответы
Привет. Помгу
Помгу
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
ЕГЭ
10 класс
11 класс
Химия
похожие вопросы 5
150 Алгебра 9 класс Макарычев Помогите решить графически
Решите графически уравнение:
а) х3 = 2; б) х3 = 4; в) х3 = -5.
ЭкзаменыАлгебра9 классМакарычев Ю.Н.ГДЗ
Когда скорость изменения функции будет наибольшей или наименьшей? Алгебра 10-11 класс Колмогоров Упр 308
Совсем я в точных науках не сильна) Кто поможет?) Найдите значения аргумента из промежутка [-2; 5], при которых скорость изменения (Подробнее…)
ГДЗ11 классКолмогоров А.Н.Алгебра
Васильевых.
Укажите предложение, в котором средством выразительности речи является эпитет.
1) — Скрипка маленькая, её на (Подробнее…)
ГДЗРусский языкОГЭ9 классВасильевых И.П.
16. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)… Цыбулько И. П. Русский язык ЕГЭ-2017 ГДЗ. Вариант 13.
16.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
ЕГЭ-2017 Цыбулько И. П. Русский язык ГДЗ. Вариант 13. 18. Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)…
18.
Расставьте все знаки препинания: укажите цифру(-ы), на месте которой(-ых)
в предложении должна(-ы) стоять запятая(-ые). (Подробнее…)
(Подробнее…)
ГДЗЕГЭРусский языкЦыбулько И.П.
Вычисление тройных интегралов: теория и примеры
- Понятие тройного интеграла
- Вычисление тройного интеграла путём уменьшения кратности
- Расстановка пределов интегрирования при переходе к последовательности трёх интегралов
- Замена переменных в тройном интеграле и цилиндрические координаты
- Тройной интеграл в сферических координатах
- Приложения тройного интеграла
Тройные интегралы – это аналог двойного интеграла для функции трёх переменных, заданной как f(M) = f(x, y, z).
Записывается тройной интеграл так:
.
Здесь V – пространственная (трёхмерная) фигура,
ограниченная плоскостями, выражения которых (равенства) даны в задании вычисления тройного интеграла. V называют также замкнутой ограниченной областью трёхмерного пространства.
Вычислить тройной интеграл — значит найти число, равное объёму тела V или, что то же самое — области V.
Практически каждый может понять смысл вычисления тройного интеграла «на своей шкуре». Точнее — «под шкурой», а ещё точнее — по своим органам дыхания — лёгким. Вне зависимости от того, знаете ли вы об этом или не знаете, в лёгких человека свыше 700 миллионов альвеол — пузырьковых образований, оплетённых сетью капилляров. Через стенки альвеол происходит газообмен. Поэтому можно рассуждать так: объём газа в лёкгих, можно представить в виде некоторой компактной области. А состоит этот объём из маленьких объёмов, сосредоточенных в альвеолах. Ключевую роль в этом сравнении играет именно огромное количество альвеол в лёгких: как мы увидим в следующем абзаце, через такое «огромное количество малостей» математически как раз и формулируется понятие тройного интеграла.
Почему именно тройной интеграл служит для нахождения объёма тела V?
Пусть область V разбита на n произвольных областей Δvi,
причём под этим обозначением подразумевается не только каждая маленькая область, но и её объём. В каждой такой
маленькой области выбрана произвольная точка Mi, а f(Mi) — значение функции f(M) в этой точке. Теперь будем максимально увеличивать число таких
маленьких областей, а наибольший диаметр Δvi —
наоборот, уменьшать. Можем составить интегральную сумму вида
В каждой такой
маленькой области выбрана произвольная точка Mi, а f(Mi) — значение функции f(M) в этой точке. Теперь будем максимально увеличивать число таких
маленьких областей, а наибольший диаметр Δvi —
наоборот, уменьшать. Можем составить интегральную сумму вида
.
Если функция f(M) = f(x, y, z) непрерывна, то будет существовать предел интегральных сумм вида, указанного выше. Этот предел и называется тройным интегралом.
В этом случае функция f(M) = f(x, y, z) называется интегрируемой в области V; V — областью интегрирования; x, y, z — переменными интегрирования, dv (или dx dy dz) — элементом объёма.
Как и в случае двойных интегралов, вычисление тройных интегралов сводится к вычислению интегралов
меньшей кратности.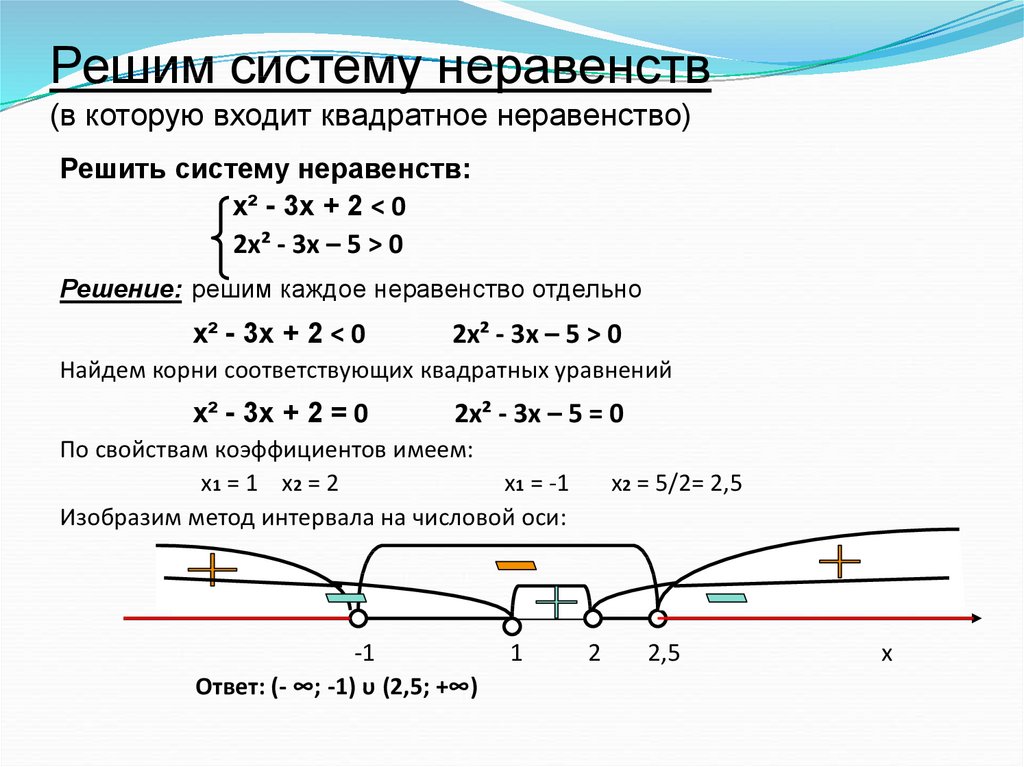
Рассмотрим трёхмерную область
Чтобы применять переход к интегралам меньшей кратности, требуется, чтобы трёхмерная область V была правильной. Она правильна тогда, когда прямая, параллельная оси Oz, пересекает границу области V не более чем в двух точках. Правильными
трёхмерными областями являются, например, прямоугольный параллелепипед, эллипсоид, тетраэдр. На рисунке ниже —
прямоугольный параллелепипед, который встретится нам в первом примере на решение задач.
Чтобы наглядно представить отличие правильности от неправильности, добавим, что поверхности области по высоте у правильной области не должны быть вогнуты вовнутрь. На рисунке ниже — пример неправильной области V — однополостный гиперболоид, поверхность которого прямая, параллельная оси Oz (красного цвета), пересекает более чем в двух точках.
Мы будем рассматривать только правильные области.
Итак, область V — правильная. Тогда для любой функции f(x, y, z), непрерывной в области V, справедлива формула
Эта формула позволяет свести вычисление тройного интеграла к последовательному вычислению внутреннего определённого интеграла по переменной z (при постоянных x и y
Переходя от двойного интеграла к повторному, получаем следующую формулу для вычисления тройного интеграла:
Таким образом, для вычисления тройного интеграла требуется последовательно вычислить три
определённых интеграла.
Вычисляются эти интегралы от самого внутреннего (по переменной z) к самому внешнему (по переменной x). Для удобства восприятия последовательности вычислений три «вложенных» интеграла можно записать так:
.
Из этой записи уже однозначно видно, что:
- сначала нужно интегрировать функцию f(x, y, z) по переменной z, а в качестве пределов интегрирования взять уравнения z = z1(x, y) и z = z2(x, y) поверхностей ограничивающих область V снизу и сверху;
- получившийся на предыдущем шаге результат интегрировать по переменной y, а в качестве пределов интегрирования взять уравнения y = y1(x) и y = y2(x) поверхностей, ограничивающих область V с боковых сторон;
- получившийся на предыдущем шаге результат интегрировать по переменной x, а в качестве пределов
интегрирования взять уравнения x = a и x = b поверхностей, ограничивающих область V по глубине.

Пример 1. Пусть от тройного интеграла можно перейти к повторному интегралу
—
последовательности трёх определённых интегралов. Вычислить этот повторный интеграл.
Решение. Вычисление повторного интеграла всегда начинается с последнего интеграла. В нашем случае применяем формулу 10 из таблицы интегралов:
.
Вычислим второй интеграл — по переменной y (применяя формулу 7 из таблицы интегралов):
.
Теперь вычисляем самый внешний интеграл — по переменной x (применяя все ту же формулу 7):
.
Ответ: данный повторный интеграл и соответствующий ему тройной интеграл равен 10.
Пример 2. Вычислить тройной интеграл
,
где V — параллелепипед, ограниченный плоскостями x = − 1, x = + 1, y = 0, y = 1, z = 0, z = 2.
Решение. Пределы интегрирования для всех трёх определённых интегралов однозначно заданы уравнениями поверхностей, ограничивающих параллелепипед. Поэтому сразу сводим данный тройной интеграл к последовательности трёх определённых интегралов:
.
Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:
.
Вычисляем интеграл «в серединке» — по переменной y. Получаем;
.
Теперь вычисляем самый внешний интеграл — по переменной x:
Ответ: данный тройной интеграл равен -2.
Пример 3. Вычислить тройной интеграл
,
где V — пирамида, ограниченная плоскостью x + y + z = 1
и координатными плоскостями x = 0, y = 0, z = 0. Область V проецируется на плоскость xOy в треугольник D, как показано
на рисунке ниже.
Область V проецируется на плоскость xOy в треугольник D, как показано
на рисунке ниже.
Решение. Расставим сначала пределы интегрирования. Для интеграла по переменной z нижний предел интегрирования задан однозначно: z = 0. Чтобы получить верхний предел, выразим z из x + y + z = 1. Получаем 1 − x − y. Для интеграла по переменной y нижний предел интегрирования задан однозначно: y = 0. Для получения верхнего предела выразим y из x + y + z = 1, считая при этом, что z = 0 (так как линия расположена в плоскости xOy). Получаем: 1 − x.
Сводим данный тройной интеграл к последовательности трёх определённых интегралов:
.
Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:
.
Вычисляем средний интеграл — по переменной y. Получаем:
Наконец, вычисляем самый внешний интеграл — по переменной x:
Ответ: данный тройной интеграл равен 1/8.
Вычислить тройной интеграл самостоятельно, а затем посмотреть решение
Пример 4. Вычислить тройной интеграл
,
где V — пирамида, ограниченная плоскостью x + y + z = 1 и координатными плоскостями x = 0, y = 0, z = 0.
Посмотреть правильное решение и ответ.
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Интеграл
Бывает, что студенты, у которых не вызывает особых трудностей непосредственное вычисление
интегралов, не могут освоиться в расстановке пределов интегрирования при переходе от тройного интеграла к
последовательности трёх определённых интегралов. В этом деле действительно требуется некоторая натренированность.
В первом примере область интегрирования V представляла собой параллелепипед,
с которым всё понятно: со всех сторон его ограничивают плоскости, а значит, пределы интегрирования однозначно
заданы уравнениями плоскостей. Во втором примере — пирамида: здесь уже требовалось чуть больше подумать и выразить
один из пределов из уравнения. А если область V ограничивают не плоские
поверхности? Нужно, конечно, определённым образом осмотреть область V.
В этом деле действительно требуется некоторая натренированность.
В первом примере область интегрирования V представляла собой параллелепипед,
с которым всё понятно: со всех сторон его ограничивают плоскости, а значит, пределы интегрирования однозначно
заданы уравнениями плоскостей. Во втором примере — пирамида: здесь уже требовалось чуть больше подумать и выразить
один из пределов из уравнения. А если область V ограничивают не плоские
поверхности? Нужно, конечно, определённым образом осмотреть область V.
Начнём с примера «пострашнее», чтобы почувствовать «обстановку, приближенную к боевой».
Пример 5. Расставить пределы интегрирования при переходе от тройного интеграла, в котором область V — эллипсоид
.
Решение. Пусть центр эллипсоида — начало координат, как показано на рисунке выше. Посмотрим на эллипсоид снизу.
Снизу его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена
ниже плоскости xOy. Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение
со знаком минус будет нижним пределом интегрирования по переменной z:
Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение
со знаком минус будет нижним пределом интегрирования по переменной z:
.
Теперь посмотрим на эллипсоид сверху. Здесь его ограничивает поверхность, являющаяся той части поверхности эллипсоида, которая расположена выше оси xOy. Следовательно, нужно выразить из уравнения эллипсоида z и полученное выражение будет верхним пределом интегрирования по переменной z:
.
Проекцией эллипсоида на плоскость xOy является эллипсоид. Его уравнение:
.
Чтобы получить нижний предел интегрирования по переменной y, нужно выразить y из уравнения эллипсоида и взять полученное выражение со знаком минус:
.
Для верхнего предела интегрирования по переменной y то же выражение со знаком плюс:
.
Что касается интегрирования по переменной x, то область V ограничена по глубине плоскостями. Следовательно, пределы интегрирования по переменной x можно представить как координаты задней и передней границ области. В случае эллипсоида ими будут взятые с отрицательным и положительным знаками величины длин полуоси a: x1 = − a и x2 = a.
Таким образом, последовательность интегралов для вычисления объёма эллипсоида следующая:
,
где «игрек первое», «игрек второе», «зет первое» и «зет второе» — полученные выше выражения. Если у Вас есть желание и отвага вычислить этот интеграл и, таким образом, объём эллипсоида, то вот ответ: 4πabc/3.
Следующие примеры — не такие страшные, как только что рассмотренный. При этом они предполагают
не только расстановку пределов интегрирования, но и вычисление самого тройного интеграла. Проверьте,
чему вы научились, следя за решением «страшного» примера. Думать при расстановке пределов всё равно
придётся.
Проверьте,
чему вы научились, следя за решением «страшного» примера. Думать при расстановке пределов всё равно
придётся.
Пример 6. Вычислить тройной интеграл
,
если область интегрирования ограничена плоскостями x + y = 1, x + 2y = 4, y = 0, y = 1, z = 1, z = 5.
Решение. «Курортный» пример по сравнению с примером 5, так как пределы интегрирования по «игрек» и «зет» определены однозначно. Но придётся разобраться с пределами интегрирования по «иксу». Проекцией области интегрирования на плоскость xOy является трапеция ABCD.
В этом примере выгоднее проецировать трапецию на ось Oy, иначе, чтобы вычислить тройной
интеграл, на придётся разделить фигуру на три части. В примере 4 мы начинали осмотр области интегрирования
снизу, и это обычный порядок. Но в этом примере мы начинаем осмотр сбоку или, если так проще, положили
фигуру набок и считаем, что смотрим на неё снизу. Можем найти пределы интегирования по «иксу»
чисто алгебраически. Для этого выразим «икс» из первого и второго уравнений, данных в условии примера.
Из первого уравения получаем нижний предел 1 − y, из
второго — верхний 4 − 2y. Сведём данный тройной
интеграл к последовательности трёх определённых интегралов:
Можем найти пределы интегирования по «иксу»
чисто алгебраически. Для этого выразим «икс» из первого и второго уравнений, данных в условии примера.
Из первого уравения получаем нижний предел 1 − y, из
второго — верхний 4 − 2y. Сведём данный тройной
интеграл к последовательности трёх определённых интегралов:
.
Внимание! В этом примере самый внешний интеграл — не по переменной «икс», а по переменной «игрек», а «средний» — по переменной «икс»! Здесь мы применили смену порядка интегрирования, с которой ознакомились при изучении двойного интеграла. Это связано с тем, что, как уже говорилось, мы начали осмотр области интегрирования не снизу, а сбоку, то есть спроецировали её не на ось Ox, на на ось Oy.
Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:
.
Вычисляем средний интеграл — по переменной x. Получаем:
Получаем:
.
Наконец, вычисляем самый внешний интеграл — по переменной y:
Ответ: данный тройной интеграл равен 43.
Пример 7. Вычислить тройной интеграл
,
если область интегрирования ограничена поверхностями x = 0, y = 0, z = 2, x + y + z = 4.
Решение. Область V (пирамида MNRP) является правильной. Проекцией области V на плоскость xOy является треугольник AOB.
Нижние пределы интегрирования по всем переменным заданы в условии примера.
Найдём верхний предел интегирования по «иксу». Для этого выразим «икс» из четвёртого уравнения,
считая «игрек» равным нулю, а «зет» равным двум. Получаем x = 2.
Найдём верхний предел интегирования по «игреку». Для этого выразим «игрек» из того же четвёртого
уравнения, считая «зет» равным двум, а «икс» — переменной величиной. Получаем y = 2 − x. И, наконец,
найдём верхний предел интегрирования по переменной «зет». Для этого выразим «зет» из того же
четвёртого уравнения, считая «игрек» и «зет» переменными величинами. Получаем z = 4 − x − y.
Получаем y = 2 − x. И, наконец,
найдём верхний предел интегрирования по переменной «зет». Для этого выразим «зет» из того же
четвёртого уравнения, считая «игрек» и «зет» переменными величинами. Получаем z = 4 − x − y.
Сведём данный тройной интеграл к последовательности трёх определённых интегралов:
.
Вычисляем самый внутренний интеграл — по переменной z, считая икс и игрек константами. Получаем:
.
Вычисляем средний интеграл — по переменной y. Получаем:
.
Вычисляем самый внешний интеграл — по переменной x и окончательно находим данный тройной интеграл:
Ответ: данный тройной интеграл равен 2.
Если проекцией области интегрирования на какую-либо из координатных плоскостей
является круг или часть круга, то тройной интеграл проще вычислисть, перейдя к цилиндрическим координатам. Цилиндрическая система координат является обобщением полярной системы координат на пространство. В системе цилиндрических координат точка M характеризуется тремя величинами
(r, φ, z), где r — расстояние от начала координат до проекции N точки M на плоскость xOy, φ — угол между вектором ON и положительным
направлением оси Ox, z — аппликата точки M (рисунок ниже).
Цилиндрическая система координат является обобщением полярной системы координат на пространство. В системе цилиндрических координат точка M характеризуется тремя величинами
(r, φ, z), где r — расстояние от начала координат до проекции N точки M на плоскость xOy, φ — угол между вектором ON и положительным
направлением оси Ox, z — аппликата точки M (рисунок ниже).
Прямоугольные координаты x, y, z с цилиндрическими координатами r, φ, z связывают формулы
x = rcosφ,
y = rsinφ,
z = z.
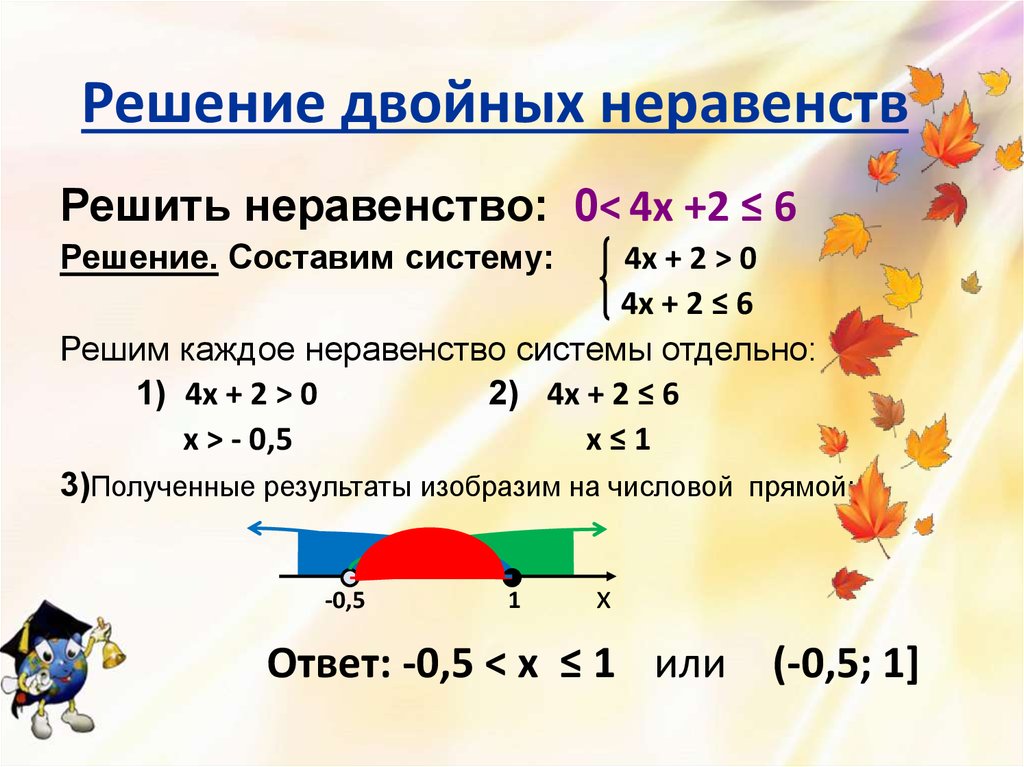
Для того, чтобы в тройном интеграле перейти к цилиндрическим координатам, нужно подынтегральную функцию выразить в виде функции переменных r, φ, z:
.
То есть переход от прямогольных координат к цилиндрическим осуществляется следующим образом:
.
Тройной интеграл в цилиндрических координатах вычисляется так же как и в декартовых прямоугольных координатах, путём преобразования в последовательность трёх определённых интегралов:
Пример 8. Вычислить тройной интеграл
переходом к цилиндрическим координатам, где V — область, ограниченная поверхностями и .
Решение. Так как область V на плоскость xOy проектируется в круг , то
координата φ изменяется в пределах от 0 до 2π, а координата r — от r=0 до r=1. Постоянному значению
в пространстве соответствует цилиндр .
Рассматривая пересечение этого цилиндра с областью V, получаем изменение
ординаты z от z = r² до z = 1.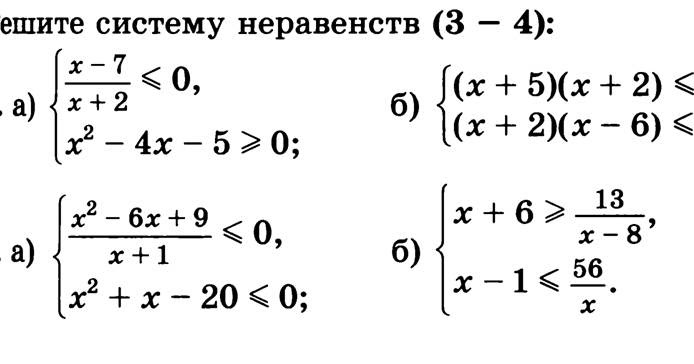 Переходим к цилиндрическим координатам и получаем:
Переходим к цилиндрическим координатам и получаем:
Ответ: данный тройной интеграл равен π/6.
Если область интегрирования в тройном интеграле представляет собой шар или часть шара, то проще вычислить тройной интеграл в сферических координатах. В сферических координатах точку M характеризуют три величины (ρ, φ, θ), где ρ — расстояние от точки M до начала координат 0, φ — угол между вектором ON и положительным направлением оси Ox (N — проекция точки M на плоскость xOy), θ — угол между вектором OM и положительным направлением оси Oz.
Сферические координаты связаны с прямоугольными декартовыми координатами соотношениями
x = ρsinθcosφ,
y = ρsinθsinφ,
z = ρcosθ.
Элемент объёма в сферических координатах выражается следующим образом:
.
Таким образом, переход от прямоугольных декартовых координат в тройном интеграле к сферическим координатам осуществляется по формуле:
Чтобы вычислить тройной интеграл в сферических координатах, нужно поступить так же, как при вычислениях в прямоугольных декартовых и цилиндрических координатах — перейти к повторным интегралам (последовательности трёх определённых интегралов):
Пример 9. Вычислить тройной интеграл
переходом к сферическим координатам, где V — область, ограниченная неравенствами и .
Решение. Снизу область интегрирования ограничена конической поверхностью
, а сверху — сферой
. Так как область
интегирования представляет собой часть шара, перейдём к сферическим координатам. Перепишем подынтегральную
функцию:
Перепишем подынтегральную
функцию:
Учитывая, что , получаем
Расставим пределы интегрирования и перепишем последний полученный интеграл в виде трёх повторных интегралов. По рисунку видно, что , , . Поэтому
Итак, тройной интеграл вычислен. Так как все три интеграла — независисмые друг от друга, мы смогли интегрировать каждый отдельно и результаты перемножить.
Вычисление объёма тела. Объём области V равен тройному интегралу по этой области, если подынтегральная функция равна 1:
.
Вычисление массы неоднородного тела. Массу неоднородного тела с плотностью ρ = ρ(x, y, z) можно вычислить по формуле:
.
Статические моменты материального тела.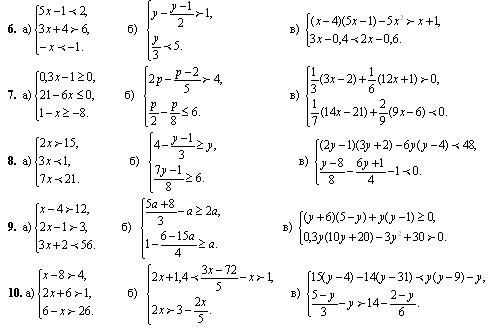 Статические моменты относительно плоскостей xOy, xOz, yOz материального тела с плотностью ρ = ρ(x, y, z)
можно вычислить по формулам:
Статические моменты относительно плоскостей xOy, xOz, yOz материального тела с плотностью ρ = ρ(x, y, z)
можно вычислить по формулам:
Моменты инерции материального тела. Моменты инерции относительно плоскостей xOy, xOz, yOz материального тела с плотностью ρ = ρ(x, y, z) можно вычислить по формулам:
Моменты инерции относительно осей Ox, Oy, Oz определяются по формулам:
Центр тяжести материального тела. Координаты центра массы C(xc, yc, zc) материального тела с плотностью ρ = ρ(x, y, z) определяются по формулам:
Пример 10. Вычислить объём тела, ограниченного поверхностями
,
,
.
Вычислить объём тела, ограниченного поверхностями
,
,
.
Решение. Одна их поверхностей — — цилиндрическая поверхность (образующая параллельна оси Oz), то есть проекция области на плоскость xOy совпадает с фигурой, которую ограничивает линия , или . Эта линия изображена на рисунке ниже.
Таким образом, записываем тройной интеграл в цилиндрических координатах и вычисляем его:
Ответ: объём тела равен 176 единиц объёма.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Пройти тест по теме Кратные и криволинейные интегралы
Кратные и криволинейные интегралы
- Вычисление двойных интегралов
- Двойные интегралы в полярных координатах
- Вычисление тройных интегралов
- Вычисление криволинейных интегралов
- Интегралы по замкнутому контуру, формула Грина
- Вычисление поверхностных интегралов
Поделиться с друзьями
Решение сложных неравенств | Начальная алгебра
Результаты обучения
- Описывать множества как пересечения или объединения
- Использовать обозначение интервала для описания пересечений и объединений
- Использование графов для описания пересечений и объединений
- Решение сложных неравенств — ИЛИ
- Решить сложные неравенства в форме или и выразить решение графически и через интервал
- Решение составных неравенств — И
- Выразить решения неравенств графически и с интервальной записью
- Найдите решения сложных неравенств в форме [латекс]а<х
- Решение абсолютных неравенств
- Решение одношаговых и многошаговых неравенств, содержащих абсолютные значения
- Определить случаи, когда нет решений абсолютных неравенств
Используйте запись интервала для описания наборов чисел как пересечений и объединений
Когда два неравенства соединяются словами и , решение составного неравенства происходит, когда оба неравенства верны одновременно. Это перекрытие или пересечение решений каждого неравенства. Когда два неравенства соединены словом или , решение составного неравенства происходит, когда или из неравенств верны. Решение представляет собой комбинацию или объединение двух отдельных решений.
Это перекрытие или пересечение решений каждого неравенства. Когда два неравенства соединены словом или , решение составного неравенства происходит, когда или из неравенств верны. Решение представляет собой комбинацию или объединение двух отдельных решений.
В этом разделе мы научимся решать сложные неравенства, которые соединяются словами И и ИЛИ. Во-первых, это поможет увидеть некоторые примеры неравенств, интервалов и графиков составных неравенств. Это поможет вам правильно описать решения сложных неравенств.
Диаграммы Венна используют концепцию пересечений и объединений, чтобы показать, сколько общего у двух или более объектов. Например, эта диаграмма Венна показывает пересечение людей, которые разбивают вам сердце, и тех, кто ежедневно расшатывает вашу уверенность. Очевидно, Сесилия обладает обоими этими качествами; поэтому она является пересечением двух.
В математических терминах рассмотрим неравенство [латекс]x\lt6[/латекс] и [латекс]х\gt2[/латекс]. Как бы мы интерпретировали, какими могут быть числа x , и как бы выглядел интервал?
Как бы мы интерпретировали, какими могут быть числа x , и как бы выглядел интервал?
На словах x должно быть меньше 6 , и в то же время должно быть больше 2, очень похоже на приведенную выше диаграмму Венна, где Сесилия одновременно разбивает вам сердце и ежедневно подрывает вашу уверенность. Давайте посмотрим на график, чтобы увидеть, какие числа возможны с этими ограничениями.
Числа, общие для обеих линий на графике, называются пересечением двух неравенств [latex]x\lt6[/latex] и [latex]x\gt2[/latex]. Это называется ограниченным неравенством и записывается как [latex]2\lt{x}\lt6[/latex]. Подумайте об этом на минуту. x должно быть меньше 6 и больше двух — значения x будут попадать между двумя числами . В записи интервала это выглядит как [латекс]\влево(2,6\вправо)[/латекс]. График будет выглядеть так:
С другой стороны, если вам нужно представить две вещи, которые не имеют общих элементов или признаков, вы можете использовать объединение. На следующей диаграмме Венна показаны две вещи, которые не имеют общих черт или элементов, но часто рассматриваются в одном и том же приложении, например онлайн-покупки или банковские операции.
На следующей диаграмме Венна показаны две вещи, которые не имеют общих черт или элементов, но часто рассматриваются в одном и том же приложении, например онлайн-покупки или банковские операции.
В математических терминах, например, [latex]x>6[/latex] или [latex]x<2[/latex] — это неравенство, к которому присоединяются слова или . Используя интервальную запись, мы можем описать каждое из этих неравенств отдельно:
[latex]x\gt6[/latex] совпадает с [latex]\left(6, \infty\right)[/latex] и [latex]x<2[/latex] совпадает с [latex ]\влево(\infty, 2\вправо)[/латекс]. Если мы описываем решения неравенств, какой эффект имеют или ? Мы говорим, что решения – это либо действительные числа, меньшие двух 90 057, либо 90 058 действительных чисел, большие 6. Вы понимаете, почему нам нужно записывать их как два отдельных интервала? Давайте посмотрим на график, чтобы получить четкое представление о том, что происходит.
Если вы поместите оба этих неравенства на график, мы увидим, что они не имеют общих чисел. Это то, что мы называем союзом, как упоминалось выше. Обозначение интервала, связанное с объединением, представляет собой большую букву U, поэтому вместо записи или мы соединяем наши интервалы большой буквой U, например:
Это то, что мы называем союзом, как упоминалось выше. Обозначение интервала, связанное с объединением, представляет собой большую букву U, поэтому вместо записи или мы соединяем наши интервалы большой буквой U, например:
[латекс]\влево(\infty, 2\вправо)\чашка\ left(6, \infty\right)[/latex]
Общепринято строить интервалы, начинающиеся с крайнего левого значения на числовой прямой в качестве левого значения, например [latex]\left(2,6 \right)[/latex], где 2 меньше 6. Число справа должно быть больше числа слева.
Пример
Нарисуйте график составного неравенства [latex]x\gt3[/latex] или [latex]x\le4[/latex] и опишите набор x -значений, которые удовлетворяют ему с интервал.
Показать решение
Примеры
Нарисуйте график составного неравенства: [latex]x\lt5[/latex] и [latex]x\ge-1[/latex] и опишите множество x — значения, которые будут его удовлетворять с интервалом.
Показать раствор
Примеры
Нарисуйте график сложного неравенства [латекс]x\lt{-3}[/латекс] и [латекс]x\gt{3}[/латекс] и опишите множество x — значения, которые будут удовлетворять его с интервалом.
Показать решение
В следующем видео представлены два примера того, как рисовать неравенства с участием И, а также записывать соответствующие интервалы.
Решение составных неравенств в форме или
Как мы видели в предыдущем разделе, решение составного неравенства, состоящего из двух неравенств, соединенных словом или , представляет собой объединение решений каждого неравенства. Объединения позволяют нам создать новый набор из двух элементов, которые могут иметь или не иметь общих элементов.
В этом разделе вы увидите, что некоторые неравенства необходимо упростить, прежде чем их решение можно будет записать или изобразить в виде графика.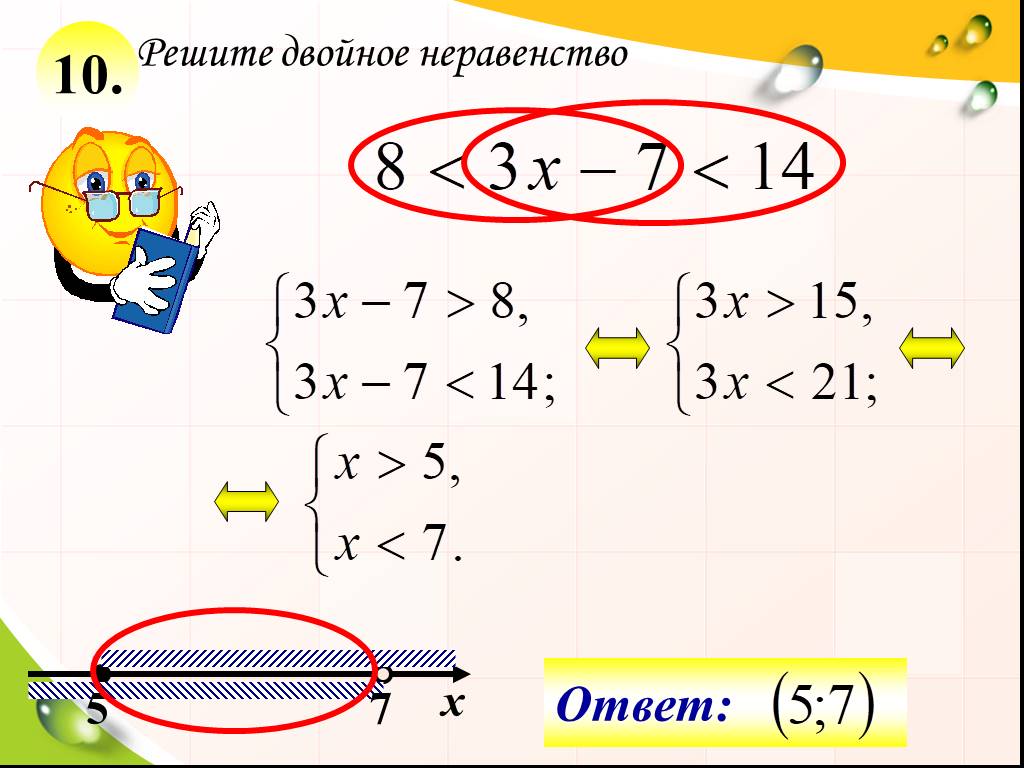
В следующем примере вы увидите пример решения одношагового неравенства в форме ИЛИ. Обратите внимание, как каждое неравенство обрабатывается независимо до конца, где решение описывается в терминах обоих неравенств. Для решения составных неравенств вы будете использовать те же свойства, что и для решения обычных неравенств.
Не забывайте применять свойства неравенства при решении сложных неравенств. В следующем примере используется деление на отрицательное значение, чтобы изолировать переменную.
Пример
Найдите y . [latex]2y+7\lt13\text{ или }−3y–2\lt10[/latex]
Показать решение
В последнем примере окончательный ответ включал решения, интервалы которых перекрывались, в результате чего ответ включал все числа на числовой прямой. На словах мы называем это решение «все действительные числа». Любое действительное число даст истинное утверждение либо для [latex]y<3\text{, либо для }y\ge -4[/latex], если его заменить на 9. 0057 х .
0057 х .
Пример
Найдите z . [латекс]5z-3\gt-18[/латекс] или [латекс]-2z-1\gt15[/латекс]
Показать решение
Следующее видео содержит пример решения составного неравенства с участием ИЛИ и построения соответствующего графика.
В следующем разделе вы увидите примеры решения составных неравенств, содержащих числа и .
Решить сложные неравенства в форме
и и представить решение графически Решением составного неравенства, состоящего из двух неравенств, соединенных словами и , является пересечение решений каждого неравенства. Другими словами, оба утверждения должны быть истинными одновременно. Решением составного неравенства и являются все решения, общие для этих двух неравенств. Как мы видели в предыдущих разделах, именно здесь два графика перекрываются.
В этом разделе мы увидим больше примеров, когда мы должны упростить сложные неравенства, прежде чем мы сможем выразить их решения графически или с интервалом.
Пример
Решить для x : [латекс] \displaystyle {5}{x}-{2}\le{3}\text{ и }{4}{x}{+7}>{3} [/latex]
Показать решение
Составные неравенства в форме [латекс]a
Вместо разделения составного неравенства в форме [латекс]a
В видео ниже вы увидите еще один пример решения неравенства в форме [latex]a Чтобы решить неравенства вида [latex]a Решение сложного неравенства с числами и всегда совпадает с решением каждого неравенства. Есть три возможных исхода сложных неравенств, соединенных словами и : В приведенном ниже примере составное неравенство не имеет решения, поскольку неравенства не пересекаются. Давайте применим то, что вы знаете о решении уравнений, содержащих абсолютные значения, и то, что вы знаете о неравенствах, для решения неравенств, содержащих абсолютные значения. [латекс]\влево|х\вправо|\leq 4[/латекс] Это неравенство читается как «абсолютное значение x меньше или равно 4». Если вас попросят решить для x , вы хотите узнать, какие значения x отстоят на 4 единицы или менее от 0 на числовой прямой. Вы могли бы начать с размышлений о числовой прямой и о том, какие значения x удовлетворяют этому уравнению. 4 и [латекс]−4[/латекс] находятся на расстоянии четырех единиц от 0, поэтому они являются решениями. 3 и [латекс]-3[/латекс] также являются решениями, потому что каждое из этих значений меньше, чем на 4 единицы от 0. Так же как 1 и [латекс]-1[/латекс], 0,5 и [латекс]-0,5[ /latex] и так далее — существует бесконечное количество значений для x , которые будут удовлетворять этому неравенству. График этого неравенства будет иметь две замкнутые окружности, 4 и [латекс]−4[/латекс]. Расстояние между этими двумя значениями на числовой прямой окрашено в синий цвет, поскольку все эти значения удовлетворяют неравенству. Решение можно записать так: Неравенство: [латекс]-4\leq x\leq4[/латекс] Интервал: [латекс]\влево[-4,4\вправо][/латекс] Ситуация немного отличается, когда знак неравенства стоит «больше» или «больше или равно». Рассмотрим простое неравенство [латекс]\влево|х\вправо|>3[/латекс]. Опять же, вы могли бы подумать о числовой прямой и о том, какие значения числа x больше, чем на 3 единицы от нуля. На этот раз 3 и [латекс]−3[/латекс] не включены в решение, поэтому оба этих значения отмечены незакрашенными кружками. 2 и [латекс]-2[/латекс] не будут решениями, потому что они не более чем в 3 единицах от 0. Но 5 и [латекс]-5[/латекс] будут работать, как и все значения, расширяющие слева от [латекс]−3[/латекс] и справа от 3. График будет выглядеть так, как показано ниже. Решение этого неравенства можно записать так: Неравенство : [латекс]x<−3[/латекс] или [латекс]x>3[/латекс]. Интервал: [latex]\left(-\infty, -3\right)\cup\left(3,\infty\right)[/latex] В следующем видео вы увидите примеры решения и выразить решение абсолютных неравенств с использованием И и ИЛИ. Для любого положительного значения a и x, одной переменной или любого алгебраического выражения: Рассмотрим еще несколько примеров неравенств, содержащих абсолютные значения. Как и в случае с уравнениями, могут быть случаи, когда неравенство не имеет решения. Составное неравенство — это утверждение из двух утверждений о неравенстве, связанных вместе либо словом , либо словом , либо словом и . Иногда составное неравенство и отображается символически, например [latex]a Абсолютные неравенства можно решить, переписав их с помощью составных неравенств. Первым шагом к решению абсолютных неравенств является выделение абсолютного значения. Следующий шаг — решить, работаете ли вы с неравенством ИЛИ или с неравенством И. Если неравенство больше числа, мы будем использовать ИЛИ. Если неравенство меньше числа, мы используем И. Помните, что если мы получим абсолютное значение больше или меньше отрицательного числа, решения не будет. Чтобы решить составное неравенство, сначала разделите его на два неравенства. Определите, должен ли ответ быть объединением множеств («или») или пересечением множеств («и»). Затем решите оба неравенства и график. Если неясно, является ли неравенство объединением множеств или пересечением множеств, то ##проверьте каждую область##, чтобы увидеть, удовлетворяет ли она составному неравенству. 4≤2 x и 2 x ≤8 (пересечение множеств) 2 x ≤8 2≤ х и х ≤4. 5≤ + 5 и +5 < 6 (пересечение множеств) +5 < 6 0≤ x и x < 3. 3( x — 2) < 9 3( х — 2) > 15 x < 5 или x > 7. 2 х ≤ x — 3 или x < 3 x — 4 (объединение наборов) x < 3 x — 4 x ≤ — 3 или x > 2. Какую бы операцию вы ни выполняли над средней частью неравенства, вы также должны выполнить ее с каждой из внешних частей. Обратите особое внимание на деление или умножение на отрицание.
Какую бы операцию вы ни выполняли над средней частью неравенства, вы также должны выполнить ее с каждой из внешних частей. Обратите особое внимание на деление или умножение на отрицание. Случай 1: Описание Решением могут быть все значения между двумя конечными точками Неравенства [latex]x\le{1}[/latex] и [latex]x\gt{-1}[/latex], или в виде ограниченного неравенства: [latex]{-1}\lt{x}\le {1}[/латекс] Интервал [латекс]\влево(-1,1\вправо][/латекс] Графики Случай 2: Описание Решение может начинаться в точке на числовой прямой и продолжаться в одном направлении. 
Неравенства [латекс]x\gt3[/латекс] и [латекс]x\ge4[/латекс] Интервал [латекс]\влево[4,\infty\вправо)[/латекс] Графики Случай 3: Описание В тех случаях, когда два неравенства не перекрываются, составное неравенство не имеет решения Неравенства [латекс]x\lt{-3}[/латекс] и [латекс]x\gt{3}[/латекс] Интервалы [латекс]\влево(-\infty,-3\вправо)[/латекс] и [латекс]\влево(3,\infty\вправо)[/латекс] График Решение неравенств, содержащих абсолютные значения
 Начнем с простого неравенства.
Начнем с простого неравенства.

Написание решений неравенств с абсолютными значениями
Неравенство абсолютного значения Эквивалентное неравенство Обозначение интервала [латекс]\влево|{х}\вправо|\ле{а}[/латекс] [латекс]{-a}\le{x}\le{a}[/латекс] [латекс]\влево[-а, а\вправо][/латекс] [латекс]\левый| х \право|\lt{a}[/латекс] [латекс]{-a}\lt{x}\lt{a}[/латекс] [латекс]\влево(-а, а\вправо)[/латекс] [латекс]\левый| х \право|\ge{ а}[/латекс] [латекс]{x}\le\text{−a}[/latex] или [латекс]{x}\ge{ a}[/latex] [латекс]\влево(-\infty,-a\право]\чашка\влево[a,\infty\вправо)[/латекс] [латекс]\левый| х \right|\gt\text{a}[/latex] [латекс]\displaystyle{x}\lt\text{−a}[/latex] или [латекс]{x}\gt{a}[/latex] [латекс]\влево(-\infty,-a\вправо)\чашка\влево(a,\infty\вправо)[/латекс] 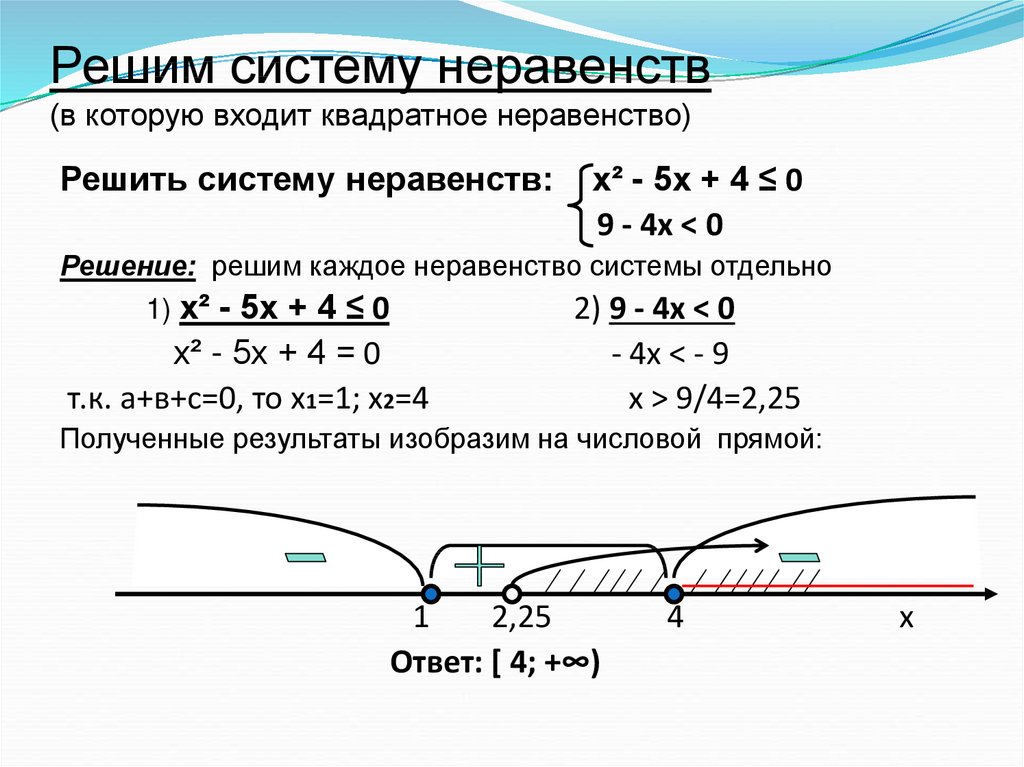
Определите случаи неравенств, содержащих абсолютные значения, которые не имеют решений
Резюме

Составные неравенства: Составные неравенства | SparkNotes
Пример 1 : Решить и построить график: 4≤2 x ≤8
4≤2 x ≤
2≤ x
х ≥2 ≤82
х ≤4 
График:
Пример 2 : Решите и постройте график: { x : 5≤ +5 < 6}
5≤ + 5 0≤
0≤ x < 1
х < 3
График:
Пример 3 : Решите и постройте график: 3( x — 2) < 9 или 3( x — 2) > 15 (объединение множеств) х — 2 < 3
х < 5
х — 2 > 5
х > 7
График:
Пример 4 : Решите и постройте график: { x : 2 x ≤ x — 3}∪{ x : x < 3 x 9 0017 — 4}
2 x ≤ x — 3 х ≤ — 3
-2 х < - 4
х >2 

