Тригонометрическая таблица, объяснение тригонометрических тождеств и примеры
Основные понятия тригонометрии, тригонометрические функции, тригонометрическая таблица
Расстояния или высоты можно найти с помощью некоторых математических методов, которые относятся к разделу математики, называемому «тригонометрия». Слово «тригонометрия» происходит от греческих слов
«три» — три,
«гон» — стороны и
«метрон» — мера треугольника.
некоторые отношения сторон прямоугольного треугольника к его острым углам, называемые тригонометрическими отношениями угла.
Область возникла в эллинистическом мире в 3 веке до нашей эры из приложений геометрии к астрономическим исследованиям.
Применение тригонометрии в реальном мире
• В древности она использовалась в астрономии для определения расстояния до звезд
• Определение радиуса Земли
• Определение высоты холмов, зданий, деревьев и т. д.
• Навигация – самолеты, корабли и т.
д.
• Оборона
Тригонометрия имеет множество применений в современном мире. Без нее многие современные отрасли и науки просто не существовали бы.
Только представьте, как люди могли измерить высоту горы Эверест!
Человеку было бы практически невозможно взять в руки измерительную ленту и взобраться на гору, чтобы измерить высоту.
Тогда как они это сделали?
Тригонометрия подходит для этого
Шесть тригонометрических функций
Существуют три основные тригонометрические функции:
1. Функция синуса (Sin)
2. Функция косинуса (Cos)
3. Функция тангенса (Tan)
Остальные три тригонометрические функции обратны Тригонометрическая функция, описанная выше
1. Функция косекса (Косек) { обратная функция синуса}
2. Функция секанса (сек) { обратная функция косинуса}
3. Функция котангенса (Cot) { обратная функция тангенса}
Нахождение тригонометрических функций в прямоугольном треугольнике
Специальные названия сторон в прямоугольном треугольнике
Гипотенуза :- Гипотенуза прямоугольного треугольника всегда является стороной, противоположной прямому углу.
Это самая длинная сторона прямоугольного треугольника.
Перпендикуляр :
Это сторона, всегда противоположная опорному углу, указанному на изображении.
Основание (примыкающее к углу theta(θ) :
Сторона, содержащая данный базовый угол.
Существуют три основные тригонометрические функции:
Тригонометрические функции, обратные трем тригонометрическим функциям как отношение длины гипотенузы к длине противолежащего катета.
Также ,
1/sinA=cosecA
4. Секанс sec(A) является обратной величиной cos(A)
Также ,
1/cosA=secA
5. Котангенс cot(A) является обратной величиной tan(A)
Определяется как отношение длины прилежащей стороны к длине противоположной сторона
ПРИМЕЧАНИЕ:
Тригонометрическая функция Sin A используется как краткая форма для «синуса угла A», что означает отношение перипердикуляра и гипотенузы.
sin A не является произведением «sin» и «sin». А’ как «грех», отделенный от угла, не имеет смысла. 92, после чего можно определить все остальные тригонометрические отношения угла. Тригонометрические таблицы
представляют собой некоторые стандартные значения тригонометрических соотношений определенных углов, а именно
0°, 30°, 45°, 60° и 90°. Существуют простые приемы и логика, чтобы запомнить так много значений, и, запомнив только 5 значений, другие 25 могут найти легко.
Тригонометрические формулы дополнительных углов
Перед изучением тригонометрических таблиц
повторим тригонометрические формулы дополнительных углов.
sinx=cos(90°-x)
cosx=sin(90°-x)
tanx=cot(90°-x)
cotx=tan(90°-x)
secx=cosec(90°-x)
cosecx=sec(90°-x)
Приведенное выше соотношение можно использовать для определения значений стандартных углов как
, например ∶sin30°=cos(90°-30°)=cos60°
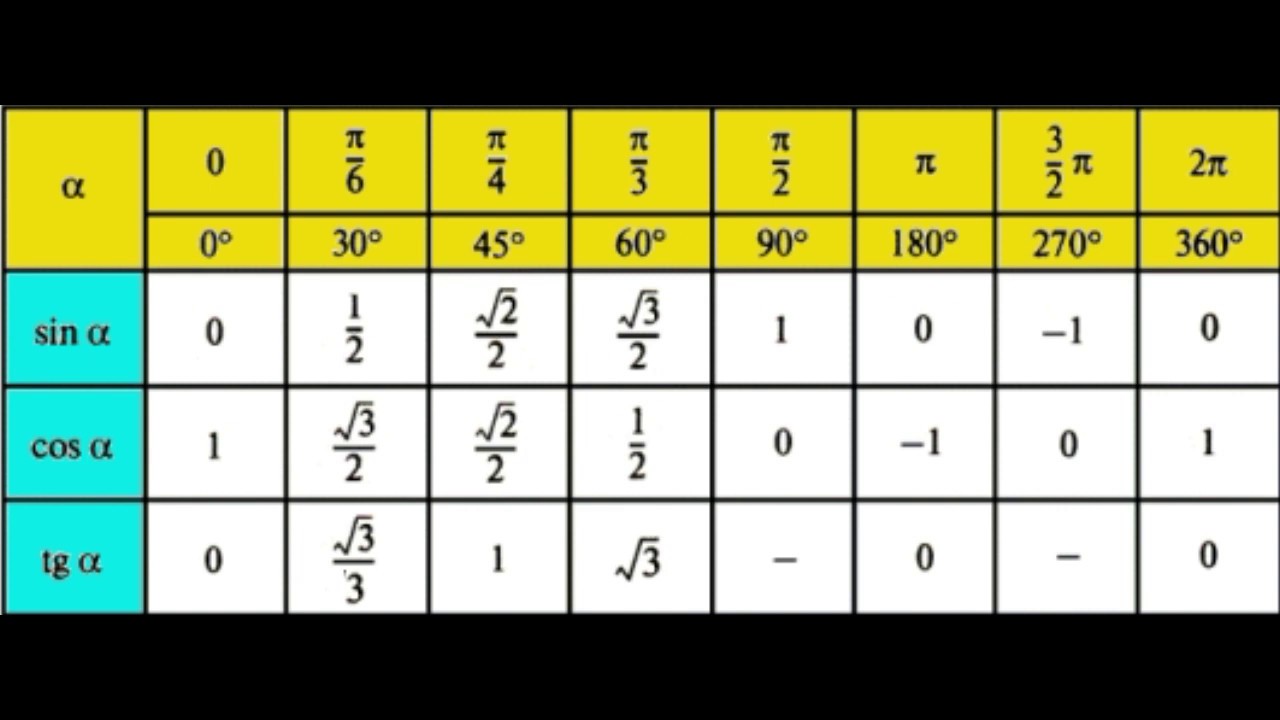
Таким образом, значения этих двух будут одинаковыми, и аналогичным образом значения многих тригонометрических таблиц продолжают повторяться в двух или более местах.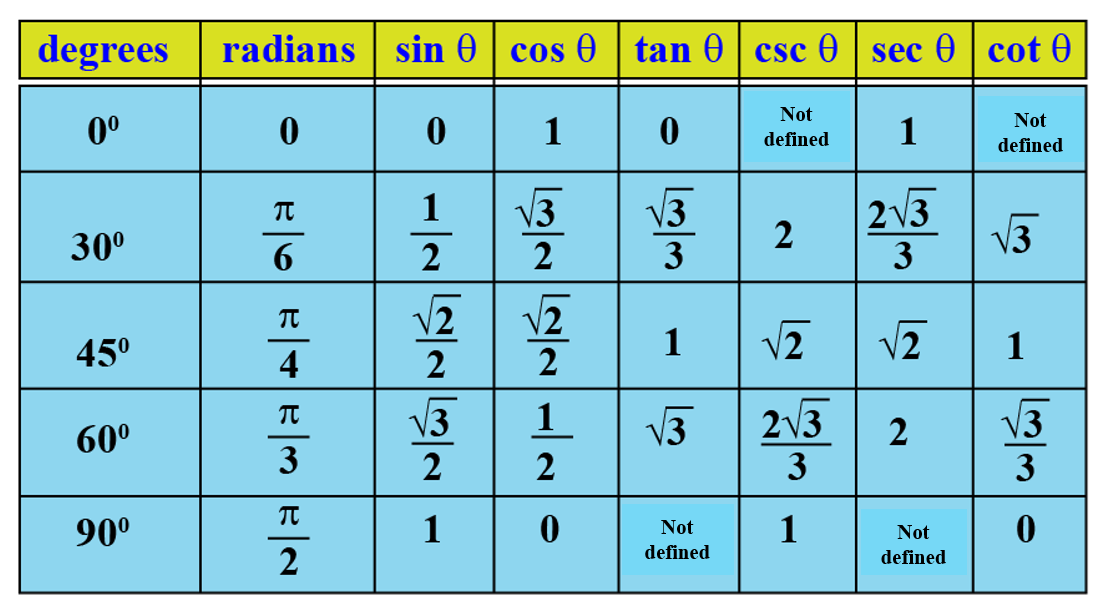
Тригонометрическая таблица наиболее часто используемых углов.
Тригонометрические таблицы обычно используются для нахождения высоты и расстояний. Обычно для конкретных углов 0°, 30°, 45°, 60° и 90°, как показано в таблице тригонометрии, используются значения шести тригонометрических соотношений. решать задачи по тригонометрии. Эти значения получаются путем нахождения отношения длин прямоугольного треугольника и углов прямоугольного треугольника. В тригонометрии для расчета отношения крайне важно распознать опорный угол, так как в соответствии с ним вычисляются только шесть тригонометрических отношений.
Таким образом, 0°, 30°, 45°, 60° и 90° в тригонометрии называются стандартным и удельным углами.
Тригонометрическая таблица состоит из значений тригонометрического отношения определенных стандартных углов, включая 0°, 30°, 45°, 60°, 90° в табличном формате. Вычислить значения тригонометрических отношений в этих тригонометрических таблицах и разработать закономерности, чтобы запомнить их наизусть, — чрезвычайно тривиальная работа.
СОВЕТЫ И РЕКОМЕНДАЦИИ ДЛЯ ЗАПОМНЕНИЯ ТРИГОНОМЕТРИЧЕСКОЙ ТАБЛИЦЫ: Есть 30 значений, которые необходимо запомнить, 5 из которых можно выучить, а другие можно найти. Даже у этих пяти значений есть концептуальная хитрость.
Теперь мы создадим таблицу, используя шаблон, который поможет запомнить все значения за очень короткое время.
КЛЮЧ ДЛЯ ЗАПОМНЕНИЯ ТРИГОНОМЕТРИЧЕСКОЙ ТАБЛИЦЫ
Самый простой способ найти тригонометрическую таблицу
Приведенные ниже шаги должны выполняться для независимого составления таблицы в любом месте и в любое время.
Эта таблица также известна как таблица Sin Cos.
ШАГ 1: создание таблицы путем записи углов и тригонометрических углов
Создайте строки и столбцы и освободите место для записи компонентов таблицы с указанными углами 0°, 30°, 45°, 60° и 90° в верхнем ряду и все шесть тригонометрических соотношений по порядку в первом столбце.
Во-первых, все три основных соотношения, за которыми следуют их обратные величины, как показано в таблице выше и указано здесь: sinθ, cosθ, tanθ, cosecθ, secθ и cotθ.
ШАГ 2: Присвоение углов
Запишите углы 0°, 30°, 45°, 60° и 90° в порядке возрастания и присвойте им значения 0,1,2,3,4 в соответствии с рисунком нижеприведенный.
Благодаря этой простой логике и пониманию запоминание тригонометрической таблицы становится чрезвычайно легким для изучения.
Часто задаваемые вопросы.
Вопрос. Что такое тригонометрия?
Ответ. Тригонометрия – это раздел математики, который устанавливает отношения между тремя сторонами и углами треугольника. Он выражается в форме отношения. Тригонометрия определяет тригонометрические функции, такие как sinθ, cosθ, tanθ, cosecθ, secθ и cotθ, в частности.
Вопрос. Что такое тригонометрические тождества?
Ответ.
Тригонометрическое тождество представляет собой уравнение, включающее тригонометрические отношения угла. Связь устанавливается с помощью теоремы Пифагора.
Тригонометрическое тождество, если оно истинно для всех значений угла.
Важные тригонометрические идентичности:
(i) sin 2 θ+ cos 2 θ = 1
(II) 1+ TAN 2 θ = SEC
(III) 1+ COT 2 θ
(III) 1+ Cot 2 θ
(III) 1+ Cot 2 ou = cosec 2 θ
Вопрос. Какие существуют виды тригонометрии?
Ответ. В настоящее время используются четыре типа тригонометрии, а именно
a. Базовая тригонометрия
б. Плоская тригонометрия
с. Сферическая тригонометрия и
d. Аналитическая тригонометрия
Вопрос. Что такое тригонометрические таблицы?
Ответ. Тригонометрическая таблица — это таблица, содержащая набор значений некоторых конкретных углов, а именно 0°, 30°, 45°, 60° и 90°.
Значения всех тригонометрических функций при указанных углах приведены в этой таблице. Эта таблица имеет решающее значение для решения многих типов тригонометрических задач. Используемые углы могут быть выражены как в градусах, так и в радианах. Обычно используется практика в градусах.
Вопрос. Для чего нужны тригонометрические таблицы?
Ответ. Тригонометрические таблицы очень полезны при решении тригонометрических задач, связанных с тригонометрическими отношениями конкретных углов. Более широкое использование этой таблицы заключается в разработке новых технологий, специально предназначенных для компьютерного программирования и оцифровки. Навигация, гражданское строительство, архитектура, машиностроение и многие другие области. Тригонометрические таблицы не ограничены только каким-то определенным углом, они могут быть расширены до углов больше 9.0 градусов.
Вопрос. Почему тригонометрия используется для измерения высоты и расстояний?
Ответ.