Длина вектора — как найти? Формулы и примеры
Поможем понять и полюбить математику
Начать учиться
Сегодня мы поговорим с вами о таких понятиях, как вектор и его длина. Эти термины достаточно популярны в алгебре, геометрии и физике. С их помощью можно решать как очень легкие задачи, так и комплексные с разными физическими величинами и математическими правилами. Сложная ли эта тема? Нет, совсем несложная, но очень и очень важная, поэтому мы посвятим сегодняшнюю статью ей. Приятного чтения!
Что такое векторы и какими они бывают
Как обычно, мы начнем с самого важного: с определения.
Вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.
Вектор обозначают знаком →, например . Как вы заметили, вектор можно выразить одной латинской буквой, а можно — сочетанием двух букв, которыми мы назовем точками начала и конца вектора.
Нулевой вектор — вектор, начало которого совпадает с его концом. Обозначается он так: .
Как вы уже знаете, векторы бывают коллинеарными и неколлинеарными, сонаправленными и противоположно направленными. Теперь давайте подумаем, что объединяет все виды векторов без исключения. Правильно, у всех есть длина! О том, что это такое, мы и поговорим дальше.
Узнай, какие профессии будущего тебе подойдут
Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас
Длина вектора
Длиной или модулем вектора называется длина направленного отрезка, определяющего вектор.
Иногда в математике длину вектора называют модулем. Это легко запомнить, так как длина вектора обозначается с помощью знака | |. Например: . Альтернативное название длины вектора дает нам отличную подсказку: она не может быть отрицательной, в какую бы сторону вектор ни был направлен.
А вот нулевой — пожалуйста!
Длина нулевого вектора всегда равна нулю.
Здесь вам может стать интересно, зачем нам нужно знать, как найти длину вектора, и это очень хороший вопрос. Причин может быть множество, но мы выделим несколько главных:
Чтобы определить равенство векторов, необходимо знать их длины. Векторы являются равными, если равны их длины, и сами векторы — сонаправленные.
Вычислив модуль вектора, мы можем рассчитать другие величины.
Например, в физике сила — это векторная величина, т. е. имеет направление. Если вычислить модуль силы, мы можем рассчитать массу тела, его ускорение и т. д.
В геометрии с помощью длины векторов мы можем определить угол между ними, их скалярное произведение.
Достаточно весомые аргументы для нахождения этой величины, правда? Самое время перейти от слов к делу: давайте научимся вычислять длину вектора через свои координаты!
Как можно найти длину вектора по его координатам
Используя прямоугольную систему координат, нарисуем вектор АВ (х, у) из точки (0; 0).
Давайте обозначим длину вектора |АВ1| = у, длину вектора |АА1| = х. Треугольники АА1В и АВ1В являются прямоугольными, где АВ — гипотенуза. Теперь вспомните, как можно найти длину гипотенузы, зная длины катетов. Верно, через теорему Пифагора! Составим выражение для АВ:
Это значит, чтобы найти длину вектора нужно взять квадратный корень из суммы квадратов его координат. В общем виде эту формулу для длины вектора записывают так — длина вектора :
Если мы будем рассматривать векторы в трехмерном пространстве, формулу нахождения длины вектора можно рассчитать так:
Давайте разберемся, как работают эти формулы для нахождения длины вектора, на примерах. Вы можете решать задания самостоятельно, а потом свериться с нами: так будет еще эффективнее!
Найдите модуль вектора .
Решение:
Ответ:
Пример № 2
Проведите вычисление длины вектора по его координатам {-2; 0; 5}.
Решение:
Ответ:
Пример № 3
Определите координату х вектора , если его координата по у равна 6, а длина вектора 10.
Решение:
,
,
,
.
,
,
,.
Ответ: .
Уверены, что у вас все блестяще получилось!
Как найти длину вектора по двум точкам
Давайте подумаем, как решать задачи, если нам не даны координаты вектора.
Для этого нужно понять, как найти длину вектора по двум точкам — координатам начала и конца. Вспомним: координаты вектора с точкой А (х_а; у_а) и В (х_в; у_в) можно рассчитать так: (х_в – х_а; у_в – у_а). А значит, длину вектора мы определим, если подставим эти выражения в формулу для ее нахождения:
Пример № 4
Найти длину вектора , если В (4; 6), С (-2; 0).
Решение:
Ответ:
Как найти длину вектора по теореме косинусов
Пришло время разобраться, как длина вектора связана с теоремой косинусов. К сожалению, не во всех задачах дано нужное количество информации, чтобы определить длину вектора — тут-то нам и поможет теорема. Вспомним ее!
Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Итак, чтобы определить длину стороны треугольника, нужно сложить квадраты двух других сторон, вычесть удвоенное произведение длин сторон на косинус угла между ними и взять корень из полученного числа. Так мы получим формулу нахождения длины вектора через теорему косинусов.
Предположим, что нам необходимо узнать длину вектора или . Тогда, чтобы воспользоваться теоремой косинусов, нам нужно найти длину векторов и и угол между ними.
Пример № 5
Длины векторов и равны 5 и 12 соответственно, а угол между ними равен π/3. Проведите вычисление длины вектора .
Решение:
Ответ:
Сегодня мы обсудили с вами все основные моменты, которые касаются длины вектора: изучили теорию и дополнили ее базовыми задачами. Дело осталось за малым — выучить весь материал и практиковаться! В этом вам помогут курсы по профильной математике в школе Skysmart.
Уникальная платформа, учителя-профессионалы, индивидуальная программа — уроки просто созданы для того, чтобы стать уверенными в математике. Ждем вас на занятиях и до новых встреч!
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Дарья Вишнякова
К предыдущей статье
Плоскость
К следующей статье
Компланарность векторов
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
Векторное Произведение Векторов. Свойства, определение
Поможем понять и полюбить математику
Начать учиться
156.
4K
«Право руля!» и «Держим вектор правее» — звучит по-разному, а смысл один: направление движения судна. В этой статье продолжим двигаться по волнам геометрии и изучим новую тему — векторное произведение векторов.
Определение векторного произведения
Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Как найти координаты точки мы рассказали в этой статье.
Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.
Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.
Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.
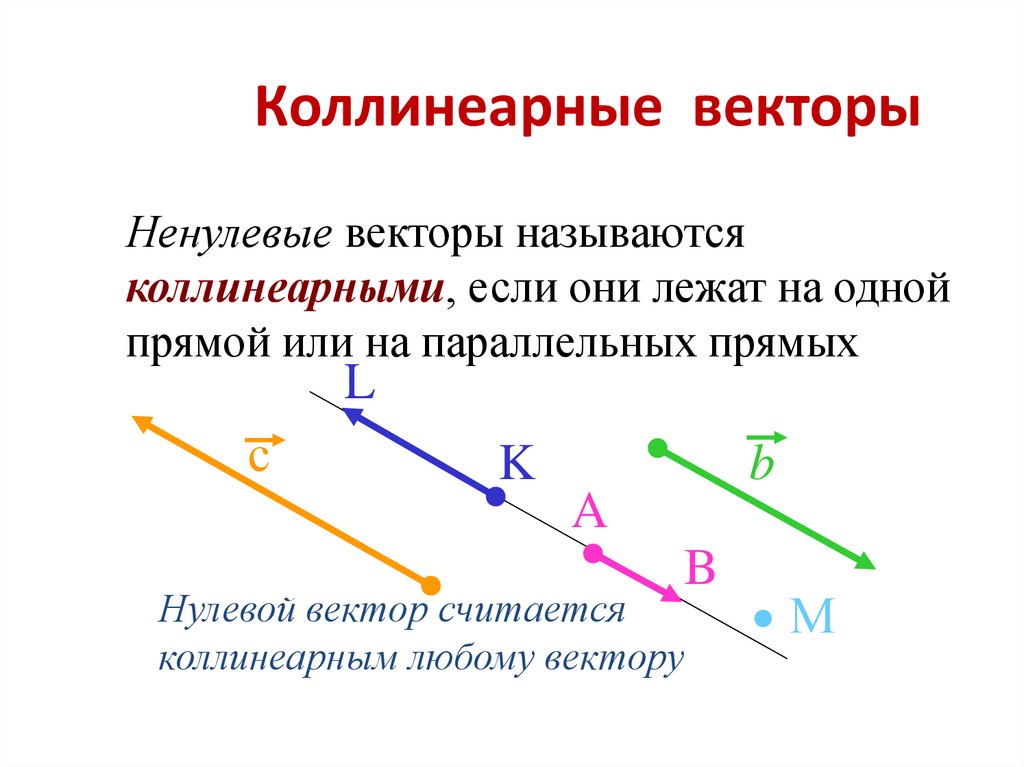
Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.
Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.
Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.
Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.
Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.
Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.
Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.
В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.
И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.
Еще не устали от теории? Онлайн-школа Skysmart предлагает обучение на курсах по математике — много практики и поддержка внимательных преподавателей!
Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:
- он является нулевым, если векторы →a и →b коллинеарны;
- он перпендикулярен и вектору →a и вектору →b;
- длина векторного произведения равна произведению длин векторов →a и →b на синус угла между ними
- тройка векторов →a, →b, →c ориентирована так же, как и заданная система координат.
Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.
Векторное произведение двух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:
Векторное произведение векторов →a и →b обозначается как [→a • →b].
Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.
Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.
Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:
- Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
- Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
- Если определитель равен нулю, то векторы компланарны (линейно зависимы).
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Координаты векторного произведения
Рассмотрим векторное произведение векторов в координатах.
Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор
, где
→i, →j, →k — координатные векторы.
Это определение показывает нам векторное произведение в координатной форме.
Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:
Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи.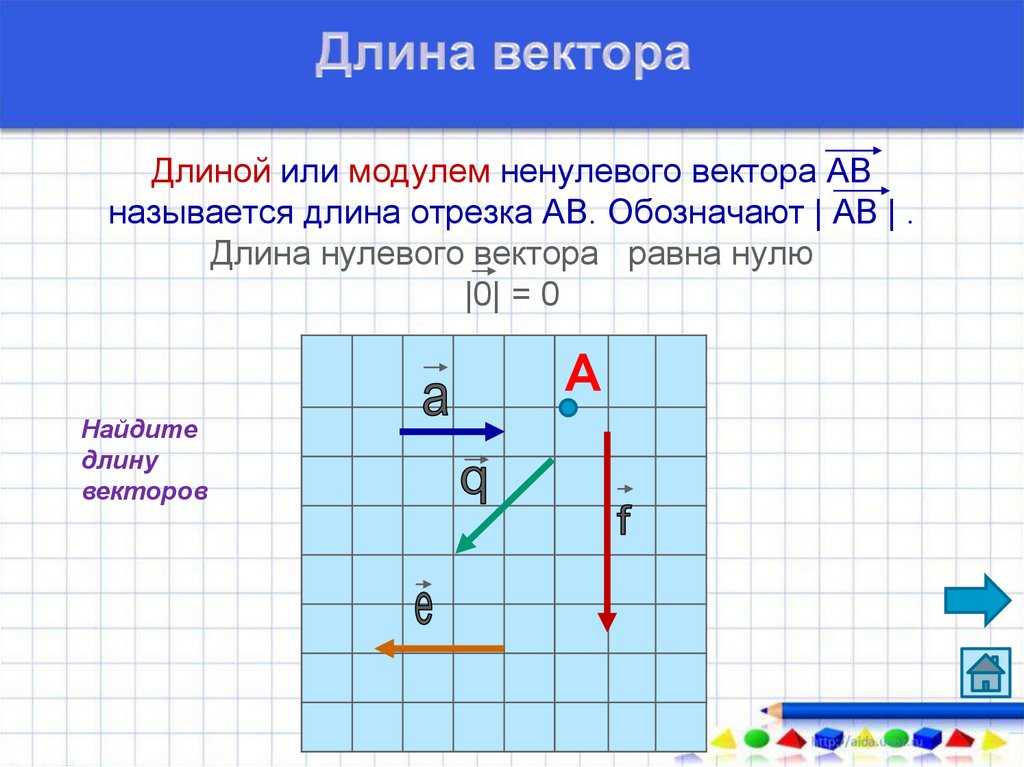
Более того, эти два определения векторного произведения эквивалентны.
Свойства векторного произведения
Векторное произведение в координатах представляется в виде определителя матрицы:
На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:
- Антикоммутативность
- Свойство дистрибутивности
или
- Сочетательное свойство
или
, где λ произвольное действительное число.
Для большей ясности докажем свойство антикоммутативности векторного произведения.
По определению
и
Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
что доказывает свойство антикоммутативности векторного произведения.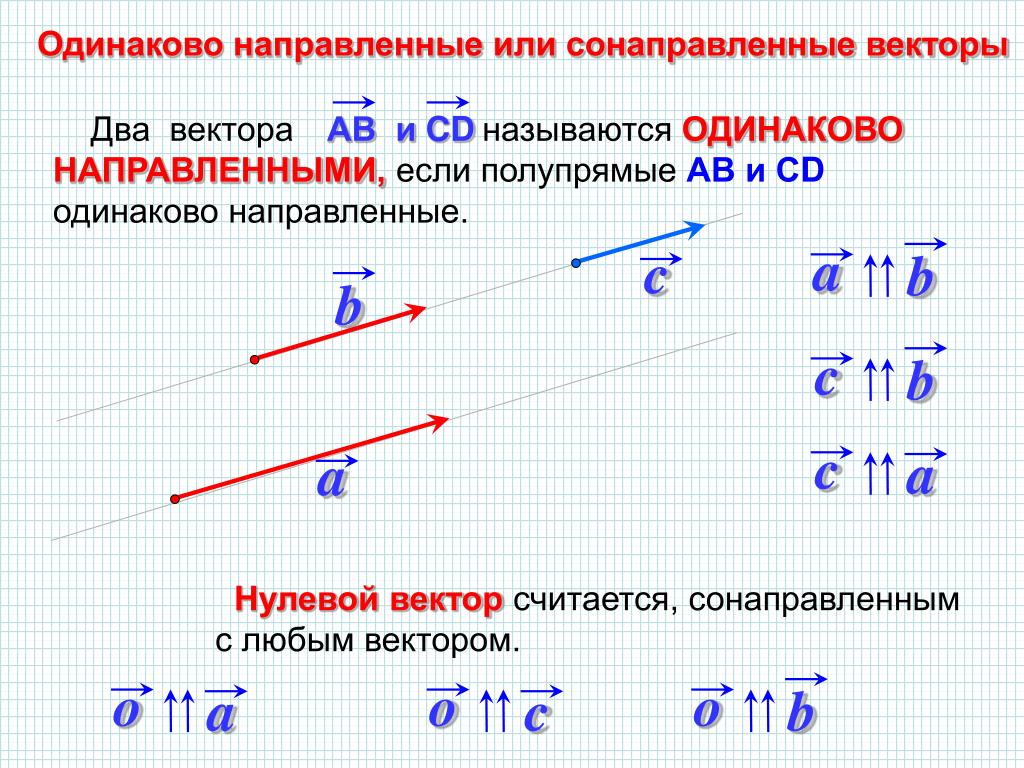
Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).
Примеры решения задач
Пример 1
а) Найти длину векторного произведения векторов →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
б) Найти площадь параллелограмма, построенного на векторах →a и →b, если |→a| = 2, |→b| = 3, ∠(→a, →b) = π/3.
Как решаем:
а) По условию требуется найти длину векторного произведения. Подставляем данные в формулу:
Ответ:
Так как в задаче речь идет о длине, то в ответе указываем размерность — единицы.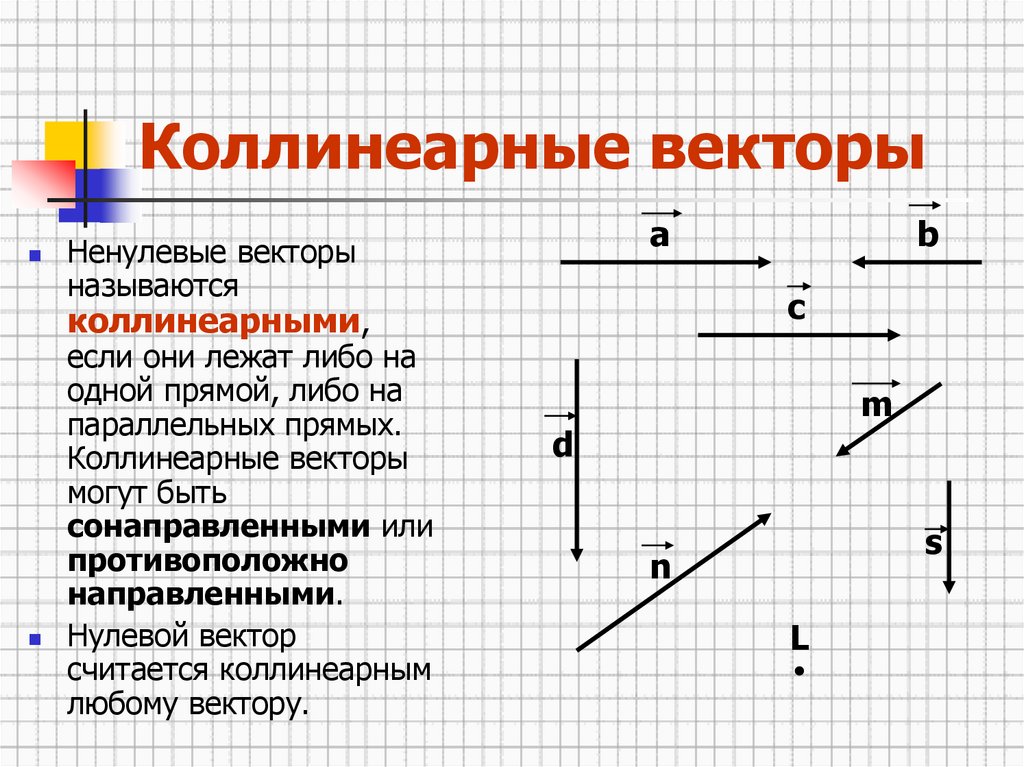
б) По условию требуется найти площадь параллелограмма, который построен на векторах →a и →b. Площадь такого параллелограмма численно равна длине векторного произведения:
Ответ:
Пример 2
Найти |[-3→a x 2→b]|, если |→a| = 1/2, |→b| = 1/6, ∠(→a, →b) = π/2.
Как решаем:
По условию снова нужно найти длину векторного произведения. Используем нашу формулу:
Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
Выносим константу за пределы модуля, при этом модуль позволяет убрать знак минус. Длина же не может быть отрицательной.
Ответ:
Пример 3
Даны вершины треугольника A (0, 2, 0), B (-2, 5,0), C (-2, 2, 6). Найти его площадь.
Как решаем:
Сначала найдём векторы:
Затем векторное произведение:
Вычислим его длину:
Подставим данные в формулы площадей параллелограмма и треугольника:
Ответ:
Геометрический смысл векторного произведения
По определению длина векторного произведения векторов равна
А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.
Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.
Физический смысл векторного произведения
В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.
Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F].
Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
239.
9K
Теорема косинусов и синусов
К следующей статье
423.2K
Длина окружности
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
интуиция — Каково направление нулевого (нулевого) вектора?
спросил
Изменено 1 год, 5 месяцев назад
Просмотрено 29 тысяч раз
$\begingroup$
Чтобы быть более точным, мне интересно знать , если интуиция, что евклидов нулевой вектор не имеет определенного направления на самом деле правильно, и если есть строгая формулировка, которая подкрепляет его.
Записи Википедии о нулевом векторе, похоже, согласуются с этой интуицией, но, как всегда, не следует слепо доверять Википедии: в одном месте утверждается, что нулевой вектор » ортогонален всем другим векторам с тем же число компонентов, », а в другом утверждается, что « два вектора можно считать ортогональными тогда и только тогда, когда их скалярное произведение равно нулю и они имеют ненулевую длину».0015 » Поправьте меня, если я ошибаюсь, но эти два утверждения противоречат друг другу.
Этот вопрос возник у меня в голове, когда я услышал, как кто-то утверждает, что, поскольку евклидов вектор определяется как геометрическая сущность, имеющая как величину, так и направление, а поскольку нулевой вектор является вектором длины 0, то для нулевого вектора подходит только « направление 0,«. Лично я склонен сказать, что нулевой вектор не имеет определенного направления, но как Я сказал, что хотел бы знать, существует ли строгая формулировка, которая привела бы к такому заключению.
0005
И если поставить вопрос в менее «вызывающей дискуссию» форме, существует ли соглашение о направлении евклидова нулевого вектора?
- интуиция
- евклидова геометрия
- определение
$\endgroup$
1
$\begingroup$
Нулевой вектор не имеет определенного направления; это согласуется с тем фактом, что он ортогонален любому другому вектору. (На самом деле не имеет смысла говорить, что у него есть » направление 0 «, так как направление не является величиной; «направление 0» имеет не больше смысла, чем «направление 1» или «направление 5,873».)
В качестве альтернативы можно сказать, что он указывает во всех направлениях, но с нулевой величиной,
так как если вы возьмете любого вектора и умножите его на ноль, вы получите нулевой вектор. «Каждый
направление» — это то же самое, что «нет определенного направления»; это просто другой способ формулировки
вещи.
Это недостаток традиционного описания вектора как пары, состоящей из величина и направление: для нулевого вектора величина равна нулю, но направление является произвольным.
$\endgroup$
2
$\begingroup$
Поскольку добавление нулевого вектора к любому ненулевому вектору не меняет направление последнего, он не может иметь правильного направления из-за правила параллелограмма 🙂
$\endgroup$
$\begingroup$
Просто замечание: здесь есть некоторая соответствующая базовая алгебраическая топология. 9{n-1}$ путем определения противоположных точек.
$\endgroup$
$\begingroup$
Во-первых, нам нужно определение направления.
Как насчет этого: направлением вектора $x$ является вектор $u$ единичной длины (то есть $|u| = 1$), такой что $cx = u$ для некоторого положительного действительного числа $c $.
Из определения ясно, что если $x = 0$, то не существует $c$ такого, что $cx$ — единичный вектор.
Также ясно, что направление $d(x)$ вектора $x$ является функцией, отображающей $x$ в единичный вектор. Для любого заданного $x$ коэффициент $c$ равен просто $\frac{1}{|x|}$, поэтому функция такова: $$d(x) = \frac{x}{|x| }$$.
Ясно, что функция не определена при $x = 0$, где она вызывает деление на ноль.
$\endgroup$
$\begingroup$
Вектор может существовать с нулевой величиной и направлением. Выразите вектор как скаляр, умноженный на вектор единичной длины. Вектор единичной длины указывает направление, а скаляр представляет длину. Даже если длина стремится к нулю, у нас все еще есть направление.
Это становится очевидным, если мы используем полярные или сферические координаты.
$\endgroup$
1
$\begingroup$
Я думаю, что вектор нулевой величины может иметь направление. Рассмотрим частицу, движущуюся по окружности с постоянной скоростью. Скорость переменная, потому что меняется направление. величина ускорения равна нулю, потому что скорость постоянна. Ускорение (направленное к центру) является переменным, потому что направление меняется каждое мгновение. Ясно, что ускорение присутствует с нулевой величиной.
$\endgroup$
3
$\begingroup$
Когда мы возьмем векторное произведение двух перпендикулярных векторов, мы получим вектор, имеющий нулевую величину.
Но мы знаем направление этого вектора, используя правило большого пальца правой руки или правило винта. Итак, мы знаем направление нулевого вектора…! что вы скажете об этом?
$\endgroup$
1
линейная алгебра — Что такое интуитивное определение нулевого вектора?
Задавать вопрос
спросил
Изменено 9 лет, 6 месяцев назад
Просмотрено 10 тысяч раз
$\begingroup$
Сейчас я изучаю векторные пространства и подпространства, и одно из трех правил, определяющих, является ли что-то подпространством большего векторного пространства, состоит в том, что оно должно содержать нулевой вектор.
{3}\;\middle|\; топор+by+cz=d\право\}$. Покажите, что $U$ является подпространством в $V$ тогда и только тогда, когда $d=0$. 92$. Это также не содержит нулевой вектор.
Мне кажется, что «нулевой вектор» используется как синоним «начала», но это не соответствует определению вектора, которое мне дали. Конечно, стрелка может начинаться в начале координат и выходить наружу, но не обязательно. Любая стрелка, представляющая вектор, такая же, как и любая другая, если она имеет одинаковую длину и направление, независимо от того, где находится основание стрелки, нулевой вектор все равно должен быть нулевым вектором.
Вот я и спрашиваю… Как может нулевой вектор не быть в 92$ — операция смещения с произвольной начальной точкой. Однако это не совсем так. Мы считаем два таких смещения существенно одинаковыми, если они имеют одно и то же направление и одинаковую величину. Это существенное тождество определяет отношение эквивалентности на множестве всех таких смещений. В этом контексте вектор является классом эквивалентности, а не просто его представителем.
Современный подход состоит в том, чтобы полностью отказаться от всех этих неудобств и принять аксиоматический подход. Векторное пространство — это множество с дополнительной структурой, удовлетворяющее определенному списку аксиом. Тогда вектор по определению является элементом векторного пространства. Тогда нулевой вектор является (доказуемо) уникальным вектором в данном векторном пространстве, который ведет себя нейтрально по отношению к сложению векторов. Это и есть нулевой вектор. Следует подчеркнуть, что точное имя нулевого вектора очень чувствительно к структуре векторного пространства. Например, $\mathbb R$ с его обычной структурой векторного пространства допускает $0$ в качестве нулевого вектора. Однако для каждого $a\in \mathbb R$ можно наделить $\mathbb R$ структурой векторного пространства так, что $a$ является нулевым вектором. Вот что происходит, когда мы переходим от определения того, что такое векторы (на котором в настоящее время зависит ваше понимание векторов), к тому, чтобы не заботиться о том, что они из себя представляют, и заботиться только о том, что вы можете с ними делать (это аксиоматический подход).
Есть веская причина, по которой последнее является преобладающим выбором в современной математике. Никто не заботится, и мы не должны заботиться о том, что есть что-то. Все, что имеет значение, это то, что мы можем с этим сделать. Если вы даже не пытаетесь определить, что такое что-то, а вместо этого просто прибегаете к перечислению того, что вы можете делать с этими вещами, это избавит вас от многих головных болей и бесконечных философских споров.
Учитывая все вышесказанное, за исключением упомянутых вами случаев, когда нулевой вектор не принадлежит данному множеству, рассмотрим пустое подмножество любого векторного пространства. Это никогда не векторное подпространство, поскольку оно не содержит нулевого вектора (или любого другого вектора).
$\endgroup$
1
$\begingroup$
«Дух» $0$-вектора таков: это элемент идентичности в операции «сложения», определенной в векторном пространстве.
Таким образом, вопрос о том, содержит ли ваш набор «тот» $0$-вектор, на самом деле зависит от того, как вы определили сложение: есть ли в вашем наборе элемент $\vec{0}$, такой что $\vec{x }+\vec{0}=\vec{0}+\vec{x}=\vec{x}$ для всех $\vec{x}$ в наборе?
$\endgroup$
$\begingroup$
Вы оперируете пониманием не просто векторного пространства, а аффинного пространства . Аффинное пространство — это в основном множество, на котором (транзитивно) действует векторное пространство. Векторы — это «направления», а аффинное пространство интуитивно состоит из точек в пространстве. Любые две точки определяют вектор смещения: уникальный вектор, который вы используете для перехода от одной точки к другой. Таким образом, вектор можно более или менее отождествить с классом эквивалентности пар точек с данным вектором в качестве вектора смещения.
Вы думаете: «Дано любое непустое подмножество аффинного пространства, в этом пространстве есть две точки с нулевым вектором смещения».
2$ — векторное пространство; это твой 92$. Важно отличать позиции (точки) от ходов (векторов).
Во многом это верно: «Дано непустое множество $S\subseteq A$ позиций, существует позиция $s\in S$, для которой у нас есть возможность не перемещаться». (Не двигаться эквивалентно смещению на $0\in V$.) Это соответствует тому, что вы думаете. Но идея подпространства — это наборов ходов, а не набор позиций, поэтому подмножество $M\subseteq V$. Действительно, в общем случае существуют наборы перемещений $M\subseteq V$, которые не содержат опции [идти в никуда]. Например, пусть $M=\{(0,1)\}$; это набор, содержащий движение [подняться на одну единицу]. Это не то же самое, что двигаться в никуда. Таким образом, даже несмотря на то, что все позиции допускают ход [никуда не ведут], не все наборы ходов содержат ход [никуда не идут]. 92}$. Линия, являющаяся подпространством, всегда будет натянута на один вектор. Если у нас есть линия в пространстве, которая не может быть натянута на один вектор, то является ли это векторным пространством (как может линия, не содержащая начало координат, рассматриваться как некоторая произвольная $(x,y)$)? Для подпространства $U$ имеется достаточно большое количество $x$ и $y$, где $x,y \in \mathbb{F}$ не удовлетворяют $x + y = 1$.