Площадь треугольника через радиус вписанной окружности: как найти, формула
Содержание:
-
Формула 1Площадь треугольника через радиус вписанной окружности
- Как найти, теорема и доказательство, формула
- Примеры решения задач с ответами
Содержание
-
Формула 1Площадь треугольника через радиус вписанной окружности
- Как найти, теорема и доказательство, формула
- Примеры решения задач с ответами
Формула 1Площадь треугольника через радиус вписанной окружности
Как найти, теорема и доказательство, формула
Теорема 1
Площадь треугольника равна произведению полупериметра данного треугольника на радиус вписанной в него окружности.
Формула 1
S=pr где p — полупериметр,
r — радиус вписанной окружности,
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
a, b, c — стороны треугольника.
Доказательство:
Пусть у ΔABC стороны равны a, b, c. AС=а, АВ=b, ВС=с. В ΔABC вписана окружность с центром в точке О и радиусом r.
Проведем отрезки ОА и ОС. Радиус r является высотой ΔАОС, проведенной к АС, по свойству касательной к окружности и ее радиуса. Так как площадь треугольника равна половине произведения основания и проведенной к этому основанию высоты,
\(S_{\Delta AОC}=\frac12a·r.\)
Таким же образом найдем площади треугольников АОВ и ВОС.
\(S_{\Delta AОВ}=\frac12b·r, \)
\(S_{\Delta BОC}=\frac12c·r. 2). \)
2). \)
По теореме Пифагора найдем АВ и затем вычислим р — полупериметр ΔАВС, р=32 (см).
Радиус вписанной окружности \(r=\frac{S_{\Delta АВС}}р=96:32=3 (см).\)
Диаметр вписанной окружности равен 6 см, а высота ΔКВМ, проведенная к КМ равна 2 см.
Коэффициент подобия ΔАВС и ΔКВМ равен \(\frac14.\)
Значит \(КМ=\frac14·АС=3 (см).\)
Ответ: КМ=3 см.
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Примечание . Это часть урока с задачами по геометрии (раздел стереометрия, задачи о сфере). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом на форуме .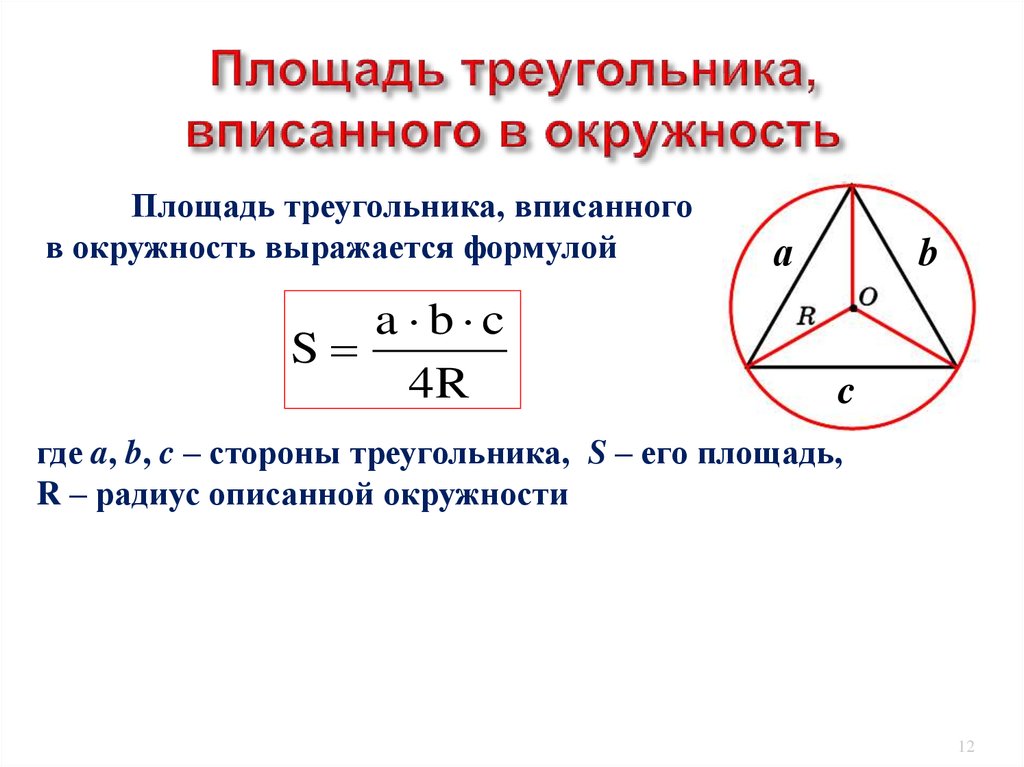 В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√». Задача В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√». Задача В сферу вписан конус, образующая которого равна l, а угол при вершине осевого сечения равен 60 градусов. Найдите площадь сферы. Решение . Площадь сферы найдем по формуле: Поскольку в сферу вписан конус, проведем сечение через вершину конуса, которое будет равнобедренным треугольником. Поскольку угол при вершине осевого сечения равен 60 градусам, то треугольник — равносторонний (сумма углов треугольника — 180 градусов, значит остальные углы (180-60) / 2 = 60 , то есть все углы равны). Откуда радиус сферы равен радиусу окружности, описанного вокруг равностороннего треугольника. Сторона треугольника по условию равна l . То есть Таким образом площадь сферы S = 4π(√3/3 l) 2 Ответ : площадь сферы равна 4/3πl 2 . ЗадачаЕмкость имеет форму полусферы (полушара). Длина окружности основания равна 46 см. На 1 квадратный метр расходуется 300 граммов краски. Сколько необходимо краски, чтобы покрасить емкость? Решение . Откуда площадь основания равна Площадь сферы найдем по формуле: Соответственно площадь полусферы Общая площадь поверхности фигуры равна: Теперь вычислим расход краски (учтем, что расход дан на квадратный метр, а вычисленное значение в квадратных сантиметрах, то есть в одном метре 10 000 квадратных сантиметров) ЗадачаРешение.
|
| V = | 4 | π R 3 = | 1 | π D 3 |
| 3 | 6 |
Формула. Площадь поверхности сферы через радиус или диаметр:
S = 4π R 2 = π D 2
Уравнение сферы
1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат
x 2 + y 2 + z 2 = R 2
2. Уравнение сферы с радиусом R и центром в точке с координатами (x 0 , y 0 , z 0) в декартовой системе координат :
(x — x 0) 2 + (y — y 0) 2 + (z — z 0) 2 = R 2
Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.
Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.
Основные свойства сферы и шара
1. Все точки сферы одинаково удалены от центра.
2. Любое сечение сферы плоскостью является окружностью.
3. Любое сечение шара плоскостью есть кругом.
4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.
5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.
6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.
7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.
8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются , а в плоскости пересечения образуется круг.
Секущая, хорда, секущая плоскость сферы и их свойства
Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.
Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).
Определение. Секущая плоскость — это плоскость, которая пересекает сферу.
Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг . Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).
Любая хорда, проходящая через центр сферы (шара) является диаметром.
Хорда является отрезком секущей прямой.
Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:
d
Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m
Местом сечения секущей плоскости на сфере всегда будет малая окружность , а на шаре местом сечения будет малый круг . Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r
такого круга можно найти по формуле:
Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r
такого круга можно найти по формуле:
r = √R 2 — m 2 ,
Где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.
Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.
Касательная, касательная плоскость к сфере и их свойства
Определение. Касательная к сфере — это прямая, которая касается сферы только в одной точке.
Определение. Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.
Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения
Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.
Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h
называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Высотой сегмента h
называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента.
Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:
S = 2π Rh
Шар и сфера — это прежде всего геометрические фигуры, и если шар — это геометрическое тело, то сфера — это поверхность шара. Этими фигурами интересовались еще многие тысячи лет назад до н.э.
Впоследствии когда было открыто, что Земля — это шар, а небо — небесная сфера, получило развитие новое увлекательное направление в геометрии — геометрия на сфере или сферическая геометрия. Для того, чтобы рассуждать о размере и объеме шара, нужно сначала дать ему определение.
Шар
Шаром радиуса R с центром в точке О в геометрии называют тело, которое создано всеми точками пространство, имеющими общее свойство. Эти точки находятся на расстоянии, не превышающем радиуса шара, то есть заполняют все пространство меньше радиуса шара во все стороны от его центра. Если мы рассмотрим только те точки, которые равноудалены от центра шара — мы будем рассматривать его поверхность или оболочку шара.
Если мы рассмотрим только те точки, которые равноудалены от центра шара — мы будем рассматривать его поверхность или оболочку шара.
Как можно получить шар? Мы можем вырезать из бумаги круг и начать его вращать вокруг его же диаметра. То есть диаметр круга будет осью вращения. Образованная фигура — будет шар. Поэтому шар называют также телом вращения. Потому что он может быть образован путем вращения плоской фигуры — круга.
Возьмем какую-нибудь плоскость и разрежем ею наш шар. Подобно тому как мы режем ножом апельсин. Кусок, который мы отсечем от шара, называется шаровым сегментом.
В Древней Греции умели не только работать с шаром и сферой, как с геометрическими фигурами, например, использовать их при строительстве, а также умели расчитывать площадь поверхности шара и объем шара.
Сферой иначе называется поверхность шара. Сфера — это не тело — это поверхность тела вращения. Однако так как и Земля и многие тела имеют сферическую форму, например капля воды, то изучение геометрических соотношений внутри сферы получило большое распространение.
Например, если мы соединим две точки сферы между собой прямой линией, то эта прямая линия назовется хордой, а если эта хорда пройдет через центр сферы, который совпадает с центром шара, то хорда назовется диаметром сферы.
Если мы проведем прямую линию, которая коснется сферы всего в одной точке, то эта линия будет называться касательной. Кроме того, эта касательная к сфере в этой точке будет перпендикулярна к радиусу сферы, проведенному в точку касания.
Если мы продолжим хорду до прямой в одну и другую сторону от сферы, то эта хорда станет называться секущей. Или можно сказать иначе — секущая к сфере содержит в себе ее хорду.
Объем шара
Формула для вычисления объема шара имеет вид:
где R — радиус шара.
Если нужно найти объем шарового сегмента — воспользуйтесь формулой:
V сег =πh 2 (R-h/3), h — высота шарового сегмента.
Площадь поверхности шара или сферы
Чтобы вычислить площадь сферы или площадь поверхности шара (это одно и то же):
где R — радиус сферы.
Архимед очень любил шар и сферу, он даже попросил оставить на его гробницу рисунок, на котором в цилиндр вписан шар. Архимед считал, что объем шара и его поверхность равны двум третьим от объема и поверхности цилиндра, в который вписан шар»
Очень часто людям требуется узнать точный размер какого-то объекта. На производстве, строительстве, моделировании и многом-многом другом точность является одним из главных правил. В природе очень распространены идеальные фигуры. Одним из таких тел является сфера. В стереометрии понятию «шар» даётся следующее определение: сфера – геометрическое место точек, равноудалённых от одной единственной – центра сферы. Расстояние, на котором находятся все эти точки, является постоянным и называется радиусом. Радиус является основным параметром и очень важно уметь вычислять его значение. Для проведения этой операции существует множество способов, как практических, так и теоретических. В большинстве из них фигурирует понятие числа «Пи», в котором обязательно нужно разобраться. Число «Пи» является постоянным иррациональным трансцендентным числом. Это значит, что его десятичная запись является бесконечной. Сама константа определяется отношением длины окружности к её радиусу. С древности учёные вычисляли значение этого числа, на данный момент известно уже более миллиарда знаков после запятой. На практике и, в частности, в данной статье понадобится не слишком точное значение данной константы. И хоть первые десять знаков выглядят как 3.3, чтобы найти радиус сферы будет использоваться округлённое значение 3,4.
Число «Пи» является постоянным иррациональным трансцендентным числом. Это значит, что его десятичная запись является бесконечной. Сама константа определяется отношением длины окружности к её радиусу. С древности учёные вычисляли значение этого числа, на данный момент известно уже более миллиарда знаков после запятой. На практике и, в частности, в данной статье понадобится не слишком точное значение данной константы. И хоть первые десять знаков выглядят как 3.3, чтобы найти радиус сферы будет использоваться округлённое значение 3,4.
Первый способ годится, если имеется реальное сферическое тело, например, мяч для игры в настольный теннис. Как вычислить его радиус? Для этого достаточно использовать штангенциркуль, а именно поместить в раствор циркуля шарик, таким образом будет получено значение его диаметра. Оно равно сорока миллиметрам, если берётся стандартная модель. Теперь остаётся лишь поделить диаметр пополам и получится точное значение радиуса, а именно 20 мм. Для подобных случаев формула будет иметь вид R = D/2, (где R — радиус, а D – диаметр сферы) . 3 = (V * 3/4) / Pi. После извлечения корня кубического получится R = sqrt((V * 3/4) / Pi) . Обозначение “sqrt” означает кубический корень. Теперь стоит подставить объём в формулу и произвести вычисления: R = sqrt((48 * 3/4) / Pi) = sqrt(36 / Pi) = sqrt(1,8) = 2,4. Важное внимание следует уделить размерности в этом случае, ведь объём дан в литрах, а ответ требуется дать в величинах, измеряющих длину.
3 = (V * 3/4) / Pi. После извлечения корня кубического получится R = sqrt((V * 3/4) / Pi) . Обозначение “sqrt” означает кубический корень. Теперь стоит подставить объём в формулу и произвести вычисления: R = sqrt((48 * 3/4) / Pi) = sqrt(36 / Pi) = sqrt(1,8) = 2,4. Важное внимание следует уделить размерности в этом случае, ведь объём дан в литрах, а ответ требуется дать в величинах, измеряющих длину.
Стоит отметить, что 1 литр равен одному дециметру кубическому, следовательно ответ получен в дециметрах. Ответ: 2,5 дециметров или 2,5 сантиметра. Для всех подобных задач радиус можно вычислить с помощью формулы R = sqrt((V * 3/4) / Pi) , где R – радиус, sqrt – корень кубический, а V – объём шара. На практике, не имея возможность вычислить диаметр, но имея возможность найти объём шара, радиус сферы можно рассчитать с помощью воды и мензурки. Для этого нужно налить 100 мл воды в мензурку, полностью опустить в неё шар, зафиксировать новое значение. Из него вычесть 100 мл — это и будет объём шара. Далее производить действия по аналогии с последней задачей.
Далее производить действия по аналогии с последней задачей.
какова площадь круга радиусом 1 единиц?
Вот ответ на вопросы типа: как найти площадь круга с радиусом 1 единиц?
| ||||||||||||
Площадь круга с радиусом 1 равна 3,142 | |
Изображение кружка = 1d = 2C = 6,28 | А = πr 2 = π(d2) 2 А = С 2 4π π = 3,1415A = площадь C = окружность или периметр r = радиус , d = диаметр |
Площадь круга в пересчете на
радиуса :Площадь = π·r 2 = 3,14·1 2 = 3,14 квадратных единиц (*)
Площадь круга относительно
диаметра :Площадь = π·(d2) 2 = 3,14·(22) 2 = 3,14·(1) 2 = 3,14 квадратных единиц (*)
Площадь круга относительно
длины окружности :Площадь = С 2 4π = 6,28 2 4π = 39,48(4·3,14) = 39,4812,56 = 3,14 квадратных единиц (*)
(*) 3,1415926535898 единиц, точно или ограничено точностью этого калькулятора (13 знаков после запятой).
Примечание: для простоты указанные выше операции были округлены до 2 знаков после запятой, а число π округлено до 3,14.
Используйте приведенный ниже калькулятор площади круга, чтобы найти площадь круга по заданному радиусу или другим параметрам. Для расчета площади вам достаточно ввести положительное числовое значение в одно из 3-х полей калькулятора. Вы также можете увидеть в нижней части калькулятора пошаговое решение.
Формула площади круга
Вот три способа найти площадь круга (формулы):
Формула площади круга по радиусу
A = πr 2
Формула площади круга по диаметру
A = π(d2) 2
Формула площади круга по окружности
A C2 4π
См. ниже некоторые определения, связанные с формулами:
Окружность
Окружность – это линейное расстояние вокруг края круга.
Радиус
Радиусом круга является любой из отрезков линии от его центра до периметра. Радиус равен половине диаметра или r = d2.
Радиус равен половине диаметра или r = d2.
Диаметр
Диаметр окружности — это любой отрезок прямой линии, проходящий через центр окружности и концы которого лежат на окружности. Диаметр в два раза больше радиуса или d = 2·r.
Греческая буква π
π обозначает число Пи, которое определяется как отношение длины окружности к ее диаметру или π = Cd . Для простоты можно использовать Pi = 3,14 или Pi = 3,1415. Пи — иррациональное число. Первые 100 цифр числа Пи: 3,14159.26535 8979323846 2643383279 5028841971 6939937510 5820974944 5923078164 0628620899 8628034825 3421170679 …
Note:
If you input the radius in centimeters, you will get the answer in square centimeters (cm²), if in inches, will get the answer in square inches (дюйм²) и т. д. …
Окружность часто неправильно пишется как окружность.
Пример расчета площади круга
- Площадь круга с радиусом 4456
- Площадь круга с радиусом 3,8 дюйма
- Площадь круга радиусом 9,2
- Площадь круга радиусом 10 футов
- Площадь круга радиусом 18,9 дюйма
- Площадь круга с окружностью 6,4
- Площадь окружности 18,9 дюйма
- Площадь круга диаметром 11,9 фута
- Площадь круга диаметром 19,4 фута
геометрия — Площадь круга на сфере
Задавать вопрос 92.


 Рiшення .
Рiшення .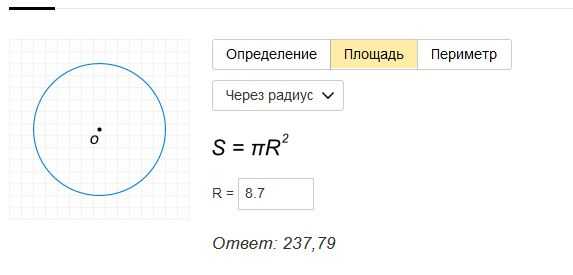 Скоротимо отриманий дріб. Неважко відмітити, що співвідношення площ двох куль дорівнює співвідношенню квадратів їх радіусів. По умові завдання це співвідношення рівне m/n
Скоротимо отриманий дріб. Неважко відмітити, що співвідношення площ двох куль дорівнює співвідношенню квадратів їх радіусів. По умові завдання це співвідношення рівне m/n