Формулы алгебры: Математические формулы по алгебре и геометрии для ЕГЭ

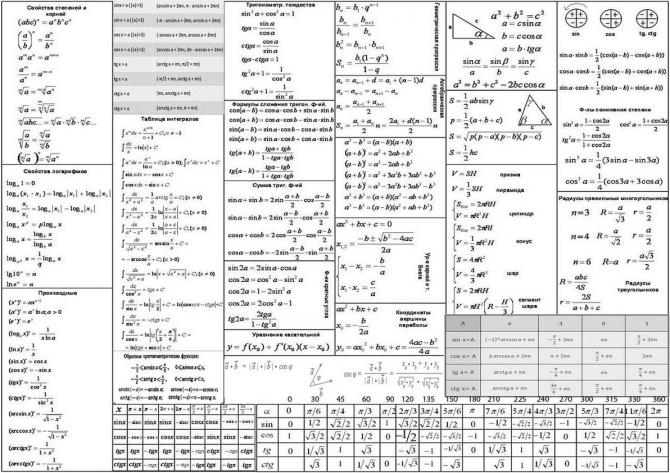
Математические формулы по алгебре и геометрии для ЕГЭ

Математические формулы по алгебре и геометрии для ЕГЭ

Как выучить все формулы по математике к ЕГЭ

Чтобы сдать ЕГЭ по математике, необходимо знать математические формулы из школьного курса алгебры и геометрии.

Для того, чтобы запомнить формулы школьной математики, желательно держать в течение всего года на видном месте шпаргалку с красиво написанными формулами. Таким образом подключается зрительная память и формулы лучше запоминаются.

Проверяйте себя время от времени: попробуйте написать все важные математические формулы по памяти, а затем проверьте. На самом деле, формул, которые надо выучить наизусть, не так много. И целого учебного года вполне достаточно, чтобы все выучить.

Многие алгебраические, геометрические, тригонометрические формулы можно быстро вывести прямо на экзамене, если Вы их забыли. Но на это придется потратить какое-то время. Поэтому преимущество получают те школьники, которые выучили формулы.
Зная математические формулы наизусть, можно гораздо быстрей решить сложные задачи по алгебре, тригонометрии и геометрии на ЕГЭ.

Мы собрали самые важные формулы из школьного курса математики, которые надо выучить для успешной сдачи ЕГЭ.

Математические формулы школьного курса алгебры

 

Степени и корни

Формулы сокращенного умножения

Квадратный трехчлен: квадратное уравнение, формулы Виета, разложение на множители

Логарифмические формулы

Формулы тригонометрии

 

Основные формулы тригонометрии

Тригонометрические уравнения

Значения тригонометрических функций

Формулы приведения

Сумма и разность углов

Формулы двойного и тройного аргумента

Формулы половинного аргумента

Сумма и разность тригонометрических функций

Произведение тригонометрических функций

Формулы дифференциального исчисления

Формулы векторной алгебры из школьного курса математики

Формулы арифметической и геометрической прогрессии

Геометрические формулы школьного курса математики для ЕГЭ

Планиметрия

Стереометрия

Выучить формулы по математике – это еще не все, что надо для успешной сдачи ЕГЭ.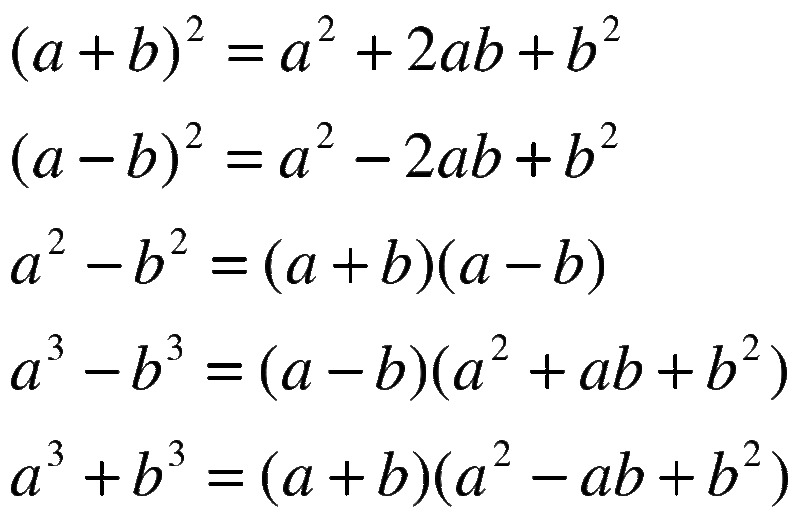 Наверх DIV >

Алгебра – основные понятия и формулы. Готовимся к ЕГЭ по Математике

Оглавление:

• Арифметический квадратный корень
• Модуль числа
• Свойства модулей
• Корни и степени
• Логарифмы

В школьном курсе алгебры не так уж много теории. Намного больше практики, то есть секретов и приемов решения задач. Хороший репетитор-математик вряд ли будет читать вам на каждом уроке длинные лекции.

Он скажет: «Смотри, как решаются такие задачи!»

И все-таки минимальное знание теории необходимо. Основные понятия и формулы надо знать наизусть.

Например, что такое квадратный корень из неотрицательного числа?

Что такое модуль числа?

Для каких чисел существуют логарифмы?

Чем действительные числа отличаются от рациональных?

Как узнать, что число делится на 11?

На этой странице – все основные темы и понятия алгебры, необходимые учащимся 10-11 класса. И еще – полезная информация о том, как считать быстро и без калькулятора и как легко запоминать формулы.

Числовые множества

Делимость чисел

Правила округления чисел 

Таблица квадратов натуральных чисел и формулы сокращенного умножения

ЕГЭ без ошибок. Считаем быстро и без калькулятора

Как запоминать формулы

Основы логики. Система условий, совокупность условий

Квадратный корень

Корни и степени

Логарифмы

Модуль числа

Число e

Проверь себя. Помнишь ли ты основные понятия алгебры?

к оглавлению ▴

Арифметический квадратный корень

— Арифметический квадратный корень из числа a — это такое неотрицательное число, квадрат которого равен a.

Посмотрим, какие задания на тему «Арифметический квадратный корень» чаще всего встречаются в вариантах ЕГЭ и ОГЭ по математике.

1. Вычислите:

Решение:

Мы применили одну из формул сокращенного умножения – квадрат разности.

Ответ: 18.

2. Избавьтесь от иррациональности в знаменателе:
(в алгебре считается, что в задаче ответ без квадратных корней в знаменателе выглядит более красиво).

a) б)

Решение:

а) Числитель и знаменатель дроби умножим на одно и то же число, равное знаменателю дроби.

б) Числитель и знаменатель дроби умножим на одно и то же число, сопряженное знаменателю.

Что значит «сопряженное»?

Выражение a+b называют сопряженным выражению a-b, а выражение a-b будет сопряженным выражению a+b.

Мы используем формулу разности квадратов:

Поэтому

Получим:

Ответ: а) б)

В вариантах ОГЭ по математике есть также задачи на сравнение арифметических квадратных корней.

3. Сравните числа и

Решение:

Мы не будем искать приближенное значение корня из 3,26. Ясно, что без калькулятора это сделать сложно. Зато два рациональных числа можно легко сравнить между собой.

Запишем число 1,8 как

Мы сравниваем и Из этих чисел больше то, для которого больше подкоренное выражение. Сравним числа 3,26 и 3,24. Конечно, тогда значит,

Ответ:

4. Между какими целыми последовательными числами заключено число ?

Решение:

Так как то значит

Ответ:

к оглавлению ▴

Модуль числа

— Определение модуля числа:

— Что такое ?  Запомним:

5. Вычислите а) б) в)

Решение:

а) Мы применили формулу

б)

в)

Ответ: а) ; б) ; в)

6. Вычислите значение выражения при

Решение:

Если то

Ответ: 5

к оглавлению ▴

Свойства модулей

1) Модуль любого числа неотрицателен.

2) любые числа.

3) любые числа.

4) любые числа.

5) любое число,

к оглавлению ▴

Корни и степени

— Знаешь ли ты, что

корни второй, третьей, четвертой, пятой, n-ной степени можно записывать просто как степени? И это намного удобнее. Например,

Напомним, что корень третьей степени из а – такое число, при возведении которого в третью степень получается число а.

Аналогично, корень четвертой степени из а – такое неотрицательное число, при возведении которого в четвертую степень получается число а.

Тема Корни и степени подробно здесь.

к оглавлению ▴

Логарифмы

Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a , чтобы получить b.

При этом

Перечислим основные формулы для логарифмов:

По определению, — это показатель степени, в которую надо возвести число a, чтобы получить число b:

Формула (1) называется основным логарифмическим тождеством.
Вот еще один вариант записи основного логарифмического тождества:

Логарифм произведения равен сумме логарифмов:

Логарифм частного равен разности логарифмов:

Логарифм степени – это показатель степени, умноженный на логарифм:

Есть также формула, когда основанием логарифма является число в некотоой степени. Показатель степени основания логарифма тоже «спрыгивает», но в виде обратного числа:

Наконец, важнейшая формула перехода к новому основанию:

В частности, если c = b, то , и тогда:

Из этих формул можно получать новые.

7. Например, докажем полезное свойство логарифма:

Доказательство:

По формуле перехода к новому основанию получим:

Отсюда

8. Докажем тождество:

Доказательство:

Решим примеры на вычисление.

9. Вычислите:

Решение: Применили формулы перехода к новому основанию и логарифма произведения.

10. Вычислите:

Решение:

Применили формулу перехода к новому основанию и формулу логарифма степени.

Спасибо за то, что пользуйтесь нашими статьями. Информация на странице «Алгебра – основные понятия и формулы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ. Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий. Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена: 08.04.2023

Формулы алгебры

• Главная

• Узнать

• Алгебра

• Что такое алгебра
• Алгебра в повседневной жизни
• Основные алгебраические термины
• Методы решения по алгебре
• Линейные, нелинейные уравнения
• Алгебра Формулы
• Коммутативные Ассоциативные законы
• Формула расстояния
• Метод фольги
• Формула средней точки
• Скобки Правила
• Квадратное уравнение
• Квадратичная формула
• Полиномиальные операции
• Полиномиальное сложение
• Полиномиальное вычитание
• Полиномиальное умножение
• Многочлен длинного деления
• Графики полиномиальных функций 92` + 10`x` + 25

  Explanation:

  ---

  Binomial Theorem Example

  
  

  Example 1:

  
  

  Example 2:

  ---

  Sum / Difference Formula Example

  
  

  Example 1:

  
  

  Example 2:

  Популярные ссылки по алгебре

  
  
  • Что такое алгебра
  • Алгебра в повседневной жизни
  • Основные алгебраические термины
  • Методы решения по алгебре
  • Линейные, нелинейные уравнения
  • Алгебра Формулы
  • Коммутативные ассоциативные законы
  • Формула расстояния
  • Метод фольги
  • Формула средней точки
  • Скобки Правила
  • Квадратное уравнение
  • Квадратичная формула
  • Полиномиальные операции
  • Полиномиальное сложение
  • Полиномиальное вычитание
  • Полиномиальное умножение
  • Многочлен длинного деления
  • Графики полиномиальных функций

  Спираль

  Станьте участником сегодня!

   Зарегистрируйтесь (бесплатно)

  Вы член? Войти!

   Войдите в свою учетную запись

  Алгебраические формулы — различные алгебраические формулы, используемые в математике

  Алгебраические формулы — это основные формулы, используемые для упрощения алгебраических выражений. Алгебраические формулы составляют основу для решения различных сложных задач. Алгебраические формулы полезны при решении алгебраических уравнений, квадратных уравнений, многочленов, уравнений тригонометрии, вероятностных вопросов и других.

  Алгебраические формулы — тождества

  Тождество — это уравнение, истинное во всех смыслах для любых значений, присвоенных переменным. Алгебраические тождества используются для решения различных уравнений. Для алгебраических тождеств LHS всегда равно RHS.

  Algebraic Identities

  Some important algebraic identities are

  (a + b) 2	a 2 + b 2 + 2ab
  (a – b) 2	a 2 + b 2 – 2ab
  (a + b)(a – b)	a 2 – b 2
  (x + a) (x + b)	x 2 + 2(a + b) + ab

  Что такое алгебраические формулы?

  Алгебраические формулы — это уравнения, требующие алгебраического выражения по обе стороны от «равно», т. е. как по левой, так и по правой стороне. Алгебраические формулы, как правило, верны для всех значений. Алгебраическая формула упрощает алгебраические уравнения и требуется для решения различных математических задач. Алгебраические формулы для различных классов обсуждаются ниже в этой статье.

  Алгебраические формулы для 8-го класса

  Алгебраические формулы для 8-го класса обсуждаются ниже в этой статье. Для трех переменных a, b и c различные алгебраические формулы таковы: ² – 2ab + b ²

• (а + b)(a – b) = а ² – b ²
• (а + b) ³ 5 а ² б + 3аб ² + b ³
• (a – b) ³ = a ³ – 3a ² b + 3ab ² – b ³
• a ³ + b ³ = (a + b)(a ² – ab + b ² )
• a ³ – b ³ = (a – b)(a ² + ab + b 2
  6 6)
• (a + b + c) ² = a ² + b ² + c ² + 2ab + 2bc + 2ca

Алгебраические формулы для 9 класса

Для 9 класса очень полезны формулы логарифмов. Они полезны для вычисления очень сложных задач на умножение и деление. Экспоненциальная форма 3 ² = 9 может быть легко преобразована в логарифмическую форму, как log ₃ 9 = 2. Кроме того, сложное умножение и деление можно легко преобразовать в сложение и вычитание, следуя логарифмическим формулам.

Важные наиболее часто используемые формулы логарифмической алгебры обсуждаются ниже:

• log _a (xy) = log _a x + log _a y
• log _a (x/y) = log _a x – log _a y
• log _a x ^m = m log _a x
• log _a a = 1 
• log _a 1 = 0

Законы экспоненты используются для решения задач с большей степенью. Некоторые из общих законов показателей степени с одинаковыми основаниями, имеющими разные степени, и разными основаниями, имеющими одинаковую степень, полезны для решения сложных экспоненциальных членов.

Более высокие экспоненциальные значения могут быть легко решены без какого-либо расширения экспоненциальных членов. Эти экспоненциальные законы также полезны для вывода некоторых логарифмических законов.

• A ^M × A ^N = A ^{M + N}
• A ^M /A ^N = ^{M — N}
63 (A ) M M M M M M M M M). ^MN
• (AB) ^M = A ^M × B ^M
• A ⁰ = 1
• A ^-M = 1.
• 9018. 9018. . 9015. . . . . . 10

  «Квадратная формула» — важная алгебраическая формула, с которой знакомятся учащиеся 10-го класса. Она используется для решения общих квадратных уравнений. Общая форма любого квадратного уравнения ax ² + bx + c = 0 , где x — переменная a, b — коэффициент, c — константа. Есть два способа решения этого квадратного уравнения.

  • Решение с использованием алгебраического метода
  • Использование квадратичной формулы

  Другими важными формулами, используемыми в классе 10, являются

  • n-й член, a _n = a + (n – 1) d
  • Сумма первых n членов, S _n = n/2 [2a + (n – 1) d]

  Формулы для геометрической последовательности

  Для любой заданной геометрической последовательности {a, ar, ar ² ,…}

  • N -й срок, A _N = A R ^N — 1
  • Сумма первых N -членов, S _N = A (1 — R ^N ). 1 – r)
  • Сумма бесконечных членов при r<1, S = a / (1 – r)

  Формулы алгебры для 11-го класса

  Формулы алгебры для 11-го класса, которые в основном используются, представляют собой формулы перестановок и комбинаций. Если требуются разные расположения r вещей из n доступных вещей, то используются формулы перестановки, тогда как формулы комбинаций используются для нахождения различных групп r вещей из n доступных вещей.

  Важные формулы перестановок и комбинаций:

  Формула факториала:

  n! = n × (n – 1) × (n – 2) × … × 3 × 2 × 1

  Формулы перестановки:

  ⁿ P _r = n! / (н – р)!

  Комбинированная формула:

  ⁿ C _r = n!/[r!(n−r)!]

  Биномиальная теорема — еще одна формула, которая имеет огромное значение для учащихся 11-го класса.

  Формулы алгебры для 12-го класса

  Важные формулы для учащихся 12-го класса включают формулы векторной алгебры. Эти формулы обсуждаются ниже,

  Возьмите любые три вектора, a, b и c, затем

  • Для вектора a = x i+y j+z k тогда величина |a| =√(x ² +y ² +z ² ).
  • Единичный вектор вдоль a равен a / |a|
  • Скалярное произведение двух векторов a и b определяется как a ⋅ b = |a| |б| cos θ
    , где θ — угол между векторами a и b.
  • Перекрестное произведение векторов a и b определяется как a × b = |a| |б| sin θ
    , где θ — угол между векторами a и b.
  • Скалярное тройное произведение трех векторов a, b и c определяется как [a b c ] = a ⋅ (b × c) = (a × b) ⋅ c.

  Также, проверка

  • Алгебраические идентификации полиномов
  • Векторная алгебра
  • Процентная формула

  Решающие примеры на Algebra Formulas

  9085 Пример. ) ² с помощью алгебраических формул.

  Решение:

  Использование алгебраической формулы,

  (A + B) ² = A ² + B ² + 2AB

  (2x + 3) ² = (2x)

  2 28 2

  2

  2

  2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2 9018 2

  (2x + 3) ² . 2 + 2 × 2x × 3

  (2x + 3) ² = 4x ² + 9 + 12x

  используя алгебраические формулы.

  Решение:

  Используя алгебраическую формулу,

  (a – b) ² = a ² + b ² – 2ab

  (5x – 3y) ² = (5x) ² – 9 х 9 + (3y) 2 90 × 3y

  (5 – 3) ² = 25x ² + 9y ² – 30xy

  Пример 3. Найдите значение 105×95 с помощью алгебраических формул.

  Решение:

  Используя алгебраическую формулу,

  (a + b)(a – b) = a ² – b ²

  105 × 95 = (100+5) (100-5)
  = 100 ² -5 ²
  = 10000-25
  = 9975

  Пример 4: Найдите Короты квадратного уравнения. x ² +6x+8=0 используя алгебраические формулы для квадратных уравнений.

  Решение:

  Данное квадратное уравнение равно x ² + 6x + 8 = 0

  Сравнение вышеприведенного уравнения с ax ² +bx+c=0, c=1, a=1, =8 

  Подставляя значения в квадратную формулу, получаем, 8))] / 2(1)
     = [−6 ± √(36 − 4(1)(8))] / 2
     = [−6 ± √(36 − 32)] / 2
     = [−6 ± √4] / 2
     = (-6 + 2)/2 и (-6 – 2)/2
     = -4/2 и -8/2
     = -2 и -4

  Таким образом, значения x равны -2 и -4

  Часто задаваемые вопросы по формулам алгебры

  Вопрос 1: Какая формула для числа ² – б ² по алгебре?

  Ответ:

  Формула для ² -B ² Определена в алгебре

  A ² -B ^{2 A 2 -B 2 A . Эту формулу также называют формулой разности квадратов.}

  Вопрос 2: Что такое алгебраические выражения?
  Ответ:

  Алгебраические выражения представляют собой комбинации переменных и констант с использованием арифметических операций, таких как сложение, вычитание, умножение и деление.

  No related posts.