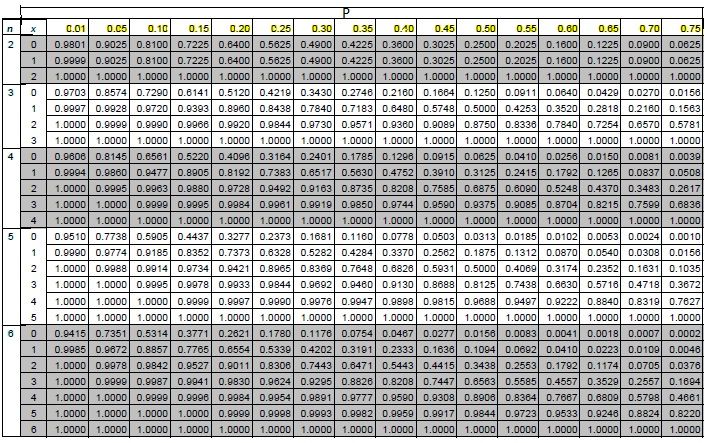
Таблица значений функции пуассона: Таблица значений функции Пуассона | matematicus.ru

Таблица значений функции Пуассона | matematicus.ru

22.02.2019 Artman Таблицы

Значения функции Пуассона

---

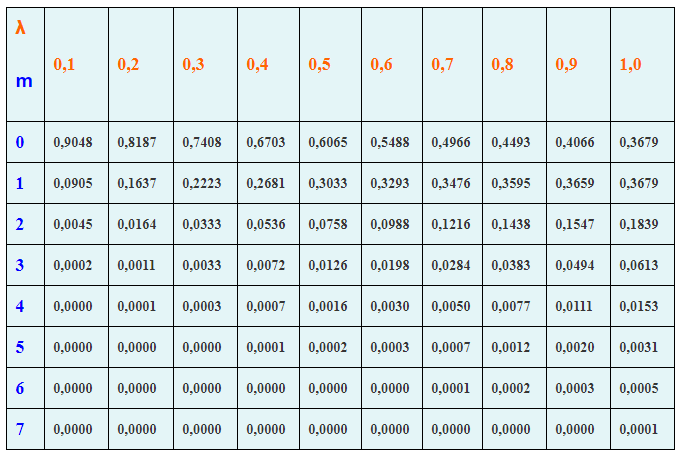
λ m	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1,0
0	0,9048	0,8187	0,7408	0,6703	0,6065	0,5488	0,4966	0,4493	0,4066	0,3679
1	0,0905	0,1637	0,2223	0,2681	0,3033	0,3293	0,3476	0,3595	0,3659	0,3679
2	0,0045	0,0164	0,0333	0,0536	0,0758	0,0988	0,1216	0,1438	0,1547	0,1839
3	0,0002	0,0011	0,0033	0,0072	0,0126	0,0198	0,0284	0,0383	0,0494	0,0613
4	0,0000	0,0001	0,0003	0,0007	0,0016	0,0030	0,0050	0,0077	0,0111	0,0153
5	0,0000	0,0000	0,0000	0,0001	0,0002	0,0003	0,0007	0,0012	0,0020	0,0031
6	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0001	0,0002	0,0003	0,0005
7	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0000	0,0001

 

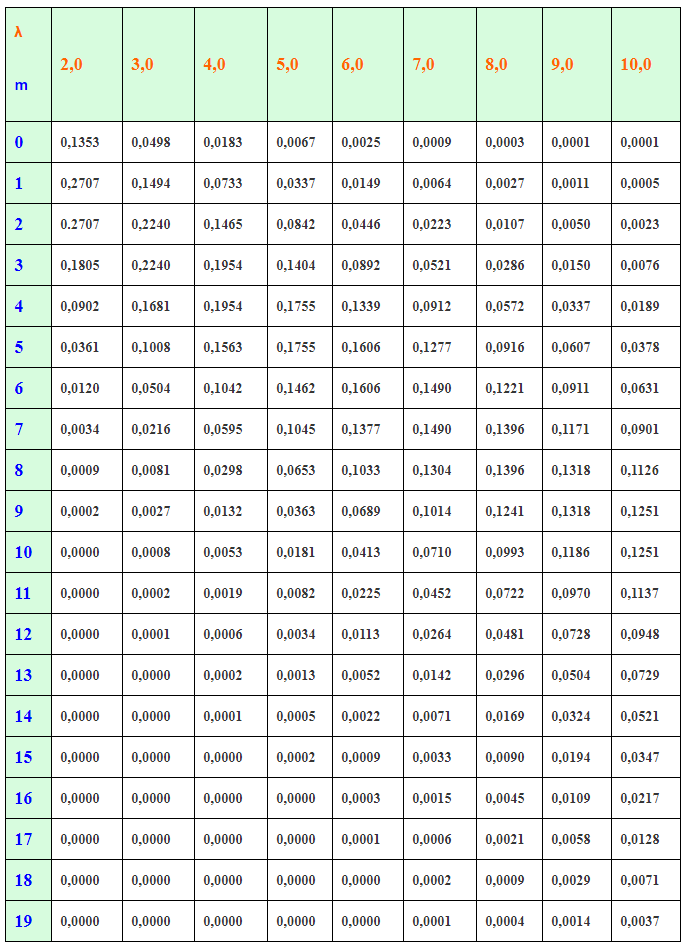
λ m	2,0	3,0	4,0	5,0	6,0	7,0	8,0	9,0	10,0
0	0,1353	0,0498	0,0183	0,0067	0,0025	0,0009	0,0003	0,0001	0,0001
1	0,2707	0,1494	0,0733	0,0337	0,0149	0,0064	0,0027	0,0011	0,0005
2	0. 2707	0,2240	0,1465	0,0842	0,0446	0,0223	0,0107	0,0050	0,0023
3	0,1805	0,2240	0,1954	0,1404	0,0892	0,0521	0,0286	0,0150	0,0076
4	0,0902	0,1681	0,1954	0,1755	0,1339	0,0912	0,0572	0,0337	0,0189
5	0,0361	0,1008	0,1563	0,1755	0,1606	0,1277	0,0916	0,0607	0,0378
6	0,0120	0,0504	0,1042	0,1462	0,1606	0,1490	0,1221	0,0911	0,0631
7	0,0034	0,0216	0,0595	0,1045	0,1377	0,1490	0,1396	0,1171	0,0901
8	0,0009	0,0081	0,0298	0,0653	0,1033	0,1304	0,1396	0,1318	0,1126
9	0,0002	0,0027	0,0132	0,0363	0,0689	0,1014	0,1241	0,1318	0,1251
10	0,0000	0,0008	0,0053	0,0181	0,0413	0,0710	0,0993	0,1186	0,1251
11	0,0000	0,0002	0,0019	0,0082	0,0225	0,0452	0,0722	0,0970	0,1137
12	0,0000	0,0001	0,0006	0,0034	0,0113	0,0264	0,0481	0,0728	0,0948
13	0,0000	0,0000	0,0002	0,0013	0,0052	0,0142	0,0296	0,0504	0,0729
14	0,0000	0,0000	0,0001	0,0005	0,0022	0,0071	0,0169	0,0324	0,0521
15	0,0000	0,0000	0,0000	0,0002	0,0009	0,0033	0,0090	0,0194	0,0347
16	0,0000	0,0000	0,0000	0,0000	0,0003	0,0015	0,0045	0,0109	0,0217
17	0,0000	0,0000	0,0000	0,0000	0,0001	0,0006	0,0021	0,0058	0,0128
18	0,0000	0,0000	0,0000	0,0000	0,0000	0,0002	0,0009	0,0029	0,0071
19	0,0000	0,0000	0,0000	0,0000	0,0000	0,0001	0,0004	0,0014	0,0037

12096

Теория вероятностей

Теория вероятностей

Вентцель Е. С. Теория вероятностей: Учеб. для вузов. — 6-е изд. стер. — М.: Высш. шк., 1999.— 576 c. Книга представляет собой один из наиболее известных учебников по теории вероятностей и предназначена для лиц, знакомых с высшей математикой и интересующихся техническими приложениями теории вероятностей. Она представляет также интерес для всех тех, кто применяет теорию вероятностей в своей практической деятельности. В книге уделено большое внимание различным приложениям теории вероятностей (теории вероятностных процессов, теории информации, теории массового обслуживания и др.). Оглавление Глава 1. Введение ПРЕДИСЛОВИЕ 1.1. Предмет теории вероятностей Теория вероятностей: 1.2. Краткие исторические сведения Глава 2. Основные понятия теории вероятностей 2.1. Событие. Вероятность события 2.2. Непосредственный подсчет вероятностей 2.3. Частота, или статистическая вероятность, события 2. 4. Случайная величина 2.5. Практически невозможные и практически достоверные события. Принцип практической универсальности Глава 3. Основные теоремы теории вероятностей 3.1. Назначение основных теорем. Сумма и произведение событий 3.2. Теорема сложения вероятностей 3.3. Теорема умножения вероятностей 3.4. Формула полной вероятности 3.5. Теорема гипотез (формула Бейеса) Глава 4. Повторение опытов 4.1. Частная теорема о повторении опытов 4.2. Общая теорема о повторении опытов Глава 5. Случайные величины и их законы распределения 5.1. Ряд распределения. Многоугольник распределения 5.2. Функция распределения 5.3. Вероятность попадания случайной величины на заданный участок 5.4. Плотность распределения 5.5. Числовые характеристики случайных величин. Их роль и назначение 5.6. Характеристики положения (математическое ожидание, мода, медиана) 5.7. Моменты. Дисперсия. Среднее квадратичное отклонение 5.8. Закон равномерной плотности 5. 9. Закон Пуассона Глава 6. Нормальный закон распределения 6.1. Нормальный закон распределения и его параметры 6.2. Моменты нормального распределения 6.3. Вероятность попадания случайной величины, подчиненной нормальному закону, на заданный участок. Нормальная функция распределения 6.4. Вероятное (срединное) отклонение Глава 7. Определение законов распределения случайных величин на основе опытных данных 7.1. Основные задачи математической статистики 7.2. Простая статистическая совокупность. Статистическая функция распределения 7.3. Статистический ряд. Гистограмма 7.4 Числовые характеристики статистического распределения 7.5. Выравнивание статистических рядов 7.6. Критерии согласия Глава 8. Системы случайных величин 8.1. Понятие о системе случайных величин 8.2. Функция распределения системы двух случайных величин 8.3. Плотность распределения системы двух случайных величин 8.4. Законы распределения отдельных величин, входящих в систему. Условные законы распределения 8.5 Зависимые и независимые случайные величины 8.6. Числовые характеристики системы двух случайных величин. Корреляционный момент. Коэффициент корреляции 8.7. Система произвольного числа случайных величин 8.8. Числовые характеристики системы нескольких случайных величин Глава 9. Нормальный закон распределении дли системы случайных величин 9.1. Нормальный закон на плоскости 9.2 Эллипсы рассеивания. Приведение нормального закона к каноническому виду 9.3. Вероятность попадания в прямоугольник со сторонами, параллельными главным осям рассеивания 9.4. Вероятность попадания в эллипс рассеивания 9.5. Вероятность попадания в область произвольной формы 9.6. Нормальный закон в пространстве трех измерений. Общая запись нормального закона для системы произвольного числа случайных величин Глава 10. Числовые характеристики функций случайных величин 10.1. Математическое ожидание функции. Дисперсия функции 10.2. Теоремы о числовых характеристиках 10. 3. Применения теорем о числовых характеристиках Глава 11. Линеаризация функций 11.1. Метод линеаризации функций случайных аргументов 11.2. Линеаризация функции одного случайного аргумента 11.3. Линеаризация функции нескольких случайных аргументов 11.4. Уточнение результатов, полученных методом линеаризации Глава 12. Законы распределения функций случайных аргументов 12.1. Закон распределения монотонной функции одного случайного аргумента 12.2. Закон распределения линейной функции от аргумента, подчиненного нормальному закону 12.3. Закон распределения немонотонной функции одного случайного аргумента 12.4. Закон распределения функции двух случайных величин 12.5. Закон распределения суммы двух случайных величин. Композиция законов распределения 12.6. Композиция нормальных законов 12.7. Линейные функции от нормально распределенных аргументов 12.8. Композиция нормальных законов на плоскости Глава 13. Предельные теоремы теории вероятностей 13. 1. Закон больших чисел и центральная предельная теорема 13.2. Неравенство Чебышева 13.3. Закон больших чисел (теорема Чебышева) 13.4. Обобщенная теорема Чебышева. Теорема Маркова 13.5. Следствия закона больших чисел: теоремы Бернулли и Пуассона 13.6. Массовые случайные явления и центральная предельная теорема 13.7. Характеристические функции 13.8. Центральная предельная теорема для одинаково распределенных слагаемых 13.9. Формулы, выражающие центральную предельную теорему и встречающиеся при ее практическом применении Глава 14. Обработка опытов 14.1. Особенности обработки ограниченного числа опытов. Оценки дли неизвестных параметров закона распределения 14.2. Оценки для математического ожидания и дисперсии 14.3. Доверительный интервал. Доверительная вероятность 14.4. Точные методы построения доверительных интервалов для параметров случайной величины, распределенной по нормальному закону 14.5. Оценка вероятности по частоте 14.6. Оценки для числовых характеристик системы случайных величин 14.7. Обработка стрельб 14.8. Сглаживание экспериментальных зависимостей по методу наименьших квадратов Глава 15. Основные понятия теории случайных функций 15.1. Понятие о случайной функции 15.2. Понятие о случайной функции как расширение понятия о системе случайных величин. Закон распределения случайной функции 15.3. Характеристики случайных функций 15.4. Определение характеристик случайной функции из опыта 15.5. Методы определения характеристик преобразованных случайных функций по характеристикам исходных случайных функций 15.6. Линейные и нелинейные операторы. Оператор динамической системы 15.7. Линейные преобразования случайных функций 15.7.1. Интеграл от случайной функции 15.7.2. Производная от случайной функции 15.8. Сложение случайных функций 15.9. Комплексные случайные функции Глава 16. Канонические разложения случайных функций 16.1. Идея метода канонических разложений. Представление случайной функции в виде суммы элементарных случайных функций 16.2. Каноническое разложение случайной функции 16.3. Линейные преобразования случайных функций, заданных каноническими разложениями Глава 17. Стационарные случайные функции 17.1. Понятие о стационарном случайном процессе 17.2. Спектральное разложение стационарной случайной функции на конечном участке времени. Спектр дисперсий 17.3. Спектральное разложение стационарной случайной функции на бесконечном участке времени. Спектральная плотность стационарной случайной функции 17.4. Спектральное разложение случайной функции в комплексной форме 17.5. Преобразование стационарной случайной функции стационарной линейной системой 17.6. Применения теории стационарных случайных процессов к решению задач, связанных с анализом и синтезом динамических систем 17.7. Эргодическое свойство стационарных случайных функций 17.8. Определение характеристик эргодической стационарной случайной функции по одной реализации Глава 18. 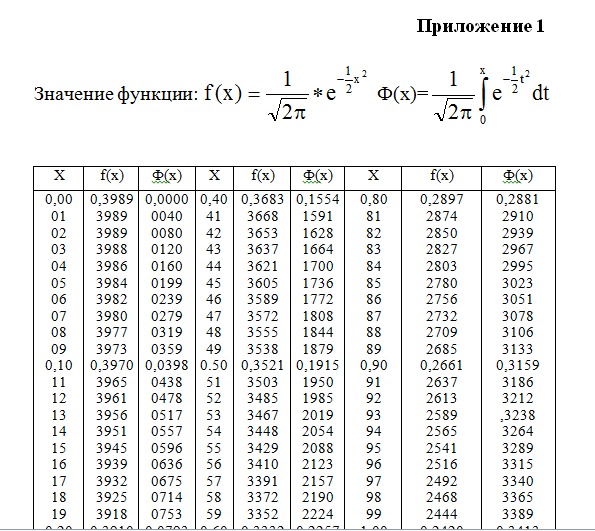Основные понятия теории информации 18.1. Предмет и задачи теории информации 18.2. Энтропия как мера степени неопределенности состояния физической системы 18.3. Энтропия сложной системы. Теорема сложения энтропий 18.4. Условная энтропия. Объединение зависимых систем 18.5. Энтропия и информация 18.6. Частная информация о системе, содержащаяся в сообщении о событии. Частная информация о событии, содержащаяся в сообщении о другом событии 18.7. Энтропия и информация для систем с непрерывным множеством состояний 18.8. Задачи кодирования сообщений. Код Шеннона-Фэно 18.9. Передача информации с искажениями. Пропускная способность канала с помехами Глава 19. Элементы теории массового обслуживания 19.1. Предмет теории массового обслуживания 19.2. Случайный процесс со счетным множеством состояний 19.3. Поток событий. Простейший поток и его свойства 19.4 Нестационарный пуассоновский поток 19.5. Поток с ограниченным последействием (поток Пальма) 19. 6. Время обслуживания 19.7. Марковский случайный процесс 19.8. Система массового обслуживания с отказами. Уравнения Эрланга 19.9. Установившийся режим обслуживания. Формулы Эрланга 19.10. Система массового обслуживания с ожиданием 19.11. Система смешанного типа с ограничением по длине очереди Приложения Таблица 1 Значения нормальной функции распределения Таблица 2. Значения экспоненциальной функции Таблица 3. Значения нормальной функции Таблица 4. Значения “хи-квадрат” в зависимости от r и p Таблица 5. Значения удовлетворяющие равенству Таблица 6. Таблица двоичных логарифмов целых чисел от 1 до 100 Таблица 7. Таблица значений функции Таблица 8. Значения распределение Пуассона

Распределение Пуассона – определение, формула, таблица, примеры

Распределение Пуассона – это теоретическая дискретная вероятность, известная также как функция массы вероятности распределения Пуассона.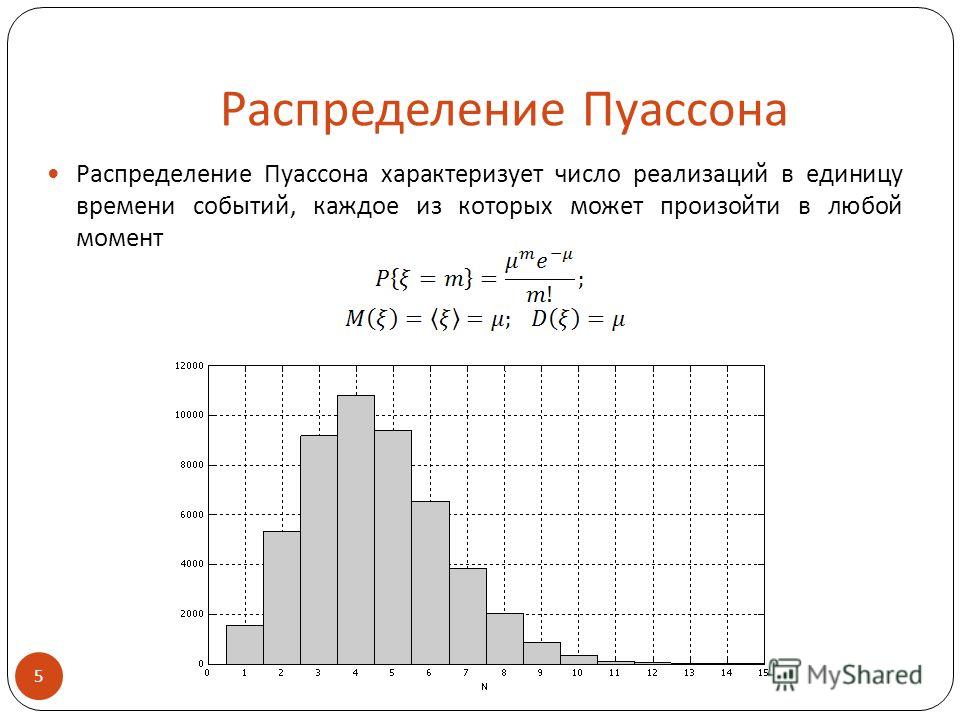 Он используется для нахождения вероятности независимого события, которое происходит в фиксированный интервал времени и имеет постоянную среднюю скорость. Функция массы вероятности распределения Пуассона также может использоваться в других фиксированных интервалах, таких как объем, площадь, расстояние и т. Д. Случайная величина Пуассона будет относительно описывать явление, если во многих испытаниях было мало успехов. Распределение Пуассона используется как предельный случай биномиального распределения, когда количество испытаний неограниченно велико. Если распределение Пуассона моделирует то же биномиальное явление, λ заменяется на np. Распределение Пуассона названо в честь французского математика Дени Пуассона.

1.	Что такое распределение Пуассона?
2.	Формула распределения Пуассона
3.	Свойства распределения Пуассона
4.	Таблица распределения Пуассона
5.	Применение распределения Пуассона
6.	Часто задаваемые вопросы о распределении Пуассона

Что такое распределение Пуассона?

Определение распределения Пуассона используется для моделирования дискретной вероятности события, когда независимые события происходят через фиксированный интервал времени и имеют известную постоянную среднюю скорость. Другими словами, распределение Пуассона используется для оценки того, сколько раз событие может произойти в течение заданного периода времени. λ — параметр скорости Пуассона, указывающий ожидаемое значение среднего числа событий в фиксированном временном интервале. Распределение Пуассона широко используется как в бизнесе, так и в биологии.

Давайте попробуем понять это на примере, центр обслуживания клиентов получает 100 звонков в час, 8 часов в день. Как мы видим, вызовы не зависят друг от друга. Вероятность числа вызовов в минуту имеет распределение вероятности Пуассона. В минуту может быть любое количество вызовов, независимо от количества вызовов, полученных в предыдущую минуту. Ниже приведена кривая вероятностей для фиксированного значения λ функции, следующей распределению Пуассона:

Если нам нужно найти вероятность того, что в час может быть получено более 150 звонков, колл-центр мог бы улучшить свои стандарты обслуживания клиентов, используя больше услуг и удовлетворяя потребности своих клиентов, основываясь на понимании Распределение Пуассона.

Формула распределения Пуассона

Формула распределения Пуассона используется для определения вероятности события, которое происходит независимо, дискретно в течение фиксированного периода времени, когда средняя скорость возникновения постоянна во времени. Формула распределения Пуассона применяется, когда существует большое количество возможных исходов. Для случайной дискретной переменной X, которая следует распределению Пуассона, а λ — это средняя норма ценности, тогда вероятность x определяется как:
f(x) = P(X=x) = (e ^-λ λ ^x )/x!

Где

• х = 0, 1, 2, 3. ..
• e — число Эйлера (e = 2,718)
• λ — средняя скорость ожидаемого значения, а λ = дисперсия, также λ>0

Среднее значение и дисперсия распределения Пуассона

Для распределения Пуассона, в котором λ является средней скоростью, для фиксированного интервала времени среднее значение распределения Пуассона и значение дисперсии будут одинаковыми. Таким образом, для X, следующего за распределением Пуассона, мы можем сказать, что λ является средним значением, а также дисперсией распределения.

Отсюда: E(X) = V(X) = λ

где

• E(X) — ожидаемое среднее значение
• V(X) это дисперсия
• λ > 0

Свойства распределения Пуассона

Распределение Пуассона применимо к событиям, которые имеют большое количество редких и независимых возможных событий. Ниже приведены свойства распределения Пуассона. В распределении Пуассона

• События независимы.
• Может произойти среднее количество успехов только за указанный период времени. Два события не могут произойти одновременно.
• Распределение Пуассона ограничено, когда число испытаний n неопределенно велико.
• среднее = дисперсия = λ
• np = λ конечно, где λ постоянно.
• Стандартное отклонение всегда равно квадратному корню из среднего значения μ.
• Точная вероятность того, что случайная величина X со средним значением μ = a определяется выражением P(X = a) = μ ^а / а! е ^-мк
• Если среднее значение велико, то распределение Пуассона приблизительно является нормальным распределением.

Таблица распределения Пуассона

Подобно биномиальному распределению, мы можем иметь таблицу распределения Пуассона, которая поможет нам быстро найти функцию массы вероятности события, которое соответствует распределению Пуассона. Таблица распределения Пуассона показывает разные значения распределения Пуассона для различных значений λ, где λ>0. Здесь, в приведенной ниже таблице, мы видим, что для P(X = 0) и λ = 0,5 значение функции массы вероятности составляет 0,6065 или 60,65%.

Применение распределения Пуассона

Существуют различные приложения распределения Пуассона. Случайные величины, которые следуют распределению Пуассона, следующие:

• Для подсчета количества дефектов готового продукта
• Для подсчета количества умерших в стране от любой болезни или стихийного бедствия
• Для подсчета количества зараженных растений в поле
• Для подсчета количества бактерий в организмах или радиоактивного распада атомов
• Для расчета времени ожидания между событиями.

Важные примечания

• Формула распределения Пуассона: f(x) = P(X=x) = (e ^-λ λ ^x )/x!.
• Для распределения Пуассона λ всегда больше 0.
• Для распределения Пуассона среднее значение и дисперсия распределения равны.

☛

Также проверьте:

• Распределитель Пуассона Формула
• Вероятность
• Данные
• Дискретные данные

Часто задаваемые вопросы о распределении Пуассона

Что такое распределение Пуассона?

Определение распределения Пуассона гласит, что это дискретная вероятность события, при котором независимые события происходят в фиксированном интервале времени и имеют известную постоянную среднюю скорость.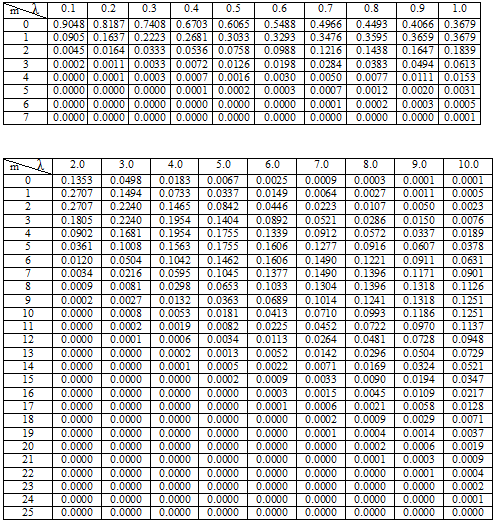 Другими словами, для фиксированного интервала времени можно использовать распределение Пуассона для измерения вероятности возникновения события. Распределение Пуассона широко используется как в бизнесе, так и в биологии.

Что такое лямбда в распределении Пуассона?

В распределении Пуассона лямбда — это средняя скорость значения функции. Его также называют средним значением распределения Пуассона. Для распределения Пуассона дисперсия также совпадает со средним значением функции, поэтому лямбда также является дисперсией функции, следующей за распределением Пуассона.

Каковы характеристики распределения Пуассона?

Основной характеристикой распределения Пуассона является то, что это дискретная вероятность события. События в распределении Пуассона независимы. Возникновение событий определяется в течение фиксированного интервала времени. Значение лямбда всегда больше 0 для распределения Пуассона.

В чем разница между распределением Пуассона и биномиальным распределением?

Для распределения Пуассона размер выборки неизвестен, но для биномиального распределения размер выборки фиксирован.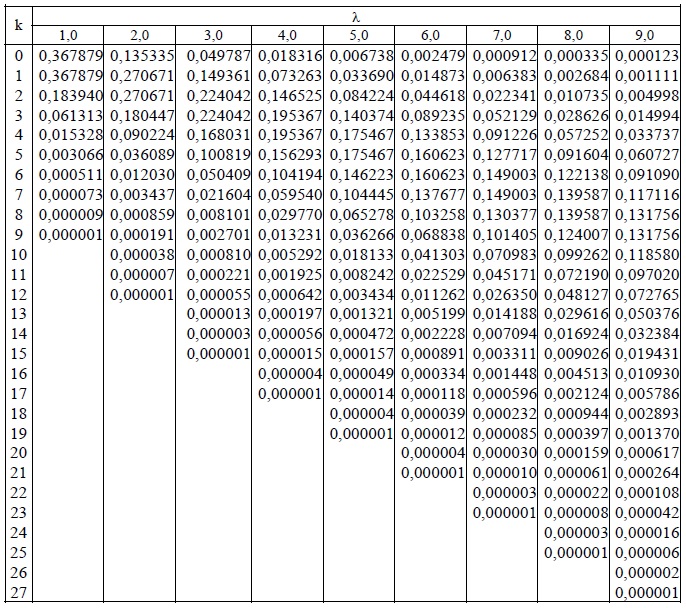 Распределение Пуассона может иметь любое значение размера выборки и всегда больше 0, тогда как биномиальное распределение имеет фиксированный набор значений размера выборки.

Как рассчитать распределение Пуассона?

Распределение Пуассона рассчитывается по формуле распределения Пуассона. Формула вероятности функции, подчиняющейся распределению Пуассона: f(x) = P(X=x) = (e ^-λ λ ^x )/x!

Где

• х = 0, 1, 2, 3…
• e — число Эйлера
.
• λ — средняя скорость значения и дисперсии, также λ>0

Где мы используем распределение Пуассона?

Распределение Пуассона используется во многих областях. Он имеет широкое применение в сфере бизнеса. Бизнесмены используют его, чтобы предсказать будущее бизнеса, рост и упадок бизнеса. Распределение Пуассона используется в биологии, особенно для оценки количества потомков в мутации через фиксированный период времени.

Распределение Пуассона

Распределение Пуассона — это дискретное распределение вероятностей, которое описывает вероятность того, что независимое событие произойдет определенное количество раз в течение фиксированного интервала времени, расстояния, площади или объема и т. д.

Например, конкретный красный свет может включаться в среднем 2000 раз в месяц. Каждое событие независимо, потому что человек, проехавший на красный свет, не влияет на то, когда следующий человек проедет на красный свет. В часы пик в течение заданного промежутка времени будет работать больше красных светофоров, чем в непиковые часы. Количество включений красного света в течение каждой минуты имеет распределение Пуассона.

Распределение Пуассона имеет следующую функцию массы вероятности (pmf):

, где λ — ожидаемое значение случайной величины, X, а e ≈ 2,718 — число Эйлера. PMF распределения Пуассона можно использовать только для определения вероятностей, связанных со случайной величиной, при следующих условиях:

• Случайная величина X является дискретной случайной величиной, а не непрерывной случайной величиной.
• Ожидаемое значение равно дисперсии, или λ = σ ² , λ > 0,
• События независимы друг от друга; появление одного события не влияет на вероятность появления другого.
• События взаимоисключающие; они не могут происходить одновременно.
• Предполагается, что средняя скорость, с которой происходят события, постоянна; скорость не зависит от какого-либо отдельного случая.

Если вышеизложенное верно, то X является случайной величиной Пуассона и имеет распределение Пуассона. Затем связанные вероятности можно найти, оценив плотность плотности распределения Пуассона на желаемом интервале или используя кумулятивные таблицы распределения Пуассона.

Пример

Данный светофор включается в среднем 5 раз в месяц.

1. Найдите вероятность того, что в любой месяц свет загорится 8 раз.
2. Найти вероятность того, что в любой месяц свет будет включаться не менее 3 раз.

я. λ = 5 и x = 8, поэтому:

Таким образом, существует примерно 6,5%-ная вероятность того, что свет будет включаться 8 раз в любой заданный месяц.

ii. Вероятность того, что свет включится не менее 3 раз, можно определить как 1 — P(X ≤ 2):

Таким образом, существует около 88% вероятности того, что свет будет включаться по крайней мере 3 раза в любой месяц.