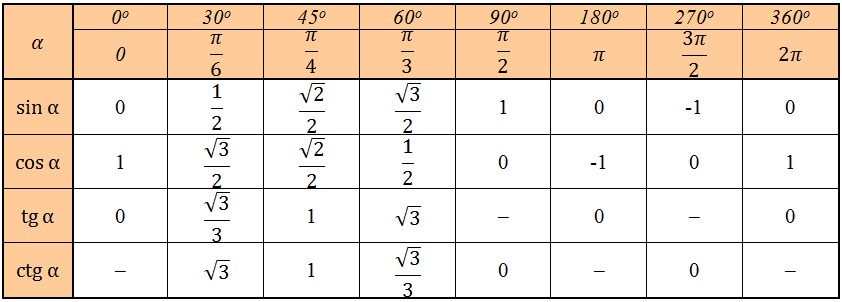
| ТАБЛИЦА ЗНАЧЕНИЙ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Таблица значений тригонометрических функций составлена для углов в 0, 30, 45, 60, 90, 180, 270 и 360 градусов и соответствующих им значений углов врадианах. Из тригонометрических функций в таблице приведены синус, косинус, тангенс, котангенс, секанс и косеканс. Для удобства решения школьных примеров значения тригонометрических функций в таблице записаны в виде дроби с сохранением знаков извлечения корня квадратного из чисел, что очень часто помогает сокращать сложные математические выражения. Для тангенса и котангенса значения некоторых углов не могут быть определены. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций стоит прочерк. Принято считать, что тангенс и котангенс таких углов равняется бесконечности. На отдельной странице находятся формулы приведения тригонометрических функций. В таблице значений для тригонометрической функции синус приведены значения для следующих углов: sin 0, sin 30, sin 45, sin 60, sin 90, sin 180, sin 270, sin 360 в градусной мере, что соответствует sin 0 пи, sin пи/6, sin пи/4, sin пи/3, sin пи/2, sin пи, sin 3 пи/2, sin 2 пи в радианной мере углов. В таблице значений тригонометрических функций нестандартных углов приводятся значения синуса, косинуса, тангенса и котангенса для углов в градусах 15, 18, 22,5, 36, 54, 67,5 72 градусов и в радианах пи/12, пи/10, пи/8, пи/5, 3пи/8, 2пи/5 радиан. Значения тригонометрических функций выражены через дроби и корни квадратные для упрощения сокращения дробей в школьных примерах. | |||
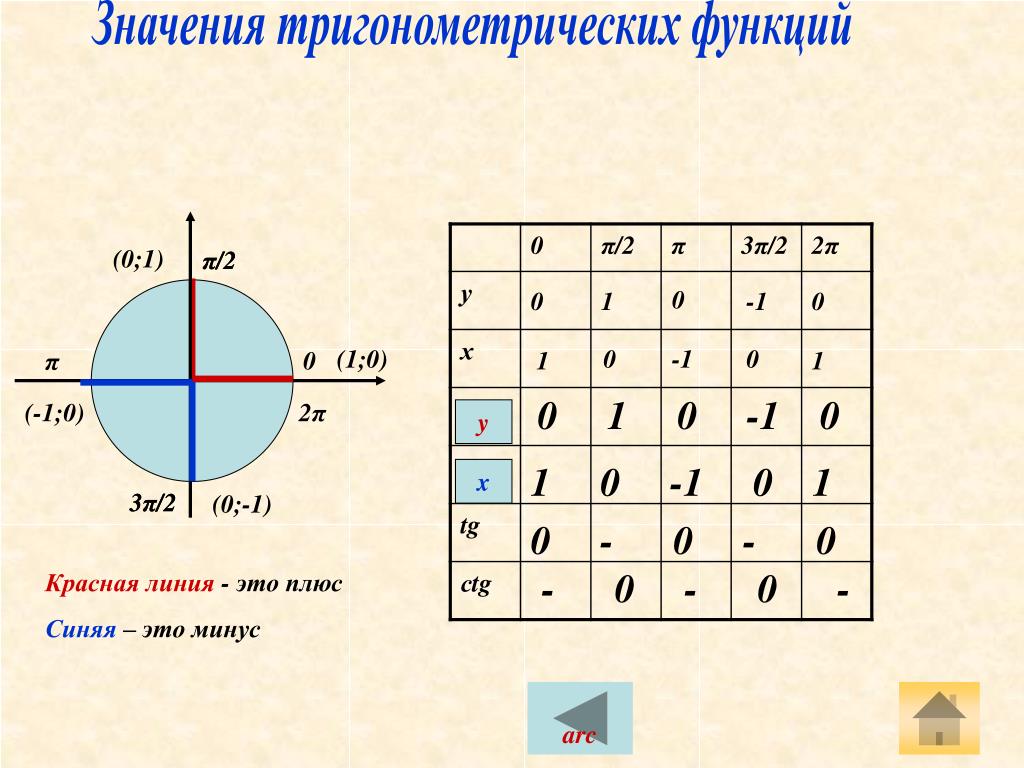
| Вопросы для проверки Определите знаки тригонометрических функций в зависимости от того, в какой четверти находится аргумент | Программа зачета 9 м класса по алгебре и началам математического анализа Определение тригонометрических функций. Основное тригонометрическое тождество. Следствия из него | ||
| Программа коллоквиума по теории пределов, дифференциальному исчислению… Понятие функции (отображения). Область определения функции и множество её значений. График функции. Способы задания функции | Что такое отношение, кортеж, атрибут? Содержит ли какую-либо информацию таблица, в которой нет полей? Может ли существовать такая таблица? | ||
| Лабораторная работа №6 Категория финансовых функций Excel обеспечивает расчет различных параметров при решении задач учета амортизации активов. 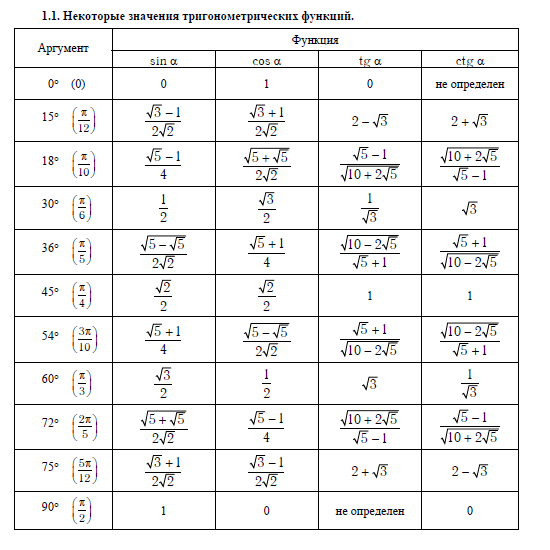 Перечень… Перечень… | Тригонометрия формулы решения простейших тригонометрических уравнений | ||
| Функции нескольких переменных При рассмотрении функций нескольких переменных ограничимся подробным описанием функций двух переменных, т к все полученные результаты… | Таблица цен на тарифные планы для организаций Вашему вниманию представлена таблица тарифных планов, которая состоит из 3 основных тарифов: Экономный, Средний и Оптимальный. Тарифы… | ||
| Система, объект, взаимодействие объектов, основные свойства системы Закон поведения системы- функция, связывающая изменения выходных значений потоков от выходных значений. Целевая ф-ия системы и ограничения-… | Вопросы к государственному экзамену для студентов Предел и непрерывность функций одной и нескольких переменных. Свойства функций, непрерывных на отрезке |
Значения тригонометрических функций основных углов
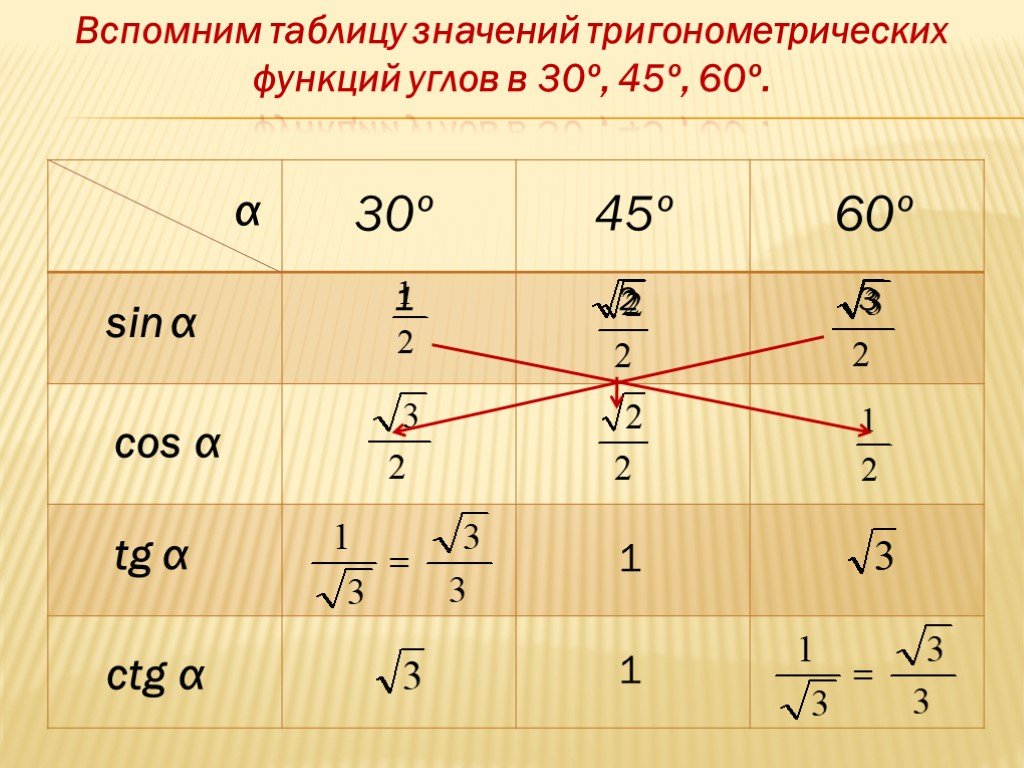
Найдём значения тригонометрических функций для углов в 30°, 45° и 60°. 2}{4}} = \frac{c\sqrt2}{2}\), одновременно и \(AC = \frac{c\sqrt2}{2}\)
2}{4}} = \frac{c\sqrt2}{2}\), одновременно и \(AC = \frac{c\sqrt2}{2}\)
sin 45° = \( \frac{BC}{AB} = \frac{\frac{c\sqrt2}{2}}{c} = \frac{\sqrt2}{2} \approx 0,7071 \)
tg 45°= \( \frac{BC}{AC} = 1 \)
cos 45°= \( \frac{BC}{AB} = \frac{\sqrt2}{2} \approx 0,7071 \)
3) Для угла в 60°
Значения тригонометрических функций для угла в 60° можно найти из того же треугольника, из которого нашли значения тригонометрических функций для угла в 30°, так как если ∠A = 30°, то ∠В = 60°.
Тогда
sin 60° = \( \frac{AC}{AB} = \frac{\sqrt3}{2} \approx 0,8660 \)
tg 60° = \( \frac{AC}{BC} = \sqrt3 \approx 1,7321 \)
cos 60° = \( \frac{BC}{AB} = \frac{1}{2} = 0,5\)
Таблица значений тригонометрических функций для углов в 30°, 45° и 60°.
|
УГОЛ |
СИНУС |
КОСИНУС |
ТАНГЕНС |
|
30о |
\( \frac{1}{2}=0,5 \) |
\( \frac{\sqrt3}{2}\approx 0,8660 \) |
\( \frac{\sqrt3}{3}\approx 0,5774 \) |
|
45о |
\( \frac{\sqrt2}{2}\approx 0,7071 \) |
\( \frac{\sqrt2}{2}\approx 0,7071 \) |
1 |
|
60о |
\( \frac{\sqrt3}{2}\approx 0,8660 \) |
\( \frac{1}{2}=0,5 \) |
\( \sqrt3 \approx 1,7321 \) |
Рассматривая эту таблицу, можно заметить, что синус и тангенс острого угла возрастают при увеличении угла, а косинус при увеличении угла убывает.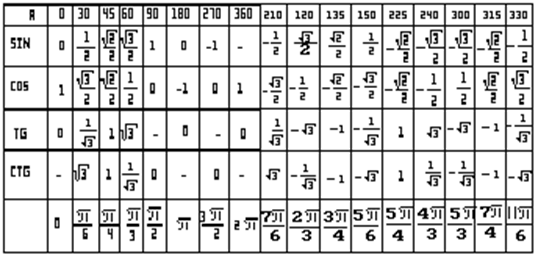
При уменьшении угла синус и тангенс убывают, а кoсинус возрастает.
Дополнительными углами называются два угла, которые в сумме составляют 90°. Такими углами, в частности, являются острые углы прямоугольного треугольника.
Углы А и В в прямоугольном треугольнике ACB являются дополнительными углами, так как
∠A + ∠B = 90°; ∠A = 90° — ∠B; ∠В = 90° — ∠A
Рассмотрим соотношения между тригонометрическими функциями дополнительных углов.
1) \( sinA = \frac{a}{c}; cosB = \frac{a}{c} \), т. e. синус данного угла равен косинусу дополнительного угла.
2) \( cosA = \frac{b}{c}; sinB = \frac{b}{c} \), т.е. косинус данного угла равен синусу дополнительного угла.
3) \( tgA = \frac{a}{b}; ctgB = \frac{a}{b} \), т.е. тангенс данного угла равен котангенсу дополнительного угла.
4) \( ctgA = \frac{b}{a}; tgB = \frac{b}{a} \), т.e. котангенс данного угла равен тангенсу дополнительного угла.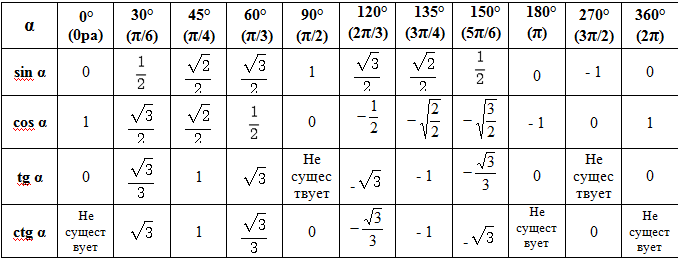
Знание соотношений между тригонометрическими функциями дополнительных углов важно для понимания устройства тригонометрических таблиц.
9.2: Графики тригонометрических функций — Математика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 41324
- Ричард В. Беверидж
- Общественный колледж Клэтсопа 9{\circ} .\)
Ниже мы видим график этих точек, нанесенных на оси координат.
При построении графика тригонометрических функций мы обычно используем радианы по оси \(x\), поэтому график обычно выглядит следующим образом:
График стандартного синуса начинается в нулевой точке, затем увеличивается до максимального значения 1 между 0 и \(\frac{7}{3}\) радиан.
 Затем он снова уменьшается до 0 при
Затем он снова уменьшается до 0 при
максимумГрафики синуса и косинуса иногда называют «синусоидой» или «синусоидой», и они могут быть очень полезны при моделировании явлений, происходящих в волнах. . Примерами этого являются приливы и отливы; звуковые волны и музыка; электричество; и продолжительность дня в течение года. Стандартные графики синусов и косинусов должны быть изменены, чтобы соответствовать конкретному приложению, чтобы они эффективно моделировали ситуацию. Идеи, которые мы рассмотрим далее, объяснят, как модифицировать графики синуса и косинуса, чтобы они соответствовали множеству различных ситуаций.

Существует четыре аспекта функций синуса и косинуса, которые следует учитывать при построении графика. Это:
1) Амплитуда графика
2) Период графика
3) Вертикальный сдвиг графика
4) Фазовый сдвиг графика
Амплитуда
Амплитуда функции синуса или косинуса относится к максимальное и минимальное значения функции. На стандартных графиках синуса и косинуса максимальное значение равно 1, а минимальное значение равно \(-1 .\). Амплитуда составляет половину разницы между максимальным и минимальным значениями. На стандартных графиках разница между максимумом и минимумом равна \(1-(-1)=2 ;\) половина от этого равна 1, поэтому амплитуда стандартных функций синуса и косинуса равна \(1 .\)Значение амплитуды также является абсолютным значением коэффициента синуса или косинуса. На стандартном графике \(y=\sin x,\) коэффициент синусоидальной функции равен \(1,\), поэтому амплитуда равна \(1 .\) В функции \(y=2 \sin x, \) все значения \(y\) будут умножены на 2, а амплитуда функции будет равна \(2 .

Отрицательное значение коэффициента перед тригонометрической функцией не изменит амплитуду функции, но изменит форму функции. Например, функция:
имеет амплитуду \(1,\), но график будет отличаться от графика \(y=\sin x\) Все \(y\) -значения функции \(y=-\sin x \) будет иметь противоположный знак, поскольку \(y\) -значения функции \(y=\sin x .\) График для \(y=-\sin x\) показан ниже:
Обратите внимание, что из-за отрицания \(y\) -значений график начинается с \(0,\), как и стандартная функция синуса, но график \(y=-\sin x\) сначала идет к минимуму значение перед повторным пересечением через 0 до максимального значения.Аналогично, график \(y=-\cos x\) начинается с минимального значения, затем переходит через 0 и достигает максимального значения, возвращается обратно через 0 и снова заканчивается минимальным значением.
Период
Период графика показывает, сколько времени требуется графику для завершения одного полного цикла значений. В стандартных функциях синуса и косинуса период равен \(2 \pi\) радианам. Функция завершает одну «волну» и возвращается в исходное положение между 0 и \(2 \pi .\). Коэффициент перед переменной в функции синуса или косинуса будет влиять на период графика. В общем выражении \(y=A\sinBx,\) значение \(A\) влияет на амплитуду функции, а значение \(B\) влияет на период функции.
В стандартных функциях синуса и косинуса период равен \(2 \pi\) радианам. Функция завершает одну «волну» и возвращается в исходное положение между 0 и \(2 \pi .\). Коэффициент перед переменной в функции синуса или косинуса будет влиять на период графика. В общем выражении \(y=A\sinBx,\) значение \(A\) влияет на амплитуду функции, а значение \(B\) влияет на период функции.Если мы рассмотрим таблицу значений стандартного синуса, то увидим, как коэффициент при переменной \(x\) повлияет на период графика. Начиная с таблицы из стандартной функции синуса:
Если мы создадим аналогичную таблицу для функции \(y=\sin(2 x),\), то мы увидим, как это повлияет на график:
В предыдущей таблице мы видим, что функция \(y=\sin (2 x)\) завершает один полный цикл между 0 и \(\pi\) радианами вместо стандартного от 0 до \(2 \ pi\) радиан. График для этих точек показан ниже. Координаты для \(x\) -значений между 9Также показаны 0046 \(\pi\) и \(2 \pi\) радиан.

На этом графике видно две полные волны между 0 и \(2 \pi\) радиан или одна полная волна между 0 и \(\pi\) радиан. Итак, в функции синуса или косинуса вида \(y=A \sin B x,\) амплитуда будет \(|A|\), а период будет \(\frac{2 \pi}{b } .\) Стандартный график для одного полного цикла функции \(y=\sin (2 x)\) показан ниже:
Обратите внимание, что, поскольку период был сокращен вдвое, \(x\) -координаты, соответствующие максимуму, минимуму и нулю \(y\) -координаты сокращаются вдвое какПример 1
9{\circ}\) или \(2 \pi\) радиан. Эти \(x\) -значения производят «критические» y-значения нуля, максимума и минимума.
График одного полного периода функции \(y=-2 \sin 3 x\)
Амплитуда в этом случае равна \(2,\), но поскольку коэффициент отрицателен, этот график синуса будет начинаться с сначала идет к минимальному значению. Период графика будет равен \(\frac{2 \pi}{B},\) или в данном случае \(\frac{2 \pi}{3}\) вместо \(2 \pi .\) Чтобы определить \(х\) -значения для максимального, минимального и нулевого \(у\) -значения, мы должны изучить, как они определяются для стандартной синусоиды.
В стандартном синусоидальном или косинусоидальном графике расстояние от каждого «критического значения» графика
до следующего всегда представляет собой «скачок» на \(\frac{\pi}{2}\) вдоль \(х\) -ось. Это четверть периода: \(\frac{2 \pi}{1} * \frac{1}{4}=\frac{\pi}{2} .\) Таким образом, чтобы определить метки для критические значения графика по оси \(x\), следует взять новый период и умножить на \(\frac{1}{4}\)
Функция, с которой мы работаем, это \(y=-2 \sin 3 x,\), поэтому, чтобы найти новый период, мы вычислили \(\frac{2 \pi}{B},\), который был \(\ frac{2 \pi}{3} .\) Затем, чтобы правильно пометить ось \(x\), мы должны взять \(\frac{2 \pi}{3}\) и умножить на \( \фракция{1}{4}\)
\[ \frac{2 \pi}{3} * \frac{1}{4}=\frac{2 \pi}{12}=\frac{2 \pi}{6}
\] Итак, критические значения по оси \(x\) будут:
\[ \frac{1 \pi}{6}, \frac{2 \pi}{6}, \frac{3 \pi}{6}, \text { и } \frac{4 \pi}{6}
\] Мы хотим выразить их в наименьших терминах, поэтому обозначим их как \(\frac{\pi}{6}, \frac{\pi}{3}, \frac{\pi}{2},\) и \(\frac{2 \pi}{3} . \) График начнется с нуля, затем (поскольку значение коэффициента \(A\) отрицательно) он опустится до минимального значения при \(\ frac{\pi}{6},\) обратно к нулю в точке \(\frac{\pi}{3},\), затем до максимума в точке \(\frac{\pi}{2}\) и обратно до нуля в \(\frac{2 \pi}{3}\), чтобы завершить один полный период графика. График этой функции показан ниже. Обратите внимание, что минимальное значение y равно -2, а максимальное значение \(y\) равно 2, потому что \(A=2\)
\) График начнется с нуля, затем (поскольку значение коэффициента \(A\) отрицательно) он опустится до минимального значения при \(\ frac{\pi}{6},\) обратно к нулю в точке \(\frac{\pi}{3},\), затем до максимума в точке \(\frac{\pi}{2}\) и обратно до нуля в \(\frac{2 \pi}{3}\), чтобы завершить один полный период графика. График этой функции показан ниже. Обратите внимание, что минимальное значение y равно -2, а максимальное значение \(y\) равно 2, потому что \(A=2\)
Давайте рассмотрим пример с косинусоидальным графиком.Пример 2
График одного полного периода функции \(y=5 \cos \frac{2}{3} x\)
Амплитуда функции равна 5, так как \(A=5,\), поэтому максимум значение y будет равно 5, а минимальное значение \(y\) будет равно \(-5 .\). Период графика будет равен \(\frac{2 \pi}{B}\), что в данном случае равно \(\frac{2 \pi}{7}=2 \pi * \frac{3}{2}=3 \pi .\) Таким образом, период равен 3 \(\pi .\) Критические значения вдоль \(x\) -ось будет начинаться с 0 и будет разделена «скачками» \(3 \pi * \frac{1}{4}=\frac{3 \pi}{4} .
\[ 0, \frac{3 \pi}{4}, \frac{6 \pi}{4}, \frac{9 \pi}{4}, \text { и } \frac{12 \pi}{4}
\] Мы хотим выразить их в наименьших терминах, чтобы обозначить их как \(\frac{3 \pi}{4}, \frac{3 \pi}{2}, \frac{9 \pi}{4}\) и \(3 \pi .\) График начнется с максимального \(y\) -значения 5 при \(x=0,\), затем он пойдет к нулю при \(x=\frac{3 \ pi}{4},\) до минимального \(y\) -значения -5 в точке \(x=\frac{3 \pi}{2},\) обратно через 0 в точке \(x=\frac {9 \pi}{4},\), а затем до максимального \(y\) -значения 5 при \(x=3 \pi\), чтобы завершить один полный период графика. График \(y=5 \cos \frac{2}{3} x\). показано ниже.Определение уравнения по графику
\) Итак, чтобы написать уравнение для тригонометрической функции, нам нужно определить значения \(A\) и \(B\).
Иногда вам дадут график и попросят определить уравнение, которое удовлетворяет условиям, видимым на графике. До сих пор мы обсудили только два из возможных преобразований тригонометрической функции — амплитуду и период. Помните, что в уравнении вида \(y=A \sin B x\) или \(y=A \cos B x,\) амплитуда равна \(|A|\), а период равен \(\frac {2 \pi}{B} .
Пример 3Определите уравнение, удовлетворяющее данному графику.
Во-первых, обратите внимание, что максимальное значение \(y\) для графика равно 3, а минимальное равно -3. Это означает, что амплитуда равна \(3 .\). Затем мы видим, что существует один полный период функции между 0 и \(\pi\), это означает, что период равен \(\pi\). Из этой информации мы знаем, что \(A=3\) и что период графика равен \(\pi\). Поскольку период \(P=\frac{2 \pi}{B},\), то мы знаем, что \(B=\frac{2 \pi}{P} .\) Итак, \(B=\frac{ 2 \пи}{\пи}=2\)Наконец, этот график начинается с \(y\) -значения \(5,\), которое является максимальным \(y\) -значением. Затем он идет к 0 и вниз к минимуму, обратно через 0, а затем обратно к максимуму, чтобы сформировать одну полную волну. поскольку это сигнатура функции косинуса, ответом на эту задачу будет:
\[ y=5 \cos \frac{8}{9} x
\]Упражнения 2.
 2
2
Определите амплитуду и период для каждой задачи и постройте график одного периода функции. Определите важные точки на осях \(x\) и \(y\).
1. \(y=\cos 4 x\)
2. \(y=-\sin 2 x\)
3. \(y=3 \sin 3 x\)
4. \(y=-2 \cos 5 x\)
5. \(y=4 \cos \frac{1}{2} x\)
6. \(y=2 \sin \frac{1}{3} x\)
7 , \(y=-\frac{1}{2} \sin \frac{2}{3} x\)
8. \(y=-3 \cos \frac{1}{5} x\)
9. \(y=-4 \sin 6 x\)
10. \(y=3 \sin 4 x\)
11. \(\quad y=2 \cos \frac{1}{2} x\ )
12. \(\quad y=3 \cos \frac{1}{3} x\)
Определите уравнение, удовлетворяющее заданному графику.Эта страница под названием 9.2: Графики тригонометрических функций распространяется под лицензией CC BY-NC-SA и была создана, изменена и/или курирована Ричардом В. Бевериджем.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Ричард В.
 Беверидж
Беверидж
- Лицензия
- CC BY-NC-SA
- Включено
- да
- Теги
- источник[1]-math-37214
Значения таблицы тригонометрии | Тригонометрическая таблица
Что такое тригонометрия?
Тригонометрия происходит от греческих слов trigonon («треугольник») и metron («измерять»). Это раздел математики, изучающий отношения между сторонами и углами треугольника. Он связан с прямоугольными треугольниками, где один угол, как известно, всегда равен 90 градусам. Мы изучаем его на уроках математики, задаваясь вопросом, где еще его можно использовать?! Вы были бы удивлены, узнав, что он находит применение в других разделах математики, например, в комплексных числах, бесконечных рядах, логарифмах и исчислении.
 Мы используем принципы тригонометрии в различных других областях.
Мы используем принципы тригонометрии в различных других областях.Тригонометрические отношения — синус, косинус, тангенс
Синус, косинус и тангенс — три основные тригонометрические функции или отношения. Мы знаем их лучше как sin, cos и tan.
Теперь давайте возьмем прямоугольный треугольник, чтобы лучше понять эти функции. Самая длинная сторона — гипотенуза, а противоположные ей стороны — прилежащая и противолежащая стороны.
При изучении тригонометрии помните, что:
- Соприкасающиеся стороны и углы называются смежный, и, таким образом, каждая сторона имеет два смежных угла.
- Стороны и углы, которые не соприкасаются, называются противоположными .
- В прямоугольном треугольнике сторона, противоположная прямому углу, называется гипотенузой , а две оставшиеся стороны называются катетами .
- Если даны два угла или две стороны, то с ними можно работать для измерения остальных деталей.

Единичный круг
Единичный круг — один из наиболее ценных инструментов класса триггеров. Единичный круг — отличный способ вычислить углы cos, sin и tan напрямую, поскольку радиус равен 1. Считайте тета углом.
Длина гипотенузы равна радиусу единичной окружности, который равен 1. Следовательно, мы можем записать тригонометрические отношения как:
Sin θ y/1 = y
Cos θ x/1 = x
Tan θ y/x
Что такое значения тригонометрической таблицы?
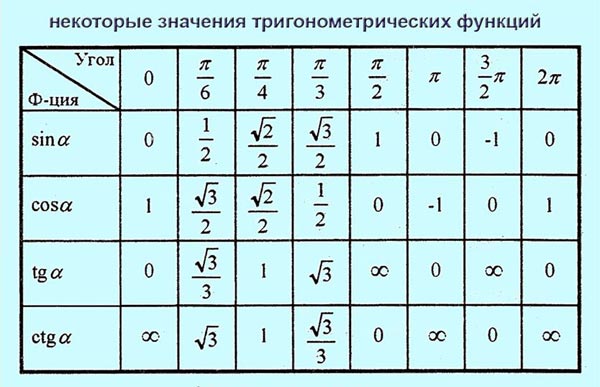
Для определения углов и расстояний разработана таблица значений тригонометрии. Основными функциями в тригонометрии являются синус, косинус и тангенс. Таблица тригонометрических значений помогает найти значения углов, таких как 0°, 30°, 45°, 60° и 9°.0°. Он состоит из тригонометрических соотношений – синуса (sin), косинуса (cos), тангенса (tan), косеканса (cosec), секанса (sec), котангенса (cot).
Как запомнить таблицу тригонометрии?
Таблица отношений тригонометрии зависит от формул тригонометрии.

Ниже приведены несколько шагов для запоминания таблицы тригонометрии.
Прежде чем начать, постарайтесь запомнить приведенные ниже формулы тригонометрии.
- sin x = величина, обратная косекансу = противоположность / гипотенуза
- cos x = обратная секанс = смежная / гипотенуза
- tan x = величина, обратная котангенсу = противоположная / смежная
- cot x = обратная величина касательной = смежная/противоположная
- сек x = величина, обратная косинусу = гипотенуза / смежная
- cosec x = (обратное значение синуса) = гипотенуза / противоположное
Шаги по созданию диаграммы тригонометрической таблицы:
- Шаг 1. Создание таблицы
Создайте таблицу с верхней строкой, в которой перечислены углы, такие как 0°, 30°, 45°, 60°, 90°, и запишите в первый столбец все тригонометрические функции, такие как sin, cos, tan, cosec, sec, cot.
- Шаг 2: Определите значение sin.

- Шаг 3: Определите значение cos.
- Шаг 4: Определите значение тангенса.
- Шаг 5: Определите стоимость детской кроватки.
Значение cot равно обратному значению tan. Значение cot при 0° получится путем деления 1 на значение tan при 0°. Таким образом, значение будет:
детская кроватка 0° = 1/0 = бесконечно или не определено
Таким же образом таблица для детской кроватки приведена ниже.
- Шаг 6: Определите значение cosec.
- Шаг 7: Определите значение сек.
Это углы, через которые могут быть представлены различные тригонометрические функции.
Некоторые стандартные углы, используемые в тригонометрии: 0º, 30º, 45º, 60º, 90º.
Тригонометрические углы могут быть выражены через тригонометрические отношения следующим образом:
- θ = sin-1 (перпендикуляр/гипотенуза)
- θ = cos-1 (основание/гипотенуза)
- θ = tan-1 (Перпендикуляр/Основание)
Учащимся, изучающим математический анализ в средней школе, требуется прочная база по тригонометрии.
 Это потому, что тригонометрические функции часто используются в вопросах. Например, в Calculus тригонометрические функции используются для анализа вращающихся тел .
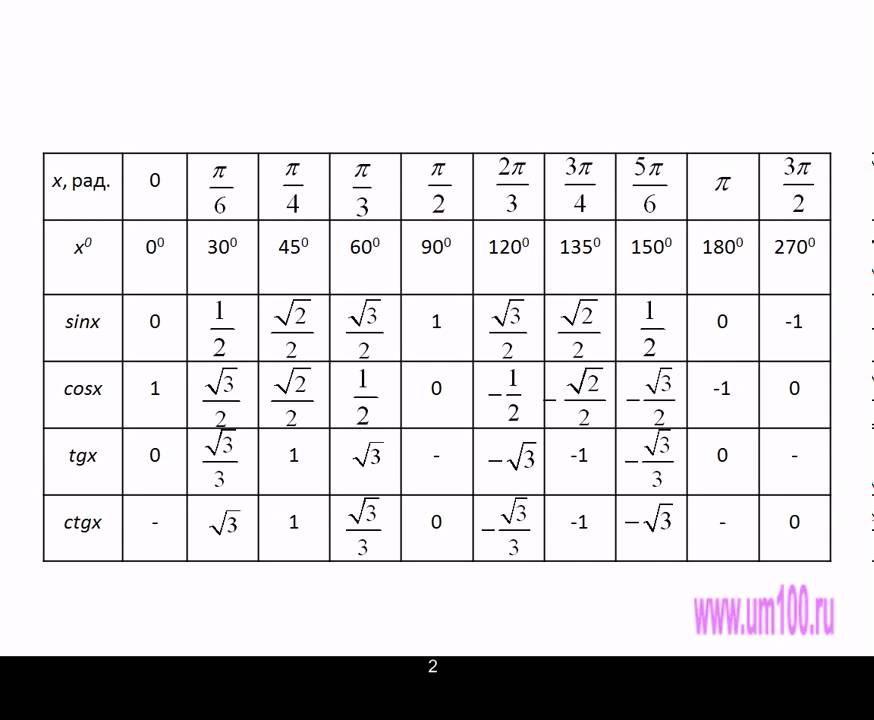
Это потому, что тригонометрические функции часто используются в вопросах. Например, в Calculus тригонометрические функции используются для анализа вращающихся тел .Кроме того, в курсе математики почти все делается в радианах. В следующей таблице приведены некоторые основные углы как в градусах, так и в радианах.
Degree 0 30 45 60 90 180 270 360 Radians 0 π/6 π /4 π/3 π/2 π 3π/2 2π Вы можете обратиться к следующему для дополнительного чтения:
Тригонометрия
Тригонометрические хитрости
Чтобы узнать об эффективных стратегиях, которые сделают вас ниндзя в математике, читайте наш блог
2 в математике ?
Тригонометрия и ее приложенияКонечно, овладение тригонометрией открывает двери для профессии учителя и исследовательской работы, требующей ее знаний.
 Но помните, как было сказано выше, о других областях, на которые сегодня влияет это понятие? Ну …..
Но помните, как было сказано выше, о других областях, на которые сегодня влияет это понятие? Ну …..Калькулятор тригонометрических функций используется для изменения волновых моделей в звуках музыкальной индустрии. Музыкальные продюсеры и звукорежиссеры используют его для создания музыки, которая нравится слушателям. Кто бы мог подумать!
Кроме того, архитекторы используют тригонометрию при возведении зданий, чтобы создать иллюзию изогнутых поверхностей конструкций. Он находит свое применение в сейсмостойких зданиях за счет улучшения конструкции и элементов.
В фильмах показана тригонометрия при запуске ракет и размещении спутников в требуемом положении в космосе. Несомненно, для расчета их скоростей используется тригонометрия, которая должна быть точной, чтобы избежать несчастных случаев.
И не забывайте, индустрия видеоигр работает благодаря тригонометрии. Интересно, как? Он используется для установки препятствий, других структур, которые появляются на вашем экране, и расчета пути всего, что брошено или запущено в игре игроком из любой точки игры.
 Так что ботаники правят везде!!
Так что ботаники правят везде!!Часто задаваемые вопросы по тригонометрии
W Кто нашел тригонометрию?
В современном виде тригонометрия была создана греческим астрономом Гиппархом. Он первым построил таблицу значений тригонометрической функции.
Что такое тригонометрия?
Тригонометрия происходит от греческих слов trigonon («треугольник») и metron («измерять»). Это раздел математики, изучающий взаимосвязь между сторонами и углами. Он ассоциируется с прямоугольными треугольниками, где один угол, как известно, всегда равен 90 градусам. Мгновенно привлекают посетителей.
Сколько существует тригонометрических соотношений?
Существует шесть тригонометрических соотношений.
Шесть тригонометрических отношений : синус (sin), косинус (cos), тангенс (tan), котангенс (cot), косеканс (cosec) и секанс (sec).
Тригонометрия проста?
Обязательно! Тригонометрия является неотъемлемой частью математики.
 Он касается соотношения между сторонами и углами треугольников. Вы можете быстро овладеть им, если подойдете к нему правильно. Если у вас возникнут какие-либо трудности с этим, не стесняйтесь обращаться к нам
Он касается соотношения между сторонами и углами треугольников. Вы можете быстро овладеть им, если подойдете к нему правильно. Если у вас возникнут какие-либо трудности с этим, не стесняйтесь обращаться к намКаковы основные функции тригонометрии?
Существуют три основные функции тригонометрии: функция синуса, функция косинуса и функция тангенса.
Есть ли короткий способ запомнить значения таблицы тригонометрии?
Наиболее часто используемая аббревиатура для запоминания этих соотношений — SOHCAHTOA, что означает «Синус, противоположный гипотенузе, Косинус, смежный с гипотенузой, Тангенс, противоположный смежному».
Почему важна тригонометрия?
Тригонометрия больше не ограничивается использованием в классе. Вы будете поражены, узнав, что:
- Архитекторы используют тригонометрию при возведении зданий, чтобы создать иллюзию изогнутых поверхностей на конструкциях.
- Музыкальные продюсеры и звукорежиссеры используют его для создания музыки, которая нравится слушателям.

- Он используется для установки препятствий, других структур, которые появляются на вашем экране, и расчета пути всего, что брошено или запущено в видеоигре.
Нужно ли мне хорошее знание тригонометрии, чтобы преуспеть в математике?
Да. Прочная основа тригонометрии помогает мне понимать и выполнять вычисления в классе исчисления. Это потому, что тригонометрические функции часто используются в вопросах. Например, в исчислении тригонометрические функции используются для анализа вращающихся тел.
Как я могу преуспеть в математике?
Действительно, математика вызывает беспокойство у многих учащихся. Но все, что вам нужно сделать, это следовать приведенным ниже советам, и вы сможете легко понять математику и получить по ней высокие баллы.
- Сосредоточьтесь на слабых местах, которые требуют более тяжелой работы.
- Не отвлекайтесь и всегда держите свои гаджеты и телефон подальше во время учебы.

- Откройте для себя математику в уме, так как она делает математику увлекательной и упрощает расчеты.
Получите помощь от способных и опытных наставников Edulyte .
Почему мне важно записаться на курсы по математике?
Основы преподаваемой математики являются основой вашего образования в колледже и будущего. Поэтому очень важно получить правильное руководство и хорошо усвоить знания. Просмотрите наши списки репетиторов и их курсы. Найдите тот, который соответствует вашим требованиям, и убедитесь в хорошем результате!
Будет ли онлайн-урок математики таким же эффективным, как очное обучение?
Конечно. Онлайн-сессии экономят время и обеспечивают большую гибкость. Вы можете легко сосредоточиться на учебе, не беспокоясь ни о чем другом.
Похожие блоги
Математика
By Geet 12 февраля 2021 г. 0
Лишь немногие освоили математику и оказались среди великих математиков.


 Школьная таблица синусов.
Школьная таблица синусов. 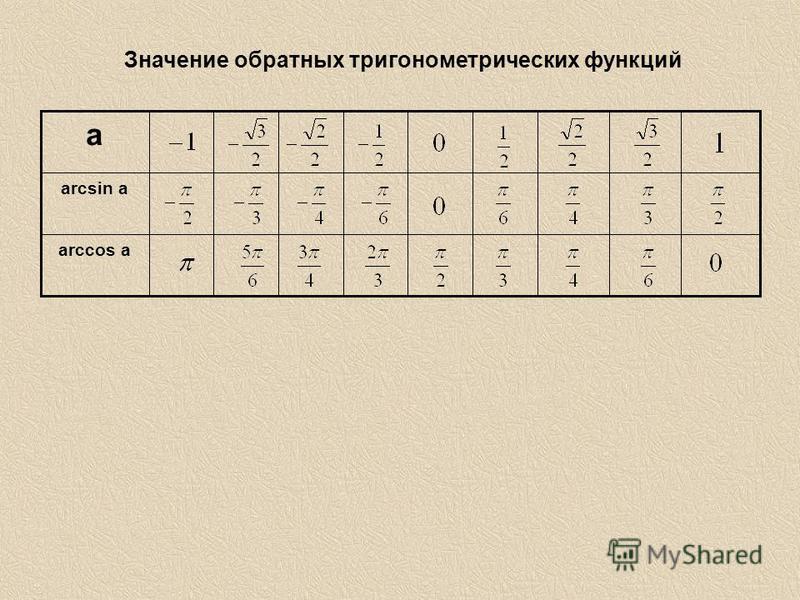 Следующие значения тригонометрических функций котангенса не определены ctg 0, ctg 180, ctg 360, ctg 0 пи, ctg пи, ctg 2 пи и считаются равными бесконечности.
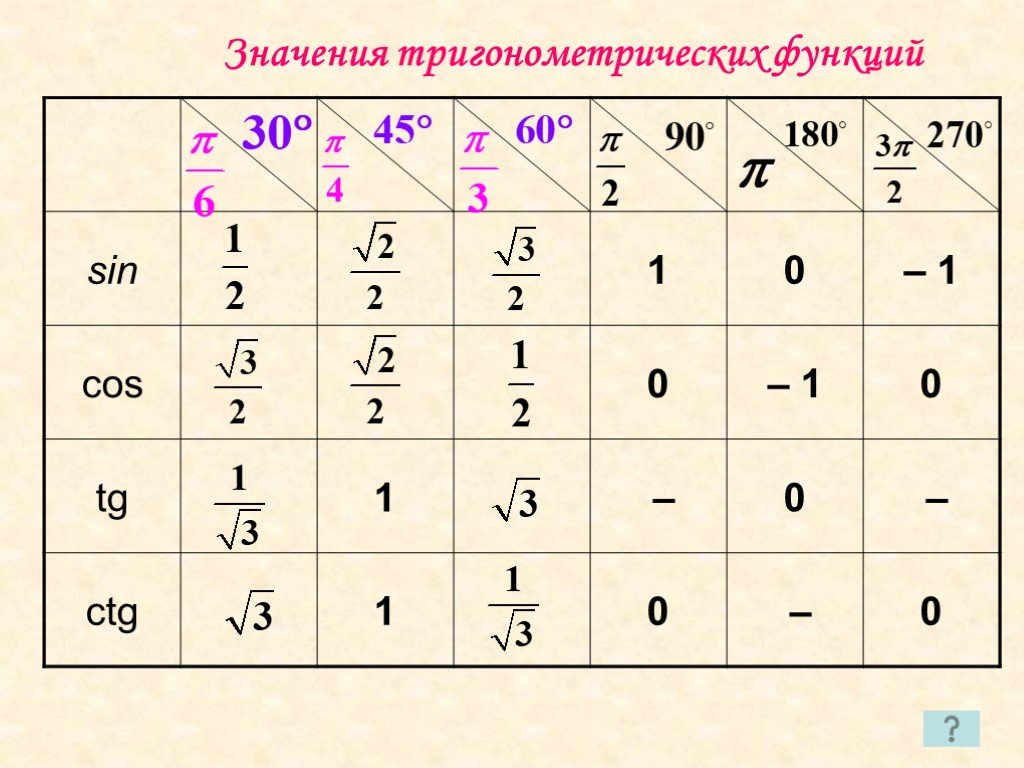
Следующие значения тригонометрических функций котангенса не определены ctg 0, ctg 180, ctg 360, ctg 0 пи, ctg пи, ctg 2 пи и считаются равными бесконечности.  Специально для блондинок значения косинуса подчеркнуты зелененькой черточкой,чтоб меньше путаться. Так же очень наглядно представлен перевод градусов в радианы, когда радианы выражены через пи.
Специально для блондинок значения косинуса подчеркнуты зелененькой черточкой,чтоб меньше путаться. Так же очень наглядно представлен перевод градусов в радианы, когда радианы выражены через пи.  Синусы и косинусы меняются местами, точно так же, как тангенс и котангенс. Это связано с симметричностью значений тригонометрических функций.
Синусы и косинусы меняются местами, точно так же, как тангенс и котангенс. Это связано с симметричностью значений тригонометрических функций.  Косинус является четной тригонометрической функцией — значение косинуса для отрицательного угла будет положительным. При умножении и делении тригонометрических функций необходимо соблюдать правила знаков.
Косинус является четной тригонометрической функцией — значение косинуса для отрицательного угла будет положительным. При умножении и делении тригонометрических функций необходимо соблюдать правила знаков. Затем он снова уменьшается до 0 при
Затем он снова уменьшается до 0 при 
 В стандартных функциях синуса и косинуса период равен \(2 \pi\) радианам. Функция завершает одну «волну» и возвращается в исходное положение между 0 и \(2 \pi .\). Коэффициент перед переменной в функции синуса или косинуса будет влиять на период графика. В общем выражении \(y=A\sinBx,\) значение \(A\) влияет на амплитуду функции, а значение \(B\) влияет на период функции.
В стандартных функциях синуса и косинуса период равен \(2 \pi\) радианам. Функция завершает одну «волну» и возвращается в исходное положение между 0 и \(2 \pi .\). Коэффициент перед переменной в функции синуса или косинуса будет влиять на период графика. В общем выражении \(y=A\sinBx,\) значение \(A\) влияет на амплитуду функции, а значение \(B\) влияет на период функции.

 \) График начнется с нуля, затем (поскольку значение коэффициента \(A\) отрицательно) он опустится до минимального значения при \(\ frac{\pi}{6},\) обратно к нулю в точке \(\frac{\pi}{3},\), затем до максимума в точке \(\frac{\pi}{2}\) и обратно до нуля в \(\frac{2 \pi}{3}\), чтобы завершить один полный период графика. График этой функции показан ниже. Обратите внимание, что минимальное значение y равно -2, а максимальное значение \(y\) равно 2, потому что \(A=2\)
\) График начнется с нуля, затем (поскольку значение коэффициента \(A\) отрицательно) он опустится до минимального значения при \(\ frac{\pi}{6},\) обратно к нулю в точке \(\frac{\pi}{3},\), затем до максимума в точке \(\frac{\pi}{2}\) и обратно до нуля в \(\frac{2 \pi}{3}\), чтобы завершить один полный период графика. График этой функции показан ниже. Обратите внимание, что минимальное значение y равно -2, а максимальное значение \(y\) равно 2, потому что \(A=2\) 
 2
2  Беверидж
Беверидж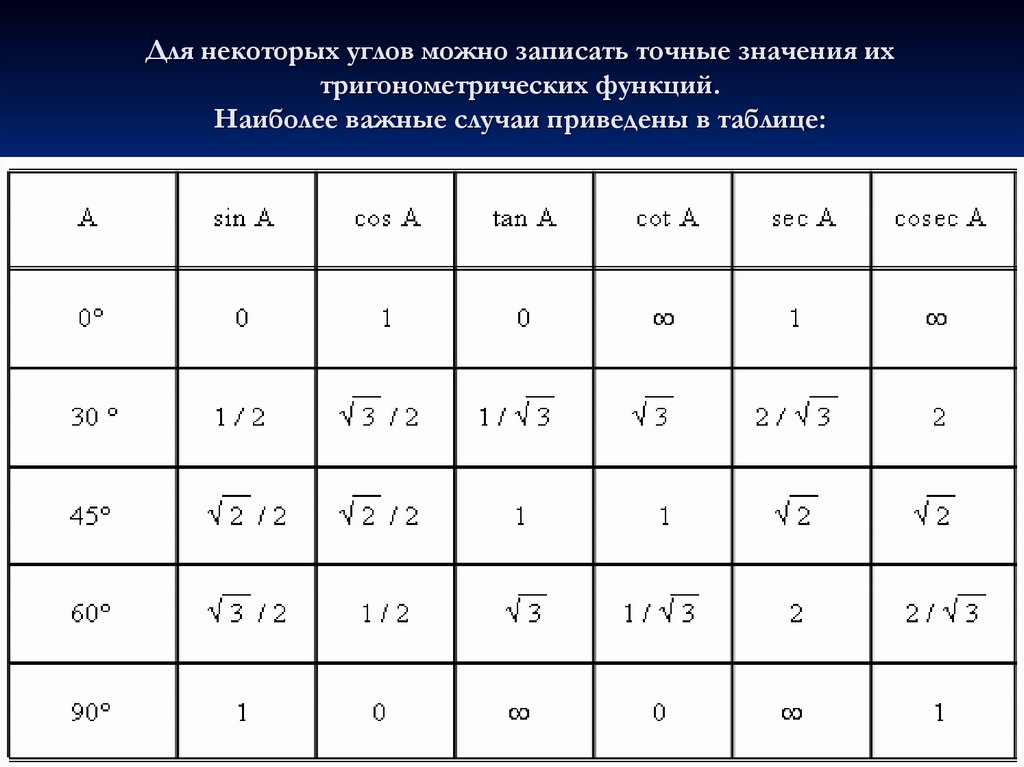 Мы используем принципы тригонометрии в различных других областях.
Мы используем принципы тригонометрии в различных других областях.

 Это потому, что тригонометрические функции часто используются в вопросах. Например, в Calculus тригонометрические функции используются для анализа вращающихся тел .
Это потому, что тригонометрические функции часто используются в вопросах. Например, в Calculus тригонометрические функции используются для анализа вращающихся тел .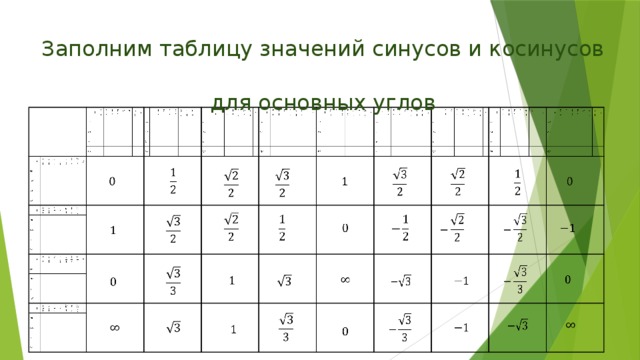 Но помните, как было сказано выше, о других областях, на которые сегодня влияет это понятие? Ну …..
Но помните, как было сказано выше, о других областях, на которые сегодня влияет это понятие? Ну ….. Так что ботаники правят везде!!
Так что ботаники правят везде!! Он касается соотношения между сторонами и углами треугольников. Вы можете быстро овладеть им, если подойдете к нему правильно. Если у вас возникнут какие-либо трудности с этим, не стесняйтесь обращаться к нам
Он касается соотношения между сторонами и углами треугольников. Вы можете быстро овладеть им, если подойдете к нему правильно. Если у вас возникнут какие-либо трудности с этим, не стесняйтесь обращаться к нам

