Тригонометрия. Таблица значений тригонометрических функций
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Тригонометрия
в двух словах2. Числовая окружность
Мы хорошо представляем, что такое числовая прямая – это прямая, на которой мыотмечаем числа.
Что получится, если мы согнём числовую прямую в кольцо?
Мы получим числовую окружность!
Давайте договоримся, что её начало (точка 0) будет расположено справа:
0
4.
 Движение по числовой окружностиПоложительное движение
Движение по числовой окружностиПоложительное движениеОтрицательное движение
(для отметки положительных чисел):
(для отметки отрицательных чисел):
против движения часовой стрелки!
по движению часовой стрелки!
1
0
0
0
-1
5. Единицы измерения на числовых окружностях
Часы:Градусы:
12
Радианы:
П
2
90
45
9
3
6
180
0
270
П
П
4
0
6. Макеты
Для удобства можно использовать макеты радианных мер на окружности:у
3П
4
у
П
2
П
4
2П
3
П
2
П
3
5П
6
П
0
5П
4
3П
2
7П
4
х
П
6
П
0
7П
6
11П
6
4П
3
3П
2
5П
3
х
7. Что такое синус (sin)?
Поместим числовую окружность на координатную плоскость:у
Обозначим проекцию точки П/4 на оси 0у.
П
2
М
П
Полученная точка M и есть синус (sin П/4)
П
4
0
х
8.
 Что такое косинус (cos)?Поместим числовую окружность на координатную плоскость:
Что такое косинус (cos)?Поместим числовую окружность на координатную плоскость:у
Обозначим проекцию точки П/4 на оси 0х.
П
2
П
Полученная точка K и есть косинус (cos П/4)
П
4
K
0
х
9. Как найти значение синуса?
Мы уже поняли, что синус – это координата на оси Оу (координата точки M).Но синус — это также и длина отрезка ОM.
у
Найдём длину отрезка ОM.
Мы знаем, что радиус нашей окружности равен 1.
Следовательно, OL=1.
М
П
0
L
Мы также знаем, что угол в точке L =30°.
х
Из курса школьной геометрии мы помним, что
«Катет, лежащий против угла 30°, равен половине гипотенузы»
Следовательно, OM=0,5 или 1/2
10. Выполните подобное вычисление 1000 раз и…
…и, с большой долей вероятности, вы станетесумасшедшим гением в тригонометрии.
11. Принцип «хорошей лени»
К счастью, большинство из нас очень скоро заметит, что производит одни и те жевычисления много раз.
 А не проще ли записать уже найденные однажды значения,
А не проще ли записать уже найденные однажды значения,например, в таблицу?
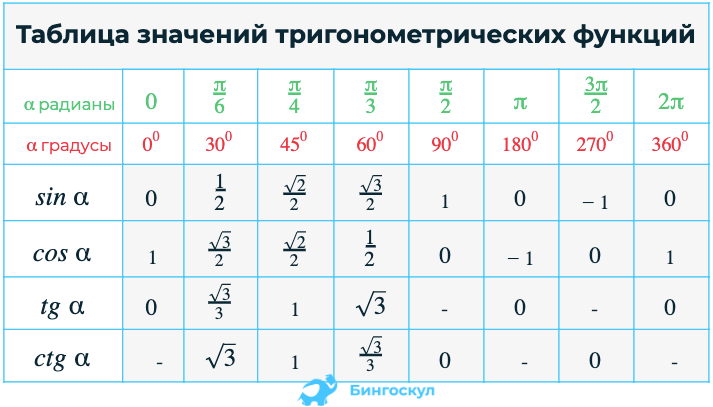
12. Таблица значений тригонометрических функций
Математики за долго до нас уже применили принцип «хорошей лени» и посчиталивсе необходимые значения.
Берите и пользуйтесь!
English Русский Правила
Таблица значений обратных тригонометрических функций
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
Ниже представлена таблица со значениями обратных тригонометрических функций: арксинусов (arcsin), арккосинусов (arccos), арктангенсов (arctg) и арккотангенсов (arcctg).
В радианах:
microexcel. ru
ru
В градусах:
| Значение | arcsin α | arccos α | arctg a | arcctg α |
| -√3 | — | — | -60° | 150° |
| -1 | -90° | 180° | -45° | 135° |
| -√3/2 | -60° | 150° | 89°» data-order=»-40.89°»>-40.89° | 130.89° |
| -√2/2 | -45° | 135° | -35.26° | 26°» data-order=»125.26°»>125.26° |
| -√3/3 | -35.26° | 125.26° | -30° | 120° |
| -1/2 | -30° | 120° | 57°» data-order=»-26.57°»>-26.57° | 116.57° |
| 0 | 0° | 90° | 0° | 90° |
| 1/2 | 30° | 60° | 57°» data-order=»26.57°»>26.57° | 63.43° |
| √3/3 | 35.26° | 54.74° | 30° | 60° |
| √2/2 | 45° | 45° | 26°» data-order=»35.26°»>35.26° | 54.74° |
| √3/2 | 60° | 30° | 40.89° | 11°» data-order=»49.11°»>49.11° |
| 1 | 90° | 0° | 45° | 45° |
| √3 | — | — | 60° | 30° |
microexcel. ru
ru
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
Тригонометрическая таблица соотношений | Таблица тригонометрических функций
Дата последнего обновления: 16 апреля 2023 г.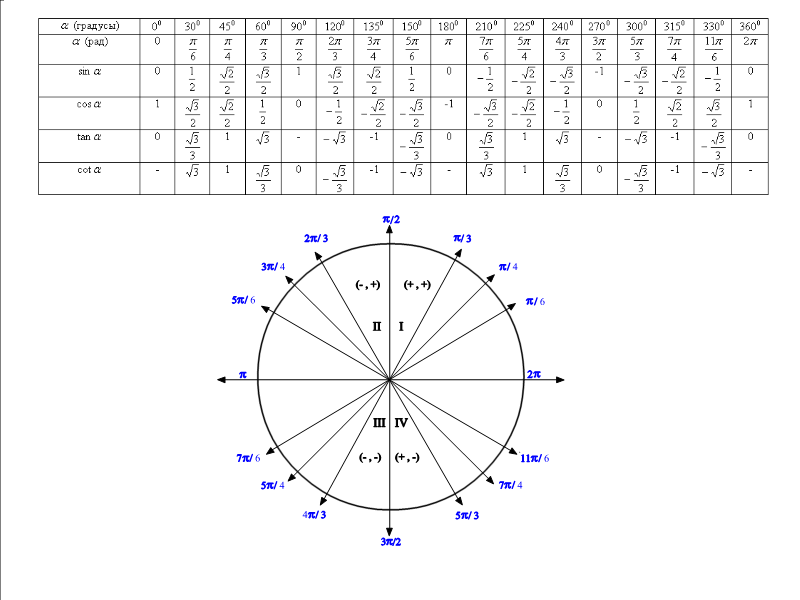
•
Всего просмотров: 441,6 тыс.
•
Просмотров сегодня: 4,11 тыс.
В математике эти тригонометрические таблицы полезны в большом количестве областей тригонометрии. До того, как мы познакомились с карманными калькуляторами, у нас были с собой тригонометрические таблицы. В каждой тригонометрической таблице есть определенные значения, которые помогут вам очень легко решить ваши суммы и уравнения. Тригонометрическая таблица содержит значения sin, cos, tan, cosec и sec при различных тета, и здесь тета — это значение угла в градусах.
Если говорить о том, что же такое эта тригонометрия, то тригонометрия – это раздел математики, который занимается изучением отношений, в том числе отношений длины треугольника и его углов. Как правило, тригонометрия связана с прямоугольным треугольником, треугольником, в котором считается, что он лежит под углом 90 градусов. Он используется не только для решения математических задач, но и в области навигации, а также в других областях науки и техники.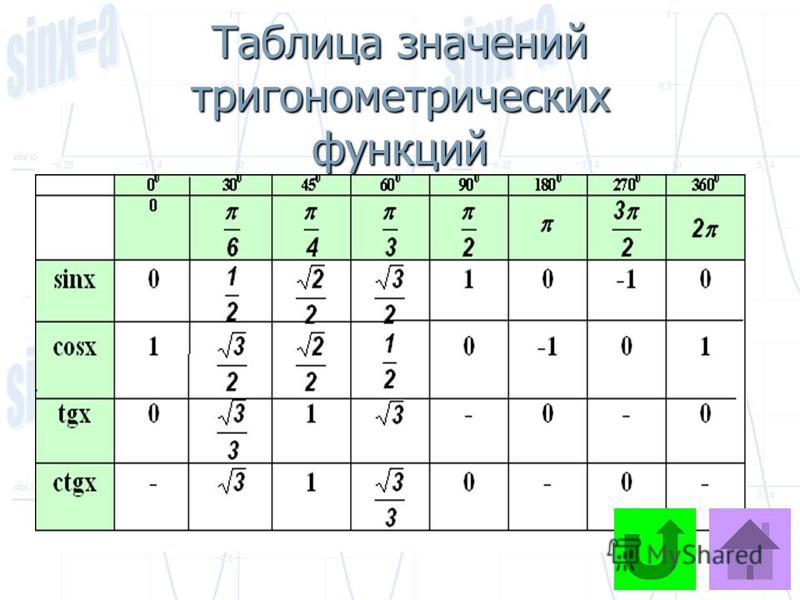
Тригонометрическая таблица содержит значения тригонометрических отношений, таких как синус, косинус, тангенс, котангенс, косеканс и секанс от 0 до 360°. Применяя значения от 0 до 360° в этих тригонометрических соотношениях, мы получаем следующие значения, перечисленные в таблице значений тригонометрии:
Углы (в градусах) 0 3 9090 | 330° | 45° | 60° | 90° | 180° | 270° | 360° | ||||||||
0 | π/6 | π/4 | π/3 | π/2 | 2π | ||||||||||
грех | 0 | 1/2 | \[\frac{1}{\sqrt{2}}\] | \[{\frac{\sqrt{2}}\[3}{sq}2q \] | 1 | 0 | -1 | 0 | |||||||
cos | 1 | \[3 9 {\ sqrt{3}] | \[\frac{1}{\ sqrt{2}}\] | 1/2 | 0 | -1 | 5 9003 0003 | ||||||||
рыжевато-коричневый | 0 | \[\frac{1}{\sqrt{3}}\] | 1 | \[\sqrt{3}\] | Не определено | 0 | 9009 3 Не определено 2 1 | ||||||||
детская кроватка | Не определено | \[\sqrt{3}\] | 1 | \[\frac{1}{\sqrt{3}}\] 3 | 0 | Не определено | |||||||||
cosec | Не определено | 2 | ] \[\frac{2}{\sqrt{ 3}}\] | 1 | Не определено | -1 | Не определено 9 8 | 032 сек | 1 | \[\frac{2 }{\sqrt{3}}\] | \[\sqrt{2}\] | 2 | Не определен | -1 | 9003 31 |
В этой таблице вы со всеми тригонометрическими значениями.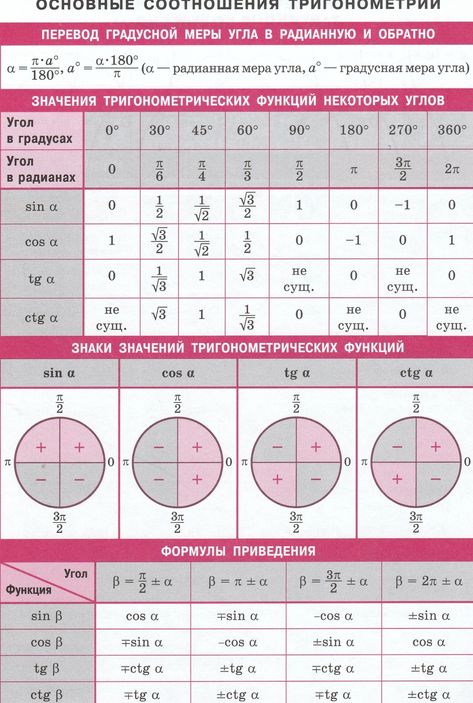 Эта таблица является основой для решения ряда сумм и уравнений с помощью тригонометрической формулы. Часто наблюдается, что многие формулы выводятся из этих тригонометрических величин. Эта тригонометрическая таблица представляет собой набор всех тригонометрических значений, но под разными углами. 0° 30° 45° 60° и 90° считаются стандартными углами тригонометрических величин.
Эта таблица является основой для решения ряда сумм и уравнений с помощью тригонометрической формулы. Часто наблюдается, что многие формулы выводятся из этих тригонометрических величин. Эта тригонометрическая таблица представляет собой набор всех тригонометрических значений, но под разными углами. 0° 30° 45° 60° и 90° считаются стандартными углами тригонометрических величин.
Подробнее о тригонометрической таблице
В таблице тригонометрических значений мы видим, что тригонометрические отношения связаны друг с другом, вариации возникают при взятии различных тригонометрических отношений сина, косинуса, секанса, косеканса, тангенса и котангенса.
По запросу тригонометрические функции генерируются также калькуляторами и современными компьютерами, но с использованием специальных библиотек этих математических кодов. Эти тригонометрические таблицы значительно облегчат вашу работу. Вам просто нужно выучить эту таблицу и большинство сумм, вы сможете легко их решить.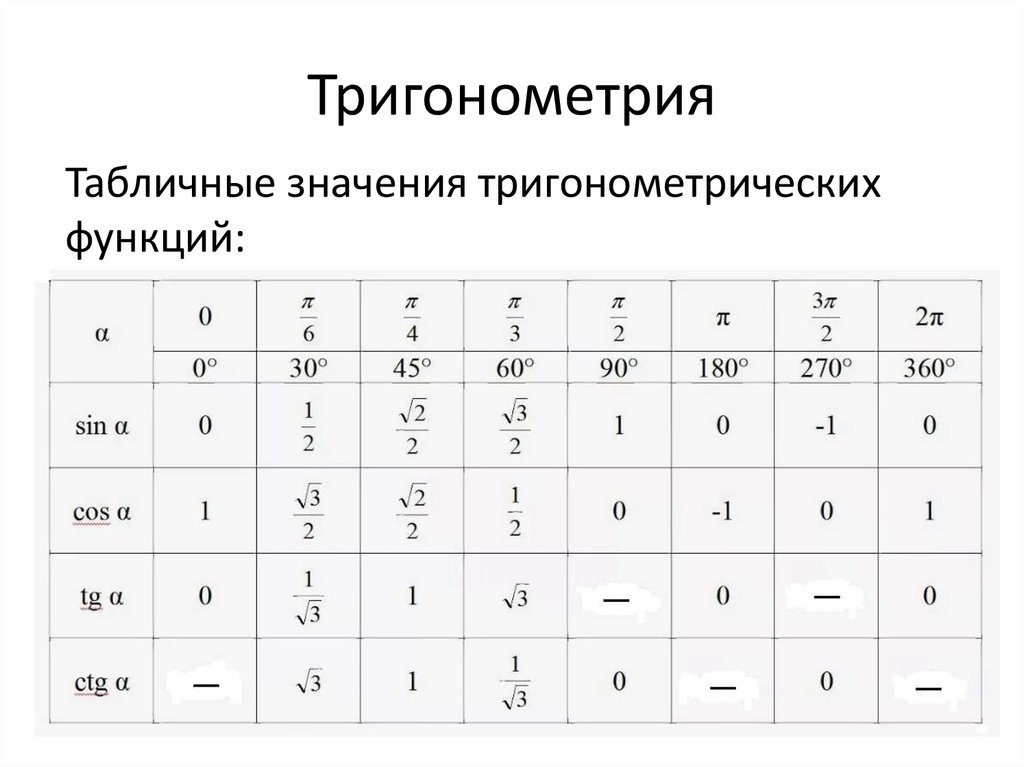
Тригонометрическая таблица состоит из следующих взаимосвязанных между собой тригонометрических соотношений – синуса, косинуса, тангенса, косеканса, секанса, котангенса. Короче говоря, эти отношения можно записать как sin, cos, tan, cosec, sec и cot.
\[sin = \frac{perpendicular} {гипотенуза}\]
\[ cos = \frac{base} {гипотенуза}\]
\[tan = \frac{perpendicular}{base}\]
\[cosec = \frac{hypotenuse}{perpendicular}\]
Применение тригонометрии в других связанных научных и математических областях огромно, поскольку расстояния на земле, а также в космосе оценивались в древнем мире при тщательном использовании и применении. тригонометрии.
В вычислениях можно легко разобраться, если запомнить таблицу функций, наиболее известную как тригонометрическая таблица. Это находит применение в нескольких областях. Некоторые из них включают в себя навигационную науку, географию, инженерию, геометрию и т. д. Тригонометрическая таблица была причиной того, что большинство цифровых разработок сегодня происходит такими темпами, поскольку первые механические вычислительные устройства нашли применение благодаря тщательному использованию тригонометрии.
д. Тригонометрическая таблица была причиной того, что большинство цифровых разработок сегодня происходит такими темпами, поскольку первые механические вычислительные устройства нашли применение благодаря тщательному использованию тригонометрии.
Таблица тригонометрических соотношений дает нам значения стандартных тригонометрических углов, таких как 0°, 30°, 45°, 60° и 9°.0°. Эти значения имеют повышенный приоритет по сравнению с другими, поскольку наиболее важные проблемы используют эти соотношения. Поэтому очень важно знать и помнить соотношения этих стандартных углов.
Запоминание таблицы тригонометрии будет полезно, так как она находит множество применений, и существует множество способов запоминания таблицы. Автоматическое знание тригонометрических формул приведет к выяснению таблицы и значений. Таблица соотношений тригонометрии зависит от формул тригонометрии точно так же, как все функции тригонометрии взаимосвязаны друг с другом.
Тригонометрические функции
Теперь, если говорить о том, что представляют собой эти тригонометрические функции, то эти тригонометрические функции являются функциями прямоугольного треугольника.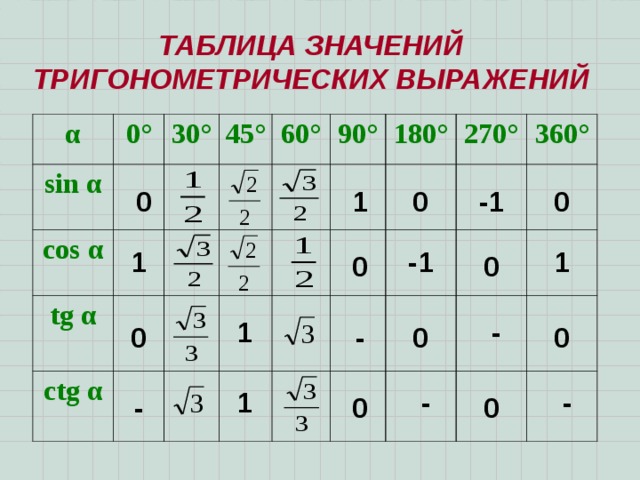 Этих тригонометрических функций в основном шесть, и они следующие:
Этих тригонометрических функций в основном шесть, и они следующие:
функция Sin
функция Cos
функция Tan
3 функция SecФункция детской кроватки
0 70 Функция Cosec
Эти функции в основном помогут вам решить проблемы и разобраться с рядом понятий.
Тригонометрические функции дополнительных углов
Перед попыткой начать лучше попытаться запомнить эти значения и знать следующие тригонометрические формулы. Потому что, если вы заранее хорошо знаете формулы, только тогда вам будет легко пробовать вопросы. Каждая функция связана с соответствующей ей функцией. Как и в приведенных ниже формулах, вы заметите, что функция sin связана с функцией cos и наоборот. Кроме того, функция is связана с функцией tan и наоборот. Другая, функция sec, также связана с функцией кроватки и наоборот.
Кроме того, функция is связана с функцией tan и наоборот. Другая, функция sec, также связана с функцией кроватки и наоборот.
sin x = cos (90°− x)
cos x = sin (90°− x)
tan x = cot (90°− x)
cot x = tan (90°− x)
sec x = cot (90°− x)
cot x = sec (90°− x)
1/sin x = 1/cos x = sin x
1/cos x = sec x
1/sec x = cos x
1/tan x = cot x
1/cot x = tan x
Шаги для создания тригонометрической таблицы:
Шаг 1: Нарисуйте табличный столбец с требуемыми углами, такими как 0, 30, 45 , 60, 90 в верхнем ряду и все 6 тригонометрических функций, таких как синус, косинус, тангенс, косеканс, секанс и котангенс в первом столбце.
Шаг 2: Найдите значение синуса требуемого угла.
Чтобы определить значение sin, мы последовательно делим все значения от 0, 1, 2, 3 и 4 на 4, а затем извлекаем квадратный корень. Например, чтобы найти значение 0°, мы напишем \[\sqrt{(\frac{{0}}{4})}\], т. е. 0, или чтобы найти значение 30°, мы напишем \[\sqrt{(\frac{{1}}{4})}\], т. е. \[\frac{1}{2}\]. Таким образом, соответствующие значения от 0 до 360° равны
Например, чтобы найти значение 0°, мы напишем \[\sqrt{(\frac{{0}}{4})}\], т. е. 0, или чтобы найти значение 30°, мы напишем \[\sqrt{(\frac{{1}}{4})}\], т. е. \[\frac{1}{2}\]. Таким образом, соответствующие значения от 0 до 360° равны
Угол в градусах | Значение |
0 | 0 |
| 3 0 9032 | |
45 | \[\frac{1}{ \sqrt{2}}\] |
60 | \[\frac{\sqrt{3}}{2}\] |
180 | 1 |
270 | -1 |
360 | 50350350303 0
Шаг 3: Найдите значение косинуса требуемого угла.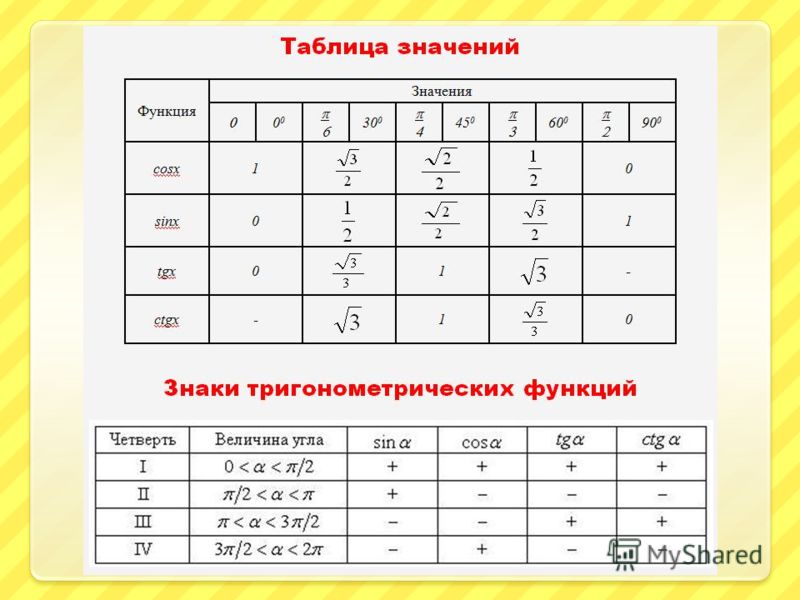
Значения cos таблично противоположны значениям углов sin.
Это означает, что любое значение степени sin (0 — x) совпадает со значением степени cos (90 — x). Чтобы найти значение cos, разделите на 4 в порядке, обратном греху, т. е. последовательно от 4, 3, 2, 1 и 0 на 4 и извлеките квадратный корень.
Например, чтобы найти значение 0°, мы напишем √(4/4), т. е. 1, или чтобы найти значение 30°, мы напишем \[\sqrt{(\frac{{3} {2})}\], т. е. \[{(\frac{\sqrt{3}}{2})}\]. Таким образом, соответствующие значения от 0 до 360°:
Угол в градусах | Значение | 5 |
1 | ||
30 | \[\frac{\sqrt{3}}{2}\] | |
45 | \[\frac{1}{\sqrt{2}}\] | |
1 2 3 5 3 90 90 /2 | ||
90 | 0 | |
180 | -1 | |
270 | ||
360 | 1 |
значение тангенса искомого угла.
Тангенс равен синусу, деленному на косинус. тангенс x = грех x/cos x.
Чтобы найти значение tan 30, делим sin 30 на cos 30 и получаем требуемое значение, т.е. \[\frac{(\frac{1}{2})}{(\frac{\sqrt{3 }}{2})} = \frac{1}{\sqrt{3}}\], другие соответствующие значения:
Угол в градусах Значение | |
0 | 0 |
30 | \[\frac{1}{\sqrt{3}}\] |
| 5 90 | 1 |
60 | √3 |
90 | \[\infty\] | 10 80 35 | 0 |
270 | \[\infty\ ] |
360 | 0 |
Шаг 5: Определите стоимость детской кроватки.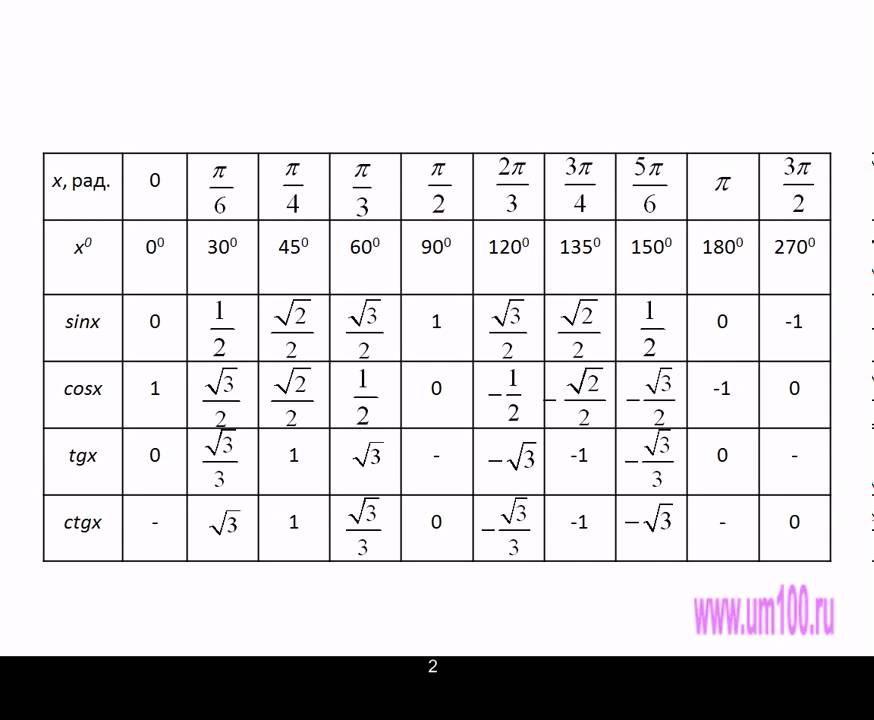
Значение кроватки можно определить по всем обратным значениям тангенса.
Итак, для каждого значения значение кроватки равно 1/тан. Поскольку кроватка x = cos x/sin x. Таким образом, соответствующие значения являются просто обратными величинами загара.
Угол в градусах | Значение |
0 | \[\infty\] |
| 3 0 032 \[{\sqrt{3}}\] | |
45 | 1 |
60 | \[1{\sqrt{3}}\] | 00 |
180 | \[\infty\] |
270 | 0 |
360 |
Шаг 6: Найдите значение косеканса искомого угла.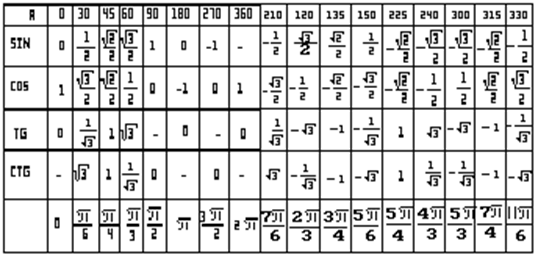
Значение cosec для любого угла является обратным значением sin для этого конкретного угла. Таким образом, соответствующие значения будут обратны значениям sin x.
Шаг 7: Определите значение сек.
Значение sec для любого угла является обратной величиной cos этого конкретного угла. Итак, обратные величины cos равны:
Следуя вышеуказанным шагам, вы сможете легко создать эту таблицу самостоятельно, и как только вы поймете, как создать эту таблицу, вы сможете легко научиться этому. Изучение этой таблицы так же важно, как и решение сумм с использованием этих таблиц, потому что, если вы выучили только таблицу, вы сможете использовать ее быстро, не тратя времени. Решение вопроса станет для вас гораздо более легкой задачей, так как вы будете знать о значениях заранее, и вам просто нужно вспомнить значение, и вы получите ответ.
Угол в градусах | 3 | Значение31 | 0 | 1 |
30 | \[2{\sqrt{3} }\] | |||
45 | \[{\sqrt{2}}\] | |||
1 2 3 2 3 9003 9003 | ||||
90 | \[\infty\] | |||
180 | -1 1 2 2 2 | \[\infty\] | ||
360 | 1 |
Список формул тригонометрии
1. Сложные углы
Сложные углы
9
cos A cos B + sin A cos B = cos (A – B) 9{2}\] A
(tan A + tan B)/(1 – tan A tan B) = tan (A + B)
(tan A – tan B)/(1 + tan A tan B) = tan (A – B)
sin2A = sin (A + A) = sinA.cosA + cosA.sinA = 2sinA.cosA
2. Сумма и разность синусов и косинусов
sin (A+B) + sin (A-B) = 2 sin A cos B
sin (A+B) – sin (A-B) = 2 cos A sin B
cos (A+B) + cos (A-B) = 2 cos A cos B 9{2}A}{2tanA}\]
4. Кратные и дольные углы
Кратные и дольные углы
Тригонометрическая таблица, формула, диаграмма, функции и значения
Тригонометрическая таблица
функции для часто используемых стандартных углов 0°, 30°, 45°, 60°, 90° и нестандартных углов 180°, 270° и 360° . Тригонометрия — это тема и глава математики, которая включает в себя изучение отношений между длиной и углами треугольника. Тригонометрия играет важную роль в класс 10, 11 и 12 предметы по математике и на многих конкурсных экзаменах некоторые вопросы задаются из тригонометрии . Прежде чем приступить к изучению тригонометрии, вы должны запомнить таблицу тригонометрии, которая обсуждается ниже.
Тригонометрическая таблица от 0° до 360°
Таблица тригонометрических соотношений помогает найти значения обычных тригонометрических углов, таких как 0°, 30°, 45°, 60° и 90°, а также необычных углов, таких как 180°, 270° и 360°. Он состоит из тригонометрических соотношений. Шесть тригонометрических соотношений: синус, косинус, тангенс, котангенс, косеканс и секанс.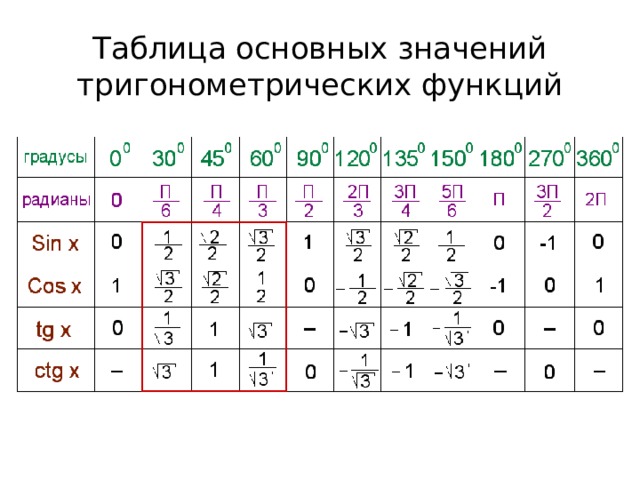 Эти отношения могут быть записаны кратко как sin, cos, tan, cosec, sec и cot. Значения тригонометрических отношений стандартных углов необходимы для решения задач по тригонометрии в 10, 11, 12 классах и на любых конкурсных экзаменах. Поэтому необходимо запомнить значения тригонометрических соотношений от 0° до 360°. Посмотрим на таблицу тригонометрии и значения функций от 0° до 360°.
Эти отношения могут быть записаны кратко как sin, cos, tan, cosec, sec и cot. Значения тригонометрических отношений стандартных углов необходимы для решения задач по тригонометрии в 10, 11, 12 классах и на любых конкурсных экзаменах. Поэтому необходимо запомнить значения тригонометрических соотношений от 0° до 360°. Посмотрим на таблицу тригонометрии и значения функций от 0° до 360°.
| Тригонометрическая таблица | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Углы 4 9003 4 63 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° | | ||||||||
| sin | 0 | 1/2 | 1/√2 | √3/2 | 2 1 90 -10 | |||||||||||
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 | 19003 9003 10640 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 |
| детская кроватка | ∞ | √3 | 1 | 1/√3 | ∞0 | ∞ | ||||||||||
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ | ||||||||
| 2/√3 | √2 | 2 | ∞ | -1 | ∞ | 1 | ||||||||||
| Тригонометрическая таблица | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0° | π/6 | π/4 | π/3 | π/2 | π | 9032 3π/2| 4 3 2π | | ||||||||||
| грех | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 09003 8 09003 031 | cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | -1 | 0 | 1 |
| 5 4 желто-коричневый | 6 | 1/√3 | 1 | √3 | ∞ | 0 | ∞ | 0 | |||||||||
| детская кроватка | ∞ | √3 | 1 | 1/√3 | 0 | ∞ 2 | 5 0 | 0 900 5 | |||||||||
| косек | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ | |||||||||
| сек | 1 0/3 | 9032 | √2 | 2 | ∞ | -1 | ∞ | 1 | |||||||||
Уловки с таблицей тригонометрии
Запоминание таблицы тригонометрии поможет вам решить вопросы по тригонометрии, очень легко запомнить таблицу тригонометрии для стандартных углов от 0° до 90° . Если вы знаете формулы тригонометрии, то запомнить таблицу тригонометрии очень легко. Таблица соотношений тригонометрии зависит от формул тригонометрии. Здесь мы предлагаем некоторые приемы и формулы тригонометрической таблицы, которые обсуждаются ниже.
Если вы знаете формулы тригонометрии, то запомнить таблицу тригонометрии очень легко. Таблица соотношений тригонометрии зависит от формул тригонометрии. Здесь мы предлагаем некоторые приемы и формулы тригонометрической таблицы, которые обсуждаются ниже.
- sin (90°− θ) = cos θ
- cos (90°− θ) = sin θ
- tan (90°− θ) = cot θ
- cot (90°− θ) = tan θ
- cosec (90°− θ) = sec θ
- sec (90°− θ) = cosec θ
- 1/sin θ = cosec θ
- 1/cos θ = sec θ
- 1/tan θ = cot θ
Таблица таблицы тригонометрии
Значения тригонометрических функций для углов 0°, 30°, 45°, 60° и 90° в таблице тригонометрии обычно используются для решения задач и вопросов по тригонометрии. Таким образом, 0°, 30°, 45°, 60° и 90° называются стандартными углами. Таблица таблицы тригонометрии для стандартных ангелов приведена ниже. вы можете скачать таблицу тригонометрической таблицы для будущего использования и изучения значений тригонометрической таблицы.
Тригонометрическая таблица для тригонометрических функций
В тригонометрии есть шесть тригонометрических функций: синус, косинус, тангенс, секанс, косеканс и котангенс . Он также известен как sin, cos, tan, cosec, sec и cot. Таблица тригонометрии для каждой тригонометрической функции обсуждается ниже.
Таблица тригонометрии для функции sin
Таблица тригонометрии для функции sin приведена ниже. Значение sin0° равно 0, а значение sin 90° равно 1. Значение sin 30° равно 1/2, а значение sin 45° равно 1/√2.
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° 90 32 90 32 900 32 270° | 360° | ||
| sin | 0 | 1/2 | 1/√2 | √3/2 | 1 | 0 | -1 | 0 |
Тригонометрическая таблица для cos
Таблица тригонометрической функции для косинуса приведена ниже.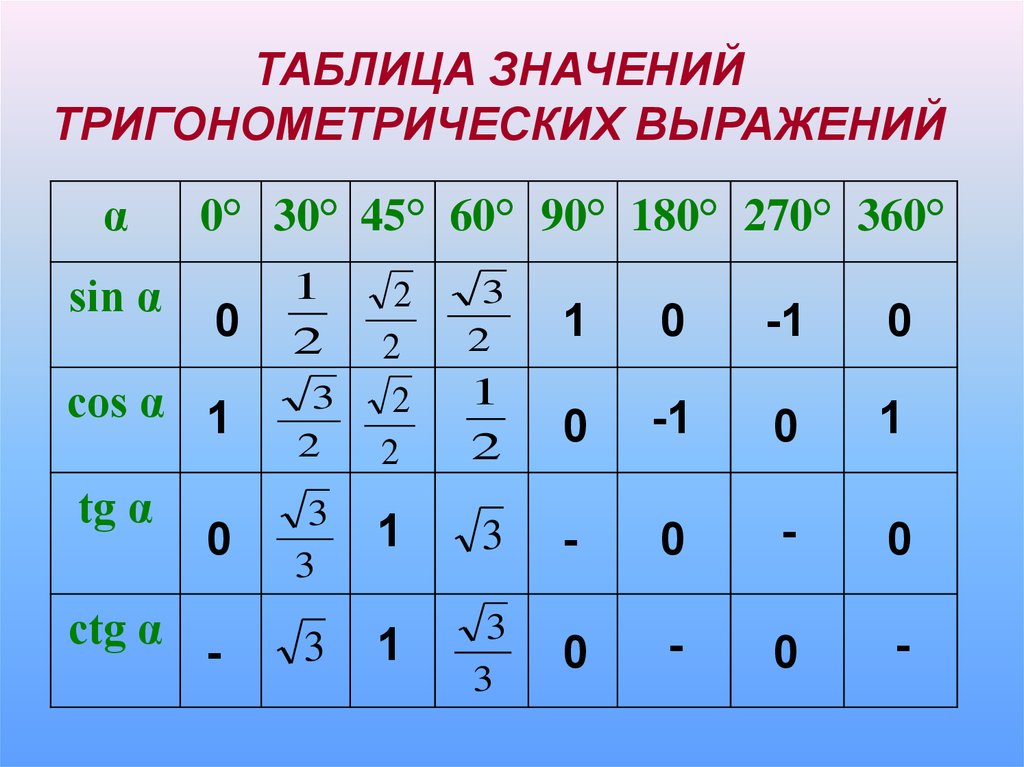 Значение cos 0° равно 1, а значение cos 90° равно 0. Это прямо противоположно функции sin от 0° до 90°.
Значение cos 0° равно 1, а значение cos 90° равно 0. Это прямо противоположно функции sin от 0° до 90°.
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° 90 32 90 32 900 32 270° | 360° |
| cos | 1 | √3/2 | 1/√2 | 1/2 | 0 | 5 09032 -1032 1 |
Тригонометрическая таблица для загара
Таблица тригонометрии для функции тангенса приведена ниже. Значение тангенса 30° равно 1/√3, а значение тангенса 60° равно √3.
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° | 1 | цвет 50 | ∞ | 0 |
Тригонометрический стол для детской кроватки
Таблица тригонометрии для функции кроватки приведена ниже. Значение раскладушки 30° равно √3, а значение раскладушки 60° равно 1/√3.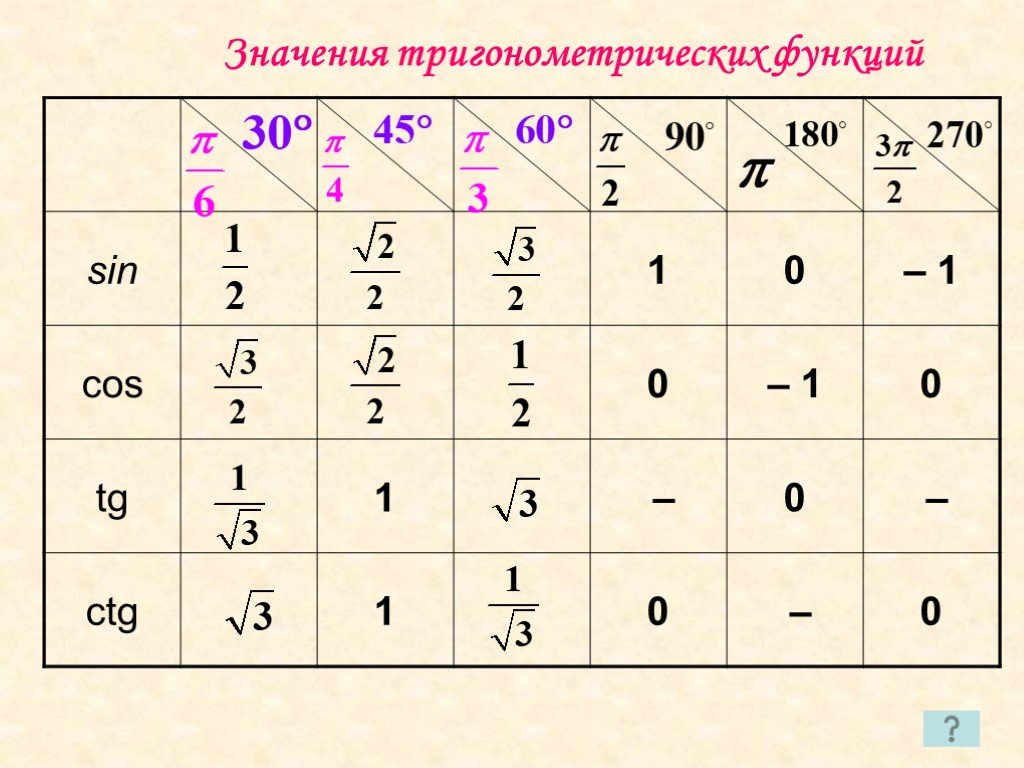
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| кроватка | ∞ | 9003 01 02032 √3 3 51/√3 | 0 | ∞ | 0 | ∞ |
Таблица тригонометрии для функции cosec
Таблица тригонометрии для функции cosec обсуждается ниже. Значение cosec 45° равно √2, а значение cosec 30° равно 2.
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° | 90031 косек 32 ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
Таблица тригонометрии для сек
Таблица тригонометрии для функции сек обсуждается ниже. Значение секунды 45° равно √2, а значение секунды 30° равно 2.
