Таблицы тригонометрических функций, основные значения
Оглавление
Время чтения:: 6 минут
1 128
Для начала определим понятие «тригонометрические функции».
Определение
С помощью тригонометрических функций выражается зависимость длин сторон треугольников от острых углов при гипотенузе. Употребление тригонометрических функций довольно широко. Астрономия, физика, медицина – это неполный перечень использования тригонометрических функций.
Из учебника геометрии нам известно, что к тригонометрическим функциям относятся синус (sin), косинус (cos), тангенс(tg), котангенс(ctg), секанс (sec) и косеканс (cosec). В данной статье мы разберем первые четыре.
Следуя тригонометрическим определениям функций sin, cos, tg и ctg можно найти их значения для углов 0 и 90 градусов:
sin 0⁰= 0, cos 0⁰=1, tg 0⁰=0, ctg 0⁰ — не определяется;
sin 90⁰=1, cos 90⁰=0, ctg 90⁰=0, tg 90° — не определяется.
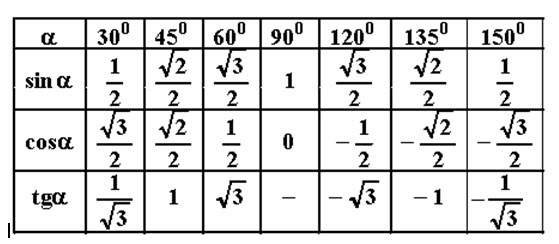
На уроках геометрии изучая прямоугольные треугольники в основном вычисляют тригонометрические функции углов 0°, 30°, 45°, 60° и 90°.
Извлеченные значения тригонометрических функций для углов были составлены в таблицу, которую называют таблица тригонометрических функций, таблица значений тригонометрических функций, таблицей тригонометрических функций углов и т.д
Используя формулы приведения, тригонометрическая таблица может быть увеличена до угла 360° и 2π радиан:
Используя особенности цикличности тригонометрических функций, любой угол, отличный от уже известного на 360°, может быть посчитан и занесен в таблицу. Например, тригонометрическая функция для угла 30° будет иметь такое же значение и для угла 30°+360°, и для угла 30°+2⋅360°, и для угла 30°+3⋅360° и т.д.
При помощи таблицы значений углов тригонометрических функций можно найти величину всех углов единичной окружности.
Как пользоваться таблицей тригонометрических функций
Для того чтобы посчитать тригонометрическую функцию, достаточно отыскать нужную тригонометрическую функцию и значение угла или радиан в таблице. Там где пересекаются строка с функцией и столбец со значением, будет необходимое значение тригонометрической функции.
Там где пересекаются строка с функцией и столбец со значением, будет необходимое значение тригонометрической функции.
На изображении, представленном ниже, можно проследить, каким образом определить значение тангенса 30⁰, которое равно:
Точно также используется расширенная тригонометрическая таблица. Главным достоинством ее использования является подсчет тригонометрической функции практически любого угла. Например, с легкостью мы можем найти значение
cos 1230° = cos (1230°−360°) = cos (870°−360°) = cos (510°−360°) = cos 150°:
Нет времени решать самому?
Наши эксперты помогут!
Контрольная
| от 300 ₽ |
Реферат
| от 500 ₽ |
Курсовая
| от 1 000 ₽ |
Таблица тригонометрических функций Брадиса
Если вам необходимо найти значение какого-то угла для его целого значения, целых градусов и целых минут, то можно воспользоваться таблицами Брадиса. Существует 2 вида таблицы: таблица для sin и cos и таблица для tg и ctg.
Таблицы Брадиса помогают найти максимально приближенное значение тригонометрических функций.
Как использовать таблицы Брадиса
Попробуем на практике как работать с таблицами Брадиса.
Пользуясь таблицей Брадиса для синусов, вычислим sin 24°36′. Для этого в столбце слева таблицы синусов и косинусов выбираем значение градусов – 24°, а в верхней строке обнаруживаем значение минут – 36′. На их пересечении получаем необходимое значение:
sin 24°36′. = 0,4163.
Для того чтобы найти значения sin 24°37′ необходимо обратиться к поправке в правой части таблицы. В нашем примере к значению 36′, которое есть в таблице, нужно прибавить поправку для 1′ , которая равна 0,0003. Получаем: sin24°37′=0,4163+0,0003=0,4166.
Чтобы посчитать значение sin24°40′ также воспользуемся поправкой в правой части таблицы. В этом случае от значения 42′, которое есть в таблице, отнимаем поправку для 2′, которая равна 0,0005. Получим: sin24°40′ = 0,4179 — 0,0005 = 0,4174.
Чтобы расчищать косинус, выполняем те же манипуляции, но градусы смотрим в правом столбце, а минуты – в нижней колонке таблицы. Например, cos 15°=0,9655. Для значений тангенса до 90° и котангенса малого угла поправок нет.
Для закрепления полученных знаний найдем tg 76°34′. Согласно таблице он 4,187.
Найдем ctg 12°36′=4,474.
Урок 4. Натуральные тригонометрические таблицы
ВИДЕО УРОК
При решении треугольников приходится находить значения тригонометрических функций заданных углов, а также отыскивать величины углов по имеющимся значениям тригонометрических функций этих углов. Обе эти задачи решаются с помощью таблиц значений тригонометрических функций, так называемых натуральных таблиц.
Как пользоваться таблицей Брадиса ?
Дадим краткое
описание устройства таких таблиц, имеющихся в книге В. Брадиса <<Четырёхзначные
математические таблицы>>, и объясним, как ими пользоваться.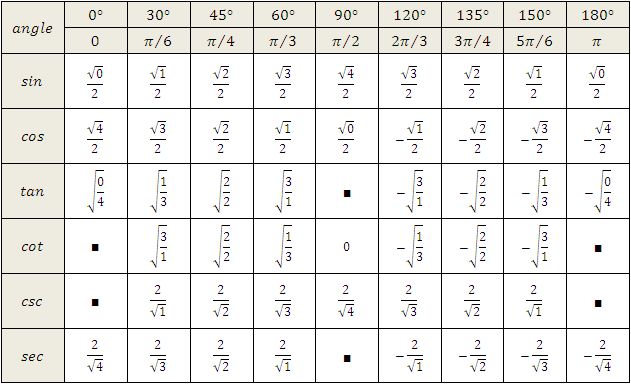 В книге В. Брадиса
таблицы значений тригонометрических функций помещены под номерами VIII, IX, X.
В книге В. Брадиса
таблицы значений тригонометрических функций помещены под номерами VIII, IX, X.
С помощью таблицы VIII можно находить значения синусов и косинусов всех острых углов, содержащих целое число градусов и минут, а также решать обратную задачу, то есть отыскивать угол по данному значению его синуса или косинуса с точностью до одной минуты.
В этой таблице в первом слева столбце под буквой А (Arkus (аркус) – по латыни означает дуга) помещены числа градусов, содержащихся в угле, а в первой верхней строке указаны числа минут в угле.
Название <<синусы>> (вверху страницы) связано с первым левым столбцом таблицы и её первой верхней строкой. Это показано на изображённой здесь части рамки таблицы VIII.
Покажем на примерах, как пользоваться таблицами.
ПРИМЕР:
Найти sin 25°.
РЕШЕНИЕ:
На пересечении строки, начинающейся с 25°, и столбца с пометкой 0‘ читаем 4226. Это – число десятитысячных. Число же целых
Это – число десятитысячных. Число же целых
sin 25° ≈ 0,4226.
ОТВЕТ: sin 25° ≈ 0,4226
Здесь и в подобных случаях следует ставить знак ≈, так как таблицы дают вообще приближённые значения тригонометрических функций.
Так же просто находятся синусы углов, выражающихся целым числом градусов и числом минут, кратным 6.
ПРИМЕР:
Найти sin 25°42‘.
РЕШЕНИЕ:
Это число находится на пересечении строки с пометкой 25° слева и столбца с пометкой 42‘ сверху. ОТВЕТ: sin 25°42‘ ≈ 0,4337
Из рассмотренной таблицы значений синусов следует, что функция sin α при изменении угла α изменяется неравномерно. Но если угол α изменяется не более чем на 6‘, то можно допустить, что приращение значения sin α пропорционально приращению значения угла
 Можно доказать, что ошибка в окончательном результате, происходящая благодаря
такому допущению, менее 0,0001,
а при отыскания значения угла α по данному значению sin α эта ошибка не
превосходит угла в 1‘.
Можно доказать, что ошибка в окончательном результате, происходящая благодаря
такому допущению, менее 0,0001,
а при отыскания значения угла α по данному значению sin α эта ошибка не
превосходит угла в 1‘.Таким образом, по таблицам В. Брадиса мы можем вести вычисления с точностью до 4-го знака, а при отыскании угла – с точностью до угла в 1‘.
Если нужна большая точность, то приходится обращаться к другим таблицам.
ПРИМЕР:
Найти sin 25°20‘.
РЕШЕНИЕ:
Находим в таблице синусы углов ближайшего меньшего и ближайшего большего, чем данный угол. Имеем:
sin 25°18‘ ≈ 0,4274,
sin 25°24‘ ≈ 0,4289.
Приращению угла на 6‘ соответствует табличная разность в
0,0015 (0,4289 – 0,4274),
а приращению угла в 2‘
соответствует приращение синуса, равноеЭту поправку в 0,0005 надо
прибавить к значению синуса угла sin 25°18‘, так как большему углу, то есть углу sin 25°20‘,
соответствует больший синус.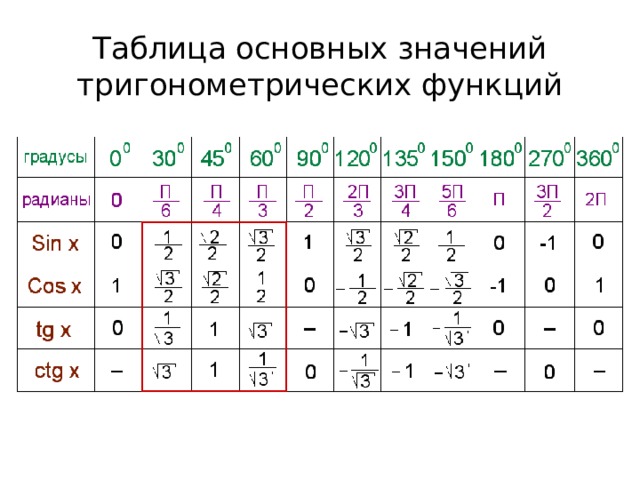
Поэтому получим:
ОТВЕТ: sin 25°20‘ ≈ 0,4279
В таблицах В. Брадиса имеются поправки для sin α, когда α изменяется на 1‘, 2‘ и 3‘. Эти поправки даны числом единиц последнего разряда. Они помещены справа в последних трёх колонках таблицы.
В приведённом выше
примере в колонке поправок под пометкой 2‘, в строке 25°, читаем
ПРИМЕР:
Найти sin 14°47‘.
РЕШЕНИЕ:
В данном случае следует взять из таблицы синус ближайшего большого угла, то есть угла 14°48‘.Тогда имеем:
ПРИМЕР:
Найдите
sin 70°36ʹ.
РЕШЕНИЕ:
Находим
число градусов в крайнем левом столбике таблицы, число минут – в верхней части
таблицы. На пересечении соответствующей строки и столбика находим искомое число 0,9432.ОТВЕТ:
На пересечении соответствующей строки и столбика находим искомое число 0,9432.ОТВЕТ:
sin 70°36ʹ = 0,9432.
ПРИМЕР:
Найдите
sin 74°55ʹ.
РЕШЕНИЕ:
В таблице находим синус угла, ближайшего к данному:
sin 74°54ʹ = 0,9655.Потом в столбиках поправок (в правой части таблицы) находим поправку на 1ʹ. Эта поправка равняется 0,0001. Учитывая, что с ростом угла от 0° до 90° синус также растет, найденную поправку добавляем. Следовательно, имеем:
sin 74°55ʹ = 0,9655 + 0,0001 = 0,9656.
ОТВЕТ:
sin 74°55ʹ = 0,9656.
Точно также устроена таблица тангенсов углов от 0° до 76°. (таблица IX) и таков же порядок пользования ею.
В таблице тангенсов, начиная с 60°, число целых даётся для тангенса каждого угла.
Таблица значений
косинусов углов от 0° до 90° (таблица
VIII) построена так: название <<косинусы>>
помещено внизу страницы.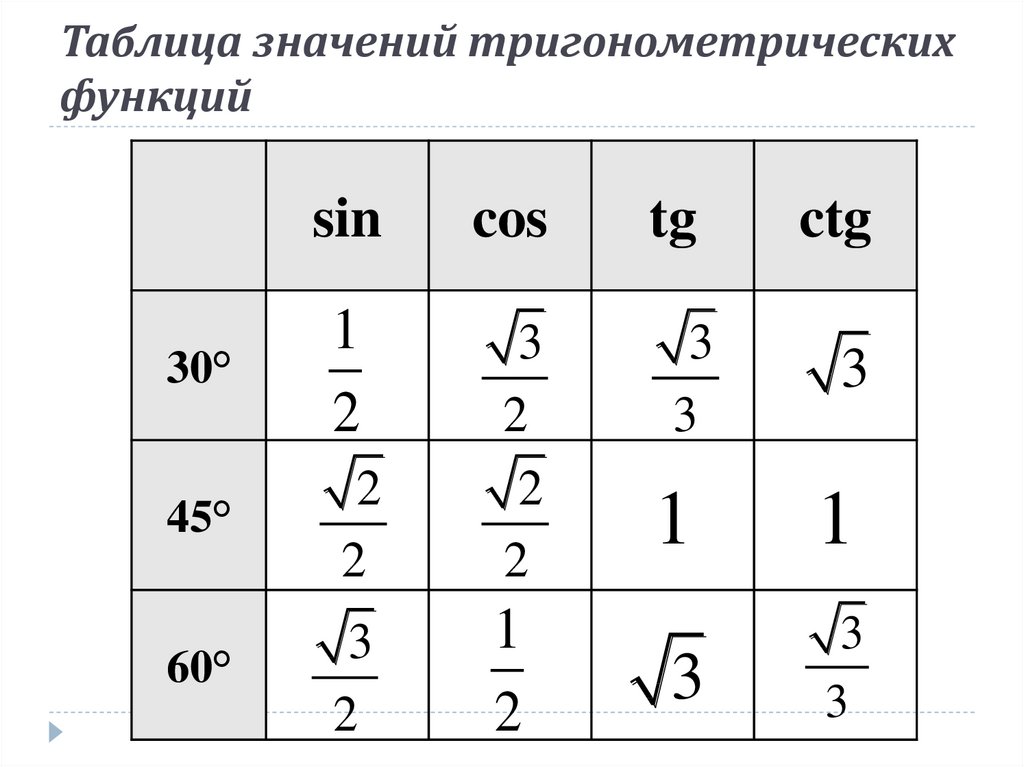 К этому названию относятся правый (4-й от края) столбец с буквой
К этому названию относятся правый (4-й от края) столбец с буквой
ПРИМЕР:
Найти cos 24°18‘.
РЕШЕНИЕ:
Это число находится на пересечении строки с пометкой 24° справа и столбца с пометкой 18‘ снизу. ОТВЕТ: cos 24°18‘ ≈ 0,9114
При отыскании косинусов углов, не содержащихся в таблице, вычисления ведутся несколько иначе, чем в случае нахождения синуса угла, так как косинус острого угла – функция убывающая. В силу этого при увеличении угла на 1‘, 2‘, 3‘ соответствующую поправку для косинуса следует вычитать из найденного в таблицах значения косинуса. Поясним это на примере.
ПРИМЕР:
Найти cos 40°25‘.
РЕШЕНИЕ:
ПРИМЕР:Найти cos 62°10‘.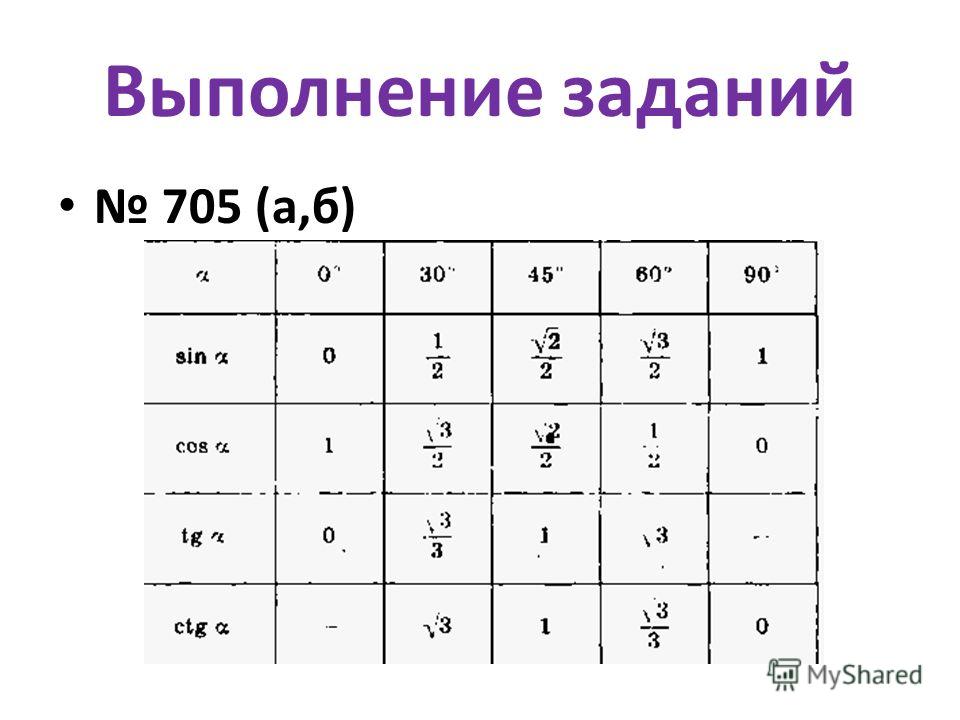
РЕШЕНИЕ:
В данном случае берём из таблицы косинус ближайшего большего угла, то есть угла 62°12‘.Тогда имеем:
ПРИМЕР:
Найдите
соs 16°12ʹ.
РЕШЕНИЕ:
Число градусов ищем в правой части таблице (в столбике А), число минут – в нижней части таблицы. На пересечении соответствующего рядка и столбика находим искомое число 0,9603.ОТВЕТ:
соs 16°12ʹ = 0,9603.
ПРИМЕР:
Найдите
соs 18°50ʹ.
РЕШЕНИЕ:
За таблицами находим значение косинуса угла, ближайшего к данному углу.
соs 18°48ʹ = 0,9466.
 Следовательно, имеем:
Следовательно, имеем:соs 18°50ʹ = 0,9466 – 0,0002 = 0,9464.
ОТВЕТ:
соs 18°50ʹ = 0,9464.
Точно так же, как таблица значений косинусов, построена таблица значений котангенсов углов от 14° до 90° (таблица IX). Таков же и порядок пользования ею.
Решение обратной задачи, то есть отыскание угла по заданному значению тригонометрической функции этого угла, производится с помощью тех же таблиц.
ПРИМЕР:
Найти угол α, если дано, что
sin α = 0,9037.
РЕШЕНИЕ:
аходим по таблицам число, наиболее близкое к данному,и соответствующий этому числу угол:
sin 64°36‘ ≈ 0,9033.
Данный синус на 4 единицы последнего разряда больше найденного в таблицах. Против поправки 4, стоящей в последней колонке строки 64°, вверху читаем 3‘. На основании этого записываем:
Следовательно α = 64°39‘.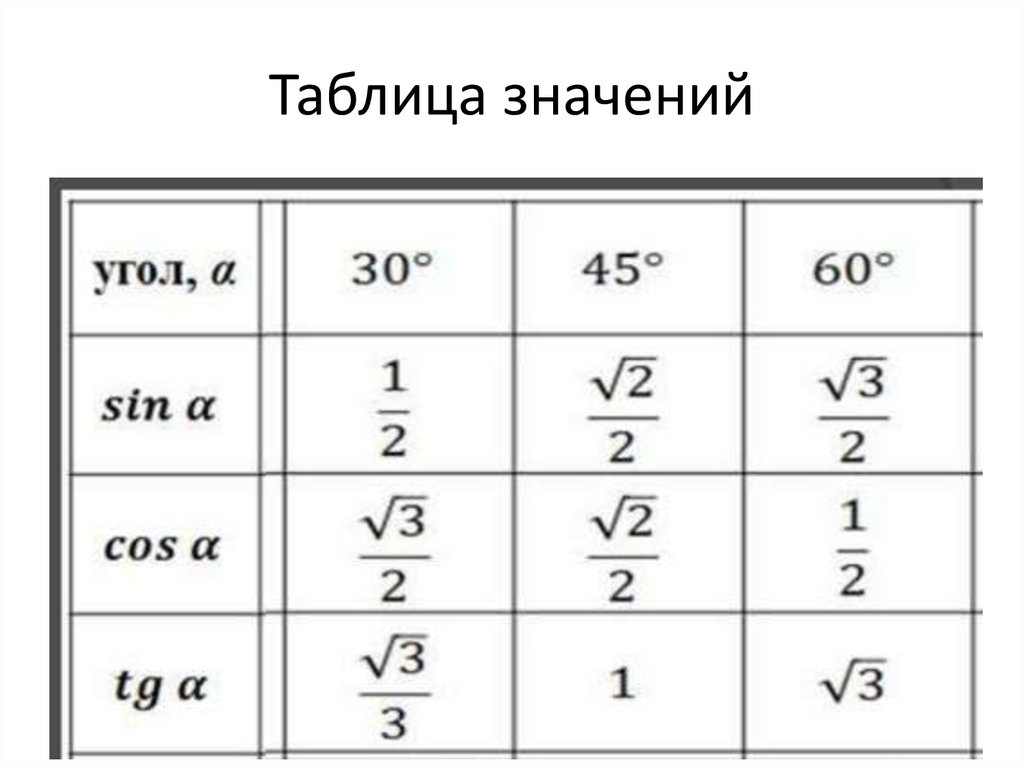
ОТВЕТ: α = 64°39‘
ПРИМЕР:
Найти угол α, если дано, что
соs α = 0,4501.
РЕШЕНИЕ: Следовательно α = 63°15‘.
ОТВЕТ: α = 63°15‘
ПРИМЕР:
Найти угол α, если дано, что
tg α = 1,4542.
РЕШЕНИЕ:
В таблице IX наиболее близко к данному значению тангенса число 1,4550, большее числа 1,4542.
В таком случае имеем:
Следовательно α = 55°29‘.
ОТВЕТ: α = 55°29‘
Таблица X позволяет находить значения тангенсов
углов от
76° до 89°59‘ и котангенсов
от 0°1‘ до 14° непосредственно, без интерполяции (при
изменении угла в указанных пределах линейная интерполяция вносит ошибку уже
в 4-й знак, вот почему необходимо в этих
случаях пользоваться таблицей X).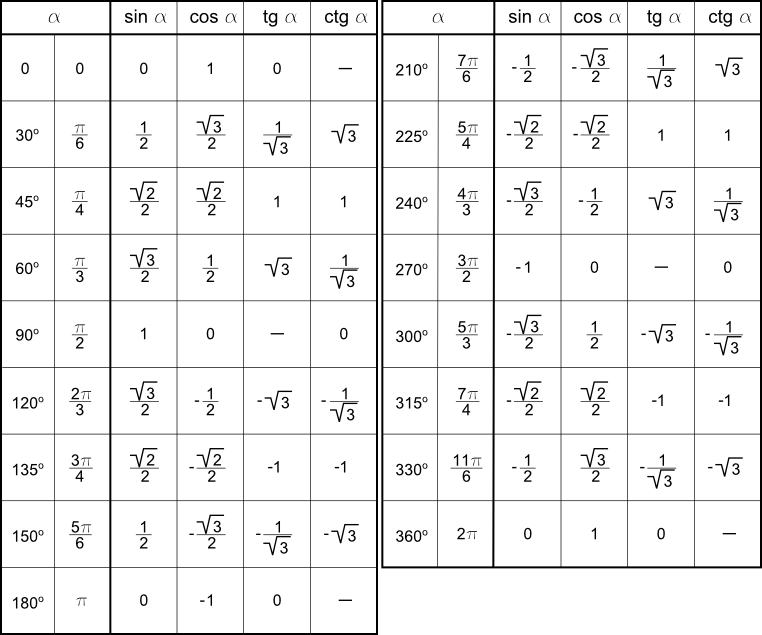 Также с помощью этой таблицы решается и
обратная задача – отыскание угла по заданному значению тангенса или котангенса
этого угла.
Также с помощью этой таблицы решается и
обратная задача – отыскание угла по заданному значению тангенса или котангенса
этого угла.
ПРИМЕР:
Найти sin 1,2610.
РЕШЕНИЕ:
Пользуясь таблицей, находим градусное выражение угла, содержащего 1,2610 радиана. Это угол 72°15‘.Тогда имеем:
sin 1,2610 = sin 72°15‘ = 0,9524.
ПРИМЕР:
Найти sin 0,0419 и tg 0,0419.
РЕШЕНИЕ:
Имеем:
sin 0,0419 = sin 2°24‘ = 0,0419,
tg 0,0419 = tg 2°24‘ = 0,0419,
Результаты показывают, что угол 2°24‘ настолько мал, что синус и тангенс этого угла имеют одинаковые первые четыре десятичных знака с радианной мерой этого угла.
ПРИМЕР:
Дано:
соs х = 0,7600.
Найти в радианах угол х.
РЕШЕНИЕ:
Сначала находим по таблице, что х = 40°32‘, а затем по таблице
х = 0,7075.
ПРИМЕР:
Вычислить
sin 1.
РЕШЕНИЕ:
Имеем:
sin 1 ≈ 57°18‘ ≈ 0,8415.
ПРИМЕР:
ВычислитьРЕШЕНИЕ:
Имеем:
Задания к уроку 4
Формула Sin Cos Tan — значения, таблица, примеры и часто задаваемые вопросы
Sin, Cos и Tan — это основные отношения тригонометрии, которые используются для изучения отношений между углами и соответствующими сторонами треугольника. Эти отношения изначально определены для прямоугольного треугольника с использованием теоремы Пифагора.
Что такое Sin Cos Tan в тригонометрии?
Давайте разберемся с Sin, Cos и Tan в тригонометрии, используя формулы и примеры.
Треугольник, один из углов которого равен 90° называется прямоугольным треугольником. У него есть стороны, называемые основанием, перпендикуляром (высотой) и гипотенузой. Прямоугольный треугольник следует теореме Пифагора.
Прямоугольный треугольник следует теореме Пифагора.
- Основание: Сторона, содержащая угол, называется основанием треугольника.
- Перпендикуляр (высота): Сторона, образующая 90° с основанием, называется перпендикуляром или высотой треугольника.
- Гипотенуза: Самая длинная сторона треугольника называется гипотенузой треугольника.
Sin, Cos и Tan — отношения сторон любого прямоугольного треугольника. В прямоугольном треугольнике ABC, приведенном выше для угла C, Sin, Cos и Tan составляют = Перпендикуляр / Основание = AB / BC
Значения Sin Cos Tan
Значения Sin, Cos и Tan представляют собой значения конкретных углов прямоугольного треугольника. В тригонометрии значения Sin, Cos и Tan различны для разных значений углов в треугольнике. Для каждого конкретного угла значения sin, cos и tan представляют собой фиксированное отношение сторон.
Далее в статье мы разберемся с формулами Sin Cos Tan.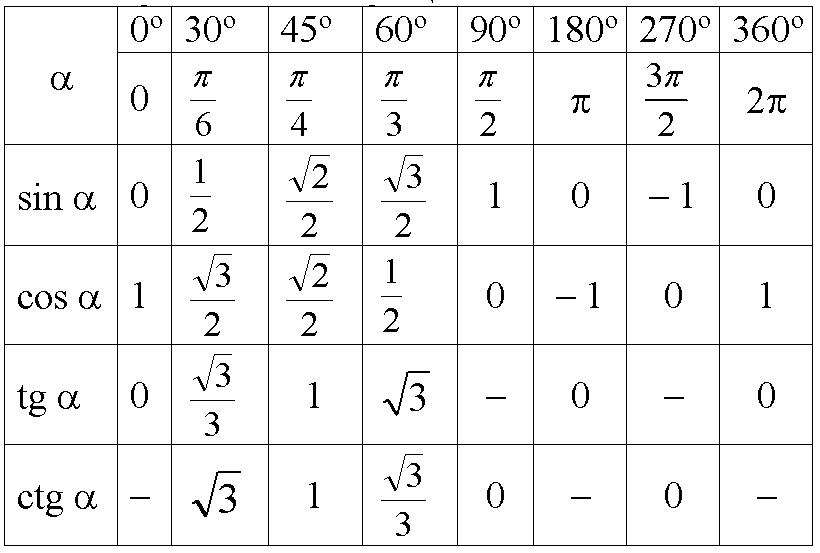
Формулы Sin Cos Tan
Функции Sin, Cos и Tan определяются как отношения сторон (противоположная, прилежащая и гипотенуза) прямоугольного треугольника. Формулы для любого угла θ sin, cos и tan:
- sin θ = Противоположный/Гипотенуза
- cos θ = Прилегающий/Гипотенуза
- tan θ = Противоположный/Примыкающий
Есть еще три гонометрические функции, которые обратны sin, cos и tan, которые являются cosec, sec и cot соответственно, таким образом,
- cosec θ = 1 / sin θ = гипотенуза / противоположность
- сек θ = 1 / cos θ = гипотенуза / соседняя
- Cot θ / 1 / tan θ = соседний / противоположный
Тригонометрические функции
Тригонометрические функции
функции также называют тригонометрическими отношениями. Существуют три основные и важные тригонометрические функции: синус, косинус и тангенс.
- Тригонометрическая функция синуса записывается как sin , косинус как cos, и тангенс как tan в тригонометрии.
- Есть еще три тригонометрические функции: cosec , sec и cot , , которые являются обратными sin , cos , и2 .
- Эти функции можно вычислить для прямоугольного треугольника.
Пусть прямоугольный треугольник с основанием b, перпендикуляром p и гипотенузой h образует с основанием угол θ. Тогда тригонометрические функции задаются следующим образом:
Трюк для запоминания SIN, COS, TAN CANTION
Тригонометрические функции
Формула тригонометрических функций
sin θ
1117 stindul (P / H)
COS θ
- COSθ = Base / Hypotenus0023
tan θ = sin θ/cos θ
- tanθ = perpendicular/base
- tanθ = p / b or θ = tan -1 ( p / b)
cosecθ = 1/sin θ
- cosecθ = гипотенуза/перпендикулярный
- cosecθ = h/p или θ = cosec -1 (H/p)
9017 Sec.
- сек θ = гипотенуза / основание
- secθ = h / b or θ = sec -1 (h / b)
cotθ = 1/tan θ
- cotθ = base/perpendicular
- cotθ = b / p или θ = COT -1 ( B / P)
Запомните
. производить красоту
Некоторые люди имеют sinθ (некоторые) = перпендикуляр(люди)/гипотенуза(есть) вьющиеся черные волосы производить красоту tanθ (to)= перпендикуляр(производить)/основание(красота) Тригонометрические функции для некоторых основных углов
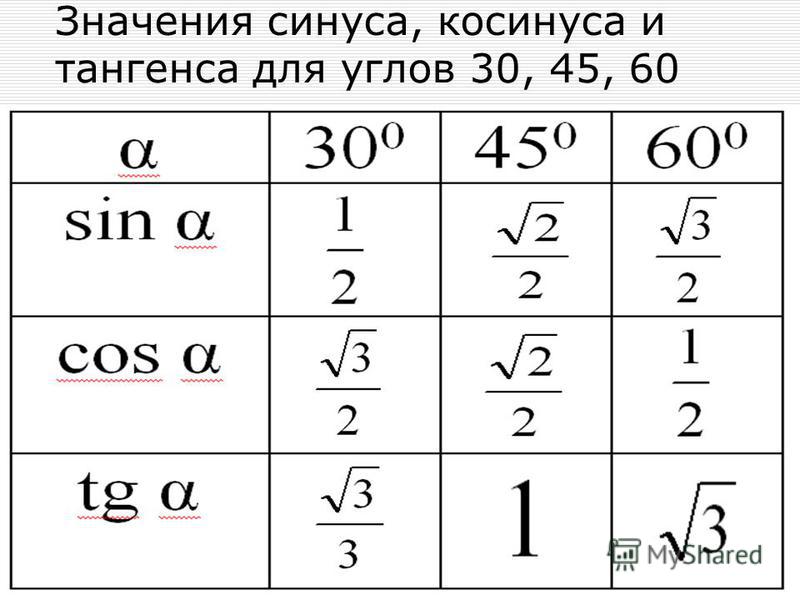
В тригонометрии основные углы 0°, 30°, 45°, 60° и 90°. В приведенной ниже тригонометрической таблице приведены значения тригонометрических функций для основных углов:
θ 0 ° 30 ° 45 ° 60 ° 90 ° SIN SIN SIN. 3/2
1 cos 1 √3/2 1/√2 1/2 0 tan 0 1/√3 1 √3 ∞ косек ∞ 2 √2 2/√3 1 1 2/√3 √2 2/√3 √2 2/√3 √2 2/√3 √2 2/√3 . ∞ √3 1 1/√3 0 SIN, COS, TAN Диаграмма
- . СИНА и COSECANT Функции являются положительными в первом и втором и втором и отрицательном в треть. четвертые квадранты.
- Функции косинуса и секанса положительны в первом и четвертом квадрантах и отрицательны во втором и третьем квадрантах.
- Функции тангенса и котангенса положительны в первом и третьем квадрантах и отрицательны во втором и четвертом квадрантах.
градусов Quadrant Знак греха Знак COS Знак TAN Знак COSEC Знак SEC Знак из COT Знак Знаки COT 0108 0 ° до 90 ° 1 ST Квадрант +(положительный) +(положительный) +(положительный) +(положительный) +(положительный) +(положительный) (положительный) (положительный) + (положительный) +(положительный) + (положительный +(положительный) 90 ° до 180 ° 2 ND Квадрант +(положительный) -(отрицательный) -(отрицательный) +(положительный) -негатив) (негатив) +(положительный) -негатив) +(положительный -(отрицательный) 180° до 270° 3 RD Квадрант -(отрицательный) -(отрицательный) +(положительный) -(отрицательный) -(отрицательный) +(положительный) 4 777777777777777777777777777777777777777777777777777777777777777777777 27 27 2777777777777 27 27777777777 27 27777777777 2777 360° 4 th quadrant –(negative) +(positive) -(negative) -(negative) +(positive) -(negative) Взаимные тождества
Функция косеканса является обратной функцией функции синуса и наоборот.
Точно так же функция секанса является обратной функцией функции косинуса, а функция котангенса является обратной функцией функции тангенса.
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ
- cosec θ = 1/sin θ
1 0 9 0 9 0 9 cts θ = 1/cos = 1/tan θPythagorean Identities
Pythagoras Идентификации тригонометрических функций:
- SIN 2 θ + COS 2 θ = 1
- SEC 2 2 θ = 1
- SEC 2 2 θ = 1
- SEC 2 2 .
- cosec 2 θ – cot 2 θ = 1
Идентификация отрицательного угла
Отрицательный угол функции косинуса всегда равен положительному косинусу угла, тогда как отрицательный угол функции синуса и тангенса равен отрицательному синусу и тангенсу угла.
- sin ( — θ) = — sin θ
- cos ( — θ) = cos θ
- tan ( — θ) = — tan θ
Также, проверьте
- Тригонометрические уровни
- ТРИДЕРИЧЕСКИЙ
Решенные примеры для формулы синуса косинуса тангенса
Пример 1: Стороны прямоугольного треугольника: основание = 3 см, перпендикуляр = 4 см, гипотенуза = 5 см.
Найдите значение sin θ, cos θ и tan θ.
Решение:
Учитывая, что
Основание (B) = 3 см,
Перпендикуляр (P) = 4 см
Гипотенуза (H) = 3 см
sinθ = P/H = 4/5
cosθ = B/H = 3/5
tanθ = P/H = 4/3
Пример 2. Стороны прямоугольного треугольника равны основанию = 3 см, перпендикуляру = 4 см и гипотенузе = 5 см. Найдите значение cosecθ, secθ и cotθ.
Решение:
Учитывая, что основание (b) = 3 см, перпендикуляр (p) = 4 см и гипотенуза (h) = 5 см
Из формулы тригонометрических функций: sinθ = H / P = 5/4
secθ = 1/cosθ = H / B= 5/3
cotθ = 1/tanθ = B / P = 3/4
Пример 3. Найдите θ, если основание = √3 и перпендикуляр = 1 прямоугольного треугольника.
Решение:
Поскольку перпендикуляр и основание прямоугольного треугольника заданы, используется тангенс θ.
tan θ = perpendicular/base
tan θ = 1/√3
θ = tan -1 (1/√3) [Из тригонометрической таблицы]
θ = 30 °
θ = 30 °
θ = 30 °
θ = 30 °
0012 Пример 4. Найдите θ, если основание = √3, а гипотенуза = 2 прямоугольного треугольника.Решение:
Поскольку основание и гипотенуза прямоугольного треугольника заданы, используется cosθ.
cos θ = base/hypotenuse
cos θ = √3/2
θ = cos -1 (√3/2) [Из тригонометрической таблицы]
= 30 °
Пример 5 30 °
9000 2 . : Найдите θ, если перпендикуляр = 1 и гипотенуза = 2 прямоугольного треугольника.Решение:
Поскольку перпендикуляр и гипотенуза прямоугольного треугольника заданы, используется sinθ.
sinθ = перпендикуляр/гипотенуза
sinθ = 1/2
θ = sin -1 (1/2) [Из тригонометрической таблицы]
= 30 °
FAQS на Sine Cosine Cosine Tangent Tangent Tangstent
029929929929929929292924.
Вопрос 1: Каковы значения sin 60°, cos 60° и tan 60°?Ответ:
Значения sin 60°, cos 60° и tan 60° is,
- sin 60° = √3/2
- cos 60° = 1/2
- tan 60° = 014
Вопрос 2: Каково значение sin 90°?
Ответ:
Значение sin 90° равно 1.
Вопрос 3: Какой угол в cos дает значение 0?
Ответ:
Угол в cos дает значение 0 равно 90° как cos 90° = 0
Вопрос 4: Как найти значение тангенса θ, используя sin θ и cos θ?
Ответ:
Значение TAN θ определяется формулой,
- TAN θ = sin θ/cos θ
Тригонометрия на пальцах — интуиция
9002 As Mays Kylow , тригонометрия — это раздел математики, изучающий отношения между длинами сторон и углами треугольников. В тригонометрии используются три основные функции: синус, косинус, тангенс, , которые обычно обозначаются как sin, cos, tan соответственно.
В тригонометрии используются три основные функции: синус, косинус, тангенс, , которые обычно обозначаются как sin, cos, tan соответственно. Давайте рассмотрим, что делает каждая из вышеперечисленных функций. Давайте также научимся делать тригонометрию на пальцах.
В непрямоугольных треугольниках мы используем законы синусов и законы косинусов для определения длин сторон и углов.
Тригонометрия широко используется во многих сферах нашей жизни, особенно в строительстве, астрономии, физике, электронной музыке, бортовой технике, морской технике, навигации, медицине, картографии, электричестве и т. д.
Давайте посмотрим на одно из практических применений тригонометрии в нашей жизни.
Задача :
Крыша вашего дома образует треугольник, как показано ниже.
Необходимо рассчитать длины скатов крыши AB и BC при заданных углах подъема A и C .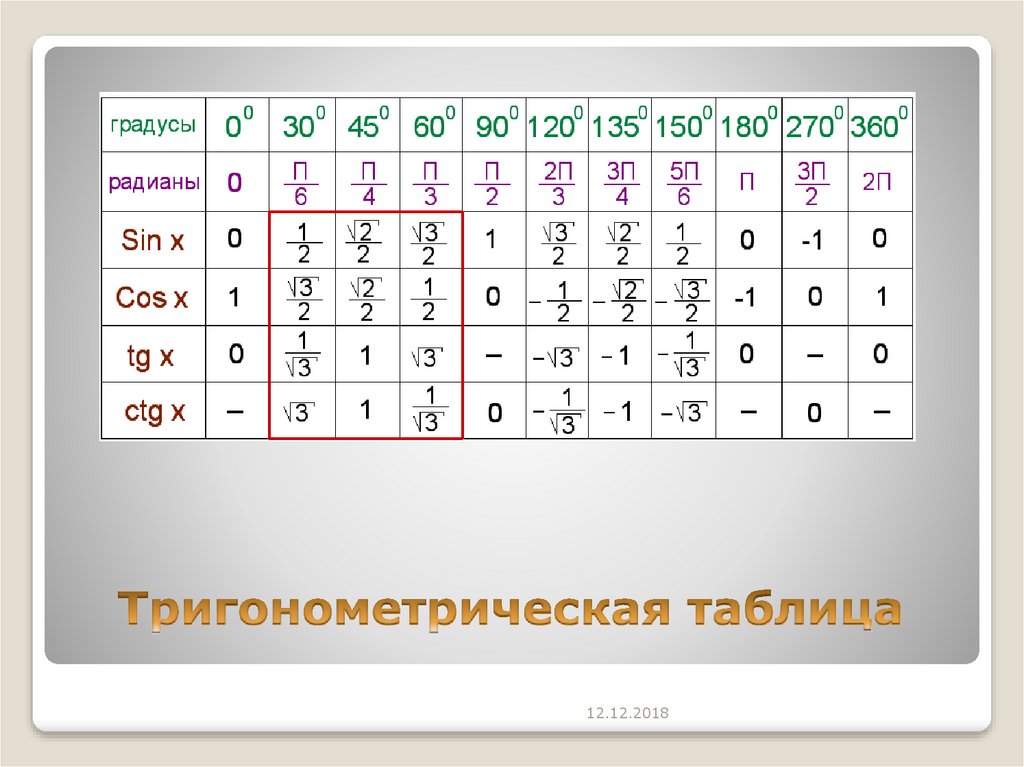 Мера угла B = 180 o – (A + B) = 180 o – (35 o + 41 o ) = 104 или .
Мера угла B = 180 o – (A + B) = 180 o – (35 o + 41 o ) = 104 или .
Теперь давайте рассмотрим еще одну задачу по тригонометрии, с которой мы обычно сталкиваемся в школе.
Нам часто приходится вычислять значения тригонометрических функций, таких как sin 41 , cos 30 , tan 90 , sin 45 , …. sin X , cos X , tan X и так далее .
Оценить значения этих функций для любого угла не так уж и просто, но есть некоторые из них, которые очень распространены и часто используются. Наиболее распространенные углы: 0, 30, 45, 60 и 90 , и для этих углов нам обычно приходится запоминать таблицу «Тригонометрических соотношений стандартных углов», которая может показаться сложной и похожей на «ракетостроение».
Хорошей новостью является то, что вы можете использовать пальцы левой руки, чтобы легко найти соотношение функций синуса и косинуса.


 3/2
3/2
 Точно так же функция секанса является обратной функцией функции косинуса, а функция котангенса является обратной функцией функции тангенса.
Точно так же функция секанса является обратной функцией функции косинуса, а функция котангенса является обратной функцией функции тангенса. Найдите значение sin θ, cos θ и tan θ.
Найдите значение sin θ, cos θ и tan θ. 
