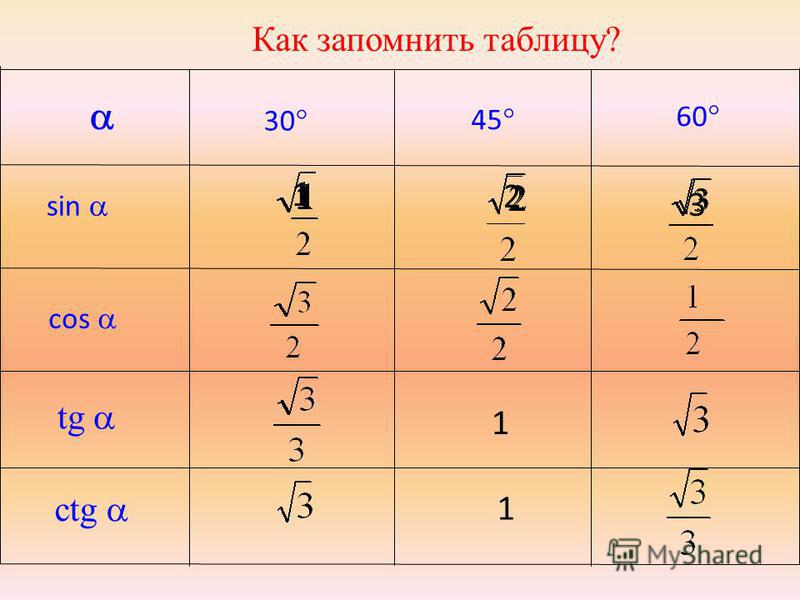
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |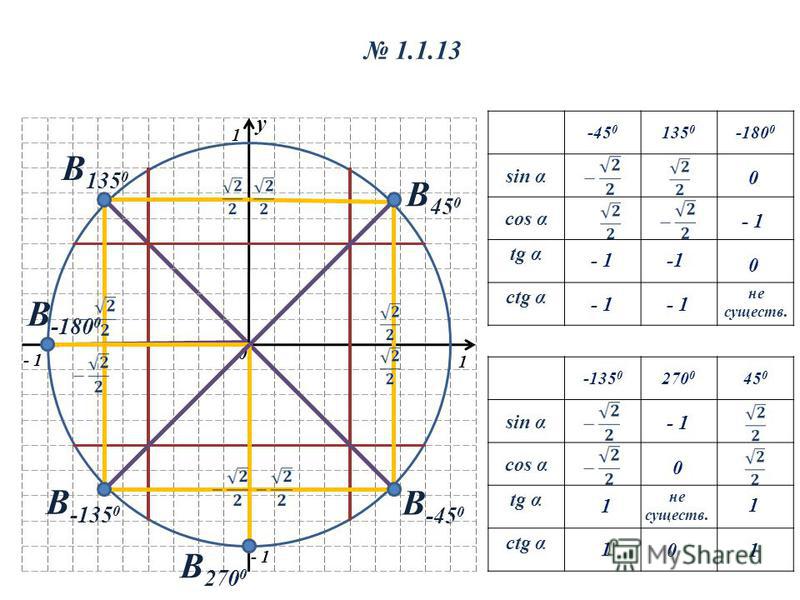
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |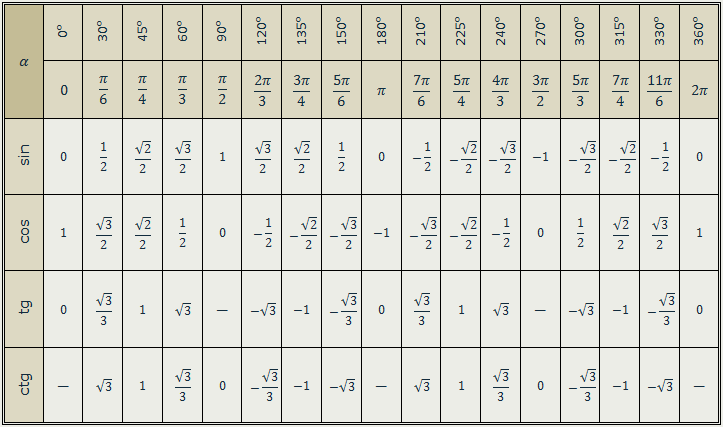
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |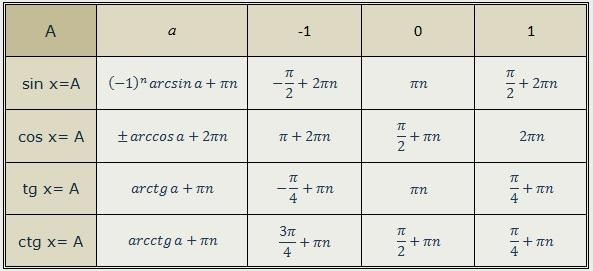
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | sin(120 град. ) | ||
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Значения косинуса
- Математические сомнения
- Тригонометрия
- Функции
- Косинус
Тригонометрическая функция косинуса дает значение для каждого угла прямоугольного треугольника и называется значением косинуса.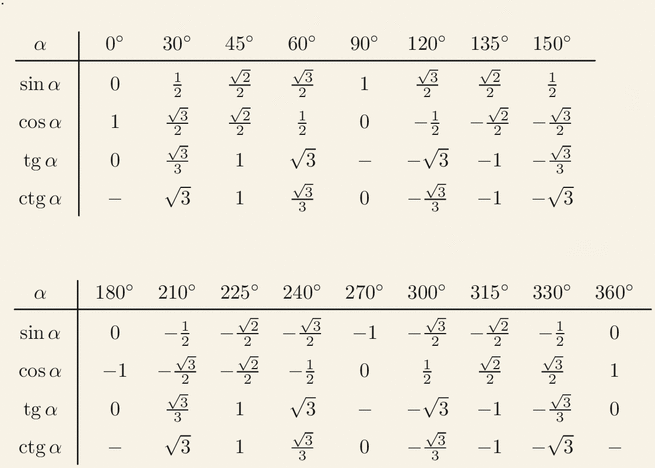
В тригонометрии существует несколько значений косинуса, но в основном используются пять значений косинуса, и они также используются для математического получения оставшихся значений функции косинуса.
Специальные значения функции косинуса для некоторых стандартных углов перечислены здесь с математическими доказательствами в табличной форме. Следующая диаграмма косинусов действительно полезна для изучения продвинутой тригонометрической математики. 92-x-6 = 0$ по методу факторинга
График Sin, Cos
График Sin, CosГрафик функций синуса и косинуса
График функции синуса. В качестве первого шага мы пройдемся по кругу и сгенерируем значения функций синуса и косинуса. Поскольку некоторые углы имеют особенно хорошие ответы, которые, похоже, нравятся составителям учебников, мы будем использовать углы, относящиеся к 30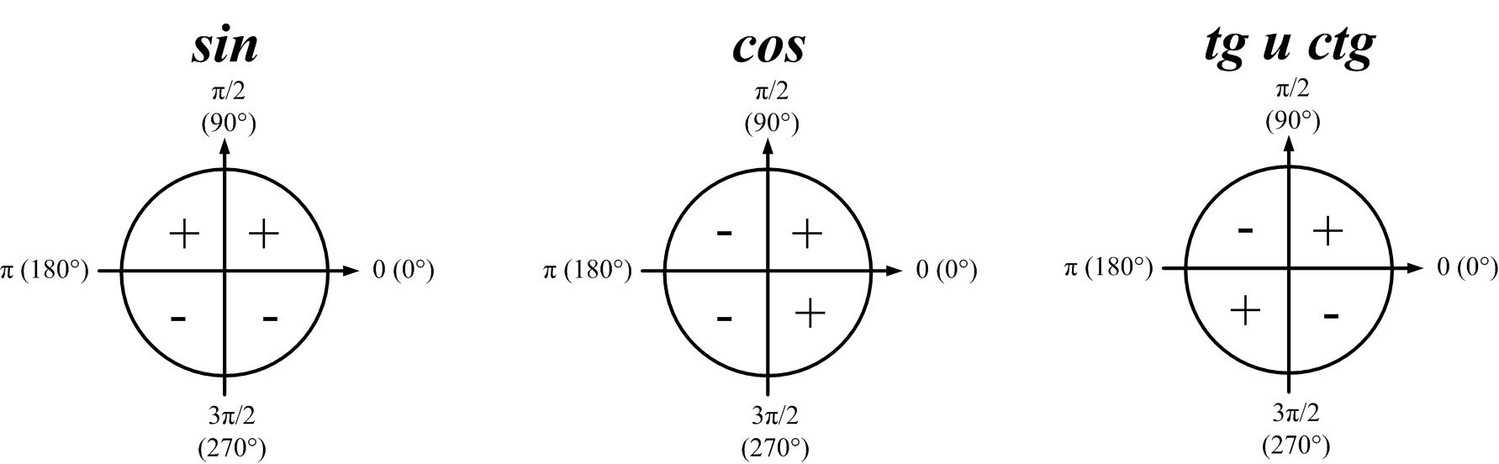 
Помните, что для единичного круга координата x точки — это косинус, а координата y точки — синус.
Из таблицы и графика видно несколько вещей. Во-первых, и синус, и косинус варьируются от -1 до +1. «Диапазон» функций синуса и косинуса составляет от -1 до +1, а домен включает все значения по оси x. Во-вторых, мы можем заметить, что когда x = 0, значение синуса равно 0. Таким образом, график синусоидальной функции будет начинаться в начале координат, увеличиваться до тех пор, пока не достигнет 1, затем уменьшаться до 0, затем станет отрицательным до -1 и, наконец, пойдет снова вернуться к 0.
Для синусоидальной функции заметим, что при x = 0 синусоидальная функция находится на средней линии (ось x в данном случае). По мере увеличения x функция увеличивается, достигая 1 в 90 или . Затем синус уменьшается, достигая 0 в точке 180 o , после чего становится отрицательным, достигая наконец -1 в точке 270 o . С этого момента до 360 o синус увеличивается, пока не вернется к 0 o .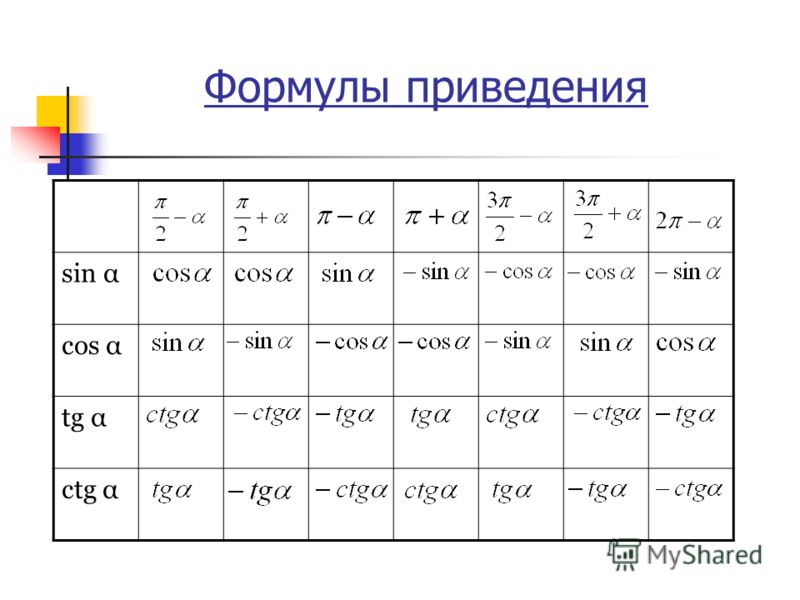
Для функции косинуса заметим, что при x = 0 функция косинуса максимальна, 1. По мере увеличения x функция уменьшается, достигая 0 при 90 o . Затем косинус становится отрицательным, достигая -1 в точке 180 o , после чего остается отрицательным, но приближается к 0, достигая, наконец, 0 в точке 270 или . С этого момента до 360 o косинус становится положительным и увеличивается.
| Угол | Синус(A) | Косинус(A) |
|---|---|---|
| 0 или | 0,0 | 1,0 |
| 30 или | 0,50 | 0,8660 |
| 45 или | 0,7071 | 0,7071 |
| 60 или | 0,8660 | 0,50 |
| 90 или | 1,0 | 0,0 |
| 120 o | 0,8660 | -0,50 |
| 135 o | 0,7071 | -0,7071 |
| 150 o | 0,5 | -0,8660 |
| 180 о | 0,0 | -1,0 |
| 210 или | -0,50 | -0,8660 |
| 225 o | -0,7071 | -0,7071 |
| 240 или | -0,8660 | -0,50 |
| 270 о | -1,0 | 0,0 |
| 300 o | -0,8660 | 0,50 |
| 315 o | -0,7071 | 0,7071 |
| 330 о | -0,50 | 0,8660 |
На рисунках ниже представлены графики функций синуса (рисунок слева) и косинуса (рисунок справа).