Пример числа которое является действительным но не является рациональным: натуральные, целые, рациональные, иррациональные, действительные

Какие числа называются Рациональными? Примеры и Определение

Поможем понять и полюбить математику

Начать учиться

190.2K

В переводе с латыни слово «рациональный» значит число, расчёт, нумерация, рассуждение, разум. Давайте узнаем, что значит рациональное число и перечислим его свойства.

Определение рациональных чисел

Рациональное число — это число, которое можно представить в виде положительной или отрицательной обыкновенной дроби или числа ноль. Если число можно получить делением двух целых чисел, то это число рациональное.

Рациональные числа — это те, которые можно представить в виде

где числитель m — целое число, а знаменатель n — натуральное число.

Рациональные числа – это все натуральные, целые числа, обыкновенные дроби, бесконечные периодические дроби и конечные десятичные дроби.

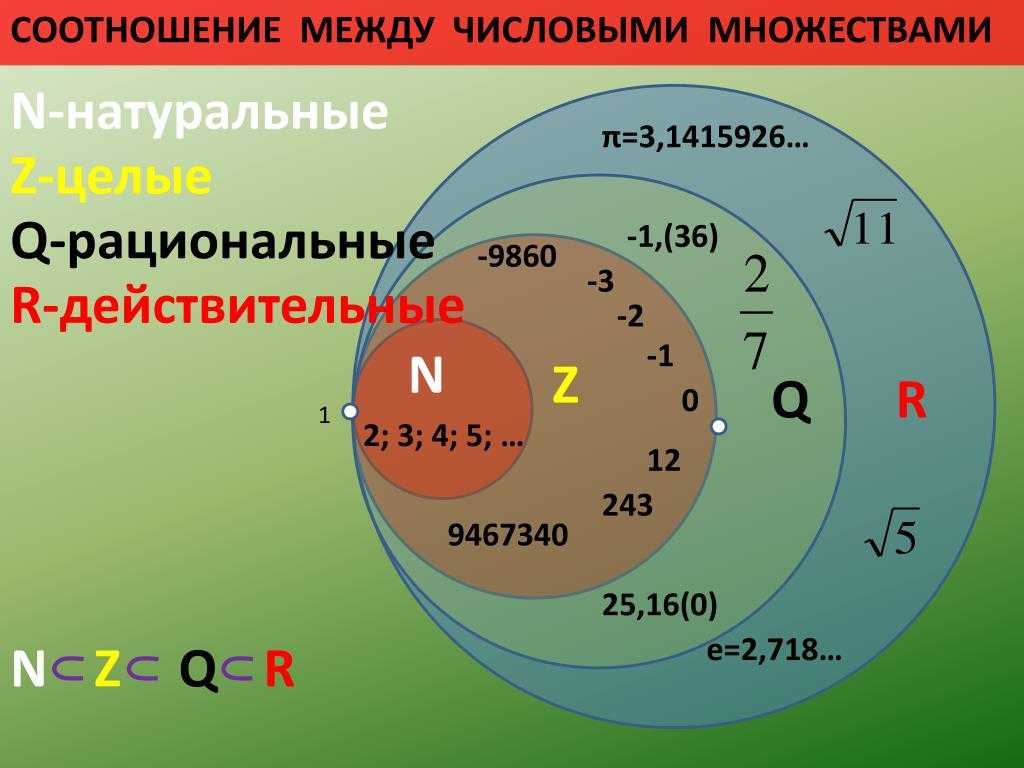
Множество рациональных чисел принято обозначать латинской буквой Q.

Примеры рациональных чисел:

• десятичная дробь 1,15 — это 115/100;
• десятичная дробь 0,5 — это 1/2;
• целое число 0 — это 0/1;
• целое число 6 — это 6/1;
• целое число 1 — это 1/1;
• бесконечная периодическая дробь 0,33333… — это 1/3;
• смешанное число — это 25/10;
• отрицательная десятичная дробь -3,16 — это -316/100.

 

Узнай, какие профессии будущего тебе подойдут

Пройди тест — и мы покажем, кем ты можешь стать, а ещё пришлём подробный гайд, как реализовать себя уже сейчас

Свойства рациональных чисел

У рациональных чисел есть определенные законы и ряд свойств — рассмотрим каждый их них. Пусть а, b и c — любые рациональные числа.

Основные свойства действий с рациональными числами Переместительное свойство сложения: a + b = b + a. Сочетательное свойство сложения: (a + b) +c = a + (b + c). Сложение рационального числа и нейтрального элемента (нуля) не изменяет это число: a + 0 = a. У каждого рационального числа есть противоположное число, а их сумма всегда равна нулю: a + (-a) = 0. Переместительное свойство умножения: ab = ba. Сочетательное свойство умножения: (a * b) * c = a * (b * c). Произведение рационального числа и едины не изменяет это число: a * 1 = a. У каждого отличного от нуля рационального числа есть обратное число. Их произведение равно единице: a * a−1 = 1. Распределительное свойство умножения относительно сложения: a * (b + c) = a * b + a * c.

Кроме основных перечисленных есть еще ряд свойств:

 

1. Правило умножения рациональных чисел с разными знаками: (-a) * b = -ab. Такая фраза поможет запомнить: «плюс на минус есть минус, и минус на плюс есть минус».


2. Правило умножения отрицательных рациональных чисел: (−a) * (−b) = ab. Запомнить поможет фраза: «минус на минус есть плюс».


3. Правило умножении произвольного рационального числа на нуль: a * 0 = 0 или 0 * a = 0. Докажем это свойство.

   Мы знаем, что 0 = d + (-d) для любого рационального d, значит a * 0 = a * (d + (-d)).

   Распределительный закон позволяет переписать выражение:

   a * d + a * (−d), а так как a * (−d) = -ad, то a * d + a * (-d) = a * d + (-ad).

   Так получилась сумма двух противоположных чисел, которая в результате дает нуль, что доказывает равенство a * 0 = 0.

Мы перечислили только свойства сложения и умножения.

На множестве рациональных чисел вычитание и деление можно записать, как обратные к сложению и умножению. То есть, разность (a — b) можно записать, как сумму a + (-b), а частное a/b равно произведению a * b−1, при b ≠ 0.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Определение иррационального числа

Иррациональное число — это действительное число, которое невозможно выразить в форме деления двух целых чисел, то есть в рациональной дроби

Оно может быть выражено в форме бесконечной непериодической десятичной дроби.

Бесконечная периодическая десятичная дробь — это такая дробь, десятичные знаки которой повторяются в виде группы цифр или одного и того же числа.

Примеры:

• π = 3,1415926…
• √2 = 1,41421356. ..
• e = 2,71828182…
• √8 = 2.828427…
• -√11= -3.31662…

Обозначение множества иррациональных чисел: латинская буква I.

Действительные или вещественные числа — это все рациональные и иррациональные числа: положительные, отрицательные и нуль.

Свойства иррациональных чисел:

• результат суммы иррационального числа и рационального равен иррациональному числу;
• результат умножения иррационального числа на любое рациональное число (≠ 0) равен иррациональному числу;
• результат вычитания двух иррациональных чисел равен иррациональному числу или рациональному;
• результат суммы или произведения двух иррациональных чисел равен рациональному или иррациональному, например: √2 * √8 = √16 = 4).

Различие между целыми, натуральными и рациональными числами

Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое: один банан, две тетрадки, десять стульев.

А вот, что точно не является натуральным числом:

• Нуль — целое число, которое при сложении или вычитании с любыми числами в результате даст то же число. Умножение на ноль дает ноль.
• Отрицательные числа: -1, -2, -3, -4.
• Дроби: 1/2, 3/4, 5/6.

Целые числа — это натуральные числа, противоположные им и нуль.

Если два числа отличаются друг от друга знаком — их называют противоположными: +2 и -2, +7 и -7. Знак «плюс» обычно не пишут, и если перед числом нет никакого знака, значит оно положительное. Числа, перед которыми стоит знак «минус», называют отрицательными.

Какие числа называются рациональными мы уже знаем из первой части статьи. Повторим еще раз.

Рациональные числа — это конечные дроби и бесконечные периодические дроби.

Например:

Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит целым числам, а знаменатель — натуральным. Поэтому во множество рациональных чисел входит множество целых и натуральных чисел.

Но не все числа можно назвать рациональными. Например, бесконечные непериодические дроби не принадлежат множеству рациональных чисел. Так √3 или 𝜋 (число пи) нельзя назвать рациональными числами.

 

Шпаргалки для родителей по математике

Все формулы по математике под рукой

Лидия Казанцева

Автор Skysmart

К предыдущей статье

159.8K

Как найти среднюю линию треугольника?

К следующей статье

530. 4K

Теория вероятностей, формулы и примеры

Получите план обучения, который поможет понять и полюбить математику

На вводном уроке с методистом

1. Выявим пробелы в знаниях и дадим советы по обучению

2. Расскажем, как проходят занятия

3. Подберём курс

Является ли каждое действительное число рациональным или иррациональным? – Обзоры Вики

Это действительные числа, которые мы не можем записать как отношение pq, где p и q — целые числа, при этом q≠0. По факту, каждое действительное число является либо рациональным числом, либо иррациональным числом. Никакое число не может быть одновременно рациональным и иррациональным!

Следовательно, является ли каждое натуральное число действительным числом? Да, цель не каждое действительное число является натуральным числом. Натуральные числа — это набор целых положительных чисел {1, 2, 3,…}, которые также являются действительными числами. Однако действительные числа также включают отрицательные числа, дроби и т. д., ни одно из которых не является натуральным числом.

Всякое ли иррациональное число является рациональным числом? «Является каждый иррациональный рациональное число?» Нет. Рациональные числа — это те, которые могут быть выражены как отношение (доля) двух целых чисел; иррациональные числа — это те, которые не могут быть выражены таким образом. Между этими двумя категориями нет пересечения.

Дополнительно Что такое каждое иррациональное число? иррациональное число, любое действительное число, которое не может быть выражено как частное двух целых чисел. Например, среди целых чисел и дробей нет числа, равного квадратному корню из 2. … Каждое иррациональное число может быть выражено как бесконечное десятичное расширение без регулярно повторяющихся цифр или групп цифр.

Как иррациональные числа используются в реальной жизни? Инженерные револьверы по конструированию вещей для реальной жизни и несколько вещей, таких как обработка сигналов, расчет силы, спидометр и т. д. использовать иррациональные числа. Исчисление и другие области математики, в которых используются эти иррациональные числа, широко используются в реальной жизни. Иррациональные числа используются косвенно.

Что такое каждое рациональное число?

Каждое рациональное число целое число.

Всякое ли иррациональное число является целым числом? Поскольку иррациональные числа не могут быть выражены как отношение двух целых чисел, отсюда следует, что иррациональные числа не могут быть целыми числами, и наоборот.

Что такое действительные и рациональные числа? Рациональными считаются числа, которые можно представить в виде отношения двух целых чисел, причем знаменатель не равен нулю. Действительные числа – это те, которые может быть представлен на действительной числовой прямой. … не может быть выражено как отношение двух целых чисел, как рациональные числа, но может быть представлено в прямой числовой строке.

Как действительные числа используются в реальной жизни?

Большинство чисел, с которыми мы работаем каждый день, являются действительными числами. . К ним относятся все деньги в вашем кошельке, статистика, которую вы видите в спорте, или измерения, которые мы видим в поваренных книгах. Все эти числа можно представить в виде дроби (нравится нам это или нет).

Также Каковы примеры действительных чисел? В математике действительное число — это значение непрерывной величины, которое может представлять расстояние вдоль линии. Реальные числа включают как рациональные, так и иррациональные числа. Рациональные числа, такие как целые числа (-5, 0, 9), дроби (1/2,7, 8/2.5, 7) и иррациональные числа, такие как √XNUMX, π и т. д., являются действительными числами.

Всякое ли целое число является рациональным числом?

Рациональное число — это число, которое может быть выражено в виде p/q, где q не должно быть равно 0… Но это не целое число, а десятичное. Таким образом, рациональное число может быть или не быть целым числом, но каждое целое число является рациональным числом.

Реально или рационально? Число рациональное (записывается как отношение двух целых чисел), но оно также реальные . Все рациональные числа также являются действительными числами.
…

Тип десятичной дроби	Рациональный или иррациональный	Примеры
Нагрузочный	Рациональный	0.25 (золото) 1.3 (золото)
Непрерывный и повторяющийся	Рациональный	0.66… (золото) 3.242424… (золото)

Что такое действительные числа и недействительные числа?

Реальные числа могут быть положительными или отрицательными.и включите число ноль. Их называют действительными числами, потому что они не являются мнимыми, а это другая система чисел. Мнимые числа — это числа, которые невозможно определить количественно, например квадратный корень из -1.

Что такое недействительные числа?

Наблюдения и советы этой статьи мы подготовили на основании опыта команды числа не действительные, а мнимые называются недействительными или недействительными числами. Недействительные числа не могут быть представлены на числовой прямой. I. Комплексные числа: 4+i5 , где «i» представляет йоту, которая равна √−1 .

Как найти действительные числа? Абсолютное значение числа — это его расстояние от нуля на числовой прямой. Действительные числа — это числа, которые не являются мнимыми, то есть все числа, кроме квадратного корня из -1 и бесконечности. Чтобы найти абсолютное значение действительного числа, найдите его расстояние от нуль в числовой строке.

Что такое рациональное и иррациональное число? Рациональные числа – это те числа, которые целые и может быть выражено в виде x/y, где и числитель, и знаменатель являются целыми числами, тогда как иррациональные числа — это те числа, которые не могут быть выражены дробью. … Иррациональные числа включают surds и специальные числа, такие как π.

Что такое рациональное и иррациональное число на примере?

Рациональное число — это число, которое можно представить в виде P/Q, где P и Q — целые числа, а Q ≠ 0.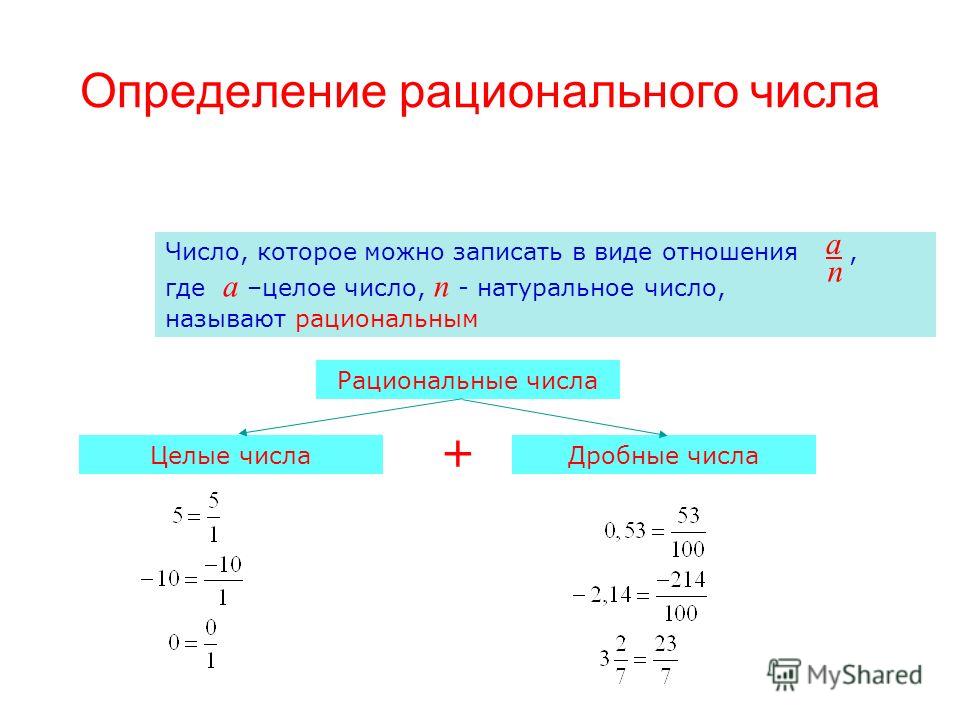 Но иррациональное число нельзя записать в виде простых дробей. ⅔ это пример рациональных чисел, тогда как √2 — иррациональное число.

Почему каждое рациональное число является действительным числом? Верно или ложно? Ага это правда….

Что такое действительное число в математике?

действительное число, в математике, количество, которое может быть выражено в виде бесконечного десятичного разложения. … Действительные числа включают положительные и отрицательные целые числа и дроби (или рациональные числа), а также иррациональные числа.

Что такое рациональные и иррациональные числа? Рациональные числа — это числа, которые можно представить в виде дроби или части целого числа.. (примеры: -7, 2/3, 3.75) Иррациональные числа — это числа, которые нельзя представить в виде дроби или отношения двух целых чисел. Нет конечного способа выразить их. (примеры: √2, π, е)

Что такое реальное число 10-го класса?

Реальные числа просто комбинация рациональных и иррациональных чисел, в системе счисления. В общем, над этими числами можно производить все арифметические действия, и их можно представить в числовой строке.

Ноль реальный или мнимый? Квадрат мнимого числа bi равен −b². Например, 5i — мнимое число, а его квадрат равен −25. По определению, ноль считается как действительным, так и мнимым.

Иррациональные числа

Иррациональное число — это действительное число, которое нельзя записать в виде простой дроби:

  1,5 рационально, но π иррационально

Иррациональное означает

Нерациональное (без соотношения)

Давайте посмотрим, что делает число рациональным или иррациональным…

Рациональные числа

A Rational Число можно записать как 0003 Отношение двух целых чисел (т.е. простой дроби).

Пример: 1,5 является рациональным, поскольку его можно записать как отношение 3/2

Пример: 7 рационально, потому что его можно записать как отношение 7/1

Пример 0,333. .. (3 повторения) также является рациональным, поскольку его можно записать как отношение 1/3

 

Иррациональные числа

Но некоторые цифры нельзя записать как отношение двух целых чисел…

…их называют Иррациональные Числа .

Пример:

π (Pi) — известное иррациональное число.

π  = 3,1415926535897932384626433832795… (и больше)

Мы не можем s записать простую дробь, которая равна Пи.

Популярное приближение ²² / ₇ = 3,1428571428571… близко, но неточное .

Еще одна подсказка заключается в том, что десятичная дробь продолжается вечно, не повторяясь.

Не может быть записан как дробь

Это иррационально потому что его нельзя записать как отношение (или дробь),
не потому что это безумие!

Таким образом, мы можем определить, является ли число рациональным или иррациональным, попробовав записать число в виде простой дроби.

Пример:

9,5 можно записать в виде простой дроби следующим образом:

9,5 = 19 2

Итак, это рациональное число (и поэтому не иррациональное )

Вот еще несколько примеров:

Номер		Как дробь		Рациональное или Иррациональное?
1,75		7 4		Рационал
.001		1 1000		Рационал
√2 (квадратный корень из 2)		?		Неразумно !

Квадратный корень из 2

Давайте посмотрим на квадратный корень из 2 более внимательно.

Когда мы рисуем квадрат размера «1», каково расстояние по диагонали?

Ответ: квадратный корень из 2 , который равен 1.4142135623730950…(и т.д.)

… на самом деле мы не может записать квадратный корень из 2, используя отношение двух чисел…

… (вы можете узнать , почему , на странице «Иррационально ли это?»)…

… и так мы знаем это иррациональное число .

Известные иррациональные числа

		Пи — известное иррациональное число. Люди вычислили число Пи с точностью до квадриллиона знаков после запятой, но закономерности до сих пор нет. Первые несколько цифр выглядят так: 3.1415926535897932384626433832795 (и еще…)
		Число e (число Эйлера) — еще одно известное иррациональное число. Люди также вычислили e до большого количества знаков после запятой без какой-либо закономерности. Первые несколько цифр выглядят так: . 2,7182818284590452353602874713527 (и еще…)
		Золотое сечение — иррациональное число. Первые несколько цифр выглядят так: . 1.61803398874989484820… (и еще…)
		Многие квадратные корни, кубические корни и т. д. также являются иррациональными числами. Примеры: √3 1.7320508075688772935274463415059 (и т. д.) √99 9,9498743710661995473447982100121 (и т. д.)

Но √4 = 2 рационально, а √9 = 3 рационально. ..

… так что не все корни иррациональны.

 

Примечание по умножению иррациональных чисел

Взгляните на это:

• π × π = π ² известно, что иррационально
• Но √2 × √2 = 2 равно рациональному

Так что будьте осторожны… умножение иррациональных чисел может дать рациональное число!

 

Забавные факты….

По-видимому Гиппас (один из учеников Пифагора) открыл иррациональные числа при попытке записать квадратный корень из 2 в виде дроби (считается, что с помощью геометрии). Вместо этого он доказал квадратный корень из 2·9.0093 нельзя было записать в виде дроби, поэтому иррационально .

Но последователи Пифагора не могли принять существование иррациональных чисел, и говорят, что Гиппас был утоплен в море в наказание богов!

 

434 435 1064 2022 3987 1065 3988 2023 2990 2991

Существуют ли действительные числа, которые не являются ни рациональными, ни иррациональными?

Конечно, «традиционный» ответ — нет, не существует действительных чисел, которые не были бы ни рациональными, ни иррациональными. Однако, будучи противоположным человеком, позвольте мне предложить альтернативную интерпретацию, которая дает другой ответ.

Что делать, если вы используете интуитивистскую логику? — ПиРулез

В интуиционистской логике, где отвергается закон исключенного третьего (LEM) $P\vee\lnot P$, все становится несколько сложнее. Пусть $x\in \Bbb Q$ означает, что существуют два целых числа $p,q$, для которых $x=p/q$. Тогда традиционная интерпретация «$x$ иррациональна» — это $\lnot(x\in\Bbb Q)$, но вместо этого мы будем называть это «$x$ иррационально». Утверждение «$x$ не рационально», то есть $\lnot\lnot(x\in\Bbb Q)$, подразумевается $x\in\Bbb Q$, но не эквивалентно ему. 9{-\mu}$, где $x$ — приближаемое действительное число, $p/q$ — рациональное приближение, а $\mu$ — положительная действительная постоянная. Мы измеряем точность аппроксимации величиной $|x-p/q|$, но не позволяем знаменателю (а значит, и числителю, поскольку $p/q$ близко к $x$) быть слишком большими, требуя, чтобы аппроксимация быть в степени $q$. Чем больше $\mu$, тем меньше пар $(p,q)$ удовлетворяют уравнению, поэтому мы можем найти наименьшую верхнюю границу $\mu$ такую, что существует бесконечно много взаимно простых решений $(p,q)$ к уравнению, и это определяет меру иррациональности $\mu(x)$. Есть хорошая теорема из теории чисел, которая гласит, что мера иррациональности любого иррационального алгебраического числа равна $2$, а мера иррациональности трансцендентного числа равна $\ge2$, а мера иррациональности любого рационального числа равна $1$. 9{-2}$ имеет бесконечно много взаимно простых решений. Тогда $x\in\Bbb I\to x\notin\Bbb Q$, т.е. иррациональное число нерационально, а в классической логике $x\in\Bbb I\leftrightarrow x\notin\Bbb Q$, значит, это эквивалентно обычному определению иррационального. Это определение считается более конструктивным, потому что оно не утверждает отрицательное (что $x=p/q$ приводит к противоречию), а дает бесконечную последовательность хороших приближений, подтверждающих иррациональность числа.