«знаки синуса косинуса тангенса и котангенса »
МОУ Луговская СОШ
Урок алгебры в 9 классе по теме
«Знаки синуса, косинуса, тангенса и котангенса .»
Учитель Коробенко И.В.
стаж работы 13 лет
2007 год
Цель:
— выяснить, какие знаки имеют синус, косинус и тангенс в
различных четвертях;
— формировать способность к использованию знаков
тригонометрических функций для упрощения выражений и
нахождения значений выражений.
— развивать умение классифицировать и устанавливать
взаимосвязи, формировать умение работать самостоятельно;
— тренировать способность к рефлексии собственной
деятельности.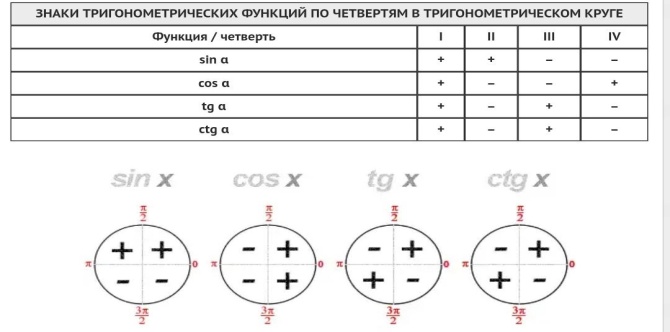
Тип урока: изучение и первичное закрепление нового материала.
Организационные формы урока: парная, групповая, индивидуальная.
Методы: деятельностный.
Средства обучения: учебник, таблица значений тригонометрических
функций для углов 30, 45, 60, 90. Карточки с
дифференцированной самостоятельной работой для
работы в парах .
Организационный момент.
Актуализация знаний
У. Какую тему изучаем?
Д. Тригонометрические выражения.
У. Что узнали на прошлом уроке по теме «Тригонометрические выражения»?
Д. Определение синуса, косинуса, тангенса и котангенса угла α.
У. Дайте определение синуса, косинуса, тангенса и котангенса угла α (Слайд 1)
Д.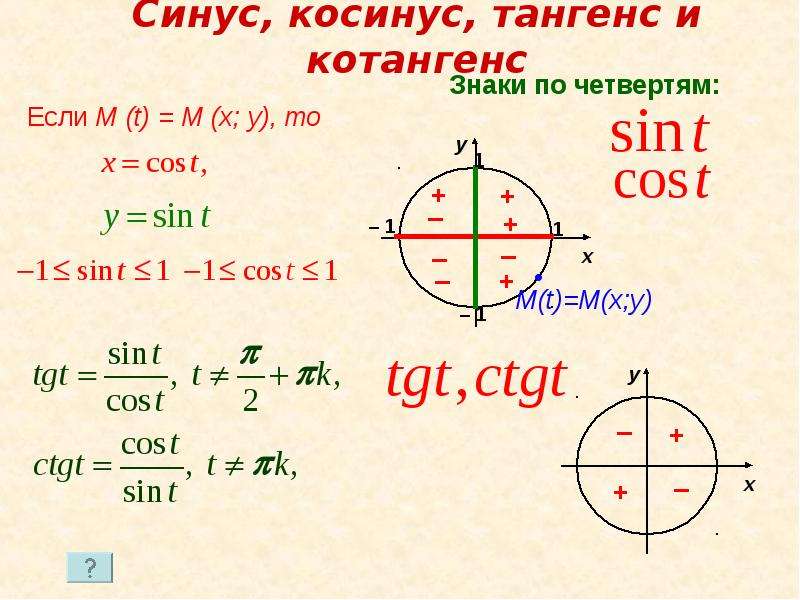 Рассказывают
определение синуса, косинуса, тангенса
и котангенса угла α..
Рассказывают
определение синуса, косинуса, тангенса
и котангенса угла α..
У. Для какого значения α тангенс не определен? Почему?
Д. Для угла 90. Тангенс – это отношение синуса угла α к косинусу угла α, косинус 90 равен 0, а делить на 0 нельзя.
У. Для того, чтобы проверить свои знания по теме тригонометрические выражения, предлагаю вам сыграть в игру «Тригонометрические шахматы»
Д. Выполняют работу по вариантам с проверкой в парах.
У. Проверьте свои ответы.
Ответы первого и второго варианта равны.
У. Что помогло быстро найти значения тригонометрических выражений?
Д. Знание таблицы значений синуса, косинуса, тангенса и котангенса углов 0, 30, 45, 60, 90.
Сообщение темы и целей урока.
У. На сколько групп можно разбить данные углы?
0, 30, 45, 90, 120, 135, 150, 180, 210, 225, 240, 270, 300, 315, 330, 360 (Слайд 2).
Д. На четыре группы
по четвертям, в которых находятся углы.
У. Значениями тригонометрических функций для углов 0, 30, 45, 60, 90 вы уже владеете и умеете применять на практике, но для удобства нахождения значения тригонометрических выражений математики нашли значения синуса, косинуса, тангенса и котангенса для этих углов.
Слайд 3.
У. Проведем наблюдение. Рассмотрите таблицу. В чем отличие значений тригонометрических функций первой четверти от остальных значений?
Д. Появляются отрицательные значения (отличаются знаками).
У. Попробуйте сформулировать тему урока (Слайд 4).
Д. Формулируют тему урока.
У, Попробуйте сформулировать цель урока, используя слова узнать и учиться.
Д, Формулируют цель урока.
У. Как вы думаете, зачем надо знать какие знаки имеют тригонометрические функции в той или иной четверти?
Д. Высказывают свои мнения.
У. Где используются эти знания?
Д. Предлагают свои варианты.
У. С одним великим
астрономом, математиком и физиком мне
хотелось бы вас сегодня познакомить.
Гаусс Карл Фридрих (1777-1855) – немецкий математик, астроном и физик. Еще студентом написал «Арифметические исследования», определившие развитие теории чисел до нашего времени. Занимался геодезией и вычислительной астрономией.
«Не считать ничего сделанным, если еще кое – что осталось сделать». К.Ф. Гаусс
У. О чем заставляют задуматься эти слова?
Д. Высказывают свое мнение.
У. Любое дело начатое вами должно быть закончено.
У.Попробуйте сформулировать свое предположение. Отчего зависят знаки тригонометрических функций?
Д. Высказывают свои предположения.
У. Вы считаете, что зависят от четверти, тогда попробуйте определить знаки синуса, косинуса, тангенса и котангенса угла в каждой четверти. Работать будете в группах. Заполните карточку № 1 (приложение №1 ).
Д. Заполненную карточку крепят к доске.
У. Итак, вы считаете,
что знаки тригонометрических функций
зависят от четверти, в которой расположен
угол, и знаки по четвертям распределяются
следующим образом.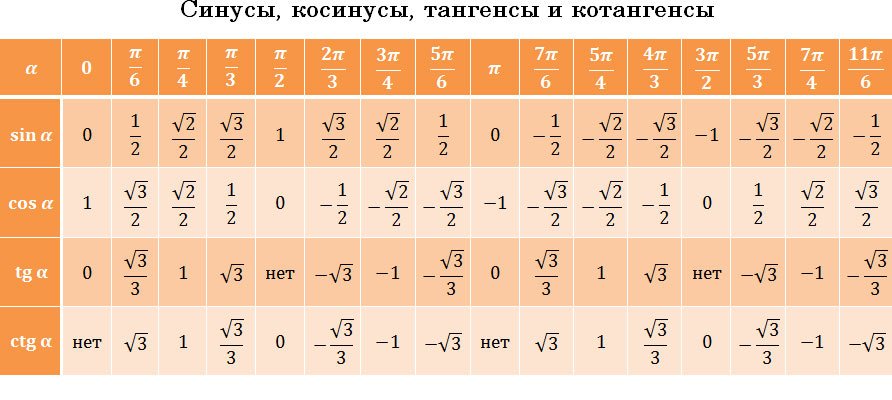
Формирование новых знаний (работа в группах).
У. Это предположение вам предстоит проверить, работая в группах.
У. Прочитайте п.29 учебника. Ответьте на следующие вопросы (Слайд 5).
— Какие знаки имеют sinα, cosα, tgα и ctgα в каждой из координатных четвертей?
— Попробуйте объяснить распределение знаков тригонометрических функций по четвертям (слайд 4).
У. Если после чтения п. 29 вы изменили мнение о распределении знаков по четвертям, можете карточку №1 заменить на карточку № 2.
Д. Работаю в группах.
У. Проверим работу каждой группы.
Д. Отвечают на вопрос и поясняют знаки каждой тригонометрической функции по четвертям.
Первичное закрепление (Физминутка).
У. Вы плодотворно потрудились, пришло время для физминутки.
1. Зарядка для глаз (слайд № 6).
У. на тригонометрическом
круге найдите четверти в которых sinα
положителен, cosα
отрицателен, tgα
и ctgα
положительны.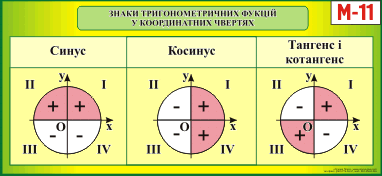
2. Физминутка.
У. Пробуем применить полученные знания на практике. Какой знак имеют sinα, cosα, tgα и ctgα для углов. Если «+», то встаньте, а если «-«, то вставать не надо.
На доске таблица
Α | sinα, | cosα, | tgα | Ctgα |
48 | + | + | + | + |
137 | + | — | — | — |
200 | — | — | + | + |
306 | — | + | — | — |
Знаки тригонометрических
функций закрыты.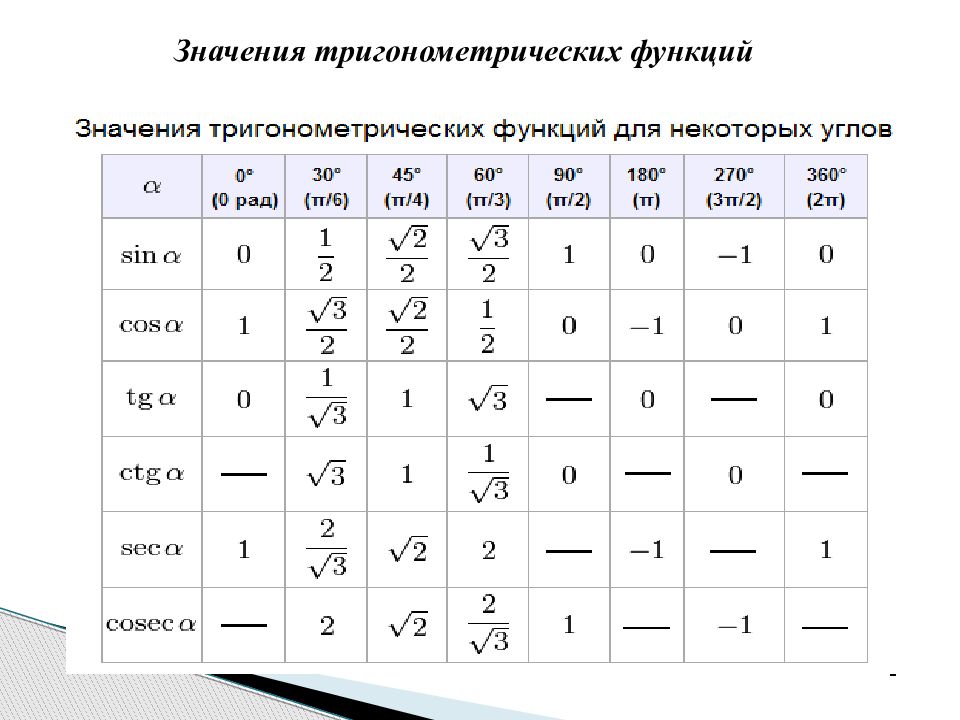 Учитель показывает
угол и функцию. Постепенно учитель
открывает всю таблицу.
Учитель показывает
угол и функцию. Постепенно учитель
открывает всю таблицу.
Тренировочные упражнения. Дифференцированная самостоятельная работа в парах.
У. Теперь вы готовы выполнять тренировочные упражнения, работая в парах.
Карточка № 3 Приложение № 2)
Д. Работают самостоятельно, проверяя правильность выполнения заданий в парах.
Итог урока.
У. Пришло время подвести итог урока.
У. Какова тема урока?
У. Что важно запомнить ?
У. Где можете применить знания, полученные на уроке?
У. Какие ошибки допустили? И почему?
— У вас на столах лежат карточки приготовьтесь выполнить задание с этими карточками. Распределитесь на пары. Каждая пара, выходя к доске, встает в нужную координатную четверть. Обоснуйте свой выбор.
Дети выполняют значение.
У. Вспомним слова Гаусса. Что еще надо сделать на этом уроке, чтобы урок считать законченным?
Д. Оценить свою
работу.
Оценить свою
работу.
Рефлексия.
У. Оцените свою работу на уроке, оцените работу группы и оцените урок.
Домашнее задание.
Приложение 1.
Карточка № 1, № 2.
у
у
х х
у
у
х х
Приложение 2.
Вариант I. | Вариант
II. | ||
А -1 | А – 1 | ||
Выясните, какой знак имеет выражение, и выпишите только со знаком «+» со знаком «-« sin179, cos280, tg175, ctg359, cos410, tg500, sin(-75), cos(-116). | |||
Проверка. Если у вас нет совпадений, то вы выполнили задание верно. | |||
А-2 | А-2 | ||
Определите знак выражения и выпишите только положительные отрицательные sin100 cos300, sin190 tg200, cos320ctg17, cos400 tg170. | |||
Проверка. | |||
Б – 1 | Б – 2 | ||
Для каких значений аргумента α, заключенных в промежутке от 0ْْْْ до 360ْ, знаки sinα и cosα совпадают различны | |||
Проверка. Если у вас нет совпадений, то вы выполнили задание верно. | |||
Б — 2 | Б — 2 | ||
Из каждой пары выражений выпишите наибольшее наименьшее | |||
Проверка. | |||
В — 1 | В – 1 | ||
В какой четверти находится точка, соответствующая числу α, если sinα + cosα= -1,4 sinα — cosα= 1,4 | |||
Проверка учителем. | |||
В — 2 | В – 2 | ||
Пусть α, β и γ – углы треугольника. Какой знак имеет сумма: sinα+ sin β + sin γ cosα+ cos β + cos γ tgα+ tg β + tg γ | |||
Проверка
учителем. Как быстро получить любую формулу приведенияДля начала обратите внимание, что все формулы имеют похожий вид:
Здесь нужно пояснить термин «кофункция» — это та же самая функция с добавлением или убиранием приставки «ко-». То есть, для синуса кофункцией будет косинус, а для косинуса – синус. С тангенсом и котангенсом – аналогично.
Функция: Кофункция:
Таким образом, например, синус при применении этих формул никогда не поменяется на тангенс
или котангенс, он либо останется синусом, либо превратиться в косинус. |
В числителе и знаменателе получились одинаковые косинусы. Сокращаем их. |
||
|
\(= 18\) |
Записываем ответ |
||
Ответ: \(18\)
Пример. Найдите значение выражения \(\frac{3 \sin{(\pi-a)}-\cos(\frac{\pi}{2}+a) }{\cos {(\frac{3\pi}{2}-a)}}\)
Решение:|
\(\frac{3 \sin{(\pi-a)}-\cos(\frac{\pi}{2}+a) }{\cos {(\frac{3\pi}{2}-a)}}=\) |
Рассмотрим первое слагаемое числителя: \(\sin(π-a)\). Воспользуемся формулами приведения, выведя ее самостоятельно:
Таким образом, \(\sin(π-a)=\sina\) |
|
|
\(=\frac{3 \sin{a}-\cos(\frac{\pi}{2}+a) }{\cos {(\frac{3\pi}{2}-a)}}=\) |
Второе слагаемое числителя: \(\cos{(\frac{π}{2} + a)}\):
Таким образом, \(\cos{(\frac{π}{2} + a)}=-\sina\) |
|
|
\(=\frac{3 \sin{a}-(-\sin{a}) }{\cos {(\frac{3\pi}{2}-a)}}=\) |
Теперь знаменатель: \(\cos(\frac{3π}{2} — a)\). |
|
|
\(=\frac{3 \sin{a}-(-\sin{a}) }{-\sin {a}}=\) |
Раскрываем скобки и приводим подобные слагаемые. |
|
|
\(=\frac{3 \sin{a}+\sin{a}}{-\sin {a}}=\frac{4\sin{a}}{-\sin{a}}\) |
Сократив на \(\sin{a}\), получаем ответ. |
|
|
\(=\frac{4 }{-1}=\)\(-4\) |
Ответ: \(-4\)
Пример. Вычислить чему равен \(ctg(-a-\frac{7π}{2})\), если \(tg\) \(a=2\)
Решение:
|
\(ctg(-a-\frac{7π}{2}) =\) |
Здесь сразу формулу приведения применять нельзя, так как аргумент нестандартный. |
|
|
\(= ctg(-\frac{7π}{2}-a) =\) |
Уже лучше, но все еще есть проблемы – «точка привязки» с минусом, а такого аргумента у нас нет. Избавимся от минуса, вынеся его за скобку внутри аргумента. |
|
|
\(= ctg(-(\frac{7π}{2}+a)) =\) |
Теперь вспомним о том, что котангенс – функция нечетная, то есть |
|
|
\(= — ctg(\frac{7π}{2}+a) =\) |
Несмотря на то, что точка привязки \(\frac{7π}{2}\) мы все равно можем использовать формулы приведения, потому что \(\frac{7π}{2}\) лежит на пересечении одной из осей и числовой окружности (смотри пояснение ниже). |
|
|
\(= — (- tg\) \(a) = tg\) \(a = 2\) |
Готов ответ. |
Ответ: \(2\)
Еще раз проговорим этот важный момент: с точки зрения формулы приведения \(\frac{7π}{2}\) — это тоже самое, что и \(\frac{3π}{2}\). Почему? Потому что \(\frac{7π}{2}=\frac{3π+4π}{2}=\frac{3π}{2}+\frac{4π}{2}=\frac{3π}{2}+2π\). Иными словами, они отличаются ровно на один оборот \(2π\). А на значения тригонометрических функций количество оборотов никак не влияет:
\(cos\) \(t=cos (t+2π)=cos (t+4π)=cos (t+6π)= …=cos (t-2π)=cos (t-4π)=cos (t-6π)…\)
\(sin\) \(t=sin (t+2π)=sin (t+4π)=sin (t+6π)= .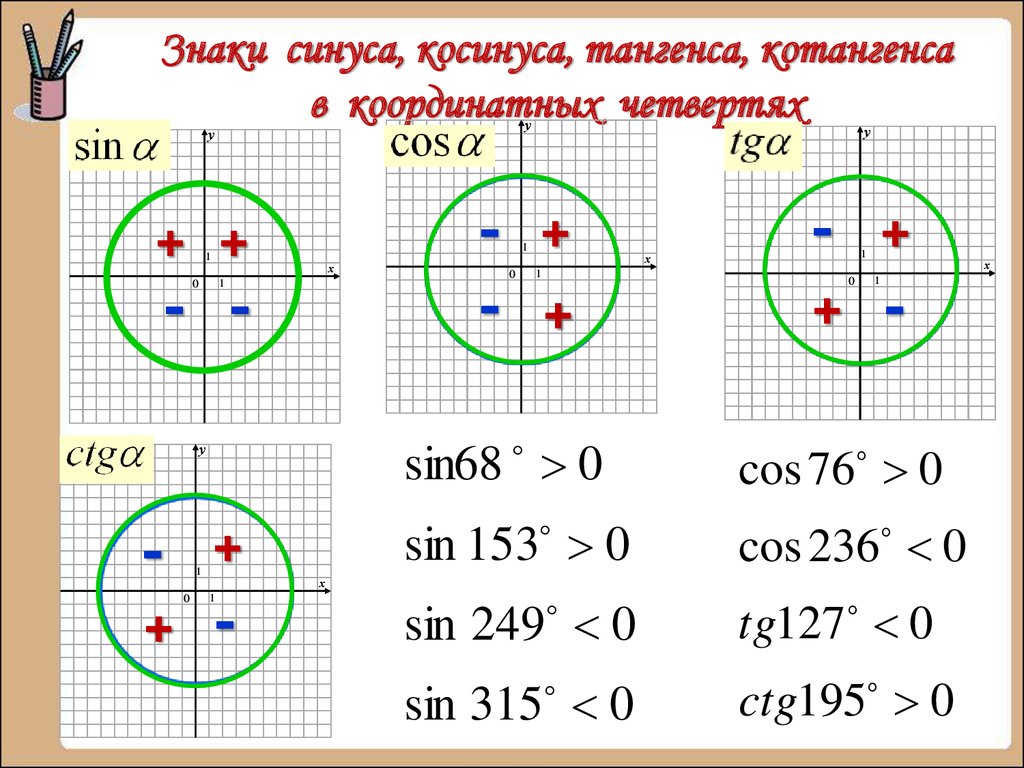 ..=sin (t-2π)=sin (t-4π)=sin (t-6π)…\)
..=sin (t-2π)=sin (t-4π)=sin (t-6π)…\)
Аналогично с тангенсом и котангенсом (только у них «оборот» равен \(π\)).
\(tg\) \(t=tg(t+π)=tg(t+2π)=tg(t+3π)= …=tg(t-π)=tg(t-2π)=tg(t-3π)…\)
\(ctg\) \(t=ctg(t+π)=ctg(t+2π)=ctg(t+3π)= …=ctg(t-π)=ctg(t-2π)=ctg(t-3π)…\)
Таким образом, \(-ctg(\frac{7π}{2}+a)=- ctg(\frac{3π}{2}+2π+a)=- ctg(\frac{3π}{2}+a)\).
То есть, для определения знака и необходимости смены функции важно лишь местоположение «точки привязки», а не её значение, поэтому так расписывать не обязательно (но можно если вы хотите впечатлить своими знаниями учительницу).
Ответы на часто задаваемые вопросы
Вопрос: Есть ли формулы приведения с аргументами \((\frac{π}{3}-a)\),\((\frac{π}{4}+a)\),\((\frac{7π}{6}+a)\) или тому подобное?
Ответ: К сожалению, нет. В таких ситуациях выгодно использовать формулы разности и суммы аргументов. Например, \(cos(\frac{π}{3}-a)=cos\frac{π}{3} cosa+sin\frac{π}{3} sina=\frac{1}{2}cosa+\frac{\sqrt{3}}{2} sina\).
Например, \(cos(\frac{π}{3}-a)=cos\frac{π}{3} cosa+sin\frac{π}{3} sina=\frac{1}{2}cosa+\frac{\sqrt{3}}{2} sina\).
Смотрите также Как доказать тригонометрическое тождество?
Скачать статьюПримечание . В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/». См. также полезные материалы: Для определения значения тригонометрической функции , найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Синус пи, косинус пи, тангенс пи и других углов в радианахПриведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах . Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан. Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам. Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180 . Примеры : 2. Косинус пи . 3. Тангенс пи Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)
Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов0, 15, 30, 45, 60, 90 … 360 градусов (цифровые значения «как по таблицам Брадиса»)
|
Тригонометрическая таблица. Cинус, косинус, тангенс и котангенс
Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
Прежде всего напомню простой, но очень полезный вывод из урока «Что такое синус и косинус? Что такое тангенс и котангенс?»
Вот этот вывод:
Синус, косинус, тангенс и котангенс накрепко связаны со своими углами. Знаем одно — значит, знаем и другое.
Другими словами, у каждого угла есть свой неизменный синус и косинус. И почти у каждого — свой тангенс и котангенс. Почему почти? Об этом ниже.
Это знание здорово помогает в учёбе! Существует масса заданий, где требуется перейти от синусов к углам и наоборот. Для этого существует таблица синусов. Аналогично, для заданий с косинусом — таблица косинусов. И, как вы уже догадались, существует таблица тангенсов и таблица котангенсов. )
Таблицы бывают разные. Длинные, где можно посмотреть, чему равен, скажем, sin37°6’. Раскрываем таблицы Брадиса, ищем угол тридцать семь градусов шесть минут и видим значение 0,6032. Понятное дело, запоминать это число (и тысячи других табличных значений) совершенно не требуется.
В сущности, в наше время длинные таблицы косинусов синусов тангенсов котангенсов не особо-то и нужны. Один хороший калькулятор заменяет их полностью. Но знать о существовании таких таблиц не мешает. Для общей эрудиции.)
И зачем тогда этот урок?! — спросите вы.
А вот зачем. Среди бесконечного количества углов существуют особые, о которых вы должны знать всё . На этих углах построена вся школьная геометрия и тригонометрия. Это, своего рода, «таблица умножения» тригонометрии. Если вы не знаете, чему равен, например, sin50°, никто вас не осудит.) Но если вы не знаете, чему равен sin30°, будьте готовы получить заслуженную двойку…
Таких особых углов тоже прилично набирается. Школьные учебники обычно любезно предлагают к запоминанию таблицу синусов и таблицу косинусов для семнадцати углов. Ну и, разумеется, таблицу тангенсов и таблицу котангенсов для тех же семнадцати углов… Т.е. предлагается запомнить 68 значений. Которые, между прочим, очень похожи между собой, то и дело повторяются и меняют знаки. Для человека без идеальной зрительной памяти — та ещё задачка…)
Мы пойдём другим путём. Заменим механическое запоминание на логику и смекалку. Тогда нам придётся зазубрить 3 (три!) значения для таблицы синусов и таблицы косинусов. И 3 (три!) значения для таблицы тангенсов и таблицы котангенсов. И всё. Шесть значений запомнить легче, чем 68, мне кажется…)
Все остальные необходимые значения мы будем получать из этих шести с помощью мощной законной шпаргалки — тригонометрического круга. Если вы не изучали эту тему, сходите по ссылочке, не ленитесь. Этот круг не только для этого урока нужен. Он незаменим для всей тригонометрии сразу . Не пользоваться таким инструментом просто грех! Не хотите? Дело ваше. Заучивайте таблицу синусов. Таблицу косинусов. Таблицу тангенсов. Таблицу котангенсов. Все 68 значений для разнообразных углов.)
Итак, начнём. Для начала разобьём все эти особые углы на три группы.
Первая группа углов.
Рассмотрим первую группа углов из семнадцати особых . Это 5 углов: 0°, 90°, 180°, 270°, 360°.
Вот так выглядит таблица синусов косинусов тангенсов котангенсов для этих углов:
Угол х(в градусах) | 0 | 90 | 180 | 270 | 360 |
Угол х(в радианах) | 0 | ||||
sin x | 0 | 1 | 0 | -1 | 0 |
cos x | 1 | 0 | -1 | 0 | 1 |
tg x | 0 | не сущ. | 0 | не сущ. | 0 |
ctg x | не сущ. | 0 | не сущ. | 0 | не сущ. |
Желающие запомнить — запоминайте. Но сразу скажу, что все эти единички и нолики очень путаются в голове. Гораздо сильнее, чем хочется.) Поэтому включаем логику и тригонометрический круг.
Рисуем круг и отмечаем на нём эти самые углы: 0°, 90°, 180°, 270°, 360°. Я эти углы отметил красными точками:
Сразу видно, в чём особенность этих углов. Да! Это углы, которые попадают точно на оси координат! Собственно, поэтому-то и путается народ… Но мы путаться не будем. Разберёмся, как находить тригонометрические функции этих углов без особого запоминания.
Кстати, положение угла в 0 градусов полностью совпадает с положением угла в 360 градусов. Это значит, что синусы, косинусы, тангенсы у этих углов совершенно одинаковы. Угол в 360 градусов я отметил, чтобы замкнуть круг.
Предположим, в сложной стрессовой обстановке ЕГЭ вы как-то засомневались… Чему равен синус 0 градусов? Вроде ноль… А вдруг единица?! Механическое запоминание такая штука. В суровых условиях сомнения грызть начинают…)
Спокойствие, только спокойствие!) Я подскажу вам практический приём, который выдаст стопроцентно правильный ответ и начисто уберёт все сомнения.
В качестве примера разберёмся, как чётко и надёжно определить, скажем, синус 0 градусов. А заодно, и косинус 0. Именно в этих значениях, как ни странно, частенько люди путаются.
Для этого на круге нарисуем произвольный угол х . В первой четверти, чтобы недалеко от 0 градусов было. Отметим на осях синус и косинус этого угла х, всё чин-чинарём. Вот так:
А теперь — внимание! Уменьшим угол х , приблизим подвижную сторону к оси ОХ. Наведите курсор на картинку (или коснитесь картинки на планшете) и всё увидите.
Теперь включаем элементарную логику!. Смотрим и размышляем: как ведёт себя sinx при уменьшении угла х? При приближении угла к нулю? Он уменьшается! А cosx — увеличивается! Остаётся сообразить, что станет с синусом, когда угол схлопнется совсем? Когда подвижная сторона угла (точка А) уляжется на ось ОХ и угол станет равным нулю? Очевидно, и синус угла уйдёт в ноль. А косинус увеличится до… до… Чему равна длина подвижной стороны угла (радиус тригонометрического круга)? Единице!
Вот и ответ. Синус 0 градусов равен 0. Косинус 0 градусов равен 1. Совершенно железно и безо всяких сомнений!) Просто потому, что иначе быть не может.
Совершенно аналогично можно узнать (или уточнить) синус 270 градусов, например. Или косинус 180. Нарисовать круг, произвольный угол в четверти рядышком с интересующей нас осью координат, мысленно подвигать сторону угла и уловить, чем станет синус и косинус, когда сторона угла уляжется на ось. Вот и всё.
Как видите, для этой группы углов ничего заучивать не надо. Не нужна здесь таблица синусов… Да и таблица косинусов — тоже.) Кстати, после нескольких применений тригонометрического круга все эти значения запомнятся сами по себе. А если забудутся — нарисовал за 5 секунд круг и уточнил. Куда проще, чем звонить другу из туалета с риском для аттестата, правда?)
Что касается тангенса и котангенса — всё то же самое. Рисуем на круге линию тангенса (котангенса) — и всё сразу видно. Где они равны нулю, а где — не существуют. Что, не знаете про линии тангенса и котангенса? Это печально, но поправимо.) Посетили Раздел 555 Тангенс и котангенс на тригонометрическом круге — и нет проблем!
Если вы поняли, как чётко определить синус, косинус, тангенс и котангенс для этих пяти углов — я вас поздравляю! На всякий случай сообщаю, что вы теперь можете определять функции любых углов, попадающих на оси. А это и 450°, и 540°, и 1800°, и ещё бесконечное количество…) Отсчитал (правильно!) угол на круге — и нет проблем с функциями.
Но, как раз, с отсчётом углов и случаются проблемы да ошибки… Как их избежать, написано в уроке: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в градусах. Элементарно, но очень помогает в борьбе с ошибками.)
А вот урок: Как нарисовать (отсчитать) любой угол на тригонометрическом круге в радианах — покруче будет. В смысле возможностей. Скажем, определить на какую из четырёх полуосей попадает угол
вы сможете за пару секунд. Я не шучу! Именно за пару секунд. Ну конечно, не только 345 «пи»…) И 121, и 16, и -1345. Любой целый коэффициент годится для мгновенного ответа.
А если угол
Подумаешь! Верный ответ получается секунд за 10. Для любого дробного значения радианов с двойкой в знаменателе.
Собственно, этим и хорош тригонометрический круг. Тем, что умение работать с некоторыми углами он автоматически расширяет на бесконечное множество углов.
Итак, с пятью углами из семнадцати — разобрались.
Вторая группа углов.
Следующая группа углов — это углы 30°, 45° и 60°. Почему именно эти, а не, к примеру, 20, 50 и 80? Да как-то сложилось так… Исторически.) Дальше будет видно, чем хороши эти углы.
Таблица синусов косинусов тангенсов котангенсов для этих углов выглядит так:
Угол х(в градусах) | 0 | 30 | 45 | 60 | 90 |
Угол х(в радианах) | 0 | ||||
sin x | 0 | 1 | |||
cos x | 1 | 0 | |||
tg x | 0 | 1 | не сущ. | ||
ctg x | не сущ. | 1 | 0 |
Я оставил значения для 0° и 90° из предыдущей таблицы для завершённости картины.) Чтобы было видно, что эти углы лежат в первой четверти и возрастают. От 0 до 90. Это пригодится нам дальше.
Значения таблицы для углов 30°, 45° и 60° надо запомнить. Зазубрить, если хотите. Но и здесь есть возможность облегчить себе жизнь.) Обратите внимание на значения таблицы синусов этих углов. И сравните со значениями таблицы косинусов…
Да! Они одни и те же! Только расположены в обратном порядке. Углы возрастают (0, 30, 45, 60, 90) — и значения синуса возрастают от 0 до 1. Можете убедиться с калькулятором. А значения косинуса — убывают от 1 до нуля. Причём, сами значения одни и те же. Для углов 20, 50, 80 так бы не получилось…
Отсюда полезный вывод. Достаточно выучить три значения для углов 30, 45, 60 градусов. И помнить, что у синуса они возрастают, а у косинуса — убывают. Навстречу синусу.) На половине пути (45°) они встречаются, т.е синус 45 градусов равен косинусу 45 градусов. А дальше опять расходятся… Три значения можно выучить, правда?
С тангенсами — котангенсами картина исключительно та же самая. Один в один. Только значения другие. Эти значения (ещё три!) тоже надо выучить.
Ну вот, практически всё запоминание и закончилось. Вы поняли (надеюсь), как определять значения для пяти углов попадающих на оси и выучили значения для углов 30, 45, 60 градусов. Всего 8.
Осталось разобраться с последней группой из 9 углов.
Вот эти углы:
120°; 135°; 150°; 210°; 225°; 240°; 300°; 315°; 330°. Для этих углов надо железно знать таблицу синусов, таблицу косинусов и т.д.
Кошмар, правда?)
А если добавить сюда углы, типа: 405°, 600°, или 3000° и много-много такого же красивого?)
Или углы в радианах? Например, про углы:
и многие другие, вы должны знать всё .
Самое забавное, что знать это всё — невозможно в принципе. Если использовать механическую память.
И очень легко, фактически элементарно — если использовать тригонометрический круг. Если вы освоите практическую работу с тригонометрическим кругом, все эти ужасные углы в градусах будут легко и элегантно сводиться к старым добрым:
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
1. Тригонометрические функции представляют собой элементарные функции, аргументом которых является угол . С помощью тригонометрических функций описываются соотношения между сторонами и острыми углами в прямоугольном треугольнике. Области применения тригонометрических функций чрезвычайно разнообразны. Так, например, любые периодические процессы можно представить в виде суммы тригонометрических функций (ряда Фурье). Данные функции часто появляются при решении дифференциальных и функциональных уравнений.
2. К тригонометрическим функциям относятся следующие 6 функций: синус , косинус , тангенс ,котангенс , секанс и косеканс . Для каждой из указанных функций существует обратная тригонометрическая функция.
3. Геометрическое определение тригонометрических функций удобно ввести с помощью единичного круга . На приведенном ниже рисунке изображен круг радиусом r=1. На окружности обозначена точка M(x,y). Угол между радиус-вектором OM и положительным направлением оси Ox равен α.
4. Синусом угла α называется отношение ординаты y точки M(x,y) к радиусу r:
sinα=y/r.
Поскольку r=1, то синус равен ординате точки M(x,y).
5. Косинусом угла α называется отношение абсциссы x точки M(x,y) к радиусу r:
cosα=x/r
6. Тангенсом угла α называется отношение ординаты y точки M(x,y) к ee абсциссе x:
tanα=y/x,x≠0
7. Котангенсом угла α называется отношение абсциссы x точки M(x,y) к ее ординате y:
cotα=x/y,y≠0
8. Секанс угла α − это отношение радиуса r к абсциссе x точки M(x,y):
secα=r/x=1/x,x≠0
9. Косеканс угла α − это отношение радиуса r к ординате y точки M(x,y):
cscα=r/y=1/y,y≠0
10. В единичном круге проекции x, y точки M(x,y) и радиус r образуют прямоугольный треугольник, в котором x,y являются катетами, а r − гипотенузой. Поэтому, приведенные выше определения тригонометрических функций в приложении к прямоугольному треугольнику формулируются таким образом:
Синусом угла α называется отношение противолежащего катета к гипотенузе.
Косинусом угла α называется отношение прилежащего катета к гипотенузе.
Тангенсом угла α называется противолежащего катета к прилежащему.
Котангенсом угла α называется прилежащего катета к противолежащему.
Секанс угла α представляет собой отношение гипотенузы к прилежащему катету.
Косеканс угла α представляет собой отношение гипотенузы к противолежащему катету.
11. График функции синус
y=sinx, область определения: x∈R, область значений: −1≤sinx≤1
12. График функции косинус
y=cosx, область определения: x∈R, область значений: −1≤cosx≤1
13. График функции тангенс
y=tanx, область определения: x∈R,x≠(2k+1)π/2, область значений: −∞
14. График функции котангенс
y=cotx, область определения: x∈R,x≠kπ, область значений: −∞
15. График функции секанс
y=secx, область определения: x∈R,x≠(2k+1)π/2, область значений:secx∈(−∞,−1]∪∪}
Статьи по теме:
Вклады чрезвычайно популярны в России, поскольку для их открытия не нужно соблюдать кучу условий, главное — располагать минимально необходимой суммой.Дорогие читатели! Статья рассказывает о типовых способах решения юридических вопросов, но каждый случай и | Врач – весьма востребованная профессия на территории Российской Федерации. Во всём мире представители медицинской отрасли очень ценятся и получают за свой труд немалые деньги. Но, к сожалению, этого нельзя сказать о России. Несмотря на всю престижность |
Я положила деньги под проценты в банк. Нужно ли потом платить НДФЛ ?Спасибо большое,Ира, Москва.Налоговый кодекс предусматривает ситуации, в которых с дохода по вкладу надо заплатить НДФЛ . Однако подобные ситуации были возможны несколько лет назад. Сейча | Хранение денег в иностранном банке – вариант того, как обезопасить свои средства от неожиданностей отечественной экономики. Причины, по которым стоит открыть вклад в иностранном банке Основная цель вклада за рубежом – это надежное сохранение средств. Ст |
Примечание . В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/». См. также полезные материалы: Для определения значения тригонометрической функции , найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов. Синус пи, косинус пи, тангенс пи и других углов в радианахПриведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах . Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан. Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам. Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180 . Примеры : 2. Косинус пи . 3. Тангенс пи Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)
Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач. Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов0, 15, 30, 45, 60, 90 … 360 градусов (цифровые значения «как по таблицам Брадиса»)
|
Тригонометрические формулы. Таблица углов. Формулы приведения
Факт 1.
\(\bullet\) Таблица синусов, косинусов, тангенсов и котангенсов углов из первой четверти:
Факт 2.
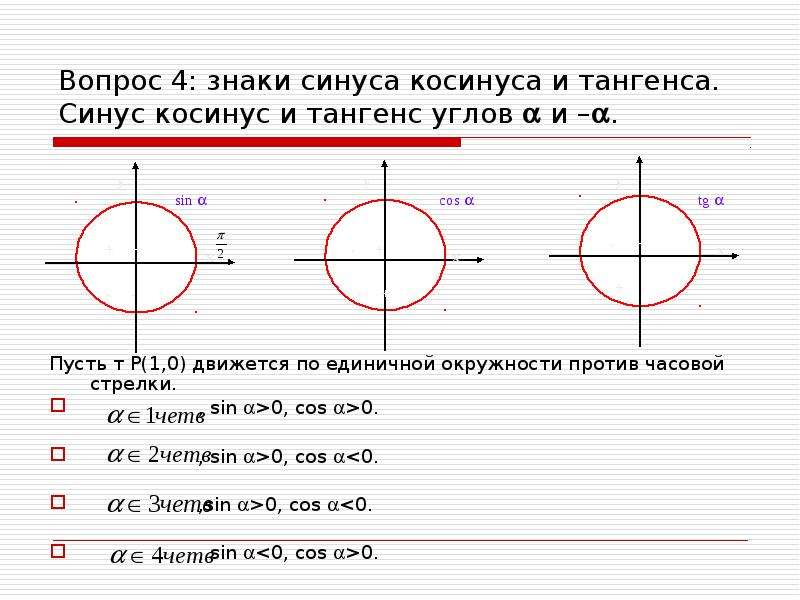
\(\bullet\) Знаки синуса, косинуса:
Так как \(\mathrm{tg}\,\alpha=\dfrac{\sin\alpha}{\cos\alpha}\) и \(\mathrm{ctg}\,\alpha=\dfrac{\cos\alpha}{\sin\alpha}\), то тангенс и котангенс положительны в \(I\) и \(III\) четвертях и отрицательны во \(II\) и \(IV\) четвертях.
Факт 3.
Формулы приведения.
\(\bullet\) Случай 1. Если угол можно представить в виде \(n\cdot \pi\pm \alpha\), где \(n\in\mathbb{N}\), то \[\sin(n\cdot \pi\pm
\alpha)=\bigodot \sin\alpha\] где на месте \(\bigodot\) стоит знак синуса угла \(n\cdot \pi\pm \alpha\). \[\cos(n\cdot \pi\pm
\alpha)=\bigodot \cos\alpha\] где на месте \(\bigodot\) стоит знак косинуса угла \(n\cdot \pi\pm \alpha\).
Знак угла можно найти, определив, в какой четверти он находится. Пользуясь таким правилом, предполагаем, что угол \(\alpha\) находится в \(I\) четверти.
\(\bullet\) Случай 2. Если угол можно представить в виде \(n\cdot \pi+\dfrac{\pi}2\pm\alpha\), где \(n\in\mathbb{N}\), то \[\sin\left(n\cdot \pi+\dfrac{\pi}2\pm
\alpha\right)=\bigodot \cos\alpha\] где на месте \(\bigodot\) стоит знак синуса угла \(n\cdot \pi+\dfrac{\pi}2\pm \alpha\). \[\cos\left(n\cdot \pi+\dfrac{\pi}2\pm
\alpha\right)=\bigodot \sin\alpha\] где на месте \(\bigodot\) стоит знак косинуса угла \(n\cdot \pi+\dfrac{\pi}2\pm \alpha\).
Знак определяется таким же образом, как и в случае \(1\).
Заметим, что в первом случае функция остается неизменной, а во втором случае — меняется (говорят, что функция меняется на кофункцию).
Алгоритм применения формул приведения для тангенса и котангенса полностью аналогичен.
Пример 1. Найти \(\cos \dfrac{13\pi}{3}\).
Преобразуем угол: \(\dfrac{13\pi}{3}=\dfrac{12\pi+\pi}{3}=4\pi+\dfrac{\pi}3\), следовательно, \(\cos \dfrac{13\pi}{3}=\cos \left(4\pi+\dfrac{\pi}3\right)=\cos\dfrac{\pi}3=\dfrac12\)
Пример 2. Найти \(\sin \dfrac{17\pi}{6}\).
Преобразуем угол: \(\dfrac{17\pi}{6}=\dfrac{18\pi-\pi}{6}=3\pi-\dfrac{\pi}6\), следовательно, \(\sin \dfrac{17\pi}{6}=\sin \left(3\pi-\dfrac{\pi}6\right)=\sin\dfrac{\pi}6=\dfrac12\)
Пример 3. Найти \(\mathrm{tg}\,\dfrac{15\pi}4\).
Преобразуем угол: \(\dfrac{15\pi}4=\dfrac{16\pi-\pi}4=4\pi-\dfrac{\pi}4\), следовательно, \(\mathrm{tg}\,\dfrac{15\pi}4=\mathrm{tg}\left(4\pi-\dfrac{\pi}4\right)= -\mathrm{tg}\,\dfrac{\pi}4=-1\)
Пример 4. Найти \(\mathrm{ctg}\,\dfrac{19\pi}3\).
Преобразуем угол: \(\dfrac{19\pi}3=\dfrac{18\pi+\pi}3=6\pi+\dfrac{\pi}3\), следовательно, \(\mathrm{ctg}\,\dfrac{19\pi}3=\mathrm{ctg}\left(6\pi+\dfrac{\pi}3\right)= \mathrm{ctg}\,\dfrac{\pi}3=\dfrac{\sqrt3}3\)
Таблица точных значений тригонометрических функций
В этой статье собраны таблицы синусов, косинусов, тангенсов и котангенсов. Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360 градусов ( 0, π/6, π/4, π/3, π/2, …, 2π радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.
Навигация по странице.
Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов
Тригонометрические определения синуса, косинуса, тангенса и котангенса позволяют указать значения тригонометрических функций для углов 0 и 90 градусов:
, а котангенс нуля градусов не определен, и
, а тангенс 90 градусов не определен.
В курсе геометрии из прямоугольных треугольников с углами 30 , 60 и 90 градусов, а также 45 , 45 и 90 градусов находятся значения синуса, косинуса, тангенса и котангенса углов 30, 45 и 60 градусов:
,
и
.
Занесем указанные значения тригонометрических функций для углов 0 , 30 , 45 , 60 и 90 градусов ( 0 , π/6 , π/4 , π/3 , π/2 радиан) в таблицу, назовем ее таблицей основных значений синуса, косинуса, тангенса и котангенса.
Используя формулы приведения, только что составленную таблицу синусов, косинусов, тангенсов и котангенсов можно расширить, дополнив значениями тригонометрических функций для углов 120 , 135 , 150 , 180 , 210 , 225 , 240 , 270 , 300 , 315 , 330 и 360 градусов ( 0, π/6, π/4, π/3, π/2, …, 2π радиан). При этом она принимает следующий вид.
Опираясь на свойство периодичности синуса, косинуса, тангенса и котангенса, таблицу основных значений тригонометрических функций можно расширить еще, заменив углы 0, 30, 45, 60, 90, …, 360 градусов соответственно на , где z – любое целое число. Из такой таблицы можно найти значения для всех углов, которым соответствуют точки единичной окружности, указанные на чертеже ниже.
Основные значения тригонометрических функций, собранные в заполненной выше таблице, желательно знать наизусть, так как они очень часто используются при решении задач.
Как пользоваться таблицей синусов, косинусов, тангенсов и котангенсов?
Использовать таблицу синусов, косинусов, тангенсов и котангенсов основных углов 0, 30, 45, 60, 90, …, 360 градусов очень просто – она дает непосредственные значения тригонометрических функций, находящиеся на пересечении соответствующей строки, указывающей название тригонометрической функции, и столбца, указывающего данное значение угла.
Например, значение косинуса угла 60 градусов находится на пересечении строки, в крайней левой ячейке которой находится запись cos , и столбца, в верхней ячейке которого записан угол 60 градусов. Так из таблицы находим, что значение косинуса 60 градусов равно одной второй. Для разъяснения приведем графическую иллюстрацию.
Расширенная таблица основных значений тригонометрических функций используется аналогично. С помощью расширенной таблицы основных значений синуса, косинуса, тангенса и котангенса можно сразу указать, например, чему равен тангенс угла 1 020 градусов. Он равен минус корню из трех, так как . Проиллюстрируем это.
Таблицы синусов и косинусов, тангенсов и котангенсов Брадиса
Таблицы синусов, косинусов, тангенсов и котангенсов Брадиса разделены на таблицу синусов и косинусов, а также на таблицу тангенсов и котангенсов. Причем таблица тангенсов и котангенсов состоит из двух частей – тангенсы углов, близких к 90 градусов, и котангенсы малых углов вынесены в отдельную таблицу.
В таблицах Брадиса с точностью до четырех знаков после десятичной запятой приведены приближенные значения синусов и косинусов, а также четыре цифры приближенных значений тангенсов и котангенсов острых углов, содержащих целое число градусов и целое число минут.
Сначала дадим таблицу Брадиса, имеющую название таблица Брадиса: синусы и косинусы.
Теперь приведем таблицу тангенсов углов от 0 до 76 градусов и котангенсов углов от 14 до 90 градусов.
Наконец, осталось заполнить таблицу Брадиса тангенсов углов, близких к 90 градусам, и котангенсов малых углов. Она содержит непосредственные приближенные значения тангенсов углов от 76 до 90 градусов и котангенсов углов от 0 до 14 градусов.
Как пользоваться таблицами синусов и косинусов, тангенсов и котангенсов Брадиса?
Осталось разобраться, как пользоваться таблицей синусов и косинусов, а также таблицами тангенсов и котангенсов Брадиса.
Значение синуса угла находится в таблице синусов на пересечении строки, содержащей в крайней левой ячейке нужное число градусов, и столбца, содержащего в верхней ячейке нужное число минут. Например, из таблицы синусов Брадиса можно определить, что синус 17 градусов 42 минут приближенно равен 0,3040 , вот иллюстрация тому, как это значение было найдено.
Несложно заметить, что в верхней строке минуты идут по порядку через шесть. А как определять значения, если количество минут имеет промежуточное значение, например 44 ? Для этого нужно внести соответствующую поправку, которую дают три крайних правых столбца таблицы. Например, синус 17 градусов 44 минут равен 0,3046 , так как синус 17 градусов 42 минут равен 0,3040 , и требуется еще поправка на 2 минуты в плюс, равна 0,0006 . Поправки содержатся в трех крайних правых столбцах таблицы синусов и косинусов Брадиса.
Если бы нам нужно было найти синус 17 градусов 47 минут, то от значения синуса 17 градусов 48 минут 0,3057 мы бы отняли поправку на 1 минуту, равную 0,0003 . В итоге мы получим искомое значение, равное 0,3054 .
Для нахождения значений косинусов используется та же таблица синусов и косинусов Брадиса. Однако следует ориентироваться на нижнюю строку при выборе соответствующего значения градуса и на четвертую справа строку при выборе нужного числа минут.
Например, косинус 20 градусов равен 0,9397 .
Другой пример: значение косинуса 20 градусов 2 минут равно 0,9397−0,0002=0,9395 , а значение косинуса 20 градусов 5 минут равно 0,9391+0,0001=0,9392 (обратите внимание: что нужно быть внимательным со знаками поправок, нужно помнить, что при возрастании острого угла его косинус убывает).
Таблица тангенсов и котангенсов Брадиса углов от 0 до 76 градусов и котангенсов углов от 14 до 90 градусов используется абсолютно аналогично таблице синусов и косинусов.
К примеру, тангенс 75 градусов 44 минут равен 3,923+0,010=3,933 , а котангенс 32 градусов 50 минут равен 1,5517−0,0020=1,5497 . Вот тому графические иллюстрации.
Таблица тангенсов углов, близких к 90 градусов, и котангенсов малых углов содержит значения тангенсов и котангенсов, не нуждающиеся в поправках. Для примера найдем значение тангенса угла 78 градусов 37 минут, оно равно 4,967 .
А котангенс угла 2 градуса 13 минут равен 25,83 .
Если угол выходит за пределы от 0 до 90 градусов, то сначала следует использовать формулы приведения и перейти к вычислению значения тригонометрической функции, аргумент которой заключен между 0 и 90 градусами. А если угол выражен в радианах, то прежде чем использовать таблицы Брадиса для нахождения синуса, косинуса, тангенса или котангенса данного угла, его нужно перевести в градусы (этому вопросу посвящен материал статьи перевод градусов в радианы и обратно).
В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса . Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90. 360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90. градусов. Определение данных величин дают определить значение функций углов в 0 и 90 градусов:
sin 0 0 =0, cos 0 0 = 1. tg 0 0 = 0, котангенс от 0 0 будет неопределенным
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0,тангенс от 90 0 будет неопределенным
Если взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3 , ctg 60 0 = √3/3
Изобразим все полученные значения в виде тригонометрической таблицы:
Таблица синусов, косинусов, тангенсов и котангенсов!
Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как:
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 0 0 +360 0 *z . 330 0 +360 0 *z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.
Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:
В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020 0 = 300 0 +360 0 *2. Найдем по таблице.
Для более поиска тригонометрических значений углов с точностью до минут используются таблицы Брадиса. Подробная инструкция как ими пользоваться на странице по ссылке.
Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.
Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса – которая поделена на две части (tg угла до 90 градусов и ctg малых углов).
Синус и косинус
tg угла начиная с 0 0 заканчивая 76 0 , ctg угла начиная с 14 0 заканчивая 90 0 .
tg до 90 0 и ctg малых углов.
Разберемся как пользоваться таблицами Брадиса в решении задач.
Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.
Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.
При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 – 0,0003 = 0,3054
При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 20 0 = 0.9397
Значения tg угла до 90 0 и cot малого угла, верны и поправок в них нет. К примеру, найти tg 78 0 37мин = 4,967
а ctg 20 0 13мин = 25,83
Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
При решении математических задач часто используются тригонометрические функции, поэтому знание значений этих функций для часто используемых углов просто необходимо.
В приведенной ниже таблице записаны значения тригонометрических функций аргумент которых задан в градусах (в первой строке) и в радианах (во второй строке). Это позволяет перевести значение популярных углов из градусов в радианы. Значения тригонометрических функций стоят на пересечении строки функции и столбца искомого угла.
Значения тригонометрических функций чаще всего требуются при решении геометрических задач.
знаков тригонометрических функций
Признаки тригонометрических функций в каждом квадранте
Мы знаем, что \ (\ cos \ alpha = \ large {\ frac {x} {r}} \ normalsize. \) Поскольку \ (r \ gt 0, \) знак функции косинуса зависит только от знака \ (x. \) Следовательно, косинус положительный в квадрантах \ (1 \ text {st} \) и \ (4 \ text {th} \) и отрицательный в \ (2 \ text {nd} \) ) и \ (3 \ text {rd} \) квадранты.
Рисунок 1.Рассмотрим функцию синуса \ (\ sin \ alpha = \ large {\ frac {y} {r}} \ normalsize.\) Его знак определяется знаком \ (y. \) Следовательно, синус положительный в квадрантах \ (1 \ text {st} \) и \ (2 \ text {nd} \) и отрицательный в квадранты \ (3 \ text {rd} \) и \ (4 \ text {th} \).
Рисунок 2.Ясно, что взаимные функции \ (\ sec \ alpha = \ large {\ frac {1} {{\ cos \ alpha}}} \ normalsize \) и \ (\ csc \ alpha = \ large { \ frac {1} {{\ sin \ alpha}}} \ normalsize \) имеют те же знаки, что и \ (\ cos \ alpha \) и \ (\ sin \ alpha, \) соответственно.
Знаки тангенса и котангенса зависят от знаков синуса и косинуса.Касательная и котангенс положительны, когда \ (x \) и \ (y \) оба положительны или оба отрицательны. \ prime = \ alpha — \ pi} = {\ frac {{7 \ pi}} {6} — \ pi} = {\ frac {\ pi} {6}.2} \ alpha = 1. \]
Если мы знаем одну из тригонометрических функций угла и квадрант, в котором находится угол, мы можем определить все остальные тригонометрические функции этого угла. Это можно сделать, используя тождества, перечисленные выше, и определения тригонометрических функций. Обратите внимание, что если тригонометрическое выражение содержит частное, оно действительно только для тех углов, при которых знаменатель не равен нулю.
Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.
Пример 1
Вычислить \ (\ sin \ alpha \) и \ (\ cot \ alpha \), если \ (\ cos \ alpha = \ large {\ frac {5} {{13}}} \ normalsize \) и угол \ (\ alpha \) лежит в квадранте \ (4 \ text {th} \).Пример 2
Вычислить \ (\ cos \ theta \) и \ (\ tan \ theta \), если \ (\ sin \ theta = — \ large {\ frac {24} {{25}}} \ normalsize \) и угол \ ( \ theta \) лежит в квадранте \ (3 \ text {rd} \).Пример 3
Найдите \ (\ cos \ alpha \), если \ (\ tan \ alpha = 5 \) и угол \ (\ alpha \) лежит в квадранте \ (3 \ text {rd} \).Пример 4
Найдите \ (\ sin \ beta \), если \ (\ cot \ beta = -3 \) и угол \ (\ beta \) лежит в квадранте \ (2 \ text {nd} \).Пример 5
Найдите значения шести тригонометрических функций \ (\ alpha = \ large {\ frac {{2 \ pi}} {3}} \ normalsize. \)Пример 6
Найдите значения шести тригонометрических функций \ (\ beta = \ large {\ frac {{5 \ pi}} {4}} \ normalsize. \)Пример 7
Определите знак выражения \ [\ sin \ frac {{13 \ pi}} {6} \ cos \ frac {{11 \ pi}} {7} \ tan \ frac {{9 \ pi}} {8}.\]Пример 8
Определите знак выражения \ [\ tan \ left ({- \ frac {{2 \ pi}} {5}} \ right) \ cot \ left ({- \ frac {{5 \ pi}} {7}} \ right) \ sec \ left ({- \ frac {{8 \ pi}} {9}} \ right). \]Пример 1.
Вычислить \ (\ sin \ alpha \) и \ (\ cot \ alpha \), если \ (\ cos \ alpha = \ large {\ frac {5} {{13}}} \ normalsize \) и угол \ (\ alpha \) лежит в квадранте \ (4 \ text {th} \).Решение.
Функция синуса отрицательна в квадранте \ (IV.2}}} = {- \ sqrt {1 — \ frac {{25}} {{169}}}} = {- \ sqrt {\ frac {{144}} {{169}}}} = {- \ гидроразрыв {{12}} {{13}}.} \]
Функция котангенса определяется как
.\ [{\ cot \ alpha = \ frac {{\ cos \ alpha}} {{\ sin \ alpha}}} = {\ frac {{\ frac {5} {{13}}}} {{- \ frac {{12}} {{13}}}}} = {- \ frac {5} {{12}}.} \]
Пример 2.
Вычислить \ (\ cos \ theta \) и \ (\ tan \ theta \), если \ (\ sin \ theta = — \ large {\ frac {24} {{25}}} \ normalsize \) и угол \ ( \ theta \) лежит в квадранте \ (3 \ text {rd} \).2}}} = {- \ sqrt {1 — \ frac {{576}} {{625}}}} = {- \ sqrt {\ frac {{49}} {{169}}}} = {- \ гидроразрыв {7} {{25}}.} \]Используя определение тангенса, имеем
\ [{\ tan \ theta = \ frac {{\ sin \ theta}} {{\ cos \ theta}}} = {\ frac {{- \ frac {{24}} {{25}}}} { {- \ frac {7} {{25}}}}} = {\ frac {{24}} {7}.} \]
Пример 3.
Найдите \ (\ cos \ alpha \), если \ (\ tan \ alpha = 5 \) и угол \ (\ alpha \) лежит в квадранте \ (3 \ text {rd} \). 2} \ alpha}.\ prime \) — это особый угол. Для него легко найти значения триггерных функций:\ [{\ sin \ frac {\ pi} {3} = \ frac {{\ sqrt 3}} {2}, \; \;} \ kern0pt {\ cos \ frac {\ pi} {3} = \ frac {1} {2}, \; \;} \ kern0pt {\ tan \ frac {\ pi} {3} = \ sqrt 3, \; \;} \ kern0pt {\ cot \ frac {\ pi} {3 } = \ frac {1} {{\ sqrt 3}}, \; \;} \ kern0pt {\ sec \ frac {\ pi} {3} = 2, \; \;} \ kern0pt {\ csc \ frac { \ pi} {3} = \ frac {2} {{\ sqrt 3}}.} \]
В квадранте \ (2 \ text {nd} \) синус и косеканс положительны, а косинус, секанс, тангенс и котангенс отрицательны.Следовательно,
\ [{\ sin \ frac {{2 \ pi}} {3} = \ frac {{\ sqrt 3}} {2}, \; \;} \ kern0pt {\ cos \ frac {{2 \ pi}} } {3} = — \ frac {1} {2}, \; \;} \ kern0pt {\ tan \ frac {{2 \ pi}} {3} = — \ sqrt 3, \; \;} \ kern0pt {\ cot \ frac {{2 \ pi}} {3} = — \ frac {1} {{\ sqrt 3}}, \; \;} \ kern0pt {\ sec \ frac {{2 \ pi}} { 3} = — 2, \; \;} \ kern0pt {\ csc \ frac {{2 \ pi}} {3} = \ frac {2} {{\ sqrt 3}}.} \]
Пример 6.
Найдите значения шести тригонометрических функций \ (\ beta = \ large {\ frac {{5 \ pi}} {4}} \ normalsize. \)Решение.\ prime: \)
\ [{\ sin \ frac {\ pi} {4} = \ frac {{\ sqrt 2}} {2}, \; \;} \ kern0pt {\ cos \ frac {\ pi} {4} = \ frac {{\ sqrt 2}} {2}, \; \;} \ kern0pt {\ tan \ frac {\ pi} {4} = 1, \; \;} \ kern0pt {\ cot \ frac {\ pi} {4} = 1, \; \;} \ kern0pt {\ sec \ frac {\ pi} {4} = \ sqrt 2, \; \;} \ kern0pt {\ csc \ frac {\ pi} {4} = \ sqrt 2.} \]
В квадранте \ (3 \ text {rd} \) тангенс и котангенс положительны, а все остальные тригонометрические функции отрицательны. Следовательно,
\ [{\ sin \ frac {{5 \ pi}} {4} = — \ frac {{\ sqrt 2}} {2}, \; \;} \ kern0pt {\ cos \ frac {{5 \ pi }} {4} = — \ frac {{\ sqrt 2}} {2}, \; \;} \ kern0pt {\ tan \ frac {{5 \ pi}} {4} = 1, \; \;} \ kern0pt {\ cot \ frac {{5 \ pi}} {4} = 1, \; \;} \ kern0pt {\ sec \ frac {{5 \ pi}} {4} = — \ sqrt 2, \; \;} \ kern0pt {\ csc \ frac {{5 \ pi}} {4} = — \ sqrt 2.} \]
Пример 7.
Определите знак выражения \ [\ sin \ frac {{13 \ pi}} {6} \ cos \ frac {{11 \ pi}} {7} \ tan \ frac {{9 \ pi}} {8}. \]Решение.
Угол \ (\ large {\ frac {{13 \ pi}} {6}} \ normalsize \) лежит в квадранте \ (1 \ text {st} \):
\ [{\ frac {{12 \ pi}} {6} \ lt \ frac {{13 \ pi}} {6} \ lt \ frac {{15 \ pi}} {6},} \; \; \ Rightarrow {2 \ pi \ lt \ frac {{13 \ pi}} {6} \ lt 2 \ pi + \ frac {\ pi} {2}.} \]
Следовательно, \ (\ sin \ kern-2pt \ large {\ frac {{13 \ pi}} {6}} \ normalsize \) имеет положительный знак.
Угол \ (\ large {\ frac {{11 \ pi}} {7}} \ normalsize \) находится в квадранте \ (4 \ text {th} \):
\ [{\ frac {{21 \ pi}} {{14}} \ lt \ frac {{22 \ pi}} {{14}} \ lt \ frac {{28 \ pi}} {{14}}] ,} \; \; \ Rightarrow {\ frac {{3 \ pi}} {2} \ lt \ frac {{22 \ pi}} {{14}} \ lt 2 \ pi,} \; \; \ Rightarrow {\ frac {{3 \ pi}} {2} \ lt \ frac {{11 \ pi}} {7} \ lt 2 \ pi.} \]
Следовательно, \ (\ cos \ large {\ frac {{11 \ pi}} {7}} \ normalsize \) имеет положительный знак.
Угол \ (\ large {\ frac {{9 \ pi}} {8}} \ normalsize \), очевидно, находится в квадранте \ (3 \ text {rd} \), поэтому \ (\ tan \ kern-2pt \ large {\ frac {{9 \ pi}} {8}} \ normalsize \) имеет положительный знак.
Поскольку все три компонента положительны, их произведение также положительно:
\ [\ sin \ frac {{13 \ pi}} {6} \ cos \ frac {{11 \ pi}} {7} \ tan \ frac {{9 \ pi}} {8} \ gt 0. \ ]
Пример 8.
Определите знак выражения \ [\ tan \ left ({- \ frac {{2 \ pi}} {5}} \ right) \ cot \ left ({- \ frac {{5 \ pi}} {7}} \ right) \ sec \ left ({- \ frac {{8 \ pi}} {9}} \ right). \]Решение.
Угол \ ({- \ large {\ frac {{2 \ pi}} {5}} \ normalsize} \) лежит в квадранте \ (4 \ text {th} \), где касательная отрицательна.Действительно,
\ [{- \ frac {{5 \ pi}} {{10}} \ lt — \ frac {{4 \ pi}} {{10}} \ lt 0,} \; \; \ Rightarrow {- \ frac {\ pi} {2} \ lt — \ frac {{4 \ pi}} {{10}} \ lt 0,} \; \; \ Rightarrow {- \ frac {\ pi} {2} \ lt — \ frac {{2 \ pi}} {5} \ lt 0.} \]
Угол \ ({- \ large {\ frac {{5 \ pi}} {7}} \ normalsize} \) находится в квадранте \ (3 \ text {rd} \), где котангенс положительный:
\ [{- \ frac {{14 \ pi}} {{14}} \ lt — \ frac {{10 \ pi}} {{14}} \ lt — \ frac {{7 \ pi}} {{ 14}},} \; \; \ Rightarrow {- \ pi \ lt — \ frac {{5 \ pi}} {7} \ lt — \ frac {\ pi} {2}.} \]
Угол \ ({- \ large {\ frac {{8 \ pi}} {9}} \ normalsize} \) также принадлежит квадранту \ (3 \ text {rd} \), где секущая отрицательна:
\ [{- \ frac {{18 \ pi}} {{18}} \ lt — \ frac {{16 \ pi}} {{18}} \ lt — \ frac {{9 \ pi}} {{ 18}},} \; \; \ Rightarrow {- \ pi \ lt — \ frac {{8 \ pi}} {9} \ lt — \ frac {\ pi} {2}.} \]
Итак, \ (2 \) из \ (3 \) множителей отрицательны, а один положителен. Понятно, что их товар положительный:
\ [{\ tan \ left ({- \ frac {{2 \ pi}} {5}} \ right) \ cot \ left ({- \ frac {{5 \ pi}} {7}} \ right) \ sec \ left ({- \ frac {{8 \ pi}} {9}} \ right)} \ gt {0.} \]
Тригонометрических идентичностей
Вы могли бы сначала прочитать о тригонометрии!
Прямой треугольник
Тригонометрические тождества — это уравнения, которые верны для прямоугольных треугольников. (Если это не прямоугольный треугольник, перейдите на страницу «Треугольники».)
Каждая сторона прямоугольного треугольника имеет имя:
Соседний всегда находится рядом с углом
И Напротив находится напротив угла
Мы скоро будем играть со всеми видами функций, но помните, что все возвращается к этому простому треугольнику с:
- Угол θ
- Гипотенуза
- Соседний
- Напротив
Синус, косинус и тангенс
Три основных функции в тригонометрии — это синус, косинус и тангенс.
Это всего лишь длины одной стороны делится на другой
Для прямоугольного треугольника с углом θ :
Функция синуса: | sin ( θ ) = Противоположность / Гипотенуза |
Функция косинуса: | cos ( θ ) = Соседний / Гипотенуза |
Касательная функция: | tan ( θ ) = противоположный / смежный |
Для данного угла θ каждое отношение остается неизменным
независимо от того, насколько большой или маленький треугольник
Когда мы разделим синус на косинус, получим:
sin (θ) cos (θ) = Противоположно / Гипотенуза Соседний / Гипотенуза = Противоположно Соседний = tan (θ)
Итак, мы можем сказать:
Это наш первый Тригонометрический идентификатор .
Косеканс, секанс и котангенс
Мы также можем разделить «наоборот» (например, Соседний / Противоположный вместо Противоположный / Соседний ):
Косекансная функция: | csc ( θ ) = Гипотенуза / Напротив |
Секущая функция: | сек ( θ ) = Гипотенуза / Соседний |
Котангенс Функция: | детская кроватка ( θ ) = рядом / напротив |
Пример: когда Противоположность = 2 и Гипотенуза = 4, тогда
sin (θ) = 2/4 и csc (θ) = 4/2
На основании всего, что мы можем сказать:
грех (θ) = 1 / csc (θ)
cos (θ) = 1 / сек (θ)
загар (θ) = 1 / детская кроватка (θ)
И наоборот:
csc (θ) = 1 / sin (θ)
сек (θ) = 1 / cos (θ)
детская кроватка (θ) = 1 / tan (θ)
А еще у нас есть:
детская кроватка (θ) = cos (θ) / sin (θ)
Теорема Пифагора
Следующие тригонометрические тождества мы начнем с теоремы Пифагора:
Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат a плюс квадрат b равен квадрату c: a 2 + b 2 = c 2 |
Деление на c 2 дает
a 2 с 2 + б 2 с 2 знак равно с 2 с 2
Это можно упростить до:
( a c ) 2 + ( б c ) 2 = 1
Итак, a / c — это Противоположность / Гипотенуза , что составляет sin (θ)
И b / c — это Соседний / Гипотенуза , что составляет cos (θ)
Так (a / c) 2 + (b / c) 2 = 1 также можно записать:
Примечание:- sin 2 θ означает найти синус θ, , затем возвести результат в квадрат и
- sin θ 2 означает возвести θ в квадрат, затем выполнить синусоидальную функцию
Пример: 32 °
Использование только 4 десятичных разряда :
- sin (32 °) = 0.5299 …
- cos (32 °) = 0,8480 …
Теперь посчитаем sin 2 θ + cos 2 θ :
0,5299 2 + 0,8480 2
= 0,2808 … + 0,7191 …
= 0,9999 …
Мы очень близки к 1, используя всего 4 десятичных знака. Попробуйте использовать на своем калькуляторе , возможно, вы получите лучшие результаты!
Связанные идентификационные данные включают:
sin 2 θ = 1 — cos 2 θ
cos 2 θ = 1 — sin 2 θ
tan 2 θ + 1 = sec 2 θ
tan 2 θ = sec 2 θ — 1
детская кроватка 2 θ + 1 = csc 2 θ
детская кроватка 2 θ = csc 2 θ — 1
Как вы их помните? Упомянутые до сих пор личности можно запомнить |
Но подождите… Это еще не все!
Есть еще много идентификаторов … вот некоторые из наиболее полезных:
Идентичности с противоположным углом
грех (-θ) = -sin (θ)
cos (−θ) = cos (θ)
тангенс (-θ) = -тан (θ)
Двойные углы идентификации
Идентификаторы с половинным углом
Обратите внимание, что «±» означает, что это может быть или один , в зависимости от значения θ / 2
Тождества суммы углов и разностей
Обратите внимание, что это означает, что вы можете использовать плюс или минус, а средство — использовать противоположный знак.
sin (A B) = sin (A) cos (B) cos (A) sin (B)
cos (A B) = cos (A) cos (B) sin (A) sin (B)
загар (A B) = загар (A) загар (B) 1 загар (A) загар (B)
детская кроватка (A B) = детская кроватка (A) детская кроватка (B) 1 детская кроватка (B) детская кроватка (A)
Треугольники
Существуют также идентичности треугольников, которые применяются ко всем треугольникам (а не только к прямоугольным треугольникам).
7.4. Другие тригонометрические функции
Мы исследовали ряд свойств тригонометрических функций. Теперь мы можем продвинуться дальше в отношениях и получить некоторые фундаментальные идентичности. Идентичности — это утверждения, которые верны для всех значений входных данных, на которых они определены. Обычно идентичность можно вывести из уже известных нам определений и отношений. Например, тождество Пифагора, которое мы узнали ранее, было получено из теоремы Пифагора и определений синуса и косинуса.
Пример \ (\ PageIndex {6} \): Использование идентичностей для упрощения тригонометрических выражений
Упростить \ (\ frac {\ sec t} {\ tan t}. \)
Решение
Мы можем упростить это, переписав обе функции в терминах синуса и косинуса.
\ [\ begin {array} {lll} \ dfrac {\ sec t} {\ tan t} & = \ dfrac {1 / \ cos t} {\ sin t / \ cos t} & \ text {Чтобы разделить функции, мы умножаем на обратную. 2 t = 1 \).2 t & = \ dfrac {25} {169} \\ \ sin t & = ± \ sqrt {\ dfrac {25} {169}} \\ \ sin t & = ± \ dfrac {\ sqrt {25}} { \ sqrt {169}} \\ \ sin t & = ± \ dfrac {5} {13} \ end {align} \]
Знак синуса зависит от значений y в квадранте, где расположен угол. Поскольку угол находится в квадранте IV, где значения y отрицательны, его синус отрицательный, \ (- \ frac {5} {13} \).
Остальные функции можно вычислить с помощью тождеств, связывающих их с синусом и косинусом.
\ [\ begin {align} \ tan t & = \ dfrac {\ sin t} {\ cos t} = \ dfrac {- \ frac {5} {13}} {\ frac {12} {13}} = — \ dfrac {5} {12} \\ \ sec t & = \ dfrac {1} {\ cos t} = \ dfrac {1} {\ frac {12} {13}} = \ dfrac {13} {12 } \\ \ csc t & = \ dfrac {1} {\ sin t} = \ dfrac {1} {- \ frac {5} {13}} = — \ dfrac {13} {5} \\ \ cot t & = \ dfrac {1} {\ tan t} = \ dfrac {1} {- \ frac {5} {12}} = — \ dfrac {12} {5} \ end {align} \]
Упражнение \ (\ PageIndex {7} \):
Если \ (\ sec (t) = — \ frac {17} {8} \) и \ (0 Решение \ (\ cos t = — \ frac {8} {17}, \ sin t = \ frac {15} {17}, \ tan t = — \ frac {15} {8} \) \ (\ csc t = \ frac {17} {15}, \ cot t = — \ frac {8} {15} \) Как мы обсуждали в начале главы, функция, которая повторяет свои значения через равные промежутки времени, известна как периодическая функция . Тригонометрические функции периодические. Для четырех тригонометрических функций, синуса, косинуса, косеканса и секанса, оборот одного круга или \ (2π \) приведет к одинаковым результатам для этих функций.А для тангенса и котангенса только половина оборота даст одинаковые результаты. Другие функции также могут быть периодическими. Например, продолжительность месяцев повторяется каждые четыре года. Если x x представляет собой продолжительность, измеряемую в годах, а \ (f (x) \) представляет количество дней в феврале, тогда \ (f (x + 4) = f (x) \). Этот образец повторяется снова и снова во времени. Другими словами, каждые четыре года в феврале гарантированно будет такое же количество дней, как и 4 годами ранее. Положительное число 4 — это наименьшее положительное число, которое удовлетворяет этому условию и называется периодом.Период — это самый короткий интервал, в течение которого функция выполняет один полный цикл — в этом примере период равен 4 и представляет время, необходимое нам, чтобы убедиться, что в феврале такое же количество дней. СРОК ФУНКЦИОНИРОВАНИЯ Период \ (P \) повторяющейся функции f f — это число, представляющее интервал, такой что \ (f (x + P) = f (x) \) для любого значения \ (x \). Период функций косинуса, синуса, секанса и косеканса равен \ (2π \). Период функций касательной и котангенса равен \ (π \). Пример \ (\ PageIndex {8} \): поиск значений тригонометрических функций Найдите значения шести тригонометрических функций угла \ (t \) на основе рисунка \ (\ PageIndex {9} \) . Решение \ [\ begin {align *} \ sin t & = y = — \ dfrac {\ sqrt {3}} {2} \\ \ cos t & = x = — \ dfrac {1} {2} \\ \ tan t & = \ dfrac {\ sin t} {\ cos t} = \ dfrac {- \ frac {\ sqrt {3}} {2}} {- \ frac {1} {2}} = \ sqrt {3 } \\ \ sec t & = \ dfrac {1} {\ cos t} = \ dfrac {1} {- \ frac {1} {2}} = — 2 \\ \ csc t & = \ dfrac {1} {\ sin t} = \ dfrac {1} {- \ frac {\ sqrt {3}} {2}} = — \ dfrac {2 \ sqrt {3}} {3} \\ \ cot t & = \ dfrac {1} {\ tan t} = \ dfrac {1} {\ sqrt {3}} = \ dfrac {\ sqrt {3}} {3} \ end {align *} \] Упражнение \ (\ PageIndex {8} \) Найдите значения шести тригонометрических функций угла \ (t \) на основе рисунка \ (\ PageIndex {10} \) . Решение \ (\ begin {align} \ sin t & = — 1, \ cos t = 0, \ tan t = \ text {Undefined} \\ \\ sec t & = \ text {Undefined}, \ csc t = — 1, \ cot t = 0 \ end {align} \) Пример \ (\ PageIndex {9} \): поиск значения тригонометрических функций Если \ (\ sin (t) = — \ frac {\ sqrt {3}} {2} \) и \ (\ cos (t) = \ frac {1} {2} \), найдите \ (\ sec (t), \ csc (t), \ tan (t), \ cot (t). \) Решение \ [\ begin {align} \ sec t & = \ dfrac {1} {\ cos t} = \ dfrac {1} {\ frac {1} {2}} = 2 \\ \ csc t & = \ dfrac {1} {\ sin t} = \ dfrac {1} {- \ frac {\ sqrt {3}} {2}} — \ dfrac {2 \ sqrt {3}} {3} \\ \ tan t & = \ dfrac {\ sin t} {\ cos t} = \ dfrac {- \ frac {\ sqrt {3}} {2}} {\ frac {1} {2}} = — \ sqrt {3} \\ \ cot t & = \ dfrac {1} {\ tan t} = \ dfrac {1} {- \ sqrt {3}} = — \ dfrac {\ sqrt {3}} {3} \ end {align} \] Упражнение \ (\ PageIndex {9} \): Если \ (\ sin (t) = \ frac {\ sqrt {2}} {2} \) и \ (\ cos (t) = \ frac {\ sqrt {2}} {2}, \) find \ (\ sec (t), \ csc (t), \ tan (t), \) и \ (\ cot (t) \). Решение \ (\ sec t = \ sqrt {2}, \ csc t = \ sqrt {2}, \ tan t = 1, \ cot t = 1 \) М. Борна Для угла θ в прямоугольном треугольнике, как показано, мы назовем стороны как: Мы, , определяем три тригонометрических отношения синус θ , косинус θ и тангенс θ следующим образом (мы обычно записываем их в сокращенной форме sin θ cos θ и tan θ ): `sin theta = текст (напротив) / текст (гипотенуза)` cos \ theta = text (смежный) / text (гипотенуза) `tan theta = text (напротив) / text (смежный)` Чтобы запомнить это, многие люди используют SOH CAH TOA, то есть: S дюйм θ = O pposite / H ypotenuse, C os θ = A djacent / H ypotenuse и T an θ = O pposite / A djacent Часто бывает полезно использовать обратные отношения, в зависимости от проблемы.(Говоря простым языком, величина, обратная дроби, находится путем переворачивания дроби.) «косеканс» \ θ` является обратной величиной «синуса» \ θ`, «секанс» \ θ` является обратной величиной «косинус» \ θ`, и «Котангенс» \ θ` является обратной величиной «тангенса» \ θ` Обычно мы записываем их в краткой форме как `csc \ θ`,` sec \ θ` и `cot \ θ` . (В некоторых учебниках « csc » пишется как « cosec ». Это то же самое.) `csc \ theta = text (гипотенуза) / текст (напротив)` sec \ theta = text (гипотенуза) / текст (рядом) `cot \ theta = text (смежный) / text (напротив)` Важное примечание: Существует большая разница между csc θ и sin -1 θ . Итак, на вашем калькуляторе не используйте кнопку sin -1 , чтобы найти csc θ . Мы познакомимся с идеей sin -1 θ в следующем разделе, Значения тригонометрических функций. Для угла в стандартном положении мы определяем тригонометрические отношения в виде x , y и r : `sin theta = y / r« cos theta = x / r` `tan theta = y / x` Обратите внимание, что мы все еще определяем sin θ as «opp» / «hyp» `; cos θ как «adj» / «hyp» `и tan θ as «opp» / «adj» `, , но мы используем конкретные значения x -, y — и r , определяемые точкой ( x , y ), через которую проходит терминальная сторона.2) ` Неудивительно, что обратные отношения определяются аналогичным образом в терминах значений x -, y — и r — следующим образом: `csc \ theta = r / y« sec \ theta = r / x` `детская кроватка \ theta = x / y` Мы увидим несколько примеров нахождения точных значений в следующем разделе «Значения тригонометрических функций». 2. Синус, косинус, тангенс и обратные отношения
Взаимные тригонометрические отношения
Тригонометрические функции на плоскости
x-y Таблицы тригонометрических функций
Таблицы тригонометрических функций
Пример 1: Что такое синус 48 °?
Пример 2: Какой угол имеет косинус 0,3912?
Хотя калькулятор может легко найти тригонометрические функции дробной угловой меры, это может быть неверно, если вам нужно использовать таблицу для поиска значений.Таблицы не могут перечислить всех углов. Поэтому для нахождения значений между перечисленными в таблице значениями необходимо использовать приближение. Этот метод известен как линейная интерполяция . Предполагается, что различия в значениях функций прямо пропорциональны разнице размеров углов на малых интервалах . Это не совсем так, но дает лучший ответ, чем просто использование ближайшего значения в таблице. Этот метод проиллюстрирован в следующих примерах.
Пример 3 : Используя линейную интерполяцию, найдите tan 28,43 °, учитывая, что tan 28,40 ° = 0,5407 и tan 28,50 ° = 0,5430.
Задайте пропорцию с помощью переменной x .
Поскольку x — это разница между tan 28,40 ° и tan 28,43 °,
Пример 4: Найдите угол первого квадранта α, где cos α ≈ 0,2622, учитывая, что cos 74 ° ≈ 0,275 и стоимость 75 ° ≈ 0,2588.
Задайте пропорцию с помощью переменной x .
Следовательно, α ≈ 74,0 ° + 0,8 ° ≈ 74,8 °
Существует интересная техника аппроксимации для нахождения синуса и тангенса углов, которые меньше 0,4 радиана (приблизительно 23 °). Синус и тангенс углов меньше 0,4 радиана примерно равны угловой мере. Например, используя радиан, sin0,15 ≈ 0,149 и tan 0,15 ≈ 0,151.
Пример 5: Найдите θ на рисунке без использования таблиц тригонометрии или калькулятора для определения значений любых тригонометрических функций.
Рисунок 1
Чертеж для примера 5.
Поскольку sin θ = 5/23 ≈ 0,21739, размер угла может быть приблизительно равен 0,217 радиан, что составляет примерно 12,46 °. На самом деле ответ ближе к 0,219 радиан, или 12,56 ° — довольно близко для приближения. Если использовать теорему Пифагора для нахождения третьей стороны треугольника, этот процесс также можно использовать для касательной.
Пример 6: Найдите величину острого угла α с точностью до минуты, если tan α = 0,8884.
С помощью калькулятора
Изучите формулы с легкостью на сайте embibe.com.
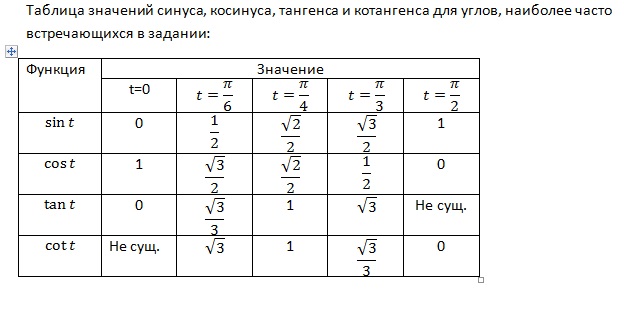
Таблица тригонометрии: Таблица тригонометрии содержит значения различных тригонометрических соотношений для стандартных углов, например 0 °, 30 °, 45 °, 60 ° и 90 °. Синус, косинус, тангенс, котангенс, секанс и косеканс — это шесть тригонометрических отношений.Таблица тригонометрии показывает значения этих тригонометрических соотношений для разных углов. Знание этих значений может облегчить решение различных тригонометрических задач.
Тригонометрия — это раздел математики, который занимается соотношением сторон и углов треугольника. Обычно это связано с прямоугольными треугольниками, при этом один из трех углов треугольника является прямым углом. Это помогает упростить вычисления и решить широкий спектр геометрических задач.
Например, если вы находитесь на террасе высокого здания известной высоты и на другой стороне дороги, напротив здания, есть почтовый ящик, ваше положение на крыше здания (точка A), подножие здания (точка B) и расположение почтового ящика (точка C) образуют прямоугольный треугольник. Вы можете легко рассчитать ширину дороги с помощью тригонометрии. Существуют различные применения тригонометрии в области строительства, летной техники, криминологии, морской биологии, инженерии и т. Д.
Эта статья предоставит вам таблицу тригонометрических соотношений и приемы для запоминания формул таблицы тригонометрии, чтобы вы могли напрямую использовать их для решения задач.
Таблица тригонометрии: тригонометрическая формула, отношение и угол | Формула таблицы тригонометрии
Как упоминалось выше, таблица тригонометрии содержит значения тригонометрических отношений (синус, косинус, тангенс, котангенс, секанс и косеканс) стандартных углов. Давайте посмотрим на таблицу тригонометрических соотношений:
| Углы в градусах | 0 ° | 30 ° | 45 ° | 60 ° | 903 | π / 6 | π / 4 | π / 3 | π / 2 | |||||
| sin | 0 | 0 | 2√3 / 2 | 0 | ||||||||||
| cos | 1 | √3 / 2 | 1 / √2 | 1/2 | 0 | |||||||||
| tan | 0 | 0 | 0 90 √3 | 1 | √3 | Не определено | ||||||||
| Детская кроватка | Не определено | √3 | 1 | 1 / √3 | 0 | 2 | 903 | √2 | 2 | Неопределенный | ||||
| кодексов | Неопределенный | 2 | √2 | 2 / √3 | 1 |
Таблица тригонометрии, 360 °, 360 °, 360 °
Давайте также посмотрим на значения этих тригонометрических отношений для 180 °, 270 ° и 360 °.
| Углы в градусах | 180 ° | 270 ° | 360 ° | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Углы в 903 90π2 /2 | 2π | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| sin | 0 | -1 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cos | -1 | 0 | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 0321 903 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| колыбель | Не определено | 0 | Не определено | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| сек | -1 | Не определено | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| cosec | Не определено | 9329 | Не определено | 902 Изучение таблицы тригонометрии: уловка для изучения таблицы тригонометрических соотношений | Трюк с тригонометрическим столом
0 ° → 0 30 ° → 1 45 ° → 2 60 ° → 3 90 ° → 4 | 3 найдите значения синуса углов , разделите число, соответствующее углу, на 4, а затем возьмите квадрат.
| sin0 ° | \ (\ sqrt {\ frac {0} {4}} = 0 \) |
| sin30 ° | \ (\ sqrt {\ frac {1} {4}} = 1/2 \) |
| sin 45 ° | \ (\ sqrt {\ frac {2} {4}} = 1 / √2 \) |
| sin60 ° | \ (\ sqrt {\ frac {3} {4}} = √3 / 2 \) |
| sin 90 ° | \ (\ sqrt {\ frac {4} {4}} = 1 \) |
Теперь мы знаем следующие формулы тригонометрии :
sin (π — \ (\ theta \)) = \ (\ sin \ theta \) ↠ Формула 1 sin (π + \ (\ theta \)) = — \ (\ sin \ theta \) ↠ Формула 2 sin (2π — \ (\ theta \)) = — \ (\ sin \ theta \) ↠ Формула 3 |
Используя эти формулы, давайте теперь найдем значения синуса углов 180 ° ( π ), 270 ° ( 3π / 2 ) и 360 ° ( 2π ), которые находятся во 2-м, третьем и 4-й квадрант соответственно:
sin180 ° = sinπ = sin (π — 0 °) = sin0 ° = 0 (по формуле 1) sin270 ° = sin (3π / 2) = sin (π + 90 °) = -sin90 ° = -1 (по формуле 2) sin360 ° = sin2π = sin (2π — 0 °) = -sin0 ° = 0 (по формуле 3) |
Таблица Trigo: определение значений косинуса стандартных углов
Чтобы определить значения косинуса стандартных углов от 0 ° до 90 °, мы просто присваиваем в обратном порядке, т.е.э .:
0 ° → 4 30 ° → 3 45 ° → 2 60 ° → 1 90 ° → 0 |
Теперь мы разделим число, соответствующее углам, на 4 и возьмем квадрат.
| cos0 ° | \ (\ sqrt {\ frac {4} {4}} = 1 \) |
| cos30 ° | \ (\ sqrt {\ frac {3} {4}} = √3 / 2 \) |
| cos45 ° | \ (\ sqrt {\ frac {2} {4}} = 1 / √2 \) |
| cos60 ° | \ (\ sqrt {\ frac {1} {4}} = 1/2 \) |
| cos90 ° | \ (\ sqrt {\ frac {0} {4}} = 0 \) |
Теперь мы знаем следующие формулы тригонометрии :
cos (π — \ (\ theta \)) = — \ (\ cos \ theta \) ↠ Формула 4 cos (π + \ (\ theta \)) = — \ (\ cos \ theta \) ↠ Формула 5 cos (2π — \ (\ theta \)) = \ (\ cos \ theta \) ↠ Формула 6 |
Теперь найдем значения косинуса углов 180 ° ( π ), 270 ° ( 3π / 2 ) и 360 ° ( 2π ) по этим формулам:
cos180 ° = cosπ = cos (π — 0 °) = -cos0 ° = -1 (с использованием формулы 4) cos270 ° = cos (3π / 2) = cos (π + 90 °) = -cos90 ° = 0 (по формуле 5) cos360 ° = cos2π = cos (2π — 0 °) = cos0 ° = 1 (по формуле 6) |
Определение значений тангенса стандартных углов
Мы знаем, что:
\ (\ tan \ theta \) = \ (\ frac {1} {\ cot \ theta} \) = \ (\ frac {\ sin \ theta} {\ cos \ theta} \) ↠ Формула 7 |
Нам уже известны значения синуса и косинуса стандартных углов.Подставляя эти значения в приведенную выше формулу (Формула 7), теперь мы можем легко вычислить значения тангенса этих углов.
| tan0 ° | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| tan30 ° | 1 / √3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| tan45 ° | 103 | 903 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| tan90 ° | Неопределенный | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| tan180 ° | 0 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| tan270 ° | Неопределенный | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 9322 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Котангенс стандартных углов Мы знаем, что:
Нам известны значения синуса и косинуса стандартных углов.Подставляя эти значения в приведенную выше формулу (Формула 8), теперь мы можем легко вычислить значения котангенса этих углов.
|


 Если у вас
нет совпадений, то вы выполнили задание
верно.
Если у вас
нет совпадений, то вы выполнили задание
верно.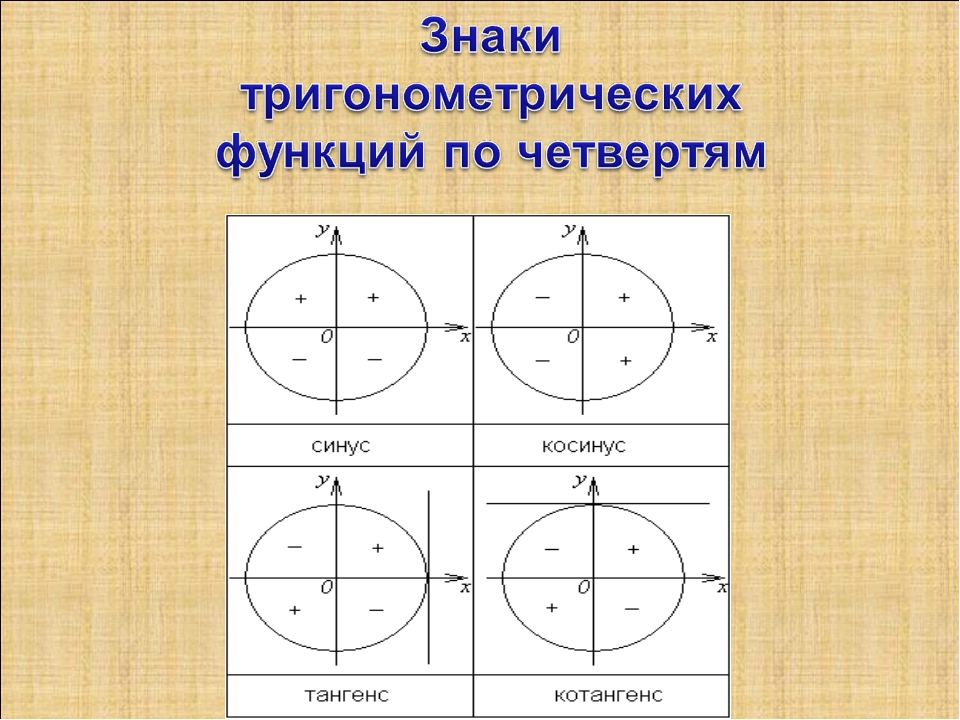 Если у вас
нет совпадений, то вы выполнили задание
верно.
Если у вас
нет совпадений, то вы выполнили задание
верно. °-a\). К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.
°-a\). К счастью, учить наизусть формулы привидения вам не придется, потому что есть легкий и надежный способ вывести нужную за пару секунд.
 °}}=\)
°}}=\)
 Значит, знак будет плюс;
Значит, знак будет плюс; Его мы разобрали выше, он равен минус синусу. \(\cos(\frac{3π}{2} — a)=-\sin{a}\)
Его мы разобрали выше, он равен минус синусу. \(\cos(\frac{3π}{2} — a)=-\sin{a}\) Что не так? Прежде всего, \(a\) стоит первой, хотя должна быть после «точки привязки». Поменяем местами слагаемые аргумента, сохраняя знаки.
Что не так? Прежде всего, \(a\) стоит первой, хотя должна быть после «точки привязки». Поменяем местами слагаемые аргумента, сохраняя знаки. \((\frac{7π}{2}+a)\) это четвертая четверть, и котангенс там отрицателен. «Точка привязки» — вертикальная, то есть функцию меняем. Окончательно имеем \(ctg(\frac{7π}{2}+a)=-tg a\) .
\((\frac{7π}{2}+a)\) это четвертая четверть, и котангенс там отрицателен. «Точка привязки» — вертикальная, то есть функцию меняем. Окончательно имеем \(ctg(\frac{7π}{2}+a)=-tg a\) .
 Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.
Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.
 Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.
Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач. Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360
градусов (0, π/6, π/4, π/3, π/2, …, 2π
радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.
Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360
градусов (0, π/6, π/4, π/3, π/2, …, 2π
радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.