Таблица углов тригонометрия: Таблица тригонометрических функций.

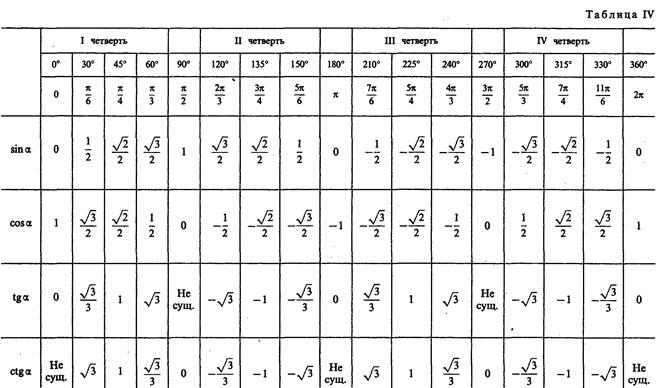
Таблица тригонометрических функций

Опять возвращаемся к пройденному: зная тригонометрическую функцию мы знаем соответствующий угол и наоборот.

Мы уже вскользь касались таблиц Брадиса. Между тем, эти таблицы бывают разные. Есть даже такие, где есть возможность узнать, например, sin49⁰8^,, достаточно выбрать необходимый угол и получить искомый результат. На сегодняшний день с помощью хорошего калькулятора можно вычислить любую тригонометрическую функцию за несколько секунд, но все-таки среди огромного количества таблиц и значений существует таблица с особыми углами. Об этих углах мы изучаем в школьной программе практически все, на них построена вся геометрия и тригонометрия, это их «основа основ». Если Вас спросят, например, чему равен sin40⁰, и вы не сможете ответить – не страшно, но если вы не будете знать значение синуса угла из числа особых, например, sin30⁰ — готовьтесь к плохой оценке.

Значения тригонометрических функций для таких особых углов свели в таблицу, широко известную как таблица тригонометрических функций. Таких особых углов насчитывается семнадцать, но их можно разделить на 3 группы. Рассмотрим их поближе.

Первая группа углов.

Сюда входят пять углов: 0⁰, 90⁰, 180⁰, 270⁰, 360⁰.

Вот так выглядит таблица с тригонометрических функций для этих углов:

Эту таблицу желательно знать наизусть, но гораздо проще и, главное, полезнее для ума уметь выводить их самостоятельно. Как? – спросите Вы. Воспользовавшись тригонометрическим кругом, который представляет собой обычный круг с центром, находящимся в нуле системы координат XY, с отмеченными табличными углами 0⁰, 90⁰, 180⁰, 270⁰, 360⁰:

Как видно из рисунка, особенность этих углов заключается в том, что они в точности попадают на оси координат. Так как круг занимает все 360⁰, углы 0⁰ и 360⁰ сходятся в одной точке, надеюсь, это понятно. Из этого вытекает одно очень полезное обстоятельство, что собственно и видно в таблице – тригонометрические функции у этих углов абсолютно одинаковы.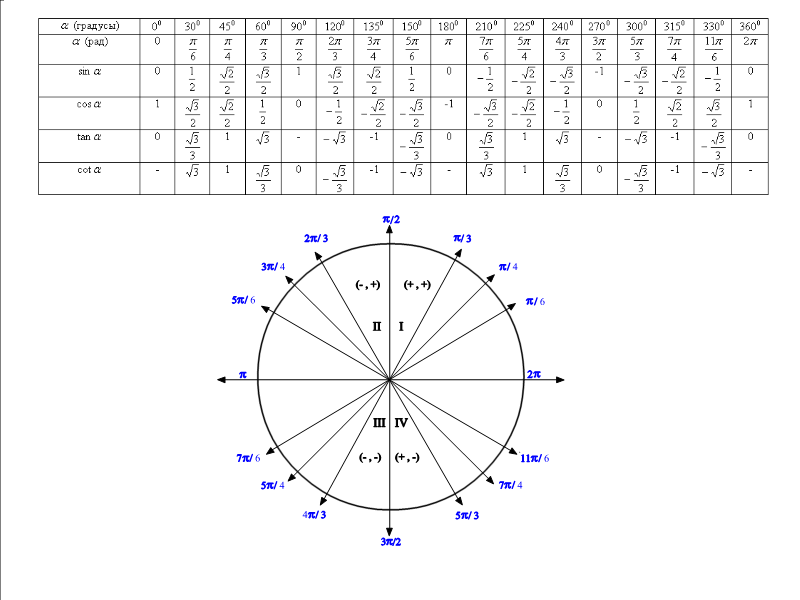

Допустим идет экзамен, и вот в ответственный момент Вас посетили смутные сомнения – синус 0⁰ равен 0 или 1? Вот тут-то Вас и спасет один чудный прием, с помощью которого Вы получите абсолютно правильный ответ, без каких бы то ни было сомнений.

Возьмем тот же злополучный sin0⁰, заодно и cos0⁰ посчитаем (именно с этими значениями обычно и случается путаница). Воспользуемся нашим кругом и нарисуем любой понравившийся угол х, но такой, который бы лежал в первой четверти. Далее отмечаем на осях sin и cos этого угла:

А теперь возьмем и уменьшим наш угол, вот так:

Что нам подсказывает логика? При уменьшении угла х синус также уменьшается. А косинус? Правильно – увеличивается. Что же произойдет с синусом, когда угол превратится в 0 и точка А окажется на оси Х? Он также исчезнет, т.е. станет равен 0. При этом косинус вырастет до длины подвижной части угла (радиуса тригонометрического круга), т.е. 1!

Вот мы и вычислили искомые синус и косинус нуля, причем быстро, а главное – надежно.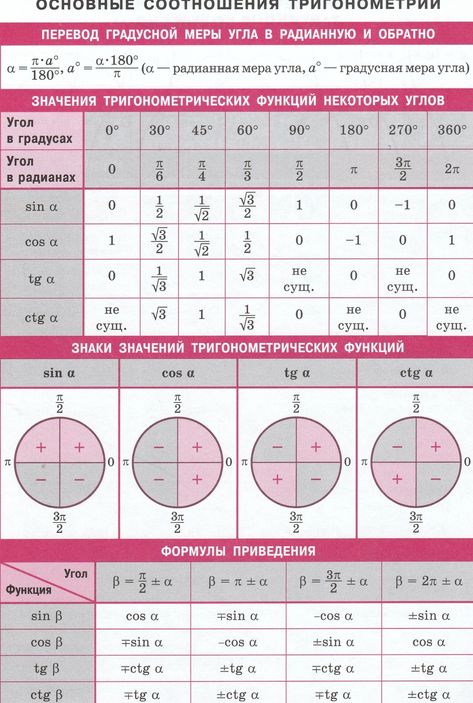 Правда – очень удобно?

Аналогично можно вычислить синус 180⁰ или косинус 270⁰.

Как видите, эта группа углов не нуждается в заучивании, достаточно воспользоваться волшебным кругом, это ведь проще, чем искать таблицу или вспоминать – правильно или неправильно.

Это же касается тангенса и котангенса. Нарисуем на круге линию тангенса или котангенса и нам всё становится видно — где он равен нулю, а где — не существует.

Идем дальше.

Вторая группа углов.

Сюда относятся следующие углы: 30⁰, 45⁰ и 60⁰. Для них также существуют табличные значения тригонометрических функций:

Я вставил сюда значения для 0⁰ и 90⁰ для завершённости первой четверти круга, мы используем это в дальнейшем.

Эти значения также необходимо знать наизусть. Но и здесь есть одна полезная особенность. Значения синусов и косинусов совпадают с точностью до наоборот, т.е. при возрастании угла от 0⁰ до 90⁰ его синус увеличивается от 0 до 1, а косинус наоборот – уменьшается от 1 до 0. Это же правило касается тангенсов и катангенсов, только значения другие. Получается, что достаточно записать это правило в память и учить станет намного меньше. Для остальных углов не из этой компании это правило уже не работает, скажем для 20⁰ или 40⁰.

Переходим к следующей группе.

Третья группа углов.

Сюда входят углы:120⁰, 135⁰, 150⁰, 210⁰, 225⁰, 240⁰, 300⁰, 315⁰, 330⁰. Для них просто надо твердо знать таблицу sin и cos.

Присмотревшись к этой группе углов, мы заметим, что она состоит из углов первых двух групп. Давайте проверим:

120⁰ = 90⁰ + 30⁰

135⁰ = 90⁰ + 45⁰

150⁰ = 90⁰ + 60⁰ и т.д.

Можно для разнообразия использовать не сумму, а разность:

120⁰ = 180⁰ — 60⁰

150⁰ = 180⁰ — 30⁰ и т.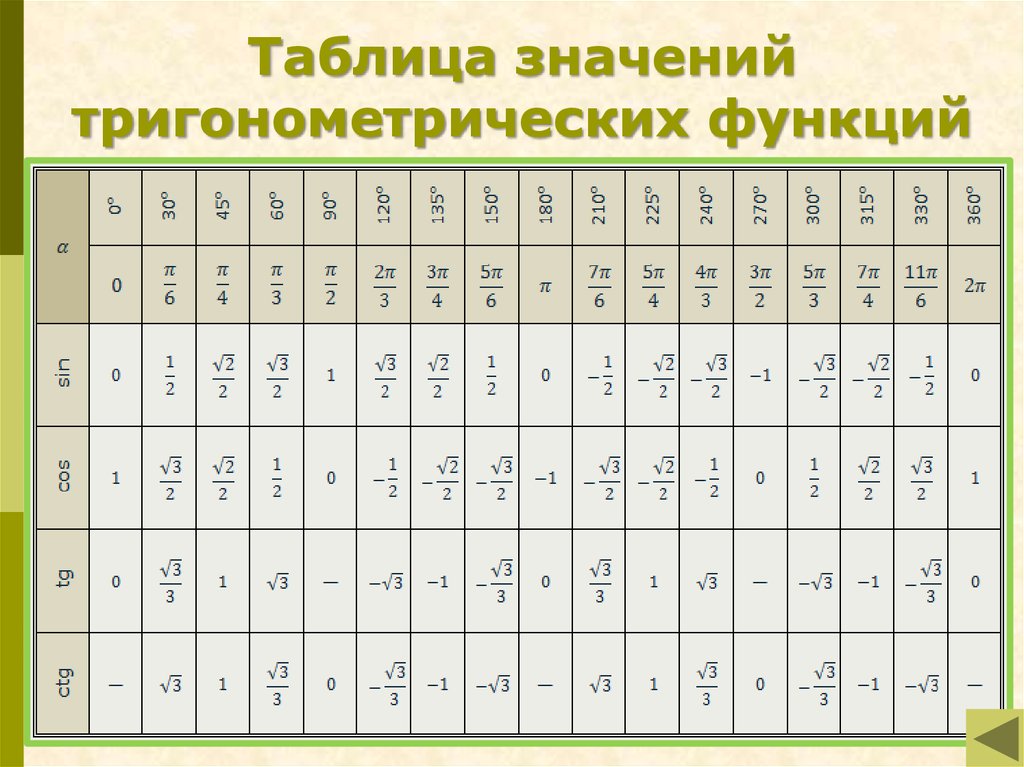 д.

Однако не будем спешить. Если Вы подумали, что это же правило действует и для синусов и косинусов, то Вы ошибаетесь. Синус суммы углов совсем не равен сумме синусов каждого угла. Но разложив угол третьей группы на сумму или разность углов из первой и второй групп мы упростим себе задачу нахождения соответствующей ему тригонометрической функции, причем не используя таблицу sin и cos.

Посмотрим, как это работает на практике. Допустим, надо найти cos150⁰.

Смотрим внимательно – из каких особых углов состоит наш угол. Советую выбирать в качестве угла из первой группы 180⁰ или 360⁰, потом станет понятно почему. Ближе всех расположен угол 180⁰:

150⁰ = 180⁰ — 30⁰

Далее нарисуем знакомый тригонометрический круг, отмечаем угол 150⁰ и получаем точку А на круге и смежный угол 30⁰. Другими словами, мы взяли подвижную сторону угла, на которой уместилась точка А, когда она находилась на оси Х, и отмотали по часовой стрелке на 30⁰.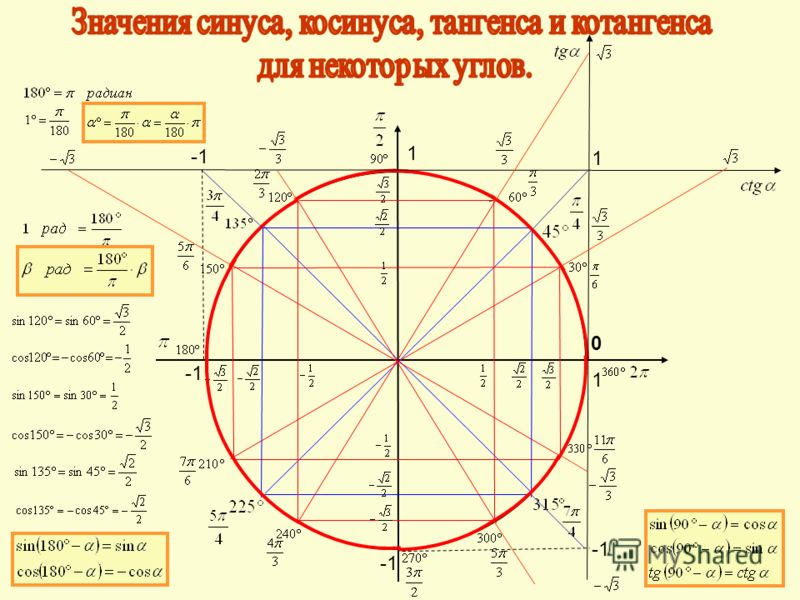 При этом получили вот такую картину:

Зелёным цветом мы обозначили угол 150⁰ и его cos, а красным — вспомогательный угол в 30⁰, правда отметили его мы не по правилам, что легко поправимо:

Правильные 30⁰ отсчитаны от положительной полуоси Х. Этот угол, как и его косинус, отметим синим цветом.

Сразу становится видно, что cos150⁰ равен cos30⁰, но с противоположным знаком, ведь треугольники справа и слева одинаковы. А уж cos30⁰ мы знаем, как табличный, и тогда:

cos150⁰ = — cos30⁰ = — /2

Аналогично можно найти sin150⁰. Снова воспользуемся тригонометрическим кругом, только теперь отмечаем синус угла синус на оси У:

И снова отмечаем правильный угол в 30⁰ и его синус. Опять мы видим, что sin 150⁰ и 30⁰ равны. Пускай углы в 30⁰ находятся вне треугольников, ведь всё равно, треугольники — одинаковые.

Получаем:

sin150⁰ = sin30⁰ = 1/2

Итак, к чему же мы пришли? Любой угол из третьей группы легко разлаживается на сумму или разность углов 180⁰ (или 360⁰) и 30, 45, 60 (смотря что подойдёт). Значит, мы всегда получим на тригонометрическом круге вспомогательный угол 30⁰, 45⁰ или 60⁰. И нет абсолютно никакой разницы, в какой из 4-х четвертей получится вспомогательный угол. Достаточно лишь изобразить правильный угол, расположенный в первой четверти, и найти одинаковые треугольники и сравнить их синусы (косинусы). Вот и все. И не надо зубрить таблицу тригонометрических функций для этих углов.

Еще небольшой примерчик.

Необходимо найти cos240⁰. Обойдемся без таблицы тригонометрических функций. Разложим угол на два:

240⁰ = 180

0 + 60⁰

Рисуем тригонометрический круг:

Мы видим, что вспомогательный угол 60⁰ находится в третьей четверти, треугольники одинаковые, поэтому ясно, что cos240⁰ = cos60⁰, но со знаком «минус», т. к. попадает на отрицательную полуось Х. Получаем:

cos240⁰ = — cos60⁰ = -1/2

заметка: для изучающих иностранные языки курсы английского языка (http://www.anglo-club.ru/napravleniya-obucheniya.html) придутся кстати.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

Таблица прямых и обратных тригонометрических функций, онлайн калькулятор

В данной таблице тригонометрических функций углов представлены значения, которые используются в большинстве геометрических задач.

Для решения математических задач часто используют тригонометрические функции, которые, обычно, выражают зависимость величины сторон треугольника от его углов. В этом списке:

• синус (sin)
• косинус (cos)
• тангенс (tg)
• котангенс (ctg)

Для того чтобы найти их значение предлагаем Вам воспользоваться нашей таблицей тригонометрических функций основных углов:

Как пользоваться таблицей

Алгоритм работы с таблицей довольно прост:

1. В первом столбце выбираем значение угла (например, 30 градусов).
2. В первой строке выбираем необходимую функцию (например, cos).
3. Находим место их пересечение (в данном случае, 3/2).

Если Вам надо узнать значение обратных тригонометрических функций угла (arcsin, arccos, arctg, arcctg) необходимо совершить действия в обратном порядке:

1. В первой строке выбираем функцию (если Вам известен arccos, то берем cos).
2. Выбираем значение угла (например, -1).
3. В первом столбце определяем угол, которому соответствует значение (в данном случае, 180 градусов).

Обратите внимание на то, что в таблице представлены стандартные тригонометрические углы (30, 60, 90, 180, 270 и 360 градусов). В ситуации, когда Вам дано другое значение (например, 87 градусов), рекомендуем воспользоваться нашими онлайн-калькуляторами.

Калькулятор расчета тригонометрических функций

Алгоритм работы с нашим калькулятором очень прост. Из выпадающего списка Тригонометрическая функция необходимо выбрать подходящую, например: косинус.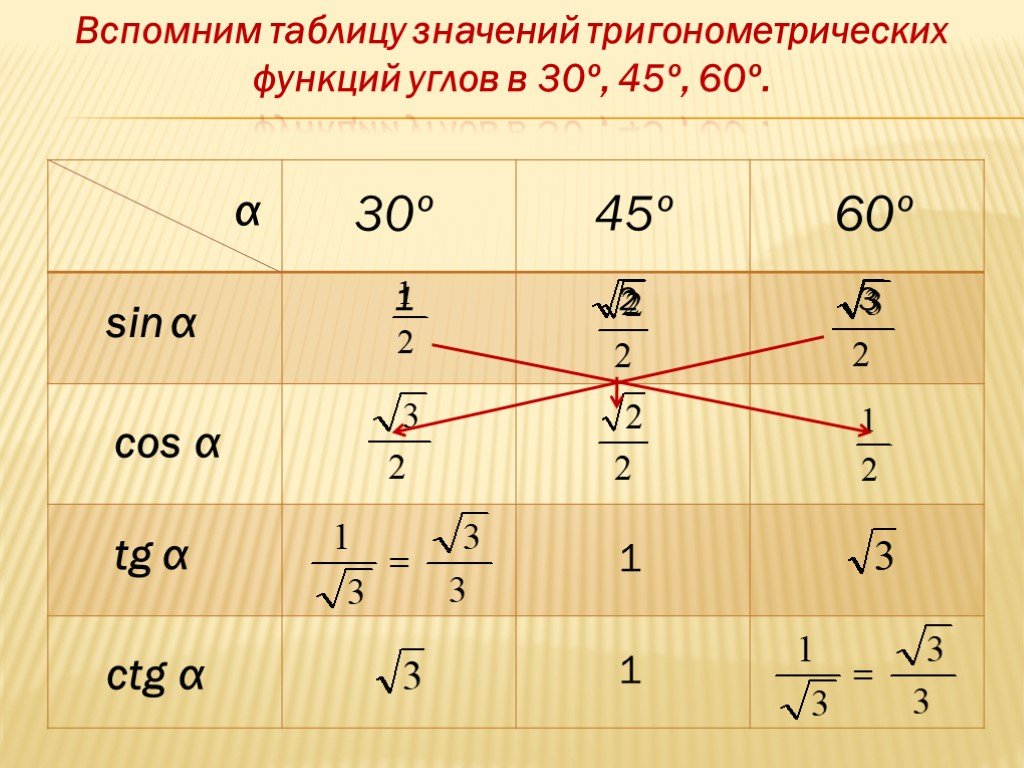 В поле Угол, градусов необходимо ввести значение угла в градусах. Можно ввести дробное значение угла, разделяя дробную часть запятой или точкой, например: 78,14 или 78.14. Обратите внимание: после запятой идут не минуты (или секунды), а дробная часть угла! То есть 45,5 это 45 градусов и 30 минут.

После того как Вы ввели значение угла и выбрали функцию нажмите на кнопку Вычислить значение. В поле Результат появится значение тригонометрической функции Вашего угла. Если были введены неверные данные, то калькулятор сообщит Вам об этом.

Калькулятор расчета обратных тригонометрических функций

Для вычисления обратных тригонометрических функций (arcsin, arcos, arctg, arcctg) Вам необходимо выбрать саму функцию из выпадающего списка. Далее в поле Значение триг. функции угла: ввести целое или дробное ее значение, например: 1 или 0.57(0,57). Нажать на кнопку Вычислить значение. Результатом будет величина угла в градусах.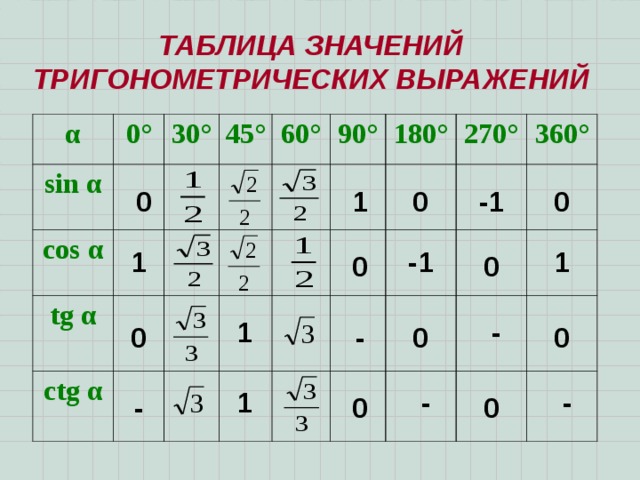

Обратите внимание: значения arcsin и arcсos не могут быть больше 1 и меньше -1!

Скорее всего, Вам будет интересно:

• Свойства вписанной в треугольник окружности
• Третий признак равенства треугольников формулировка и доказательство
• Как найти область определения функции онлайн
• Первый признак равенства треугольников: формулировка и доказательство (7 класс)
• Свойства медианы в прямоугольном треугольнике с доказательствами
• Свойства прямоугольной трапеции
• Средняя линия трапеции: чему равна, свойства, доказательство теоремы
• Пьеса Островского «Гроза» читать онлайн или скачать pdf
• Состав служебного программного обеспечения
• Сообщение о пчелах по биологии для 2-7 класса

ТАБЛИЦА ТРИГОНОМЕТРИЧЕСКИХ СООТНОШЕНИЙ И ТРИГОНОМЕТРИЧЕСКИЕ СООТНОШЕНИЯ КОНКРЕТНЫХ УГЛОВ угол \ тета . Теперь посмотрим, как этот угол \тета связан с тригонометрическими соотношениями и как он образует таблицу тригонометрических соотношений?

Угол \theta в тригонометрических соотношениях, связанный с углом \theta прямоугольного треугольника.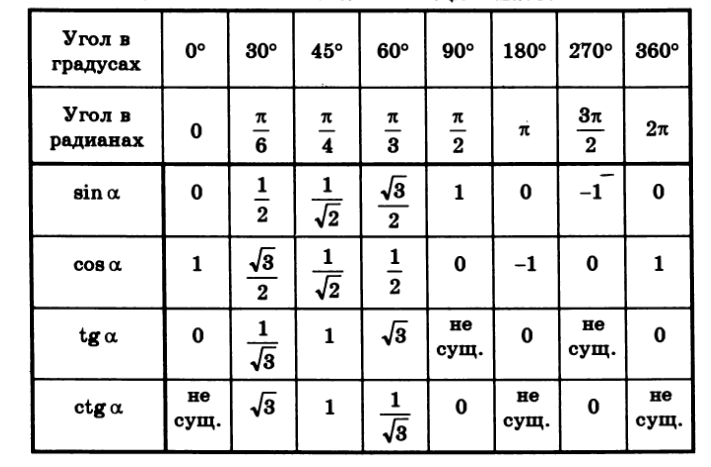

Имейте это в виду, это поможет вам глубже понять концепцию. Для прямоугольного треугольника угол \ тета находится в пределах от 0 до 9.0005 или до 90 ^или . [Почему \тета не может превышать 90 ^o ? Комментарий ниже]

ТРИГОНОМЕТРИЧЕСКИЕ СООТНОШЕНИЯ ПОД КОНКРЕТНЫМИ УГЛАМИ

Все тригонометрические отношения имеют некоторое значение для каждого угла. Эту концепцию можно лучше понять на примере.

Пример: Sin 30

^o

Что на самом деле означает Sin 30 ^o . Он имеет 2 компонента.

– 1 ^st – это Sin , то есть тригонометрическое отношение.

– 2 ^nd равно 30 ^o , что является тригонометрическим углом \тета прямоугольного треугольника.

Для большей ясности давайте разберемся с этим в отношении прямоугольного треугольника ABC.

Для этого прямоугольного треугольника ABC мы знаем, что Sin равен AB/AC, то есть отношение перпендикуляра к гипотенузе.

Среднее значение для прямоугольного треугольника ABC с тригонометрическим углом \ тета как 30 ^o отношение перпендикуляра (AB) и гипотенузы (AC) будет равно Sin 30 ^или .

Рассчитайте отношение перпендикуляра (AB) и гипотенузы (AC) любого случайного прямоугольного треугольника с углом \theta как 30 ^o . Он будет равен 0,5, что является фиксированным. Вы можете попробовать это с любым размером треугольника, просто тригонометрический угол должен быть 30 ^o .

Из приведенной выше анимации мы получили sin 30 ^o  равно 0,5. Аналогичным образом мы можем вычислить значение для всех углов и для всех тригонометрических отношений.

 Вы можете использовать калькулятор для перекрестной проверки.

ТРИГОНОМЕТРИЧЕСКАЯ ТАБЛИЦА

До сих пор мы понимали, что каждое тригонометрическое отношение имеет фиксированное значение относительно угла \theta .

Запомнить все значения будет невозможно. Поэтому мы ограничимся только некоторыми конкретными углами, которые показаны ниже в ТРИГОНОМЕТРИЧЕСКОЙ ТАБЛИЦЕ.

Тригонометрическая таблица показывает углы слева направо и тригонометрические отношения сверху вниз.

Не пытайтесь грабить Тригонометрическую таблицу. Попытайтесь понять это. В следующем посте рассматривается техника запоминания тригонометрической таблицы.

Если вы хотите узнать производные каждого угла относительно каждого тригонометрического отношения, нажмите здесь, чтобы получить БЕСПЛАТНУЮ видеолекцию о том же.

Эксперимент @ Дома

Нарисуйте случайные треугольники с тригонометрическим углом \тета как 30 ^o , 45 ^o и 60 ^o . И измерьте тригонометрические отношения с помощью тригонометрических сторон и проверьте правильность таблицы.

НЕ забудьте прокомментировать результаты.

Вопросы

В) Найдите стороны AB и BC на рисунке?

Во-первых, определите тригонометрические стороны.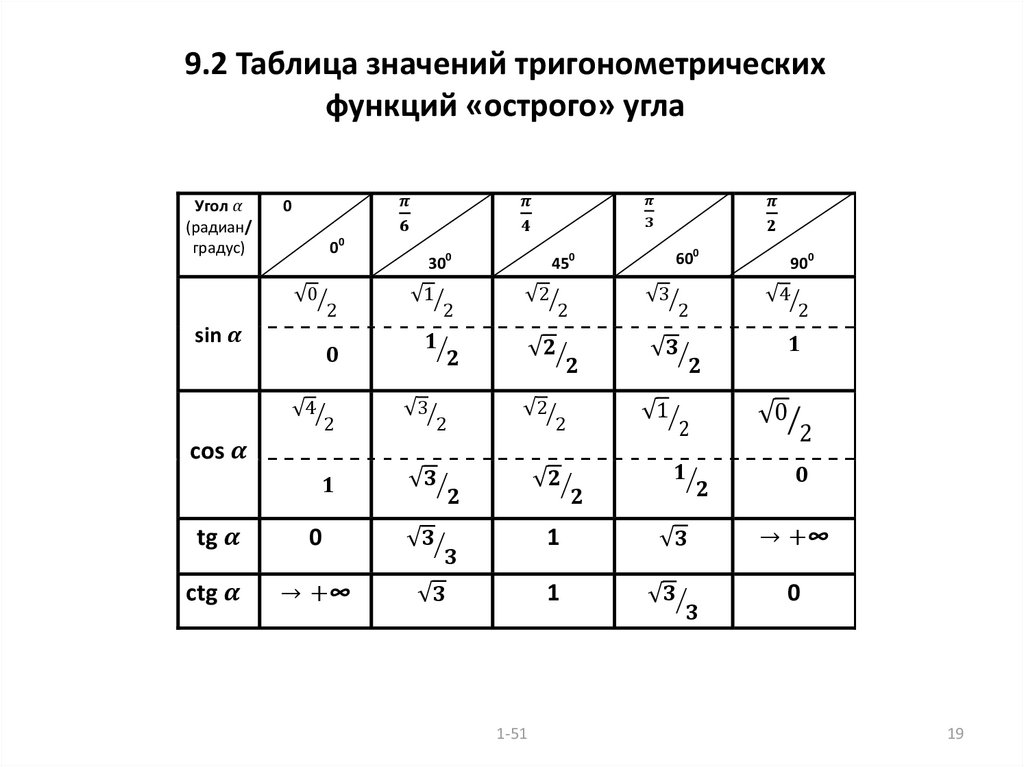 Нажмите здесь, чтобы узнать, как идентифицировать тригонометрические стороны.

AC= P = Перпендикуляр = 5

AB = B = Основание = ?

до н.э. = H = Гипотенуза = ?

Нам нужно найти основание B и гипотенузу H. 

Сначала найдем гипотенузу. Применимое соотношение между перпендикуляром и гипотенузой:

См. тригонометрическую таблицу для значения Sin 30 ^o .

Мы получили гипотенузу H как 10. т.е. сторона BC равна 10. У нас есть 2 стороны треугольника ABC. Давайте вычислим третью недостающую сторону B.

Мы получили все 3 стороны треугольника ABC.

Альтернативный подход к вопросу:

Как только мы получили гипотенузу H, мы также можем использовать Пифагор, чтобы найти 3-ю недостающую сторону Базы. [Комментарий ниже с полным ответом]

Вопрос к вам:

В) Найдите длины всех сторон и всех углов прямоугольного треугольника, приведенного ниже? Площадь треугольника равна 50 \sqrt { 3 }.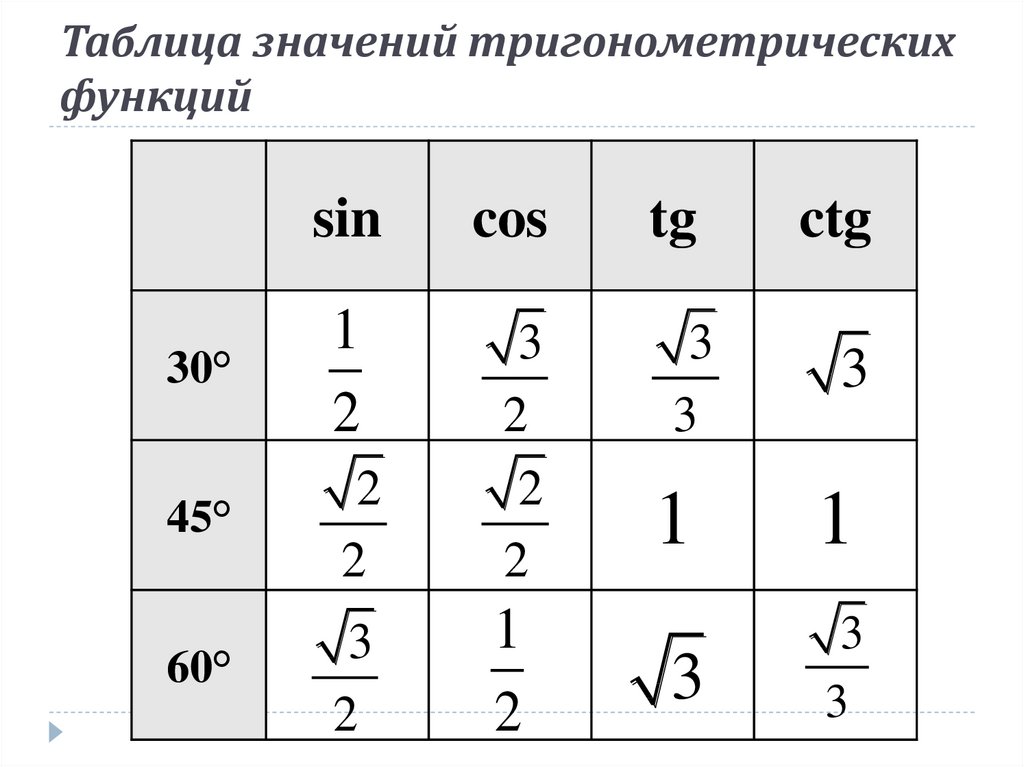

[Вставьте свой ответ в раздел комментариев]

[Спросите подсказку в разделе комментариев]

Посмотрите полное видео этой лекции с помощью

Animation Tool.

(Визуализируйте концепцию совершенно по-другому)

Это бесплатно

Узнать больше

Тригонометрическая таблица — Изучите CBSE

Тригонометрическая таблица : Тригонометрия — это раздел математики, занимающийся изучением длины, углов и их взаимосвязей в треугольнике. Тригонометрические соотношения применимы только для прямоугольных треугольников, один из углов которых равен 90 ^o

Тригонометрическую таблицу составляют следующие взаимосвязанные между собой тригонометрические соотношения – sin, cos, tan, cos , сек, койка.

• sin (обратная величина косеканса)  = напротив гипотенузы
• cos (обратное значение секанса)  = соседний по гипотенузе
• тангенс (обратное значение котангенса)  = напротив соседнего
• cot (обратное касательной)  = смежное над противоположным
90 171 косек (обратное значение синуса) = гипотенуза относительно противоположного 90 172 90 171 сек (обратное косинусу) = гипотенуза относительно соседнего 90 172

В вычислениях можно легко разобраться, если запомнить таблицу функций, наиболее известную как Тригонометрическая таблица . Это находит применение в нескольких областях. Некоторые из них включают навигационные видеоигры, авиацию, науку, географию, инженерию, геометрию и т. д. Тригонометрическая таблица помогла во многих разработках и в области машиностроения для первых инноваций.

Таблица соотношений Trig дает нам значения стандартных тригонометрических углов, таких как 0°, 30°, 45°, 60° и 90°. Эти значения имеют повышенный приоритет по сравнению с другими, поскольку наиболее важные проблемы используют эти соотношения. Поэтому очень важно знать и помнить соотношения этих стандартных углов.

Советы по запоминанию тригонометрической таблицы

Тригонометрическая таблица

Запоминание таблицы тригонометрии будет полезно, так как она находит множество применений, и существует множество способов запоминания таблицы. Автоматическое знание формул, соотношений и тождеств тригонометрии приведет к выяснению таблицы и значений. Таблица тригонометрических соотношений зависит от формул тригонометрии точно так же, как все функции тригонометрии взаимосвязаны друг с другом.

Прежде чем начать, лучше попытаться запомнить эти значения и знать следующие тригонометрические отношения дополнительных углов.

• sin x = cos (90∘−x)
• потому что х = грех (90∘−х)
• загар x = детская кроватка (90∘−x)
• кроватка х = загар (90∘−x)
• сек х = детская кроватка (90∘−x)
• раскладушка x = сек (90∘−x)

Взаимные соотношения тригонометрических отношений

• 1 / sin x = cosec x
• 1 / cos х= сек х
• 1/сек х= cos х
• 1 / коричневый x= детская кроватка x
• 1 / детская кроватка x= светло-коричневый x
• 1/ cosec x = sin x

шагов для создания тригонометрической таблицы:

Шаг 1 : Нарисуйте табличный столбец с требуемыми углами, такими как 0, 30 ^o , 45 ^o , 60 ^o , 90 ^o , 18 0 ^или , 270 ^или , 360 ^или в верхнем ряду и все 6 тригонометрических функций, таких как синус, косинус, тангенс, косеканс, секанс и котангенс в первом столбце.