Тангенс 1 градуса: Таблица тангенсов и котангенсов

alexxlab / / Разное

Содержание

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значение
cos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74
Найти точное значение		tan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81
Найти точное значение		sin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Синус, косинус, тангенс, котангенс произвольного угла. Радианная мера угла. Синус, косинус, тангенс и котангенс числа

В данной статье рассмотрим темы, которые встречаются в заданиях ЕГЭ по математике и содержатся в разделе алгебры, в ходе изучения темы подробно рассмотрим определения, используемые в теме, просмотрим рисунки, радианную меру углов, а также будем решать примерные задания. Темы, содержащиеся в статье, рассматриваются в соответствии с кодификатором, задающим элементы содержания заданий для выпускников образовательных организаций.

Переходим к более подробному изучению темы.

Для понятия о тригонометрических функциях следует рассмотреть окружность, радиус которой является единичным. У окружности есть центр, находящийся в начале координат, он расположен непосредственно на координатной плоскости. Для того, чтобы определить данную функцию, будем рассматривать вектор ОР. Он берёт начало в центре заданной окружности. Р – есть точка окружности. С помощью вектора ОР образуется угол с прилегающей осью, названной ОХ. ОР будет равен: OR = R = 1.

Рассмотрим соответствующий рисунок (рис. 1).

При проведении перпендикуляра из Р к оси ОХ получается прямоугольный треугольник, у которого есть гипотенуза и она равна единице.

При движении радиуса-вектора по часовой стрелке, будет получено отрицательное направление. А если радиус будет двигаться против часовой стрелки – положительное направление.

Для того чтобы осуществить вычисления синуса угла альфа, нужно обозначить на плоскости координату У. Как же получить это значение? Следует помнить, что в треугольнике, являющемся прямоугольным, синус произвольного угла будет равен отношению катета, являющегося противолежащим по отношению к гипотенузе. Получаем:

Sin a = У0 / R.

Радиус равен единице, исходя из этого: sin a = у0.

В окружности, являющейся единичной, ордината не должна быть больше единицы, а также меньше минус единицы: -1 < sin a < 1.

Синус будет являться положительным в первых и вторых четвертях окружности, являющейся единичной. Синус будет принимать отрицательное значение в третьей и четвёртой четверти окружности, являющейся единичной.

Выходит, для того чтобы получить косинус угла альфа, нужно определить на плоскости координату Х.

Косинус произвольного угла в треугольнике, являющемся прямоугольным, составляет отношение катета к гипотенузе. Получаем:

Cos a = х0 / R.

Поэтому, радиус равен единице, соответственно, cos a = x0.

У окружности, являющейся единичной, абсцисса не должна быть больше единицы и меньше минус единицы: -1 < cos a < 1.

Таким образом, косинус будет положительным в следующих четвертях окружности, являющейся единичной:

– В первой четверти;

– В четвёртой четверти.

Отрицательным:

– Во второй четверти;

– В третьей четверти.

Тангенсом угла, являющегося произвольным, считают отношение синуса и косинуса.

Представим произвольный треугольник, при условии, что он является прямоугольным. Здесь тангенсом будет отношение катета, названного противолежащим по отношению к прилежащему катету.

Если мы будем рассматривать единичную окружность – отношение её ординаты к абсциссе.

Получаем:

tg a = sin a / cos a; tg a = y0 / x0.

Следовательно, тангенс может быть при нулевом значении абсциссы, при этом, угол должен быть прямым. Тангенс вправе принимать и другие значения, такие как отрицательные и положительные.

Положительное значение тангенс будет иметь в первых и третьих четвертях окружности, являющейся единичной. Отрицательным тангенс является в четвёртой и второй четвертях.

Перейдём к рассмотрению котангенса. Котангенс угла, являющегося произвольным – косинус по отношению к синусу.

При рассмотрении прямоугольного треугольника это прилежащий катет по отношению к противолежащему:

Ctg a = cos a / sin a;

Ctg a = х0 / у0.

Если угол альфа равен нулю, то котангенса не существует. Это обусловлено тем, что в знаменателе дроби находится ордината.

Котангенс так же как и тангенс, в четвертях окружности, имеет такие же значения.

Рассмотрим примеры заданий, а в точности — неравенства:

– Если n принадлежит Z, то:

Sin (a + 2 пn ) = sin a;

Cos ( a + 2 пn ) = cos a.

– Также, если n принадлежит Z, то:

Tg ( a + пn ) = tg a;

Ctg ( a + пn ) = ctg а.

Перейдём к рассмотрению радианной меры угла. Рассмотрим единичную окружность (рис. 2).

Проводим дугу, которая будет равна радиусу окружности. Далее нужно соединить центр с концами данной дуги с помощью радиана. Один градус будет равен п 180 радиан. Один радиан соответственно, будет равен 180п. При этом, окружность будет равняться 2п.

Само понятие радиана открыл Томас Мюир и Джеймсон Томпсон в 1870 году. Таким образом, учёные измеряли углы на протяжении большого количества времени. К примеру, учёный Эйлер проводил исследования, он измерял углы с помощью длины дуги, которая отрезана в окружности, являющейся единичной.

Решим задачу ЕГЭ по математике на данную тему.

Нужно найти углы, при мере радиуса равной п / 2, п / 4, п / 8.

П / 2 * 180 / п = 90 градусов.

П / 4 * 180 / п = 45 градусов.

П / 8 * 180 / п = 22, 5 градуса.

Следует запомнить, что:

– 30 градусов равны п / 6;

– 45 градусов равны п / 4;

– 60 градусов равны п / 3;

– 90 градусов равны п / 2;

– 120 градусов равны 4п / 6;

– 180 градусов равны п.

Синус, тангенс, косинус, котангенс числа

Определением вышеописанных понятий считают число, равное синусу, косинусу, тангенсу и котангенсу в t радиан.

Синусом, косинусом, тангенсом и котангенсом числа t считают число, равное синусу, косинусу, тангенсу и котангенсу в t радиан.

Рассмотрим пример. Для любого действительного числа на окружности, являющейся единичной, определять точку. При этом, центр окружности должен находиться в начале системы координат. Все данные находят с помощью данной точки.

Начальной точкой окружности является точка А. Её координатами будут ( 1; 0 ). Пусть t – положительное число. Данному числу будет соответствовать точка, в неё осуществит переход изначальная точка. Если t отрицательное, то ему будет соответствовать точка, в которую осуществит переход исходная точка при направлении против часовой стрелки.

Рассмотрим определения основных понятий темы.

Синусом числа t является ордината точки окружности, являющейся единичной, она соответствует числу t. То есть sin t = y.

Косинусом числа t называют абсциссу точки окружности, являющейся единичной, она соответствует числу t. Получается: cos t = x.

Тангенсом числа t считают отношение ординаты к абсциссе точки окружности, являющейся единичной, она соответствует числу t. То есть: tg t = yx = sin t cos t.

Следует запомнить данные определения, а также необходимые неравенства, они пригодятся при решении заданий ЕГЭ по математике.

Данные определения не противоречат определению, которое дано в начале этой темы. Точка, лежащая на окружности, соответствует числу t, а также имеет совпадение с точкой. В эту точку переходит исходная точка, это происходит после осуществления поворота на угол, равный t радиан.

В процессе подготовки к экзамену рекомендуем внимательно просмотреть демоверсию ЕГЭ по математике базового уровня, а также решить примерные задания по теме. В демонстрационном варианте содержатся необходимые пояснения к ЕГЭ. Его назначением является ознакомление с примерным содержанием КИМОВ, заданиями, а также уровнем их сложности.

Тан 1 градус — найти значение Тан 1 градус .

. . Тангенс 1 градус в радианах записывается как тангенс (1° × π/180°), т. е. тангенс (0,017453…). В этой статье мы обсудим методы определения значения тангенса 1 градуса на примерах.

  • Tan 1° в десятичном виде: 0,0174550. . .
  • Тан (-1 градус): -0,0174550. . .
  • Tan 1° в радианах: загар (0,0174532 . . . .)

Каково значение Tan 1 градусов?

Значение тангенса 1 градуса в десятичной системе равно 0,017455064. . .. Tan 1 градус также может быть выражен с использованием эквивалента данного угла (1 градус) в радианах (0,01745 . . .)

Мы знаем, используя преобразование градусов в радианы, θ в радианах = θ в градусах × (пи/ 180°)
⇒ 1 градус = 1° × (π/180°) рад = 0,0174. . .
∴ тангенс 1° = тангенс (0,0174) = 0,0174550. . .

Объяснение:

Для тангенса 1 градуса угол 1° находится в диапазоне от 0° до 90° (первый квадрант). Поскольку функция тангенса положительна в первом квадранте, значение тангенса 1° = 0,0174550. . .
Поскольку функция тангенса является периодической функцией, мы можем представить тангенс 1° как тангенс 1 градусов = тангенс (1° + n × 180°), n ∈ Z.
⇒ тангенс 1° = тангенс 181° = тангенс 361° и так далее.
Примечание: Поскольку тангенс является нечетной функцией, значение тангенса (-1°) = -тангенса (1°).

Методы определения значения Тан 1 градусов

Функция тангенса положительна в 1-м квадранте. Значение тангенса 1° указано как 0,01745. . .. Мы можем найти значение tan 1 градусов по:

  • Используя Unit Circle
  • Использование тригонометрических функций

Тангенс 1 градус с помощью единичной окружности

Чтобы найти значение тангенса 1 градус с помощью единичной окружности:

  • Поверните ‘r’ против часовой стрелки, чтобы образовать угол 1° с положительной осью x.
  • Тангенс 1 градуса равен координате y (0,0175), деленной на координату x (0,9). 998) точки пересечения (0,9998, 0,0175) единичной окружности и r.

Следовательно, значение тангенса 1° = y/x = 0,0175 (приблизительно).

Тангенс 1° в терминах тригонометрических функций

Используя формулы тригонометрии, мы можем представить тангенс 1° как:

  • sin(1°)/cos(1°)
  • ± sin 1°/√(1 — sin²(1°))
  • ± √(1 — cos²(1°))/cos 1°
  • ± 1/√(косек²(1°) — 1)
  • ± √(сек²(1°) — 1)
  • 1/кроватка 1°

Примечание. Поскольку 1° находится в 1-м квадранте, окончательное значение тангенса 1° будет положительным.

Мы можем использовать тригонометрические тождества для представления tan 1° как

  • cot(90° — 1°) = cot 89°
  • -кроватка(90° + 1°) = -кроватка 91°
  • -тангенс (180° — 1°) = -тангенс 179°

☛ Также проверьте:

  • загар 45 градусов
  • загар 10 градусов
  • загар 0 градусов
  • загар 35 градусов
  • загар 73 градуса
  • загар 195 градусов

Примеры использования Tan 1 градусов

  1. Пример 1: Используя значение тангенса 1°, найдите: (sec²(1°) — 1).

    Решение:

    Мы знаем, (sec²(1°) — 1) = (tan²(1°)) = 0,0003
    ⇒ (сек²(1°) — 1) = 0,0003

  2. Пример 2: Упрощение: 8 (tan 1°/cot 89°)

    Решение:

    Мы знаем tan 1° = cot 89°
    ⇒ 8 tan 1°/cot 89° = 8 (tan 1°/tan 1°)
    = 8(1) = 8

  3. Пример 3. Найдите значение 5 тангенсов (1°)/10 тангенсов (179°).

    Решение:

    Используя тригонометрические тождества, мы знаем, что tan(1°) = -tan(180° — 1°) = -tan 179°.
    ⇒ тангенс (1°) = -тангенс (179°)
    ⇒ Значение 5 tan(1°)/10 tan(179°) = -5/10 = -1/2

перейти к слайдуперейти к слайдуперейти к слайду

 

Готовы увидеть мир глазами математика?

Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.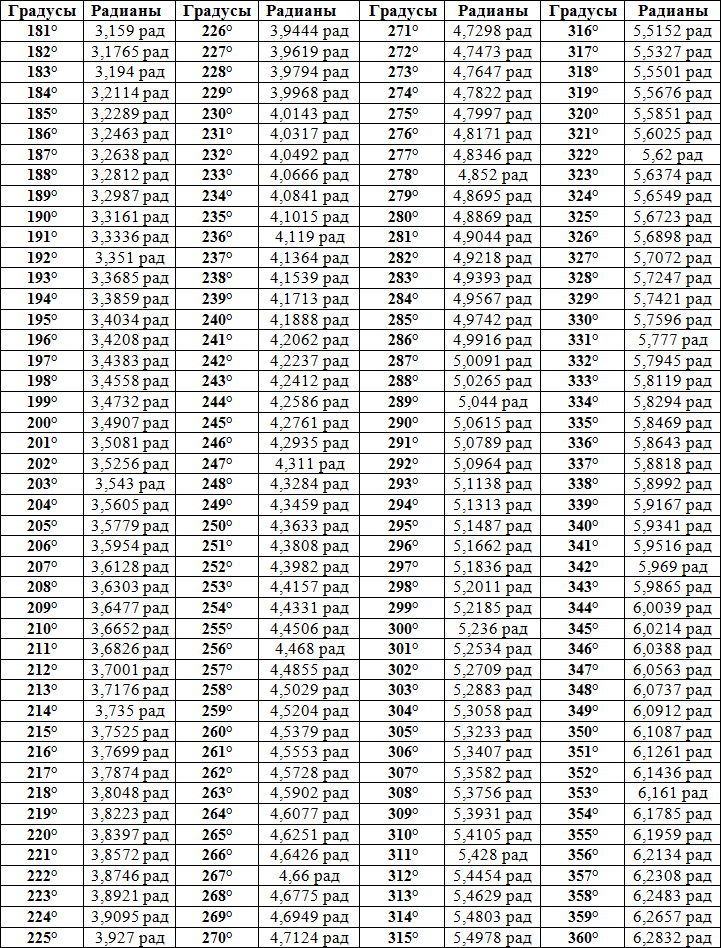

Запишитесь на бесплатный пробный урок

Часто задаваемые вопросы о Tan 1 Degrees

Что такое Tan 1 Degrees?

Тангенс 1 градус — значение тангенса тригонометрической функции для угла, равного 1 градусу. Значение тангенса 1° равно 0,0175 (приблизительно).

Каково точное значение тангенса в 1 градусе?

Точное значение тангенса 1 градуса может быть задано с точностью до 8 знаков после запятой как 0,01745506.

Как найти значение тангенса в 1 градусе?

Значение тангенса в 1 градусе можно рассчитать, построив угол 1° с осью x и затем найдя координаты соответствующей точки (0,9998, 0,0175) на единичной окружности. Значение tan 1° равно координате y (0,0175), деленной на координату x (0,9998). ∴ tan 1° = 0,0175

Каково значение Tan 1 в градусах с точки зрения Sin 1°?

Используя тригонометрические тождества, мы можем записать tan 1° через sin 1° как tan(1°) = sin 1°/√(1 — sin²(1°)) . Здесь значение sin 1° равно 0,0175.

Как найти тангенс 1° с точки зрения других тригонометрических функций?

Используя формулу тригонометрии, значение тангенса 1° может быть выражено через другие тригонометрические функции следующим образом:

  • sin(1°)/cos(1°)
  • ± sin 1°/√(1 — sin²(1°))
  • ± √(1 — cos²(1°))/cos 1°
  • ± 1/√(косек²(1°) — 1)
  • ± √(сек²(1°) — 1)
  • 1/кровать 1°

☛ Также проверьте: Тригонометрическая таблица

 

Скачать БЕСПЛАТНЫЕ учебные материалы

Тригонометрия

Рабочие листы по математике и
наглядная программа

Tan-1 Calculator

9 0002 Создано Анной Щепанек, доктором философии

Отзыв Давиде Борчиа

Последнее обновление: 02 февраля 2023 г.

Содержание:
  • Что такое tan-1 в математике?
  • Как обозначается арктангенс?
  • Как пользоваться этим калькулятором tan-1?
  • Инструменты Omni, связанные с этой темой
  • Часто задаваемые вопросы

Калькулятор тангенса 1 всегда готов помочь вам с уравнениями вида тангенс 1(х) = y . Мы здесь, чтобы помочь вам понять, что означают эти уравнения и как их решать.

Что такое tan-1 в математике?

Обозначение tan-1 может означать две разные вещи в математике:

  • tan-1(x) = 1/tan(x) = cot(x) , т. е. здесь мы имеем дело с мультипликативной инверсией; или
  • tan-1(x) = arctan(x) , поэтому обратная функция тангенса . Мы отвечаем здесь на вопрос , каков угол, тангенс которого равен x .

Люди, которые пишут tan-1 , чаще всего имеют в виду последнее значение: зачем вам печатать tan-1(x), если можно просто написать cot(x)? Однако иногда вам нужно будет догадаться из контекста.

Как видите, обозначение tan-1 может быть очень запутанным, и его следует избегать. Если вы имеете в виду котангенс, используйте cot(x) . Что следует использовать для обратной тангенса? Мы обсудим это сейчас.

Как обозначается арктангенс?

Наиболее распространенное обозначение для обратной тангенса arctan(x) . Префикс дуги берет свое начало в том, что при использовании единичной окружности и измерении углов в радианах угол x радиан будет соответствовать дуге, длина которой также равна x . Следовательно, «угол, тангенс которого равен х», совпадает с «дугой, тангенс которой равен х» .

В языках программирования обратная тангенс часто сокращается до atan(x) .

Как пользоваться этим калькулятором tan-1?

Калькулятор tan-1 очень прост в использовании. Просто введите число в поле и наслаждайтесь результатами в мгновение ока!

Например, если вам нужно определить tan-1(2) , просто введите 2 в поле x . Вы увидите, что результат равен 1,2490 радиан, то есть немного больше, чем 71,5° . Обратите внимание, что калькулятор позволяет конвертировать * между радианами и градусами , вам не нужно делать это вручную или искать дополнительные инструменты!

Помимо этого калькулятора tan-1, в Omni есть несколько других инструментов, объясняющих обратную сторону тангенса под разными углами (каламбур). Вот они:

  • Калькулятор арктангенса;
  • Обратный калькулятор Тан;
  • Калькулятор тангенса дуги; и
  • Калькулятор арктангенса.

Часто задаваемые вопросы

Как найти тангенс 1 отрицательных чисел?

Чтобы определить тангенс 1 отрицательного числа, выполните следующие действия:

  1. Запишите абсолютное значение вашего числа. Другими словами, избавьтесь от знака минус.
  2. Найдите тангенс-1 абсолютного значения, которое вы нашли на шаге 1.
  3. Возьмите результат и поставьте перед ним знак минус. Формально: найти напротив числа .
  4. Это ваш результат! Мы применили здесь формулу tan-1(-x) = -tan-1(x) для каждого действительного числа x .

Что такое tan-1 для -1?

Ответ: -45° , или эквивалентно -π/4 рад . Чтобы получить этот результат, вы должны использовать формулу tan-1(-x) = -tan-1(x) .

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *