Бесконечные пределы и асимптоты
Помимо конечных пределов, у последовательностей бывают бесконечные (см. раздел Пределы и ограниченность в главе 5). У функций тоже!
12.1Бесконечные пределы в конечных точках
12.1.1Существование предела и ограниченность
Из лекции 5 мы знаем, что сходящаяся последовательность ограничена. Для функций можно сформулировать аналогичное утверждение.
Теорема 1. Пусть функция f(x) имеет предел при x→x0. Тогда она ограничена на некоторой проколотой окрестности точки x0. Иными словами, найдутся такие C и δ∗>0, что для всех x∈˚Uδ∗(x0) выполняется неравенство |f(x)|<C.
Доказательство. По определению предела, для всякого ε>0 найдётся такое δ=δ(ε)>0, что для всех x из проколотой δ-окрестности x0 выполняется неравенство |f(x)−b|<ε.
Положим δ∗:=δ(1) (то есть возьмём ε=1). Тогда для всех
x из проколотой δ∗-окрестности точки x0 выполняется неравенство
|f(x)−b|<1.
По неравенству треугольника,
|f(x)|≤|f(x)−b|+|b−0|<1+|b|.
Положим C=1+|b|. Тогда ˚Uδ∗(x0) — искомая окрестность точки x0. Теорема доказана.∎
Доказательство очень похоже на доказательство аналогичной теоремы для последовательностей, и даже проще: в случае с последовательностями нужно было отдельно рассматривать начальный отрезок. За это мы платим тем фактом, что утверждение об ограниченности распространяется не на всю область определения функции, а лишь на некоторую проколотую окрестность точки x0.
Пример 1. Рассмотрим функцию f(x)=1/x. Она имеет предел при x→1, однако не является ограниченной на всей области определения.
12.1.2Бесконечные пределы
В том случае, когда функция не является ограниченной ни в какой проколотой
окрестности точки x0, она не может иметь предела в этой точке. Однако,
опять аналогично ситуациям с последовательностями, мы можем определить, что
означает, что функция стремится к бесконечности в точке x0.
Определение 1. Пусть функция f(x) определена в некоторой проколотой окрестности точки x0. Говорят, что её предел в этой точке равен бесконечности, если для всякого C найдётся такая δ>0, что для всех x из проколотой δ-окрестности точки x0 выполняется неравенство: |f(x)|>C. Формально:
∀C∈R ∃δ>0 ∀x∈R:0<|x−x0|<δ⇒|f(x)|>C.
∀C∈R ∃δ>0 ∀x∈R:0<|x−x0|<δ⇒|f(x)|>C.
Записывают:
limx→x0f(x)=∞.
Пример 2. Функция f(x)=1x стремится к бесконечности при x→0. Дейстительно, возьмём любоое C. Если C≤0, условие |1/x|>C выполнено автоматически. Если C>0, положим δ=1/C. Тогда если |x|<δ, то |1/x|=1/|x|>1/δ=C.
Пример 3. Функция
f(x)={1/x,x∈Q,0,x∉Q,
Опять же, аналогично последовательностям, помимо просто бесконечности, бывает плюс бесконечность и минус бесконечность:
Определение 2. Пусть функция f(x) определена в некоторой проколотой окрестности точки x0. Говорят, что её предел в этой точке равен плюс бесконечности (минус бесконечности), если для всякого C найдётся такая δ>0, что для всех x из проколотой δ-окрестности точки x0 выполняется неравенство: f(x)>C (соответственно, f(x)<C).
Упражнение 1. Запишите эти три определения в кванторах.
Пример 4. Неверно, что 1/x→+∞ при x→0: когда x приближается к нулю слева (то есть становится очень маленьким по модулю, но отрицательным), 1/x становится большим по модулю, но тоже отрицательным. В то же время, 1/(x2)→+∞ при x→0: знаменатель всегда положительный при x≠0, и когда он маленький по модулю, дробь становится очень большой.
Наконец, можно рассматривать односторонние бесконечные пределы.
Упражнение 2. Придумайте определения для утверждений limx→x+0f(x)=+∞,
limx→x+0f(x)=−∞, limx→x−0f(x)=+∞,
limx→x−0f(x)=−∞ самостоятельно, объединяя определение
2 и определения 11 и 12
из лекции 10.
Упражнение 3. Снова рассмотрим функцию f(x)=1/x. Докажите, что
limx→0+1x=+∞
и
limx→0−1x=−∞.
Определение 3. Заметим, что если функция стремится к какой-нибудь из бесконечностей
(неважно, плюс, минус или просто бесконечности) когда x стремится к x0
с какой-нибудь стороны, график y=f(x) приближается к вертикальной прямой
x=x0 когда x приближается к x0 (слева или справа). В этом случае
прямая x=x0 называется
Пример 5. Рассмотрим функцию
f(x)=x−1×2−1.
Знаменатель обнуляется в двух точках: x=1 и x=−1. При приближении к
точке x=−1 знаменатель стремится к нулю, а числитель к −2. Значит, дробь
стремится к бесконечности (без знака, т.к. знаменатель может быть
положительным или отрицательным, в зависимости от того, с какой стороны
приближаемся). У функции есть вертикальная асимптота x=−1.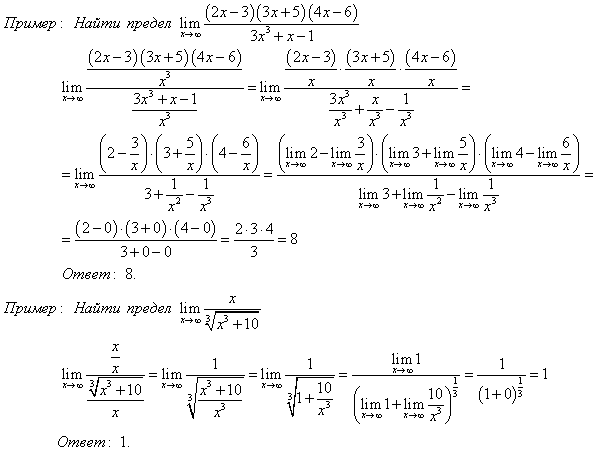
В точке x=1
обнуляется и числитель, и знаменатель. Чтобы найти предел в этой точке,
сократим дробь на (x−1). Получится выражение 1/(x+1). Оно имеет предел,
равный 1/2 при x→1. Значит, вертикальной асимптоты x=1 у функции
нет.
Рис. 12.2: У функции f(x)=x−1×2−1 есть единственная вертикальная асимптота: x=−1.
12.2Пределы на бесконечности
Другой тип пределов функций, связанный с бесконечностями — это предел при x стремящемся к бесконечности.
12.2.1Конечные пределы на бесконечности и горизонтальные асимптоты
Определение 4. Пусть функция f(x) определена для всех достаточно больших по модулю значений x, то есть найдётся такое C∗, что f(x) определена для всех x, для которых |x|>C∗. Говорят, что предел функции f(x) при x стремящемся к бесконечности равен b, если для всякого ε>0 найдётся такое C, что для всех x, если |x|>C, то |f(x)−b|<ε.
Определение 5. Пусть функция f(x) определена для всех достаточно больших значений x, то
есть найдётся такое C∗, что f(x) определена для всех x>C∗.
Говорят,
что предел функции f(x) при x стремящемся к плюс бесконечности равен
b, если для всякого ε>0 найдётся такое C, что для всех x>C
верно неравенство |f(x)−b|<ε.
Определение 6. Пусть функция f(x) определена для всех достаточно больших по модулю отрицательных значений x, то есть найдётся такое C∗, что f(x) определена для всех x<C∗. Говорят, что предел функции f(x) при x стремящемся к минус бесконечности равен b, если для всякого ε>0 найдётся такое C, что для всех x<C верно неравенство |f(x)−b|<ε.
Обозначения:
limx→∞f(x)=b,limx→+∞f(x)=b,limx→−∞f(x)=b.
Упражнение 4. Докажите, что если limx→∞f(x)=b, то limx→+∞f(x)=b и limx→−∞f(x)=b. Верно и обратное: если limx→+∞f(x)=b и limx→−∞f(x)=b, то limx→∞f(x)=b. Докажите и это.
Пример 6. Функция f(x)=1/x стремится к нулю при x→∞. (Докажите!)
Пример 7. Функция f(x)=ex стремится к нулю при x→−∞, а предел при x→+∞ не существует.
Определение 7. Если функция стремится к какому-то числу при x→+∞ или x→−∞,
её график приближается к горизонтальной прямой y=b.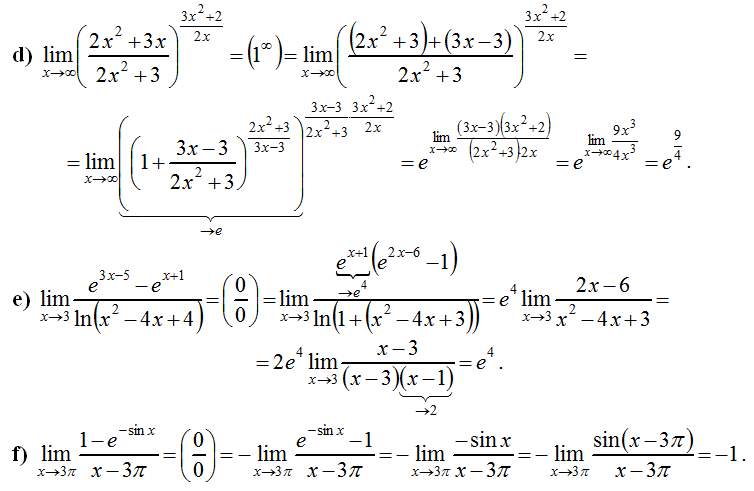
Рис. 12.3: Прямая y=0 является горизонтальной асимптотой функции f(x)=(sinx)/x.
Вопрос 1. Сколько вертикальных асимптот может быть у функции?
Сколько угодно, даже бесконечное число.
Верный ответ. Это правда. Например, у тангенса их бесконечно много.
Тоже не больше двух.
Неверный ответ. У функции f(x)=1/(x(x−1)(x+1)) их три!
Сколько угодно, но конечное число.
Неверный ответ. Что насчёт тангенса?
Вопрос 2. Рассмотрим два предела: предел функции limx→+∞sin(πx) и предел последовательности limn→∞sin(πn). Что вы можете про них сказать?
Неверный ответ.
Этого не может быть из определения предела по Гейне.
Они оба существуют и равны.
Неверный ответ. Это вряд ли. Функция sinπx может принимать значения 1 или −1 для сколь угодно больших x.
Они оба не существуют.
Неверный ответ. А что вы можете сказать про последовательность {sin(πn)}? Найдите несколько её членов.
Предел функции существует, а предел последовательности нет.
Неверный ответ. Этого не может быть из определения предела по Гейне.
Предел последовательности существует, а предел функции нет.
Верный ответ. И правда! Последовательность на самом деле состоит из нулей и её предел равен нулю. А функция sinπx может принимать значения 1 или −1 для сколь угодно больших x, и значит не имеет предела.
12.2.2Бесконечные пределы на бесконечности
Мы рассмотрели бесконечные пределы в конечных точках и конечные пределы на
бесконечности.
Можно скрестить ужа с ежом и получить бесконечные пределы
при x стремящемся к бесконечности.
Определение 8. Пусть функция f(x) определена для всех достаточно больших значений x, то есть найдётся такое C∗, что f(x) определена для всех x>C∗. Говорят, что предел функции f(x) при x стремящемся к плюс бесконечности равен плюс бесконечности, если для всякого D найдётся такое C, что для всех x>C верно неравенство f(x)>D. Записывают:
limx→+∞f(x)=+∞.
Упражнение 5. Придумайте определения для остальных комбинаций бесконечностей.
Пример 8. Функция f(x)=x2 стремится к плюс бесконечности при x→∞, а функция f(x)=x3 стремится просто к бесконечности при x→∞.
Пример 9. Рассмотрим функцию
f(x)=11+e−x.
При x→+∞ функция e−x стремится к нулю (она равна 1/ex, и раз ex становится очень-очень большим, e−x становится очень близким к нулю). По арифметике пределов,
limx→+∞11+e−x=11+0=1.
При x→−∞ функция e−x стремится к плюс бесконечности. В этом случае знаменатель дроби также стремится к плюс бесконечности. Поскольку числитель равен 1, значение дроби стремится к нулю (см. утверждение 2 из лекции 7, где шла речь про «арифметику бесконечностей»). Значит
limx→−∞11+e−x=0.
У нашей функции две горизонтальные асимптоты: y=0 и y=1. (И вообще это важная функция — так называемая «сигмоида», встречается в эконометрике и нейросетях.)
Рис. 12.4: У функции f(x)=1/(1+e−x) две горизонтальные асимптоты: y=0 и y=1.
12.2.3Наклонные асимптоты
Пусть limx→∞f(x)=∞. Тогда функция не может иметь горизонтальных асимптот. Однако её график по-прежнему может приближаться к какой-нибудь прямой — только не горизонтальной.
Пример 10. Рассмотрим функцию
f(x)=x+1x.
Её предел при x→∞ равен бесконечности, и когда x стремится к
бесконечности, график функции неограниченно приближается к прямой y=x.
Рис. 12.5: У функции f(x)=x+1x есть наклонная асимптота y=x.
Действительно, давайте возьмём большое значение x=x0 и посчитаем «расстояние по вертикали» между графиком функции и прямой y=x для этого значения x. (Иными словами, мы проведём вертикальную прямую x=x0 и посмотрим на расстояние между точками пересечения этой прямой и графиков y=f(x) и y=x.) Это расстояние вычисляется как |f(x)−x|=|1/x|. Оно стремится к нулю при x→∞.
Определение 9. Прямая y=kx+b называется наклонной асимптотой функции f(x) (или её графика), если хотя бы один из пределов
limx→+∞(f(x)−(kx+b)),
или
limx→−∞(f(x)−(kx+b))
равен нулю.
Как искать наклонные асимптоты? На эту тему есть рецепт.
Утверждение 1. Наклонная асимптота y=kx+b при x→+∞ у функции f(x) существует
тогда и только тогда, когда существуют пределы
limx→+∞f(x)x=k;limx→+∞(f(x)−kx)=b.
(12.1)(12.2)
При этом они обязаны равняться указанным значениям (k и b).
Доказательство. Докажем в одну сторону. Пусть y=kx+b является наклонной асимптотой функции f(x) при x→+∞. Тогда
limx→+∞f(x)x=limx→+∞f(x)−(kx+b)+(kx+b)x==limx→+∞(f(x)−(kx+b)x+k+bx)=k
limx→+∞f(x)x==limx→+∞f(x)−(kx+b)+(kx+b)x==limx→+∞(f(x)−(kx+b)x+k+bx)=k
Предел первого слагаемого равен нулю, поскольку числитель стремится к нулю (по предположению), а знаменатель к бесконечности.
Со вторым пределом ещё проще:
limx→+∞(f(x)−kx)=limx→+∞((f(x)−(kx+b)+b)=b.
limx→+∞(f(x)−kx)==limx→+∞((f(x)−(kx+b)+b)=b.
В обратную сторону. Пусть существует предел (12.2) и он равен b. Тогда
limx→+∞(f(x)−(kx+b))=limx→+∞(f(x)−kx)−b=b−b=0.
limx→+∞(f(x)−(kx+b))==limx→+∞(f(x)−kx)−b=b−b=0.
Утверждение доказано.
∎
Конечно, можно сформулировать и доказать аналогичное утверждение для x→−∞.
Таким образом, чтобы найти наклонные асимптоты, нужно сперва найти предел (12.1). Если он не существует, наклонной асимптоты (для этой бесконечности) точно нет. Если существует, нужно найти предел (12.2). Если этот предел существует, прямая y=kx+b является наклонной асимптотой.
Пример 11. Может так случиться, что предел (12.1) существует, а предел (12.2) нет. Например, это верно для функции f(x)=sinx.
12.3Заключение
Главная цель математического анализа — научиться «заглядывать в бесконечность». В этой лекции мы серьезно продвинулись в этом навыке.
← Предыдущая глава Следующая глава →
| 1 | Trovare la Derivata — d/dx | натуральный логарифм x | |
| 2 | Вычислим интеграл | интеграл натурального логарифма x по x | |
| 3 | Trovare la Derivata — d/dx | e^x | |
| 4 | Вычислим интеграл | интеграл e^(2x) по x | |
| 5 | Trovare la Derivata — d/dx | 1/x | |
| 6 | Trovare la Derivata — d/dx | x^2 | |
| 7 | Trovare la Derivata — d/dx | 1/(x^2) | |
| 8 | Trovare la Derivata — d/dx | sin(x)^2 | |
| 9 | Trovare la Derivata — d/dx | sec(x) | |
| 10 | Вычислим интеграл | интеграл e^x по x | |
| 11 | Вычислим интеграл | интеграл x^2 по x | |
| 12 | Вычислим интеграл | интеграл квадратного корня из x по x | |
| 13 | Trovare la Derivata — d/dx | cos(x)^2 | |
| 14 | Вычислим интеграл | интеграл 1/x по x | |
| 15 | Вычислим интеграл | интеграл sin(x)^2 по x | |
| 16 | Trovare la Derivata — d/dx | x^3 | |
| 17 | Trovare la Derivata — d/dx | sec(x)^2 | |
| 18 | Вычислим интеграл | интеграл cos(x)^2 по x | |
| 19 | Вычислим интеграл | интеграл sec(x)^2 по x | |
| 20 | Trovare la Derivata — d/dx | e^(x^2) | |
| 21 | Вычислим интеграл | интеграл в пределах от 0 до 1 кубический корень из 1+7x по x | |
| 22 | Trovare la Derivata — d/dx | sin(2x) | |
| 23 | Trovare la Derivata — d/dx | tan(x)^2 | |
| 24 | Вычислим интеграл | интеграл 1/(x^2) по x | |
| 25 | Trovare la Derivata — d/dx | 2^x | |
| 26 | График | натуральный логарифм a | |
| 27 | Trovare la Derivata — d/dx | cos(2x) | |
| 28 | Trovare la Derivata — d/dx | xe^x | |
| 29 | Вычислим интеграл | интеграл 2x по x | |
| 30 | Trovare la Derivata — d/dx | ( натуральный логарифм от x)^2 | |
| 31 | Trovare la Derivata — d/dx | натуральный логарифм (x)^2 | |
| 32 | Trovare la Derivata — d/dx | 3x^2 | |
| 33 | Вычислим интеграл | интеграл xe^(2x) по x | |
| 34 | Trovare la Derivata — d/dx | 2e^x | |
| 35 | Trovare la Derivata — d/dx | натуральный логарифм 2x | |
| 36 | Trovare la Derivata — d/dx | -sin(x) | |
| 37 | Trovare la Derivata — d/dx | 4x^2-x+5 | |
| 38 | Trovare la Derivata — d/dx | y=16 корень четвертой степени из 4x^4+4 | |
| 39 | Trovare la Derivata — d/dx | 2x^2 | |
| 40 | Вычислим интеграл | интеграл e^(3x) по x | |
| 41 | Вычислим интеграл | интеграл cos(2x) по x | |
| 42 | Trovare la Derivata — d/dx | 1/( квадратный корень из x) | |
| 43 | Вычислим интеграл | интеграл e^(x^2) по x | |
| 44 | Вычислить | e^infinity | |
| 45 | Trovare la Derivata — d/dx | x/2 | |
| 46 | Trovare la Derivata — d/dx | -cos(x) | |
| 47 | Trovare la Derivata — d/dx | sin(3x) | |
| 48 | Trovare la Derivata — d/dx | 1/(x^3) | |
| 49 | Вычислим интеграл | интеграл tan(x)^2 по x | |
| 50 | Вычислим интеграл | интеграл 1 по x | |
| 51 | Trovare la Derivata — d/dx | x^x | |
| 52 | Trovare la Derivata — d/dx | x натуральный логарифм от x | |
| 53 | Trovare la Derivata — d/dx | x^4 | |
| 54 | Оценить предел | предел (3x-5)/(x-3), если x стремится к 3 | |
| 55 | Вычислим интеграл | интеграл x^2 натуральный логарифм x по x | |
| 56 | Trovare la Derivata — d/dx | f(x) = square root of x | |
| 57 | Trovare la Derivata — d/dx | x^2sin(x) | |
| 58 | Вычислим интеграл | интеграл sin(2x) по x | |
| 59 | Trovare la Derivata — d/dx | 3e^x | |
| 60 | Вычислим интеграл | интеграл xe^x по x | |
| 61 | Trovare la Derivata — d/dx | y=x^2 | |
| 62 | Trovare la Derivata — d/dx | квадратный корень из x^2+1 | |
| 63 | Trovare la Derivata — d/dx | sin(x^2) | |
| 64 | Вычислим интеграл | интеграл e^(-2x) по x | |
| 65 | Вычислим интеграл | интеграл натурального логарифма квадратного корня из x по x | |
| 66 | Trovare la Derivata — d/dx | e^2 | |
| 67 | Trovare la Derivata — d/dx | x^2+1 | |
| 68 | Вычислим интеграл | интеграл sin(x) по x | |
| 69 | Trovare la Derivata — d/dx | arcsin(x) | |
| 70 | Оценить предел | предел (sin(x))/x, если x стремится к 0 | |
| 71 | Вычислим интеграл | интеграл e^(-x) по x | |
| 72 | Trovare la Derivata — d/dx | x^5 | |
| 73 | Trovare la Derivata — d/dx | 2/x | |
| 74 | Trovare la Derivata — d/dx | натуральный логарифм 3x | |
| 75 | Trovare la Derivata — d/dx | x^(1/2) | |
| 76 | Trovare la Derivata — d/d@VAR | f(x) = square root of x | |
| 77 | Trovare la Derivata — d/dx | cos(x^2) | |
| 78 | Trovare la Derivata — d/dx | 1/(x^5) | |
| 79 | Trovare la Derivata — d/dx | кубический корень из x^2 | |
| 80 | Вычислим интеграл | интеграл cos(x) по x | |
| 81 | Вычислим интеграл | интеграл e^(-x^2) по x | |
| 82 | Trovare la Derivata — d/d@VAR | f(x)=x^3 | |
| 83 | Вычислим интеграл | интеграл 4x^2+7 в пределах от 0 до 10 по x | |
| 84 | Вычислим интеграл | интеграл ( натуральный логарифм x)^2 по x | |
| 85 | Trovare la Derivata — d/dx | логарифм x | |
| 86 | Trovare la Derivata — d/dx | arctan(x) | |
| 87 | Trovare la Derivata — d/dx | натуральный логарифм 5x | |
| 88 | Trovare la Derivata — d/dx | 5e^x | |
| 89 | Trovare la Derivata — d/dx | cos(3x) | |
| 90 | Вычислим интеграл | интеграл x^3 по x | |
| 91 | Вычислим интеграл | интеграл x^2e^x по x | |
| 92 | Trovare la Derivata — d/dx | 16 корень четвертой степени из 4x^4+4 | |
| 93 | Trovare la Derivata — d/dx | x/(e^x) | |
| 94 | Оценить предел | предел arctan(e^x), если x стремится к 3 | |
| 95 | Вычислим интеграл | интеграл (e^x-e^(-x))/(e^x+e^(-x)) по x | |
| 96 | Trovare la Derivata — d/dx | 3^x | |
| 97 | Вычислим интеграл | интеграл xe^(x^2) по x | |
| 98 | Trovare la Derivata — d/dx | 2sin(x) | |
| 99 | Вычислить | sec(0)^2 | |
| 100 | Trovare la Derivata — d/dx | натуральный логарифм x^2 |
— Вопрос об ограничениях в команде lim и масштабе в пакете mathtools — TeX
Это дополнительный вопрос относительно ограничений в команде \lim и пакете mathtools .
Для начала, как я могу сделать так, чтобы ограничения начинались с начала символа lim, а не перед ним? Это означает, что символ предела и пределы не должны быть центрированы.
Также в пакете mathtool, если я использую опцию масштабирования, то пределы масштабируются, но, как мне кажется, вокруг точки, и чем меньше масштаб, тем больше становится вертикальный зазор между пределами и символом предела. Как я могу это исправить, чтобы вертикальное пространство перенаправлялось так же, как и оригинал в команде lim? И почему это происходит?
Это код, который я использовал в некоторых случаях, он принадлежит Питеру Гриллу, который опубликовал его, чтобы ответить на мой предыдущий вопрос.
\documentclass[12pt]{статья}
\usepackage{mathtools}
\usepackage{graphicx}
\usepackage{расчет}
% http://tex.stackexchange.com/questions/60453/reduction-font-size-in-equation/
\newcommand*{\Scale}[2][4]{\scalebox{#1}{$#2$}}%
\newcommand*{\Resize}[2]{\resizebox{#1}{!}{$#2$}}%
\начать{документ}
\noindent
Без \verb|\mathclap|:
\[ \lim_{n\to +\infty}x(n) \]
Но с \verb|\mathclap|::
\[ \lim_{\mathclap{n \to +\infty}}x(n) \]
Использование \verb|\scriptstyle| изменить размер:
\[ \lim_{\scriptscriptstyle n \to +\infty} х (n) \]
Использование \verb|\Scale|
\[ \lim_{\Масштаб[0,5]{n \to +\infty}} x(n) \]
Использование \verb|\Resize|
\[ \lim_{\Resize{\widthof{$\lim{}$}}{n \to +\infty}} x(n) \]
\конец{документ}
- позиционирование
- математические операторы
Стеки делают это очень простым.
Выравнивание задается параметром режима ( \stackalignment ), зазор задается необязательным аргументом стека. Использование \useanchorwidth говорит о том, что ширина отступа не должна влиять на расстояние до следующего элемента. EDITED для использования \mathop .
\documentclass{статья}
\usepackage[usestackEOL]{стековый движок}
\usepackage{graphicx}
\стекМатематика
\def\stackalignment{l}\def\useanchorwidth{T}
\начать{документ}
\[
\ mathop {\ stackunder [3pt] {\ lim} {\ scriptstyle n \ rightarrow + \ infty}} x (n)
\]
\[
\ mathop {\ stackunder [2.5pt] {\ lim} {\ scriptscriptstyle n \ rightarrow + \ infty}} x (n)
\]
\[
\mathop{\stackunder[2pt]{\lim}{\scalebox{.33}{$n\rightarrow+\infty$}}} x(n)
\]
\конец{документ}
Если \usearchorwidth было определено как {F} вместо {T} , результат будет выглядеть так:
параметры могут быть непосредственно включены в синтаксис, что имеет дополнительное преимущество, заключающееся в том, что их вызов непроницаем для текущих настроек режима.
\documentclass{статья}
\usepackage[usestackEOL]{стековый движок}
\usepackage{graphicx}
\стекМатематика
\начать{документ}
\[
\ mathop {\ stackengine {3pt} {\ lim} {\ scriptstyle n \ rightarrow + \ infty} {U} {l} {F} {T} {S}} x (n)
\]
\[
\ mathop {\ stackengine {2.5pt} {\ lim} {\ scriptscriptstyle n \ rightarrow + \ infty} {U} {l} {F} {T} {S}} x (n)
\]
\[
\mathop{\stackengine{2pt}{\lim}{\scalebox{.33}{$n\rightarrow+\infty$}}{U}{l}{F}{T}{S}} x(n)
\]
\конец{документ}
5
Это не работает в нижних или верхних индексах (это может быть сделано так):
\documentclass{article}
\makeatletter
\newcommand{\awfullim}{\@ifnextchar _{\@awfullim}{\lim}}
\newcommand{\@awfullim}[2]{% #1 равно _
\settowidth{\dimen0}{$\lim$}%
\settowidth{\dimen2}{$\scriptstyle#2$}%
\ifdim\dimen2<\dimen0
\lim_{#2}%
\еще
\addtolength{\dimen2}{-\dimen0}%
\kern-\dimen2 \lim_{\kern\dimen2 #2}%
\fi
}
\ сделать другое
\начать{документ}
\[
\awfullim_{x\to0^+}f(x)=\awfullim_{y\to+\infty}f(1/y)
\]
\конец{документ}
Имя, которое я использовал, говорит о том, насколько мне нравится эта идея.
;-)
4
символов. Как настроить вертикальное позиционирование \lim, чтобы аргумент выравнивался по всему стеку лимитов, а не только по слову «lim»? - TeX
Вот решение, которое повышает или понижает медиану любого оператора до медианы его аргумента.
\documentclass{статья}
\usepackage{аммат}
\usepackage{settobox}
\usepackage[noactivechars]{mathstyle}
\newsavebox{\opbox}
\newsavebox{\argbox}
\newlength{\opheight}
\newlength{\opdepth}
\newlength{\argheight}
\newlength{\argdepth}
\newcommand\vcenterop[2]{%
\edef\savedstyle{\currentmathstyle}
\savebox{\opbox}{\(\savedstyle #1\)}
\savebox{\argbox}{\(\savedstyle #2\)}
\settoboxheight{\opheight}{\opbox}
\settoboxdepth{\opdepth}{\opbox}
\settoboxheight{\argheight}{\argbox}
\settoboxdepth{\argdepth}{\argbox}
\addtolength{\argheight}{-\opheight}
\addtolength{\argheight}{-\argdepth}
\addtolength{\argheight}{\opdepth}
\mathop{\raisebox{0,5\argheight}{\usebox{\opbox}}} \mathord{\usebox{\argbox}}
}
\начать{документ}
\начать{выравнивать*}
&\textstyle\vcenterop{\lim_{x \to 0}}{f(x)} &\textstyle\vcenterop{\lim_{x \to 0}}{\frac{f(x)}{g(x) }} \\
&\vcenterop{\lim_{x \to 0}}{f(x)} &\vcenterop{\lim_{x \to 0}}{\frac{f(x)}{g(x)}} \\
&\lim_{x \to 0} f(x) &\lim_{x \to 0} \frac{f(x)}{g(x)} \\
&\vcenterop{\log_2}{f(x)^2} &\vcenterop{\log_2}{\frac{f(x)^2}{g(x)^2}} \\
&\log_2 f(x)^2 &\log_2 \frac{f(x)^2}{g(x)^2}
\конец{выравнивание*}
\конец{документ}
Также можно было бы повысить или понизить аргумент, а не оператор, или центрировать оба на математической оси, как это делает Мико для \lim .
По запросу Себастьяно
Вот как это выглядит с некоторыми рукописными шрифтами.
\documentclass{статья}
\usepackage{юникод-математика}
\usepackage{settobox}
\usepackage[noactivechars]{mathstyle}
\defaultfontfeatures{ Лигатуры=TeX, Масштаб=MatchLowercase}
% Tillana — это бесплатный шрифт от Indian Type Foundry, доступный по адресу:
% https://github.com/itfoundry/tillana/
% VAG Handwriting — это бесплатный шрифт от VAG Design, доступный по адресу:
% https://www.fontsquirrel.com/fonts/VAG-HandWritten
\setmainfont{VAG-HandWritten.otf}
\setmathfont{GFS Неоэллинская математика}
\setmathfont[range={"03C0,"2013-"2014,"2018-"201A,"201C-"201E,"2021-"2022,
"2026", "2030", "2039"-"203А", "2044", "20АС", "20БА", "20БД",
2113, 2122, 2126, 212Е, 2202, 2206, 220F, 2211,
2212, 2215, 221А, 221Е, 222Б, 2246, 2260, 2264,
"2265", "25КА}
]{Тиллана-Regular.otf}
\setmathfont[range=bfup/{латиница,латиница,число}
]{Tillana-Semibold.
