Степенная функция с нечетным показателем степени , ее свойства и график 9 класс онлайн-подготовка на Ростелеком Лицей |
Тема: Числовые функции
Урок: Степенная функция с нечетным показателем степени её свойства и график
1. Введение
Мы рассмотрим свойства и график степенной функции с нечетным показателем степени т.е. функции вида
2. Функция и её свойства
Рассмотрим функцию (рис. 1).
График проходит через три фиксированные характерные точки:
Прочтем график и сформулируем свойства функции.
2. Функция нечетная, График симметричен относительно начала координат.
3. Функция возрастает.
4. Не ограничена ни сверху, ни снизу.
5 .Не имеет ни наибольшего, ни наименьшего значения.
6. Функция непрерывна. Это значит, что кривую можно изобразить, не отрывая карандаша от бумаги.
7.
8. Выпукла вверх при выпукла вниз при .
3. Функция и её свойства
Рассмотрим свойства иных степенных функций с нечетным показателем степени.
Функция
1.
2. Функция нечетная,
3. График проходит через три фиксированные точки:
4. Функция возрастает.
5. Не ограничена ни сверху, ни снизу.
6. Нет ни наибольшего, ни наименьшего значения.
7. Функция непрерывна.
8.
9. Выпукла вверх при выпукла вниз при
4. Примеры
Рассмотрим взаимное расположение кривых на примере функций (рис. 2).
Например,
Рассмотренное свойство является ключом к решению ряда задач.
1. Найдитеи постройте график функции.
Решение:
График получим из известного нам графика путем сдвига на две единицы вправо (рис.
3).
Отметим точки пересечения с осями.
Ответ:
2. График данной функции получаем из графика функции сдвигом на одну единицу вверх (рис. 4).
Ответ:
5. Свойство функции с нечетным показателем
Мы изучаем степенные функции с нечетным показателем степени. Все они монотонно возрастают на всей области определения. Отметим важное свойство:
Если функция возрастает, а функция убывает, и если уравнение имеет корень, то этот корень – единственный (рис. 5).
6. Решение задач
Рассмотрим примеры:
1. Решить уравнение
решить неравенство
Решение:
Корень
Функция монотонно возрастает, функция монотонно убывает, корень есть, значит, он единственный.
Решением неравенства является луч
Ответ:
2. Построить график кривой
Решить уравнение
Решить неравенство
Решение:
Построим график функции Для этого график функции сдвинем на 3 вправо вдоль оси x и на 1 вниз вдоль оси y(рис.
7).
Функция монотонно возрастает, поэтому прямая пересекает кривую только в одной точке. Это точка
Решением неравенства является луч На этом промежутке кривая расположена выше оси x.
Ответ:
3. Найти область значений функции где
Решение:
Если x то yвозрастает и
Ответ:
4. Определить число решений системы
Решение:
Построим график каждой функции. График функции симметричное отображение графика относительно оси x.Если монотонно возрастает, то монотонно убывает.
График функции получаем сдвигом графика на 6 вниз вдоль оси у(рис. 9).
Функция монотонно возрастает, и если кривые пересекаются, то только в одной точке.
Ответ: Система имеет только одно решение.
7. Заключение
Мы рассмотрели график и свойства степенной функции с нечетным показателем степени. На следующем уроке мы рассмотрим задачи на степенную функцию с натуральным показателем.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб.для общеобразоват. учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб.для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4 .Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т.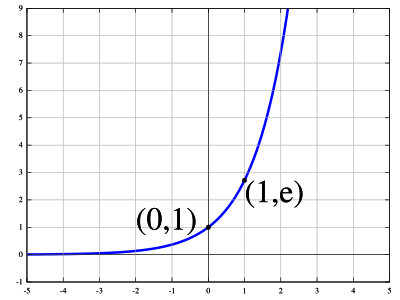
Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.:ил.
Рекомендованные ссылки на ресурсы интернет
1. Открытая математика (Источник).
2. Задачи (Источник).
3. Решу ЕГЭ (Источник).
Рекомендованное домашнее задание
Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил.
№№306, 307(б, г), 310, 308(а, в).
Дифференцирование e в степени x
LearnPracticeDownload
Дифференцирование e в степени x — это процесс определения производной e в степени x по x, который математически записывается как d(e x )/дх. Экспоненциальная функция имеет форму f(x) = a x , где «a» — действительное число, а x — переменная. e в степени x является экспоненциальной функцией с основанием (a), равным числу Эйлера «e», а дифференцирование e в степени x равно e в степени x, то есть самой себе.
Записывается как d(e x )/dx = e x .
Познакомимся с дифференцированием e в степени x и некоторыми вариациями функции e в степени x. Мы определим дифференцирование e в степени x, используя различные методы, включая первый принцип дифференцирования и производную экспоненциальной функции, а также несколько примеров для лучшего понимания.
| 1. | Какова дифференциация e в степени x? |
| 2. | Дифференциация e в Power x Formula |
| 3. | Дифференцирование e в степени x с использованием первого принципа |
| 4. | Дифференцирование e в степени x с использованием производной от a x |
| 5. | Часто задаваемые вопросы о дифференциации e в степени x |
Какова дифференциация e в степени x?
Дифференциация e в степени x равна e в степени x, потому что производная экспоненциальной функции с основанием ‘e’ равна e x .
Математически это обозначается как d(e x )/dx = e x . e в степени x является экспоненциальной функцией с основанием, равным «e», которое известно как «число Эйлера». Оно записывается как f(x) = e x , где e — число Эйлера, а его значение приблизительно равно 2,718. Дифференцирование e в степени x может быть выполнено с использованием различных методов, таких как первый принцип дифференцирования и производная х .
Дифференциация e в Power x Formula
Предположим, что y = e x ⇒ ln y = ln e x ⇒ ln y = x. Дифференцируя это по x, мы имеем (1/y) dy/dx = 1 ⇒ dy/dx = y ⇒ dy/dx = e x . Если мы продифференцируем e в степени x относительно x, мы получим d(e x )/dx = e x . Следовательно, формула дифференцирования e в степени x:
Дифференцирование e в степени x с использованием первого принципа производных
Далее мы докажем, что дифференцирование e в степени x равно e x , используя первый принцип дифференцирования.
Мы знаем, что для двух экспоненциальных функций, если основания одинаковы, мы складываем степени. Для доказательства производной e в степени x воспользуемся следующими формулами показательных функций и производных:
- f'(x) = lim h→0 [f(x + h) — f(x) ] / ч
- е х + ч = е х .e ч
- lim x→0 (e x — 1) / x = 1
Используя приведенные выше формулы, мы имеем
d(e x )/dx = lim h→0 [e x + h — e x ] / h
= lim ч→0 [e x .e h — e x ] / h
= lim h→0 e x [e h — 1] / h
= е х лим ч→0 [e h — 1] / h
= e x × 1
= e x
Таким образом, мы доказали, что дифференцирование e в степени x равно e в степени x .
Дифференцирование e в степени x с использованием производной от a
x Показательная функция имеет форму f(x) = a x , где ‘a’ — константа (действительное число), а x — переменная.
Производная показательной функции f(x) = a x равно f'(x) = (ln a) a x . Используя эту формулу и подставляя значение a = e в f'(x) = (ln a) a x , мы получаем дифференцирование e в степени x, которая определяется выражением f'(x) = (ln e) e x = 1 x e x = e x [Поскольку по правилам журнала, ln e = 1]. Следовательно, производная от e в степени x равна e x .
Важные замечания о дифференцировании e в степени x:
- n -е дифференцирование e в степени x равно e x , то есть d n (e x )/dx n = e x
- Производная показательной функции с основанием e равна e x .
- Производная от e x равна ae x . Используя эту формулу, мы получаем дифференцирование e x как 1.e x = e x .
☛ Связанные темы:
- Производное e 2x 9{2}}\)
Пример 2: Определите дифференцирование e в степени x sin x.
Решение: Чтобы вычислить значение производной от e x sinx, воспользуемся правилом дифференцирования произведения.
d(e x sinx)/dx = (e x )’ sin x + (sin x)’ e x
= e x sin x + e x co с х [Потому что производная от sin x равна cos x]
= e x (sin x + cos x)
Ответ: Следовательно, дифференцирование e в степени x sin x равно e x
(sin x + cos x).
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими сертифицированными экспертами
Запишитесь на бесплатный пробный урок
Дифференциация e в степени x Вопросы
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о дифференциации e в степени x
Каково дифференцирование e в степени x в исчислении?
дифференцирование e в степени x равно e в самой степени x, потому что производная экспоненциальной функции с основанием ‘e’ равна e x .
Математически это обозначается как d(e x )/dx = e x .
Каково дифференцирование e в степени минус x?
Дифференцирование e в степени минус x равно отрицательному значению e в степени минус x, то есть d(e — x )/dx = -e x .
В чем отличие e от Power Sin x?
Дифференцирование e в степени sin x равно произведению cos x и e в степени sin x, то есть d(e sin x )/dx = cos x e sin x .
Какая производная от e в степени x log x?
Производная от e в степени x log x определяется выражением d(e x ln x )/dx = e x ln x (1 + ln x). Это следует из цепного правила.
Как найти производную показательной функции?
Производная экспоненциальной функции f(x) = a x есть f'(x) = (ln a) a x , которую можно вычислить, используя первый принцип дифференцирования.
Что такое формула экспоненциального дифференцирования?
Формула экспоненциального дифференцирования для f(x) = a x равно f'(x) = (ln a) a x .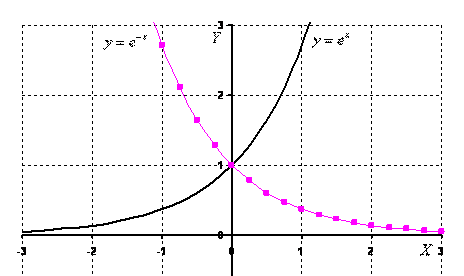
x.$$ 9х$$
является примером экспоненциального распада. Он быстро уменьшается по мере увеличения $x$, как показано на его графике.
При экспоненциальном росте $f(x)$ функция удваивается каждый раз, когда вы добавляете единицу к ее входу $x$. При экспоненциальном затухании $g(x)$ функция уменьшается вдвое каждый раз, когда вы добавляете единицу к ее входу $x$. Наличие этого времени удвоения или периода полураспада характерно для экспоненциальных функций, указывающих, насколько быстро они растут или затухают.
Параметры показательной функции
Как и в случае любой функции, действие экспоненциальной функции $f(x)$ можно описать с помощью метафоры функциональной машины, которая принимает входные данные $x$ и преобразует их в выходные данные $f(x)$.
Метафора функциональной машины полезна для введения параметров в функцию. Приведенные выше экспоненциальные функции $f(x)$ и $g(x)$ — это две разные функции, но они отличаются только изменением основания возведения в степень с 2 на 1/2.