Тангенс 180: tg 180 градусов

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значение
cos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27
Найти точное значение		sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упростить
sin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )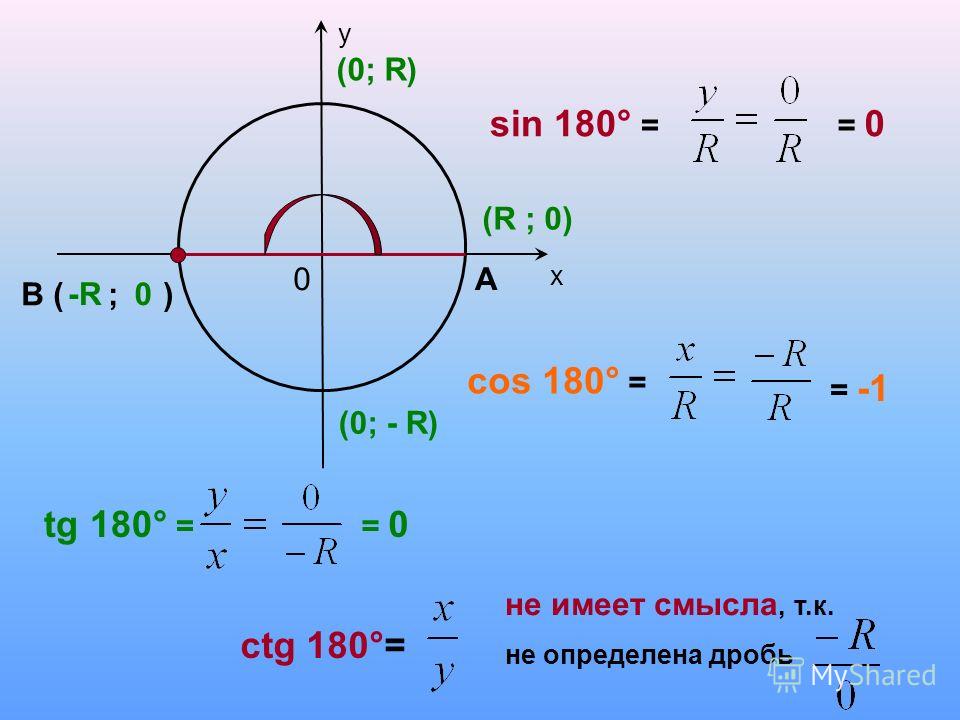
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )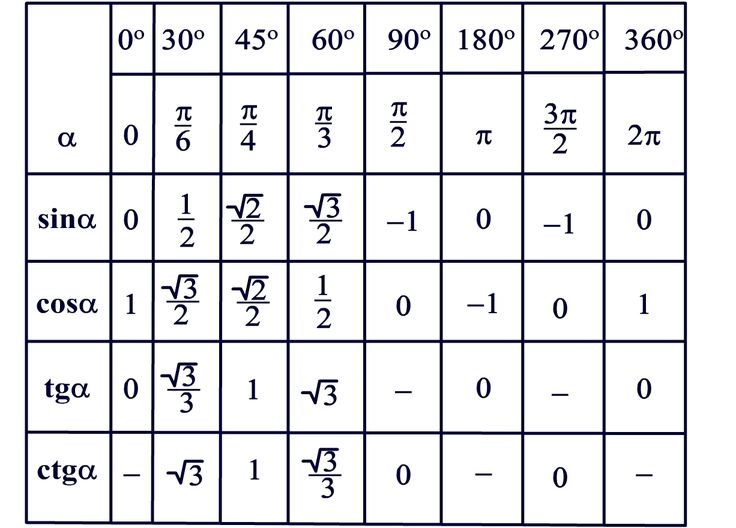
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )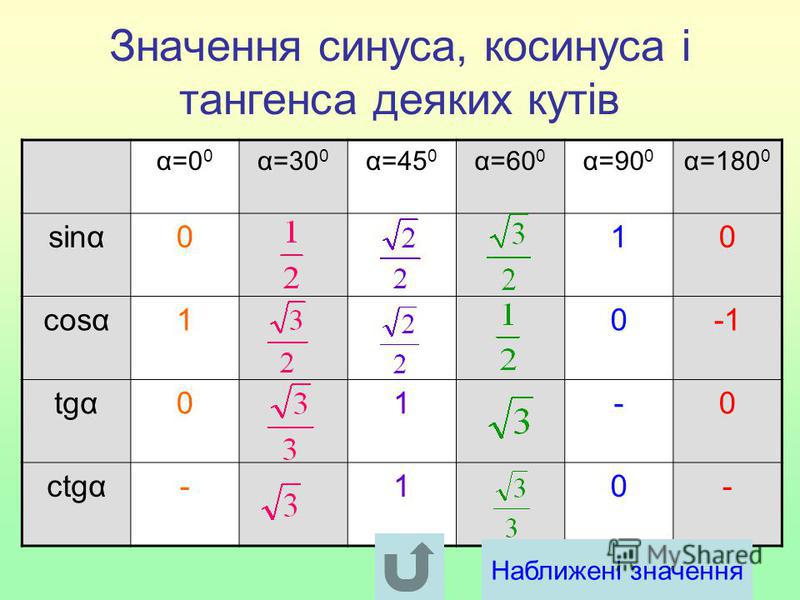
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значение
tan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значение
sin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )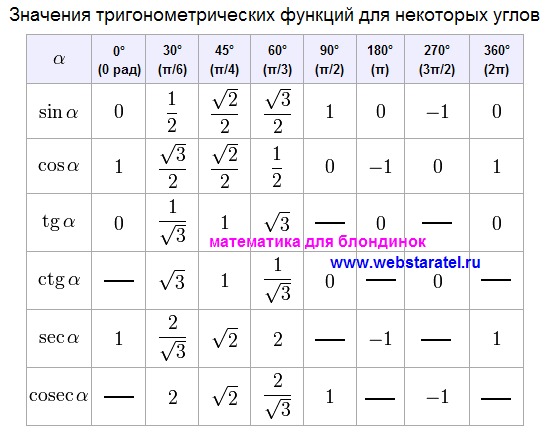
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

Таблица тангенсов углов от 0° до 180°

Тангенсом угла называется отношение синуса этого угла к косинусу:

   

Таблица тангенсов — таблица, содержащая значения тангенсов углов.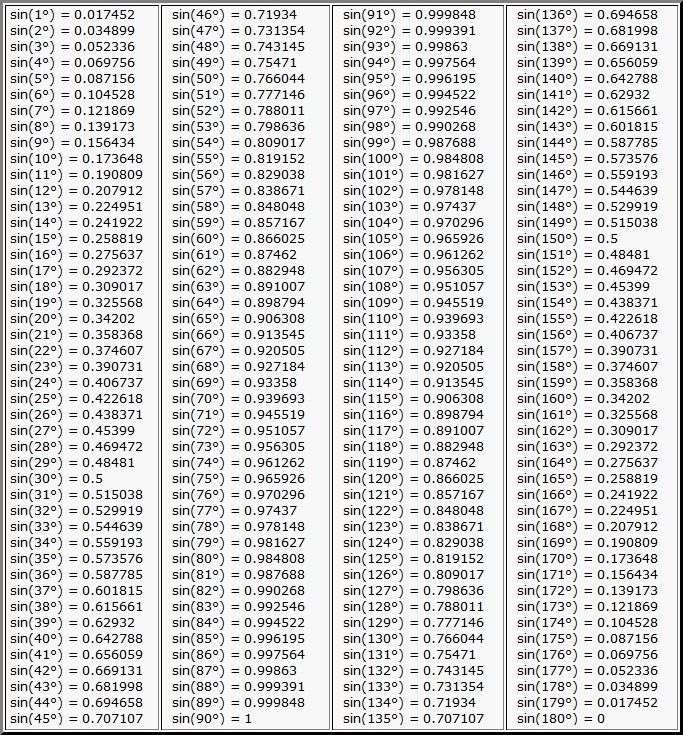 В нашей таблице вычислены тангенсы углов от 0° до 180°.

Таблицы тангенсов можно использовать при отсутствии калькулятора с тригонометрическими функциями.

Вам также могуть быть полезны таблица синусов, таблица косинусов и таблица котангенсов.

Таблица тангенсов углов 0°, 30°, 45°, 60°, 90°

Тангенс 90° не определён, так как .

Таблица тангенсов углов от 0° до 90°

tg(0°) = 0
tg(1°) = 0.017455
tg(2°) = 0.034921
tg(3°) = 0.052408
tg(4°) = 0.069927
tg(5°) = 0.087489
tg(6°) = 0.105104
tg(7°) = 0.122785
tg(8°) = 0.140541
tg(9°) = 0.158384
tg(10°) = 0.176327
tg(11°) = 0.194380
tg(12°) = 0.212557
tg(13°) = 0.230868
tg(14°) = 0.249328
tg(15°) = 0.267949
tg(16°) = 0.286745
tg(17°) = 0.305731
tg(18°) = 0.324920
tg(19°) = 0.344328
tg(20°) = 0.363970
tg(21°) = 0.383864
tg(22°) = 0. 404026
tg(23°) = 0.424475
tg(24°) = 0.445229
tg(25°) = 0.466308
tg(26°) = 0.487733
tg(27°) = 0.509525
tg(28°) = 0.531709
tg(29°) = 0.554309
tg(30°) = 0.577350
tg(31°) = 0.600861
tg(32°) = 0.624869
tg(33°) = 0.649408
tg(34°) = 0.674509
tg(35°) = 0.700208
tg(36°) = 0.726543
tg(37°) = 0.753554
tg(38°) = 0.781286
tg(39°) = 0.809784
tg(40°) = 0.839100
tg(41°) = 0.869287
tg(42°) = 0.900404
tg(43°) = 0.932515
tg(44°) = 0.965689
tg(45°) = 1
 tg(46°) = 1.03553
tg(47°) = 1.072369
tg(48°) = 1.110613
tg(49°) = 1.150368
tg(50°) = 1.191754
tg(51°) = 1.234897
tg(52°) = 1.279942
tg(53°) = 1.327045
tg(54°) = 1.376382
tg(55°) = 1.428148
tg(56°) = 1.482561
tg(57°) = 1.539865
tg(58°) = 1.600335
tg(59°) = 1.664279
tg(60°) = 1.732051
tg(61°) = 1.804048
tg(62°) = 1.880726
tg(63°) = 1.962611
tg(64°) = 2.050304
tg(65°) = 2. 144507
tg(66°) = 2.246037
tg(67°) = 2.355852
tg(68°) = 2.475087
tg(69°) = 2.605089
tg(70°) = 2.747477
tg(71°) = 2.904211
tg(72°) = 3.077684
tg(73°) = 3.270853
tg(74°) = 3.487414
tg(75°) = 3.732051
tg(76°) = 4.010781
tg(77°) = 4.331476
tg(78°) = 4.704630
tg(79°) = 5.144554
tg(80°) = 5.671282
tg(81°) = 6.313752
tg(82°) = 7.115370
tg(83°) = 8.144346
tg(84°) = 9.514364
tg(85°) = 11.430052
tg(86°) = 14.300666
tg(87°) = 19.081137
tg(88°) = 28.636253
tg(89°) = 57.289962
tg(90°) не определено

Таблица тангенсов углов от 91° до 180°

tg(91°) = -57.289962
tg(92°) = -28.636253
tg(93°) = -19.081137
tg(94°) = -14.300666
tg(95°) = -11.430052
tg(96°) = -9.514364
tg(97°) = -8.144346
tg(98°) = -7.115370
tg(99°) = -6.313752
tg(100°) = -5.671282
tg(101°) = -5.144554
tg(102°) = -4.704630
tg(103°) = -4. 331476
tg(104°) = -4.010781
tg(105°) = -3.732051
tg(106°) = -3.487414
tg(107°) = -3.270853
tg(108°) = -3.077684
tg(109°) = -2.904211
tg(110°) = -2.747477
tg(111°) = -2.605089
tg(112°) = -2.475087
tg(113°) = -2.355852
tg(114°) = -2.246037
tg(115°) = -2.144507
tg(116°) = -2.050304
tg(117°) = -1.962611
tg(118°) = -1.880726
tg(119°) = -1.804048
tg(120°) = -1.732051
tg(121°) = -1.664279
tg(122°) = -1.600335
tg(123°) = -1.539865
tg(124°) = -1.482561
tg(125°) = -1.428148
tg(126°) = -1.376382
tg(127°) = -1.327045
tg(128°) = -1.279942
tg(129°) = -1.234897
tg(130°) = -1.191754
tg(131°) = -1.150368
tg(132°) = -1.110613
tg(133°) = -1.072369
tg(134°) = -1.035530
tg(135°) = -1
 tg(136°) = -0.965689
tg(137°) = -0.932515
tg(138°) = -0.900404
tg(139°) = -0.869287
tg(140°) = -0.839100
tg(141°) = -0.809784
tg(142°) = -0.781286
tg(143°) = -0. 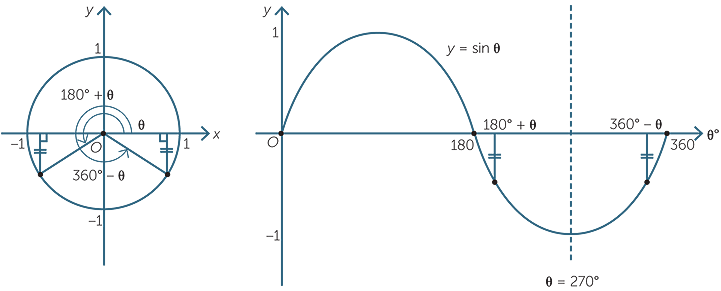753554
tg(144°) = -0.726543
tg(145°) = -0.700208
tg(146°) = -0.674509
tg(147°) = -0.649408
tg(148°) = -0.624869
tg(149°) = -0.600861
tg(150°) = -0.577350
tg(151°) = -0.554309
tg(152°) = -0.531709
tg(153°) = -0.509525
tg(154°) = -0.487733
tg(155°) = -0.466308
tg(156°) = -0.445229
tg(157°) = -0.424475
tg(158°) = -0.404026
tg(159°) = -0.383864
tg(160°) = -0.363970
tg(161°) = -0.344328
tg(162°) = -0.324920
tg(163°) = -0.305731
tg(164°) = -0.286745
tg(165°) = -0.267949
tg(166°) = -0.249328
tg(167°) = -0.230868
tg(168°) = -0.212557
tg(169°) = -0.194380
tg(170°) = -0.176327
tg(171°) = -0.158384
tg(172°) = -0.140541
tg(173°) = -0.122785
tg(174°) = -0.105104
tg(175°) = -0.087489
tg(176°) = -0.069927
tg(177°) = -0.052408
tg(178°) = -0.034921
tg(179°) = -0.017455
tg(180°) = 0

Tan 180 градусов — Найдите значение Tan 180 градусов

LearnPracticeDownload

Значение tan 180 градусов равно 0 . Тангенс 180 градусов в радианах записывается как тангенс (180° × π/180°), то есть тангенс (π) или тангенс (3,141592…). В этой статье мы обсудим методы нахождения значения тангенса 180 градусов на примерах.

  • Желто-коричневый 180°: 0
  • Желто-коричневый (-180 градусов): 0
  • Tan 180° в радианах: тангенс (π) или тангенс (3.1415926 . . . .)

Сколько стоит Тан 180 градусов?

Значение тангенса 180 градусов равно 0. Тангенс 180 градусов также может быть выражен с помощью эквивалента заданного угла (180 градусов) в радианах (3,14159 . . .)

Мы знаем, используя преобразование градусов в радианы, θ в радианы = θ в градусах × (pi/180°)
⇒ 180 градусов = 180° × (π/180°) рад = π или 3,1415 . . .
∴ tan 180° = tan(3.1415) = 0

Объяснение:

Для тангенса 180 градусов угол 180° лежит на отрицательной оси x. Таким образом, значение тангенса 180° = 0
Поскольку функция тангенса является периодической функцией, мы можем представить тангенс 180° как тангенс 180 градусов = тангенс (180° + n × 180°), n ∈ Z.
⇒ тангенс 180° = тангенс 360° = тангенс 540° и так далее.
Примечание: Поскольку тангенс является нечетной функцией, значение тангенса (-180°) = -тангенса (180°) = 0.

Методы определения значения тангенса 180 градусов

Значение тангенса 180° задается как 0. Мы можем найти значение тангенса 180 градусов по:

  • Использование тригонометрических функций
  • Использование единичного круга

Тангенс 180° в терминах тригонометрических функций

Используя формулы тригонометрии, мы можем представить тангенс 180° как:

  • sin(180°)/cos(180°)
  • ± sin 180°/√(1 — sin²(180°))
  • ± √(1 — cos²(180°))/cos 180°
  • ± 1/√(косек²(180°) — 1)
  • ± √(сек²(180°) — 1)
  • 1/кровать 180°

Примечание. Поскольку 180° лежит на отрицательной оси x, конечное значение тангенса 180° равно 0.

Мы можем использовать тригонометрические тождества для представления тангенса 180° как

  • cot(90° — 180°) = детская кроватка (-90°)
  • -кроватка(90° + 180°) = -кроватка 270°
  • -тангенс (180° — 180°) = -тангенс 0°

Tan 180 градусов с помощью единичной окружности

Чтобы найти значение tan 180 градусов с помощью единичной окружности:

  • Поверните ‘r’ против часовой стрелки, чтобы образовать угол 180° с положительной осью x.
  • Тангенс угла 180 градусов равен координате y(0), деленной на координату x(-1) точки пересечения (-1, 0) единичной окружности и r.

Отсюда значение тангенса 180° = y/x = 0

☛ Также проверьте:

  • тангенс 1 градус
  • загар 0 градусов
  • загар 15 градусов
  • тан 11 градусов
  • загар 38 градусов
  • загар 18 градусов

Примеры использования Tan 180 градусов

  1. Пример 1. Найдите значение tan 180°, используя cos 180° и sin 180°.

    Решение:

    Используя формулу загара,
    тангенс 180 ° = sin 180°/cos 180°
    ∵ sin 180° = 0 и cos 180 ° = -1
    ⇒ тангенс 180 ° = 0/(-1) = 0

  2. Пример 2: найти значение 7 tan(180°)/9загар (45°).

    Решение:

    Используя тригонометрические тождества, мы знаем, что tan(180°) = 0 и tan 45° = 1.
    ⇒ Значение 7 тангенса (180°)/9 тангенса (45°) = 0

  3. Пример 3. Найдите значение tan 180° + cot 45°.

    Решение:

    Так как tan 180° = 0 и cot 45° = 1
    ⇒ tan 180° + cot 45° = 0 + 1 = 1

перейти к слайдуперейти к слайдуперейти к слайду

 

Готовы увидеть мир глазами математика?

Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.

Запишитесь на бесплатный пробный урок

Часто задаваемые вопросы о Tan 180 Degrees

Что такое Tan 180 Degrees?

Тангенс 180 градусов — значение тангенса тригонометрической функции для угла, равного 180 градусам. Значение tan 180° равно 0.

Как найти значение Tan 180 градусов?

Значение тангенса 180 градусов можно рассчитать, построив угол 180° с осью x и затем найдя координаты соответствующей точки (-1, 0) на единичной окружности. Значение tan 180° равно координате y (0), деленной на координату x (-1). ∴ tan 180° = 0

Каково значение Tan 180° в единицах Sec 180°?

Мы можем представить функцию тангенса в терминах функции секущей, используя тригонометрические тождества, тангенс 180° можно записать как √(sec²(180°) — 1). Здесь значение sec 180° равно -1.

Каково значение Tan 180 градусов в пересчете на Cot 180°?

Поскольку функция тангенса является обратной функцией котангенса, мы можем записать тангенс 180° как 1/cot(180°).

Как найти тангенс 180° с точки зрения других тригонометрических функций?

Используя формулу тригонометрии, значение тангенса 180° может быть выражено через другие тригонометрические функции следующим образом:

  • sin(180°)/cos(180°)
  • ± sin 180°/√(1 — sin²(180°))
  • ± √(1 — cos²(180°))/cos 180°
  • ± 1/√(косек²(180°) — 1)
  • ± √(сек²(180°) — 1)
  • 1/кровать 180°

☛ Также проверьте: таблицу тригонометрии

 

Скачать БЕСПЛАТНЫЕ учебные материалы

Тригонометрия

Рабочие листы по математике и визуальный учебный план

Значение Tan 180 в градусах и радианах 9002 Примеры решения 9001 0

Сохранить

Скачать публикацию в формате PDF

Значение тангенса 180 градусов равно нулю. {\circ}\) в стандартном положении (-1, 0) 9{\circ} \right ) = 0\)

Периодичность касательной функции

Период — это продолжительность времени между двумя волнами, тогда как периодическая функция — это функция, значения которой повторяются через равные интервалы или периоды.

Поскольку выходные значения тангенса повторяются через равные промежутки времени, \( f\left ( \theta \right ) = \tan \left ( \theta \right )\) является периодической функцией. Любой другой угол с одинаковым значением тангенса для каждого угла существует на полпути вокруг единичной окружности. Следовательно, \(\pi\) является тангенциальным периодом.

Прежде чем график перескочит и снова повторится, мы можем наблюдать один непрерывный цикл из \( \frac{-\pi }{2},\frac{\pi }{2}\).

Таблица значений тангенса

Таблица значений тангенса приведена ниже:

Угол в градусах
0 0
30 \( \frac{1}{\sqrt{3}}\)
45{\circ}\)

0+1 = 1

Если вы хотите хорошо сдать экзамен по математике, то вы попали по адресу.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *

© 2015 - 2019 Муниципальное казённое общеобразовательное учреждение «Таловская средняя школа»

Карта сайта