Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД
Гипотенуза прямоугольного треугольника – это сторона, лежащая напротив прямого угла.
Катеты – стороны, лежащие напротив острых углов. Катет \(a\), лежащий напротив угла \(\alpha\), называется противолежащим (по отношению к углу \(\alpha\)). Другой катет \(b\), который лежит на одной из сторон угла \(\alpha\), называется прилежащим.
Синус острого угла в прямоугольном треугольнике равен отношению противоположного катета к гипотенузе: \(sin∠A=\frac{a}{c} \).
Косинус острого угла в прямоугольном треугольнике равен отношению прилежащего катета к гипотенузе: \(cos∠A=\frac{b}{c} \).
В прямоугольном треугольнике синус одного острого угла равен косинусу другого, и наоборот:
\(sin∠A=cos∠B;\ \sin \angle A=\cos \angle B; \ sin∠A=cos∠B\; \\ sin∠B=cos∠A; \ \sin \angle B=\cos \angle A; \ sin∠B=cos∠A.
{\circ}\)
\(1\)
\(\cos \varphi\)
\(0\)
\(\color{red}-\)
\(0\)
Тригонометрические функции 8-9 класс
Синус и косинус острого угла
Синусом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к гипотенузе.
Синус угла А обозначается sin A .
Кос инусом острого угла прямоугольного треугольника называется отношение п ри лежащего к этому углу катета к гипотенузе. Кос инус угла А обозначается cos A .
По определению,
В режиме слайдов ответы появляются после кликанья мышкой
Тангенс и котангенс острого угла
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к прилежащему.Тангенс угла
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к противолежащему. Котангенс угла А обозначается с tg A .
По определению,
В режиме слайдов ответы появляются после кликанья мышкой
Тригонометрические функции
Синус, косинус, тангенс и котангенс называют тригонометрическими функциями острого угла.
Из определения тригонометрических функций следует:
1) катет прямоугольного треугольника равен произведению гипотенузы на синус противолежащего угла;
2) катет прямоугольного треугольника равен произведению гипотенузы на косинус прилежащего угла;
3) катет прямоугольного треугольника равен произведению второго катета на тангенс противолежащего угла;
4) катет прямоугольного треугольника равен произведению второго катета на котангенс прилежащего угла.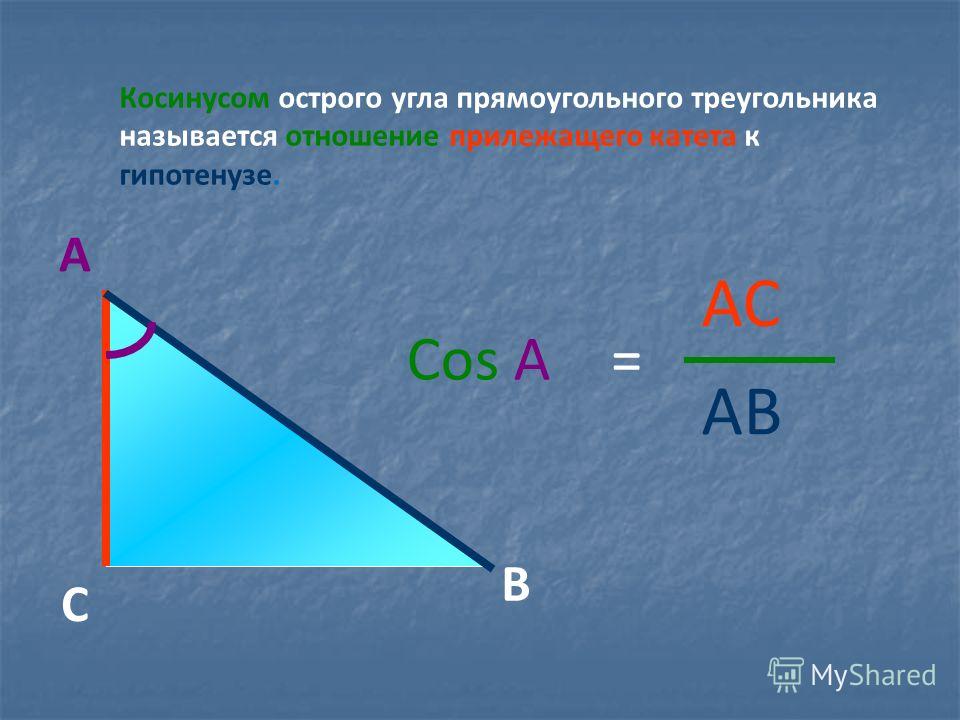
В режиме слайдов ответы появляются после кликанья мышкой
Вопрос 1
Что называется синусом острого угла прямоугольного треугольника?
Ответ: Синусом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к гипотенузе.
В режиме слайдов ответы появляются после кликанья мышкой
Вопрос 2
Как обозначается синус угла A ?
Ответ: Синус угла А обозначается sin A .
В режиме слайдов ответы появляются после кликанья мышкой
Вопрос 3
Что называется косинусом острого угла прямоугольного треугольника?
Ответ: Кос инусом острого угла прямоугольного треугольника называется отношение п ри лежащего к этому углу катета к гипотенузе.
В режиме слайдов ответы появляются после кликанья мышкой
Вопрос 4
Как обозначается косинус угла A ?
Ответ: Кос инус угла А обозначается cos A .
В режиме слайдов ответы появляются после кликанья мышкой
Вопрос 5
Что называется тангенсом острого угла прямоугольного треугольника?
Ответ: Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к прилежащему.
В режиме слайдов ответы появляются после кликанья мышкой
Вопрос 6
Как обозначается тангенс угла A ?
Ответ: Тангенс угла А обозначается tg A .
В режиме слайдов ответы появляются после кликанья мышкой
Вопрос 7
Что называется котангенсом острого угла прямоугольного треугольника?
Ответ: Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к противолежащему.
В режиме слайдов ответы появляются после кликанья мышкой
Вопрос 8
Как обозначается котангенс угла A ?
Ответ: Котангенс угла А обозначается c tg A .
В режиме слайдов ответы появляются после кликанья мышкой
Вопрос 9
Что называется тригонометрическими функциями острого угла?
Ответ: Т ригонометрическими функциями острого угла называются с инус, косинус, тангенс и котангенс .
В режиме слайдов ответы появляются после кликанья мышкой
Вопрос 10
Чему равен катет, лежащий против угла в 30 о ?
Ответ: Катет, лежащий против угла в 30 о равен половине гипотенузы.
В режиме слайдов ответы появляются после кликанья мышкой
Упражнение 1
Найдите значения тригонометрических функций угла в 3 0 о .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
Упражнение 2
Найдите значения тригонометрических функций угла в 45 о .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
Упражнение 3
Найдите значения тригонометрических функций угла в 60 о .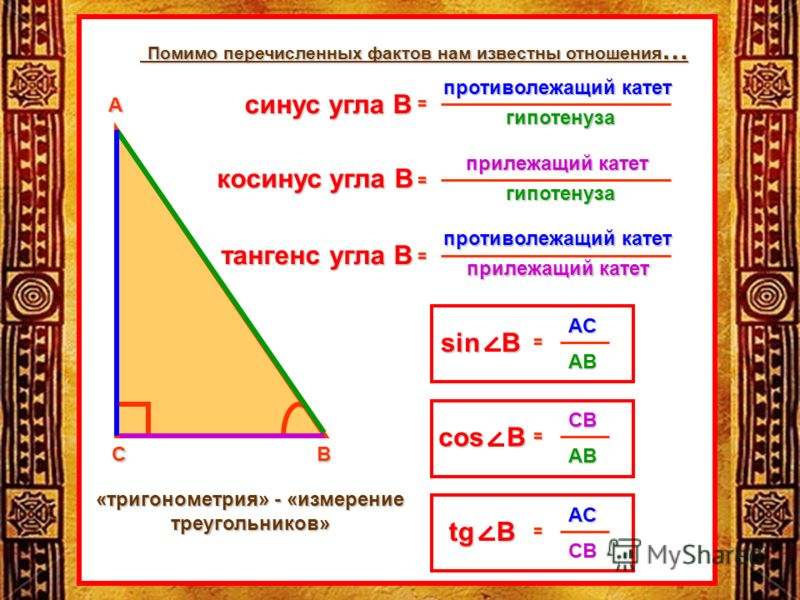
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
Упражнение 4
Найдите значения тригонометрических функций угла AOB , изображенного на рисунке .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
17
Упражнение 5
Найдите значения тригонометрических функций угла AOB , изображенного на рисунке .В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
Упражнение 6
Найдите значения тригонометрических функций угла AOB , изображенного на рисунке .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
Упражнение 7
Найдите значения тригонометрических функций угла AOB , изображенного на рисунке .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
Упражнение 8
Найдите значения тригонометрических функций угла AOB , изображенного на рисунке .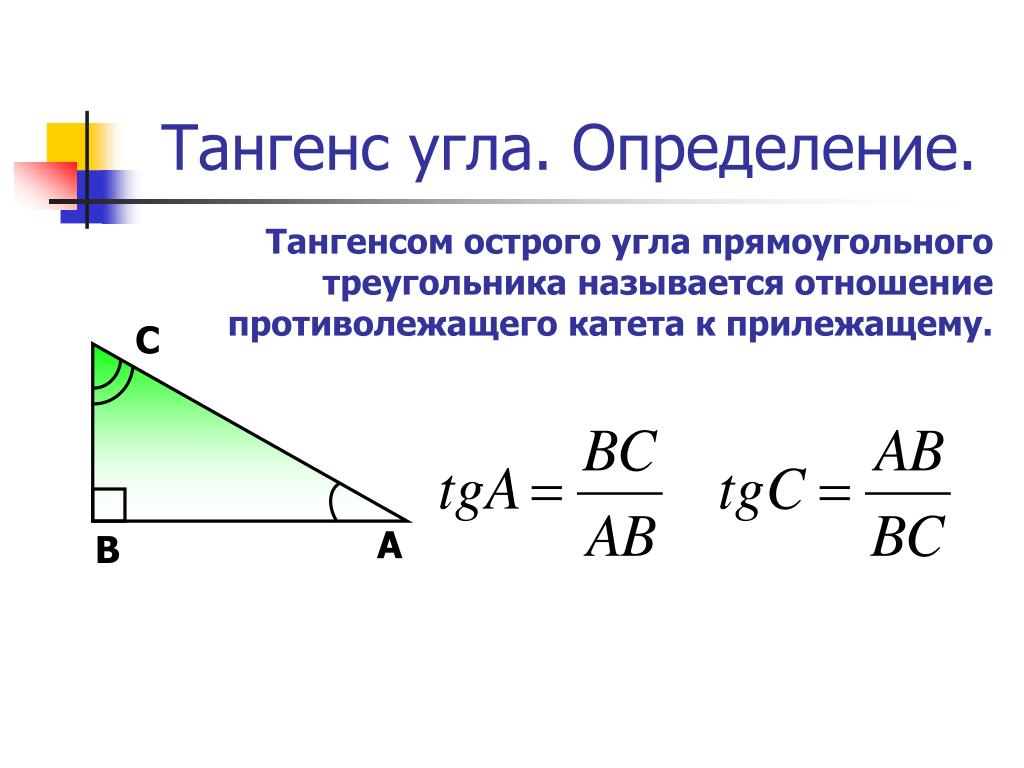
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
Упражнение 9
На клетчатой бумаге изобразите угол, тангенс которого равен: а) 1; б) 0,5; в) 2; г) 3.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
Упражнение 10
От луча OA отложите угол, тангенс которого равен: а) 1 /2 ; б) 1/3 ; в) 2.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
Упражнение 11
Может ли синус (косинус) угла быть равен ?
Ответ: Нет, значения синуса и косинуса меньше единицы .
В режиме слайдов ответы появляются после кликанья мышкой
Упражнение 12
Может ли тангенс (ко тангенс ) угла быть равен ?
Ответ: Да .
В режиме слайдов ответы появляются после кликанья мышкой
Упражнение 1 3
Катеты прямоугольного треугольника равны 12 см и 5 см.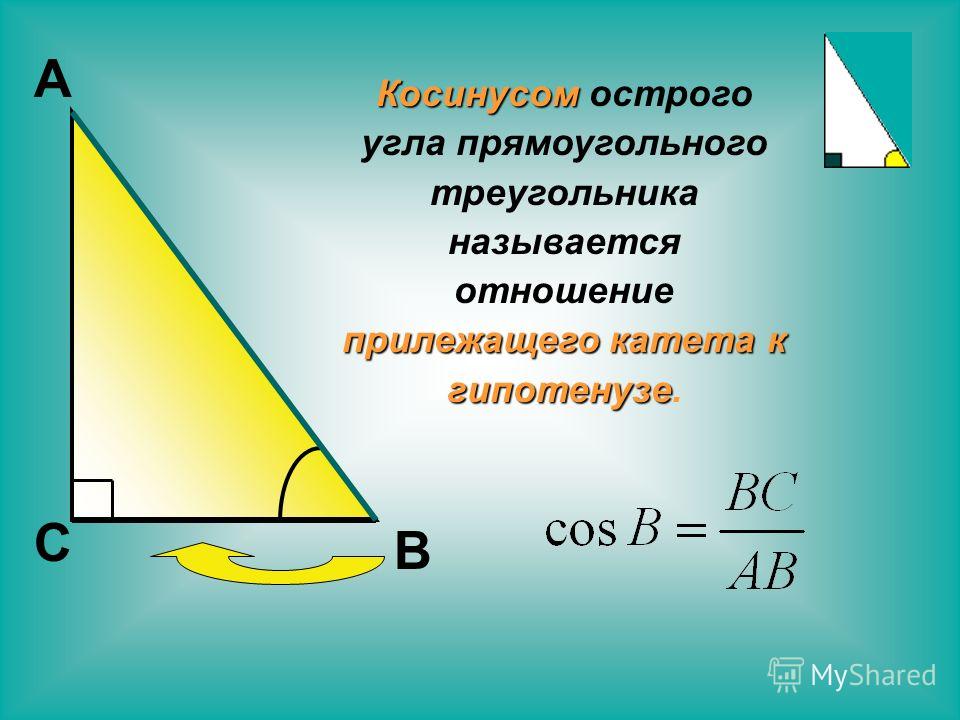
Найдите все тригонометрические функции его меньшего угла A .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
Упражнение 1 4
В треугольнике ABC угол C равен 90 о , CH – высота, AC = 5, AH = 4. Найдите :
а) sin B ;
б) cos B .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: а ) 0,8 .
б ) 0, 6.
Упражнение 1 5
В треугольнике ABC угол C равен 90 о , CH – высота, BC = 5, BH = 3. Найдите :
а) sin A ;
б) cos A .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: а) 0,6 ;
б) 0, 8 .
Упражнение 1 6
В треугольнике ABC угол C равен 90 о , AC = 5, высота CH равна 3. Найдите sin B .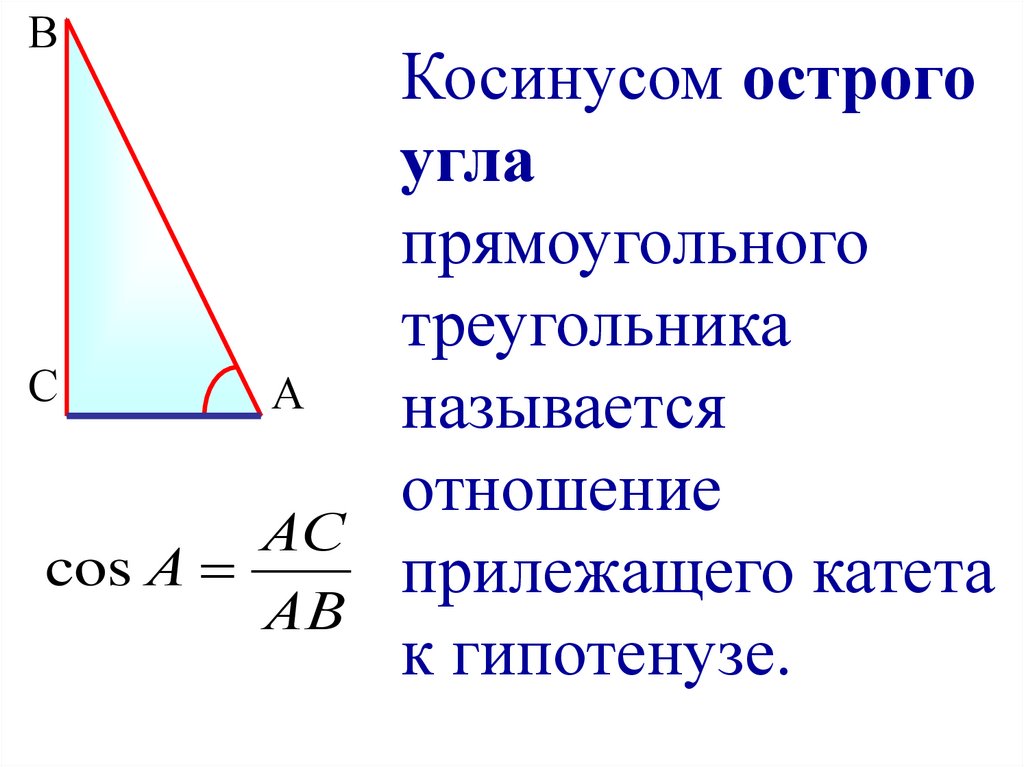
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 0,8.
Упражнение 1 7
В треугольнике ABC угол C равен 90 о , BC = 5, высота CH равна 4. Найдите sin A .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 0,6.
Упражнение 1 8
Высота, проведенная к основанию равнобедренного треугольника, равна 8 см, основание равно 12 см. Найдите синус и косинус угла A при основании треугольника.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
Упражнение 19
В треугольнике ABC AC = BC = 5, AB = 8. Найдите tg A .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 0,75.
Упражнение 20
В треугольнике ABC AC = BC , AB = 5, высота AH равна 4.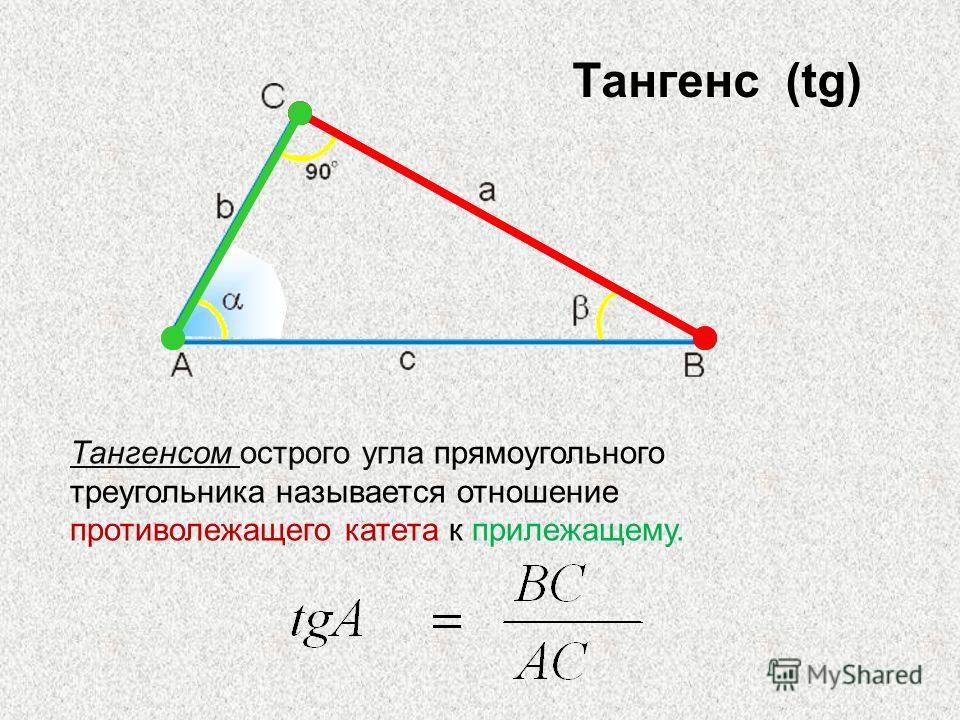
Найдите sin A .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 0,8.
Упражнение 2 1
В треугольнике ABC AC = BC , AB = 5, высота AH равна 4. Найдите cos A .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 0,6.
Упражнение 2 2
В треугольнике ABC AC = BC , AB = 5, AH – высота, BH = 3. Найдите cos A .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 0,6.
Упражнение 2 3
В треугольнике ABC AC = BC , AH – высота, sin A = 0,8. Найдите косинус угла BAH .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 0,8.
Упражнение 2 4
В треугольнике ABC AC = BC , AH – высота, sin A = 0,8.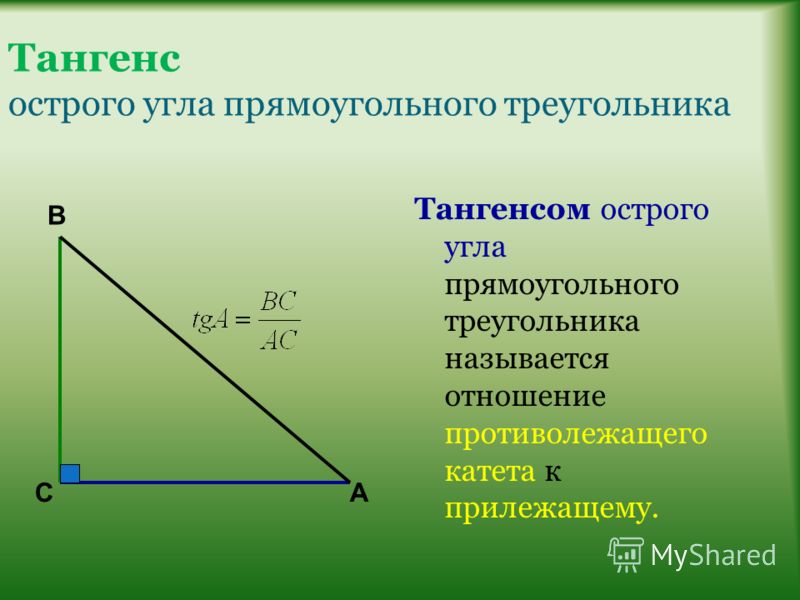
Найдите синус угла BAH .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 0,6.
Упражнение 2 5
В треугольнике ABC AB = BC , AC = 10, CH – высота, AH = 8. Найдите sin C .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 0,6.
Упражнение 26
В треугольнике ABC AB = BC , CH — высота, sin C = 0,4. Найдите косинус угла ACH .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 0,4.
Упражнение 27 *
Найдите синус угла в 18 о .
Решение. Рассмотрим золотой треугольник ABC , у которого угол C равен 36 о . Проведем высоту CH .
Если AC = 1, то AH = .
Следовательно, sin 18 о =
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
Упражнение 28 *
Найдите синус угла в 54 о .
Решение. Рассмотрим золотой треугольник ABC , у которого угол C равен 108 о . Проведем высоту CH . Если AC = 1, то
AH = Следовательно,
sin 54 о =
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
Упражнение 29 *
Найдите ко синус угла в 18 о .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
Упражнение 30 *
Найдите ко синус угла в 54 о .
В режиме слайдов ответы появляются после кликанья мышкой
Ответ:
Упражнение 31
Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. Под каким углом к направлению на запад он должен идти, чтобы вернуться домой? В ответе укажите целое число градусов. (Используйте таблицу тригонометрических функций.)
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 37 о .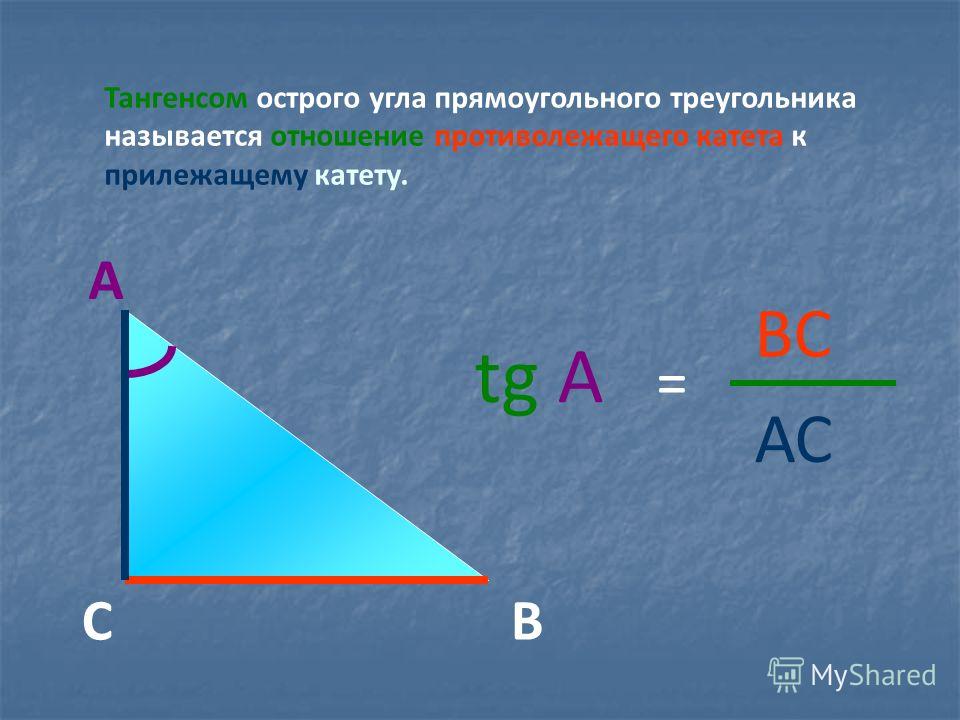
Упражнение 32
Грибник, войдя в лес, в течение двух часов шел в направлении на север, а затем с той же скоростью в течение полутора часов – на восток. Под каким углом к направлению на юг он должен идти, чтобы вернуться к месту, где он вошел в лес? В ответе укажите целое число градусов. (Используйте таблицу тригонометрических функций.)
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 37 о .
Упражнение 33
Маятник AB длиной 50 см отклонили от положения равновесия на расстояние CD , равное 12 см. Используя таблицу тригонометрических функций, найдите угол, который образует новое положение AC маятника с положением равновесия AB
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 14 о .
Упражнение 34
Горная железная дорога поднимается на 1 м на каждые 30 м пути. Используя таблицу тригонометрических функций, найдите угол подъема в градусах.
В ответе укажите приближенное значение, выражаемое целым числом градусов.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 2 о .
Упражнение 35
Человек, пройдя вверх по склону холма 1000 м, поднялся на 90 м над плоскостью основания холма. Используя таблицу тригонометрических функций, найдите (в среднем) угол наклона холма в градусах. В ответе укажите приближенное значение, выражаемое целым числом градусов.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 5 о .
Упражнение 36
Использую таблицу тригонометрических функций, найдите приближенное значение угла, под которым виден столб высотой 3 м, находящийся от наблюдателя на расстоянии 100 м. В ответе укажите целое число градусов.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 2 о .
Упражнение 37
Высота башни главного здания МГУ имени М.
В. Ломоносова равна 240 м. Под каким углом видна эта башня с расстояния 200 м? В ответе укажите приближенное значение, равное целому числу градусов.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 50 о .
Упражнение 38
Высота Останкинской телевизионной башни – 540 м. Используя таблицу тригонометрических функций, найдите угол в градусах, под которым видна башня с расстояния 2000 м.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 15 о .
Упражнение 39
Строение высоты 30 м бросает тень длиной 45 м. Используя таблицу тригонометрических функций, найдите угол наклона солнечных лучей. В ответе укажите приближенное значение, выражаемое целым числом градусов.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 34 о .
Упражнение 40
Используя таблицу тригонометрических функций, найдите угол наклона солнечных лучей, если длина тени стоящего человека в два раза меньше его роста.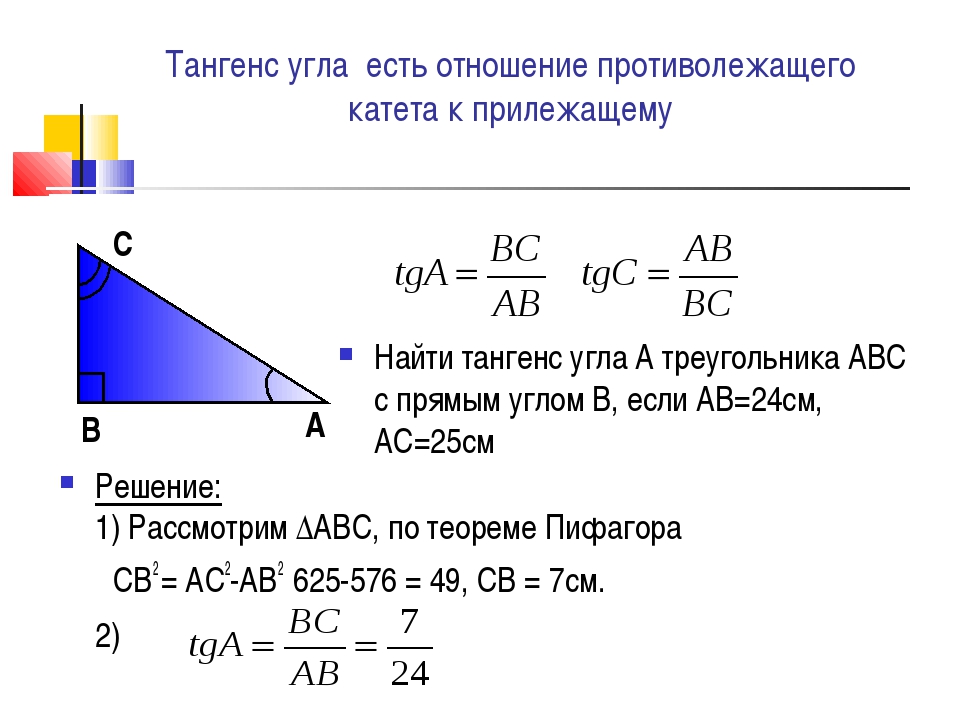
В ответе укажите приближенное значение, выражаемое целым числом градусов.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 64 о .
Упражнение 41
Лестница имеет ступеньки, ширина которых равна 30 см, а высота – 18 см. Используя таблицу тригонометрических функций, найдите угол подъема лестницы. В ответе укажите приближенное значение, выражаемое целым числом градусов.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 31 о .
Упражнение 42
Ширина дачного домика равна 6 м, ширина одного ската его двускатной крыши равна 5 м. Используя таблицу тригонометрических функций, найдите угол между стропилами крыши и потолком.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 53 о .
Упражнение 43
Ширина футбольных ворот равна 8 ярдам. Расстояние от 11-метровой отметки до линии ворот равно 12 ярдам.
Найдите угол, под которым видны ворота с 11-метровой отметки. В ответе укажите целое число градусов.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: 37 о .
A
sin A
A
tg A
sin A
A
tg A
sin A
tg A
Таблица тригонометрических функций
1,73
0,87
0,58
60 о
0,50
0,0087
0,0087
30′
30 о
1,80
0,87
61 о
0,60
0,52
0,0175
1 о
0,0175
31 о
1,88
0,88
0,62
62 о
0,53
0,035
0,035
2 о
32 о
1,96
0,89
63 о
0,65
0,54
0,05
3 о
0,05
33 о
2,02
0,90
64 о
0,68
0,56
0,07
4 о
0,07
34 о
2,15
0,91
65 о
0,70
0,57
0,09
5 о
0,09
35 о
2,25
0,91
0,73
66 о
0,59
0,10
6 о
0,11
36 о
2,36
0,92
67 о
0,75
0,60
0,12
7 о
0,12
37 о
2,48
0,93
68 о
0,78
0,62
0,14
8 о
0,14
38 о
2,61
0,93
69 о
0,81
0,63
0,16
9 о
0,16
39 о
2,78
0,94
70 о
0,84
0,64
0,17
10 о
0,18
40 о
2,90
0,95
71 о
0,87
0,66
0,19
11 о
0,19
41 о
3,08
0,95
72 о
0,9
0,67
0,21
12 о
0,21
42 о
3,27
0,96
73 о
0,93
0,68
0,23
13 о
0,23
43 о
3,49
0,96
74 о
0,97
0,69
0,24
14 о
0,25
44 о
1,00
3,73
0,97
75 о
0,71
15 о
0,26
0,27
45 о
4,01
0,97
76 о
1,04
0,72
0,28
16 о
0,29
46 о
4,33
0,97
77 о
1,07
0,73
0,29
17 о
0,31
47 о
4,71
0,98
78 о
1,11
0,32
0,74
48 о
0,31
18 о
В режиме слайдов ответы появляются после кликанья мышкой
0,33
19 о
5,15
0,98
79 о
1,15
0,75
49 о
0,34
1,19
5,67
80 о
0,98
0,36
0,77
0,34
20 о
50 о
6,31
0,99
81 о
1,23
0,78
0,36
21 о
0,38
51 о
7,12
0,99
1,28
82 о
0,37
22 о
0,79
0,40
52 о
8,14
0,992
83 о
1,33
0,80
53 о
0,42
0,39
23 о
9,51
0,994
84 о
1,38
0,81
0,41
24 о
0,45
54 о
1,43
11,43
0,996
85 о
55 о
0,47
0,42
0,82
25 о
86 о
1,48
0,998
14,30
56 о
0,44
26 о
0,83
0,49
1,54
19,08
0,999
87 о
57 о
0,51
0,45
0,84
27 о
1,60
28,64
1,00
88 о
0,47
0,85
28 о
58 о
0,53
1,66
57,29
1,00
89 о
0,86
59 о
0,55
0,48
29 о
57
Тангенс (угла)
Горячая математика касательная угла – это
тригонометрическое соотношение
между прилежащей стороной и противолежащей стороной прямоугольного треугольника, содержащего этот угол.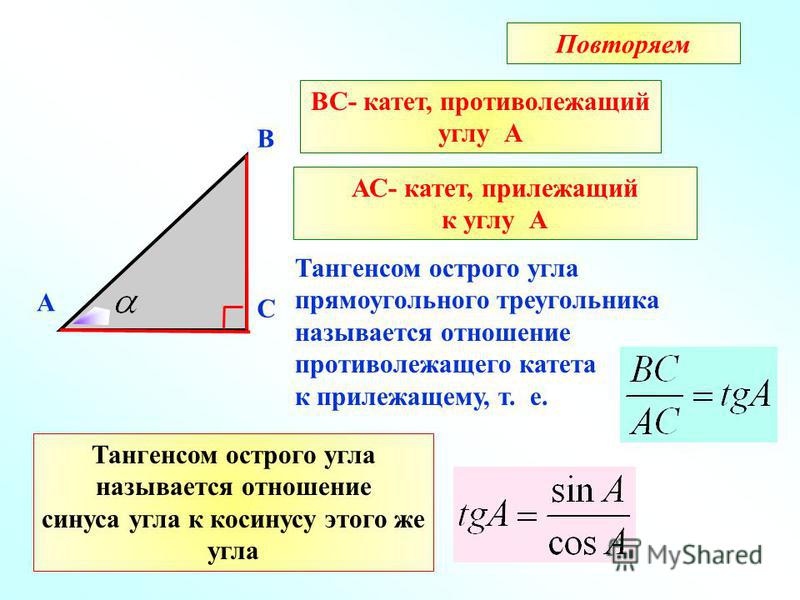
касательная знак равно длина из в нога противоположный к в угол длина из в нога соседний к в угол сокращенно «загар»
Пример:
В показанном треугольнике
загар
(
А
)
знак равно
6
8
или же
3
4
а также
загар
(
Б
)
знак равно
8
6
или же
4
3
.
Отношение тангенсов одинаково независимо от размера прямоугольного треугольника. Итак, часто проще всего рассмотреть прямоугольный треугольник с гипотенузой длины 1 .
Отношение тангенса также можно рассматривать как функцию, которая принимает разные значения в зависимости от меры угла. Вы можете измерить угол в градусах или радианы .
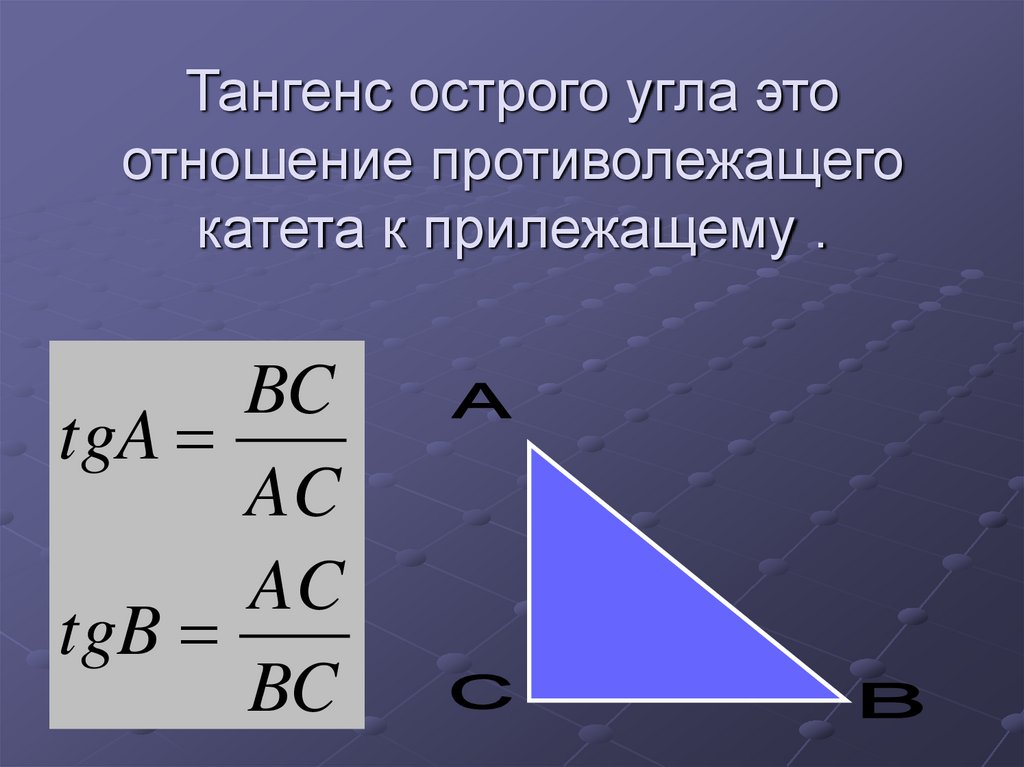
Обратная величина отношения тангенса известна как отношение котангенса угла, сокращенно «кроватка».
То есть,
котангенс знак равно длина из в нога соседний к в угол длина из в нога противоположный к в угол
В приведенном выше примере
детская кроватка
(
А
)
знак равно
7
4
а также
детская кроватка
(
Б
)
знак равно
4
7
.
Смотрите также: синус а также косинус .
Математический обзор тангенса угла
Математический обзор тангенса угла https://schooltutoring.com/help/wp-content/themes/movedo/images/empty/thumbnail.jpg 150 150 Дебора Дебора https://secure.gravatar.com/avatar/63fb4ad5c163b8f83de2f54371b9e040?s=96&d=mm&r=g
Обзор
Тангенс угла представляет собой отношение длины катета, противолежащего острому углу, к длине катета, примыкающего к острому углу прямоугольного треугольника. . Это одна из основных тригонометрических функций, связанная со многими реальными измерениями углов и навигации.
Определение
Прямоугольный треугольник имеет ряд особых соотношений между измерениями его сторон и углов.
Теорема Пифагора (a 2 + b 2 = c 2 ) относится к измерениям сторон прямоугольного треугольника. В любом прямоугольном треугольнике есть один прямой угол и два острых угла. Катеты — это стороны по обе стороны от прямого угла, а гипотенуза — длинная сторона треугольника. Если один катет измеряется как а, а другой катет как b, то гипотенуза измеряется как с. Тангенс — это отношение двух катетов угла, противолежащего углу и примыкающего к нему.
Рисунок 1: Определение касательной.
Приложения
В реальном мире есть много вещей, похожих на прямоугольные треугольники, которые необходимо измерить. Деревья растут перпендикулярно земле, мачта парусника перпендикулярна воде, а линию можно провести от вершины горы до базового лагеря на уровне моря. Маяк стоит на скале перпендикулярно морю.
Примеры
Предположим, человеку нужно посмотреть на 40 0 угол, чтобы увидеть верхушку дерева на расстоянии 75 футов.