Тангенс это отношение противолежащего катета к прилежащему: Синус, косинус и тангенс угла — урок. Геометрия, 9 класс.

Видео-урок: Тригонометрия прямоугольного треугольника: Нахождение стороны

Стенограмма видео

В этом видео мы научимся найти значение длины недостающей стороны в прямоугольном треугольнике, выбрав соответствующее тригонометрическое соотношение для данного угла. Так что же это за тригонометрические отношения?

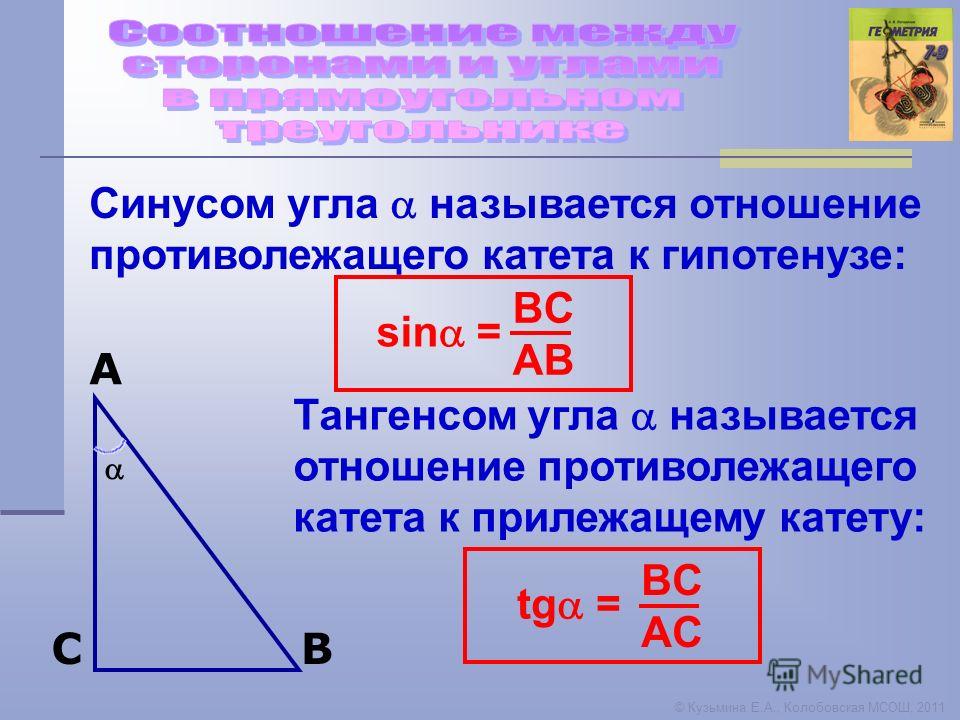
Когда у нас есть прямоугольный треугольник, мы используйте аббревиатуру SOH CAH TOA, чтобы помочь нам запомнить определения тригонометрических отношения синуса, косинуса и тангенса. Мы говорим, что грех 𝜃 равен в обратном направлении по гипотенузе. Кос угла 𝜃 равен длина смежного катета по гипотенузе. А тангенс угла 𝜃 равен длина противоположной стороны больше длины соседней стороны.

Но чтобы получить эти коэффициенты правильно, нам нужно правильно обозначить треугольник. А это значит, что мы всегда подумайте, какой угол мы используем. Вот, это наш ракурс 𝜃. Противоположная сторона – это сторона прямо напротив рассматриваемого угла. Прилегающая сторона – это сторона между углом и прямым углом. А гипотенуза всегда наибольшая сторона прямоугольного треугольника. Это прямо напротив правого угол.

Когда мы сможем вспомнить тригонометрические отношения и правильно обозначить наш прямоугольный треугольник, мы готовы начать смотря как вычислить неизвестные длины прямоугольного треугольника. Вот пример, когда нам нужно найти недостающую длину стороны.

Найдите 𝑥 на данном рисунке. Дайте ответ с точностью до двух знаков после запятой места.

Первое, что мы замечаем, это то, что это прямоугольный треугольник. Мы знаем угол и сторону длина. А это значит решить задача, нам нужно будет использовать тригонометрические соотношения.

Мы помним аббревиатуру SOH CAH ТОА. грех 𝜃 равен противоположному гипотенуза, потому что 𝜃 равна смежной по гипотенузе, а тангенс 𝜃 равно противоположному соседнему. Наша отправная точка всегда соответствующий угол. Нам дан угол 68 градусов. И поэтому мы можем обозначить противоположное боковая сторона 𝑥; соседняя сторона, сторона, равная 11; а гипотенуза всегда сторону, противоположную прямому углу.

После того, как мы пометили эти стороны, мы видим, что нам дана длина соседней стороны. И нас интересует длина противоположной стороны. Поскольку мы имеем дело с противоположное и соседнее, мы будем смотреть на отношение тангенса. Поскольку тангенс 𝜃 равен противоположные над соседними, подставляем угол 68 градусов. Противоположная сторона — это сторона, на которой мы пытаюсь найти, 𝑥.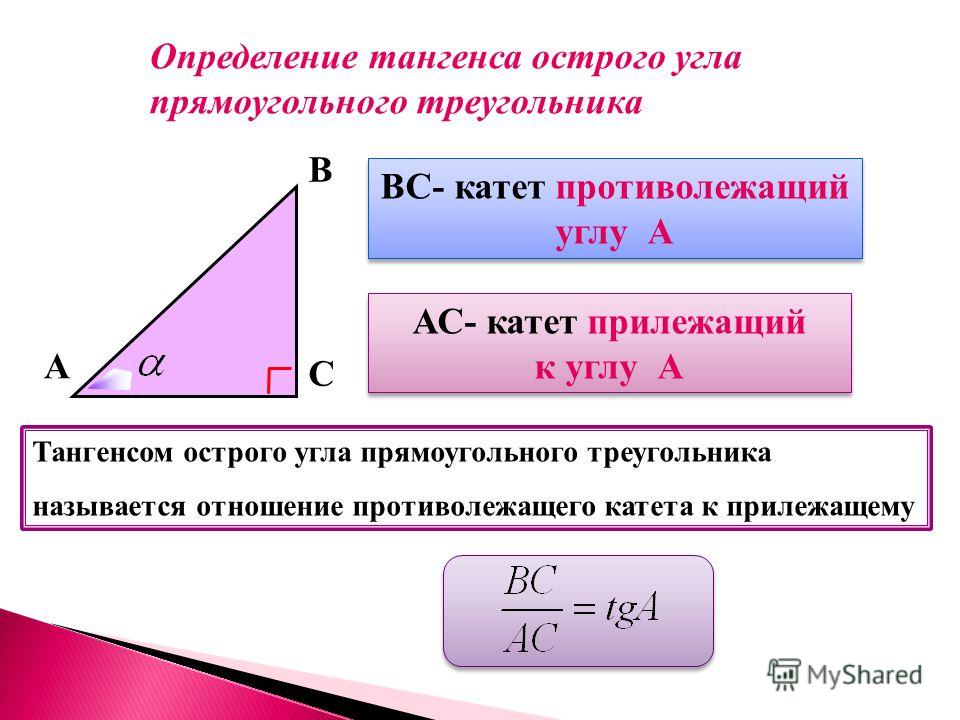

И соседние боковые меры 11.

Чтобы найти 𝑥, нам нужно изолировать его, чтобы получить его сам по себе. Мы можем сделать это, умножив оба стороны этого уравнения на 11. тангенс 68 градусов, умноженный на 11, будет равно длине стороны 𝑥. Отсюда, чтобы решить, нам нужно используйте калькулятор. Мы введем тангенс 11, умноженный на 68. градусов, и это даст нам 27,22595, продолжая. Если ваш калькулятор не возвращает это значение, вы должны проверить и убедиться, что оно установлено в градусный режим, а не в радианы.

Недостающая сторона 𝑥 равна 27.22595. Мы хотим, чтобы это было правильно до двух десятичных знаков места. Чтобы округлить до второго десятичного знака место, смотрим направо. Поскольку в третьем пятерка десятичный знак, нам нужно округлить. И мы получим, что 𝑥 равно 27.

23. Поскольку нам не заданы единицы измерения, хорошо, чтобы оставить его в этом формате. 𝑥 равно 27,23.

Вот еще пример. На этот раз нам не хватает двух длины сторон. И нам нужно решить для обоих из недостающие стороны.

Найдите значения 𝑥 и 𝑦, давая ответ с точностью до трех знаков после запятой.

Замечаем, что это право треугольник. Нам дан угол и сторона длины, а это значит, что мы можем использовать тригонометрические отношения для решения двух недостающих стороны. Запоминание аббревиатуры SOH CAH TOA, грех 𝜃 равен противоположному по гипотенузе, потому что 𝜃 равен смежный по гипотенузе, а тангенс 𝜃 равен противоположному по гипотенузе соседний. Ключ здесь для нас, чтобы обозначить этот треугольник правильно. И для этого воспользуемся данным угол в качестве нашей отправной точки.

Мы обозначаем длины сторон относительными под заданный нами угол. 𝑦 — сторона, противоположная 40-градусный угол. 𝑥 — сторона, примыкающая к 40-градусный угол. А гипотенуза всегда сторону, противоположную прямому углу.

Сначала попробуем решить для 𝑦. Если мы ищем 𝑦 и знаем гипотенузе, мы будем использовать отношение синуса, потому что грех 𝜃 противоположен гипотенуза. А это значит, что мы можем сказать, что грех 40 градусов равен 𝑦 больше 14. Поскольку наша цель — найти 𝑦, мы умножим обе части на 14. И тогда мы увидим, что 14 раз грех 40 градусов равен 𝑦. Когда мы подключаем это к нашему калькулятор, получаем 8,99902 продолжение. Если вы не получили этот ответ на ваш калькулятор, то вы должны проверить и убедиться, что вы работаете в градусов, а не в радианах.

Нам нужен ответ до трех знаков после запятой места. Итак, мы смотрим на четвертый десятичный знак место, где стоит ноль. Это означает, что мы будем округлять. 𝑦 равно 8,999. И единицы, которые мы измеряем это сантиметры. Итак, мы говорим, что 𝑦 равно 8,9.99 сантиметры.

Далее нам нужно найти 𝑥. И мы можем решить 𝑥 с двумя разные соотношения. Мы могли бы использовать соседнюю сторону и гипотенуза, которая была бы отношением косинуса. Или мы могли бы взять то, что мы нашли для 𝑦 и используйте это как противоположную сторону. И это означало бы, что мы будем использовать отношение тангенса, потому что у нас были бы противоположная и смежная стороны. В этом случае воспользуемся гипотенуза, так как это сэкономит нам немного времени.

Мы имеем дело с косинусом соотношение. У нас cos 40 градусов равен до 𝑥 более 14. Мы умножим обе части на 14. 14 умножить на 40 градусов будет равно 𝑥. Таким образом, 𝑥 будет равно 10,72462. продолжение. Округлено до третьего десятичного знака означает, что нам нужно округлить до 10,725. Опять же, единицы здесь будут измеряется в сантиметрах. И поэтому мы можем сказать, что 𝑥 равно до 10,725 см, а 𝑦 равно 8,999 сантиметров, каждое до трех знаков после запятой места.

Обратите внимание, как в этих задачах мы имели дело с недостающими длинами сторон как числитель дроби в соотношение. Давайте рассмотрим пример, где мы имеют длину стороны, которая оказывается в знаменателе этого отношения.

Найдите значения 𝑥 и 𝑦, давая ответ с точностью до трех знаков после запятой.

У нас есть прямоугольный треугольник. Нам дан угол и сторона длину и попросили найти две недостающие стороны. Для этого нам понадобится наш тригонометрические соотношения. И чтобы запомнить их, мы будем использовать СОХ КАХ ТОА. Грех 𝜃 равен противоположному над гипотенузой. Кос 𝜃 равен соседнему над гипотенузой. А загар 𝜃 равен противоположное над соседним. Ключ к решению этих проблем последовательно состоит в том, чтобы правильно обозначить треугольник. И мы обозначаем их относительно данный нам угол. Это наша отправная точка. Длина противоположной стороны равна длина стороны, прямо противоположной этому углу. Соседняя сторона находится между этим угол и прямой угол. А гипотенуза всегда напротив прямого угла.

Как только треугольник помечен, мы готовы определить, какое из соотношений нам нужно. Если мы начнем с нахождения длины стороны 𝑦, гипотенуза, и мы уже знаем противоположную сторону, 28 сантиметров, нам нужно использовать коэффициент синуса, так как коэффициент синуса включает длину противоположной стороны и гипотенуза.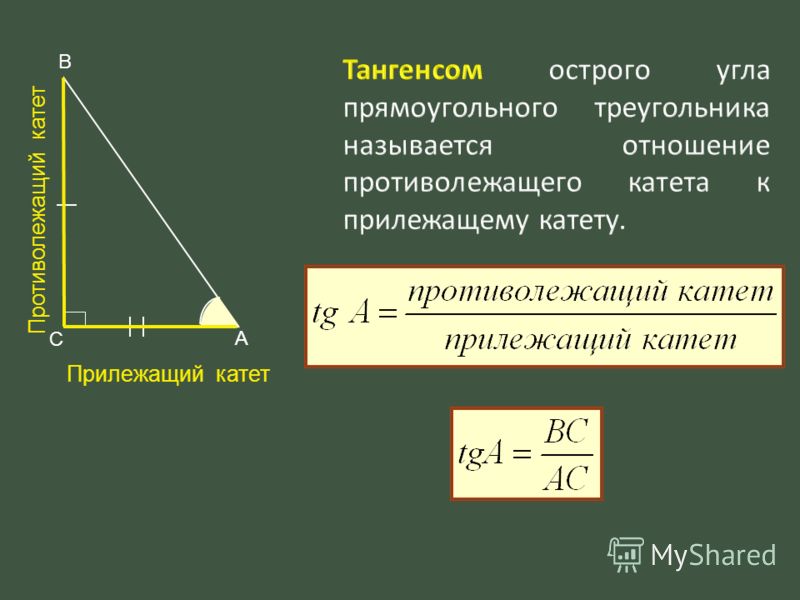

Соотношение будет выглядеть так. грех 47 градусов равен 28 над 𝑦. Когда наша переменная находится в знаменатель, потребуется два шага, чтобы найти значение.

Первое, что мы должны сделать, это умножьте обе части уравнения на 𝑦. Когда мы это делаем, мы получаем 𝑦 раз грех 47 градусов равен 28. Если цель состоит в том, чтобы изолировать 𝑦, то в этот момент нам нужно разделить обе части уравнения на грех 47 градусов. И тогда слева мы просто есть 𝑦, а справа у нас будет 28 над грехом 47 градусов.

Когда мы подключим это к калькулятор, получаем 38,28516 продолжая. Нам нужно округлить до трех десятичные знаки. Это значение округляется до 38.285. Стороны измеряются в сантиметры, поэтому единицами здесь будут сантиметры. А это значит, что мы нашли один из недостающие стороны.

Чтобы найти длину стороны 𝑥, мы есть два варианта.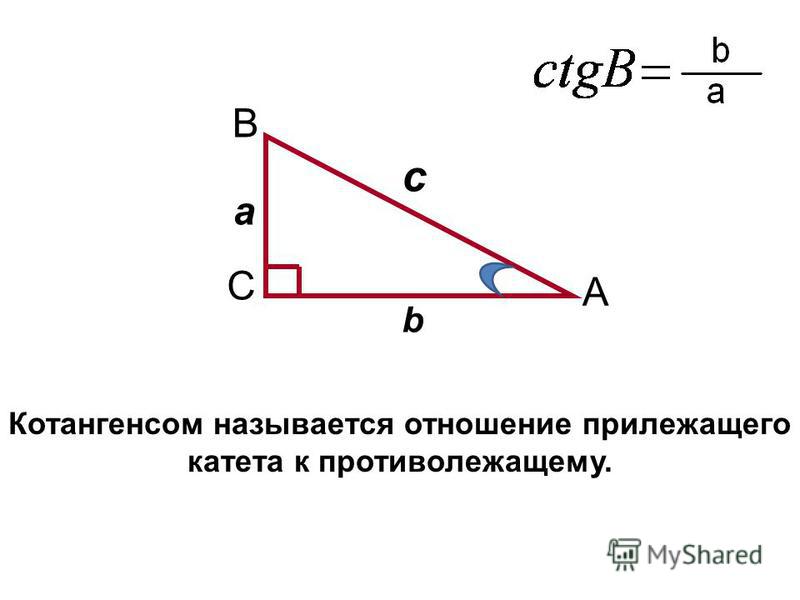 Мы могли бы использовать гипотенузу, которую мы только что найдено, 38.285. Если бы мы это сделали, мы бы имели дело с прилежащей стороной и гипотенузой, которая будет косинусом отношение. Или мы могли бы использовать 28-сантиметровый сторона. В этом случае мы будем использовать противоположная сторона и смежная сторона и потребуется отношение тангенса.

В этом случае давайте потренируемся 𝑥-переменная в знаменателе. тангенс 47 градусов равен 28 больше 𝑥. Чтобы найти 𝑥, мы сначала умножаем обе части уравнения на 𝑥. Тогда мы можем сказать, что 𝑥 раз загар 47 градусов равно 28. Чтобы изолировать 𝑥, мы делим обе стороны уравнения тангенсом 47 градусов. Итак, мы говорим, что 𝑥 равно 28. над тангенсом 47 градусов, что дает нам продолжение 26,11042. Округляем до третьего знака место, и мы получаем, что 𝑥 равно 26,110.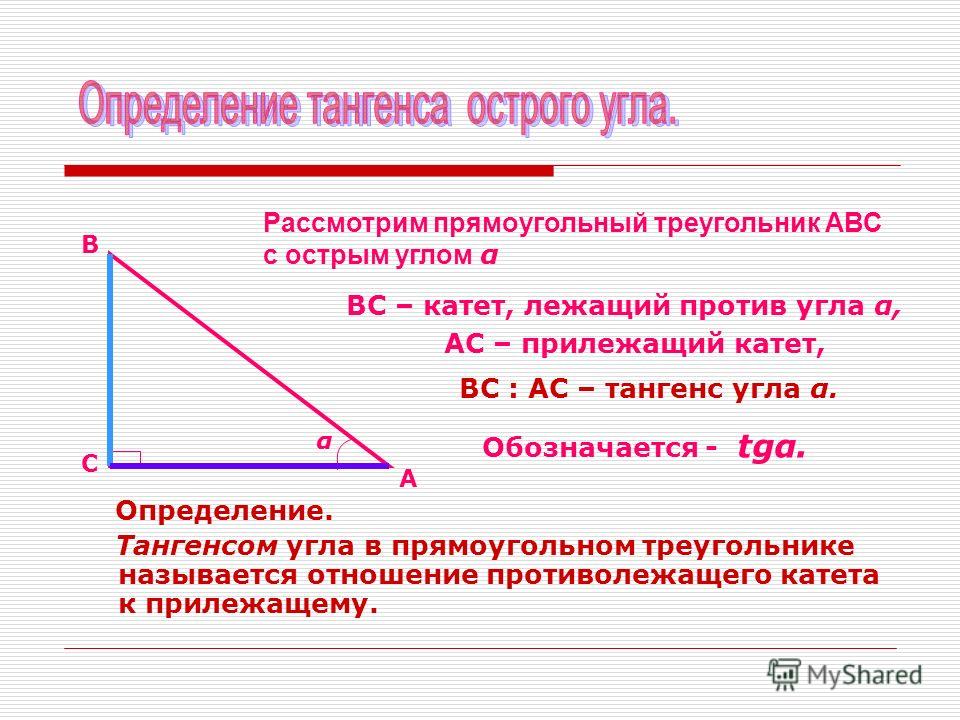 Это измеряется в сантиметры. И вот мы нашли двух пропавших без вести длины сторон. С точностью до трех знаков после запятой 𝑥 равно 26,110 см, а 𝑦 равно 38,285 см.

Давайте посмотрим на последний пример. где нам не дали схему.

Найти длину отрезка 𝐴𝐶, учитывая, что 𝐴𝐵𝐶 — прямоугольный треугольник в точке 𝐵, где грех 𝐶 равен девяти 16 и 𝐴𝐵 равно 18 сантиметрам.

В этом случае первый шаг должен начертить прямоугольный треугольник, удовлетворяющий этим условиям. У нас есть прямоугольный треугольник. Прямой угол находится в 𝐵, поэтому мы обозначьте прямой угол 𝐵. А затем добавляем 𝐴 и 𝐶. Нам говорят, что 𝐴𝐵 измеряет 18 сантиметры. И тогда у нас есть этот другой кусок информации о том, что грех 𝐶 равен девяти больше 16. Это говорит нам о том, что угол, под которым мы работа с углом 𝐶.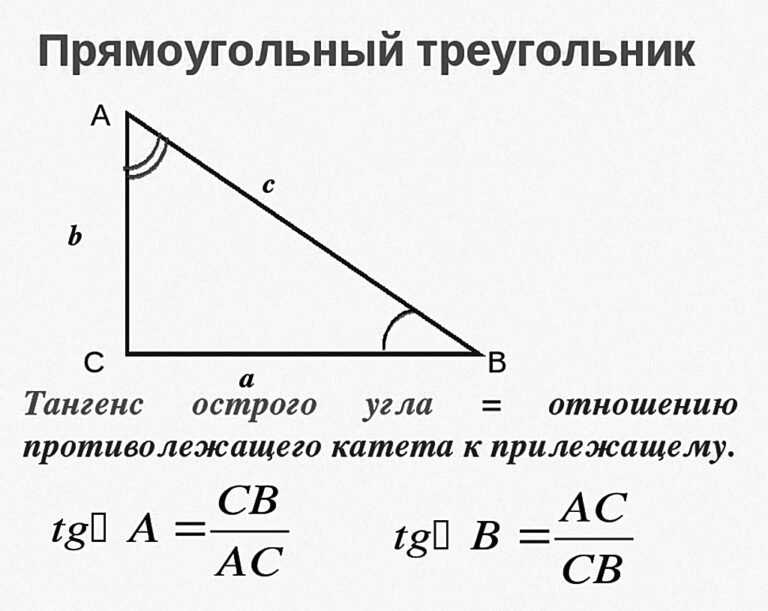 И если мы вспомним нашу аббревиатуру SOH CAH TOA, мы знаем, что синус угла равен противоположному по гипотенуза.

Если рассматриваемый угол 𝐶, обратная будет сторона 𝐴𝐵, а гипотенуза всегда сторона напротив прямого угла. Это сторона 𝐴𝐶. И так что это соотношение девять больше 16. Главное здесь помнить что эти отношения являются отношениями. Итак, грех угла 𝐶 говорит нам что на каждые девять единиц на противоположной стороне приходится 16 единиц на противоположной стороне. длина стороны гипотенузы.

Итак, мы можем сказать, что если есть 18 сантиметров на противоположной стороне, мы знаем, что девять умножить на два равно 18. И когда речь идет о соотношениях или дроби, если мы умножаем на два в числителе, нам нужно умножать на два в знаменатель. 16 умножить на два будет 32. Таким образом, мы можем сказать, что если напротив 18, гипотенуза должна быть 32. Отрезок 𝐴𝐶 — это гипотенуза, а ее длина 32 сантиметра.

Давайте теперь суммируем ключевые моменты из этого видео. Когда у нас есть прямоугольные треугольники, и мы нужно решить для одной из сторон, мы должны помнить три тригонометрических отношения, а затем выполните следующие действия. Один, пометьте стороны в треугольник как противоположный, смежный, а гипотенуза, относительно известного угол. Два, выберите правильный тригонометрическое соотношение, которое связывает известную сторону с неизвестной с помощью аббревиатуры SOH CAH TOA, чтобы помочь. И, наконец, подставьте в значения и решить уравнение.

Отношение тангенсов – определение, формула и примеры

Отношение тангенсов – это одно из тригонометрических соотношений прямоугольных треугольников. Это отношение противолежащей стороны к прилежащей относительно угла.

Формула

Рассмотрим прямоугольный треугольник ABC, где AC — гипотенуза, а AB и BC — две другие стороны прямоугольного треугольника. Таким образом, для любого угла θ в прямоугольном треугольнике

${\tan \theta =\dfrac{Противоположная сторона}{Смежная сторона}}$

Тангенс Отношение

Точно, ${\tan A=\dfrac{BC}{AB}}$ и ${\tan C=\dfrac{AB}{BC}}$

Таким образом, отношения тангенсов можно использовать для вычисления углов и стороны прямоугольного треугольника, подобные отношениям синусов и косинусов. Кроме того, можно найти отношение тангенсов для одного угла прямоугольного треугольника, отличного от прямого угла.

Учитывая отношение тангенсов ${\tan A=\dfrac{BC}{AB}}$, если известна мера угла A, можно найти отношение тангенсов угла A. Опять же, нахождение отношения тангенсов легко, если известны одна сторона и гипотенуза. Например, если известны AC и BC, то по теореме Пифагора получаем 9{2}}}}$

Нахождение отношения касательной

Рассмотрим 3 прямоугольных треугольника с разными длинами сторон, но с одинаковым углом, измеряемым θ.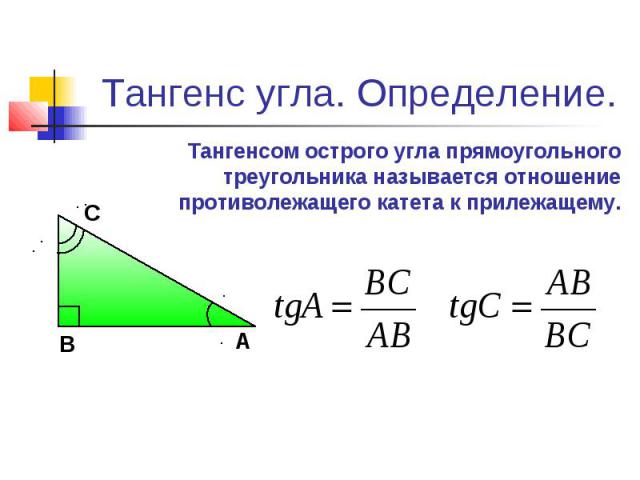 Теперь найдем отношения касательных для всех трех треугольников.

Отношение тангенса Рисунок 2 6}}$ = 1,34

. Для большого треугольника . Это конкретное отношение является тригонометрическим отношением треугольника к острому углу θ и применяется к подобным треугольникам.

Отношение тангенса Рисунок 3

Например, tan 45° = 1

Если один угол в прямоугольном треугольнике равен 45°, отношение длины противоположного катета к соседнему катету равно 1.

Таким образом, отношение тангенса равно функция, которая принимает разные значения в зависимости от меры угла. Мы можем измерить угол в градусах или радианах. Его также можно рассчитать с помощью калькулятора.

Решенные примеры

Теперь, когда мы изучили концепцию, давайте решим несколько задач.

В заданном прямоугольном треугольнике PQR найдите отношение касательных сторон ∠P и ∠R

Решение:

tan P = ${\dfrac{QR}{QP}=\dfrac{12}{5 }}$
tan R = ${\dfrac{PQ}{QR}=\dfrac{5}{12}}$

Найдите значение x в заданном прямоугольном треугольнике.

No related posts.