Экспонента обратная: Недопустимое название | Математика | Fandom

Экспоненциальная функция | это… Что такое Экспоненциальная функция?

ТолкованиеПеревод

Экспоненциальная функция

Экспонента — функция exp(x) = e^x, где e — основание натуральных логарифмов.

Содержание 1 Определение 2 Свойства 3 Экспонента от комплексного аргумента 4 Вариации и обобщения 4.1 Матричная экспонента 5 Обратная функция 6 См. также

Определение

Экспоненциальная функция может быть определена различными эквивалентными способами. Например через ряд Тейлора:

или через предел:

Здесь x — любое вещественное или комплексное число.

Свойства

• (e^x)’ = e^x, в частности
• Экспонента является единственным решением дифференциального уравнения y‘ = y с начальными данными y(0) = 1. Кроме того через экспоненту выражаются общие решения однородных дифференциальных уравнений.
• Экспонента определена на всей вещественной оси. Она всюду возрастает и строго больше нуля.
• Экспонента является выпуклой функцией.
• Обратная функция к ней — натуральный логарифм .
• Производная в нуле равна 1, поэтому касательная к экспоненте в этой точке проходит под углом 45°.
• Основное функциональное свойство экспоненты:

  exp(a + b) = exp(a)exp(b).

  • Непрерывная функция с таким свойством либо тождественно равна 0, либо имеет вид exp(ct), где c — некоторая константа.

Экспонента от комплексного аргумента

От комплексного аргумента z = x + iy экспонента определяется следующим образом:

e^z = e

^{x + iy} = e^xe^iy = e^x(cosy + isiny) (формула Эйлера)

В частности,

e^iπ + 1 = 0

Вариации и обобщения

Аналогично экспонента может быть определена для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.

Матричная экспонента

Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:

Определённый таким образом ряд сходится для любого оператора A с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы A: Следовательно, экспонента от матрицы всегда определена и сама является матрицей.

С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение с начальным условием

x(0) = x₀ имеет своим решением x(t) = exp(At)x₀.

Обратная функция

Обратной функцией к экспоненциальной функции является натуральный логарифм.
Обозначается ln(x):

ln(x) = log_e(x)

См.

также

• Экспонента комплексного переменного (обобщение)
• Показательная функция

Wikimedia Foundation. 2010.

Игры ⚽ Нужен реферат?

• Экспонента группы
• Экспансия Третьего рейха

Полезное

ЦИТМ Экспонента — MATLAB&Simulink, Инженерные сервисы, Модельно-ориентированное проектирование

Инженерные компетенции

Системы управления

• Модельно-ориентированное проектирование
• Системы автоматического управления
• Управление электроприводом
• Беспилотные и автономные технические системы
• Робототехника

Обработка сигналов

• Цифровая обработка сигналов 
• Системы связи
• Системы связи 5G
• Радиолокационные системы

Встраиваемые системы

• Встраиваемые системы
• Машины жесткого реального времени
• Верификация кода критических систем
• Сертификация и разработка систем повышенной надежности

Электроэнергетика

• Электроэнергетика

Системная инженерия

• Инженерный DevOps
• Управление интерфейсами сложных систем

Получите ответы на вопросы о продуктах и решениях компании.

Реализованные проекты

Разработка электронного блока управления электрооборудованием электробуса с помощью модельно-ориентированного проектирования

Инновационный центр «КАМАЗ» при поддержке инженеров ЦИТМ Экспонента освоил современный рабочий процесс на базе модельно-ориентированного проектирования, который позволил небольшой команде разработчиков создать систему управления электрооборудования электробуса верхнего уровня в кратчайшие сроки.

Ускорение разработки систем ЦОС в КБ Радар при помощи модельно-ориентированного проектирования

Инженеры ЦИТМ Экспонента были приглашены на базу компании «КБ Радар» для реализации алгоритмов ЦОС для систем мониторинга воздушных целей. Разработка макета приемника и средства модельно-ориентированного проектирования MATLAB позволили сократить время проекта в 5 раз.

История успеха ГСС: системное моделирование аэродинамики самолета

Привлечение специалистов ЦИТМ Экспонента для проведения мастер-классов и выполнения совместного проекта позволило наладить рабочий процесс и выработать внутренние правила моделирования в компании «ГСС».

Проверка AI концепции для Камаз

Для решения проблемы подсчета и идентификации дорогих запчастей компания «Камаз» применила решение на базе сверточных нейронных сетей, предложенное Экспонентой. В результате совместной работы были получены детально проработанная концепция и рабочий прототип.

Радио Гигабит: разработка модема на ПЛИС для радиорелейной системы связи миллиметрового диапазона с использованием методологии модельно-ориентированного проектирования

Для разработки высокоскоростного модема на ПЛИС Экспонента использовала модельно-ориентированный подход на основе среды Simulink. В результате этого решения компания «Радио Гигабит» успешно завершила проект в четырехмесячный срок.

Разработка системы управления электропривода по методу модельно-ориентированного проектирования

Автоматическая генерация кода на основе моделей MATLAB позволило разработать программное обеспечение микропроцессорной системы управления с минимальным использованием традиционных средств разработки программного кода.

Инструменты MATLAB помогли компании «Рубикон-Инновация» грамотно решить имевшиеся задачи управления.

Реализация системы видеосвязи для ЛА на основе стандарта IEEE 802.11N для концерна Вега

Инженеры ЦИТМ Экспонента применили методы модельно-ориентированного проектирования для построения системной имитационной модели, отладки алгоритмов и автоматической генерации HDL кода. В результате проект концерна «Вега» удалось сократить в 5 раз.

Системные имитационные модели передачи информации на среднеорбитальные космические аппараты и VDB GBAS

Инженеры МКБ «Компас» обратились к специалистам ЦИТМ Экспонента для создания универсальной математической системной модели, на которой можно отработать основные алгоритмические решения.

«Технодинамика» разрабатывает алгоритмы первичной обработки данных в Simulink в соответствии с КТ-178

Представитель компании «Технодинамика» поделился результатами использования продуктов MATLAB для моделирования алгоритма первичной обработки данных и генерации исходного кода микроконтроллера и его верификации. Подробности в видеоролике.

Использование MATLAB и Simulink в МГТУ им. Баумана

МГТУ им. Баумана использует MATLAB и Simulink как в учебном процессе, так и в научно-исследовательских и опытно-конструкторских разработках, так как ориентирован на самые передовые направления современной науки и техники.

Сопровождение летных испытаний летательного аппарата «ОКБ им. А. С. Яковлева» в Simulink

Использование продуктов MathWorks в процессе летных испытаний летательного аппарата позволило ускорить анализ результатов испытаний, скорректировать характеристики аппарата и обеспечить проверку изменений, вносимых в проект.

Конструкторы ФГУП ГНПРКЦ «ЦСКБ-Прогресс» моделируют ракеты в среде MATLAB

Самарское представительство компании завершило проект по внедрению продукта MATLAB от компании MathWorks – решение для технических расчетов, разработка алгоритмов и анализ данных на предприятии – в Государственном научно-производственном ракетно-космическом центре «ЦСКБ-Прогресс».

ФГУП «ГОСНИИАС» разработал модель автопилота для пилотажного тренажера среднемагистрального самолета в среде MATLAB и Simulink

Благодаря использованию продуктов MathWorks удалось сократить сроки разработки, достичь требуемой точности управления и оптимизировать передачу информации для создания приложения реального времени, имитирующее автоматическое управление пространственным положением и тягой самолета на всех режимах полета.

Русэлпром протестировал цифровое управление двумя двигателями от одного преобразователя частоты при помощи MATLAB и Simulink

Перед инженерами ЦИТМ Экспонента стояла задача экспериментальной проверки возможности группового управления двумя тяговыми асинхронными двигателями мотовоза от общего преобразователя частоты в векторном режиме с помощью моделирования в Simulink.

История успеха АО «РТИ»: оптимизация кода математического модуля на языке VHDL

Специалисты ЦИТМ Экспонента создали модели математического модуля, автоматической генерации кода и верификации относительно тестовых данных с помощью Simulink и HDL Coder для компании «РТИ».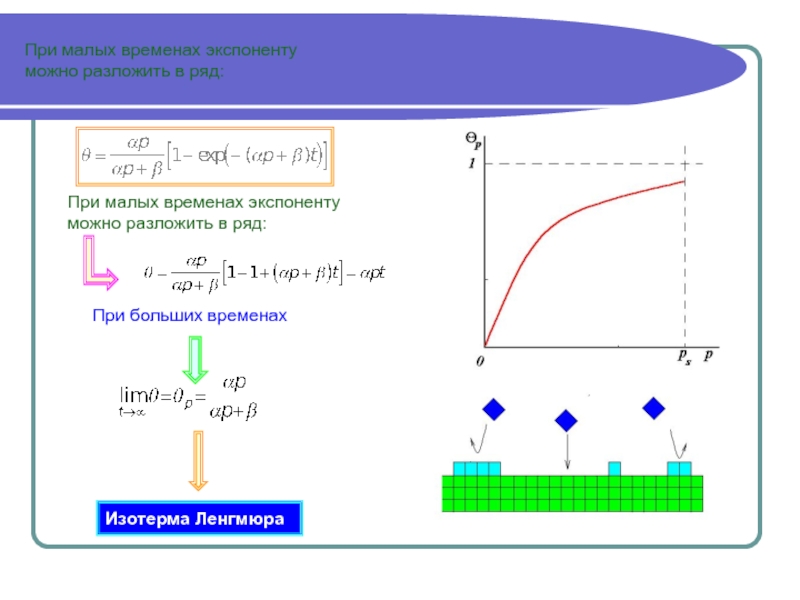

Посмотреть другие реализованные проекты >>

Мероприятия

05 апреля 2023 10:00 Конференция «Моделирование в инженерном деле»

Семинар

06 апреля 2023 10:00 Разработка системы передачи видео через радиоканал

Вебинар

11 апреля 2023 10:00 Разработка систем спутниковой связи с помощью модельно-ориентированного проектирования

Семинар

13 апреля 2023 10:00 Моделируем искусственный интеллект для агротеха

Вебинар

26 апреля 2023 10:00 Компьютерное зрение

Семинар

 Смотреть все мероприятия>> 

Публикации

20 марта 2023 10:00 Экспонента упрощает внедрение современных компетенций и высокотехнологичных продуктов в агротехе

08 февраля 2023 11:00 Экспонента запускает систему предсказательного обслуживания Экспонента. Предиктив

03 октября 2022 11:00 Применение КПМ РИТМ для моделирования электроэнергетических систем

09 августа 2022 13:00 VIII Всероссийская конференция «Технологии разработки и отладки сложных технических систем». Академические доклады

26 июля 2022 01:05 Имитационные модели реального времени электроэнергетических объектов

 Смотреть все публикации>> 

О компании

Центр Инженерных Технологий и Моделирования создан для всестороннего содействия русскоязычным инженерам в освоении передовых инструментов и технологий разработки и отладки сложных технических систем, алгоритмов и инженерного анализа данных.

ЦИТМ Экспонента дает импульс развитию и ускорению внутренних инженерных процессов заказчика, передает практические компетенции по технологиям модельно-ориентированного проектирования и Engineering Data Analytics на живых совместных проектах, через тренинги и семинары, консультационную поддержку, образовательные интернет ресурсы, примеры в исходных кодах или моделях.

Наша цель — постоянное укрепление инженерных команд заказчиков, которые знают «что делать», нашим пониманием возможностей и технологий того «как это делать быстрее и дешевле» и помощью в вопросах поиска и развития кадров.

Опыт и решения ЦИТМ Экспонента помогают сотням учебных заведений усиливать практико-ориентированность учебного процесса и последовательно формировать вычислительные компетенции будущих инженеров и ученых. Мы хорошо понимаем организационные и управленческие особенности наших заказчиков, умеем приносить пользу и развитие с учетом специфики ВУЗа или корпорации.

Продукты

• Купить MATLAB
• Simulink
• Сопровождение проектов
• Строим стенд главного конструктора

Контакты

Подписка

• Подпишитесь на новости

Нет совпадений

Продукты

${ product. header }

Сервисы

${ workflow.title }

Новость

${ news.title }

Мероприятие

${ event.title_rus }

Статичные страницы

${ page.title }

Страницы

${ page.title }

Продукты

${ product.header }

Сервисы

${ workflow.title }

Новость

${ news.title }

Мероприятие

${ event.title_rus }

Статичные страницы

${ page.title }

Страницы

${ page.title }

Выберите компанию из списка

y \mod z$, и он работает быстро, потому что включает «возведение в степень путем возведения в квадрат» (или что-то подобное). Код мгновенно запускается на моем ноутбуке.

$\endgroup$

9

Как работает обратная взвешенная интерполяция расстояния — ArcGIS Pro

Доступно с лицензией Geostatistical Analyst.

Интерполяция, взвешенная по обратному расстоянию (IDW), явно предполагает, что объекты, находящиеся близко друг к другу, более похожи, чем те, которые находятся дальше друг от друга. Чтобы спрогнозировать значение для любого неизмеренного местоположения, IDW использует измеренные значения, окружающие прогнозируемое местоположение. Ближайшие к прогнозируемому местоположению измеренные значения оказывают большее влияние на прогнозируемое значение, чем те, которые находятся дальше. IDW предполагает, что каждая измеренная точка имеет локальное влияние, которое уменьшается с расстоянием. Он дает больший вес точкам, ближайшим к местоположению прогноза, и веса уменьшаются в зависимости от расстояния, отсюда и название «взвешенное обратное расстояние». Веса, присвоенные точкам данных, показаны в следующем примере:

Иллюстрация Search Neighborhood

Окно Weights содержит список весов, присвоенных каждой точке данных, которая используется для создания прогнозируемого значения в месте, отмеченном перекрестием.

Узнайте больше о методах интерполяции, доступных в ArcGIS Geostatistical Analyst

Степенная функция

Как упоминалось выше, веса обратно пропорциональны расстоянию (между точкой данных и прогнозируемым местоположением), возведенному в степень стр . В результате с увеличением расстояния веса быстро уменьшаются. Скорость уменьшения весов зависит от значения p . Если p = 0, уменьшение с расстоянием не происходит, и поскольку каждый вес λ _i одинаков, прогноз будет средним значением всех значений данных в окрестности поиска. По мере увеличения p веса удаленных точек быстро уменьшаются. Если значение p очень велико, только ближайшие окружающие точки будут влиять на прогноз.

Уменьшение веса с расстоянием, иллюстрация

Geostatistical Analyst использует значения мощности, большие или равные 1. Когда p = 2, метод известен как взвешенная интерполяция обратного квадрата расстояния. Значение по умолчанию — p = 2, хотя нет теоретического обоснования предпочтения этого значения по сравнению с другими, и влияние изменения p следует исследовать путем предварительного просмотра вывода и изучения статистики перекрестной проверки.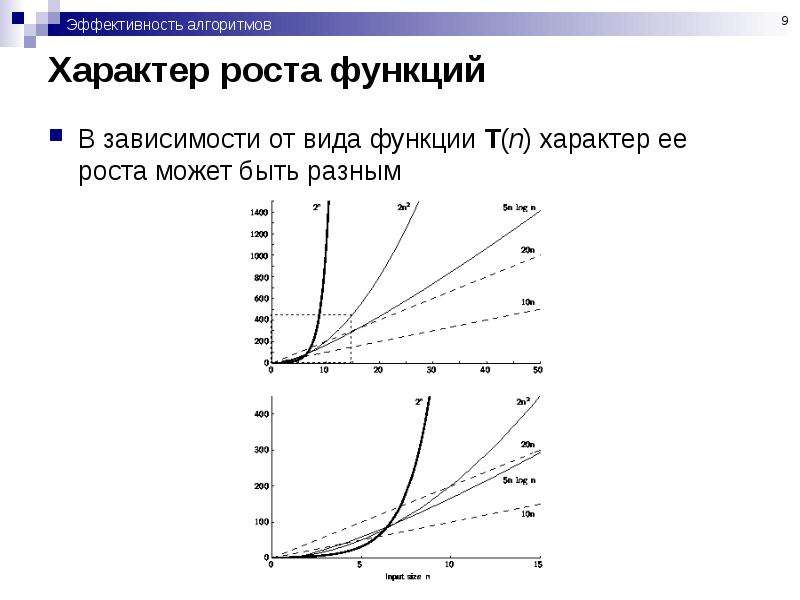

Район поиска

Поскольку объекты, расположенные близко друг к другу, больше похожи друг на друга, чем объекты, расположенные дальше, по мере удаления местоположений измеренные значения будут мало связаны со значением прогнозируемого местоположения. Для ускорения расчетов можно исключить более удаленные точки, которые мало повлияют на прогноз. В результате общепринятой практикой является ограничение количества измеренных значений путем указания области поиска. Форма окрестности ограничивает, как далеко и где искать измеренные значения, которые будут использоваться в прогнозе. Другие параметры соседства ограничивают места, которые будут использоваться в этой фигуре. На следующем изображении пять измеренных точек (соседей) будут использоваться при прогнозировании значения для местоположения без измерения, желтая точка.

Пример поиска окрестности

На форму окрестности влияют входные данные и поверхность, которую вы пытаетесь создать. Если в ваших данных нет направленных влияний, вы захотите рассмотреть точки одинаково во всех направлениях. Для этого вы определите область поиска как круг. Однако, если в ваших данных есть влияние направления, например преобладающий ветер, вы можете захотеть скорректировать его, изменив форму окрестности поиска на эллипс с большой осью, параллельной ветру. Поправка на это влияние направления оправдана, поскольку вы знаете, что места с наветренной стороны от прогнозируемого местоположения будут более похожими на удаленных расстояниях, чем местоположения, перпендикулярные ветру, но расположенные ближе к прогнозируемому местоположению.

После указания формы соседства вы можете ограничить, какие местоположения данных внутри формы должны использоваться. Вы можете определить максимальное и минимальное количество локаций для использования, а также разделить район на сектора. Если вы разделите окрестности на сектора, к каждому сектору будут применены максимальное и минимальное ограничения.

Точки, выделенные в окне просмотра данных, показывают местоположения и веса, которые будут использоваться для прогнозирования местоположения в центре эллипса (положение перекрестия). Окрестность поиска ограничена внутренней частью эллипса. В приведенном ниже примере двум красным точкам будет присвоен вес более 10 процентов. В восточном секторе одной точке (коричневой) будет присвоен вес от 5 до 10 процентов. Остальные точки в окрестности поиска получат меньшие веса.

Пример весов секторов соседства

Когда использовать IDW

Поверхность, рассчитанная с использованием IDW, зависит от выбора значения степени ( p ) и стратегии поиска соседства. IDW — это точный интерполятор, в котором максимальное и минимальное значения (см. диаграмму ниже) на интерполированной поверхности могут встречаться только в точках выборки.

Пример профиля, взвешенного по обратному расстоянию

Выходная поверхность чувствительна к кластеризации и наличию выбросов. IDW предполагает, что моделируемое явление обусловлено локальными вариациями, которые можно зафиксировать (смоделировать), определив адекватную окрестность поиска. Поскольку IDW не дает стандартных ошибок прогнозирования, обоснование использования этой модели может быть проблематичным.