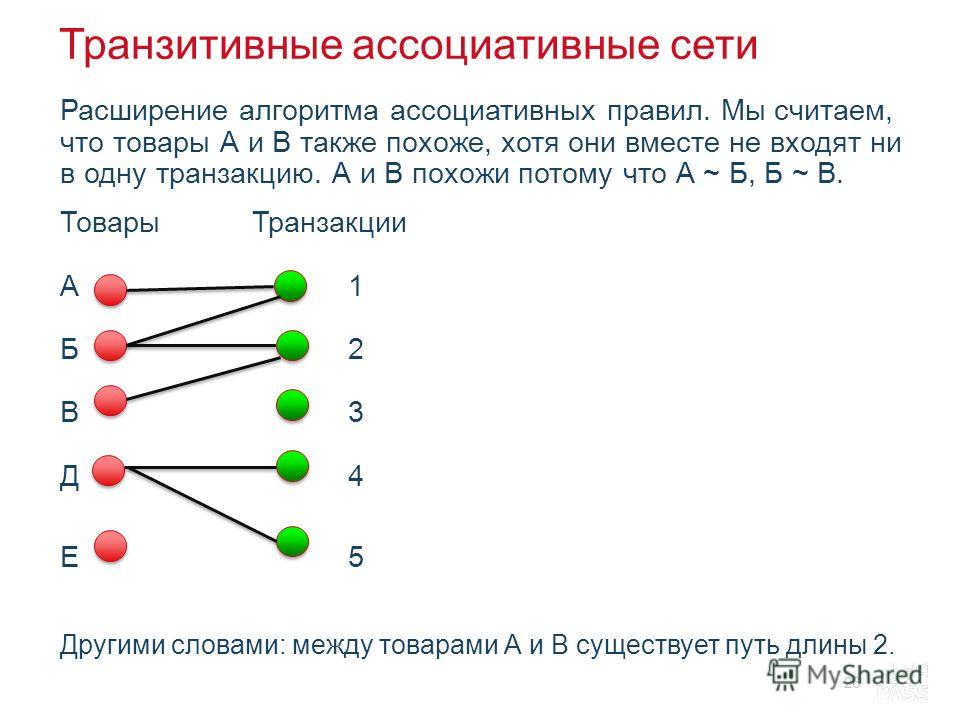
2.3. Транзитивность и транзитивное замыкание бинарного отношения
Определение 2.6. Бинарное отношение называюттранзитивным бинарным отношением, если для любых ,ииз того, чтои, вытекает, что.
Символически определение 2.6 записано формулой (2.7).
. | (2.7) |
Другими словами, отношение транзитивно, если оно покрывает все опосредованные связи между элементами. Отсюда вытекает, чтоусловием транзитивности отношения является выполнение условия
(2.8) |
Используя матрицы отношений, условие (2.8) можно переписать так:
 | (2.9) |
Пример.
На множестве ={a,b,c} задано отношение :
.
Покажем, что не является транзитивным отношением.
,
инесравнимы между собой, следовательно, не транзитивно.
Найдем более высокие степени отношения , т.е. матрицы отношений,,,…,:
,
,
,
.
Легко проверить, что …=.
Определение 2.7. Транзитивным замыканием бинарного отношения называют объединение степеней этого бинарного отношения:
. | (2. |
10)Транзитивное замыкание отношения в рассмотренном примере имеет вид.
Пусть на множестве отношениезадано графом (рис.2.4). Запишем матрицуэтого отношения и найдем его транзитивное замыкание.
Матрица отношения .
Для нахождения транзитивного замыкания будем умножать матрицу на себя, получая,,…,, до тех пор, пока не выполнится равенство. Дальнейшее умножение не будет приводить к изменению матриц.
==.
Любой элемент матрицы не превосходит соответствующий элемент матрицы, т.е.. Это означает, чтовключает все опосредованные связи между элементами, следовательно,является транзитивным бинарным отношением. Покажем, что его транзитивное замыкание совпадает с самим.
==.
Транзитивное
замыкание отношения
найдем, используя формулу (2.
10) и матрицыи:
.
Как и следовало ожидать, поскольку отношение является транзитивным отношением, оно совпадает со своим транзитивным замыканием.
Справедливы следующие утверждения.
Утверждение 1. Транзитивное бинарное отношение совпадает со своим транзитивным замыканием.
Утверждение 2. Транзитивное замыкание бинарного отношения есть наименьшее по числу элементов транзитивное отношение, содержащее данное бинарное отношение.
Утверждение 3. Транзитивное замыкание есть ближайшее к транзитивное отношение.
Использование термина «ближайшее отношение» предполагает, что между отношениями определено расстояние. Для определения расстояния между множествами используют формулу линейного расстояния (формула 2.11), или формулу евклидова расстояния (формула 2.12).
, | (2. |
11), | (2.12) |
где – расстояние между подмножествамииуниверсального множества,ихарактеристические функции этих подмножеств. Суммирование выполняется по всем элементам универсального множества.
Для бинарного отношения, заданного на множестве , универсальным множеством является множество. Если, тоназывают
, | (2.13) |
, | (2.14) |
где
– число элементов универсального
множества,,.
Не следует думать, что последовательность степеней матрицы отношения всегда имеет предел, т. е., начиная с некоторого шага , выполняется равенство. Приведем простой пример, показывающий, что это не так.
Пусть матрица отношения на множествеимеет вид.
Тогда
, ,,….,,
для любого .
Тем не менее .
|
|
Математика — это язык, на котором написана книга природы.
РЕШЕНИЕ ЗАДАЧ, КОНТРОЛЬНЫХ РАБОТ ПО ВЫСШЕЙ МАТЕМАТИКЕ                                                                                                         Галилео Галилей | |||
|
Главная Оплата Примеры Учебники |
|
|||
Изобразить P1, P2 графически. Найти P = (P2◦P1)–1.
Выписать области определения и области значений всех трех
отношений: P1, P2, Р. Построить матрицу [P2],
проверить с ее помощью, является ли отношение P2
рефлексивным, симметричным, антисимметричным, транзитивным. P1 = {(b,1),(b,4),(a,3),(a,4),(c,4),(c,2)};
P2 = {(1,1),(2,4),(2,3),(2,2),(3,3),(3,4),(4,2),(4,4)}.
матриц — Как проверить, является ли отношение транзитивным от матричного представления?
Это ответ на ваш второй вопрос об отношении $R=\{\langle 1,2\rangle,\langle 2,2\rangle,\langle 3,2\rangle\}$.
Мы можем проверить транзитивность несколькими способами.
(1) Список всех связанных пар:
$$\begin{align*} &\langle 1,2\rangle\land\langle 2,2\rangle\tag{1}\\ &\langle 2,2\rangle\land\langle 2,2\rangle\tag{2}\\ &\langle 3,2\rangle\land\langle 2,2\rangle\tag{3} \end{выравнивание*}$$
Если $R$ должен быть транзитивным, $(1)$ требует, чтобы $\langle 1,2\rangle$ было в $R$, $(2)$ требует, чтобы $\langle 2,2\rangle$ было в $R$, а $(3)$ требует, чтобы $\langle 3,2\rangle$ находилось в $R$. А поскольку все эти требуемые пары равны в $R$, $R$ действительно транзитивно.
(2) Проверить все возможные пары конечных точек. Например, чтобы увидеть, требуется ли $\langle 1,3\rangle$ для того, чтобы $R$ был транзитивным, посмотрите, существует ли «ступенька» от $1$ к $3$: существует ли $a$ такие, что $\langle 1,a\rangle$ и $\langle a,3\rangle$ принадлежат $R$? Если это так, транзитивность потребует, чтобы $\langle 1,3\rangle$ также лежало в $R$. Как оказалось, такого $a$ не существует, поэтому транзитивность $R$ не требует, чтобы $\langle 1,3\rangle$ было в $R$.
Выполните эту проверку для каждой из девяти упорядоченных пар в $\{1,2,3\}\times\{1,2,3\}$. 92=\begin{bmatrix}0&1&0\\0&1&0\\0&1&0\end{bmatrix}\begin{bmatrix}0&1&0\\0&1&0\\0&1&0\end{bmatrix}=\begin{bmatrix}0&1&0\\0&1&0\\0&1&0\ end{bmatrix}$$
подсчитывает количество путей с шагом $2$ между элементами $\{1,2,3\}$. Запись в строке $i$, столбце $j$ — это количество путей из $i$ в $j$, состоящих из $2$ шагов. (Под двухшаговым путем я имею в виду что-то вроде $\langle 3,2\rangle\land\langle 2,2\rangle$: первая пара ведет от $3$ до $2$, вторая — от $2$ до $2$. $2$, а вместе вы получите от $3$ до $2$.) 92=\begin{bmatrix}1&0&1\\0&1&0\\1&0&1\end{bmatrix}\begin{bmatrix}1&0&1\\0&1&0\\1&0&1\end{bmatrix}=\begin{bmatrix}2&0&2\\0&1&0\\2&0&2\ end{bmatrix}\;.$$
$2$ указывают на то, что существует два $2$-шаговых пути из $1$ в $1$, из $1$ в $3$, из $3$ в $1$ и из $3 $ до $3$; существует только один $2$-шаговый путь из $2$ в $2$. Например, от $1$ до $1$ у вас есть как $\langle 1,1\rangle\land\langle 1,1\rangle$, так и $\langle 1,3\rangle\land\langle 3,1\rangle$ .
2$ показывает хотя бы один двухшаговый путь, $M_R$ показывает, что одношаговый путь уже существует, и поэтому $R$ транзитивен. 92$. Если $M_R$ уже имеет $1$ в каждой из этих позиций, $R$ является транзитивным; если нет, то нет.
Сходимость степеней нечеткой транзитивной матрицы
- title={Сходимость степеней нечеткой транзитивной матрицы},
автор={Хироши Хашимото},
journal={Нечеткие множества и системы},
год = {1983},
громкость = {9},
страницы = {153-160}
}
- H. hashimoto
- Опубликовано 1983
- Компьютерная наука
- Нечеткие наборы и системы
View Via Publisher
Конвергенция продуктов Fuzzy Matrices
- S. Guu, HSING-HSING-HSIA, CHIN-TZONG
- S. GUU, HSING-HSING-HSIA, CHINGONG
- S. Guu, HSING-HSIN Информатика, Математика
Сист. нечетких множеств.
- 2001
Период степеней нечеткой матрицы
- Х.
Имаи, Юичи Окахара, М. Миякоши Информатика
Нечеткие множества Сист.
- 2000
Сходимость макс-средних арифметических степеней нечеткой матрицы
- Юнг-Йих Лур, Ян-Куэн Ву, С. Гуу
Информатика
3
3 Информатика.
- 2007
О транзитивности обобщенных нечетких матриц
- И-цзя Тан
Математика, информатика
Нечеткие множества Сист.
- 2013
Сходимость степеней s-транзитивных нечетких матриц
- W. Kołodziejczyk
Computer Science
- 1988
On Infinite Products of Fuzzy Matrices
- S. Guu, Yung-Yih Lur, Chin-Tzong Pang
Mathematics, Computer Science
SIAM Дж. Матричный анал. заявл.
- 2001
Показано, что слабая сходимость бесконечных произведений конечного числа нечетких матриц эквивалентна слабым сходимостям бесконечных произведений конечного числа ассоциированных булевых матриц.
Периодичность степеней нечетких матриц (конечные нечеткие отношения)
- Ли Цзянь-Синь
Информатика
- 1992
средние операции
- Yung-Yih Lur, Yan-Kuen Wu, S. Guu
Информатика
Инф. науч.
- 2009
Мультипликативный функционал на верхнетреугольных нечетких матрицах
- Лю Пин
Информатика, Математика
- 2015
Доказано, что существуют мультипликативный функционал F и функционал G из нечеткой алгебры в нечеткую геометрию такие, что образ нечеткой верхней матрицы треугольный под f может быть представлен как произведение всех образов его элементов главной диагонали под F и других элементов под G.0061
- В. Колодзейчик
Информатика
- 1990
Показано, что существуют решения с различными известными типами нечеткой транзитивности, а максимальное решение имеет особый новый тип так называемой α- показано транзитивность и интересное свойство сходимости натуральных степеней максимального решения.
ПОКАЗАНЫ 1-10 ИЗ 11 ССЫЛОК
СОРТИРОВАТЬ ПОРелевантности Наиболее влиятельные документыНедавность
Сходимость степеней нечеткой матрицы
- M. Thomason
Computer Science
- 1977
STRUCTURE OF FUZZY BINARY RELATIONS
- S. Ovchinnikov
Computer Science
- 1981
Similarity relations and fuzzy orderings
- L Заде
Информатика
Инф. науч.
- 1971
Классификация образов на основе нечетких отношений
Описан метод классификации образов с использованием нечетких отношений, в котором сходство между любыми двумя образами вычисляется путем использования композиции нечеткого отношения для индуцирования отношения эквивалентности.
Графы и сети
привлекательно, использование алгебры путей. Здесь матрица инцидентности графа состоит из элементов из подходящей алгебры, а система уравнений решается методами, аналогичными используемым в линейных…
Нечеткая модель поисковых систем документов
Введение в теорию нечетких подмножеств.
- C. Proctor, A. Kaufman, D. Swanson
Информатика
- 1977
Применение графов и булевых матриц в компьютерном программировании
- Р. Маримон
Информатика
- 1960
Рассмотрены элементарные свойства ориентированных графов и булевых матриц, показано, как их использование в других областях может быть связано с программированием, а также некоторые проблемы которые должны быть решены, прежде чем компьютерное программирование может быть полностью механизировано.
О графиках и асимптотиках матриц конечных булевых отношений и стохастических матриц
- D. Rosenblatt
Математика
- 1957
на графах конечных идаптотентов. Характеристика идемпотентных матриц булевых отношений конечного порядка и формальные результаты приведены на примере исследования асимптотических форм рекурсивной модели информационной системы, которая обеспечивает совместное представление процессов передачи и получения информации.
Имаи, Юичи Окахара, М. Миякоши
