| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |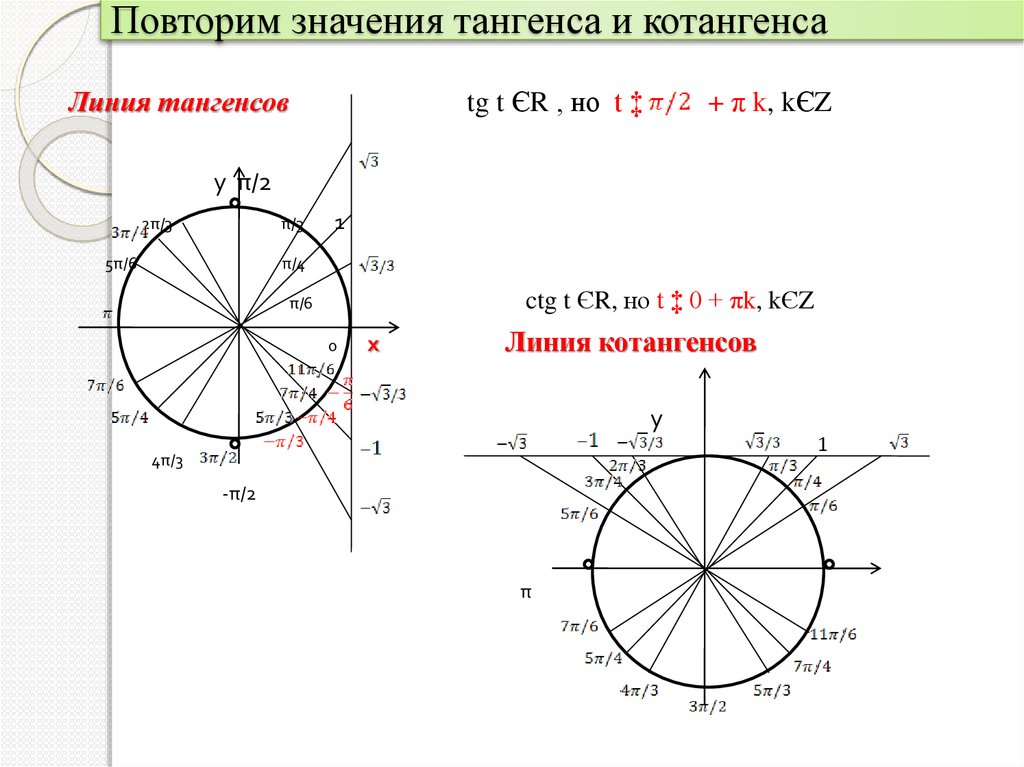
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |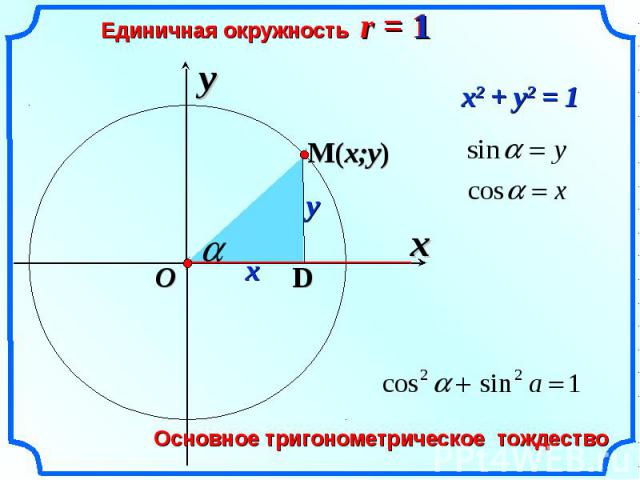
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |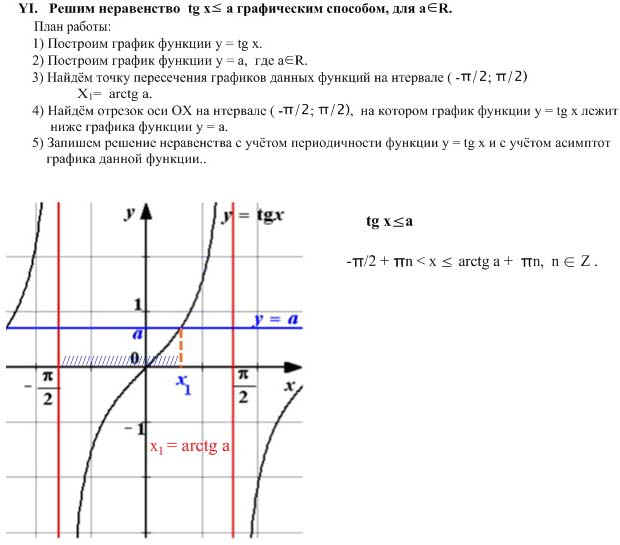
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |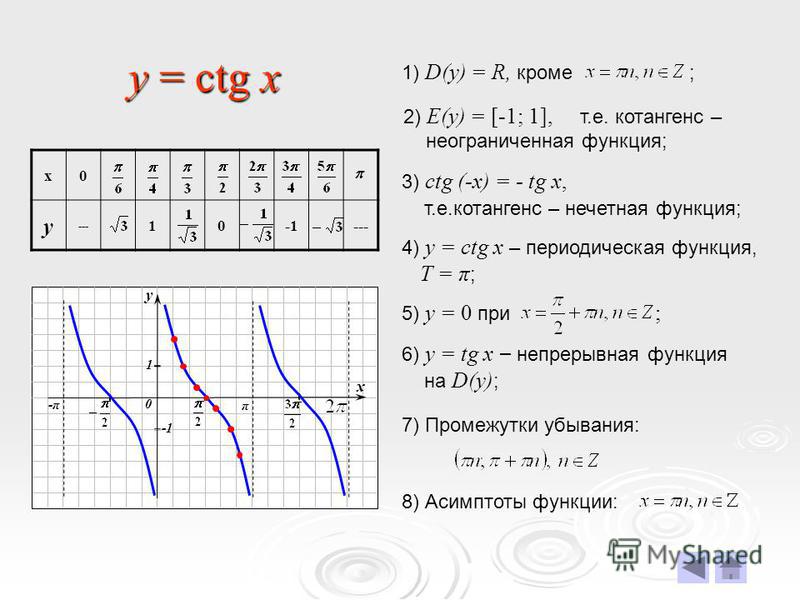
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | ||
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Уравнение tgx=a
Напомним,
что уравнение, которое содержит переменную под знаком тригонометрических
функций, называется тригонометрическим уравнением. Уравнения вида
, , и , где х – переменная,
а число , называются простейшими
тригонометрическими уравнениями.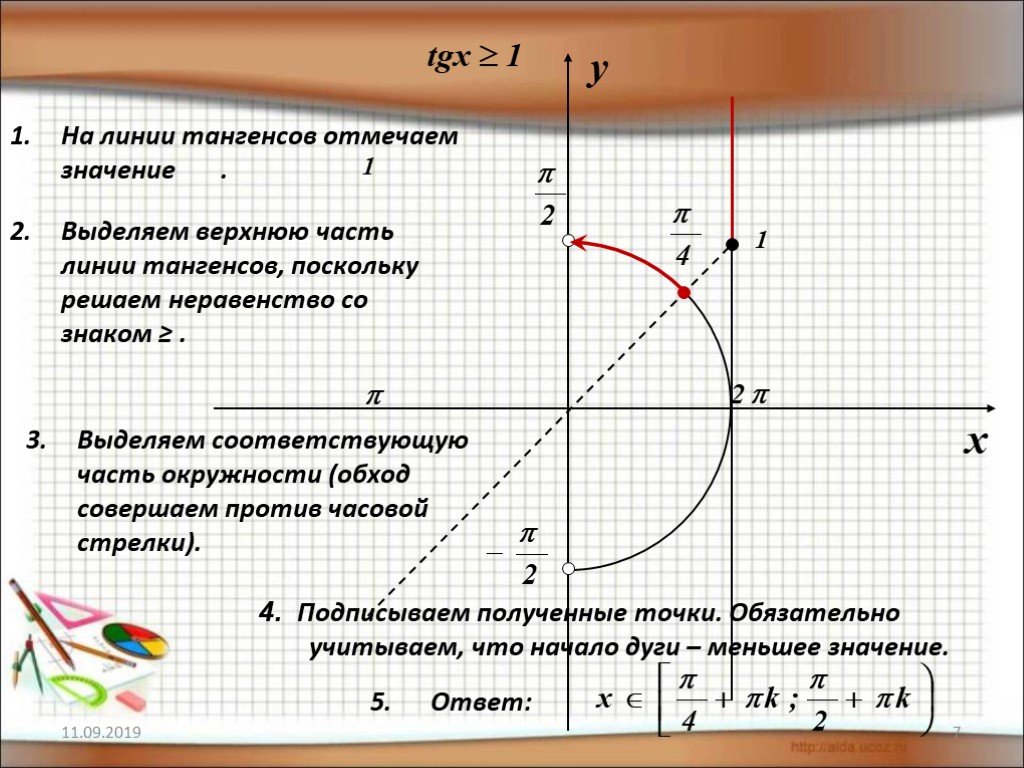
На этом уроке мы с вами подробно
рассмотрим решение уравнений вида и .
Вы уже знаете, что тангенсом угла называется отношение синуса угла к его косинусу. А котангенсом угла называется отношение косинуса угла к синусу угла .
Важно помнить, что и определены для любого угла , а их значения заключены в промежутках от минус единицы до единицы, так как координаты точек единичной окружности заключены в промежутках –1 до 1.
А вот тангенс определён только для тех углов, для которых косинус не равен нулю, так как делить на нуль нельзя. Тогда тангенс определён для любых углов, кроме .
Что касается котангенса , то он определён только для тех углов, для которых синус не равен нулю. То есть котангенс определён для любых углов, кроме .
Исходя
из определений тангенса и котангенса, следует, что и могут принимать любые действительные
значения. Значит, уравнения и имеют корни при любом
значении а.
Так как же решают такие уравнения? Давайте рассмотрим два уравнения: и .
Решение этих уравнений удобно проиллюстрировать с помощью линии тангенсов. Напомним, что тангенс икс – это ордината точки М пересечения прямой ОМ с линией тангенсов.
Итак, построим углы, тангенсы которых равны 1. Для этого через начальную точку Р проведём прямую, перпендикулярную оси абсцисс, то есть линию тангенсов. На линии тангенсов есть лишь одна точка с ординатой один. Обозначим её М. Затем через точку М и начало координат проведём прямую. Обратите внимание, эта прямая пересекает единичную окружность в двух диаметрально противоположных точках – и . Видим, у нас получился прямоугольный треугольник РОМ. Вы уже знаете, что тангенсом угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему . Найдём это отношение. Так как РО равно 1, то имеем .
Отсюда
по таблице значений . Таким образом, точка получается путём
поворота начальной точки на угол .
В свою очередь, точка получается поворотом
начальной точки на угол .
Но ведь в эти точки мы можем попасть не по одному разу. Если мы сделаем полный оборот по единичной окружности, то снова попадём в эти точки. Сделав ещё полный оборот, снова попадём в эти точки и так далее. Отсюда имеет две серии решений:
Как правило, эти серии решений совмещают и записывают как .
Решим
второе уравнение . Оно решается
аналогичным образом. Итак, построим углы, тангенсы которых равны –1. Для этого
проведём линию тангенсов. На линии тангенсов есть лишь одна точка с ординатой –1.
Обозначим её М. Затем через точку М и начало координат проведём прямую. Эта
прямая пересекает единичную окружность в двух диаметрально противоположных
точках – и . Видим, у нас получился
прямоугольный треугольник РОМ. Так как тангенс угла в прямоугольном
треугольнике – это отношение противолежащего катета к прилежащему , то . Отсюда .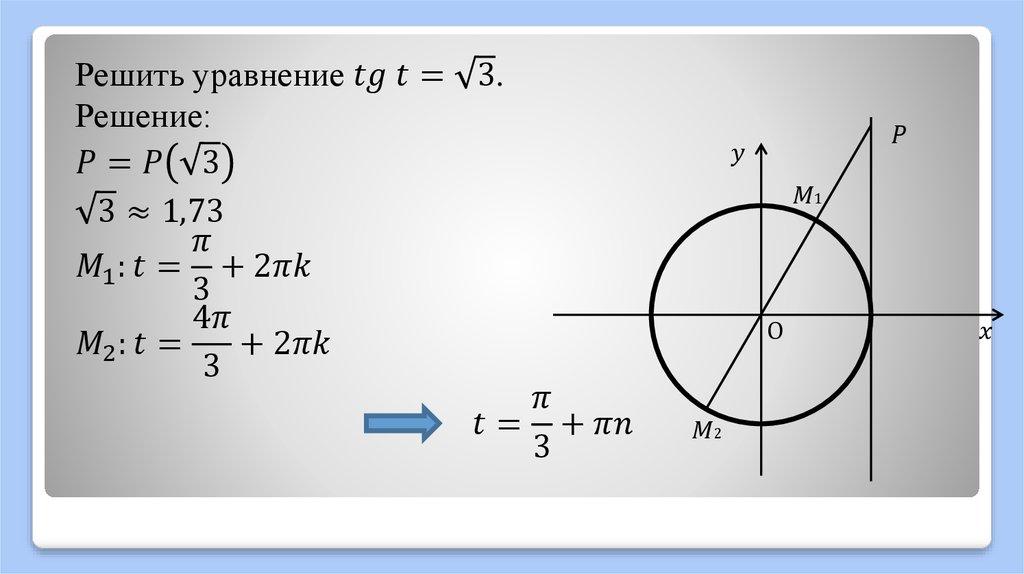
Таким образом, точка получается путём
поворота начальной точки на угол . В свою очередь, точка получается поворотом
начальной точки на угол .
Отсюда уравнение имеет две серии решений:
Как правило, эти серии решений совмещают и записывают как .
Заметим, что каждое из уравнений и имеет бесконечное множество корней. Однако на интервале каждое из этих уравнений имеет только один корень. Так, , – это корень уравнения , а , – это корень уравнения . Число называют арктангенсом числа 1. Записывают так: . Число называют арктангенсом числа –1. Записывают так: .
Кстати, «арктангенс» в переводе с латинского означает «дуга» и «тангенс». Это обратная функция.
Вообще, уравнение для любого на интервале имеет только один корень. Если , то этот корень заключён в промежутке ;
если же , то корень располагается в промежутке .
Этот
корень называют арктангенсом числа а и обозначают так .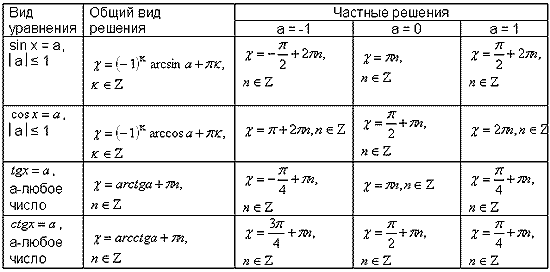
Запомните! Арктангенсом числа называется такое число , тангенс которого равен а.
, если и
Например, , так как , . , так как , .
Возвращаясь к нашему уравнению , где , можно утверждать, что все корни уравнения можно найти по формуле: . Это и есть общая формула нахождения корней уравнения .
Запомните! Для любого справедлива формула . Эта формула позволяет находить значения арктангенсов отрицательных чисел через значения арктангенсов положительных чисел.
Например, .
Уравнения
вида решаются аналогичным
образом. Отличия лишь в том, что – это абсцисса точки М
пересечения прямой ОМ с линией котангенсов. И при построении углов, котангенсы
которых нужно найти, из прямоугольного треугольника мы будем находить отношение
прилежащего катета к противолежащему, так как котангенсом
угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему
.
Вычислив
это отношение, мы найдём искомое решение уравнения.
Уравнение также имеет бесконечное множество решений при любых значениях а. Однако на интервале это уравнение для любого действительного а имеет только один корень. Если , то этот корень заключён в промежутке ;
если же , то корень располагается в промежутке .
Этот корень называют арккотангенсом числа а и обозначают так .
Запомните! Арккотангенсом числа называется такое число , котангенс которого равен а.
, если и
Например, , так как , . , так как , .
Тогда можно утверждать, что все корни уравнения можно найти по формуле: . Это и есть общая формула нахождения корней уравнения котангенс икс равно а.
Запомните!
Для любого справедлива формула . Эта формула позволяет
находить значения арккотангенсов отрицательных чисел через значения
арккотангенсов положительных чисел.
Например, .
А теперь давайте приступим к практической части нашего урока.
Задание. Решите уравнения и .
Решение.
тригонометрия — Почему $x
спросил
Изменено 11 месяцев назад
Просмотрено 17 тысяч раз
$\begingroup$
При доказательстве $\displaystyle\lim_{x\rightarrow0}\frac{\sin{x}}{x}=1$ предполагается, что $\sin{x}\leq{x}\leq\tan{x }$, а $0 $\endgroup$ $\begingroup$ $\ \ \ \bullet$ Используя подобные треугольники:
$$\color{darkgreen}{\tan t}={\color{бордовый}{\sin t}\over\color{darkblue}{\cos t}} ={
{\ text {length} ( \ color {darkgreen} {\ overline {{IZ}})}} \ over 1 } \ quad \ Longrightarrow \ quad \ color {darkgreen} {\ tan t} = \ text {length} ( \color{темно-зеленый}{\overline{IZ}})$$
$\ \ \ \bullet$ Площадь $\треугольника OIZ={1\over2}\cdot1\cdot\color{darkgreen}{\tan t}$.
Итак, $$\color{maroon}{\sin t}\lt t\lt\color{darkgreen}{\tan t}$$ при $0< t<\pi/2$.
$\endgroup$
3
$\begingroup$
Хорошо, если сравнение этих длин интуитивно понятно для вас, но если вы хотите быть строгим, проще сравнивать вложенные области, чем сравнивать длины кривых.
Обработав рисунок Дэвида Митры (см. его ответ), площадь треугольника, натянутого на линии $\cos(t)$ и $\sin(t)$, равна $\frac{1}{2} \cos (т)\sin(t)$. Эта площадь лежит внутри сектора угла $t$, который имеет площадь $\frac{t}{2}$ (доля $\frac{t}{2\pi}$ от площади всего круга $\pi$) . И, в свою очередь, площадь сектора находится внутри треугольника, натянутого на горизонтальный радиус единичной окружности и $\tan(t)$, который имеет площадь $\frac{1}{2} \tan(t)$.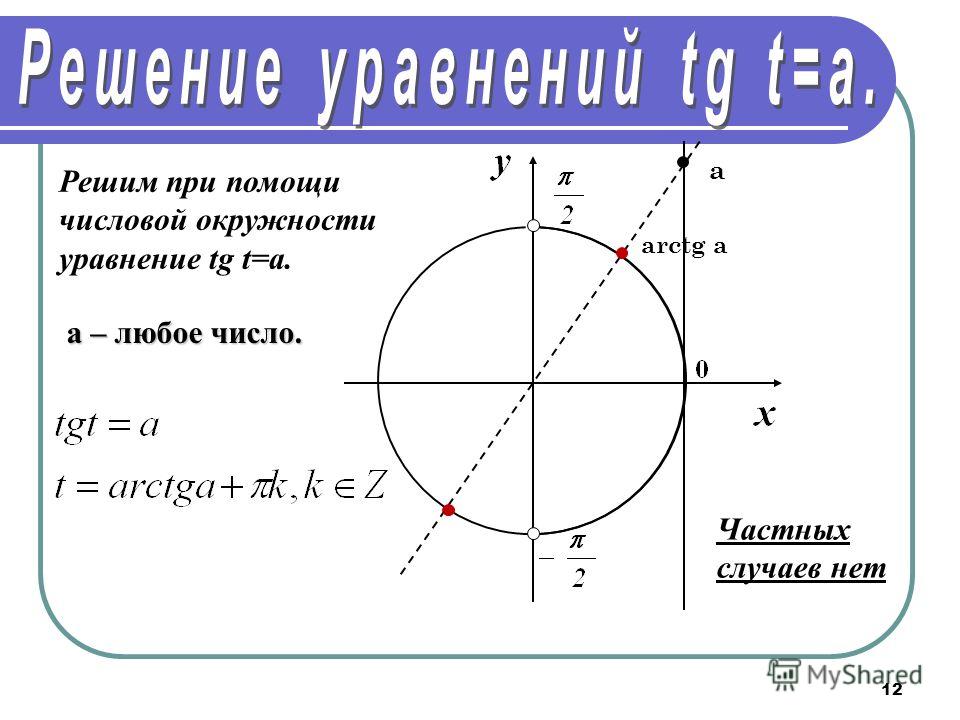
Таким образом, имеем неравенство $$\frac{1}{2} \cos(t)\sin(t) \le \frac{t}{2} \le \frac{1}{2} \tan( t)$$ Или $$\cos(t)\sin(t) \le t \le \tan(t)$$ с отменой двойки. Вы должны быть в состоянии скорректировать доказательство $\displaystyle\lim_{t \to 0}\frac{\sin(t)}{t} = 1$, чтобы использовать это немного более слабое неравенство. 92(x) \leqslant 0~,~~~~~0\lt x\lt \frac{\pi}{2},$$ Итак, $f(x)$ убывает на $0\lt x\lt \frac{\pi}{2}$. Таким образом, мы имеем $f(0)\gt f(x)$ или $f(x)\lt 0$.
$\endgroup$
2
$\begingroup$
Мой подход, вероятно, отличается от того, что вы хотите услышать:
Производная от $\tan x$ равна 1, когда $x = 0$ и возрастает. Можно легко показать, что $\tan x$ равно ( строго) выпукла при $x \in (0, \pi/2)$. А так как $y=x$ является его касательной в точке $[0,0]$, то должно выполняться неравенство $\tan x > x$.
Я не знаю, обсуждали ли вы касательные и выпуклые/вогнутые функции, но это одно из основных свойств.
Надеюсь, я хоть немного помог. Ваше здоровье.
$\endgroup$
1
$\begingroup$
Поскольку первое сравнение вам понятно….Если вы начертите единичный круг и узнаете сторону касательной, то и второе вам будет понятно.
$\endgroup$
$\begingroup$
Неравенство $$\sin x < x < \tan x $$ должно быть понятно из картинки ниже
Это из книги Людвига Бибербаха Differentialrechnung I.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
2 x-1>0$, значит, $f$ возрастает, и $f(0)=0$ .) $\tan x$ определяется как $\frac{\sin x}{\cos x}$, где они определяются своим бесконечным рядом. Что у меня есть на данный момент: 92}3$, поэтому $\tan x>x$. Однако это покрывает только область $x\le1$, и мне все еще нужно ограничить $\tan x$ на $(1,\pi/2)$. Моим лучшим приближением к $\pi$ является очень грубое $2<\pi<4$, полученное путем объединения приведенных выше оценок с формулами двойного угла (обратите внимание, что $\pi$ определяется как наименьший положительный корень из $\sin x $), поэтому я не могу закончить доказательство оценкой типа $\sin x>1/\sqrt 2$, $\cos x\le\pi/2-x$ (считая теперь, что $x\ge1\ge \pi/4$), потому что граница слишком жесткая. Любые идеи?- реальный анализ
- последовательности-ряды
- тригонометрия
- неравенство
$\endgroup$
12
$\begingroup$
Вот не очень оригинальное геометрическое доказательство.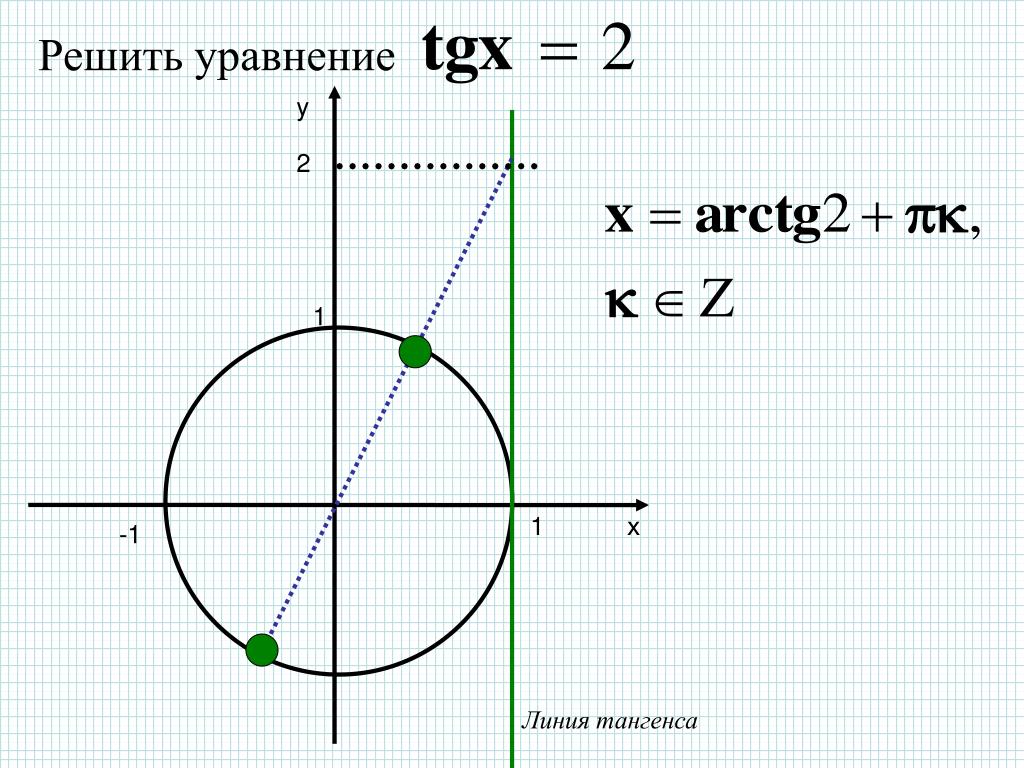
В единичной окружности $F$ начертите $\Delta ABC$ с точкой $C$ в центре $F$ и $\overline{AB}$ касательной к $F$ в точке $A$. Пусть $D$ — точка на $\overline{BC}$, а $E$ — точка на $\overline{AB}$ такая, что $\overline{DE}$ касается $F$ в точке $D$. Кроме того, пусть $\theta=\measuredangle ACB$.
Ясно, что $\tan\theta = \lvert\overline{AB}\rvert$, поскольку $\measuredangle CAB = \pi/2$ из-за касания. Кроме того, $\tan\theta=\lvert\overline{AE}\rvert+\lvert\overline{EB}\rvert$, но $\lvert\overline{ED}\rvert\lt\lvert\overline{EB}\ rvert$, так как $\lvert\overline{EB}\rvert$ — это гипотенуза $\Delta BDE$. Таким образом, у нас есть
$$\tan\theta\gt\lvert\overline{ED}\rvert+\lvert\overline{EA}\rvert$$
Из диаграммы видно, что сектор ACD $\subset$ четырехугольник ACDE, и поскольку оба множества являются выпуклыми, периметр сектора ACD $\lt$ периметр ACDE или
$$\lvert\overline{AC}\rvert+\lvert\overline{CD}\rvert+\lvert arc\:DA \rvert \lt \lvert\overline{AC}\rvert+\lvert\overline{CD}\rvert + \ lvert\overline{DE}\rvert+\lvert\overline{EA}\rvert$$
$$\lvert arc\:DA \rvert \lt \lvert\overline{DE}\rvert+\lvert\overline{EA}\rvert$$
Наконец у нас есть
$$\theta=\lvert arc\:DA \rvert \lt \lvert\overline{DE}\rvert+\lvert\overline{EA}\rvert\lt\lvert\overline{EA}\rvert+\lvert\overline{EB }\rvert=\tan\theta$$ 99/45360) + \ldots$.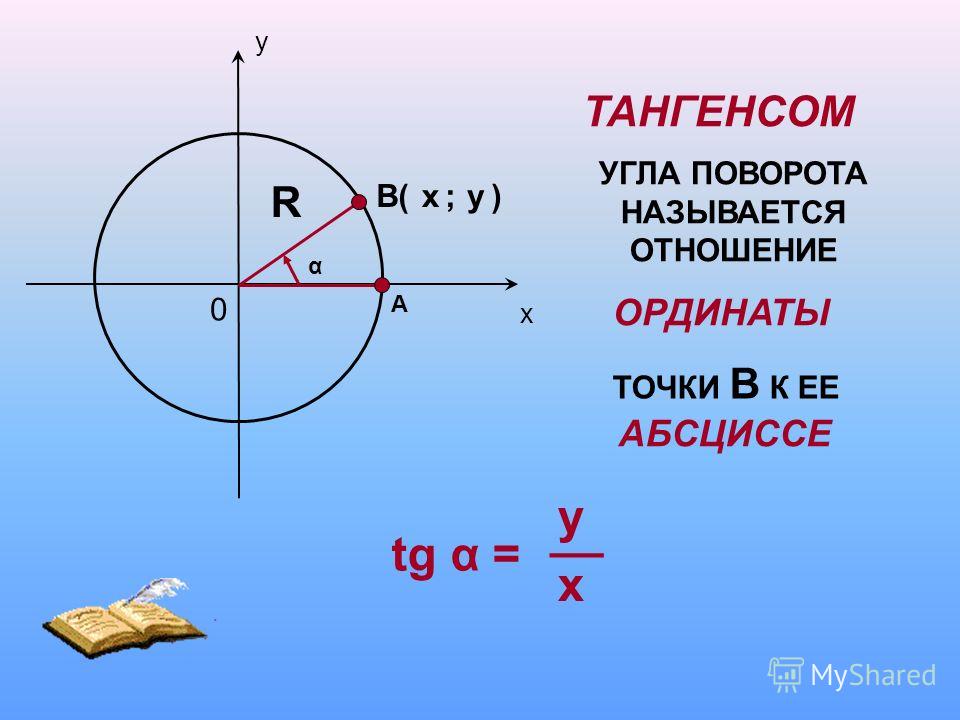
Если $0 < x < \sqrt{10}$, первая разность положительна. Соотношение слагаемых в каждой разности убывающее, поэтому если первая разность положительна, то и все остальные тоже, а сумма положительна. Таким образом, $\sin x - x \cos x > 0$ при $0 < x < \sqrt{10}$, что дает вам некоторую свободу действий, поскольку $\sqrt{10} > \pi/2$. (Первое положительное решение $\sin x — x \cos x = 0$ происходит при $x \приблизительно 4,493$ согласно WolframAlpha.)
$\endgroup$ 92-1$ гарантирует, что это так, поэтому мы можем заключить, что $\tan2x>2x$ для всех $x\in(0,1]$ таких, что $\cos 2x>0$, т. е. когда $2 x\in(0,\pi/2)$ (так как $\pi/4<1$).
PS: Этот ответ был успешно превращен в формальное доказательство. $\endgroup$
0
$\begingroup$
Эквивалентно показу того, что $\arctan t Но
$$
\arctan t=t-\frac{t^3}{3}+\frac{t^5}{5}+\cdots =\int_0^t\frac{ds}{1+s^2} $\endgroup$ 1 $\begingroup$ Нижеследующее является попыткой преобразовать «доказательство с исчислением» в доказательство без исчисления путем непосредственного выписывания всех определений. Фиксируем $a\in(0,\pi/2)$ и пусть $f(x)=\sin x-x\cos x$ и $g(x)=f(x)-xf(a)/a$ . Мы хотим доказать, что $f(a)>0$. Пусть $z$ — внутренняя экстремальная точка $g(x)$ в $(0,a)$, которая должна существовать, поскольку $g(0)=g(a)=0$ и $[0,a]$ компактен (это теорема об экстремальных значениях). Затем $$\frac{g(z+h)-g(z)}h=\frac{f(z+h)-f(z)}h-\frac{f(a)}a\le0$ $ для $h>0$, если $z$ — максимум, или для $h<0$, если $z$ — минимум. Теперь коэффициент разности равен $$\frac{f(z+h)-f(z)}h=\\
\cos z\Big(\!\frac{\sin h}h-\cos h\Big)+(\sin z-z\cos z)\frac{1-\cos h}h+\sin z\sin h+z \sin z\frac{\sin h}h.$$ Оценок в исходном вопросе достаточно, чтобы доказать, что пределы $\sin h\to0$, $\cos h\to1$, $\frac{\ sin h}h\to1$ и $\frac{1-\cos h}h\to0$ существуют как $h\to0$, поэтому разностное частное выше стремится к последнему члену, $z\sin z>0$ , и, в частности, существует $h$ вблизи $0$, такое что приведенное выше частное больше нуля.
