Уравнение кубический корень: Функция кубического корня — урок. Алгебра, 9 класс.

roots, – phrases

Sign in | English | Terms of Use

   English ⇄ ArabicBasqueBulgarianCatalanChineseChinese TaiwanChinese simplifiedCroatianCzechDanishDutchEnglishEsperantoEstonianFinnishFrenchGermanGreekHebrewHungarianIrishItalianJapaneseKoreanLatvianLithuanianMalayMalteseNorwegian BokmålPolishPortugueseRomanianRussianScottish GaelicSerbian LatinSlovakSloveneSpanishSwedishThaiTurkishUkrainianUzbek

Terms for subject Mathematics containing roots, | all forms | exact matches only

English	Russian
A corresponding limitation on the number of negative roots can be obtained by	соответствующее ограничение на число отрицательных корней может быть получено путём …
a repeated real root	кратный действительный корень (многочлена)
a root of order n	корень с порядком n
all three of the roots are	все три корня являются
an nth root of unity	из единицы
approximate root	приближённый корень
approximation of roots	приближённое вычисление корней
arithmetical root	арифметический корень
assume that the critical equation for 1 possesses distinct roots x and y	предположим, что уравнение для 1 обладает различными корнями
asymptotic root	асимптотический корень
basis of root system	базис корневой системы
chamber of root system	камера корневой системы
characteristic root	собственное значение
commensurable roots	соизмеримые корни
compact root	компактный корень
complementary root	дополнительный корень
compute a root	извлекать корень
cube root	кубический корень
cube-root	равный кубическому корню
cube-root	кубический корень
cube root	кубичный корень
cube-root extraction	извлечение кубического корня
cube root of 3	кубический корень из 3
diminution of roots	уменьшение числа корней (уравнения)
distinctive roots	различные корни (неодинаковые)
dominant root	наибольший корень (по модулю)
double root	двойной корень
Encke roots	корни Энке
equal roots	одинаковые корни
essential root	существенный корень
estimate root	оценивать значение корня
extract a root	извлекать корень
extract the root	извлекать корень
extracting a root	извлечение корня
extracting a root	извлекающий корень
extraction of a root	извлечение корня
extraction of root	извлечение корня
extraction of the root	извлечение корня
extraneous root	посторонний корень
find a root	извлекать корень
find the root	извлекать корень
find the root	извлечь корень
folded root	свёрнутый корень
fourth root	корень четвёртой степени
get to the root of a problem	проникать в существо проблемы
golden root	золотой корень
having solved this equation numerically, we can find a root of the above polynomial	решив
ill-conditioned root	плохо обусловленный корень
imaginary root	мнимый корень
in order to take the square root of a complex number, it is reasonable to convert this number into trigonometric form	извлекать квадратный корень из
in order to take the square root of a complex number, it is reasonable to convert this number into trigonometric form	тригонометрическая форма
infinite root	бесконечный корень
integer root	целочисленный корень
irrational root	иррациональный корень
irreducible root	неприводимый корень
isolate a root	отделять корень
isolate root	отделять корень
isolating of root	отделение корня
isotropic root	изотропный корень
it is very common to «polish up» a root with one or two steps of Newton-Raphson	обычно улучшают корень, используя один-два шага метода Ньютона-Рафсона
k-th root	корень k-й степени
keep in mind that Q depends on the selection of a set of positive roots via I	отметьте, что . ..
latent root	характеристический корень (vector)
latent root	собственное значение (vector)
location of roots	отделение корней (многочлена)
location of the roots of a polynomial	распределение корней
long root	длинный корень (Lie algebras)
mean-root-square	среднеквадратический (= среднеквадратичный)
mean-root-square	среднеквадратичный
mean-root-square	среднеквадратический
mean-root square error	среднеквадратическая ошибка
mean-root-square error	среднеквадратичная ошибка
mean square root	среднеквадратическое значение
mean square root	среднее значение квадратного корня
mean square root error	среднеквадратичная ошибка
multiple root	кратный корень
multiple root of an equation	кратный корень уравнения
multiple-roots case	случай нескольких корней (при решении уравнения)
multiplicity of root	неоднозначность корня
multiplicity of root	кратность корня
n-fold root	n-кратный корень
n-tuple root	n-кратный корень
negative root	отрицательный корень (rklink_01)
no two distinct roots have the same real part	никакие два различных корня не имеют одну и ту же действительную часть
noncompact root	некомпактный корень
nonessential root	несущественный корень
nonisotropic root	неизотропный корень
normalized root mean square	нормализованная среднеквадратичная величина (MichaelBurov)
once repeated root	двукратный корень
order of root	степень корня
orthogonal roots	ортогональные корни
perfect root	совершенный корень
positive root	положительный корень (rklink_01)
primitive root	первообразный корень
primitive root of unity	первообразный корень из единицы
primitive roots	первообразные корни
principal root	главный корень
principal root	главное значение корня
principal square root	главное значение квадратного корня
pseudocharacteristic root	псевдохарактеристический корень
pseudonegative root	псевдоотрицательный корень
pseudopositive root	псевдоположительный корень
pure imaginary root	чисто мнимый корень
purely imaginary root	чисто мнимый корень
quadratic root	квадратный корень
rational root	рациональный корень
rational root theorem	теорема о рациональных корнях
reduction of roots	исключение корней (уравнения)
relativistic root	релятивистский корень
repeated root	кратный корень
restricted root	ограниченный корень
root	хвост (лопатки турбины)
root	извлекать корень
root	маршрут
root cause	основная причина
root cell	корневая клетка
root-compact group	корнекомпактная группа
root-counting theorem	теорема о числе корней многочлена
root distribution	распределение корней
root estimator	оценка корня (of a mean; среднего значения)
root field	корневое поле
root-finding	поиск корней
root-finding method	метод поиска корней
root index	показатель корня
root index	показатель кореня
root isolating	отделение корня
root location	отделение корня
root locus	расположение корней
root locus	геометрическое место корней
root-mean	среднее квадратичное
root-mean-square	среднеквадратическое значение
root mean square	среднее квадратичное
root mean square	среднеквадратическое значение
root-mean-square	критерий среднеквадратичной ошибки
root mean square average	среднее квадратическое (не обязательно профиля :)) Enotte)
root mean square average is by definition the root of the average of the squares of the deviations from the average	среднее квадратичное
root-mean-square criterion	критерий среднеквадратической ошибки
root mean square deviation	ошибка среднеквадратической величины
root-mean-square deviation	среднеквадратичное отклонение
root mean square deviation	отклонение корня средней величины
root-mean-square difference	среднеквадратическое отклонение
root mean square error	отклонение корня средней величины
root-mean-square error	среднеквадратичная ошибка
root mean square error	ошибка среднеквадратической величины
root-mean-square error	средне-квадратичная ошибка (or deviation)
root-mean-square function	среднеквадратическая функция
root-mean-square norm	среднеквадратическая норма
root-mean-square sum	среднеквадратическая сумма
root-mean-square value	величина корня из квадрата среднего
root-mean-square velocity	среднеквадратическая скорость (rate, speed)
root-meansquare	среднеквадратичный
root-meansquare	среднеквадратический
root of a number	корень из числа
root of an equation	корень уравнения
root of congruence	корень сравнения
root of equation	корень управления
root of graph	корень графа
root of multiplicity n	корень кратности (n-fold root)
root of order m	корень порядка m
root of sum-of-squares	корень из суммы квадратов (квадратный)
root of tree	корень дерева
root of unity	корень из единицы
root out	выкорчевать (перен. )
root pattern	система корней
root property	корневое свойство
root sign	знак радикала
root sign	знак корня
root space	корневое пространство
root space decomposition	разложение на корневые пространства
root subspace	корневое подпространство
root subspace	корневое пространство
root-sum-of-squares method	метод вычисления суммарной величины как квадратного корня из суммы квадратов составляющих
root system	система корней
root test	признак Коши сходимости ряда
root test	признак сходимости Коши
root value	значение корня (feihoa)
root vertex	корневая вершина
Roy’s maximum root criteria	критерии максимального корня Роя
sensitivity of the root q to perturbations in the coefficients of the equation	чувствительность к возмущениям
separation of roots	разделение корней
short root	короткий корень (Lie algebras)
simple root	неразветвлённый корень
simple root	простой корень
spurious root	побочный корень
square root	квадратичный корень
square root	квадратный корень
square-root chart	таблица квадратных корней
square-root computer	устройство для вычисления квадратных корней
square-root computer	вычислитель квадратных корней
square-root generation	извлечение квадратного корня
square-root generation	преобразование типа квадратного корня
square root Kalman filter	фильтр Калмана на основе квадратного корня (clck. ru dimock)
square root of a linear binomial	квадратный корень из линейного двучлена (ssn)
square root of a quadratic polynomial	квадратный корень из квадратного трёхчлена (ssn)
square root of the mean squared error	квадратный корень из средней квадратичной ошибки (clck.ru dimock)
square root of the sum of the squares	корень квадратный из суммы квадратов составляющих (ssga.ru irksibrus1)
square root planimeter	планиметр квадратного корня
square-root principle	принцип квадратного корня
strictly positive root	строго положительный
string of roots	последовательность корней
strongly orthogonal roots	строго ортогональные корни
take root	врастать (перен. )
take root	извлекать корень
taking from under the root sign	вынесение за знак корня
taking the root	извлечение корня
taking the root of a number	извлечение корня
the equation has a root x=1	уравнение с корнем x=1
the fifth root of	корень пятой степени из
the location of the roots of a polynomial	отделение корней многочлена
the nature of these roots depends on whether D > 0	характер этих корней зависит от знака D, является ли D>0
the nature of these roots depends on whether D > 0	характер этих корней зависит от знака D
the roots of 2 are all simple	все корни уравнения 2 являются простыми
the roots of 2 are all simple	все корни уравнения 2 простые
the square root of без the	квадратный корень из
the square root of 2	корень квадратный из 2
this concept has roots stretching back into antiquity	корни этой концепции уходят в древность
transpose of square root of matrix K	транспонированный квадратный корень из матрицы К (clck. ru dimock)
triple root	трёхкратный корень
triple root	тройной корень
typical examples of irrational numbers are the numbers ( and e, as well as the principal roots of rational numbers	типичными примерами иррациональных чисел являются
unrepeated root	простой корень
with many roots	многокорневой
with multiple roots	многокорневой
x=1 is a root of the equation	уравнение с корнем x=1
zero root	равный нулю
zero root	нулевой корень
zero root	корень

Get short URL

 

Как поставить корень в Ворде: 3 простых способа

Содержание

• Способ 1: Вставка символа
  • Вариант 1: Ручной выбор символа
  • Вариант 2: Ввод и преобразование кода
• Способ 2: Вставка уравнения
• Способ 3: Microsoft Equation 3. 0 (для старых версий)
• Вопросы и ответы

Довольно часто при работе в Microsoft Word требуется выходить за рамки обычного набора текста, например, записывая различные математические выражения и уравнения. Одним из знаков, с необходимостью ввода которого можно столкнуться, является арифметический корень, и сегодня мы расскажем, как поставить его в текстовом документе.

Способ 1: Вставка символа

Проще всего добавить знак корня квадратного, кубического или n-степени в документ Ворд можно посредством вставки соответствующего символа из встроенного набора. У данной процедуры есть как минимум два варианта реализации

Вариант 1: Ручной выбор символа

Интегрированная в Word библиотека символов довольно обширна, но к счастью, все они поделены на тематические категории, что существенно упрощает поиск. Для добавления корня выполните следующее.

1. Перейдите во вкладку «Вставка»

   и нажмите по расположенному в правой части панели инструментов пункту «Символ». Из выпадающего меню выберите «Другие символы».

2. Убедитесь, что в выпадающем списке «Шрифт» установлен «(обычный текст)», а в списке «Набор» выберите «Математические операторы».
3. Необходимый знак будет представлен в первой или второй строке окна – выделите его, после чего нажмите по кнопке «Вставить».

   Символ появится в указанном вами месте документа, а значит, окно вставки можно закрыть.

К сожалению, таким образом можно добавить только квадратный корень. Зато, как несложно догадаться, в этом разделе текстового редактора можно найти множество других символов и знаков, которые отсутствуют на клавиатуре.

Читайте также: Вставка символов и специальных знаков в Ворде

Вариант 2: Ввод и преобразование кода

За каждым символом, представленным в интегрированной библиотеке Word, закреплен специальный код. Зная его и комбинацию клавиш, которая выполняет преобразование, можно значительно быстрее добавить знак арифметического корня, но, как и в предыдущем случае, только квадратного.

Обратите внимание! Узнать код любого символа, входящего во встроенный набор программы, можно из окна его вставки (предварительно выделив), там же будет указана комбинация клавиш, необходимая для преобразования, и/или кодировка, в которой это значение нужно вводить.

Код знака арифметического корня выглядит следующим образом:

221A

Просто введите указанное выше значение, предварительно переключившись на английскую раскладку, а затем, не добавляя отступ, нажмите клавиши «ALT+X» — в выбранном вами месте сразу же появится необходимый символ.

Способ 2: Вставка уравнения

Если же ваша задача заключается не просто во вставке знака квадратного корня, а и в последующем написании полноценного примера или уравнения, действовать потребуется по иному алгоритму. Преимущество изложенного ниже подхода заключается еще и в том, что таким образом можно записать не только квадратный или кубический корень, но и любой другой, представленный в n-степени.

Примечание: Добавленный таким образом символ, как и остальные элементы будущего примера, будут представлять собой не обычный текст, а блок с указанными вами значениями, для которого нельзя изменить шрифт (его стиль) и некоторые другие параметры.

1. Откройте вкладку «Вставка» и нажмите в ней по расположенному справа пункту «Уравнение».
2. На странице документа появится область для ввода будущей записи, а на ленте – группа «Работа с уравнениями» и входящая в нее вкладка «Конструктор».

   Как раз из последней и можно добавить интересующий нас знак корня – просто выберите его в группе «Символы». Рядом с кнопкой добавления квадратного есть также кубический и корень четвертой степени.

   Если же требуется записать квадратный (с уточнением степени) или кубический корень, обозначение степени в котором будет пригодным для редактирования, обратитесь к расположенной правее кнопке c одноименным названием и выберите подходящий вариант.

   В этом же меню можно найти символ для записи корня в n-степени,

   которую потребуется указать вручную.

   Также рекомендуем обратить внимание на стандартный набор формул и уравнений – вполне возможно, в нем найдется еще более подходящая для поставленных целей запись.

   Из этого же меню можно перейти к рукописному вводу арифметических выражений (отмечено цифрой 3 на скриншоте выше), которые будут распознаны программой и преобразованы в стандартный для уравнений текст.

3. Узнать более подробно о встроенном в Ворд редакторе формул и особенностях его использования можно из представленных по ссылкам ниже статей.

Подробнее:
Редактор формул в Ворде
Как в Ворде записать формулу

Преимущество данного способа перед предыдущим заключается в том, что под знак корня, представленный в виде элемента уравнения/формулы, можно вписать любую цифру, букву и даже целый пример, а для самого элемента можно задать не только квадратную и кубическую, но и любую другую степень. Если же говорить о вставленном из набора символе, то он позволяет записывать значения только сразу за ним, но не под ним.

Способ 3: Microsoft Equation 3.0 (для старых версий)

В январе 2018 года компания Microsoft выпустила обновление для всех версий Word, начиная с 2010, которое «убрало» из приложения компонент Microsoft Equation 3.0. Ранее именно он использовался для работы с формулами и уравнениями, а также для ввода всевозможных математических выражений и символов. Если вы пользуетесь версией текстового редактора, которая не поддерживается разработчиком как минимум с обозначенной выше даты или выходящие с момента ее наступления апдейты не устанавливались, добавление знака корня можно выполнить следующим образом:

Примечание: Функциональность компонента Microsoft Equation в версиях Word ниже 2010 весьма ограничена – многие уравнения и формулы им попросту не поддерживаются. Устраняется эта проблема путем преобразования документа, о чем мы рассказывали в представленной по ссылке ниже статье.

Подробнее: Использование Microsoft Equation и устранение проблем совместимости

1. Как и в предыдущих способах, перейдите во вкладку «Вставка». Далее кликните по кнопке «Объект», расположенной в группе «Текст».
2. В открывшемся диалоговом окне выберите пункт «Microsoft Equation 3.0».
3. В Ворде будет открыт дополнительный интерфейс, а именно – редактор математических формул. Внешний вид приложения при этом полностью изменится.
4. В окне «Формула» нажмите на кнопку «Шаблоны дробей и радикалов».
5. В выпадающем меню выберите знак корня, который нужно добавить. Первый — квадратный корень, второй — любой другой выше по степени (вместо значка «x» можно будет вписать степень).

Добавив знак корня в документ, вы сможете ввести под него необходимое числовое значение.

Сделав это, закройте окно «Формула» и кликните по пустому месту в документе, чтобы перейти в обычный режим работы.

Примечание: Знак корня с цифрой или числом под ним будет находиться в поле, похожем на текстовое или поле объекта «WordArt», которое можно перемещать по документу и изменять в размерах. Для этого достаточно потянуть за один из маркеров на его рамке.

Читайте также: Как повернуть текст в Word

Чтобы выйти из режима работы с объектами, просто кликните в пустом месте документа.

Совет: Чтобы вернутся в режим работы с объектом и повторно открыть окно «Формула», дважды кликните левой кнопкой мышки по полю, содержащему добавленный вами объект.

Читайте также: Как в Ворд вставить знак умножения

Как видим, даже в старых версиях текстового редактора от Майкрософт для записи символа корня, а вместе с ним и любых других арифметических выражений, лучше использовать специально предназначенный для этого компонент, а не интегрированную в приложение библиотеку символов.

Теперь вы знаете, как в Word поставить знак корня, независимо от того, какая версия текстового редактора используется – актуальная или та, что уже несколько лет не обновлялась.

1.4.3: График функций кубического корня

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

14137

График функции кубического корня

Миссис Гарсия поручает своему ученику построить график функции кубического корня \(\ y=-\sqrt[3]{(x+1)}\) в качестве домашнего задания. На следующий день она спрашивает своих учеников, в каком квадранте (квадрантах) находится их график.0026

Алендро говорит, что из-за отрицательного знака все значения и отрицательны. Поэтому его график находится только в третьем и четвертом квадранте.

Дако говорит, что его график также находится в третьем и четвертом квадрантах, но также и во втором квадранте.

Мариша говорит, что они оба неверны и что ее график функции находится во всех четырех квадрантах.

Какой из них правильный?

---

График функций кубического корня

Функция кубического корня отличается от квадратного корня. Их общие формы выглядят очень похожими, \(\ y=a \sqrt[3]{x-h}+k\), а родительский граф — \(\ y=\sqrt[3]{x}\). Однако мы можем взять корень в кубе из отрицательного числа, поэтому он будет определен для всех значений x. Построив родительский граф, мы получим:

[Рисунок 1] 9{3}\). Домен и диапазон \(\ y=\sqrt[3]{x}\) — все действительные числа. Обратите внимание, что нет «начальной точки», как у функций квадратного корня, (h,k) теперь относится к точке изгиба функции, называемой точкой перегиба .

Опишем, как получить график \(\ y=\sqrt[3]{x}+5\) из \(\ y=\sqrt[3]{x}\).

[Рисунок 2]

Мы знаем, что +5 указывает на вертикальное смещение на 5 единиц вверх. Следовательно, этот график будет выглядеть точно так же, как родительский график, сдвинутый вверх на пять единиц.

Теперь построим график \(\ f(x)=-\sqrt[3]{x+2}-3\) и найдем домен и диапазон.

[Рисунок 3]

Из предыдущей задачи мы знаем, что из родительского графика эта функция сдвинется на две единицы влево и на три единицы вниз. Отрицательный знак приведет к отражению.

Альтернативный метод: Если вы хотите использовать таблицу, это также сработает. Вот таблица, затем нанесите точки. (h,k) всегда должен быть средней точкой в ​​вашей таблице.

x	у
-27	-3
-8	-2
-1	-1
0	0
1	1
8	2
27	3

х	у
6	-5
-1	-4
-2	-3
-3	-2
-10	-1

Наконец, построим график \(\ f(x)=\frac{1}{2} \sqrt[3]{x-4}\).

-4 говорит нам, что от родительского графика функция сдвинется вправо на четыре единицы. \(\ 1 \over 2\) влияет на то, как быстро функция будет «расти». Поскольку он меньше единицы, он будет расти медленнее, чем родительский граф.

Использование графического калькулятора: Если вы хотите построить график этой функции с помощью TI-83 или 84, нажмите Y= и удалите все функции. Затем нажмите (1÷2), MATH и прокрутите вниз до 4 : \sqrt[3]{ } и нажмите ENTER .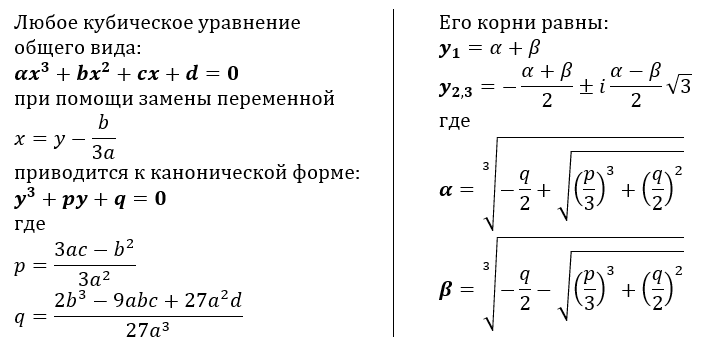 Затем введите остальную часть функции, чтобы \(\ Y=\left(\frac{1}{2}\right) \sqrt[3]{(X-4)}\). Нажмите GRAPH и отрегулируйте окно.

Важное примечание: Область определения и диапазон всех функций кубического корня являются действительными числами.

---

Пример 1

Решение

Ранее вас просили определить, кто из учащихся был прав.

Если построить график функции \(\ y=-\sqrt[3]{(x+1)}\), вы увидите, что областью определения являются все действительные числа, что делает возможными все квадранты. Однако для всех положительных значений x , y отрицательно из-за отрицательного знака перед кубическим корнем. Это исключает первый квадрант. Следовательно, Дако прав.

Пример 2

Вычислить \(\ y=\sqrt[3]{x+4}-11\), когда \(\ x=−12\).

Раствор

Подставьте \(\ x=−12\) и найдите \(\ y\).

\(\ y=\sqrt[3]{-12+4}-11=\sqrt[3]{-8}+4=-2+4=2\)

Пример 3

Опишите, как получить график \(\ y=\sqrt[3]{x+4}-11\) из \(\ y=\sqrt[3]{x}\).

Решение

Начиная с \(\ y=\sqrt[3]{x}\), вы получите \(\ y=\sqrt[3]{x+4}-11\), сдвигая влево на четыре единицы и вниз на 11 единиц.

Нарисуйте график следующих функций кубического корня. Проверьте свои графики на графическом калькуляторе.

Пример 4

\(\ y=\sqrt[3]{x-2}-4\)

Решение

Эта функция представляет собой сдвиг по горизонтали на две единицы вправо и на четыре единицы вниз.

[Рисунок 4]

Пример 5

\(\ f(x)=-3 \sqrt{x}-1\)

Решение

Эта функция является отражением \(\ y=\sqrt [3]{x}\) и увеличен в три раза. Наконец, он смещается на одну единицу вниз.

[Рис. 5]

---

Обзор

Вычислить \(\ f(x)=\sqrt[3]{2 x-1}\) для следующих значений \(\ x\).

1. ф(14)
2. ф(−62)
3. ф(20)

Нарисуйте график следующих функций кубического корня. Используйте калькулятор, чтобы проверить свои ответы.

4. \(\ y=\sqrt[3]{x}+4\)
5. \(\ y=\sqrt[3]{x-3}\)
6. \(\ f(x)=\sqrt[3]{x+2}-1\)
7. \(\ г(х)=-\sqrt[3]{х}-6\)
8. \(\ f(x)=2 \sqrt[3]{x+1}\)
9. \(\ h(x)=-3 \sqrt[3]{x}+5\)
10. \(\ y=\frac{1}{2} \sqrt[3]{1-x}\)
11. \(\ y=2 \sqrt[3]{x+4}-3\)
12. \(\ y=-\frac{1}{3} \sqrt[3]{x-5}+2\)
13. \(\ г(х)=\sqrt[3]{6-х}+7\)
14. \(\ f(x)=-5 \sqrt[3]{x-1}+3\)
15. \(\ y=4 \sqrt[3]{7-x}-8\)

---

Ответы на проблемы с обзором

Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 7.5.

---

Словарь

Срок	Определение
Общее уравнение для функции кубического корня	Общее уравнение для кубической функции корня имеет вид \(\ f(x)=a \sqrt[3]{x-h}+k\), где h — смещение по горизонтали, а k — смещение по вертикали.

---

Атрибуция изображений

1. [Рисунок 1]
   Авторы и права: Sean MacEntee
   Источник: https://www.flickr.com/photos/smemon/17323618152/in/photolist-soQ58A-5rouLK-67pQ1V-a54ocN-51ysYT-pP1VGr-6gshc-d8RVdu-nBXVi8-Nv9px-qtm3yn-dUUJmL-6ojCxV-DejJUS 51YQZG-51YQK4-5NRFCF-51CE4O-51CD2W-51CEAO-51YQF8-FDO2JF-51YPZI-51CDOS-F9SKNY-51CEMJ-JNS68-51SYC-4T1Z5J-51YQAT-51CCQV-29-21H-21H-21-21-Q-21H-21H-21H-21-21-Q-21H-21-21-Q-21-21-Q-21-21-Q-29-21-21-21. agFDN7-51ypHi-51CGdY-51CFMG-51ysUK-anJz1-51yrta-51yuA8-51CFPY-51ysrz-51CFG1
2. [Рисунок 2]
   Кредит: Шон МакЭнти
      Источник:   -6ojcxv-dejjus-51yqzg-51yqk4-5nrfcf-51ce4o-51cd2w-51ceao-51yqf8-fdo2jf-51y-51cdos-f9skny-51cemj-jns68-51sic-51z51y-51-g-51-g-51-g-51-g-51-g-51 -6ooPqQ-51CEA9-agFDN7-51ypHi-51CGdY-51CFMG-51ysUK-anJz1-51yrta-51yuA8-51CFPY-51ysrz-51CFG1
3. [Рисунок 3]
   Кредит: Шон МакЭнти
   Источник: -qtm3yn-dUUJmL-6ojCxV-DejJUS-51yqZg-51yqk4-5NrFcF-51CE4o-51CD2w-51CEao-51yqf8-fdo2Jf-51ypZi-51CDos-F9SKny-51CEmJ-jnS68-51ysyc-4t1z5J-51yqat-51CCQU-d9VTUC-51ypzB-2hVbrU-29Gjnh -4Q2Th5-ayVtXQ-6ooPqQ-51CEA9-agFDN7-51ypHi-51CGdY-51CFMG-51ysUK-anJz1-51yrta-51yuA8-51CFPY-51ysrz-51CFG1
4. [Рисунок 4]
   Авторы и права: Шон МакЭнти
   Источник: D8RVDU-NBXVI8-NV9PX-QTM3YN-DUUJML-6OJCXV-DEJJUS-51YQZG-51YQK4-5NRFCF-51CE4O-51CD2W-51CEAO-51YQF8-FDO2JF-51CD2W-51CEA-51YQF8-FDO2JF-51CD2W-51S-51YQF8-FDO2JF-51CSI-51S-51-21S-51-21-21-21-21-21-21-21-21-21-21-21-21-yqf8-jeqf8-jeqf8-jeqf8-jeqf8-jeqf8-jeqf8-j 51ypzB-2hVbrU-29Gjnh-4Q2Th5-ayVtXQ-6ooPqQ-51CEA9-agFDN7-51ypHi-51CGdY-51CFMG-51ysUK-anJz1-51yrta-51yuA8-51CFPY-51ysrz-51CFG1
5. [Рисунок 5]
   Авторы и права: Шон МакЭнти
   Источник: -pP1VGr-6gshc-d8RVdu-nBXVi8-Nv9px-qtm3yn-dUUJmL-6ojCxV-DejJUS-51yqZg-51yqk4-5NrFcF-51CE4o-51CD2w-51CEao-51yqf8-fdo2Jf-51ypZi-51CDos-F9SKny-51CEmJ-jnS68-51ysyc-4t1z5J-51yqat

---

Эта страница под названием 1. 4.3: Графики корневых функций куба распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами LibreTexts. Платформа; подробная история редактирования доступна по запросу.

ПОД ЛИЦЕНЗИЕЙ

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   СК12

   Лицензия

   СК-12

   Программа OER или Publisher

   СК-12

2. Теги

   92+3z+1=0$

   , что дает нам два разных результата:

   $-\frac{1}{6}i(\sqrt3-3i)$ и $\frac{1}{6}i(\ sqrt3+3i)$

   я также проверил в wolfram alpha и, похоже, не ошибся. это результат, полученный с каждым методом

   1)https://www.wolframalpha.com/input/?i=cuberoot%28%28z-1%29%5E3%29%3Dcuberoot%28z%5E3%29 2) https://www.wolframalpha.com/input/?i=%28z%2B1%29%5E3%3Dz%5E3

   В каких случаях неправильно извлекать кубический корень с обеих сторон? я понимаю, что это может быть проблемой с кубическим корнем, потому что квадрат необратим, но это кубический корень. 92}{1/12} \ \ = \ \ 1 \ \ , $$ с центром в точках $ \ a \ = \ -\frac12 \ , \ b \ = \ 0 \ \ $ и вершинами в точках $ \ \ a \ = \ — \ frac12 \ , \ b \ = \ \pm \ \ frac {1}{\sqrt{12}} \ \ . $ Второе уравнение представляет собой объединение «горизонтальной» прямой $ \ b \ = \ 0 \ $ и «вертикальной» прямой $ \ a \ = \ -\frac12 \ \ . $ Пересечения этих «кривых» [как видно на графике ниже] равны $ \ z \ = \ -\frac12 \ \pm \ i·\frac{1}{\sqrt{12}} \ = \ -\ frac12 \ \pm \ i·\frac{\sqrt3}{6} \ \ , $ ровно два корня, которые вы нашли. На линии $ \ \mathfrak{Re}(z)-$ нет пересечений, что указывает на то, что наше уравнение не имеет вещественных решений.

   No related posts.