Укажите наибольший отрицательный корень уравнения — dj-sensor.ru
2).√(3)ctgx+3=0
ctgx=-√(3)
x=-π/6+πk
наименьший положительный
x=5π/6=150°
4).sin(π/2-x)-cos(π+x)=cosx+cosx=2cosx
Наименьшее значаение y=-2
Достигается при cosx=-1
5). 5-cosx
Наименьшее значение 4.
Достигается при cosx=-1
Найдите наибольший отрицательный корень уравнения:
Решением уравнения cosx=a являются два корня:
Определение: Пусть число a по модулю не превосходит единицы. Арккосинусом числа a называется угол x, лежащий в пределах от 0 до Пи, косинус которого равен a.
Найдём наибольший отрицательный корень. Как это сделать? Подставим различные значения n в полученные корни, вычислим и выберем наибольший отрицательный.
Общая рекомендация для всех подобных задач: для начала берите диапазон n от –2 до 2. Если требуемое значение выявить не удалось, подставляем следующие значения x: –3 и 3, –4 и 4 и так далее.
Вычисляем:
При n = – 2 х1= 3 (– 2) – 4,5 = – 10,5 х2= 3 (– 2) – 5,5 = – 11,5
При n = – 1 х1= 3 (– 1) – 4,5 = – 7,5 х2= 3 (– 1) – 5,5 = – 8,5
При n = 0 х1= 3∙0 – 4,5 = – 4,5 х2= 3∙0 – 5,5 = – 5,5
При n = 1 х1= 3∙1 – 4,5 = – 1,5 х2= 3∙1 – 5,5 = – 2,5
При n = 2 х1= 3∙2 – 4,5 = 1,5 х2= 3∙2 – 5,5 = 0,5
Получили, что наибольший отрицательный корень равен –1,5
Найдите наименьший положительный корень уравнения:
Решением уравнения sin x = a являются два корня:
Либо (он объединяет оба указанные выше):
Определение: Пусть число a по модулю не превосходит единицы. Арксинусом числа a называется угол x, лежащий в пределах от –90 о до 90 о синус которого равен a.
Значит
Выразим x (умножим на 4 и разделим на Пи):
Найдём наименьший положительный корень.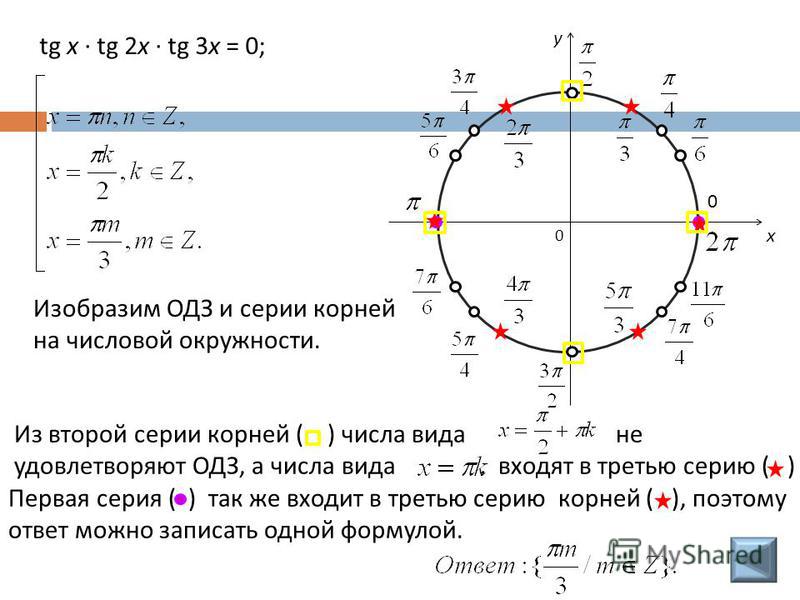
Здесь сразу видно, что при подстановке отрицательных значений n получим отрицательные корни. Поэтому будем подставлять n=0,1,2 …
При n = 0 х = (– 1) 0 + 4∙0 + 3 = 4
При n = 1 х = (– 1) 1 + 4∙1 + 3 = 6
При n = 2 х = (– 1) 2 + 4∙2 + 3 = 12
Проверим при n=–1 х=(–1) –1 + 4∙(–1) + 3 = –2
Значит наименьший положительный корень равен 4.
Найдите наименьший положительный корень уравнения:
Решением уравнения tg x = a является корень:
Определение: Арктангенсом числа a (a – любое число) называется угол x принадлежащий интервалу – 90 о до 90 о , тангенс которого равен a.
Значит
Выразим x (умножим на 6 и разделим на Пи):
Найдём наименьший положительный корень. Подставим значения n=0,1,2,3 … Отрицательные значения подставлять нет смысла, так как видно, что получим отрицательные корни:
Таким образом, наименьший положительный корень равен 0,25.
1. Укажите наибольший отрицательный корень уравнения
2sinx +1 = 0. Ответ запишите в градусах.
2. Укажите наименьший положительный корень уравнения
ctgx +3 = 0. Ответ запишите в градусах.
3. Укажите наибольший отрицательный корень уравнения
2
tgx -6 = 0. Ответ запишите в градусах.
4. Укажите наименьший положительный корень уравнения
sin(4x) =
/2 . Ответ запишите в градусах.
5. Укажите наибольший отрицательный корень уравнения
Cos(2x)cosx-sin(2x)sinx= 1. Ответ запишите в градусах.
6. Решите уравнение: cos 2x =0,5
7. Решите уравнение: tg xctg x+cosx =1
8. Решите уравнение: 2cosx+
=0
9. Решите уравнение: cos(x+2000
) =0
10. Решите уравнение: sin(
-x) — cos( +x) = -1
11.
Решите уравнение: cos(
-x)-3cos2x = 2
12. Укажите наименьший положительный корень уравнения
sin(
x)(cosx -2) =0
13. Укажите корень уравнения cos(
x)(sin2x + ) =0, принадлежащий промежутку [2;3].
14. Решите уравнение: sin 2 (x/2) – cos 2 (x/2) =
/2
15. Решите уравнение: cos x+cos2x = 2
16. Решите уравнение: 2 cos 2 (
— x)+5sinx – 4 =0
17. Решите уравнение: cos2x + 5cos(- x)+ 3=0
18. Решите уравнение: sinx —
cosx = 0
19. Решите уравнение: sin(
-x) — cos( +x) =
20. Решите уравнение: 3cos x+sin(-2x) = 0
21. Решите уравнение: 6sin 2 x +5sinxcosx+3cos 2 x=2
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Учись учиться, не учась! 10637 —
| 8008 — или читать все.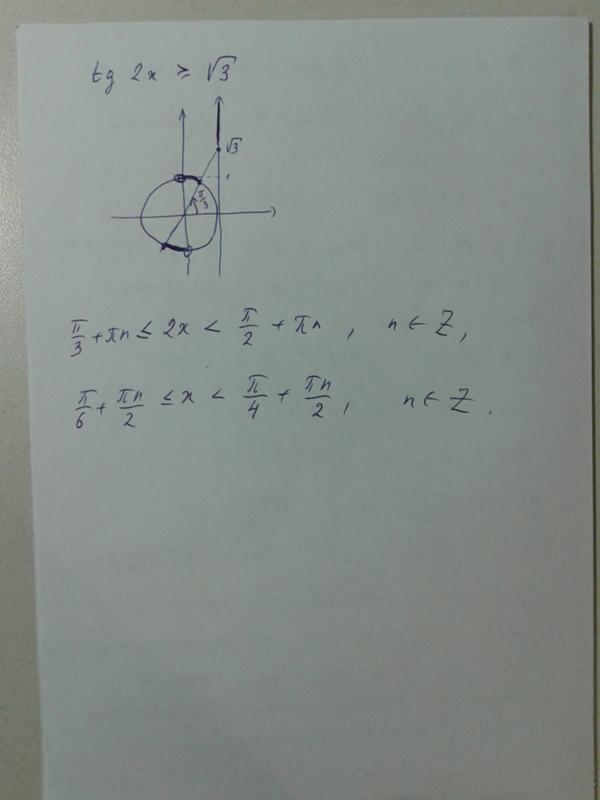
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
- Автор: Мария Сухоруких
- Распечатать
Оцените статью:
(0 голосов, среднее: 0 из 5)
Поделитесь с друзьями!
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | ||
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | соз(0) | ||
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| Найти точное значение | грех(150) | ||
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Как решить $\\tan(x) = \\sqrt 3 $?
Подсказка: Чтобы определить значение вышеприведенного вопроса, возьмем обратную тангенс с обеих сторон уравнения, чтобы вытащить x из касательной.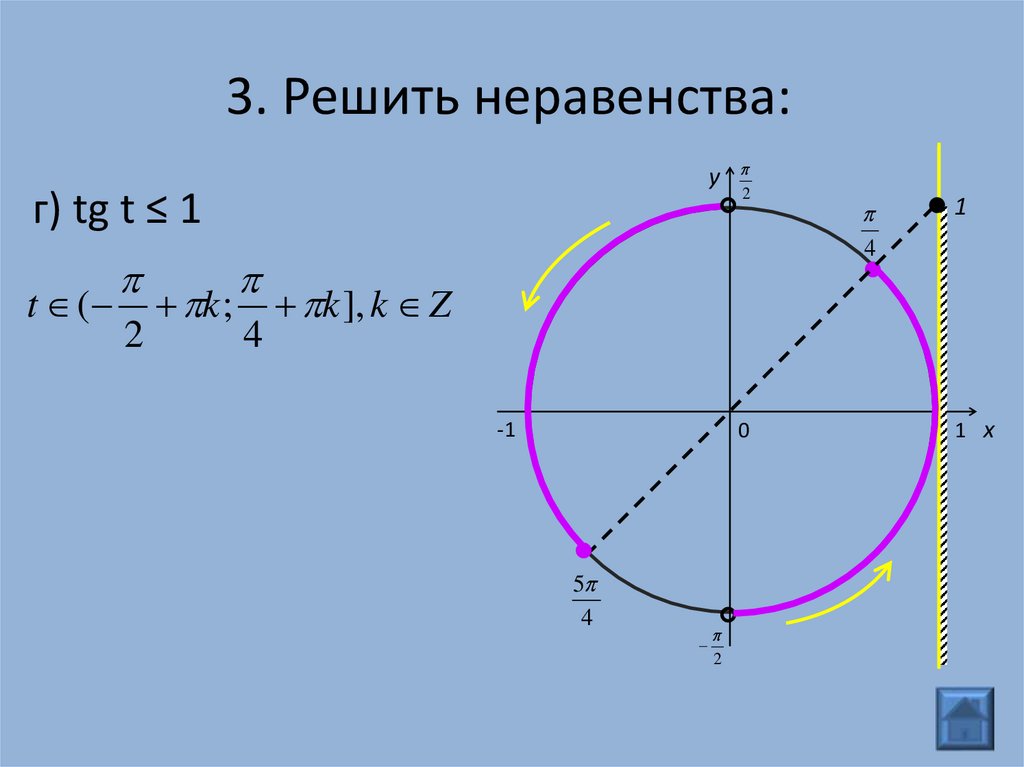
Теперь нам просто нужно найти значение, обратное тангенсу $\sqrt 3 $. Функция тангенса положительна как в 1-м, так и в 3-м квадранте, поэтому ответ существует для обоих квадрантов. Период тангенса равен $\pi $, поэтому сформулируйте свой ответ в соответствии с ним
Полное пошаговое решение:
Нам дано тригонометрическое выражение $\tan (x) = \sqrt 3 $ 9{ — 1}}\left( {\sqrt 3 } \right) = \dfrac{\pi }{3}$
Поскольку мы знаем, что функция тангенса всегда положительна как в первом, так и в третьем квадрантах.
Чтобы определить второе решение, тангенс которого равен $\sqrt 3 $, добавим исходный угол $\pi $
$x = \pi + \dfrac{\pi }{3}$
Теперь упрощая вышеизложенное,
$
x = \dfrac{{3\pi + \pi}}{3} \\
x = \dfrac{{4\pi}}{3} \\
$
$\tan (\ тета + \ пи ) = \ dfrac {{\ грех (\ тета + \ пи )}} {{\ соз (\ тета + \ пи )}} = \ dfrac {{ — \ грех (\ тета
)}}{{ — \cos (\theta)}} = \dfrac{{\sin (\theta)}}{{\cos (\theta)}} = \tan\left(\theta\right)$
Таким образом, период функции $\tan\theta$ равен $\pi $,
$\следовательно, x = \dfrac{\pi }{3} + n\pi ,\dfrac{{4\pi}}{ 3} + n\pi $ для любого целого числа n
Следовательно, решение $\tan (x) = \sqrt 3 $ равно $x = \dfrac{\pi }{3} + n\pi ,\ dfrac{{4\pi }}{3} + n\pi $ для любого целого числа n.
Дополнительная информация:
1. В математике обратные тригонометрические функции (иногда дополнительно называемые антитригонометрическими функциями или цикломатической функцией) являются обратными элементами математических функций. В частности, они являются обратными синусу, функции косинуса, тангенса, котангенса, секанса и косеканса и используются для получения точки из любой из математических пропорций точки.
Обратные тригонометрические функции обычно используются при проектировании, маршрутизации, материаловедении и расчетах.
2. В обратной тригонометрической функции областью значений являются области значений соответствующих тригонометрических функций, а областью значений являются области значений соответствующей тригонометрической функции.
3. Тригонометрия является одним из значительных разделов на протяжении всего существования математики и эту идею дал греческий математик Гиппарх.
4. Периодическая функция= Функция $f(x)$ называется периодической, если существует действительное число T > 0 такое, что $f(x + T) = f(x)$ для всех x.